Spin dynamics of paramagnetic centers with anisotropic g tensor and spin of ½

Abstract

The influence of g tensor anisotropy on spin dynamics of paramagnetic centers having real or effective spin of 1/2 is studied. The g anisotropy affects both the excitation and the detection of EPR signals, producing noticeable differences between conventional continuous-wave (cw) EPR and pulsed EPR spectra. The magnitudes and directions of the spin and magnetic moment vectors are generally not proportional to each other, but are related to each other through the g tensor. The equilibrium magnetic moment direction is generally parallel to neither the magnetic field nor the spin quantization axis due to the g anisotropy. After excitation with short microwave pulses, the spin vector precesses around its quantization axis, in a plane that is generally not perpendicular to the applied magnetic field. Paradoxically, the magnetic moment vector precesses around its equilibrium direction in a plane exactly perpendicular to the external magnetic field. In the general case, the oscillating part of the magnetic moment is elliptically polarized and the direction of precession is determined by the sign of the g tensor determinant (g tensor signature). Conventional pulsed and cw EPR spectrometers do not allow determination of the g tensor signature or the ellipticity of the magnetic moment trajectory. It is generally impossible to set a uniform spin turning angle for simple pulses in an unoriented or ‘powder’ sample when g tensor anisotropy is significant.

Introduction

Paramagnetic centers (PCs) with anisotropic g tensor possess some unique features compared to isotropic PCs because their magnetic moment does not coincide with the direction of their spin vector, and because the magnitude of the magnetic moment vector varies with the orientation of the spin. Their spins are quantized by the external magnetic field, but usually not along that field direction. The manifestation of such anisotropy in continuous wave (CW) EPR experiments has been described by Abragam and Bleaney [1, Chapters 3 and 15]. Here we examine features of the spin dynamics of PCs, having g tensors with significant anisotropy (δg~g), during the course of pulsed EPR experiments. Typical systems are paramagnetic metal ions in a diamagnetic host; paramagnetic nanoparticles; and transition metal cofactors and clusters in metalloproteins. The rapidly expanding application of pulsed EPR spectroscopy to such systems, particularly for long-range distance measurements by DEER and PELDOR methods [2], requires a thorough understanding of the unique features of spin dynamics in systems with large g anisotropy.

The EPR signal and the dipolar interactions between PCs are properties of the magnetic moment, while other features of magnetic resonance are most easily described using spin vectors. The distinction between magnetic moment and the spin vector has no practical consequences for PCs with isotropic g because the two vectors are exactly proportional to each other. This allows the Bloch equations for spin dynamics to be written in terms of either the spin vector or the magnetic moment vector for the isotropic PC, but there is no tractable form of the Bloch equations for anisotropic PCs. The spin vectors move in response to external fields in a straightforward manner in a rotating frame, yet the magnetic moment produces the signal in a microwave (mw) resonator in the laboratory frame.

These dual aspects of anisotropic PCs have prevented a unified description of their magnetic resonance. The length of the spin vectors does not depend explicitly on the orientation of the PC and varies relatively slowly via T₁ and T₂-like relaxation, while the magnetic moment is a dynamic property of spin vectors with a magnitude that depends explicitly on PC orientation and that magnitude oscillates rapidly during precession of the spin vector. The loss of equivalence between spin and magnetic moment has three important practical consequences in pulsed magnetic resonance experiments. The first consequence is that the EPR spectrum measured by pulse methods has a slightly different lineshape from that measured by CW methods. The differences need to be considered when spectral fitting is used to determine spin Hamiltonian parameters from EPR spectra measured by pulsed methods. The second important consequence of the inequivalence of spin and magnetic moment arises when mw pulses are used to manipulate spin-spin interactions and local dipolar fields. The magnetic moments behave quite differently at times from the spins and can produce rather unexpected results. The final consequence is that dipolar interactions with other spins can have a lineshape quite different from the classic Pake-like pattern.

In this contribution we examine the response of the PC to mw pulses and we consider the free induction decay (FID) and spin echo signals from PCs with anisotropic g tensors having spins (either real or effective) of ½.

Theory

The Spin Hamiltonian and the Propagator

The magnetic moment operator, $\widehat{\overrightarrow{\mu }}$, of a PC is related to its spin operator, $\widehat{\overrightarrow{S}}$, via

$$\widehat{\overrightarrow{\mu }}=-\beta \overleftrightarrow{g}\widehat{\overrightarrow{S}}.$$ (1)

Here β is the Bohr magneton, the minus sign is due to the negative charge of the electron, and g↔ is the g tensor, or, more precisely, g-matrix [3]. The properties of g↔ are considered in detail in Abragam and Bleaney [1], with a recent examination in [4]. The Zeeman interaction of the PC with an external magnetic field B⃗₀ is described by the Hamiltonian

$$\widehat{H}=-{\overrightarrow{B}}_0·\widehat{\overrightarrow{\mu }}=\beta {{\overrightarrow{B}}_0}^T\overleftrightarrow{g}\widehat{\overrightarrow{S}}.$$ (2)

The dot operator between vectors denotes the scalar dot product, while the superscript T indicates the transpose of vectors (written as columns) and matrixes. The Hamiltonian (2) has a simple form:

$$\widehat{H}=\beta B_0{g}_{\mathit{eff}}\overrightarrow{k}·\widehat{\overrightarrow{S}}=\beta B_0{g}_{\mathit{eff}}{\widehat{S}}_z$$ (3)

in a coordinate frame whose Z axis is directed along the unit vector k⃗ defining the quantization axis for the PC’s spin,

$$\overrightarrow{k}={\overleftrightarrow{g}}^T\overrightarrow{b}/g_{\mathit{eff}}.$$ (4)

Here b⃗ is the unit vector directed along the external magnetic field, B⃗₀ = B₀b⃗; and g_eff is the effective value of the g tensor

$$g_{\mathit{eff}}=\sqrt{{\overrightarrow{b}}^T\overleftrightarrow{G}\overrightarrow{b}}=\sqrt{G_{zz}},$$ (5)

where z is a lab frame axis parallel to b⃗, and G↔ is the symmetric tensor [1],

$$\overleftrightarrow{G}=\overleftrightarrow{g}{\overleftrightarrow{g}}^T.$$ (6)

The spin dynamics resulting from the Hamiltonian (3) with an arbitrary magnetic field B⃗₀ (t) is a precession of the spin around the instantaneous direction of the quantization axis in Eq. (4) with an instantaneous angular frequency ω = βB₀g_eff/ħ It is impossible to obtain a closed form description of the spin dynamics for arbitrary B⃗₀ (t) but it is possible for certain time-dependent magnetic fields relevant to magnetic resonance.

Pulsed EPR

For typical pulsed EPR experiments, the external magnetic field can be written as a sum of a strong, constant field B⃗₀ and an alternating, linearly-polarized mw field B⃗₁ = 2B₁b⃗₁ perpendicular to the static field, so that

$$\overrightarrow{B}(t)=B_0\overrightarrow{b}+2B_1{\overrightarrow{b}}_{1}p(t)cos(\omega t+\varphi (t)).$$ (7)

The unit vectors b⃗ and b⃗₁ define the z and x axes of the laboratory frame, respectively; B₁ is the strength of the mw field; p(t) equals 1 when a mw pulse is applied and 0 otherwise; and ϕ(t) is the phase of the mw pulse, usually 0, ±π/2, or π.

The system Hamiltonian with the magnetic field of Eq. (7) may be written as

$$\widehat{H}=\beta B_0{g}_{\mathit{eff}}\overrightarrow{k}·\widehat{\overrightarrow{S}}+2\beta B_{1}p(t)cos(\omega t+\varphi (t)){\overrightarrow{K}}_1·\widehat{\overrightarrow{S}},$$ (8)

with

$${\overrightarrow{K}}_1={\overleftrightarrow{g}}^T{\overrightarrow{b}}_1.$$ (9)

Although b⃗ and b⃗₁ (and the static and oscillating fields) are orthogonal, the vectors k⃗ and K⃗₁ are generally not orthogonal. The cosine of the angle between them is given by

$$cos\left(\overrightarrow{k},{\overrightarrow{K}}_1\right)=\overrightarrow{k}·{\overrightarrow{K}}_1/\left|{\overrightarrow{K}}_1\right|=G_{xz}/\sqrt{G_{zz}{G}_{xx}},$$ (10)

so that the effective mw field B₁K⃗₁ has a non-zero projection along the quantization axis k⃗ when G_xz ≠0. This mw field projection slightly modifies (in terms of the Magnus expansion, see, e.g., [5]) the spin resonance frequency and transition probability. The changes are on the order of B₁/B₀ or higher and usually may be neglected. We will ignore the component of B₁K⃗₁ along k⃗ and define k⃗₁ as the unit vector lying in the same plane as K⃗₁ and k⃗, but perpendicular to k⃗,

$${\overrightarrow{k}}_1=\left\{{\overrightarrow{K}}_1-\overrightarrow{k}\left(\overrightarrow{k}·{\overrightarrow{K}}_1\right)\right\}/g_1,$$ (11)

where g₁ was introduced by Abragam and Bleaney [1, Eq. (3.10)] as

$$g_1=\sqrt{G_{xx}-G_{xz}^2/G_{zz}}.$$ (12)

The CW EPR spectrum intensity is proportional to $g_1^2$ [1]. The Hamiltonian (8) becomes

$$\widehat{H}=\beta B_0{g}_{\mathit{eff}}\overrightarrow{k}·\widehat{\overrightarrow{S}}+2\beta B_1{g}_{1}p(t)cos(\omega t+\varphi (t)){\overrightarrow{k}}_1·\widehat{\overrightarrow{S}}.$$ (13)

The static and mw effective magnetic fields, B₀k⃗ and B₁k⃗₁, in Eq. (13) are orthogonal even for PCs with very anisotropic g tensors and are readily transformed into a rotating frame. However the anisotropy causes the rotating frame to differ in important ways from the standard rotating frame (SRF) used in magnetic resonance. The rotation axis is parallel to the quantization axis of the spin k⃗, but not always to the static field b⃗, producing a tilted rotating frame (TRF) that generally lies at some angle with respect to the lab axis system. Appendix A provides a detailed derivation of the rotating frame Hamiltonian.

The linearly-polarized mw field can be written as a sum of two counter-rotating, circularly-polarized fields,

$$2cos(\omega t+\varphi (t)){\overrightarrow{k}}_1=cos(\omega t+\varphi (t)){\overrightarrow{k}}_1+sin(\omega t+\varphi (t)){\overrightarrow{k}}_2+cos(\omega t+\varphi (t)){\overrightarrow{k}}_1-sin(\omega t+\varphi (t)){\overrightarrow{k}}_2$$ (14)

where the unit vector

$${\overrightarrow{k}}_2=\overrightarrow{k}\times {\overrightarrow{k}}_1,$$ (15)

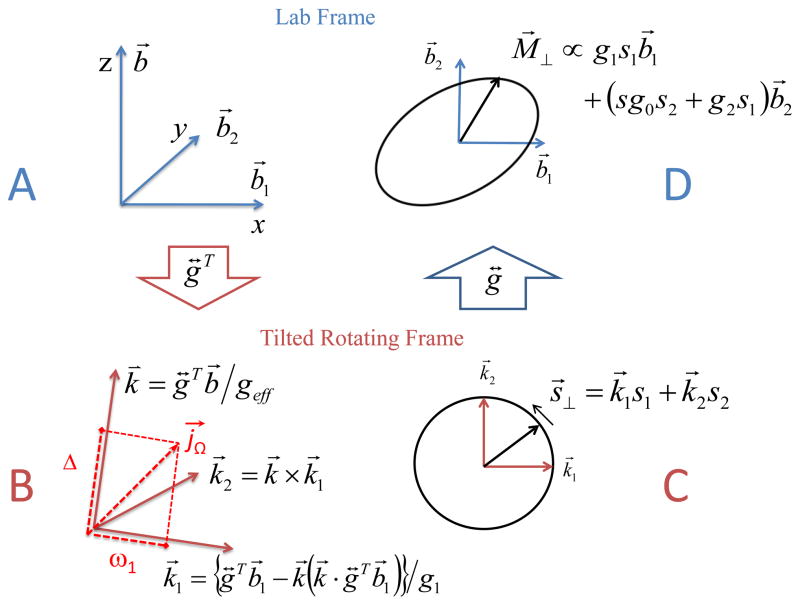
is chosen so that k⃗₁, k⃗₂, k⃗ form an orthonormal, right-hand coordinate system in the lab frame. Fig. 1A shows the lab frame with z and x axes defined by the B₀ and B₁ fields respectively, while the TRF, in Fig. 1B, has axes k⃗₁, k⃗₂ and k⃗, tilted by g↔^T. In the new TRF, the Hamiltonian (13) with the results of Appendix A becomes

Figure 1.

(A) Laboratory frame and (B) tilted rotating frame (TRF). The TRF is obtained from the lab frame by mapping its axes by g^T as described in text. The TRF basis set is labeled by the vectors. (C) The spin vector rotating in a plane perpendicular to its quantization axis k⃗ during the free precession period. (D) The magnetic moment dynamics obtained by mapping the spin vector into the lab frame by g. Spin components mapped onto the x-y plane, produce an elliptically-polarized magnetic moment path in the lab x-y plane perpendicular to b⃗. This double mapping makes all measurable quantities depend on G and on the signature of g.

$${\widehat{H}}_{\mathit{TRF}}=\left(\beta B_0{g}_{\mathit{eff}}-\hslash \omega \right)\overrightarrow{k}·\widehat{\overrightarrow{S}}+\beta B_1{g}_{1}p(t)\left\{{\overrightarrow{k}}_1·\widehat{\overrightarrow{S}}cos\varphi +{\overrightarrow{k}}_2·\widehat{\overrightarrow{S}}sin\varphi \right\}.$$ (16)

The system propagator Û_p describing the effect of a mw pulse of length t_p may be written

$${\widehat{U}}_p(t_p)=exp\left\{-\frac{i{\widehat{H}}_{\mathit{TRF}}{t}_p}{\hslash }\right\}=\widehat{E}cos\frac{\mathrm{\Omega }{t}_p}{2}-2i{\overrightarrow{j}}_{\mathrm{\Omega }}·\widehat{\overrightarrow{S}}sin\frac{\mathrm{\Omega }{t}_p}{2},$$ (17)

where Ê is the unit operator in spin space, Ω is the angular spin precession or Rabi frequency in the TRF around the effective magnetic field direction, j⃗_Ω,

$$\mathrm{\Omega }=\sqrt{{\mathrm{\Delta }}^2+{\omega }_1^2},$$ (18)

$$\mathrm{\Delta }={\omega }_0-\omega ,$$ (19)

$${\omega }_0=\beta B_0{g}_{\mathit{eff}}/\hslash ,$$ (20)

$${\omega }_1=\beta B_1{g}_1/\hslash ,$$ (21)

$${\overrightarrow{j}}_{\mathrm{\Omega }}=\frac{1}{\mathrm{\Omega }}\left[\mathrm{\Delta }\overrightarrow{k}+{\omega }_1\left({\overrightarrow{k}}_{1}cos\varphi +{\overrightarrow{k}}_{2}sin\varphi \right)\right].$$ (22)

Local fields, such as hyperfine interactions, that would contribute to ω₀ in Eq. (20) are assumed, for simplicity, to be zero. Measurements of a pulsed EPR signal usually are performed in the absence of mw irradiation, during a final free precession period. The system density matrix immediately after the last pulse may be calculated using the propagator

$${\widehat{U}}_{\mathit{prep}}={\widehat{U}}_p\left(t_{p,N}\right){\widehat{U}}_F\left({\tau }_{N-1}\right)\dots {\widehat{U}}_p\left(t_{p,2}\right){\widehat{U}}_F\left({\tau }_1\right){\widehat{U}}_p\left(t_{p,1}\right),$$ (23)

where the propagator during a free precession period simplifies to

$${\widehat{U}}_F(\tau )=\widehat{E}cos\frac{\mathrm{\Delta }\tau }{2}-2i\overrightarrow{k}·\widehat{\overrightarrow{S}}sin\frac{\mathrm{\Delta }\tau }{2},$$ (24)

with τ_j the delay between mw pulse j and (j+1), and N is the number of pulses in the sequence. The system density matrix immediately after the pulse sequence is

$${\rho }_{\mathit{prep}}={\widehat{U}}_{\mathit{prep}}{\rho }_{eq}{\widehat{U}}_{\mathit{prep}}^{+},$$ (25)

where ρ_eq is the density matrix at the start of the pulse sequence, normally at equilibrium with temperature T.

Resonance Measurements of Anisotropic PC

Spin dynamics during free precession after a series of mw pulses is simple; the properties of the propagator in Eq. (24) are well known. Willer and Schweiger [6] used a somewhat different approach to reach an equivalent description of the spin vector for anisotropic g with axial symmetry. The spin vector rotates around the quantization axis k⃗, with no variation parallel to k⃗ and precession in the k⃗₁, k⃗₂ plane perpendicular to k⃗. The spin vector traces out a circle as it precesses as shown in Fig. 1C. Although that circle is perpendicular to k⃗ in the TRF, it is tilted relative to the z axis of the lab frame, so there is an oscillating projection of the spin vector along the static field B₀. The precession frequency of the spin is ω₀ in the stationary frame and Δ in the TRF (see Eq. (19)). However, EPR spectrometers using mw detection [7] do not detect the spins or the motion of the spins; rather the signal is induced in the mw resonator by the magnetic moment. The difference between spin vector and magnetic moment was not appreciated in previous treatments of pulsed EPR in anisotropic spin systems.

The Precessing Magnetic Moment

The expectation values, s_n, of the spin vector along the n axis of the TRF, e.g., $s_1=\langle {\overrightarrow{k}}_1·\widehat{\overrightarrow{S}}\rangle =\text{Tr}\left({\overrightarrow{k}}_1·\widehat{\overrightarrow{S}}{\rho }_{\mathit{prep}}\right)$ simplify expressions for the density matrix. In the TRF, the density matrix for spins has the form ${\rho }_{\mathit{prep}}=2\left(s_1{\overrightarrow{k}}_1+s_2{\overrightarrow{k}}_2+s_3\overrightarrow{k}\right)·\widehat{\overrightarrow{S}}$, where normalization for S=1/2 is provided by $\text{Tr}{\left(S_i^2\right)}^{-1}=2$. Phase cycling in a pulsed EPR measurement makes it possible to have the average s₃ = 0, so that the density matrix can be written as

$${\rho }_{\mathit{prep}}=A\left\{sin(\mathrm{\Psi }){\overrightarrow{k}}_1·\widehat{\overrightarrow{S}}+cos(\mathrm{\Psi }){\overrightarrow{k}}_2·\widehat{\overrightarrow{S}}\right\},$$ (26)

The amplitude A and phase Ψ are easily related to s_n, allowing the density matrix to be written in the lab frame as (see Appendix A, Eq. (A12))

$${\rho }_{\mathit{prep}}^{\mathit{lab}}=A\left\{sin\left(\mathrm{\Psi }-\omega t_{\mathit{prep}}\right){\overrightarrow{k}}_1·\widehat{\overrightarrow{S}}+cos\left(\mathrm{\Psi }-\omega t_{\mathit{prep}}\right){\overrightarrow{k}}_2·\widehat{\overrightarrow{S}}\right\},$$ (27)

where t_prep is the temporal length of the preparatory pulse sequence. The density matrix evolves in the lab frame through the free precession of the spins at ω₀ around k⃗, so that for times t> t_prep

$${\rho }^{\mathit{lab}}(t)={\widehat{U}}_0\left(t-t_{\mathit{prep}}\right){\rho }_{\mathit{prep}}^{\mathit{lab}}{\widehat{U}}_0^{+}\left(t-t_{\mathit{prep}}\right).$$ (28)

Here Û₀ is the propagator Û_F written in the lab frame where Δ is replaced by ω₀, giving the precessing spin vector in Fig. 1C:

$$\begin{array}{l}{\rho }^{\mathit{lab}}(t)=A\left\{sin\left(\mathrm{\Psi }-\omega t_{\mathit{prep}}-{\omega }_0\left(t-t_{\mathit{prep}}\right)\right){\overrightarrow{k}}_1·\widehat{\overrightarrow{S}}+cos\left(\mathrm{\Psi }-\omega t_{\mathit{prep}}-{\omega }_0\left(t-t_{\mathit{prep}}\right)\right){\overrightarrow{k}}_2·\widehat{\overrightarrow{S}}\right\}\\ =A\left\{sin\left(\mathrm{\Psi }-{\omega }_{0}t+\mathrm{\Delta }{t}_{\mathit{prep}}\right){\overrightarrow{k}}_1·\widehat{\overrightarrow{S}}+cos\left(\mathrm{\Psi }-{\omega }_{0}t+\mathrm{\Delta }{t}_{\mathit{prep}}\right){\overrightarrow{k}}_2·\widehat{\overrightarrow{S}}\right\}\end{array}$$ (29)

The M_x and M_y components of magnetic moment, in the lab frame are

$$\begin{array}{l}{M}_{x(y)}(t)=\text{Tr}\left\{\left({\overrightarrow{b}}_{1(2)}·\widehat{\overrightarrow{\mu }}\right){\rho }^{\mathit{lab}}(t)\right\}\\ =-\beta \text{Tr}\left\{{\overrightarrow{b}}_{1(2)}^T\overleftrightarrow{g}\widehat{\overrightarrow{S}}{\rho }^{\mathit{lab}}(t)\right\}.\end{array}$$ (30)

The unit vector b⃗₂ = b⃗ × b⃗₁ lies along the lab y axis. Using the results in Appendix B, the x and y components of the magnetic moment, Eq. (30) and Fig. 1D, become

$$M_x(t)=-\frac{\beta }{2}{Ag}_{1}sin\left(\mathrm{\Psi }-{\omega }_{0}t+\mathrm{\Delta }{t}_{\mathit{prep}}\right),$$ (31)

$$M_y(t)=-\frac{\beta }{2}A\left\{{sg}_{0}cos\left(\mathrm{\Psi }-{\omega }_{0}t+\mathrm{\Delta }{t}_{\mathit{prep}}\right)+g_{2}sin\left(\mathrm{\Psi }-{\omega }_{0}t+\mathrm{\Delta }{t}_{\mathit{prep}}\right)\right\}.$$ (32)

Here

$$g_0=\frac{\sqrt{det\left(\overleftrightarrow{G}\right)}}{g_1{g}_{\mathit{eff}}},$$ (33)

$$g_2=\frac{G_{yx}{G}_{zz}-G_{yz}{G}_{zx}}{g_1{G}_{zz}}.$$ (34)

$$s=sgn(det(\overleftrightarrow{g}))$$ (35)

The vector k⃗₂ is not necessarily perpendicular to B⃗₀, so that the spin can have an oscillating component along the static magnetic field in Eqs. (26) and (29). However, M_z for that same system does not because M_z from ρ^lab (t) in eq. (29) contains (g↔^Tb⃗)·k⃗_n and vanishes. In other words, the spin components precess, forming a circle in a plane perpendicular to k⃗ but not necessarily perpendicular to b⃗, Fig. 1C. However, the magnetic moment vector follows an ellipse restricted to a plane that is perpendicular to the external magnetic field direction b⃗. This surprising result is accomplished by variation of the length of the magnetic moment as it precesses and is required for conservation of energy. Oscillations of M_z in the lab frame would produce oscillations of the total energy, which are impossible in a static magnetic field. Fig. 1 illustrates the relation between the laboratory frame, the tilted spin frame, the oscillating components of the spin vector and the respective components of the magnetic moment vector.

Results

The EPR Spectrum

The magnetic moment described by eqs. (31) and (32) is the sum of two linearly-polarized components along the lab x and y axes. This magnetic moment is elliptically polarized in the lab frame, and can also be written as the sum of two counter-rotating, circularly-polarized components with unequal amplitudes even though the underlying spin vector is a single, circularly-polarized entity. The vast majority of magnetic resonance spectrometers can only measure the linearly-polarized signal from M_x, although some induction spectrometers using bimodal resonators or a quasioptical design can measure M_x and M_y or either circularly-polarized component [8–10]. We restrict our attention to M_x and the EPR spectrum from conventional EPR spectrometers and consider induction spectrometers and the independent information contained in M_y in a later paper.

Modern pulsed EPR spectrometers use some form of coherent demodulation to convert or mix the mw M_x(t) signal at ω₀ to a much lower frequency signal at Δ with two quadrature components. The resulting signal can be written as a complex quantity:

$$\begin{array}{l}{M}_{det}(t^{\prime })=i\frac{\beta }{4}{g}_{1}Aexp\left(i(\mathrm{\Delta }{t}^{\prime }-\mathrm{\Psi })\right)\\ =\frac{\beta }{4}{g}_{1}A\left(-sin(\mathrm{\Delta }{t}^{\prime }-\mathrm{\Psi })+icos(\mathrm{\Delta }{t}^{\prime }-\mathrm{\Psi })\right)\end{array}$$ (36)

The M_det signal contains information only about M_x; all information of M_y is lost. Pulsed and CW EPR spectra provide identical information about the tensor G [1], because they arise from the same M_x which depends on g₁ and g_eff, see Eqs. (5), (12), (20), (21) and (31). The only quantity related directly to the g tensor which is potentially available from experimental data is the signature, s. Everything else in the EPR measurement related to g actually depends on G [1]. Unfortunately, s is obtained from M_y(t) in the lab frame which is not measured by conventional spectrometers.

Axial Symmetry

The g tensor often has axial or near-axial symmetry. In this limiting case, some simplification of equations is possible. Calculations are more convenient in the molecular frame that diagonalizes G↔ with principal values G_⊥, G_⊥ and G_||. The Z axis is defined as the axial symmetry axis and the X axis is chosen to lie in the plane containing Z and the z axis of the lab frame when these do not coincide, so that b⃗ = (sinθ, 0, cosθ)^T. In this coordinate system, b⃗₁ = (cosθcosα, sinα, − sinθcosα)^T is perpendicular to b⃗ and the angle α is zero when b⃗₁ is perpendicular to Y. Then

$$g_{\mathit{eff}}=\sqrt{G_{\perp }{sin}^2\theta +G_{\left|\right|}{cos}^2\theta }$$ (37)

$$g_1=\sqrt{G_{\perp }}\sqrt{{sin}^2\alpha +\frac{G_{\left|\right|}}{g_{\mathit{eff}}^2}{cos}^2\alpha }$$ (38)

which show that PCs with the same orientation of the external magnetic field in the molecular frame, and thus the same θ, g_eff and ω₀; nevertheless, can have different g₁ because of the angle α. The orientation of b⃗₁ with respect to the G_|| axis is significant. This means that in ‘powder’ samples, PCs having identical resonance frequencies are not identical because they respond differently to the mw field that produces the EPR signal.

Only when the unique axis of the g tensor is parallel to the external magnetic field (θ=0, $g_{\mathit{eff}}^2=G_{\left|\right|}$, and $g_1=\sqrt{G_{\perp }}$) will all the resonant PCs behave identically. And only at the g_|| feature of axial PCs can simple mw pulses be used for precise manipulations of spins because only there will all spins have the same turning angle and ω₁. This characteristic makes the g_|| feature convenient for B₁ field calibration. On the other hand, if the g tensor lacks even axial symmetry, every point in EPR powder spectrum has a distribution of turning angles, ω₁, and different signal amplitudes for PCs with the same ω₀. Willer and Schweiger [6] exploited the unique properties of the g_|| feature to measure $\sqrt{G_{\perp }}$ from spin nutation during a microwave pulse. However, the conversion of spin vector into magnetic moment in eqn. (23) of that paper confuses the lab frame with the TRF magnetic moments; a factor of g₁ is lost in the ‘proportional to’ in converting the spin vector into magnetic moment; and it is implicitly assumed that the measurement is made at the center of a symmetric EPR spectrum. Yet they succeeded in measuring g_⊥ =0.04±0.015 for Ti⁺³ in sapphire which is otherwise not readily measureable.

The Free Induction Decay

The simplest pulsed EPR signal is the FID that appears following a single mw pulse. The propagator in Eq. (23) in this case consists of the single rightmost operator. A two-step phase cycle in the form of (φ = 0, −), (φ = π, +) suppresses the spin component along k⃗. (The phase cycle notation indicates that signals or ρ^lab generated with φ=0 are subtracted from those with φ=π.) After this preparation, we obtain (see Appendix C, Eq. (C4), and Appendix D, Eqs. (D2) and (D3) for details)

$$A=2A_{1}tanh\left({\epsilon }_0/2\right),$$ (39)

$$\mathrm{\Psi }={\mathrm{\Psi }}_1,$$ (40)

where

$$sin{\mathrm{\Psi }}_i=2\frac{{\omega }_1\mathrm{\Delta }}{A_i{\mathrm{\Omega }}^2}{sin}^2\frac{\mathrm{\Omega }{t}_{p,i}}{2},$$ (41)

$$cos{\mathrm{\Psi }}_i=-\frac{{\omega }_1}{A_i\mathrm{\Omega }}sin\mathrm{\Omega }{t}_{p,i},$$ (42)

with

$$A_i=\sqrt{{\left(2\frac{{\omega }_1\mathrm{\Delta }}{{\mathrm{\Omega }}^2}{sin}^2\frac{\mathrm{\Omega }{t}_{p,i}}{2}\right)}^2+{\left(\frac{{\omega }_1}{\mathrm{\Omega }}sin\mathrm{\Omega }{t}_{p,i}\right)}^2}.$$ (43)

Here t_p,i is the length of mw pulse i in the sequence. Using Eq. (36) the FID signal is

$$M_{\mathit{FID}}(t^{\prime })=-i\frac{\beta }{2}{g}_{1}tanh\left({\epsilon }_0/2\right)exp\left(i\mathrm{\Delta }{t}^{\prime }\right)\left\{\frac{{\omega }_1}{\mathrm{\Omega }}sin\mathrm{\Omega }{t}_{p,1}+2i\frac{{\omega }_1\mathrm{\Delta }}{{\mathrm{\Omega }}^2}{sin}^2\frac{\mathrm{\Omega }{t}_{p,1}}{2}\right\}.$$ (44)

It is widely known that the Fourier transform of the FID signal reproduces the CW magnetic resonance spectrum in the frequency domain [5, 11] for isotropic g. This is no longer the case when the g tensor is anisotropic. The same frequencies appear in both spectra, but their relative intensity across the spectrum may be different. The CW EPR spectrum intensity is proportional to $g_1^2$ [1], while the intensity of a spin at frequency Δ in the Fourier Transform of the FID is

$$I_{\mathit{FID}}(\mathrm{\Delta })\propto -{ig}_1\left\{\frac{{\omega }_1}{\mathrm{\Omega }}sin\mathrm{\Omega }{t}_{p,1}+2i\frac{{\omega }_1\mathrm{\Delta }}{{\mathrm{\Omega }}^2}{sin}^2\frac{\mathrm{\Omega }{t}_{p,1}}{2}\right\}$$ (45)

which depends nonlinearly on Ωt_p,1. In the limit of a hard, small turning-angle pulse, Ωt_p,1≪1 and ω₁≫Δ, the I_FID is proportional to $g_1^2$ the same as the CW EPR spectrum. The second factor of g₁ comes from expanding the term inside the brackets for small turning angle. The same result occurs with small turning angle when the EPR spectrum is reconstructed by sweeping ω or B₀. The correspondence with the CW spectrum is lost in both limits if a large turning-angle (~π/2) pulse is used. The problem is not simply that the turning angle depends on orientation and that it is not possible to uniformly excite all spins. Even if there were an ideal composite pulse with an effective turning angle of π/2, the term in brackets would become unity and the I_FID would be proportional to g₁ and not the $g_1^2$ of the CW EPR spectrum.

Two-Pulse Electron Spin Echo

A typical phase cycle during generation of the two-pulse spin echo of

$$(0,0,-),(\pi ,0,+),(0,\pi ,-),(\pi ,\pi ,+),\left(\pi ,\frac{\pi }{2},-\right),\left(0,\frac{\pi }{2},+\right),\left(\pi ,-\frac{\pi }{2},-\right),\left(0,-\frac{\pi }{2},+\right)$$ (46)

suppresses terms which produce unwanted signals. The resulting amplitude A and phase Ψ are

$$A=-8A_1{p}_2$$ (47)

$$\mathrm{\Psi }=\mathrm{\Delta }\tau -{\mathrm{\Psi }}_1$$ (48)

with p₂ being the probability for the second mw pulse to flip the spin

$$p_2=\frac{{\omega }_1^2}{{\mathrm{\Omega }}^2}{sin}^2\frac{\mathrm{\Omega }{t}_{p2}}{2}.$$ (49)

Substitution of (47), (48) and (49) in Eq. (36) gives the ESE signal,

$$M_{\mathit{ESE}}\left(t^{\prime }\right)=-2i\beta g_1{A}_1{p}_{2}exp\left[i\left(\mathrm{\Delta }\left(t^{\prime }-\tau \right)+{\mathrm{\Psi }}_1\right)\right].$$ (50)

The signal is nearly the same as for isotropic PC [7], but ω₁, A₁, and p₂ now depend on the orientation of the PC in the lab frame. The refocusing of the magnetic moment as an echo still occurs with the peak echo intensity at t′=τ, given by

$$M_{\mathit{ESE}}\left(t^{\prime }=\tau \right)=2i\beta g_{1}tanh\left(\frac{{\epsilon }_0}{2}\right)\frac{{\omega }_1^3}{{\mathrm{\Omega }}^3}{sin}^2\frac{\mathrm{\Omega }{t}_{p2}}{2}\left\{sin\mathrm{\Omega }{t}_{p1}-2i\frac{\mathrm{\Delta }}{\mathrm{\Omega }}{sin}^2\frac{\mathrm{\Omega }{t}_{p1}}{2}\right\}$$ (51)

An EPR spectrum of the PC can be obtained from a two-pulse echo measurement, for example, by Fourier transformation of the echo shape or from the total integral of the echo as a function of B₀ at constant ω. However, the EPR spectrum is not identical to the CW EPR spectrum of the PC for the reasons discussed for FID detection. In the limit of small turning angle, the two-pulse echo response is proportional to g₁⁴, while with ‘perfect composite pulses’, it would be proportional to g₁. Although the echo is still a pair of ‘back-to-back’ FIDs, the shape is slightly different from the single pulse FID, eqn. (44), and from the Fourier transform of the CW EPR spectrum. Figure 2 compares numerically calculated echo-detected spectra for different turning angles to the CW EPR spectrum drawn using the analytic expression in Eqns.(2.149-150) of [12].

Figure 2.

Comparison of two-pulse, echo-detected EPR spectra with the CW absorption spectrum for spectrometer frequency 9.5 GHz. The g principal values were g_XX=3.0, g_YY=2.0, g_ZZ=1.0. The CW ‘stick’ spectrum was calculated using an analytic expression, and echo-detected spectra using Monte Carlo averaging over the unit sphere. The ‘noise’ in the echo-detected spectra arise from the limited number of orientations used. The mw pulse lengths were t_p1=t_p, t_p2=2t_p. The B₁ was chosen for a turning angle of π/2 for isotropic g = 2.0 at t_p=9 ns. The echo-detected and the cw shapes never coincide.

Three-Pulse Electron Spin Echo

The stimulated echo signal appears after application of three nominally π/2 mw pulses. It is often likened to a two-pulse spin echo where the second or π pulse is “divided” into two π/2 “subpulses”. A complete phase cycle of

$$\begin{array}{cccc}(0,0,0,+),& (\pi ,0,0,-),& (0,\pi ,0,-),& (\pi ,\pi ,0,+),\\ (0,0,\pi ,-),& (\pi ,0,\pi ,+),& (0,\pi ,\pi ,+),& (\pi ,\pi ,\pi ,-)\\ (0,\pi /2,\pi /2,+),& (\pi ,\pi /2,\pi /2,-),& (0,-\pi /2,\pi /2,-),& (\pi ,-\pi /2,\pi /2,+),\\ \left(0,\pi /2,-\pi /2,-\right),& (\pi ,\pi /2,-\pi /2,+),& (0,-\pi /2,-\pi /2,+),& (\pi ,-\pi /2,-\pi /2,-).\end{array}$$ (52)

prepares a density matrix in the form given in Eq. (26) (see Eq. (D10)) with

$$\begin{array}{c}A=16tanh\left(\frac{{\epsilon }_0}{2}\right)A_1{A}_2{A}_{3}sin\left(\mathrm{\Delta }\tau -{\mathrm{\Psi }}_1-{\mathrm{\Psi }}_2\right),\\ \mathrm{\Psi }={\mathrm{\Psi }}_3,\end{array}$$ (53)

giving the signal

$$M_{st}(t^{\prime })=16i\beta g_{1}tanh\left(\frac{{\epsilon }_0}{2}\right)A_1{A}_2{A}_{3}exp\left\{i\left[\mathrm{\Delta }\left(t^{\prime }-\tau \right)+{\mathrm{\Psi }}_1+{\mathrm{\Psi }}_2-{\mathrm{\Psi }}_3\right]\right\}.$$ (54)

The sixteen-step phase cycle in eq. (52) isolates the stimulated echo from all other signals including a different three-pulse echo, the virtual echo [13, 14], for isotropic and anisotropic PCs. The stimulated echo signal refocuses at time t′=τ while the virtual echo refocuses at time t′ = −τ, but each echo can be independently recovered using the appropriate phase cycle [15]. The phase cycle in eq. (52) or equivalent forms [16] recovers the stimulated echo; the cycle in Table 1 of [17] recovers the virtual echo, while that in Table 10.2.1 of [7] recovers both echoes.

With three identical pulses, eq. (54) reduces to

$$M_{st}(t^{\prime })=-16i\beta g_1{\left(\frac{{\omega }_1}{\mathrm{\Omega }}\right)}^{3}tanh\left(\frac{{\epsilon }_0}{2}\right)\left\{{sin}^2\mathrm{\Omega }{t}_p+4\frac{{\mathrm{\Delta }}^2}{{\mathrm{\Omega }}^2}{sin}^4\frac{\mathrm{\Omega }{t}_p}{2}\right\}\times exp\{i\mathrm{\Delta }(t^{\prime }-\tau )\}\left\{sin\mathrm{\Omega }{t}_p-2i\frac{\mathrm{\Delta }}{\mathrm{\Omega }}{sin}^2\frac{\mathrm{\Omega }{t}_p}{2}\right\}$$ (55)

with limiting values proportional to g₁⁴ for small turning angle pulses and g₁ for ‘perfect composite pulses”; identical to the two-pulse echo and the virtual echo.

Pulsed Electron-Electron Double Resonance

The probability for the pumping pulse to flip a spin plays an important role in the measurement of distances between spins in pulsed electron-electron double resonance (PELDOR) [2] also known as DEER. This probability is called p_B in DEER, but is the p₂ in eq. (49). When nitroxide spin labels are used in PELDOR measurements, it is necessary to account for their g tensor anisotropy only with respect to its effect on the Zeeman frequencies which can produce orientation selection. Their small g anisotropy has negligible effect on p₂. However, when one of the PCs is a metal center with substantial g anisotropy, the DEER measurement is affected: by the consequent orientation selection; by modification of the dipolar interaction; and by alteration of the spin dynamics. We briefly mention the latter two aspects assuming the A spin has minimal anisotropy (A spins are those whose signal is recorded) but the B spin has significant anisotropy (the B spins flip because of a pumping pulse at ω_B, thereby changing the local dipole field and modulating the ESE signal of the A spins).

The dipole-dipole interaction spectrum involving an anisotropic PC is different from the standard Pake pattern for isotropic spins and has been treated in [18–20]. Fortunately, the dipole splitting, and consequently the modulation frequencies of the PELDOR signal, depends only on the external magnetic field direction, b⃗, with respect to the molecular frame. It does not depend on the orientation of the x axis of the lab frame, b⃗₁, and is readily incorporated into DEER analysis.

On the other hand, p_B does depend explicitly on b⃗₁. Fortunately, if the orientation of the B spin in disordered systems is uncorrelated with the vector between A and B spins, it is necessary to integrate p_B only over the Euler angles relating the lab fame to the B spin g tensor. In the case of axial symmetry this means integration over α and θ after substitution of Eq. (38) into (49), with t_p2 changed to t_pB. When the vector between spins has a fixed orientation relative to the g axes, the dependence of p_B on b⃗ and b⃗₁ must be explicitly incorporated into the analysis.

Figure 3 shows how anisotropy of a rhombic g tensor affects the averaged p_B for different pumping field strengths. For small g anisotropy, p_B oscillates as B₁ and the nominal pulse turning angle increase, but for large anisotropy, p_B approaches the form of a linear ramp. The g anisotropy makes it impossible to characterize a mw pulse in terms of a single turning angle, particularly in multi-pulse sequences used to generate echoes. The effective mw field strength ω₁ and hence the turning angle ω₁t_p vary with the orientation of b⃗₁, making it impossible to precisely manipulate spin dynamics and difficult to optimize measurement conditions. This situation qualitatively resembles the case of an inhomogeneous B₁ field for isotropic PCs [14].

Figure 3.

The probability, p_B, for a B spin to be flipped by a mw pulse with strength, B₁, for different rhombic g tensors: g_XX=2.0+ δg/2, g_YY=2.0, g_ZZ=2.0 − δg/2. The values of δg are indicated on the figure. Note that the local maxima in p_B shift as δg increases. Calculated with mw frequency of 9.5 GHz and the magnetic field for g_eff=2.0 and pulse length of 12 ns. For significant anisotropy, the largest response occurs at the highest value of B₁. For most PELDOR signal calculations, this separate averaging of p_B is impossible due to correlation of dipole splitting with g anisotropy; rather, p_B may be obtained from the limiting PELDOR signal at long delays.

Conclusion

Many similarities exist between the spin dynamics and pulsed EPR signals of anisotropic PCs in the TRF and those of isotropic PCs in the SRF. Yet important differences do arise because the effective mw magnetic field depends on the orientation of the molecular frame with respect to the laboratory frame x axis and because EPR signals arise from the magnetic moment and not the spin. In the absence of a mw field, the spin vector has a stationary component parallel to the quantization axis and a single, circularly-polarized component precessing in a plane perpendicular to the quantization axis. The magnetic moment vector behaves quite differently. It has a stationary component, parallel to G↔B⃗₀, which generally lies in a different direction than B₀ or the quantization axis. More surprisingly, the magnetic moment vector generally has an elliptically-polarized component, moving strictly perpendicular to the stationary magnetic field B⃗₀. The signal detected by a standard pulsed EPR spectrometer measures the mw field induced by the component of the magnetic moment vector parallel to the linearly polarized field in the spectrometer mw resonator and misses those perpendicular to the mw field. The signal does not measure the spin vectors themselves, only some of their specific components.

Anisotropy of the g tensor introduces an additional parameter g₁ which alters the signal amplitude. This parameter depends only on the components of the tensor G in the lab frame. The signal amplitude may differ for PCs having the same orientation of magnetic field B⃗₀ to their molecular frames but different orientations of the mw field B⃗₁. These amplitude variations are proportional to g tensor anisotropy and may be neglected for typical organic radicals. This variation causes the EPR spectrum detected using pulsed EPR methods to depart from the CW EPR signal shape. Only in the unrealistic asymptotic limit for the FID from a small turning angle pulse exciting the whole EPR spectrum does the Fourier transform of the FID coincide with the CW spectrum.

• With g-anisotropy, electron spin and magnetic moment generally behave differently.

• Spins precess in one direction on a circular path perpendicular to g↔^TB⃗₀/g_eff

• Magnetic moment precesses in an elliptical path perpendicular to B₀.

• The orientation of B₁ relative to g does matter.

• CW EPR spectra are slightly different from the FT spectra.