Biological Phosphoryl-Transfer Reactions: Understanding Mechanism and Catalysis

Abstract

Phosphoryl-transfer reactions are central to biology. These reactions also have some of the slowest nonenzymatic rates and thus require enormous rate accelerations from biological catalysts. Despite the central importance of phosphoryl transfer and the fascinating catalytic challenges it presents, substantial confusion persists about the properties of these reactions. This confusion exists despite decades of research on the chemical mechanisms underlying these reactions. Here we review phosphoryl-transfer reactions with the goal of providing the reader with the conceptual and experimental background to understand this body of work, to evaluate new results and proposals, and to apply this understanding to enzymes. We describe likely resolutions to some controversies, while emphasizing the limits of our current approaches and understanding. We apply this understanding to enzyme-catalyzed phosphoryl transfer and provide illustrative examples of how this mechanistic background can guide and deepen our understanding of enzymes and their mechanisms of action. Finally, we present important future challenges for this field.

INTRODUCTION

Reactions at the phosphorus atom of phosphate esters and anhydrides form the chemical basis for many of the most fundamental processes in living systems. These reactions allow genetic inheritance through nucleic acids and the coupling of chemical energy to drive the thermodynamically unfavorable processes required for construction and maintenance of living cells. Phosphoryl-transfer chemistry is also crucial for basic metabolic pathways and cellular signal transduction (1–3).

Despite the importance of phosphoryl transfer, the modern reader faces a considerable challenge in approaching the literature on phosphoryl-transfer chemistry. In the 30 years since Jeremy Knowles's major review for the general reader in this series (1), many new observations have been made, some long-standing questions have been settled, and new controversies have arisen. An explosion of structural and computational data has led to new insights, but also new sources of controversy and confusion over chemical and catalytic mechanisms. Decades of work and often-unfamiliar experimental approaches can present a daunting challenge to investigators new to the field. At the same time, our current understanding of biological catalysis of phosphoryl transfer is closely linked to knowledge of mechanisms and transition states for the nonenzymatic reactions in solution. In this review, we hope to complement excellent reviews in the chemical literature (e.g., 4–11) and provide the background for the general reader to understand key experimental data and concepts, to evaluate current controversies in the literature, and to meet future challenges in the field. We have included additional discussion in the Supplemental Text (for all Supplemental Material, follow the link on the Annual Reviews home page at http://www.annualreviews.org), as well as several compiled data sets that we hope will be useful in future work.

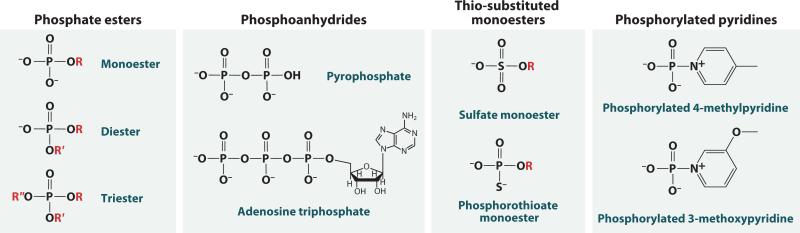
Because of their biological importance, the reactions of monosubstituted phosphates (e.g., phosphate monoesters such as glucose and inositol phosphate, and phosphoanhydrides such as ATP and pyrophosphate) and diesters, such as DNA and RNA, are emphasized. Phosphate triesters and other compounds are also discussed, as they provide important mechanistic comparisons (Figure 1). To understand how these compounds react and how enzymes catalyze their reactions, we consider four key questions:

1. Are phosphoryl-transfer reactions concerted, or do they proceed through stable intermediates? This question has largely been resolved for nonenzymatic reactions. We review the experiments and analyses that led to its resolution for monoesters, as this knowledge helps in assessing new situations, particularly in enzymatic systems where the question continues to arise.

2. How can we evaluate the structure and properties of the transition state? Transition-state theory defines catalysis as preferential stabilization of a transition state relative to the ground state (12–15). As the proficiency of an enzyme is related to its ability to recognize and stabilize the transition state, characterizing the geometry, bonding, and charge distribution of the transition state is crucial for understanding catalysis. We aim to explain the experimental approaches used to characterize phosphoryl-transfer transition states, providing the reader with the tools to critically evaluate existing and emerging data.

3. Do enzymes alter transition states from those in solution? If enzymes recognize and stabilize the transition states of the corresponding uncatalyzed reactions, then nonenzymatic transition states may be used as a guide to understand and possibly engineer stabilizing interactions. Alternatively, if enzymes alter transition states from those in solution, it will be fascinating to unravel the forces and interactions that are responsible for the change. Although much remains to be done in comparing enzymatic and nonenzymatic transition states, emerging data suggest a coherent picture.

4. How do phosphoryl-transfer enzymes achieve catalysis? Decades of intensive studies have provided detailed structural pictures and identified key enzymatic functional groups. Yet in most cases, the energetic contributions of enzymatic interactions to catalysis remain poorly accounted for or unknown. We present a perspective on mechanisms for catalyzing phosphoryl-transfer reactions, selected case studies that illustrate key principles, and future challenges and new directions.

Figure 1.

Substituted phosphates and related compounds important for biology and mechanism. Phosphate monoesters and diesters form crucial biological compounds. Phosphoanhydrides contain one or more anhydride linkages between phosphate groups. Triesters, thio-substituted compounds, and phosphorylated pyridines have contributed significantly to mechanistic understanding. The protonation states shown are the dominant forms at pH 7–8.

MECHANISTIC POSSIBILITIES

Concerted Versus Stepwise Reactions

One of the most confusing issues faced by the modern reader venturing into the mechanistic literature is whether phosphoryl-transfer reactions in solution are concerted or whether they proceed through stepwise processes with discrete intermediates. Although Knowles's 1980 review (1) was written more than two decades after seminal mechanistic results were obtained, it was still unclear at that time whether the nonenzymatic hydrolyses of phosphate monoesters were concerted or stepwise reactions. While the issue is largely resolved today, confusion persists in the literature. It is instructive to review the original data that motivated early mechanistic models, followed by the resolution of this issue from new data and a new conceptual framework.

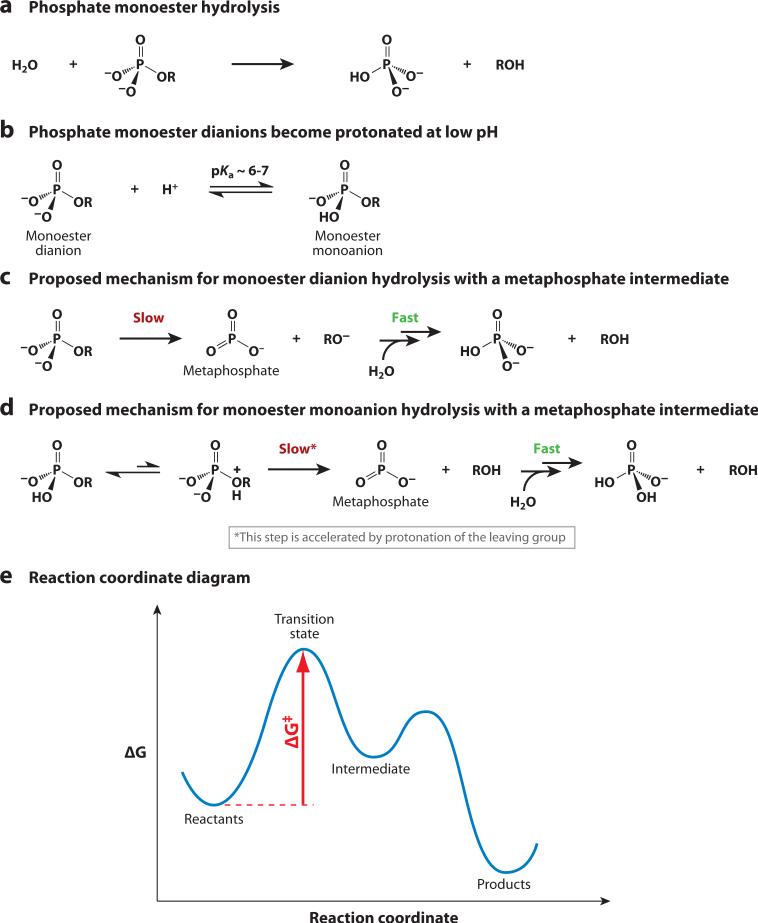
Hydrolysis reactions of phosphate monoesters (Figure 2 a) were the subject of intensive study for decades. As early as the 1950s, investigators observed that the hydrolysis rate increases by many orders of magnitude as the pH is decreased, implying that protonated phosphate monoesters (the monoanionic form) (Figure 2b) react much faster than do phosphate monoester dianions (16–18). To account for this observation, Westheimer proposed a mechanism in which the rate-determining step in phosphate monoester hydrolysis was uni-molecular decomposition to a metaphosphate intermediate, followed by rapid addition of water to produce inorganic phosphate (Figure 2c). This model explained the enhanced reactivity of phosphate monoester monoanions because the proton could shift from the phosphoryl group to the leaving group, thereby stabilizing charge buildup on the leaving group in the rate-determining step (Figure 2d).¹ An intuitively attractive feature of this model was that the negatively charged oxygen atoms could act as the “driving force” for leaving-group expulsion by donating electron density to phosphorus (18). An alternative model to explain the reactivity of phosphate monoester monoanions, in which protonation increased the electrophilicity of the phosphoryl group, could be ruled out because the monoester monoanion reacts significantly faster than the corresponding phosphate diester (Figure 1) (17, 18).

Figure 2.

Phosphate monoesters and proposed hydrolysis reaction mechanisms. (a) Hydrolysis of phosphate monoester dianion. (b) At low pH, phosphate monoesters become protonated to form monoanions (104). (c,d ) The rapid hydrolysis of these phosphate monoester monoanions led early researchers to propose that phosphate ester hydrolysis reactions proceeded through a metaphosphate intermediate. There is now strong evidence against the intermediacy of metaphosphate. (e) Reaction coordinate diagram. A transition state (‡) represents a local maximum along a reaction coordinate, whereas an intermediate exists in an energy well.

Although metaphosphate appeared to be too unstable to isolate and characterize, additional data were taken as supporting this mechanism. Entropies and volumes of activation were cited in support of unimolecular decomposition to metaphosphate (19–21), and linear free energy relationships (LFERs) and kinetic isotope effects (KIEs) suggested extensive breaking of the bond to the leaving group (19, 20, 22). We explain these techniques in later sections; here we simply emphasize that these results were consistent with the proposed reaction mechanism proceeding through a metaphosphate intermediate. However, the key flaw in this logic was that all of the data were obtained from kinetic methods that reported on properties of the transition state, not the properties of an intermediate. Although the data were consistent with a metaphosphate intermediate, they did not require one, and as we describe below, considerable data available today provide strong evidence for reactions through metaphosphate-like transition states but not metaphosphate intermediates.

The distinction between a transition state and an intermediate is apparent from reaction coordinate diagrams (as in Figure 2e). A transition state represents a local maximum along a reaction coordinate, whereas an intermediate exists in a local minimum, i.e., an energy well. Most importantly, kinetic data such as rate constants and activation parameters report on the properties of the transition state relative to the reactants (ΔG^‡) (Figure 2e). Thus, kinetic data that suggest significant breaking of the bond to the leaving group and minimal bonding to the nucleophile do not necessarily imply the existence of a metaphosphate intermediate, but rather tell us about properties of the transition state. How did this distinction cause decades of confusion in the literature? One problem was that the experimental data were challenging to interpret, but a key factor was the absence of a language or framework for describing these and other reactions. In the next section we describe a simple framework that clarifies these points and helps to frame the remainder of our discussion and evaluation of the mechanisms of phosphoryl-transfer reactions.

Two-Dimensional Reaction Coordinate Diagrams and a Continuum of Transition States

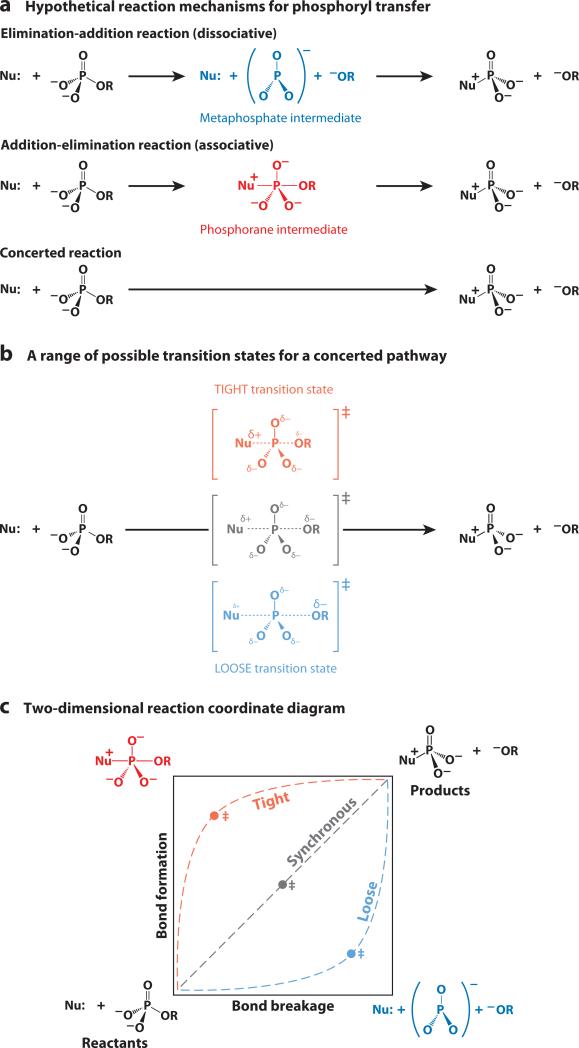
Figure 3a shows a range of hypothetical phosphoryl-transfer reaction mechanisms: a dissociative mechanism (elimination-addition), which for phosphoryl transfer would entail a metaphosphate intermediate; a concerted mechanism, an S_N2-type reaction proceeding through a single transition state with simultaneous breaking of one bond and formation of a new bond; and an associative mechanism (addition-elimination), which would entail formation of a pentavalent phosphorane intermediate. These reaction mechanisms, however, are only the limiting cases among a continuum of possibilities in which bond formation and cleavage in the transition state need not be synchronous (Figure 3b).

Figure 3.

Mechanistic possibilities in phosphoryl-transfer reactions. (a) An elimination-addition reaction through a metaphosphate intermediate (D_N + A_N), an addition-elimination reaction through a phosphorane intermediate (A_N + D_N), and a concerted reaction pathway with simultaneous bond formation and bond cleavage (A_ND_N). The parentheses give the IUPAC nomenclature (162). (b) A range of possible transition states for a concerted pathway. (c) A two-dimensional reaction coordinate diagram, also known as a More O'Ferrall-Jencks diagram (23, 24). The diagram represents a range of possible concerted reaction pathways passing through loose, synchronous, or tight transition states. Bond breaking and bond formation proceed along the x- and y-axes, respectively, and the energy axis is perpendicular to the page. The transition state is located at a maximum along the path from reactants to products, but a minimum in the direction perpendicular to the reaction pathway. The two-dimensional reaction coordinate depiction emphasizes that there is a continuum of reaction pathways, and the transition state can occur at any point along the pathway. For simplicity, the diagram above depicts symmetrical transition states halfway along each reaction pathway. Reactions proceeding through intermediates would have additional energy wells in the lower right corner for a metaphosphate intermediate and in the upper left corner for a phosphorane intermediate.

To depict this continuum of possible transition states, we introduce two-dimensional reaction coordinate diagrams, also known as More O'Ferrall-Jencks diagrams after the originators of this framework (23, 24). In the two-dimensional reaction coordinate diagram shown in Figure 3c, the reactants are depicted in the lower left corner and the products in the upper right. Bond breaking proceeds along the x-axis and bond formation proceeds along the y-axis. This two-dimensional reaction coordinate defines a three-dimensional free energy surface in which the free energy axis is perpendicular to the page. Starting from the reactants located in a free energy well at the bottom left, a reaction will proceed across this surface via the pathway with the lowest barrier. As in the one-dimensional reaction coordinate shown in Figure 2e, the transition state is a maximum along the reaction pathway, but a minimum in the direction perpendicular to the reaction pathway (i.e., it is a saddle point). The two-dimensional reaction coordinate diagram illustrates that there is a continuum of possible reaction pathways between the two extremes of an elimination mechanism via a metaphosphate intermediate in the lower right corner of Figure 3c and an addition mechanism via a phosphorane intermediate in the upper left corner.

The range of possible transition states for concerted reactions can be mapped onto the reaction coordinate diagram. Transition states in which the phosphorus atom sees an increase in the total bond order to the nucleophile and the leaving group relative to that in the reactants are referred to as tight transition states. Those with a decrease in total bond order between phosphorus and the nucleophile and leaving group are called loose transition states. Concerted reactions with similar net bond order between reactants and transition states are synchronous transition states (for a more sophisticated treatment of bond order, see Reference 25). These transition states are depicted as symmetric in Figure 3c but need not be—the nucleophile and leaving group may be bonded to phosphorus to differing extents in transition states that are early or late along the reaction pathway. For further discussion of terminology, see the sidebar Terminology for Describing Phosphoryl-Transfer Reactions.

For phosphate monoester hydrolysis reactions, a metaphosphate-like transition state can occur for a reaction pathway that proceeds near the bottom right corner, but this pathway need not proceed through a metaphosphate intermediate. Indeed, there is now strong evidence against the formation of a metaphosphate intermediate in phosphate monoester hydrolysis (26–33). Most simply, stereochemical studies demonstrate that hydrolysis proceeds with complete inversion of configuration (26, 27). This result rules out the presence of a long-lived, freely diffusing metaphosphate intermediate, because water could attack a free metaphosphate from either side to produce a racemic mixture of products (for a discussion of some specific types of reactions where racemization is observed, see Supplemental Section B). However, metaphosphate could still form, but not be long-lived enough to diffuse and racemize; such reactions are sometimes referred to as preassociation stepwise (34). Strong evidence against even transient formation of a metaphosphate intermediate came later from LFERs demonstrating that phosphoryl-transfer reactions are sensitive to the strength of a series of amine nucleophiles (28–32). The key feature of these experiments was the use of a broad range of nucleophile strengths such that a change in the rate-limiting step would have been detected if an intermediate occurred along the reaction pathway (29–32). Corresponding, although not identical, logic was subsequently applied to reactions of oxygen nucleophiles, including water, strongly suggesting that metaphosphate is not an intermediate in phosphate monoester dianion hydrolysis (33). Similarly, LFERs, stereochemical studies, and KIEs suggest that hydrolysis of phosphate monoester monoanions (Figure 2b) proceeds through a loose transition state and provide no indication of formation of a metaphosphate intermediate (20, 26, 35, 36). The interested reader should consult the original references after having read the following sections, which introduce the key concepts for understanding these LFER experiments.

As for monoesters, experimental data suggest that phosphate diesters and triesters (Figure 1) generally react through concerted processes (37, 38), although there are notable exceptions where stable phosphorane intermediates have been observed (discussed further in Supplemental Section B). The ability to compare reactivity trends among phosphate monoesters, diesters, and triesters has provided an important perspective for interpreting experimental data about transition-state properties. The experimental evidence supports monoester reactions proceeding through loose transition states, and the transition states tend toward increasing tightness from monoester to diester to triester. The next sections explain how experimental methods can allow us to infer properties of the transition state and indirectly assess the extent of bond cleavage and bond formation. Because enzymatic rate enhancements arise from preferential stabilization of the transition state relative to the ground state (12–14, 39), characterizing the structure of the transition state is a critical step toward understanding how enzymes produce their enormous rate enhancements.

TRANSITION STATES FOR PHOSPHORYL TRANSFER

No experimental methods yet exist for directly visualizing transition states for phosphoryl-transfer or other reactions in solution. However, kinetic data can provide indirect but powerful information about transition states, and systematic variation of reactants and conditions can allow more incisive feedback about the properties of the transition state. Here we review fundamental experimental approaches for characterizing phosphoryl-transfer reactions, emphasizing both the information obtained and the limitations of each approach.

Linear Free Energy Relationships

Analyses of substituent effects have been an essential part of the development of our modern understanding of organic reactivity (15, 40–43). By systematically altering the structure of a molecule and measuring the resulting effects on reaction rates and equilibria, one can characterize the transition states for chemical reactions. The idea is simple and intuitive: If a bond is broken or formed in the transition state, there will be a change in electron density and charge at that position in the progression from reactants to the transition state. Adding electron-withdrawing groups stabilizes developing negative charge and destabilizes developing positive charge, whereas adding electron-donating groups has the opposite effect (40, 42).

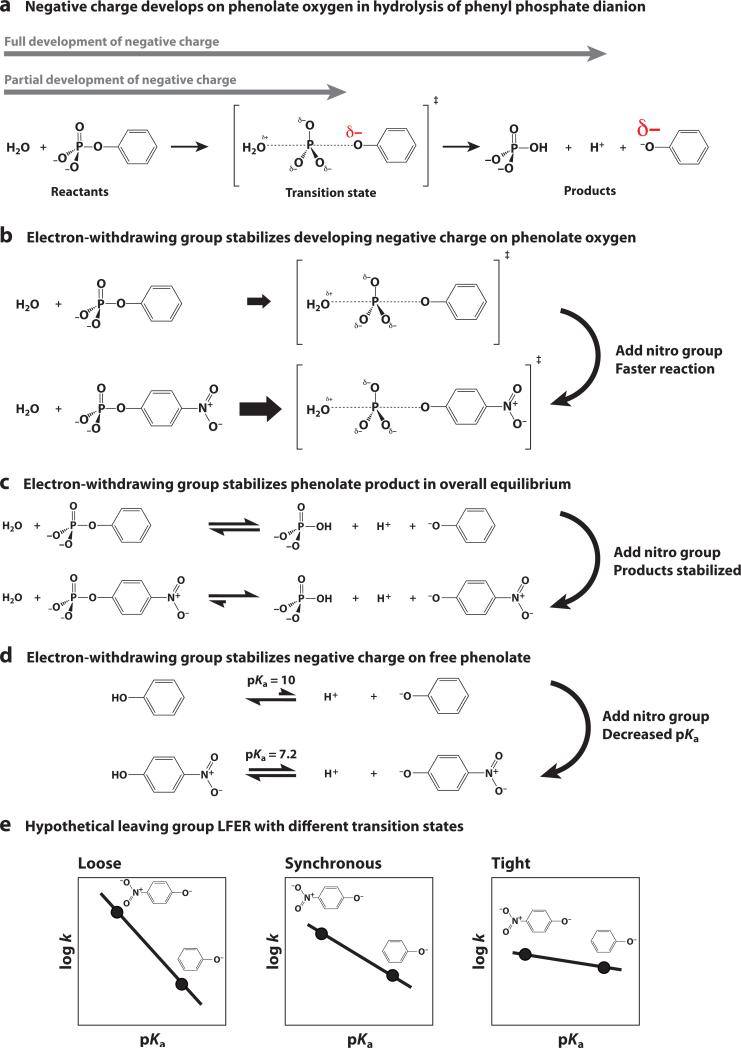
This concept is illustrated in Figure 4 with the phenolate leaving group of phenyl phosphate as an example. In the hydrolysis reaction of phenyl phosphate dianion, the P-O bond to the phenolate leaving group is broken, yielding a phenolate with a net charge of –1. In the transition state when the P-O bond is partially cleaved, charge has developed on the phenolate oxygen atom, but to a lesser extent than in the phenolate product (Figure 4a). The extent of charge buildup in the transition state relative to the products corresponds to the extent of bond cleavage in the transition state. To assess charge buildup in the transition state, electron-withdrawing and electron-donating groups are added to the leaving group. For example, adding a nitro group to the pheno-late leaving group withdraws electron density, stabilizing the charge development in the transition state and increasing the hydrolysis rate constant (Figure 4b). The degree to which the nitro group increases the rate constant depends on how much negative charge develops in the transition state of the reaction. In a loose transition state with extensive bond cleavage to the leaving group, there is a lot of charge development so electron-withdrawing groups give large rate increases. In contrast, in a very tight transition state with little bond cleavage to the leaving group, electron-withdrawing groups will have little or no effect on the reaction rate.

Figure 4.

Substituent effects can provide information about charge development in the transition state. (a) In the complete hydrolysis reaction of phenyl phosphate, the P-O bond to the leaving-group oxygen is fully broken, and negative charge develops on the phenolate oxygen. In the transition state, the P-O bond is partially broken, and negative charge partially accumulates on the phenolate oxygen. (b) Adding an electron-withdrawing p-nitro group distributes electron density away from the leaving-group oxygen in the transition state, making the partial cleavage of the P-O bond more favorable and thereby increasing the reaction rate. (c,d ) Adding a p-nitro group also withdraws electron density in the free phenolate, shifting the overall equilibrium toward products and reducing the affinity for a proton. This results in a reduced pK_a value. (e) Hypothetical linear free energy relationships (LFERs) for a series of leaving groups of differing pK_a values.

What does it mean to say that electron-withdrawing groups give large or small rate increases for reactions involving extensive or minimal bond cleavage? To quantitatively interpret the significance of an observed rate effect, it is also necessary to measure the effect on the overall equilibrium for the reaction, as this effect sets the scale for how the substituent stabilizes complete charge buildup on the leaving group (43, 44). These comparisons are performed using logarithms, which provide a common scale that is directly proportional to changes in free energy.² In the case of phenyl phosphate hydrolysis, adding an electron-withdrawing group stabilizes negative charge on the phenolate product, shifting the overall equilibrium toward the products (Figure 4c). If the resulting effects on log(k) and log(K_EQ) were the same, it would suggest that the charge development in the transition state is similar to that in the products (Figure 4a), implying that the P-O bond is nearly or fully broken in the transition state. Changes in log(k) that are small (or zero) relative to changes in log(K_EQ) suggest that the P-O bond remains mostly (or fully) intact in the transition state. The correlation between log(k) and log(K_EQ) is an example of a LFER and the slope of this LFER reflects the extent of charge buildup and bond cleavage (or formation) in the transition state.

In practice, LFERs are typically reported as plots of log(k) versus pK_a and log(K_EQ) versus pK_a rather than log(k) versus log(K_EQ), where the pK_a is that for the nucleophile or leaving group in the reaction of interest. The slopes of these so-called Brønsted plots are referred to as β_NUC for a series of rate constants with different nucleophiles, β_LG for a series of rate constants with different leaving groups, and β_EQ for comparisons of log(K_EQ) versus pK_a. The pK_a, which is also a logarithmic quantity, provides a convenient standard reference scale with which to quantify the effects of electron-withdrawing and electron-donating groups. In the phenolate example, the electron-withdrawing effect of the nitro group decreases the affinity of the substituted phenolate for a proton, reducing its pK_a value (Figure 4d). If there is substantial charge development in the transition state, as in a loose transition state, the nitro group has a large effect on rate constants relative to pK_a and the β_LG slope is steep (Figure 4e). In contrast, a tight transition state will have little charge development relative to pK_a and a resulting shallow β_LG slope. In nucleophile LFERs, a loose transition state in which the nucleophile develops a small amount of positive charge has a small, positive β_NUC value. A tight transition state develops greater positive charge, and thus a larger, positive value of β_NUC is expected.

Comparisons to pK_a values provide a useful reference for charge development because, similarly to the overall equilibrium for bond cleavage, the deprotonation equilibrium involves the development of a full –1 charge on the phenolate and because pK_a values are particularly convenient to measure. In contrast, K_EQ values are difficult to obtain, especially for reactions where one side of the equilibrium is strongly favored. Nevertheless, there is a drawback to using pK_a as a proxy for log(K_EQ).

Changes in log(K_EQ) calibrate the scale for complete bond cleavage (or formation) in the reaction of interest, but changes in pK_a report on a different reaction, i.e., deprotonation. The substituent effects can be different for deprotonation and the reaction of interest (i.e., |β_EQ| ≠ 1) (43), which makes values of β_NUC and β_LG less straightforward to interpret in terms of the extent of bond cleavage. This problem can be remedied by obtaining the ratio β_LG/β_EQ (or β_NUC/β_EQ), which corresponds to the slope of the plot of log(k) versus log(K_EQ). This value is sometimes referred to as the Leffler α parameter (40, 43, 44). This approach is convenient when direct measurement of K_EQ is challenging but an estimate of β_EQ is available, usually from a set of different but structurally related compounds. Another conceptual framework useful for interpreting β values is effective charge, which is discussed in Supplemental Section C (40, 43).

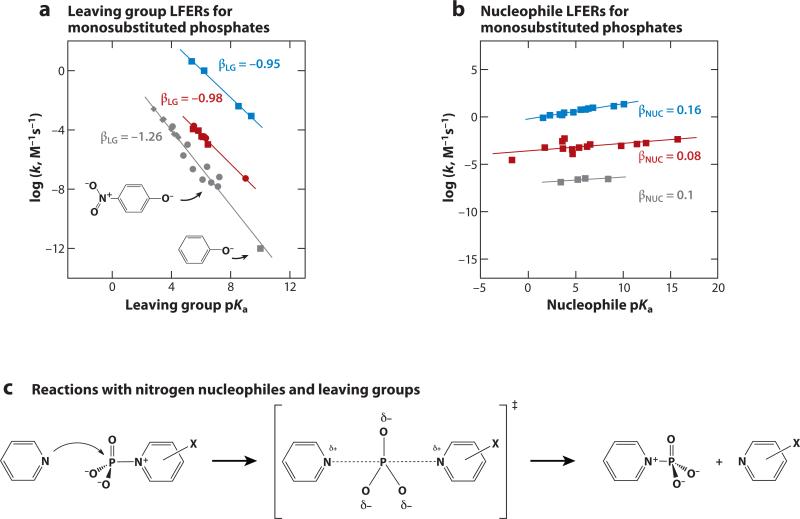
In Figure 5a,b, experimental LFERs are plotted for reactions of monosubstituted phosphoryl compounds (19, 20, 28, 31–33, 45–47) (see Supplemental Section D for additional data sets). For the hydrolysis reactions of phosphate esters, there is a large sensitivity to leaving group pK_a (β_LG = –1.26) (Figure 5a). Using a value for β_EQ of –1.35 that has been estimated for hydrolysis reactions of monoesters with oxygen leaving groups (48), we can estimate the fraction of total charge development on the leaving group in the transition state as |β_LG/β_EQ| = 0.93, suggesting that a large amount of bond breakage to the leaving group has already occurred in the transition state.

Figure 5.

Interpreting observed linear free energy relationships (LFERs). (a) Observed β_LG LFERs. In gray: substituted phosphate monoester dianions reacting with water [diamonds indicate benzoyl leaving groups (19); circles (20) and square (45) are phenolate leaving groups]. Points are indicated for phenyl phosphate and p-nitrophenyl phosphate. In red: hydrolysis reactions of phosphorylated pyridines [squares (31) and circles (33)]. In blue: morpholine nucleophile reacting with phosphorylated pyridines (47). (b) Observed β_NUC LFERs. In gray: amine nucleophiles reacting with p-nitrophenyl phosphate (28). In red: oxygen nucleophiles with phosphorylated 4-methyl pyridine (46). In blue: amine nucleophiles with phosphorylated 3-methoxypyridine (32). (c) Pyridine nucleophiles and leaving groups do not have transferrable protons and show the same trends as for oxygen nucleophiles (panels a and b).

To conclude that the transition states for these reactions are loose, we must also consider bond formation, as extensive bond cleavage to the leaving group could also be observed for a late transition state with substantial bond formation to the incoming nucleophile. To evaluate both β_NUC and β_LG, we turn to nitrogen nucleophiles and leaving groups (Figure 5c), as more complete data are available for these reactions. Here β_LG = –0.95 for reaction of morpholine with phosphorylated pyridines (47), β_NUC = 0.16 for reaction of pyridines with 3-methoxypyridine (32), and β_EQ has been estimated to be 1.05 (Figure 5a,b) (32). These values correspond to estimated charge changes of |β_LG/β_EQ = 0.90 and |β_NUC/β_EQ| = 0.15, suggesting extensive bond cleavage to the leaving group and little bond formation to the nucleophile, i.e., a loose transition state in the lower right corner of the two-dimensional reaction coordinate diagram (Figure 3c).

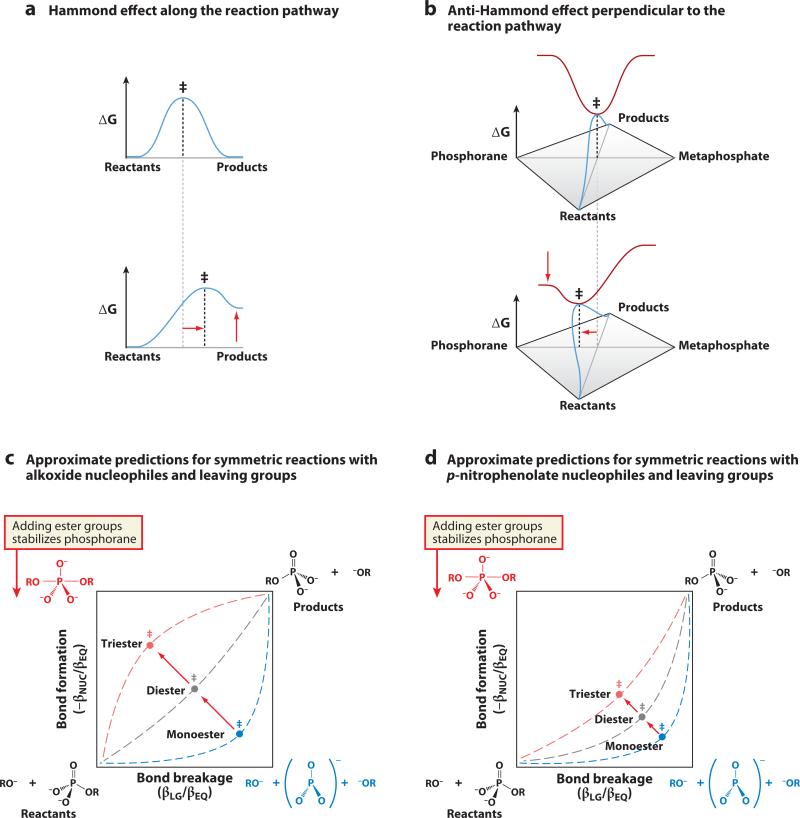
The two-dimensional reaction coordinate diagram can also be used as a conceptual tool to understand how changes in structure can change the transition state. Following is an abbreviated discussion; the reader is referred to Supplemental Section C and the original literature for more detailed treatments (44, 49, 50). According to the Hammond postulate, two states along a reaction coordinate that are close in free energy will have similar structures (44, 51). Consequently, perturbations that raise the energy of either the reactants or products result in a shift of the transition state toward the higher-energy species (Figure 6a). This logic holds along the pathway from reactants to products, where the transition state is a maximum in free energy. Perturbations that are not along the reaction path, such as those that raise the energy of either the phosphorane or metaphosphate intermediate species, have different consequences. Because the transition state represents a minimum in free energy along the direction perpendicular to the reaction pathway (e.g., along the line between the phosphorane and metaphosphate intermediate corners in Figures 3c and 6c), the transition state shifts in the direction of the stabilized species. This is sometimes referred to as an anti-Hammond effect (Figure 6b) (50).

Figure 6.

Changes in structure can alter the nature of the transition state. (a) Along the reaction pathway, the transition state is at a maximum in free energy. When the equilibrium between reactants and products changes, the transition state moves toward the species that has increased in energy. (b) Perpendicular to the reaction pathway, the transition state is at a minimum in free energy. When the equilibrium between the phosphorane and metaphosphate species changes, the transition state moves toward the species that has decreased in energy. (c) A two-dimensional reaction coordinate diagram for symmetric phosphoryl-transfer reactions with alkyl nucleophiles and leaving groups, with approximate predicted changes in transition-state structure as ester substituents are added to the phosphoryl group and the energy of the phosphorane corner decreases. (d) Similar approximate predictions for symmetric reactions with p-nitrophenolate nucleophiles and leaving groups. Whereas monoester reactions show little variability in transition state, triesters show considerable variability (as discussed further in Supplemental Section C).

Using this logic for how the transition-state structure changes in response to perturbations in the reaction free energy surface, it is possible to assess crudely the effect of adding additional substituents in the progression from monoesters to diesters to triesters. Figure 6c shows a two-dimensional reaction coordinate diagram for symmetric phosphoryl-transfer reactions with alkoxide nucleophiles and leaving groups. To a first approximation, adding an ester substituent to the phosphoryl group has no differential energetic effect on the reactants and products (especially in a symmetrical reaction where the nucleophile and leaving group are the same), so the transition state does not shift along the reaction pathway. In the direction perpendicular to the reaction pathway, the phosphorane corner has significant charge buildup on the phosphoryl group, and adding an ester substituent that withdraws electrons is expected to stabilize the phosphorane corner relative to the metaphosphate corner. Thus, adding ester groups is predicted to have anti-Hammond effects on the transition state (Figure 6b), leading to a progression from loose to tighter transition states for monoesters, diesters, and triesters (Figure 6c).

The currently available LFER data for monoester, diester, and triester reactions are generally consistent with this expectation. Indeed, the approximate positions of the transition states in Figure 6c are predicted from analyses of almost 100 LFERs reported in the literature (see Supplemental Sections C and D). Remarkably, despite this large number of LFERs, there remain many gaps in the data and, correspondingly, in our understanding. Information is particularly limited for symmetric reactions, which provide the simplest comparisons between these reactions and their transition states. Still, the available data provide a consistent picture and make strong predictions about reactions that have not yet been tested.

Interestingly, phosphate monoesters show limited variability in transition-state properties, based on the available data, whereas the variability is considerable for phosphate triesters. Panels c and d of Figure 6 depict approximate predicted transition-state positions for symmetric reactions with alkoxides and with p-nitrophenolate, respectively. For these two types of reactions, which differ in the pK_a of the nucleophile and leaving group, the position of the monoester transition state is similar—a loose transition state in the lower right corner. In contrast, triester reactions show greater variability in transition-state properties with pK_a. The available data suggest a range of possible transition states for triesters from loose to tight. In all cases, the direction of change is as predicted from consideration of Hammond and anti-Hammond effects in two-dimensional reaction coordinate diagrams; however, the size of the change differs greatly. The simplest expectation for this difference would be a shallower energy surface for triesters, but the data remain limited. Many challenges remain to obtain more systematic LFERs and to understand the origins of these different behaviors. Supplemental Section C contains additional discussion.

An important potential limitation of LFERs is that alternative mechanisms and changes to the energetic landscape can complicate the interpretation of LFERs. Indeed, the extreme view that LFERs cannot be used to evaluate reaction mechanisms has been put forth in the literature (52–54). This argument has been advanced in two ways. First, it has been suggested that proton transfers among the nucleophile, the phosphoryl oxygen atoms, and the leaving group could obscure meaningful trends related to transition-state properties (52). Although this complication can arise in some reactions, this potential problem has been eliminated in many of the fundamental studies of phosphoryl transfer through use of nitrogen nucleophiles and leaving groups such as pyridines that have no transferable protons (Figure 5) (see Supplemental Section D). The transition states characterized for these monosubstituted phosphoryl compounds are essentially indistinguishable from those for reactions of phosphate monoesters with other nitrogen and with oxygen nucleophiles. These similarities suggest an analogous mechanism for all these reactions. Finally, oxygen nucleophiles both with and without potentially transferable protons follow a single LFER with only minor deviations, providing strong evidence against intervention and complication from proton transfers in these reactions (33). For enzymatic reactions there is also evidence against this class of mechanism, termed substrate-assisted catalysis, as discussed below in Enzymatic Phosphoryl Transfer.

A second challenge to the interpretation of LFERs is based on the suggestion that transition states change with substituent pK_a (53, 54). However, this point has been covered extensively in the development and theory of LFERs (40, 49, 50, and references therein), and the experiments themselves address the question of changes in transition state with pK_a (discussed further in Supplemental Section C). Within a single LFER, curvature indicates changes in transition-state bonding over the range of compounds used to construct the LFER. Similarly, changes in the slope across a series of LFERs (e.g., a set of β_LG values obtained with different nucleophiles) suggest changes in transition-state bonding, and a constant slope suggests similar transition-state bonding. As discussed above, the data for phosphate monoesters indicate only small changes in transition-state structure with different nucleophile and leaving-group pK_a values (33). In contrast, LFERs for triesters indicate changes in the nature of the transition state with different substituent pK_a values (37, 38, 55). In both cases, the directions of the changes can be understood simply in terms of perturbations to the energy surface in a two-dimensional reaction coordinate diagram (37, 55). Thus, the LFER data, although not complete, are consistently and robustly accounted for by the current and longstanding models described above. Nevertheless, it is important to recognize that LFER data do not directly supply information about bond lengths and charges in the transition state, but rather provide empirical correlations from which transition states are inferred. More research is needed to fully understand these and other empirical relationships.

Kinetic Isotope Effects

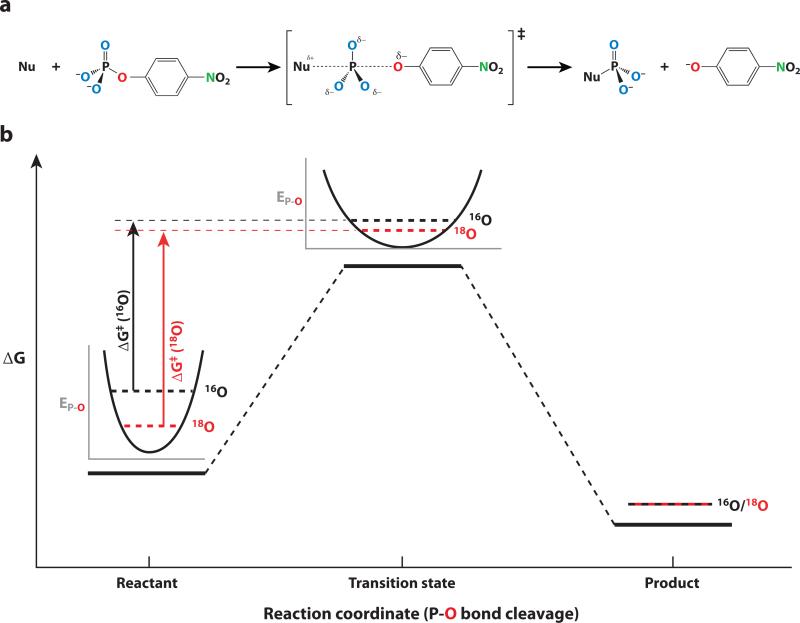
KIEs report on changes in bonding that occur in the transition state by measuring changes in reaction rates that occur when an atom in the compound of interest is substituted with a heavy isotope (Figure 7). How does isotopic substitution alter reaction rates, and how do these changes report on properties of the transition state? According to quantum mechanics, every bond has a characteristic minimum vibrational energy state, termed the zero-point energy, which depends on the strength of the bond and the masses of the atoms involved in the bond; increasing mass decreases the zero-point energy. When a bond is broken, the vibrational energy states for that bond are lost so there is no longer a difference in vibrational energy between the heavy and light isotopes. Thus, there is a larger energy barrier for cleavage of a heavy-atom substituted bond and the reaction is correspondingly slower; this leads to a “normal” KIE (k_light/k_heavy > 1) (56, 57). For bonds that are partially broken in the transition state, the difference in vibrational zero-point energy between the heavy and light isotopes decreases relative to that in the ground state, and the magnitude of the KIE corresponds to the extent of bond cleavage in the transition state (Figure 7b). In cases where bonding increases at the substituted position, for example as a result of protonation, an inverse isotope effect can be observed (k_light/k_heavy < 1). KIEs resulting from isotopic substitutions at positions of bond cleavage or formation are termed primary isotope effects.

Figure 7.

Kinetic isotope effects (KIEs) report on changes in bonding in the transition state. (a) Sites of isotopic substitution in the phosphate monoester p-nitrophenyl phosphate (pNPP) are shown in color. KIEs can be measured for multiple sites within a molecule, including the bridging oxygen at the position of bond cleavage (red ) and the nonbridging oxygen atoms of the phosphoryl group (blue). The presence of a nitrogen atom (green) in pNPP allows KIEs to be measured with the remote label method (56), as it is technically easier to measure ¹⁵N/¹⁴N than ¹⁸O/¹⁶O ratios. Recently, however, some KIEs have been determined by direct measurement of ¹⁸O/¹⁶O ratios (10, 63, 101). (b) Heavy-isotope substitution at the position of bond cleavage (red, bridging oxygen atom) slows the reaction because the difference in zero-point vibrational energy is larger in the ground state than in the transition state, leading to a larger activation barrier for the heavy-isotope-substituted molecule (56, 57). The broader vibrational potential well at the transition state reflects the weaker state of the partially broken bond.

KIEs can also be observed for isotopic substitution at positions that are not directly involved in bond cleavage or formation (i.e., secondary isotope effects). In general, bond vibrational states include stretching, bending, and torsional modes. For primary isotope effects, the dominant vibrational contribution typically comes from loss (or gain) of a stretching mode involving the groups in the bond being broken or formed. In contrast, secondary isotope effects frequently arise from changes in geometry, which can have significant effects on bending and torsional vibrational modes. For example, deuterium substitution in S_N2 displacement reactions at carbon leads to small, normal secondary KIEs due to a weaker bending mode in the trigonal planar transition-state geometry relative to the tetrahedral ground state (57). Similar geometrical changes occur for the nonbridging oxygen atoms during phosphoryl-transfer reactions. Unlike deuterium, however, the nonbridging oxygen atoms can also undergo increased or decreased bonding to the central phosphorus atom in the transition state, leading to changes in stretching vibrational modes. Thus, predicting the dominant contribution to the KIE is not straightforward. Nevertheless, trends in these KIEs can still be informative, and we hope these values can be understood more fully in the future.

Because isotope substitution is minimally invasive and can be made at multiple positions in a phosphoryl compound (Figure 7a), this approach would appear to be a powerful method to obtain information about transition states. In practice, the compounds needed are not trivial to make and the analysis requires high-precision measurements with sophisticated equipment (56). Notwithstanding these challenges, there is a large body of KIE data for phosphoryl-transfer reactions in the literature that provides a consistent picture of phosphoryl-transfer transition states. This picture complements information obtained from LFER studies.

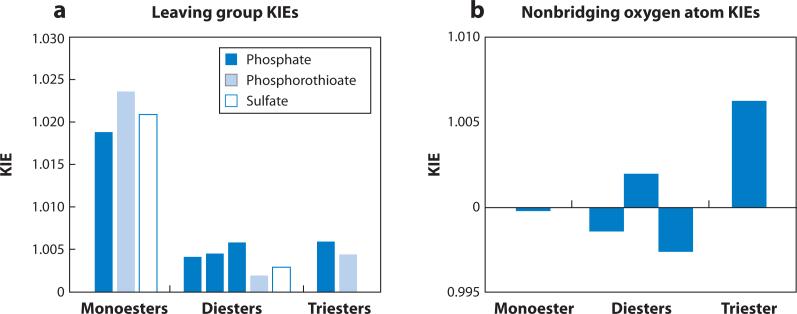
Figure 8 shows the KIEs for hydrolysis reactions of phosphate monoesters, diesters, and triesters with p-nitrophenyl leaving groups. For comparison, leaving-group KIEs for phosphorothioate and sulfate esters are also included, because these compounds display similar behaviors as their phosphate ester counterparts. Leaving-group KIEs for monoesters are large and normal, consistent with a loose transition state with significant bond cleavage to the leaving group (Figure 8a). The KIEs for diesters and triesters are significantly smaller, suggesting tighter transition states for these compounds. Nonbridging oxygen atom KIEs also exhibit a trend from monoester to triester; values for monoesters are small, whereas those for triesters are significantly larger (Figure 8b). This increase in the nonbridging KIE may arise because increasing nucleophilic participation in a tighter transition state leads to weakening of the P-O_nonbridge bond. Taken together, the KIEs suggest a trend from loose to tight transition states for phosphate monoesters, diesters, and triesters. Although the data are limited, leaving-group KIEs for triesters vary significantly with the identity of the leaving group (58, 59), consistent with the larger body of LFER data suggesting that the transition states for triester reactions are highly variable. A detailed compilation of LFER and KIE data for phosphoryl-transfer reactions supporting these general conclusions is presented in Supplemental Sections C, D, and F.

Figure 8.

Kinetic isotope effects (KIEs) for nonenzymatic phosphoryl-transfer reactions with p-nitrophenyl leaving groups (35, 59, 163–166) (includes one unpublished value from E.A. Tanifum & A.C. Hengge). Complete data tables and corresponding references are presented in the Supplemental Section F. The reactions shown are for the fully ionized species (i.e., phosphate monoester dianions and sulfate monoester monoanions, rather than the corresponding protonated forms). (a) Leaving-group KIEs (¹⁸k_bridge) for monoester hydrolysis are large, suggesting extensive bond cleavage to the leaving group in the transition state. Values of ¹⁸k_bridge are significantly smaller for diesters and triesters. Phosphorothioate and sulfate esters exhibit similar trends in their leaving-group KIEs. (b) The nonbridging oxygen atom KIE (¹⁸k_nonbridge, per oxygen atom) for phosphate monoester hydrolysis is close to unity, whereas that for triester hydrolysis is large and normal. Values for diester hydrolysis are more variable. Phosphorothioate esters are not included because the presence of sulfur at the nonbridging position significantly perturbs ¹⁸k_nonbridge (see Supplemental Section F), and sulfate esters are omitted because ¹⁸k_nonbridge is available for only a single sulfate monoester.

Because isotope effects are sensitive to changes in both bond lengths and geometry, and more generally to any changes in the vibrational environment of the labeled position (57), KIEs can be challenging to interpret in complex environments. This challenge is particularly acute in the active site of an enzyme, where protonation, metal ion interactions, and interactions with other enzyme functional groups can contribute to observed isotope effects (56, 60–63). KIEs for representative enzyme-catalyzed reactions are provided in Supplemental Section F.

Other Tools

Measurements of volumes and entropies of activation have been consistent with the trends from LFER and KIE data, suggesting loose transition states for monoesters and tighter transition states for diesters and triesters. However, a serious concern in interpreting these data is the difficulty of isolating changes in volume or entropy of the reacting system from changes due to interactions with the solvent. We present and discuss these data in Supplemental Section G.

Thio-substitution experiments have been an important tool in studying phosphoryl transfer. Substitution of a sulfur atom for an oxygen atom of a phosphate ester leads to perturbation in pK_a values, bond lengths, van der Waals radii, polarizability, and electrostatics of the resulting compound, providing valuable mechanistic comparisons in catalyzed reactions (64–67). For example, catalytic metal interactions in enzymes can be probed with “metal ion rescue” experiments, in which loss in activity upon thio-substitution can be reversed through use of thiophilic metal ions (68–72). “Sulfur rescue” experiments, in which deleterious mutations are rescued by the lowered pK_a values of thio-substituted substrates, can help to identify general acid catalysis (67, 73, 74). Thio-substitution at prochiral oxygen positions can help to identify the stereochemical course of reactions, and within the context of an active site, rate effects due to steric differences upon thio-substitution can provide probes for active-site interactions and geometry (75–78). An understanding of the nonenzymatic reactivities and properties of thio-substituted compounds, also called phosphorothioates (with nonbridging sulfur atom) and phosphorothiolates (with bridging sulfur atom), provides a foundation for these and other experiments.

Nonenzymatic reactions have been characterized for a number of thio-substituted compounds and LFER and KIE data have been collected (see Supplemental Sections E and F for data sets and references). As with phosphate esters, these results are consistent with loose transition states for monoesters and progressively tighter transition states for diesters and triesters. However, in contrast to phosphate monoesters, which proceed through concerted reactions and do not form stable metaphosphate intermediates, thiometaphosphate intermediates have been reported in some reactions of phosphorothioates (79–81). This change can be understood in the context of a two-dimensional reaction coordinate diagram, in which sulfur substitution stabilizes the metaphosphate corner sufficiently to allow formation of a metaphosphate intermediate (Figure 6). The similarity in LFER trends for phosphorothioate and phosphate monoesters, diesters, and triesters, in combination with the observation of freely dissociated thiometaphosphate, provides further support for a loose, metaphosphate-like transition state for phosphate monoester hydrolysis.

Overview of Nonenzymatic Data

The trends among all the data provide a consistent picture of the nature of the transition state for phosphate monoesters, diesters, and triesters. Monoesters appear to progress through loose transition states, diesters through more synchronous transition states, and triesters through tighter transition states. In addition, there is more variation in the nature of the transition state for triesters than for monoesters in response to variation of the pK_a values and reactivities of the attacking and leaving groups. This picture has not been challenged by new experimental observations over several decades, yet each individual experiment is subject to uncertainties and the models must be continuously evaluated with respect to new data. Although computational methods fall outside of the scope of this review, these approaches offer promise in more directly relating LFER and KIE data to transition-state structures and charge distributions. To establish confidence in the theoretical models, systematic and comprehensive experimental data sets will be needed to serve as benchmarks, and computational approaches will need to be critically assessed through robust and nontrivial predictions of previously unmeasured values.

ENZYMATIC PHOSPHORYL TRANSFER

Phosphoryl-transfer reactions can be exceptionally slow in solution (45, 82, 83), and enzymes that catalyze these reactions can have tremendous rate accelerations. For example, the first-order rate constant for attack on methyl phosphate dianion by water is less than 10^–20 s^–1—a half-life of more than one trillion years (45). Alkaline phosphatase catalyzes this hydrolysis with a second-order rate constant (k_cat/K_M) of 1.2 × 10⁶ M^–1s^–1 (84), giving a rate acceleration of more than 10²⁷-fold!³

How do enzymes achieve these large rate accelerations relative to the solution reactions? An understanding of the transition states for nonenzymatic reactions in solution can provide insight into possible strategies for enzymatic catalysis and can guide investigations of new enzymatic systems and catalytic mechanisms. In this section, we provide an overview of strategies that enzymes could employ in catalyzing phosphoryl-transfer reactions from the perspective of the nonenzymatic transition state, with an emphasis on monoesters. Earlier works have reviewed possible catalytic strategies for phosphoryl transfer (e.g., 1, 85–88), and we offer an updated perspective here, informed both by our perspective on nonenzymatic reactions and by more recent work that sheds new light on these strategies. Rather than covering specific enzyme classes and families, we refer the reader to other reviews (4–6, 89–93); we also present three enzyme case studies in the sidebars and Supplemental Text that further illustrate specific mechanistic concepts.

Activation of the Nucleophile

Three general means of nucleophilic activation have been proposed for reactions of phosphate monoesters: positioning of the nucleophile, increasing nucleophilicity, and overcoming electrostatic repulsion. The current data, as outlined below, suggest that only positioning can provide substantial catalysis in reactions proceeding via loose transition states, whereas increasing the nucleophilicity through varying the identity of the nucleophile, metal ion catalysis, or general base catalysis can contribute significantly for tighter transition states as in diesters and triesters.

Positioning

The most general hallmark of enzymes is their ability to use binding interactions and positioned groups within the folded enzyme to facilitate catalysis. This ability directly links catalysis to specificity, as is required in biology (94). The ability to attain enormous rate advantages from positioning was demonstrated in many early studies that compared inter- and intramolecular solution reactions and was explained by Page & Jencks (95), who demonstrated that such large effects could come from the removal of translational and rotational degrees of freedom upon fixing two reactants with respect to one another. Unfortunately, we still lack good estimates of how large such effects can be in enzymatic reactions (96).

In phosphoryl-transfer reactions, the nucleophile must be aligned with the phosphorus atom and the leaving group for in-line attack at phosphorus, and enzyme interactions could help to position the nucleophile in this reactive geometry. Empirical data for phosphoryl-transfer reactions suggest that positioning of the nucleophile can make a significant contribution to catalysis. This conclusion is based on exogenous rescue experiments in which the enzymatic His nucleophile of NDP kinase was replaced with noncovalently bound small-molecule nucleophiles. Comparisons between the covalent enzymatic nucleophile, noncovalently bound nucleophiles, and the nonenzymatic reaction suggest a ~10²-fold enhancement from positioning of the covalently bound enzymatic nucleophile (97). How does this observation relate to our expectation that the transition state for phosphate monoester hydrolysis has little nucleophilic participation? The simplest explanation is that even in a loose transition state there is some bond formation to the nucleophile, which requires positioning of the nucleophile with respect to the phosphoryl group. Translational entropy is lost when the two reactants no longer move independently of one another, regardless of whether the transition state is loose or tight, so a significant rate enhancement from prepositioning the reactants is possible.

Increasing the nucleophilicity

The reactivity of a nucleophile can be increased by a number of mechanisms, including removal of a proton by a general base, activation by a metal ion, or by changing the identity of the nucleophile.⁴ The potential catalytic contributions from general base catalysis or metal ion activation can be estimated using the LFER slope β_NUC, which describes the change in reaction rate as a function of nucleophile pK_a. Qualitatively, because β_NUC is small for reactions at monosubstituted phosphate centers (Figure 5), there is little advantage gained from changing the pK_a of the nucleophile through any of these routes. Quantitatively, we can calculate a maximum expected contribution using the shift in pK_a and the β_NUC value. The expected log increase in rate constant upon abstraction of a proton from a water (or similarly serine) nucleophile is the difference in pK_a between hydroxide (pK_a = 15.7) and water (pK_a = –1.7) times the β_NUC value. Thus, the increase in rate constant is estimated as

$$\Delta \left(\text{log}k\right)={\beta }_{\mathrm{NUC}}\cdot \Delta \mathrm{p}{K}_{\mathrm{a}}.$$

For monoester reactions with β_NUC = 0.1 (Figure 5), this relationship gives a value of 56-fold as the maximum rate increase, and for a hypothetical β_NUC = 0.2, a value of 3 × 10³-fold is obtained. The actual rate increase is expected to be substantially less, as concerted general base catalysis yields only partial deprotonation in the transition state and thus partial activation. There may be additional entropic barriers for having multiple simultaneous events of bond formation and proton transfer, further reducing the catalytic benefit for general base catalysis. Similar considerations apply to nucleophile activation by a metal ion. The estimated pK_a for the metal-bound alkoxide Ser-O^– · · · Zn²⁺ in the enzyme alkaline phosphatase is ~5.5 (99), giving a rate advantage of ~10-fold if β_NUC ~0.1–0.2.⁵ Overall, increasing nucleophilicity is not expected to provide a major catalytic contribution for monoester reactions with loose transition states. This point is illustrated further in the sidebar Ras GTPase: Is a General Base Necessary?

In contrast to the case for loose transition states, increasing the reactivity of the nucleophile through general base catalysis or metal ion coordination can provide larger catalytic contributions for reactions with tighter transition states. As an example, for diester reactions with β_NUC = 0.31, the above relationship gives a value for the maximum increase in rate constant of 3 × 10⁵, indicating that increasing nucleophilicity could provide a much larger contribution to catalysis for these tighter transition states, although again, general base catalysis would not be expected to capture this full value.

Overcoming electrostatic repulsion

Could an enzyme make phosphoryl transfer more favorable by reducing electrostatic repulsion between the nucleophile and the charged phosphoryl oxygen atoms? Westheimer, in his classic perspective “Why Nature Chose Phosphates” (3), suggested that this type of electrostatic repulsion accounts for the low nonenzymatic reactivity of phosphate compounds. Indeed, nonenzymatic phosphate monoester hydrolysis is extraordinarily slow relative to other biological reactions (45). But is electrostatic repulsion the culprit? The observation that no reaction of phosphate monoester dianions with hydroxide ion is observed above that with water, even at high hydroxide ion concentrations (20, 45), is consistent with the electrostatic repulsion model (100). However, an alternative explanation is provided by the small value of β_NUC for these reactions (Figure 5). As discussed above, with a β_NUC value of 0.1, the reactivity of hydroxide ion can be roughly estimated as 60-fold greater than that of water. But water is present in 55-fold greater amounts even relative to 1 M hydroxide ion at pH 14. Thus, the absence of an observable rate increase at high pH could primarily reflect the shallow dependence of the reaction rate on nucleophilicity and be unrelated to electrostatic repulsion.

A more direct experimental test of the electrostatic repulsion model comes from comparisons of the reactivity of neutral and negatively charged oxygen nucleophiles in reactions with negatively charged phosphate esters. These reactions all follow the same dependence on nucleophile pK_a, with no significant deviations between neutral and negatively charged nucleophiles (33). Similarly, there are no deviations between charged and uncharged nucleophiles when the rate constants for phosphate ester hydrolysis are compared with those for corresponding reactions with uncharged esters (46). Finally, increasing the ionic strength, which would screen and thereby diminish electrostatic repulsion, has only small effects on reaction rates; anionic nucleophiles react ~5-fold faster, whereas reactions of neutral nucleophiles are not significantly affected (46, 101). These results suggest that electrostatic repulsion between anionic nucleophiles and negatively charged phosphate esters (relative to uncharged esters) is not extensive.

If the relatively slow reactions of phosphate esters are not a consequence of electrostatic repulsion between nucleophiles and negatively charged phosphoryl groups, then mitigating electrostatic repulsion would not be a major contributor to enzymatic catalysis of these reactions. However, further study of highly charged phosphate esters such as nucleoside triphosphates is warranted to further explore this issue. For example, it has been suggested from structural data that enzymes can bind ATP with the phosphoryl oxygen atoms in an eclipsed conformation, introducing steric or electrostatic repulsion that may destabilize the bound substrate and thereby lower the reaction barrier (102, 103).

Stabilization of the Leaving Group

In contrast to the situation for the nucleophile discussed above, the leaving group develops substantial negative charge in the loose transition state relative to the ground state for phosphate monoester dianion reactions (Figure 3b). Consequently, stabilization of the developing negative charge on the leaving group can contribute significantly to catalysis of monoester reactions.

Similarly to the calculation above for nucleophilic activation, we can calculate a rough maximum rate advantage for protonating an alcohol-type leaving group such as glucose or ethanol using the difference in pK_a and the β_LG value with the following expression:

$$\Delta \left(\text{log}k\right)={\beta }_{\mathrm{LG}}\cdot \Delta \mathrm{p}{K}_{\mathrm{a}}.$$

The maximum value of ΔpK_a is the difference between the pK_a of a fully protonated leaving group (pK_a ~ –2 for protonation of water or an alcohol) and that for an alkoxide leaving group (pK_a ~ 16 for protonation of hydroxide and simple alkoxides) (104). Using a value of pK_a of 18 and the β_LG value of –1.26 (Figure 5) gives an enormous maximum estimated rate advantage of >10²⁰-fold. We emphasize that the actual expected catalytic effect will be much less. As noted above for general base catalysis, the proton will be partially rather than fully transferred in the transition state and there are entropic-like barriers for having multiple simultaneous events of bond breaking and proton transfer. For phosphate diesters and triesters, the tighter transition states and correspondingly smaller values of β_LG lead to the prediction of smaller catalytic effects from a general acid, but large values of β_LG (~1) can still occur with a tight transition state when β_EQ is also large. In these cases, general acid catalysis can provide a significant advantage.

Interactions with the Phosphoryl Oxygen Atoms: Charge, Positioning, and Geometry

The phosphoryl group (PO₃^–) that is transferred from the leaving group to the nucleophile can undergo two types of changes from the ground state to the transition state: electrostatic and geometric. The literature has generally focused on electrostatic changes, but emerging data suggest that geometry may also be important.

Electrostatic changes

A hallmark of the active sites of phosphoryl-transfer enzymes is the presence of positively charged functional groups and metal ion cofactors in the active site (1, 4, 91). These positively charged groups are often positioned to interact with the nonbridging oxygen atoms of the transferred phosphoryl group. This observation has led to frequent suggestions in the literature that these positively charged groups lead to enzymatic transition states that are tighter than those of the corresponding nonenzymatic reactions (1, 28, 87, 91, 92, 102, 105–122). Most simply, coordination of the nonbridging oxygen atoms could make the substrate behave more like a diester or triester and thus proceed through a tighter transition state.

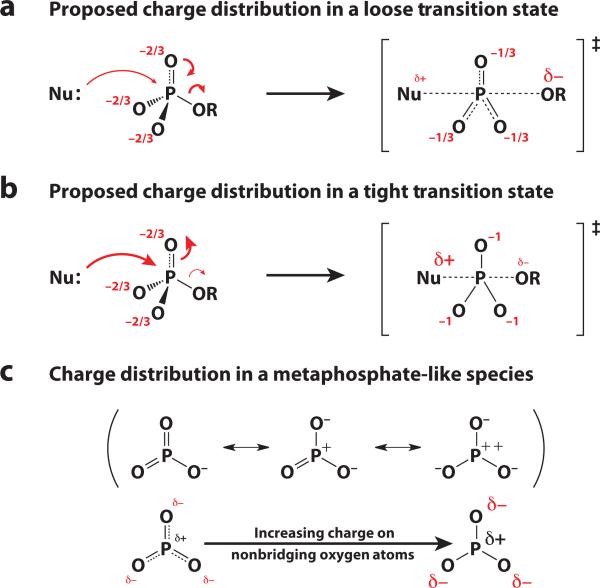
A physical model for the proposed tightening of the transition state comes from consideration of electrostatic changes in the phosphoryl group. In a loose transition state where bond cleavage to the leaving group is more advanced than bond formation to the nucleophile, there is a net loss of electrons in the phosphoryl group and the negative charge on the nonbridging oxygen atoms may decrease (Figure 9a). Indeed, to account for data suggesting extensive bond cleavage to the leaving group, early workers in the field suggested that negatively charged oxygen atoms provide the driving force to expel the leaving group (18). In contrast, in a tighter transition state, the net increase in bond order at phosphorus would be expected to lead to an increase in negative charge on the nonbridging phosphoryl oxygen atoms (Figure 9b). Thus, positively charged functional groups that are ubiquitous in phosphoryl-transfer enzyme active sites have been suggested to be better suited to stabilize the charge distribution in a tight transition state rather than a loose transition state similar to that in the nonenzymatic reaction. In terms of a two-dimensional reaction coordinate diagram, this proposal corresponds to an enzyme altering the energy surface relative to that in solution to move the transition state from the bottom right of the diagram toward the top left (Figure 6c, with positively charged functional groups behaving like additional ester substituents on the phosphoryl group).

Figure 9.

Charge distribution on the phosphoryl oxygen atoms in the transition state. Based on a simple arrow-pushing scheme, one might expect the charge on the nonbridging oxygen atoms to decrease in a loose transition state (a) and increase in a tight transition state (b) (the transition-state charges depicted are the extreme limits). However, the charge distribution for a metaphosphate-like species in a loose transition state is unknown. Three different resonance forms can be depicted with more or less charge on the nonbridging oxygen atoms (c).

Although this logic is intuitively appealing, it falls short on several counts. First, the charge distribution in a metaphosphate-like species in a loose transition state is not known, and there is no requirement that charge on the nonbridging oxygen atoms should decrease to compensate for leaving-group expulsion. Indeed, computational studies of metaphosphate in the gas phase suggest a charge distribution closer to the resonance forms on the right of Figure 9c, with significant negative charge density on the nonbridging oxygen atoms (123–125). Second, even if the charge on the nonbridging oxygen atoms does decrease in a loose transition state, positively charged functional groups in an enzyme active site may form stronger interactions in the transition state owing to changes in the geometry of the phosphoryl group that lead to better alignment of the interacting groups. This idea is discussed further in the sidebar Alkaline Phosphatase: Do Positively Charged Groups Tighten Transition States? Finally, the proposal that enzyme active sites alter the transition state from that in solution has an important unstated assumption: The energy surface surrounding the transition state must be sufficiently shallow such that the energetic benefit gained from enzyme interactions with a tighter transition state outweighs the energetic preference for a loose transition state. Empirical studies to date suggest that these interactions are insufficient to overcome the preference for a loose transition state for phosphate monoester reactions. No evidence for changes in transition-state structure has been observed upon Mg²⁺ and Ca²⁺ coordination in reactions of phosphate monoesters and anhydrides in solution, based on a lack of changes in LFER slopes, suggesting that these metal ion interactions are insufficient to alter transition-state structure (126, 127).⁶ Consideration of the p_xy coefficient (see Supplemental Section C) also suggests that monoester transition states may not be easy to change. Moreover, as experimental LFER and KIE data have begun to emerge for enzyme-catalyzed phosphate monoester reactions, changes in transition-state structure relative to solution have also not generally been observed (56, 62, 99, 133–146). Phosphoglucomutase provides an interesting example, discussed in the sidebar Phosphoglucomutase: Do Enzymes Change Mechanisms from Those in Solution?, of a case where enzymatic interactions were proposed to cause extreme tightening toward a phosphorane intermediate, but follow-up investigations suggested otherwise.

Thus, it appears unlikely that enzymes derive a catalytic advantage by shifting the energy surface toward a tighter transition state and concurrently stabilizing greater charge development on the nonbridging oxygen atoms in the transition state. Nevertheless, further investigation is in order. Most fundamentally, the charge distribution of the phosphoryl group in a loose transition state remains an open question. A challenge for the future is to develop experimental and computational tools that can confidently address this question.

The placement of active-site functional groups has also been suggested to determine the distance between entering and leaving groups in the transition state (92). This proposal makes assumptions about the nature of the energy surface for the reaction and how difficult it is to change the transition-state structure, and the structural data from X-ray crystallography and nuclear magnetic resonance provide information about ground states, not transition states. There is no indication that these distances can affect transition-state tightness.

Geometry and positioning

In nonenzymatic reactions, solvent must rearrange to accommodate reaction transition states. In contrast, enzymatic interactions are optimally positioned by the folded macromolecule for electrostatic and geometric complementarity with the transition state. These interactions include aspects discussed above such as stabilizing contacts to the leaving group. In addition, interactions between the nonbridging phosphoryl oxygen atoms and positively charged active-site groups can play important catalytic roles in positioning the phosphoryl substrate with respect to the attacking group and also in aligning the leaving group for stabilizing interactions. An open but intriguing question is whether the trigonal bipyramidal transition-state geometry can be recognized by the active site in preference to the tetrahedral ground state. For phosphate monoesters, the position and orientation of the nonbridging oxygen atoms changes in the progression from ground state to transition state (Figure 3), and for diesters preferential interactions could also be made with the substituent attached to the transferred phosphoryl group. This model implies that active-site interactions are suboptimal in the ground state owing to conformational constraints and more favorable in the transition-state geometry. Thus, even with no increase in negative charge on the nonbridging oxygen atoms, hydrogen bonding and electrostatic interactions with these atoms could potentially become stronger in the transition state as the nonbridging oxygen atoms reorient. Indeed, recent data support the possibility that enzymes can recognize small geometrical changes on the scale of a few tenths of an Ångstrom (see Reference 147). Advancing our understanding of enzyme rigidity, positioning, and dynamics is an important future challenge for phosphoryl transfer and other enzymes (96).

Determining the bond distances in phosphoryl-transfer transition states and trajectories of reaction pathways represent additional important challenges. What are the bond distances in loose or tight transition states, and do positioning interactions that place the reactants in close proximity lead to tighter transition states? For example, it has been suggested that the transition state can be loose even if the nucleophile is initially positioned in van der Waals contact with the phosphate ester (5, 8).

Challenges for the Future

We can currently identify elements of enzymatic systems that contribute to catalysis of phosphoryl transfer, but ultimately we hope to develop a quantitative, predictive understanding of the structural origins of catalysis. One major challenge for achieving that goal is in relating the empirical correlations provided by KIEs and LFERs to precise geometries and charges for all atoms in the transition state. Both experimental and computational approaches toward this goal face additional limitations caused by the complexity of the enzymatic environment. Another major challenge toward a more quantitative understanding of phosphoryl-transfer catalysis is in experimentally dissecting the roles of active-site interactions. Site-directed mutagenesis has provided crucial information, but it cannot directly assess catalytic contributions because active sites are complex and cooperative networks of interacting residues (96). Double-mutant cycles can help by assessing cooperativity of interactions, albeit imperfectly (148, 149). Comparative approaches that utilize multiple substrates, multiple enzymes, and catalytic promiscuity to further parse energetic effects are providing additional insights (84, 150–153). Yet understanding energetic contributions remains difficult, and much work remains to be done.

CONCLUSIONS

Phosphoryl-transfer enzymes have attracted enormous attention as befits their central roles in biology. Over time, different approaches to these systems have been prominent: physical organic approaches to nonenzymatic phosphoryl transfer in the 1950s, mechanistic studies of specific enzymes in the 1970s and beyond, structural studies from the 1990s to the present, and contemporary emerging computational approaches. Although each new development has been powerful and exciting, there has been a tendency to lose track of mechanistic considerations from earlier nonenzymatic studies. We hope that this review will resuscitate and broaden a fundamental understanding of phosphoryl-transfer mechanisms and that the analyses and case studies will provide motivation for current and future investigators to apply lessons and approaches from nonenzymatic studies. The understanding of biological phosphoryl transfer from these approaches is synergistic rather than additive, and the deepest understanding will come from an integration of different perspectives and methods.

Leaving group: the part of a molecule that departs in a reaction, breaking a bond to phosphorus and taking a pair of electrons

LFER: linear free energy relationship

KIE: kinetic isotope effect

Nucleophile: a species that donates an electron pair to an electrophilic atom (such as phosphorus), forming a new bond

Dissociative mechanism: a stepwise elimination-addition mechanism with a stable metaphosphate intermediate

Concerted mechanism: a single-step reaction proceeding through a single transition state

Associative mechanism: a stepwise addition-elimination mechanism with a stable pentacoordinate intermediate

Tight transition state: the phosphorus atom has more net bonding to the leaving group and nucleophile atoms than in the ground state

Loose transition state: the phosphorus atom has less net bonding to the leaving group and nucleophile atoms than in the ground state

Synchronous transition state: the total bond order of the phosphorus atom to the leaving group and nucleophile atoms is similar to that in the ground state

TERMINOLOGY FOR DESCRIBING PHOSPHORYL-TRANSFER REACTIONS.

Here we use the terms loose, synchronous, and tight to describe different types of transition states for a concerted reaction (A_ND_N). In the literature, the terms “associative” and “dissociative” have often been used to describe transition states. This usage is ambiguous because the terms have been used to refer to both the mechanism of the reaction (whether concerted or stepwise) and the structure of the transition state in a concerted reaction. Thus, the following terminology has been suggested and is used herein. An associative, or addition-elimination (A_N + D_N), mechanism is a reaction that proceeds through a phosphorane intermediate. A dissociative, or elimination-addition (D_N + A_N), mechanism is a reaction that proceeds through a metaphosphate intermediate. The parentheses give the corresponding IUPAC nomenclature (162).

RAS GTPASE: IS A GENERAL BASE NECESSARY?

Ras and related proteins catalyze GTP hydrolysis and have been studied extensively as paradigms for molecular switches that link enzymatic activity to cell-regulatory signals through conformational change. The catalytic mechanism of the Ras GTPase became a topic of extensive discussion when structural studies did not find a good candidate for a general base in the active site. To account for this observation, a new mechanism was proposed, referred to as substrate-assisted catalysis, whereby the GTP substrate would act as the catalytic base to deprotonate water, forming the more potent hydroxide nucleophile (154, 155). Although this mechanism is widely cited in the literature, subsequent experiments strongly support an alternative interpretation of the original data taken as support of this mechanism; these experiments are described in Supplemental Section J. However, a more fundamental question underlies this issue: Is there any reason to think that a general base is necessary? Studies on nonenzymatic and Mg²⁺-promoted nucleoside triphosphate hydrolysis as well as Ras-catalyzed GTP hydrolysis suggest a loose transition state for this reaction (127, 138, 139). Using β_NUC = 0.1 as reported for nucleoside triphosphate hydrolysis (127), the expected catalytic advantage for deprotonating water to form hydroxide is at most 60-fold, relative to a rate acceleration for Ras of approximately 10⁵-fold relative to the nonenzymatic reaction. Thus, although interactions with the enzyme can help to position water for nucleophilic attack, there is little expected benefit from using a general base to deprotonate the attacking water. Given consideration of the transition-state structure, additional mechanisms for RasGAP-mediated GTP hydrolysis were proposed and subsequently supported by crystallographic and functional studies (discussed further in Supplemental Section J).

ALKALINE PHOSPHATASE: DO POSITIVELY CHARGED GROUPS TIGHTEN TRANSITION STATES?

Alkaline phosphatase (AP) catalyzes phosphoryl transfer from a broad range of monoesters and is among the most proficient enzymes known. AP has considerable positive charge concentrated in its active site, including two Zn²⁺ ions and an arginine available to interact with the nonbridging phosphoryl oxygen atoms in the transition state. Could these interactions with positive charge lead to a tighter transition state, as may be expected from stabilization of the upper left corner in the two-dimensional reaction coordinate diagram? Because the active site of AP accepts a wide range of leaving groups, it has been possible to perform numerous linear free energy relationship (LFER) and kinetic isotope effect studies to probe transition-state properties in AP-catalyzed reactions. In reactions of monoesters for which the chemical step is rate limiting, all experimental evidence, described in Supplemental Section I, is consistent with transition states that do not differ from those of the nonenzymatic reactions. These observations suggest that the presence of positively charged groups does not substantially tighten the transition state. Yet arginine residues and other positively charged residues are ubiquitous in phosphoryl-transfer enzymes. What roles could they play? LFER results showed no evidence for substantial change in transition-state structure upon mutation of the active-site arginine of AP (145), but measurement of individual reaction steps indicated that arginine coordination strengthens binding by approximately 3 kcal/mol and provides 1–2 kcal/mol of additional transition-state stabilization (75). Through studies of AP and protein tyrosine phosphatase, another phosphoryl-transfer enzyme with similar arginine coordination in a very different active-site environment, it has been proposed that interactions with arginine serve to position optimally the phosphoryl group for reaction and may provide further catalysis if they are positioned to interact more strongly with the trigonal bipyramidal geometry in the transition state than the tetrahedral ground state (75, 76, 115, 136, 156, 157). Additional references and discussion of AP catalytic mechanisms are provided in Supplemental Section I.

PHOSPHOGLUCOMUTASE: DO ENZYMES CHANGE MECHANISMS FROM THOSE IN SOLUTION?

A recent X-ray crystallographic study challenged expectations from nonenzymatic reactions by reporting a stable phosphorane intermediate in phosphoryl transfer from glucose in the active site of phosphoglucomutase (158). For this reaction, a concerted process with a loose transition state is expected, and thus the observation of electron density suggestive of a stable pentacoordinate, trigonal bipyramidal species in the structure was surprising. A crystallographically observable phosphorane would represent a remarkable shift in mechanism from a transition state near the lower right of the two-dimensional reaction coordinate diagram to a long-lived stable species in the upper left corner. However, soon after this result was presented, it was suggested that the observed pentacoordinate species may not represent a reaction intermediate, but instead could represent a MgF₃^– transition-state analog arising from components from the crystallization buffer (159). Subsequent evidence from ¹⁹F and ³¹P nuclear magnetic resonance, additional X-ray experiments, and kinetic data provided strong support for the assignment of the pentavalent species as MgF₃^– (160, 161). The phosphoglucomutase story provides a reminder of the importance of synergy between kinetics, chemical mechanism, and structure for understanding enzymatic catalysis. Structural studies with transition-state analogs have advanced enzymology by providing physical models of active-site interactions. Nevertheless, structures alone cannot reveal mechanism or energetics and so must be placed in the context of functional studies. See Supplemental Section H for additional references and discussion.

SUMMARY POINTS.

1. Considerable experimental evidence supports a concerted reaction for phosphate monoesters and related compounds in nearly all cases.

2. Transition states for phosphoryl-transfer reactions can, in principle, be loose, tight, or synchronous, as defined by the net bonding of phosphorus to the nucleophile and leaving group.

3. A consistent picture of the transition states for phosphoryl transfer has emerged from LFER and KIE studies, where phosphate monoesters proceed through loose transition states, phosphate diesters through roughly synchronous transition states, and phosphate triesters through generally tighter but more variable transition states.

4. Experimental evidence suggests that, in cases tested to date, enzymatic catalysis generally does not substantially alter transition states for phosphoryl transfer from those in solution.

5. Consideration of the mechanistic data for nonenzymatic phosphoryl transfer allows evaluation of proposed catalytic mechanisms and has led to important insights into mechanisms of catalysis for enzymatic phosphoryl transfer.

FUTURE ISSUES.

1. LFER and KIE data provide empirical descriptions of transition states. A major challenge lies in translating the empirical correlations into bond distances, electronic distributions, and vibrational states.

2. Additional, systematic experimental data will be needed to achieve this goal. Computational approaches offer promise in correlating these empirical data with physical parameters, but calculations must be related to these experimental observables and provide nontrivial predictions to allow unbiased tests of the methods and results.

3. Understanding how reaction energy surfaces change in response to enzymatic stabilizing interactions is a key challenge. An ultimate goal is the development of predictive and quantitative models for phosphoryl-transfer catalysis.

4. Although not discussed here, a related important challenge is to understand how enzymatic catalysis of phosphoryl transfer is coupled to events required for biological signaling and regulation.