Mode Recognition in UV Resonance Raman Spectra of Imidazole: Histidine Monitoring in Proteins

Abstract

The imidazole side-chains of histidine residues perform key roles in proteins, and spectroscopic markers are of great interest. The imidazole Raman spectrum is subject to resonance enhancement at UV wavelengths, and a number of UVRR markers of structure have been investigated. We report a systematic experimental and computational study of imidazole UVRR spectra, which elucidates the band pattern, and the effects of protonation and deprotonation, of H/D exchange, of metal complexation, and of addition of a methyl substituent, modeling histidine itself. A consistent assignment scheme is proposed, which permits tracking of the bands through these chemical variations. The intensities are dominated by normal mode contributions from stretching of the strongest ring bonds, C₂N and C₄C₅, consistent with enhancement via resonance with a dominant imidazole π-π* transition.

1. INTRODUCTION

Histidine plays a central role in proteins because its imidazole sidechain, having a pKa near neutrality, can act as an acid or a base, and can also bind transition metal ions.^1–7 Consequently, spectroscopic probes of the histidine environment are useful in studies of protein function. The vibrational spectrum of imidazole is of current interest because of the possibility of probing histine residues with infrared and Raman spectroscopy.^8–25 The vibrational modes are strongly affected by protonation and by metal ion binding.^{12–20,23–38}

Imidazole ring vibrations occur in crowded regions of protein vibrational spectra, rendering identification difficult. FTIR difference spectroscopy on carefully matched samples of isotopically labelled protein can recover changes in certain imidazole vibrations.^39–43 Raman spectroscopy offers the advantage of selective resonance enhancement by tuning the laser to imidazole electronic transitions in the ultraviolet.^30–34 The imidazole enhancements are modest, and histidine bands are often obscured in protein UVRR spectra.⁴⁴ However, in favorable cases, bands which respond to protonation and metal binding can be detected, as reviewed by Takeuchi.^18,19 Of particular utility is the monitoring of protonation status via a strong imidazolium band found at ~1410 cm⁻¹ when the NH protons are exchanged in D₂O.27–30 NH/D exchange is also helpful in characterizing signals from metal-bound histidine residues.^19–22

These observations on proteins place a premium on understanding the imidazole vibrational modes and their compositions, and to assess the effects of protonation or deprotonation, of metal binding, and of NH/D exchange. These issues have been addressed in a number of computational and experimental studies.^{8–18,30–36} The present work combines experiment with theory in order to elucidate the UV resonance Raman (UVRR) spectral pattern for imidazole (ImH) and 4-methyl-imidazole (MeImH – Figure 1), a model for histidine, through variations in protonation status and metal binding. The aims are to (1) propose a normal mode labeling scheme for imidazole across its three protonation states, based on the computed eigenvectors; (2) compute RR spectral intensities to facilitate band identification in experimental spectra; (3) evaluate effects of ring substitution, tautomerization and NH/ND exchange in order to assign histidine spectra; (4) study effects of mono-, and di-cation binding to imidazole and imidazolate, respectively.

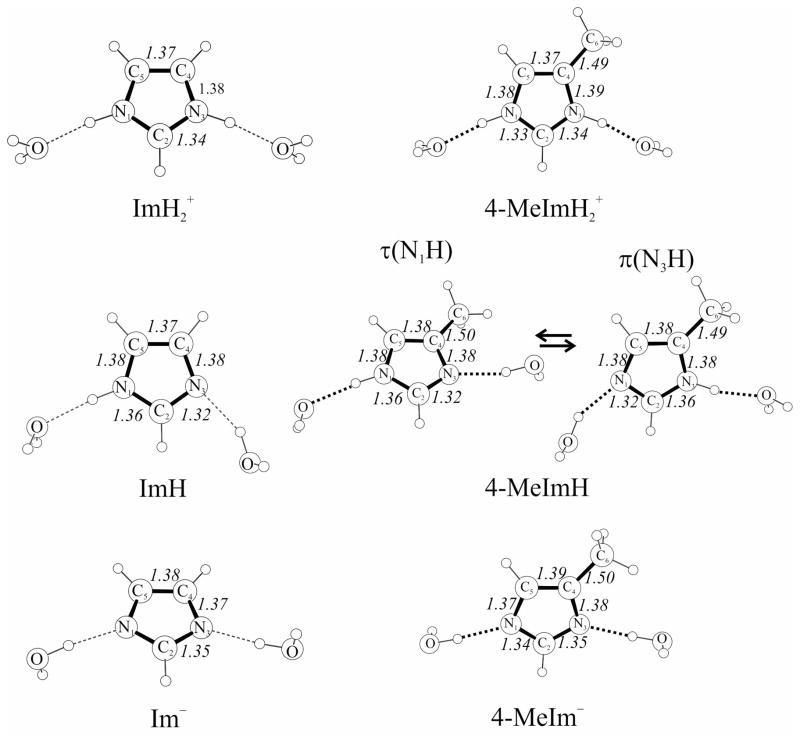
Figure 1.

Atom labeling and computed bond lengths (Å) of imidazole and 4-methylimidzole in the three protonation states. The tautomeric states of neutral 4-methylimidazole are labeled as τ(N₁H) and π(N₃H) states.

We find that DFT-computed geometries, vibrational frequencies and UVRR intensities are sufficiently accurate to permit tracking of the observed spectral bands. The main finding is that resonance enhancement is principally associated with the stretching of the N-C₂ bonds, resulting in a single dominant band for the imidazolate anion (Im⁻), and for the NH/D-exchanged imidazolium cation (ImD₂⁺). When N-H bonds are present, the N-H bending coordinates reorient the normal modes, resulting in two strong bands for un-exchanged imidazolium (ImH₂⁺). Further redistribution of intensity in neutral imidazole results from the asymmetry of having one protonated and one unprotonated N. The ImH intensity pattern is maintained in MeImH, with additional perturbation from the methyl substituent, and with the presence of alternative tautomers, τ and π (Figure 1). Protonation, and to a lesser extent metal binding, also has a pronounced effect on mode frequencies, reflecting the polarization of the ring bonds.

2. METHODS

2.1 Experimental

Imidazole (ImH), 4-methyl-imidazole (MeImH), and histidine (HisH) (Aldrich) were dissolved (0.5 M) in pH 7.4 phosphate buffer, or in 3 M aqueous HCl or 3 M aqueous NaOH, to obtain the neutral, cationic or anionic species. Imidazole adducts of the tren (triethylenetetramine) chelates of Zn²⁺ and Cu²⁺, as well as the binuclear Zn²⁺,Cu²⁺ tren chelate adduct with a bridging imidazolate, were prepared⁴⁵ and dissolved in 40 % acetonitrile in water for UVRR measurements.

RR spectra were excited at 229 nm with a frequency doubled Ar+ ion laser (Innova 300 FreD, Coherent, ~0.4 mW). Raman spectra were collected in back scattering (135 °C) geometry from sample in a spinning NMR tube, and were dispersed in a single monochromator (Spex 1269) equipped with 3600 grooves/mm grating. A back illuminated liquid N₂-cooled charge coupled device (LN-CCD, Princeton Instruments) was used as the multichannel detector. To avoid photo-degradation, a cylindrical lens was used to focus the laser beam at the sample. UVRR spectra at different laser power levels were measured and optimized.⁴⁶ Sample integrity was monitored by the absence of time-dependent changes in the Raman spectra, as well as in UV absorption spectra obtained after each measurement.

Pre-resonant Raman spectra were also obtained with 488 nm Ar⁺ laser excitation, to aid in band assignments.

Appropriate solvent backgrounds were subtracted. A 3M NaOH solution of ImH contained mostly imidazolate, but also remnant neutral species, whose contributing bands were subtracted using the imidazole spectrum obtained at neutral pH. Raman bands from acetone were used as the standard for wavenumber calibration.

Raman cross sections were obtained from experimental intensity measurements, as described elsewhere.⁴⁷ To minimize possible errors due to photo-degradation or poor data quality we used the following procedure. The RR spectrum at lower analyte concentration (C_A, 10–50 mM) in the presence of 0.2 M (C_S) SO₄²⁻ was measured. The Raman cross section for one of the strongest analyte bands was obtained using the following relation:

$${\sigma }_A={\sigma }_S\times \frac{I_A{C}_S}{I_S{C}_A}\times \frac{(A_0+A_{v_A})}{(A_0+A_{v_S})}\times {\left(\frac{v_0-v_S}{v_0-v_A}\right)}^4$$

where σ_A and σ_S are the Raman cross sections of the analyte and the intensity standard, respectively. A₀, A_νA, and A_νS, are the absorption coefficient at the wavenumbers, ν₀, ν_S, and ν_A, of the laser and of the scattered frequencies of the analyte and the standard, respectively. The last two terms in the above equation corresponds to self-absorption and frequency dependent corrections. A cross section of 420 × 10⁻³⁰ (cm²/molecule steradian) was adopted⁴⁷ for the 981 cm⁻¹ band of SO₄²⁻, whose intensity (I_S) was ratioed to that of the analyte band (I_A) using peak height measurements. Then at higher analyte concentration (0.5 M), the above σ_A value was used as reference for other analyte bands. In order to check for possible errors due to self-absorption at higher concentration, the σ_A values for all the bands at low and high concentration were predicted and found to be similar in both methods.

2.2 Computational methods

All electronic structure calculations reported in this work were performed using the Gaussian 98 suite of programs.⁴⁸ Density functional theory (DFT) using the B3LYP (Becke’s nonlocal three-parameter exchange functional in conjunction with Lee-Yang-Parr correlation functional)^49,50 was used to calculate the properties of the ground state, while the CIS (configuration interaction with singlet excited state)⁵¹ method was used to calculate the gradient in the excited state for the computation of UVRR relative intensities.¹⁵ The standard 6-31G* basis set was used throughout.

In order to model the effect of hydrogen bonding in aqueous solution, two water molecules were included, acting as H-bond acceptor from the NH group and donor to the lone pair on the unprotonated N atom.¹⁵ The geometries of all the water adducts were optimized without any symmetry constraints. Vibrational frequencies were calculated at the optimized geometries using analytical derivative techniques. No negative frequencies were found, showing that the calculated geometries were at true energy minima. Calculated vibrational frequencies were scaled using the scaled quantum mechanical (SQM)^52–56 procedure to compensate for anharmonicity and basis set incompleteness. Force constants were calculated in Cartesian coordinates, and transformed into a non-redundant set of natural internal coordinates. SQM scaling⁵⁶ was applied to the internal coordinate force constants.

The ground state results were used in conjunction with CIS to determine the forces acting at vertical excitations on the resonant excited state.^{15,30,57–59} Calculated Cartesian forces were projected on the normal mode displacements that were obtained by diagonalization of the scaled force fields. These projected forces were used to reproduce relative resonance Raman intensities for the fundamental modes.

3. RESULTS

3.1 Optimized Structures

Optimized structures are shown in Figure 1. Water molecules were added as H-bond acceptors and donors in order to improve the simulation of aqueous solution data. The effect of hydration was to shorten the C-N bonds slightly, while H-bond acceptors also lengthened the N-H bonds (by 0.01 to 0.025 Å – Table S1)

Where comparisons are possible, there is good agreement with experimentally determined bond distances (Table S1). Thus neutron diffraction distances for imidazole⁶⁰ or protonated histidine⁶¹ are within 0.01 Å of the computed distances for hydrated neutral or protonated species. Microwave data are also available for neutral imidazole,⁶² and show the expected increases and decreases in C-N and N-H bond distances.

Within the imidazole ring the shortest bonds are N-C₂, but there is pronounced asymmetry in the neutral species, 1.32 and 1.36 Å, with the longer N-C₂ bond belonging to the proton-bearing N. Adding one and then two protons to imidazolate shortens the C₄-C₅ bond by 0.01 Å at each step and also shortens the N-C₂ bonds, by 0.05 Å on average, per proton. The effect of adding a methyl group at C₄ is very small. Bond distances for the two MeImH tautomers are in agreement with the DFT-computed distances reported by Toyama et al.⁹

3.2 Normal Modes

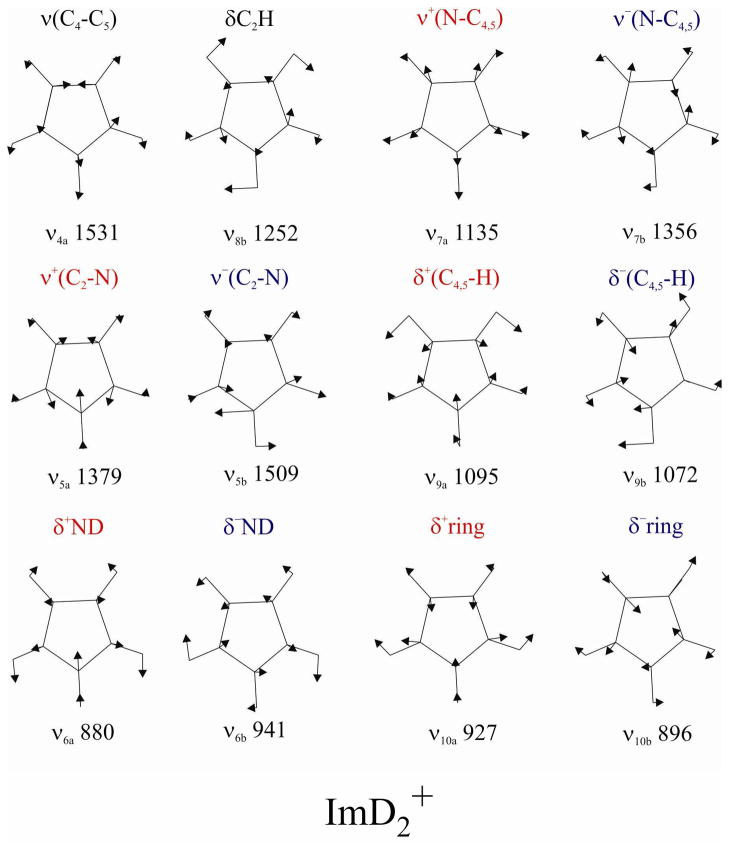
Imidazole [C_s symmetry] has six out-of-plane and fifteen in-plane vibrational modes. Protonation and deprotonation add or subtract one out-of-plane and two in-plane modes, and introduce a 2-fold symmetry axis in the mirror plane [C_2v symmetry], producing symmetric and antisymmetric in-plane modes.

Traditionally, modes are labeled in order of descending frequency within each symmetry block, starting with the totally symmetric modes. However when interpreting imidazole vibrational spectra in proteins it is desirable to correlate modes of similar composition across different protonation states. For this purpose, we have constructed a labeling scheme, in which the mode subscripts (ν_i for in-plane and γ_i for out-of-plane) increase in descending order of frequency, but are arranged in a/b pairs for modes with similar compositions that are symmetric [a] and antisymmetric [b] with respect to the two-fold axis of imidazolium and imidazolate. The labels ν_1–3 are allocated to the N-H and C-H stretching modes. These occur above the fingerprint region, and are not considered in the present work.

For imidazole itself, the a/b distinction is arbitrary, and the modes are correlated with imidazolium on one hand, and imidazolate on the other, on the basis of mode composition similarity and on frequency order. Among the in-plane modes below 2000 cm⁻¹, ImH and Im⁻ have one and two fewer modes, respectively, than ImH₂⁺. For ImH, the missing mode is allocated to ν_6b, while for Im⁻ the two missing modes are allocated to ν_6a and ν_6b, based on frequency correlations and visual matching of eigenvector patterns. These modes have particularly large contributions from N-H bending coordinates, and correlate with much lower frequency modes in NH/D isotopomers, ImD and ImD₂⁺.

Computed frequencies and isotope shifts were in reasonable agreement with experiment and with previous computations^{9,10,16,17,30,31,33,36} for ImH₂⁺ (Table S2), ImH (Table S3), Im⁻ (Table S4) MeImH₂⁺ (Table S5), MeImH (τ tautomer, Table S6 and π tautomer, Table S7) and MeIm⁻ (Table S8). The experimental frequencies (including weakly enhanced bands obtained with pre-resonant (488 nm) excitation together with ¹⁵N and C₂D isotopic shifts (Figure S1–S3)) are correlated across the three protonation states in Tables 1 and 2, while measured cross sections are listed in Table 3

Table 1.

Experimental frequencies(cm⁻¹)¹ and isotopic shifts (Δ¹⁵N, cm-¹)² for the in-plane mode of the indicated molecules.

νi	ImH2+	Δ15N	ImD2+	Δ15N	ImH	Δ15N	ImD	Δ15N	Im−	Δ15N
4a	1594	−8	1548	−3	1534	−6	1507	+1	1457	−2
5a	1456	−12	1399	−21	1428	−13	1324	−10	1248	−17
6a	1211	−7	883	--	1160	−5	861	--
7a	1130	−12	1145	−10	1134	−14	1136	−13	1141	−16
9a	1102	0	1106	0	1098	0	1106	−1	1099	−2
10a	923	--	920	−8	933	−13	912	−14	946	−21
5b	1538	−10	1527	−8	1489	−5	1485	−4	1472	−3
6b	--	--	924	--
7b	--	--	1379	--	1329	−4	1360	−18	1310	--
8b	--	--	1253	--	1259	−4	1253	−10	--	--
9b	1058	−3	1086	−1	1067	−10	1070	−4	1077	−4
10b	908	--	--	--	915	--	949	−15	930	--

¹Vibrational frequencies listed in bold numbers are from resonance Raman spectra excited at 229 nm (Figure 3) and other values are from non-resonant Raman spectra excited at 488 nm (Figure S1,S2 and S3).

²Isotopic shifts (Δ¹⁵N) are obtained from Raman spectra excited at 229 nm or 488 nm(data not shown).

Table 2.

Experimental vibrational frequencies (cm⁻¹)¹ for 4-methylimidazole and histidine in the indicated protonation states.

νi	Protonated				Neutral								Deprotonated
	MeImH2+	MeImD2+	HisH2+	HisD2+	τ-MeImH	τ-MeImD	τ-HisH	τ-HisD	π-MeImH	π-MeImD	π-HisH	π-HisD	MeIm−	His−
4a	1634	1610	1634	1610	1577	1572	1575	1561	1596	1579	1593	1570	1536	1531
5a	1490	1412	1493	1412	1454	1308	1453	1322	1426	1326	1435	1336	1260	1259
6a	1205	985	1200	992	1158	--	1164	--	1158	--	1164	--
7a	1184	1260	1186	1260	1260	1227	1286	1234	1260	--	1269	1197	1233	1235
9a	1089	1110	1097	1114	1087	1019	1090	1023	1103	1019	--	1007	1010	1009
10a	929	918	928	921	936	926	940	926	--	945	--	947	951	953
5b	1535	--	1535	1523	1494	1489	1498	1486	1494	1489	1498	1486	1441	1438
6b	1430	--	--
7b	1270	1372	--	--	1305	1375	1324	1376	1344	1366	1360	1359	1297	1315
8b	1296	--	1270	--	1231	1260	1239	1274	1231	--	1239	--	--	--
9b	1008	1023	998	1007	997	--	993	1099	1015	1100	1011	1100	1100	1104
10b	978	--	--	--	--	982	--	991	977	982	969	991	--	--

¹Vibrational frequencies listed are from resonance Raman spectra excited at 229 nm (Figure 6 & 7).

Table 3.

Resonance Raman cross section (x 10³⁰/cm².sr) ^a with 229 nm excitation for the indicated species. Values for N-deuterated species are given in parentheses.

νi	Imidazole			4-methyl-imidazole				Histidine
	ImH2+ (D2+)	ImH(D)	Im−	MeIm H2+(D2+)	MeImH [τ] (D)	MeImH [π] (D)	MeIm−	HisH2+(D2+)	HisH [τ]	HisH [π]	His −
4a	-- (0.23)	0.05 (0.21)	0.35	0.77 (1.53)	0.74 (0.58)	0.86 (0.74)	1.10	0.30 (2.36)	1.36(0.51)	0.88 (1.97)	2.18
5a	0.57 (1.49)	0.22 (1.24)	2.10	3.08 (6.92)	0.39 (2.76)	1.43 (2.02)	2.97	2.91 (12.54)	0.16(1.58)	1.27 (0.48)	3.29
6a	0.46	0.21		1.78	0.68	1.14		0.79	0.91	1.85
7a	0.03 (0.27)	0.05 (0.12)	0.07	1.74	0.48 (0.17)	--	2.02	0.55	0.42 (0.16)	0.61	2.66
9a	0.01 (0.01)	0.02 (0.18)	0.11	0.13 (0.46)	--	0.44 (0.65)	0.42	0.06 (0.42)	0.12 (0.18)	0.30 (0.12)	0.51
10a	0.08 (0.12)	0.11 (0.14)	0.23	0.73 (0.51)	0.51 (0.33)	-- (0.37)	0.34	0.19 (0.62)	0.73 (0.33)	- (0.07)	0.42
5b	0.03 (0.04)	0.05 (0.21)	0.22	0.43 (0.25)	0.16	0.15 (0.39)	0.24	0.35 (0.26)	0.66	0.33 (0.64)	0.60
6b	--			--				-
7b	--	0.44 (0.85)	--	1.69 (1.59)	1.74 (1.77)	0.55 (0.89)	--	0.55 (2.01)	1.67 (1.43)	2.24 (0.20)	-
8b	0.08	0.66 (0.36)	--	--	0.48 (0.31)	--	--	--	0.91(0.28)	1.67	-
9b	0.02(0.01)	0.03 (0.07)	0.06	0.15	--	- - (0.26)	0.15	--	0.09 (0.13)	- (0.21)	0.58
10b	--	-- (0.06)	--	0.30	--	0.26 (0.35)	--	0.07 (0.30)	-	0.06	-

^aSee txt for methodology

The in-plane eigenvectors of ImH₂⁺ are illustrated in Figure 2. The internal coordinates for N-C₂ and N-C_4,5 stretching, and for NH and C_4,5H bending segregate into in-phase [ν⁺] and out-of-phase [ν ⁻] combinations in the a and b modes. The C₄-C₅ stretch contributes only to a modes, while the C₂H bend contributes only to b modes. Bond stretch contributions to the ImH₂⁺ eigenvectors are listed in Table 4, while corresponding eigenvector elements are given in Tables S9 and S10 for Im⁻ and ImH.

Figure 2.

Eigenvectors, mode numbering and SQM frequencies (cm⁻¹) for the in-plane vibrations of ImD₂⁺.

Table 4.

Internal coordinate coefficients^a in the computed eigenvectors and vibrational frequencies(cm⁻¹) of ImH₂(H₂O)₂⁺ and ImD₂(D₂O)₂⁺

νi	Mode	ImH2(H2O)2+				ImD2(D2O)2+
		ν(C4-C5)	ν+(N-C2)	ν+(N-C4,5)	Freq.	ν(C4-C5)	ν+(N-C2)	ν+(N-C4,5)	Freq.
4a	ν(C4-C5)	0.246	−0.170	0.020	1579	−0.355	0.125	0.040	1531
5a	ν+(N-C2)	0.266	0.140	−0.204	1447	0.151	0.275	−0.223	1379
6a	δ+(N-H/D)	−0.067	−0.252	−0.051	1205	0.030	−0.032	0.052	880
7a	ν+(N-C4,5)	−0.043	0.025	−0.321	1121	0.076	0.116	0.270	1135
9a	δ+(C4,5-H)	−0.138	0.069	0.041	1093	0.127	−0.044	−0.110	1095
10a	δ+ring	0.011	0.031	−0.033	929	0.012	−0.093	0.080	927
			ν− (N-C2)	ν− (N-C4,5)			ν− (N-C2)	ν− (N-C4,5)
5b	ν− (N-C2)		0.346	0.079	1525		0.346	0.051	1509
6b	δ− (N-H/D)		0.142	−0.223	1452		0.006	−0.149	941
7b	ν− (N-C4,5)		−0.119	0.203	1315		−0.186	0.324	1356
8b	δ(C2-H)		0.130	−0.101	1178		−0.014	0.034	1252
9b	δ− (C4,5-H)		0.085	0.198	1045		−0.130	0.118	1072
10b	δ−ring		0.017	−0.060	918		−0.005	0.026	896

^aSymmetry coordinate coefficients are given for pairs of bonds related by 2-fold symmetry: ν^±(N-C₂) = (N₁-C₂ +/− N₃-C₂);ν^±(N-C_4,5) = (N₁-C₅ +/− N₃-C₄); δ^± (C_4,5-H) = (C₄-H+/−C₅-H); δ^± (N-H/D)=(C₁-H/D+/−N₃-H/D).

3.3 UVRR Spectra

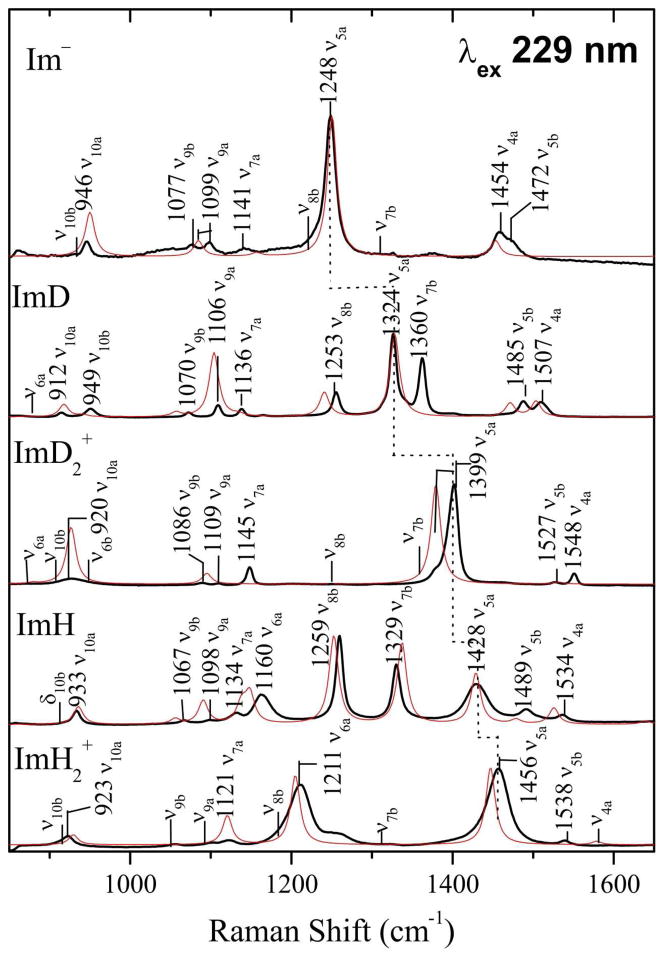
Figure 3 compares experimental (black) and computed (red) UVRR spectra for the three imidazole protonation states, as well as the NH/D isotopomers. There is generally good correspondence of the experimental and computed intensity patterns. As in our earlier study of ImH,¹⁵ a single resonant π-π* state was used in the computation of excited state gradients, the one with the highest oscillator strength in the ~200 nm region. A subsequent investigation of the effect of including additional excited states showed only minor changes in the intensity pattern.⁶³

Figure 3.

Experimental (black) and computed (red) UVRR spectra (229 nm excitation) for the indicated species in aqueous solution (di-hydrates in the computation). Mode assignments and experimental frequencies are labeled.

The most striking feature of Figure 3 is the dominance of ν_5a. In this mode, the N-C₂ and C₄-C₅ bonds stretch while the N-C_4,5 bonds contract. It is by far the strongest band for Im⁻ (1248 cm⁻¹) and also for ImD₂⁺ (1399 cm⁻¹), in which its frequency has shifted up by 151 cm⁻¹, reflecting ring bond strengthening in the cation. It shifts up another 57 cm⁻¹ in ImH₂⁺ (1456 cm⁻¹), whose spectrum now contains an equally strong band, ν_6a, which involves N-C₂ stretching, primarily, but also a significant contribution from N-H bending. There is little N-C₂ stretching in the weak ν_6a mode of ImD₂⁺ (Table 4), whose frequency is lowered drastically (883 cm⁻¹) because of the N-H/D bending contribution. Thus involvement of the N-H bending coordinate alters the mode compositions for ImH₂⁺, and intensifies ν_6a by introducing a large N-C₂ stretching contribution.

Likewise ν_4a has a large N-C₂ stretching contribution, in all the imidazole forms, but it also has a large C₄-C₅ stretching contribution which is opposite in sign. Because the N-C₂ and C₄-C₅ bonds both contract in the resonant excited state (see Discussion) the opposite phasing of their displacements leads to intensity cancellation, leaving quite weak ν_4a bands. This phasing effect on the intensities was also noted by Majoube et al.³¹

For Im⁻, ImD₂⁺ and ImH₂⁺, b modes are very weak, as expected, since, being antisymmetric, they are not enhanced by the dominant Frank-Condon mechanism, but require vibronic coupling of two excited states.^30,31,33 The 2-fold symmetry and the a/b distinction is lost in ImH and ImD, whose UVRR spectra are richer in bands, as a result. ν_5a can still be identified, at intermediate frequencies, between Im⁻ and ImD₂⁺ for ImD, and between Im⁻ and ImH₂⁺ for ImH (Figure 3). However, it is no longer dominant in ImH, for which the two strongest bands, at 1253 and 1329 cm⁻¹, correlate best with ν_8b and ν_7b. These two modes have predominantly N-C₂ stretching character in ImH (Table S3).

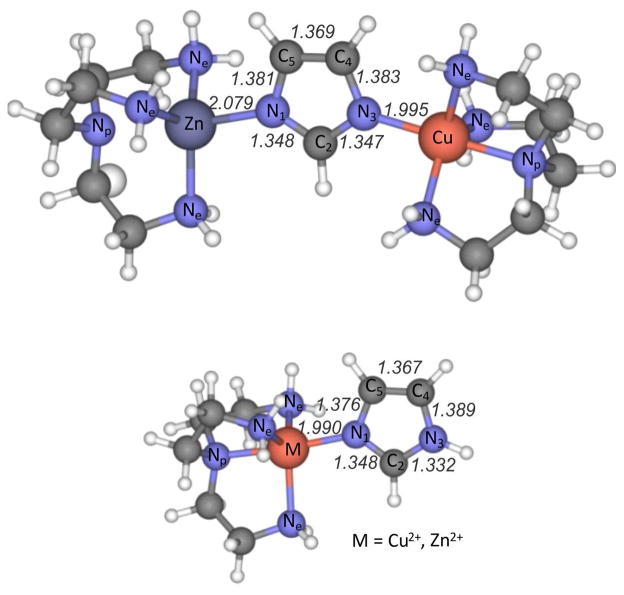
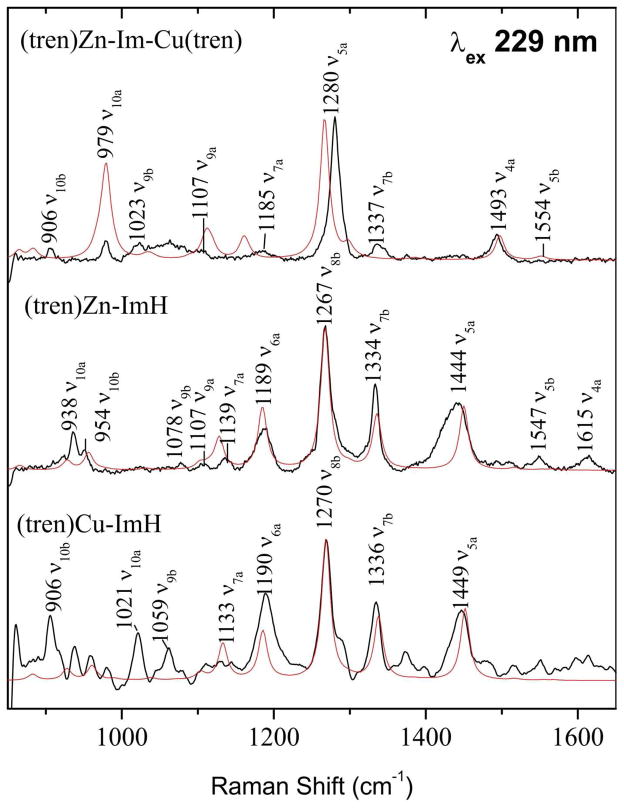
3.4 Metal Binding

To investigate the effects of metal binding we prepared the imidazole adduct of tren (triethylenetetramine) chelates of Zn²⁺ and Cu²⁺, as well as the binuclear Zn²⁺,Cu²⁺ adduct with a bridging imidazolate (Figure 4). Experimental and computed UVRR spectra were again in good agreement (Figure 5), and closely resembled those of ImH and of Im⁻, but with significant frequency increases, reflecting strengthening of the ring bonds by the electropositive metal ions. The increases are higher for two metals bound to Im⁻ than for one metal bound to ImH. As might be expected, the polarization effect is greater for protons than for metal ions. Thus the increase in ν_5a is 151 cm⁻¹ when Im⁻is bound by deuterons (ImD₂⁺) and 32 cm⁻¹ when it is bound by Zn²⁺ and Cu²⁺. Table S11 lists computed and experimental frequencies for the metal complexes.

Figure 4.

Optimized structure of imidzolate and imidazole adducts of Zn²⁺ and Cu²⁺ triethylenetetramine(tren) complexes.[The lower structure gives computed imidazole bond lengths (Å) in the [tren]-Cu-ImH complex. For [tren]-Zn-ImH, the C₄-C₅ and C₂N₃ bond lengths are same and the other CN bonds are longer by 0.001 Å. The Zn-N bond is 0.089 Å longer then the Cu-N bond].

Figure 5.

As Figure 3, but for the indicated metallo-tren complexes.

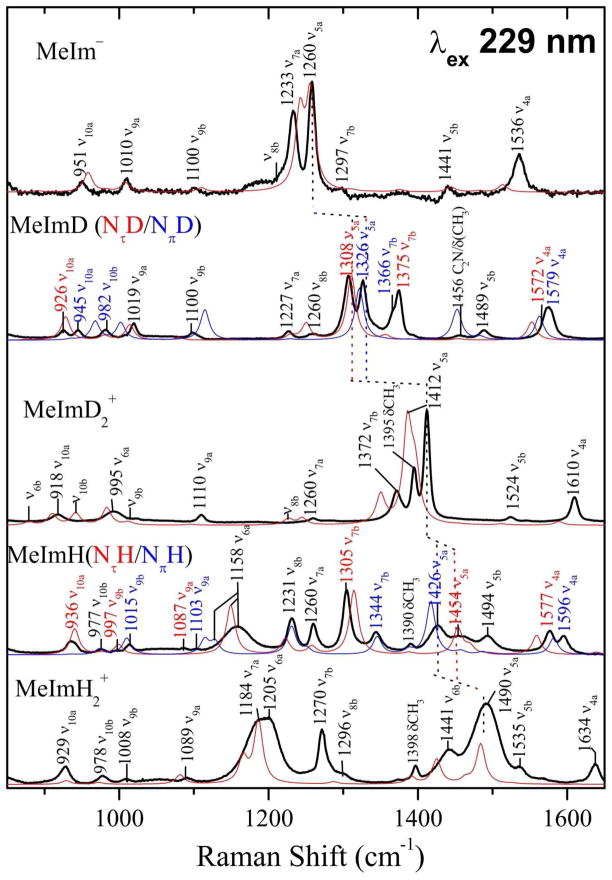
3.5 Methyl substituent and histidine

Adding a methyl substituent complicates the imidazole spectra (Figure 6), although the main features are retained. Thus ν_5a remains the strongest band for MeIm⁻ and for MeImD₂⁺, while ν_6a and ν_5a are equally strong for MeImH₂⁺, as they are for ImH₂⁺, and the frequencies of these main bands are only slightly displaced by the methyl substitution. However, introduction of the new coordinates shifts other modes, which gain intensity by proximity to the main bands: ν_7a for MeIm⁻ and MeImH₂⁺, ν_7b and the methyl umbrella mode for MeImD₂⁺. In addition b modes become activated because of symmetry lowering by the methyl substituents; ν_6b and ν_7b become prominent for MeImH₂⁺. Another notable feature is the intensification of ν_4a in all the methylated species. This likely reflects an alteration in mode composition that lessens the N-C₂/C₄-C₅ cancellation, mentioned above, although this effect is not captured in the computed spectra, which continue to show very low ν_4a intensity.

Figure 6.

As Figure 3, but for the corresponding species of 4-methylimidzole. For MeImD and MeImH, the red and blue traces are for the τ and π tautomers; band assignments are likewise labeled in red and blue. Common frequencies to both τ and π tautomers are labeled in black.

An interesting broadening effect is seen for the main bands, ν_6a and ν_5a, of MeImH₂⁺. This broadening is noticeable in ImH₂⁺ (Figure 3) but becomes more pronounced in MeImH₂⁺. The broadening is not seen for ImD₂⁺ or MeImD₂⁺. It likely reflects a distribution of H-bonded structures for the diprotonated species in H₂O (inhomogeneous broadening).

Many bands crowd the UVRR spectra of neutral MeImH and MeImD (Figure 6), reflecting equilibrium mixtures of τ and π tautomers. The tautomers have somewhat different mode compositions and frequencies, because of the ring asymmetry induced by having one protonated and one unprotonated N (Figure 1). The computed spectra are very useful in assigning the observed bands (Figure 6). Most of the corresponding bands from the two tautomers are well resolved. The assignments are in agreement with attribution of bands to the two isomers by Toyama et al,⁹ based on the temperature dependence of MeImH spectra.

The ν_4a modes of MeImH and the ν_5a modes of MeImD give rise to easily recognizable band pairs for the two tautomers, and can be used to estimate their populations. The present computation does not yield the absolute Raman cross-section. However, the fact that the τ/π tautomer population ratio estimated at room temperature is ~0.6/0.4, based on the tautomer enthalpy difference obtained from Raman measurements,⁶⁴ implies the inverse ratio for the τ/π cross sections, since the ν_4a bands of MeImH and the ν_5a bands of MeImD have essentially equal UVRR intensities (Figure 6).

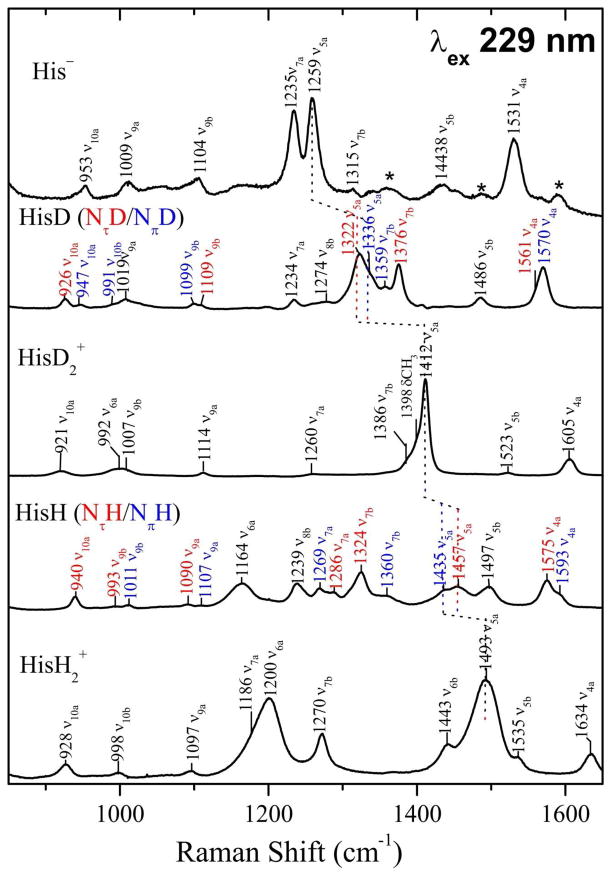
Finally, Figure 7 demonstrates that 4-methylimidazole is a good model for histidine, although the vibrational coupling to the substituent is slightly different for –CH₂R (R is the rest of the histidine molecule) than for –CH₃. All of the histidine bands can be assigned with reference to the 4-methylimidazole assignments, although the histidine bands are broader, likely reflecting a distribution of histidine conformations.

Figure 7.

Experimental UVRR spectra (229 nm excitation) for the indicated histidine species. Band assignments are based on comparison to the 4-methylimidazole modes. Asterisks mark bands in the His⁻ spectrum, which are from neutral histidine, due to imperfect subtraction.

4. DISCUSSION

The present results show that DFT/SQM force fields combined with CIS-derived excited-state gradients, give a good account of imidazole UVRR spectra, across all three protonation states. Likewise, the computations correctly reflect the effects of metal complexation, and of methyl or histidyl substituent. The intensities are modeled well enough to provide clearcut assignments of the in-plane ring modes, using a scheme that accounts for the 2-fold symmetry of diprotonated and unprotonated forms. The strength of the approach is revealed in the straightforward assignment of the crowded MeImH UVRR spectrum, to individual bands of the co-existing τ and π tautomers.

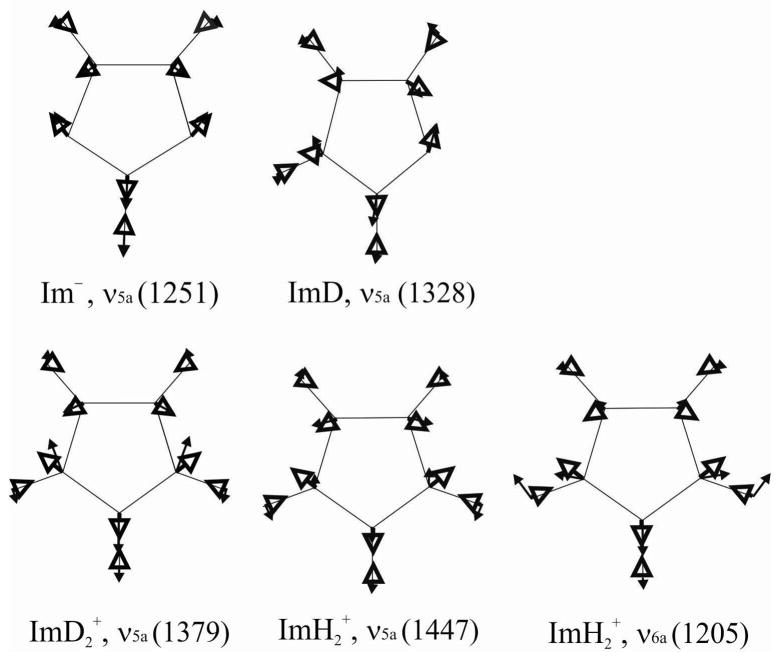
A single normal mode, ν_5a, dominates the UVRR spectra of Im⁻ and ImD₂⁺, even though its frequency is 151 cm⁻¹ higher in the latter. Figure 8 shows why this is the case. In the dominant RR mechanism (Frank-Condon or A term) the intensity is proportional to the square of the excited state displacement along the normal mode. As can be seen in Figure 8, the ν_5a eigenvector is fully aligned with the excited state displacement of the bonds in the case of Im⁻, and nearly so for ImD₂⁺. Consistent with the resonant electronic transition being from a bonding π to an antibonding π* orbital, the shorter bonds, N-C₂ and C₄-C₅ (Figure 1), lengthen in the excited state, while the longer ones, N-C₄ and N-C₅, contract. The same displacements occur in the ν_5a mode, which therefore carries most of the intensity.

Figure 8.

Eigenvectors (solid arrows) superimposed on excited state displacements (open arrows) for the indicated modes.

The ν_5a mode is also dominant in the UVRR spectrum of ImD (Figure 3), despite its asymmetry, and Figure 8 shows that its eigenvector is still well-aligned with the excited state displacements. For ImH₂⁺, one can see that the two modes that dominate the UVRR spectrum, ν_5a and ν_6a, both have eigenvectors that align with the excited state displacement. The C₄-C₅ displacement is greater for ν_5a than ν_6a, but the order is reversed for N-C₂, so that the intensity is comparable for the two modes. In contrast, ImD₂⁺ experiences a large N-C₂ displacement in ν_5a, but very little in ν_6a (not shown), which has a drastically lowered frequency because of the NH/D replacement. We note that Markham et al³⁰ made a similar argument about the effect of NH/D exchange on the UVRR spectrum of ImH₂⁺, in an early computational treatment.

These intensity mechanisms are retained in 4-methylimidazole and histidine UVRR spectra, but coupling with substituent internal coordinates perturbs the ring mode frequencies, and also induces additional intensity in modes that are weak in imidazole. A notable instance is ν_4a, a mode whose intensity is suppressed in imidazole due to out-of-phase contributions from the N-C₂ and C₄-C₅ bonds. The methyl or histydyl substituent alters the mode composition enough to lift the suppression significantly and intensify ν_4a, permitting its use as a structure marker, as advocated by Takeuchi,^18,19 who refers to it as ν(C₄=C₅).

This band has been observed to shift up several cm⁻¹ on metal binding to histidine,^18,19 an effect confirmed for imidazole in our tren-metal complexes (Figure 5). Other, lower frequency ring modes are similarly affected, but are less useful in histidine because of spectral crowding. However, bands at ~1390 and ~1340 cm⁻¹ have been identified in D₂O solutions of plastocyanin as arising from the Cu-histidine ligands.²¹ These can now be identified as ν_7b and ν_5a, shifted ~10–20 cm⁻¹ by metal coordination. A larger shift, 32 cm⁻¹, is observed for ν_5a when imidazolate is bound by two metal ions in the Cu,Zn tren adduct (Figure 5), and a similar shift has been reported for Cu,Zn superoxide dismutase,^20,28,37 in which a histidinate ligand is likewise bound to two metal ions. In this case a doublet is seen, at 1282 and 1292 cm⁻¹, corresponding to the 1235, 1259 cm⁻¹ ν_7a/ν_5a doublet of histidinate (Figure 7). Interestingly, the doublet collapses into a single band at 1287 cm⁻¹, when CN⁻ is bound to the Cu²⁺ ion in SOD; the collapse was suggested to result from altered coupling with substituent coordinates as a result of reorientation of the bridging imidazolate.²⁰

The power of spectral modeling is seen in the ready assignment of the bands in the crowded MeImH and HisH spectra (Figure 6 and 7) to separate modes of the τ and π tautomers. The well-separated ν_4a bands are well suited for tautomer identification, as are the ν_5a bands in the NH/D exchanged species.