Comparison of Secondary Structure Formation Using 10 Different Force Fields in Microsecond Molecular Dynamics Simulations

Abstract

We have compared molecular dynamics (MD) simulations of a β-hairpin forming peptide derived from the protein Nrf2 with 10 biomolecular force fields using trajectories of at least 1 μs. The total simulation time was 37.2 μs. Previous studies have shown that different force fields, water models, simulation methods, and parameters can affect simulation outcomes. The MD simulations were done in explicit solvent with a 16-mer Nrf2 β-hairpin forming peptide using Amber ff99SB-ILDN, Amber ff99SB*-ILDN, Amber ff99SB, Amber ff99SB*, Amber ff03, Amber ff03*, GROMOS96 43a1p, GROMOS96 53a6, CHARMM27, and OPLS-AA/L force fields. The effects of charge-groups, terminal capping, and phosphorylation on the peptide folding were also examined. Despite using identical starting structures and simulation parameters, we observed clear differences among the various force fields and even between replicates using the same force field. Our simulations show that the uncapped peptide folds into a native-like β-hairpin structure at 310 K when Amber ff99SB-ILDN, Amber ff99SB*-ILDN, Amber ff99SB, Amber ff99SB*, Amber ff03, Amber ff03*, GROMOS96 43a1p, or GROMOS96 53a6 were used. The CHARMM27 simulations were able to form native hairpins in some of the elevated temperature simulations, while the OPLS-AA/L simulations did not yield native hairpin structures at any temperatures tested. Simulations that used charge-groups or peptide capping groups were not largely different from their uncapped counterparts with single atom charge-groups. On the other hand, phosphorylation of the threonine residue located at the β-turn significantly affected the hairpin formation. To our knowledge, this is the first study comparing such a large set of force fields with respect to β-hairpin folding. Such a comprehensive comparison will offer useful guidance to others conducting similar types of simulations.

Introduction

Atomistic molecular dynamics (MD) simulations are a versatile tool for studying protein folding and function. They can provide detailed atomistic information, which may be difficult to obtain by experimental techniques. Increases in computational power have allowed for simulations to reach experimentally relevant time scales at the microsecond level: MD simulations have been used to study the folding of peptides and small proteins¹⁻⁹ and to model other biological systems. The current record for an atomistic simulation of protein conformational changes, as far as we know, is 1 ms reached by Shaw et al.⁷ for the 58-residue protein BPTI.

One of the major challenges in protein folding simulations is choosing an appropriate force field; see, for example, ref (10). This is due to possible biases different force fields have toward certain types of secondary structure.^3,11−14 Ideally, the force field should be fully validated with experimental data, but that is typically not possible as it would involve validation against different structures and other physical properties from a large number of independent and fully validated experiments, mission impossible because experiments have their own error sources due to, for example, instrumentation. While a completely transferable force field does not exist, modifications of existing force fields have led to improvements in agreement with experimental data.¹⁵⁻²²

In this work, we compared 10 biomolecular force fields with respect to the folding of a peptide derived from Nuclear factor erythroid 2-related factor 2 (Nrf2). Nrf2 is an important transcription factor that regulates the expression of genes responsive to oxidative stress.^23,24 The protein consists of six highly homologous regions (Neh1–6 domains). Structural analysis showed that the N-terminal Neh2 domain is intrinsically disordered, a novel class of proteins that are extremely dynamic in nature.²⁵⁻²⁹ Under homeostatic conditions, this domain binds two Kelch units of a Keap1 dimer through two separate motifs: a high affinity “ETGE” motif and a lower affinity “DLG” motif.³⁰ Crystallographic data have shown that the “ETGE” motif and its surrounding residues (residues 75–83) form a β-hairpin structure upon binding to the Kelch domain of Keap1 (PDB ids: 2FLU and 1X2R).^30,31 NMR-derived ¹H, ¹H NOEs suggest that residual structure spanning from residues 74–85, likely in the form of a β-hairpin, also exists in the free-state of Neh2.^30,31 Other experimental data have shown that a peptide containing residues 74–87 can compete with the full-length Nrf2 for binding Keap1.³¹ Here, we chose to use a 16-mer human Nrf2 peptide with the sequence ⁷²AQLQLDEETGEFLPIQ⁸⁷ for our MD simulations. This peptide contains the “ETGE” motif and should be of sufficient length to form the necessary interactions to stabilize the β-hairpin structure. It is noteworthy that the phosphorylation of Thr-80 has been shown to impair the binding to Keap1.³¹ Because Neh2 is largely disordered and lacks a tertiary structure, this β-hairpin likely folds independently, making it a good target for folding simulations.³⁰

In addition to Nrf2, several other proteins that contain “ETGE”-like motifs have been shown to interact with the Kelch domain of Keap1. These include PGAM5,³² FAC1,³³ PTMA,³⁴ p62,³⁵ WTX,³⁶ and PALB2.³⁷ Some of these Keap1 interacting proteins have only been recently discovered, which suggests that this list of targets may still be growing. Structures of PTMA (Prothymosin alpha) and p62 peptides in complex with Keap1 indicate that their “ETGE”-like motifs bind to the same region as the “ETGE” motif of Nrf2 and form similar hairpin structures in their bound states.^31,34,35 Interestingly, MD simulations from our previous work showed that the binding motifs of Nrf2 and PTMA have a tendency to form hairpin structures that resembled the bound state conformation even in the absence of Keap1.⁹ With the list of Keap1 binding partners seemingly expanding and MD simulations becoming an increasingly important and predictive tool, it is important to establish appropriate simulation protocols for these systems, including force field choice.

β-Hairpins are a type of protein supersecondary structure consisting of two hydrogen-bonded antiparallel β-strands connected by a turn. These structural elements are common in globular proteins because they reverse the direction of the protein backbone, allowing the formation of compact structures. β-Hairpin motifs are sometimes involved in protein–protein interactions, and it has been suggested that they can act as nucleation sites for protein folding.^31,38−40 In this study, we compared folding simulations of a β-hairpin peptide derived from the intrinsically disordered Neh2 domain. Starting from an unfolded structure, we performed extensive (1–2 μs each, totaling 37 μs) atomistic molecular dynamics simulations using 10 different force fields (details in next section). We selected these force fields primarily because they are commonly used in biomolecular simulations, including those of β-hairpin folding.^3,9,41,42

Force field selection is a key factor in the outcome of protein folding simulations. Although force field modifications have led to improved agreements between MD simulations and experimental data, continued testing and comparison with experimental data is required to further these advances. While studies comparing different force fields have been conducted previously, very few of them had included such a large set of force fields with respect to folding of secondary structure elements.^{3,14,19,43−45} Small proteins and peptides with folding times on the microsecond time scale are excellent systems to test and compare force fields; such trajectories provide reasonable sampling of conformations and sufficient length to examine the stability of the force field.

In this work, we compare MD simulations of a β-hairpin forming peptide derived from the protein Nrf2, performed with 10 force fields. We assess their agreements with experimental data. The effects of elevated temperatures, charge-groups,^46,47 peptide capping, and phosphorylation of Thr-80 with respect to β-hairpin formation were also examined. Despite using identical starting structures and simulation parameters, we observed clear differences among the various force fields and even between replicate simulations using the same force field. Such a comprehensive comparison will offer useful guidance to others conducting similar types of simulations and for improving force fields.

Simulation Methodology

Starting Structures

The starting structure for our MD simulations was generated on the basis of the amino acid sequence of a 16-mer human Nrf2 peptide (⁷²AQLQLDEETGEFLPIQ⁸⁷). We used the Crystallography and NMR System (CNS)⁴⁸ to generate an extended structure, which subsequently underwent simulated annealing. To avoid any potential bias to the bound-state conformation, a structure from the annealing simulations that did not resemble the bound state structure (PDB id: 2FLU) was chosen as the starting structure.³¹ The exact same starting structure was used for all simulations. For the phosphorylated peptide (pThr-80) simulations, a dianionic phosphate group (PO₄^2–) was modeled onto residue Thr-80 of the same structure using chimera.⁴⁹

Force Fields

We compared the peptide folding using the following force fields: Amber ff99SB-ILDN,^15,19,20 Amber ff99SB*-ILDN,^15,17,19,20 Amber ff99SB,^15,19 Amber ff99SB*,^15,17,19 Amber ff03,^15,16 Amber ff03*,¹⁵⁻¹⁷ GROMOS96 43a1p,^50,51 GROMOS96 53a6,^21,22 CHARMM27 (version c32b1) with CMAP,^18,52,53 and OPLS-AA/L force fields.⁵⁴⁻⁵⁶ The “*” designations on the Amber force fields indicate the presence of a modification to the backbone dihedral potentials to improve agreement with experimental data.¹⁷ The “ILDN” designation indicates the presence of a modification to the side-chain torsion potentials of isoleucine, leucine, aspartate, and asparagine to improve agreement with quantum-mechanical calculations.²⁰ Combination of the “ILDN” and ff99SB* modifications has been demonstrated recently.^44,57 For a recent summary of the evolution of the Amber ff99 and ff03 series of force fields, see the results section of ref (44). The “p” designation on the GROMOS96 43a1 force field indicates the inclusion of phosphorylated amino acid parameters to the otherwise unmodified 43a1 parameters.⁵⁰ One major difference between the GROMOS force fields and the others used in this study is that the GROMOS force fields are united atom and do not explicitly have all hydrogen atoms. The “AA” and “/L” designations on the OPLS force field indicate all-atom and the inclusion of updated dihedral parameters from the original distribution.⁵⁶

Simulations of the same peptide with residue Thr-80 phosphorylated (pThr-80) were conducted with several of the above force fields in which phosphothreonine parameters were available. These included Amber ff99SB-ILDN, GROMOS96 43a1p, and CHARMM27. Phosphothreonine parameters from refs (58) and (50) were used for the Amber ff99SB-ILDN and GROMOS96 43a1p force field simulations, respectively. Phosphothreonine parameters included in the CHARMM27 force field distribution were used.^18,53

Simulation Details

A. General Parameters

Simulations were performed using GROMACS (GROningen MAchine for Chemical Simulations) version 4.5.⁴⁷ Although GROMACS was used in this work, we expect that our findings will be applicable to other simulation software that utilizes the same force fields.⁵⁹ Cubic boxes of linear size 6 nm were used, and periodic boundary conditions were applied in all directions. Sodium (Na⁺) and chloride (Cl^–) ions were added to neutralize the system and bring the salt concentration to 0.1 M. Na⁺ and Cl^– parameters specific to each force field distribution were used.⁶⁰ Protein and nonprotein atoms were coupled to their own temperature baths, which were kept constant at 310 K using the Parrinello–Bussi algorithm.⁶¹ This approach has been shown to perform very well in biomolecular simulations.⁴⁶ Pressure was maintained isotropically at 1 bar using the Parrinello–Rahman barostat.⁶² A 2 fs time step was employed. Prior to the production runs, the energy of each system was minimized using the steepest descents algorithm. This was followed by 2 ps of position-restrained dynamics with all non-hydrogen atoms restrained with a 1000 kJ mol^–1 force constant. Initial atom velocities were taken from a Maxwellian distribution at 310 K. All bond lengths were constrained using the LINCS algorithm.⁶³ A 1.0 nm cutoff was used for Lennard-Jones interactions. Dispersion corrections for energy and pressure were applied. Electrostatic interactions were calculated using the Particle-Mesh Ewald (PME) method⁶⁴ with 0.12 nm grid-spacing and a 1.0 nm real-space cutoff. No reaction-field or cutoff methods were tested as they have previously been shown to be inferior to PME.^65,66 System coordinates were written out at 4 ps intervals during the production runs.

B. System-Specific Attributes

The protonation states of all ionizable residues were chosen on the basis of their most probable state at pH 7. Unless specified, simulations were conducted with the amino and carboxyl terminals of the peptide left uncapped (NH₃⁺ and COO^–, respectively) for each force field. When studying peptides from the interior of a protein sequence, it is common to add capping groups to the ends. This neutralizes the unphysical charges introduced by the free N- and C-termini, which can potentially disrupt the native structure. To study the effects of peptide capping, several simulations with the N- and C-terminus capped with acetyl (ACE) and NH₂ groups, respectively, were performed (Table 1). The starting structure was solvated in SPC (simple point charge), TIP3P, or TIP4P^67,68 water. The compatibility of these water models with ions has been examined in detail in ref (60). A three-point water model (SPC or TIP3P) was recommended by GROMACS for all of the force fields used in this study, with the exception of OPLS-AA/L, in which the four-point (TIP4P) water model was the recommended choice (Table 1). Simulations with TIP3P and TIP4P were conducted for this force field (Table 1). The nonphosphorylated peptide systems each contained 17 Na⁺ and 13 Cl^– ions, while for the pThr-80 systems two extra Na⁺ ions were added to neutralize the dianionic phosphate group. For each force field, a simulation was conducted without the use of charge-groups (single atom charge groups); GROMACS uses the concept of charge groups to speed up simulations; see section “Domain Decomposition” in ref (47) for details. It has recently been shown that in some situations charge-groups can lead to pronounced unphysical effects.⁴⁶ To examine the effect of charge-groups, additional simulations were conducted with the GROMOS96 and OPLS-AA/L force fields employing the default charge-groups for these force fields. Simulations performed with charge-groups are denoted with brackets around the force field name in the Results. For simulations conducted with the CHARMM27 force field, CMAP correction was applied.¹⁸ A few of the simulations were duplicated to assess reproducibility (Table 1). These systems did not use charge-groups, were prepared in the same manner as stated above, and were assigned different initial atom velocities than their originals. Duplicated simulations are denoted with bracketed sequential numbering beside the force field name in the Results. We also performed elevated temperature simulations at 330, 350, and 370 K with the Amber ff99SB*-ILDN,^15,17,19,20 Amber ff03*,¹⁵⁻¹⁷ GROMOS96 53a6,^21,22 CHARMM27 with CMAP,^18,52,53 and OPLS-AA/L force fields.⁵⁴⁻⁵⁶ Using the initial and final (after 1 μs) system configurations at 310 K, we reassigned the atom velocities at each higher temperature and performed 0.2 μs MD simulations.

Table 1. Summary of the MD Simulations.

force field	water	elevated tempa	cappedb	pThr-80c	charge-groupsd	duplicatee
Amber ff99SB-ILDN	TIP3P (7038)					Y
	TIP3P (7030)		Y			Y
	TIP3P (7036)			Y
Amber ff99SB*-ILDN	TIP3P (7038)	Y
Amber ff99SB	TIP3P (7038)					Y
Amber ff99SB*f	TIP3P (7038)					Y
Amber ff03	TIP3P (7038)
Amber ff03*	TIP3P (7038)	Y
GROMOS96 43a1p	SPC (7035)				Y
	SPC (7030)		Y
	SPC (7033)			Y	Y
	SPC (7027)		Y	Y
GROMOS96 53a6	SPC (7035)	Y			Y	Y
	SPC (7033)	Y	Y
CHARMM27	TIP3P (7038)	Y				Y
	TIP3P (7030)			Y
OPLS-AA/Lf	TIP3P (7037)	Y			Y
	TIP4P (6969)

^a“Y” indicates that elevated temperature simulations were performed at 330, 350, and 370 K from the initial and final (after 1 μs) system configurations.

^b“Y” indicates that the N and C termini of the peptide were capped with acetyl (ACE) and NH₂ groups, respectively. They were otherwise left uncapped (NH₃⁺ and COO^–, respectively).

^c“Y” indicates that residue Thr-80 was phosphorylated.

^d“Y” indicates that two simulations were performed: one with default GROMACS charge-groups and one without charge-groups.

^e“Y” indicates that two simulations, each 1 μs, were performed. Duplicates were always performed without charge-groups and were identical to the first simulation except for their initial atom velocities.

^fThe trajectory was extended to 2 μs.

In total, 28 individual 1 μs simulations were conducted, and two of these trajectories were extended to 2 μs (Amber ff99SB* and OPLS-AA/L). An additional 7.2 μs of simulations at elevated temperature was performed. The cumulative simulation time was 37.2 μs. The simulations are summarized in Table 1.

Simulation Analysis

We used either the full 1 μs trajectories or the last 0.1 μs for analysis. By restricting some analyses to the last 0.1 μs, we allowed as much time as possible for the simulations to converge to a stable conformation. Hydrogen bonds were analyzed as follows: A hydrogen bond between a donor (D–H) and an acceptor (A) was considered to be formed when the DA distance was less than 3.2 Å and the angle between the DA vector and the D–H bond (AD–H angle) was less than 35°. These geometric criteria for defining hydrogen bonds are consistent with those used in prior studies.^69,70 Secondary structure content was assessed with the DSSP algorithm.⁷¹

Results

We have compared the secondary structures and free- and bound-state contact formations in MD simulations of a β-hairpin forming peptide derived from the intrinsically disordered Neh2 domain of Nrf2 conducted with 10 different biomolecular force fields. The DSSP algorithm was used to monitor the evolution of secondary structures over the entire 1 μs trajectories. β-Hairpin formation was identified by inspection of the cluster center structures and the C_α–C_α atom pair distances during the last 0.1 μs. Resemblance to the native state was gauged via the presence or absence of experimentally determined ¹H, ¹H NOEs.³⁰ We have also compared hydrogen bonds, rmsd’s, and backbone dihedral angles in the MD structures to the peptide in complex with its binding target, Keap1.³¹ The effects of elevated temperatures, terminal capping, charge-groups, and phosphorylation of Thr-80 on hairpin folding were also assessed.

Assessing Secondary Structure Formation at 310 K

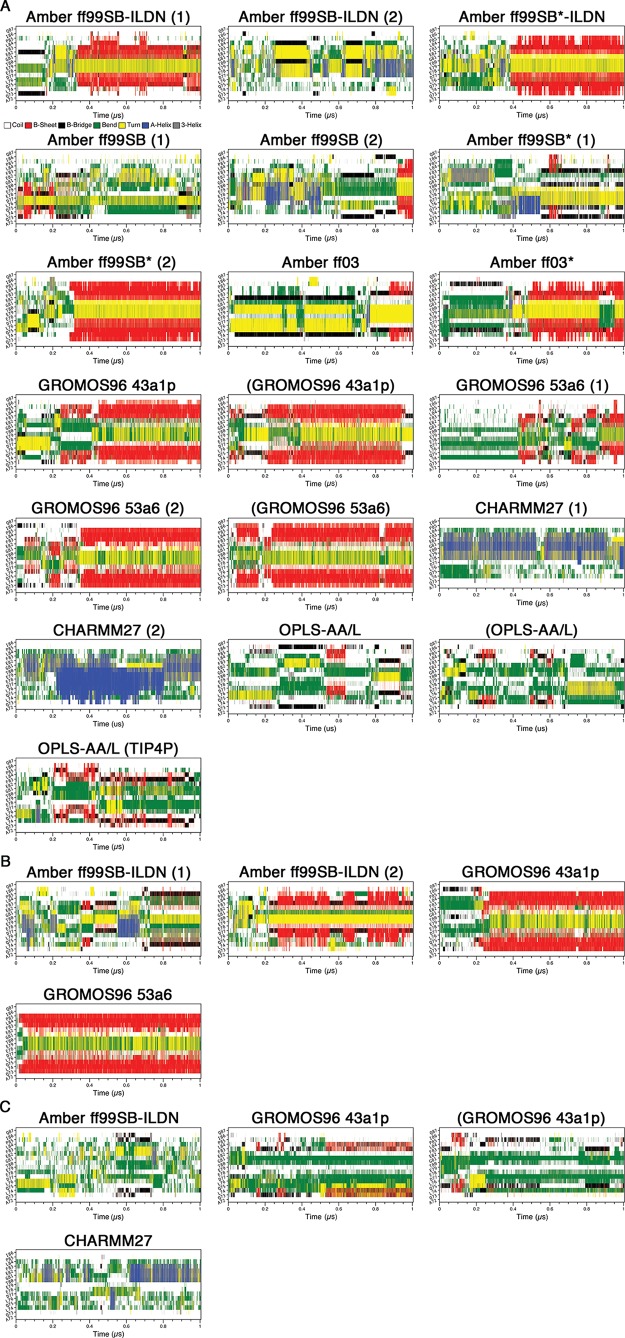
To compare the MD trajectories obtained with different force fields, we first assessed the secondary structure content over the course of our simulations at 310 K using the program DSSP.⁷¹ In this analysis, we deemed simulations that had residues from their β-turn regions (⁷⁷DEET⁸⁰) in “turn” conformations (yellow) flanked by residues in β-sheet conformations (red) simultaneously, to have formed β-hairpins (Figure 1). For the uncapped peptides, the Amber ff99SB-ILDN (1), Amber ff99SB*-ILDN, Amber ff99SB (2), Amber ff99SB* (2), Amber ff03, Amber ff03*, GROMOS96 43a1p, and GROMOS96 53a6 (1 and 2) simulations, including those which used charge-groups, appeared to adopt β-hairpins at some points in their trajectories (Figure 1A). Cluster center structures from the last 0.1 μs of the simulations, with the potential β-turn region (⁷⁷DEET⁸⁰) colored in black, are shown in Figure 2. The result clearly illustrates the 16-mer peptide folds into β-hairpin conformations by using these force fields. Intriguingly, the folding times vary greatly between ∼0.05 and >0.9 μs in these simulations (Figure 1A). The CHARMM27 simulations did not form hairpins, and DSSP plots showed that helical content was present in the peptide (Figures 1A and 2A). None of the OPLS-AA/L simulations met our criteria for hairpin formation. Instead, these simulations were enriched in “bend” conformations (green) (Figure 1A). While there was some transient turn and β-sheet content in the expected locations, there were no pronounced β-hairpin signatures (Figures 1A and 2A). Extending of the OPLS-AA/L trajectory (without charge groups and TIP3P water) to 2 μs still did not yield a native-like hairpin (data not shown).

Figure 1.

Secondary structure propensity analysis of the trajectories. Secondary structure content was assessed with the DSSP algorithm:⁷¹ coil (white), β-sheet (red), β-bridge (black), bend (green), turn (yellow), α-helix (blue), and 3₁₀ helix (gray). (A) Uncapped peptide. (B) Capped peptide. (C) pThr-80 peptide.

Figure 2.

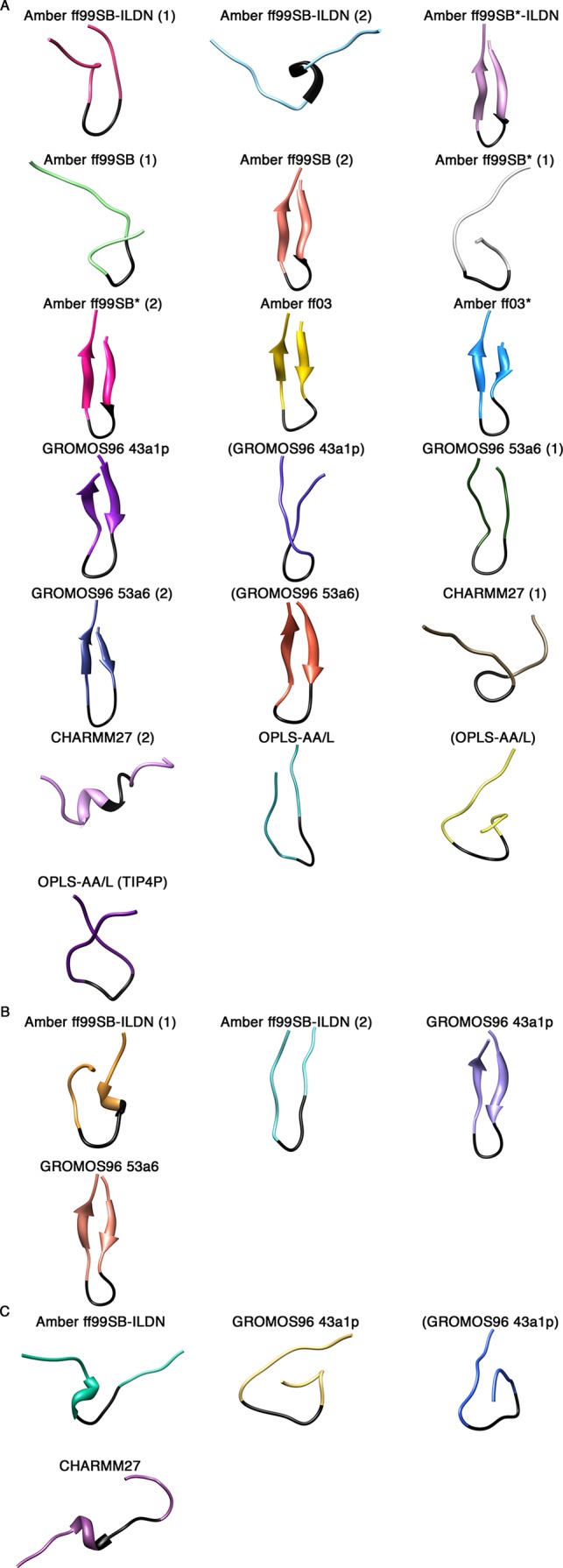
Cluster centroid structures from the last 0.1 μs of the simulations. A single cluster represented all structures in each simulation, and the center structure was extracted. (A) Uncapped peptide. (B) Capped peptide. (C) pThr-80 peptide.

There were clear differences between replicate runs using the same force fields. Specifically, the Amber ff99SB-ILDN (2), Amber ff99SB (1), and Amber ff99SB* (1) simulations did not converge upon β-hairpin conformations (Figures 1A and 2A). To determine if a longer trajectory would lead to hairpin formation, we extended the Amber ff99SB* (1) simulation to 2 μs. DSSP analysis, however, still was not indicative of a hairpin structure (data not shown).

For the capped peptides, while the Amber ff99SB-ILDN (2), GROMOS96 43a1p, and GROMOS96 53a6 simulations yielded hairpin signatures throughout large parts of the trajectories (Figure 1B), only the GROMOS96 force fields led to the formation of well-defined β-hairpins in the last 0.1 μs of the simulations (Figure 2B). Again, there were differences between the two Amber ff99SB-ILDN replicates. While the Amber ff99SB-ILDN (1) simulation did have turn and strand contents in the expected region, it appeared to be transient and not as pronounced as the Amber ff99SB-ILDN (2) hairpin signature (Figure 1B). Figure 2B shows that close to the end of the trajectory, Amber ff99SB-ILDN (1) structure adopted a short non-native helix before the turn region, while hairpin structure that is slightly displaced from the expected location was observed in the Amber ff99SB-ILDN (2) trajectory.

The phosphorylation of Thr-80 located at the turn region appears to have significant effects on the peptide folding. β-Hairpin formation was not observed in any of the pThr-80 simulations (Figures 1C and 2C). Interestingly, these simulations all displayed considerable bend content but failed to form a turn in the expected location (Figure 1C).

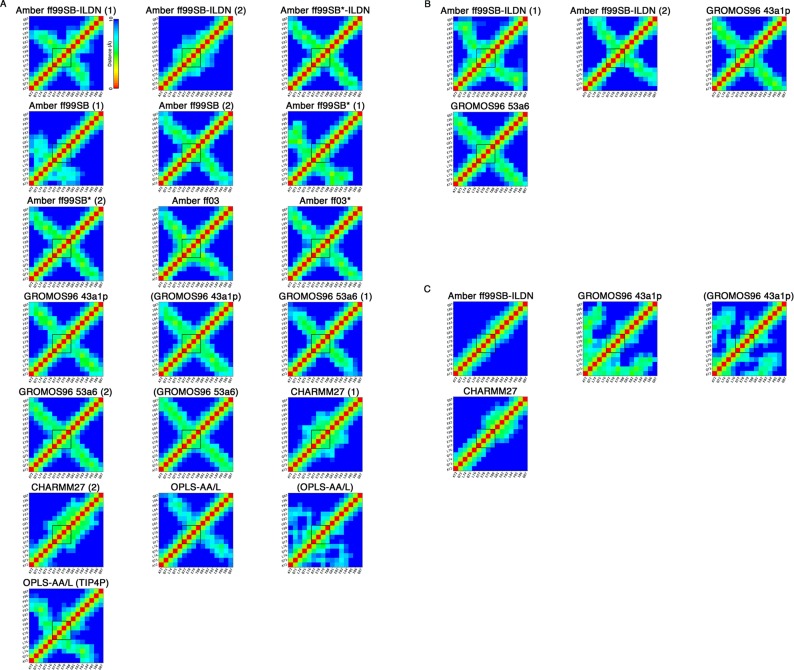
The averaged C_α–C_α atom pair distances (within 10 Å) were also plotted to identify β-hairpin formation in the simulations (Figure 3). In these plots, the β-turn (⁷⁷DEET⁸⁰) region, which the hairpin is approximately centered around, was indicated. For the uncapped peptides, the Amber ff99SB-ILDN (1), Amber ff99SB*-ILDN, Amber ff99SB (2), Amber ff99SB* (2), Amber ff03, Amber ff03*, GROMOS96 43a1p, and GROMOS96 53a6 (1 and 2) simulations, including those which used charge-groups, appeared to form β-hairpins as evidenced by the cross-strand C_α–C_α contacts centered around the β-turn (Figure 3A). Like the DSSP plots, this analysis also revealed clear differences between the replicates of Amber ff99SB-ILDN, Amber ff99SB, and Amber ff99SB* simulations. While Amber ff99SB-ILDN (2) displayed no signature of β-hairpin structure, the hairpins formed in the Amber ff99SB (1) and Amber ff99SB* (1) simulations were found in different regions as compared to the replicas (Figure 3A). The CHARMM27 simulations did not have cross-strand C_α–C_α contacts indicative of β-hairpin structures, but showed regions of compactness in the turn segment (Figure 3A). The OPLS-AA/L simulations without charge groups had some evident cross-strand contacts, but the β-turn was shifted from the expected location (Figure 3A), while the OPLS-AA/L simulation with default charge-groups did not appear to form a hairpin (Figure 3A). C_α–C_α contacts in the capped peptide simulations were indicative of hairpin structures. However, unlike the conformations observed with the GROMOS force fields, the β-hairpin in the Amber ff99SB-ILDN simulations was shifted from the expected location (Figure 3B). None of the pThr-80 simulations had cross-strand contacts evident of β-hairpin structures (Figure 3C). It is worthwhile to note that in both GROMOS96 43a1p trajectories with Thr-80 phosphorylated there was evidence of close contacts between the positively charged N-terminus and the negatively charged phosphate group (Figure 3C). Because this may represent an unphysical interaction, we performed an additional simulation with a capped version of the peptide (Table 1). In this trajectory, we still did not observe hairpin or turn formation and noticed similar close contacts between the N-terminal region and phosphate group (data not shown).

Figure 3.

C_α–C_α atom pair distances. Average C_α–C_α distances less than or equal to 10 Å during the last 0.1 μs of the MD simulations. Distances equal to or greater than 10 Å are colored blue. The black square indicates the β-turn (⁷⁷DEET⁸⁰) region. (A) Uncapped peptide. (B) Capped peptide. (C) pThr-80 peptide.

Comparison to Experimental Data

Next, we compared the results of our simulations to experimental data. To begin, we assessed how many experimentally determined atomic contacts within the Nrf2 β-hairpin were found in our simulations. Even though the free state structure of the 16-mer human Nrf2 peptide used in this study is not currently available, several atomic contacts within the β-hairpin region of mouse Nrf2 have been determined by NMR.³⁰ The mouse Nrf2 contains the same β-hairpin sequence as the human version used in this study, except with a single conservative amino acid change of L74F (Figure 4A). Given that the human and mouse Nrf2 β-hairpin sequences are nearly identical, they are expected to adopt similar structures.

Figure 4.

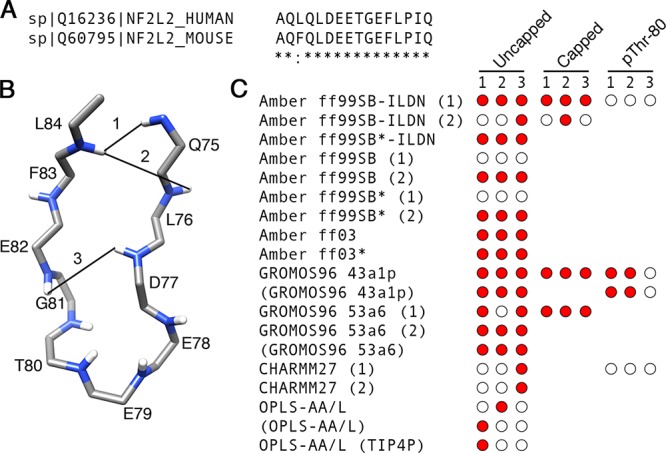
Nrf2 β-hairpin sequence alignment and native contacts. (A) Sequence alignments between the human and mouse Nrf2 β-hairpin segments were generated with ClustalW XXL.⁸¹ The Blosum scoring matrix⁸² was used, and gap penalties were set at their default values. Opening and end gap penalties were set to 10. Extending and separation gap penalties were set to 0.05. (B) Three NMR-derived cross-strand ¹H, ¹H NOEs determined by ref (30) mapped onto a model Nrf2 β-hairpin backbone structure. (C) Presence or absence of each native contact for each force field. Time-averaged distances <6 Å during the last 0.1 μs of the simulations between hydrogen atom pairs matching those observed by Tong et al.³⁰ were considered to be native contacts.

We compared the NMR-derived cross-strand ¹H, ¹H NOEs determined in ref (30) to the corresponding time-averaged distances from our MD simulations. Time-averaged distances <6 Å between hydrogen atom pairs matching those observed in³⁰ were considered to be native contacts. Because the united-atom GROMOS96 force fields used in this study do not explicitly represent every hydrogen atom, we restricted our analysis to backbone amide hydrogens, which were explicitly represented in all force fields. NOEs between adjacent residues and those involving F74 were excluded from the analysis. This reduced the number of experimentally determined native contacts used in this analysis to three (Q75 HN:L84 HN, L76 HN:L84 HN, and D77 HN:E82 HN). They are depicted in Figure 4B.

The presence or absence of each of the three contacts is shown in Figure 4C. For the uncapped peptides, the Amber ff99SB-ILDN (1), Amber ff99SB*-ILDN, Amber ff99SB (2), Amber ff99SB* (2), Amber ff03, Amber ff03*, GROMOS96 43a1p, and GROMOS96 53a6 simulations, including those which used charge-groups, had at least two of the three native contacts (Figure 4C). Once again, there were differences between the Amber replicas (Figure 4C). Notably, in the Amber ff99SB-ILDN (2), Amber ff99SB (1), and Amber ff99SB* (1) simulations, only one or none of the native contacts were present, while their replicas had all three (Figure 4C). The CHARMM27 and OPLS-AA/L simulations had only one out of the three native contacts (Figure 4C). The capped peptides were able to form all three native contacts, but differences between duplicates were also evident. The Amber ff99SB-ILDN (1) simulation had all three contacts, while its duplicate had only one (Figure 4C). Native contacts were reduced in all pThr-80 simulations as compared to their unphosphorylated counterparts (Figure 4C). Interestingly, two of the three native contacts were still present in the GROMOS96 43a1p pThr-80 trajectories (Figure 4C). In these simulations, while the two contacts in the β-sheet region of the hairpin were present, the contact in the turn region was missing (Figure 4C).

In addition to NMR-derived contacts, backbone and side chain hydrogen bonds between Asp-77 and Thr-80 are present when Nrf2 is bound to Keap1 (PDB id: 2FLU).³¹ We previously found that hydrogen bonds between these residues may also exist in the free state with high frequencies in simulations conducted with the GROMOS96 53a6 force field.⁹ Because hydrogen bonding between Asp-77 and Thr-80 may be correlated with β-hairpin formation, we calculated the frequencies of hydrogen bonding between these residues (Table 2). For the uncapped peptides, we observed high (>0.68) frequencies of Asp-77 to Thr-80 hydrogen bonding in the Amber ff99SB-ILDN (1), Amber ff99SB*-ILDN, Amber ff99SB (2), Amber ff99SB* (2), Amber ff03*, GROMOS96 43a1p, and GROMOS96 53a6 (1 and 2) simulations, including those which used charge-groups (Table 2). Like the aforementioned analyses, clear differences between some replicas were observed (Table 2). Specifically, the Amber ff99SB-ILDN (2), Amber ff99SB (1), and Amber ff99SB* (1) simulations had considerably less Asp-77 to Thr-80 hydrogen bonding as compared to their duplicates (Table 2).

Table 2. Frequency of Asp-77 to Thr-80 Hydrogen Bonding^a.

force field	uncappedb	cappedc	pThr-80d
Amber ff99SB-ILDN (1)	0.95	0.00	0.00
Amber ff99SB-ILDN (2)	0.27	0.00
Amber ff99SB*-ILDN	0.94
Amber ff99SB (1)	0.00
Amber ff99SB (2)	0.97
Amber ff99SB* (1)	0.00
Amber ff99SB* (2)	0.97
Amber ff03	0.00
Amber ff03*	0.86
GROMOS96 43a1p	0.69	0.91	0.00
(GROMOS96 43a1p)e	0.94		0.00
GROMOS96 53a6 (1)	0.90	0.92
GROMOS96 53a6 (2)	0.93
(GROMOS96 53a6)	0.91
CHARMM27	0.32		0.00
CHARMM36	0.22
OPLS-AA/L	0.00
(OPLS-AA/L)	0.00
OPLS-AA/L (TIP4P)	0.00

^aFrequencies of 1 or more hydrogen bonds during the last 0.1 μs of the trajectories. Oxygen and nitrogen atoms were acceptors. Amine groups and the hydroxyl group of Thr-80 were donors. Intraresidue hydrogen bonds were excluded from the analysis. A hydrogen bond between a hydrogen donor (D–H) and a hydrogen acceptor (A) was judged to be formed when the DA distance (r) was less than 3.2 Å, and the angle between the DA vector and the D–H bond (AD–H angle) was less than 35°.

^bValues for the peptides with unmodified N and C termini (NH₃⁺ and COO^–, respectively).

^cValues for the peptides with capped N and C termini (ACE and NH₂, respectively).

^dValues for the peptides with residue Thr-80 phosphorylated.

^eParenthetical values indicate hydrogen-bond frequencies for trajectories with default GROMACS charge groups.

It is noteworthy that in the Amber ff03 simulation, no hydrogen bonding between Asp-77 and Thr-80 was observed (Table 2). Because prior analysis showed that this trajectory formed a hairpin with three native contacts (Figure 4A), the complete lack of hydrogen bonding between these two residues was unexpected. Inspection of the trajectory showed that the side chains of Leu-76 and Asp-77 were on opposite sides of the hairpin as compared to the other simulations (data not shown). Although Asp-77 was not in an appropriate orientation to form hydrogen bonds with Thr-80, we found that the frequency of forming 1 or more hydrogen bonds between Leu-76 and Thr-80 was 0.66 in this trajectory. Low frequencies of Asp-77 to Thr-80 hydrogen bonding were found in the CHARMM27 simulations (between 0.22 and 0.32) and were completely absent in the OPLS-AA/L simulations (Table 2).

For the capped peptides, no hydrogen bonding between Asp-77 and Thr-80 was observed in the Amber ff99SB-ILDN simulations, but was present in over 90% of the structures in the last 0.1 μs of the GROMOS96 trajectories (Table 2). While the capped Amber ff99SB-ILDN (1) simulation was found to have three native contacts (Figure 4C), cluster analysis indicated that there was a short non-native helix before its β-turn region (Figure 1B). Furthermore, the DSSP plot of this trajectory did not have a typical hairpin signature (Figure 2B). These factors likely contributed to the lack of Asp-77 to Thr-80 hydrogen bonding in this trajectory (Table 2). The capped Amber ff99SB-ILDN (2) simulation had only one native contact (Figure 4C), and its β-turn was slightly displaced from the expected location (Figure 3B), factors that likely contributed to the lack of hydrogen bonding (Table 2). Hydrogen bonding between Asp-77 and Thr-80 was not observed in any of the pThr-80 simulations (Table 2).

We also compared the Nrf2 peptide structures from our simulations to that of the Keap1-bound state (PDB id: 2FLU).³¹ This comparison is interesting because the ETGE motif of the disordered Nrf2 has been shown to have a tendency to form bound state-like structure even in the absence of the target.^9,30,31 Because the Nrf2 β-hairpin does not adopt a well-defined in the free state,³⁰ we restricted the rmsd calculations to backbone atoms only.

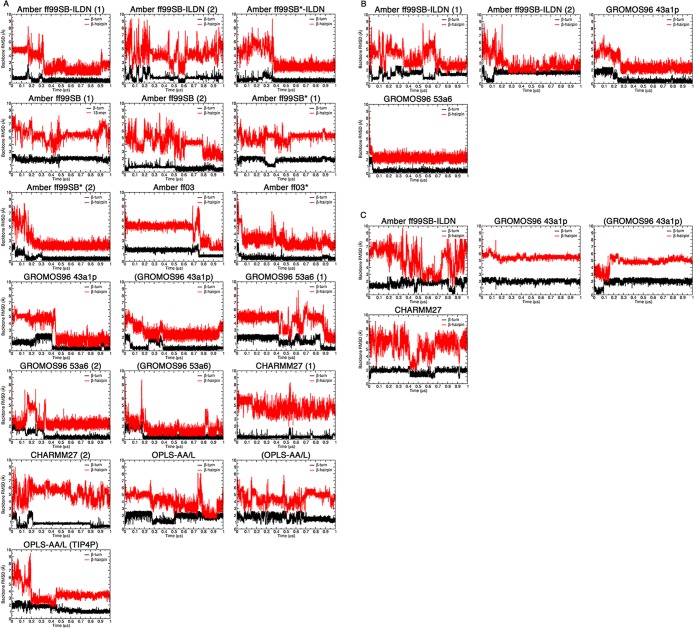
The rmsd’s were calculated separately for the β-turn, ⁷⁷DEET⁸⁰ and β-hairpin, ⁷²AQLQLDEETGEFL⁸⁴ regions. The rmsd’s throughout the trajectories are plotted in Figure 5, and average rmsd values over the last 0.1 μs are shown in Figure 6 and summarized in Tables 3–5. For the uncapped peptides, the Amber ff99SB-ILDN (1), Amber ff99SB*-ILDN, Amber ff99SB (2), Amber ff99SB* (2), Amber ff03, Amber ff03*, GROMOS96 43a1p, and GROMOS96 53a6 (1 and 2) simulations achieved average rmsd’s < 1 and <3 Å to the bound state β-turn and hairpin, respectively, including simulations that used charge-groups (Figure 6A). Again, there were some differences between replicas. The Amber ff99SB-ILDN (2) simulation had a β-turn region with an average rmsd <1 Å, but when considering the full β-hairpin, the rmsd was larger than 4.8 Å (Figure 6A). Also, the Amber ff99SB (1) and Amber ff99SB* (1) simulations had substantially higher rmsd’s as compared to their duplicates (Figures 5A and 6A). The CHARMM simulations did not lead to a bound state like β-hairpin (rmsd’s > 4 Å), but had β-turn rmsd’s below 1 Å (Figures 5A and 6A). The OPLS-AA/L simulations had both β-turn and hairpin rmsd’s greater than 1 and 3 Å, respectively (Figures 5A and 6A), indicating significant deviations from the bound-state structure.

Figure 5.

Backbone rmsd’s between the bound state and MD structures throughout the trajectories. The rmsd values were calculated for the β-turn 4-mer, ⁷⁷DEET⁸⁰ (black), and β-hairpin 13-mer, ⁷²AQLQLDEETGEFL⁸⁴ (red), by least-squares fitting the backbone atoms (N, C_α, and C) from each frame to the corresponding atoms of bound state reference structure (PDB id: 2FLU).³¹ (A) Uncapped peptide. (B) Capped peptide. (C) pThr-80 peptide.

Figure 6.

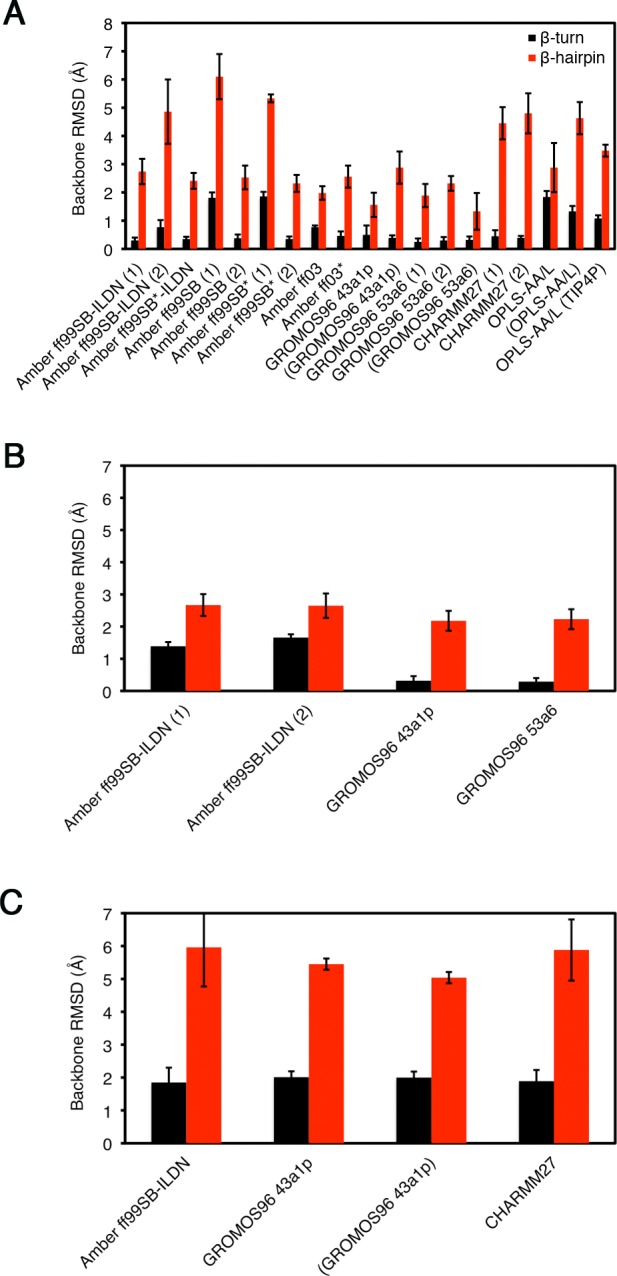
Average backbone rmsd’s between the bound state and MD structures. Average rmsd values were calculated over the last 0.1 μs of the simulations for the β-turn 4-mer, ⁷⁷DEET⁸⁰ (black), and β-hairpin 13-mer, ⁷²AQLQLDEETGEFL⁸⁴ (red), by least-squares fitting the backbone atoms (N, C_α, and C) from each frame to the corresponding atoms of bound state reference structure (PDB id: 2FLU).³¹ (A) Uncapped peptide. (B) Capped peptide. (C) pThr-80 peptide.

Table 3. Average Backbone rmsd’s between the Bound State Structure and MD Structures of the Uncapped Peptides^a.

force field	backboneb (Å) ± sdev β-turnc	backbone (Å) ± sdev β-hairpind
Amber ff99SB-ILDN (1)	0.30 ± 0.10	2.74 ± 0.45
Amber ff99SB-ILDN (2)	0.77 ± 0.25	4.86 ± 1.14
Amber ff99SB*-ILDN	0.35 ± 0.08	2.41 ± 0.28
Amber ff99SB (1)	1.81 ± 0.19	6.10 ± 0.80
Amber ff99SB (2)	0.38 ± 0.13	2.53 ± 0.42
Amber ff99SB* (1)	1.86 ± 0.16	5.33 ± 0.14
Amber ff99SB* (2)	0.35 ± 0.09	2.32 ± 0.30
Amber ff03	0.77 ± 0.06	1.98 ± 0.24
Amber ff03*	0.46 ± 0.16	2.56 ± 0.39
GROMOS96 43a1p	0.50 ± 0.33	1.56 ± 0.43
(GROMOS96 43a1p)e	0.39 ± 0.09	2.88 ± 0.57
GROMOS96 53a6 (1)	0.25 ± 0.12	1.89 ± 0.41
GROMOS96 53a6 (2)	0.30 ± 0.12	2.32 ± 0.26
(GROMOS96 53a6)	0.32 ± 0.12	1.42 ± 0.56
CHARMM27	0.45 ± 0.21	4.45 ± 0.57
CHARMM36	0.39 ± 0.07	4.80 ± 0.71
OPLS-AA/L	1.84 ± 0.21	2.88 ± 0.87
(OPLS-AA/L)	1.33 ± 0.19	4.63 ± 0.57
OPLS-AA/L (TIP4P)	1.08 ± 0.11	3.48 ± 0.21

^aAverage rmsd’s were calculated over the last 0.1 μs of the trajectories.

^bBackbone atoms include N, C_α, and C.

^cβ-Turn (⁷⁷DEET⁸⁰).

^dβ-Hairpin (⁷²AQLQLDEETGEFL⁸⁴).

^eAverage rmsd’s for trajectory with default GROMACS charge groups.

Table 5. Average rmsd’s between the Bound State Conformation and MD Structures of the pThr-80 Peptides^a.

force field	backboneb (Å) ± sdev β-turnc	backbone (Å) ± sdev β-hairpind
Amber ff99SB-ILDN	1.85 ± 0.45	5.96 ± 1.19
GROMOS96 43a1p	2.01 ± 0.18	5.45 ± 0.17
(GROMOS96 43a1p)e	2.00 ± 0.18	5.04 ± 0.17
CHARMM27	1.89 ± 0.34	5.88 ± 0.93

^aAverage rmsd’s were calculated over the last 0.1 μs of the trajectories.

^bBackbone atoms include N, C_α, and C.

^cβ-Turn (⁷⁷DEET⁸⁰).

^dβ-Hairpin (⁷²AQLQLDEETGEFL⁸⁴).

^eAverage rmsd’s for trajectory with default GROMACS charge groups.

Table 4. Average rmsd’s between the Bound State Conformation and MD Structures of the Capped Peptides^a.

force field	backboneb (Å) ± sdev β-turnc	backbone (Å) ± sdev β-hairpind
Amber ff99SB-ILDN (1)	1.39 ± 0.13	2.67 ± 0.34
Amber ff99SB-ILDN (2)	1.66 ± 0.10	2.65 ± 0.38
GROMOS96 43a1p	0.32 ± 0.14	2.18 ± 0.31
GROMOS96 53a6	0.29 ± 0.11	2.23 ± 0.31

^aAverage rmsd’s were calculated over the last 0.1 μs of the trajectories.

^bBackbone atoms include N, C_α, and C.

^cβ-Turn (⁷⁷DEET⁸⁰).

^dβ-Hairpin (⁷²AQLQLDEETGEFL⁸⁴).

For the capped peptides, both Amber ff99SB-ILDN simulations had average rmsd’s < 3 Å for the hairpin region, but their β-turns had rmsd’s > 1 Å (Figures 5B and 6B). In comparison, both GROMOS96 force fields had rmsd’s of <1 and <3 Å for the β-turn and hairpin, respectively (Figures 5B and 6B). These rmsd’s were similar to their uncapped versions (Figures 5A and 6A). It is worthwhile to note that the capped GROMOS96 53a6 simulation converged to bound state like structure in <0.05 μs, the fastest of all of the simulations (Figure 5B). Among the simulations that had bound state like rmsd’s, the amount of time it took to adopt these conformations varied between <0.05 and ∼0.9 μs, even for duplicates using the same force field (Figure 5A and B). However, once a bound state like structure was formed, it tended to remain stable. The β-turn and hairpin rmsd’s were higher in all pThr-80 simulations as compared to those of the unphosphorylated peptides (Figures 5C and 6C).

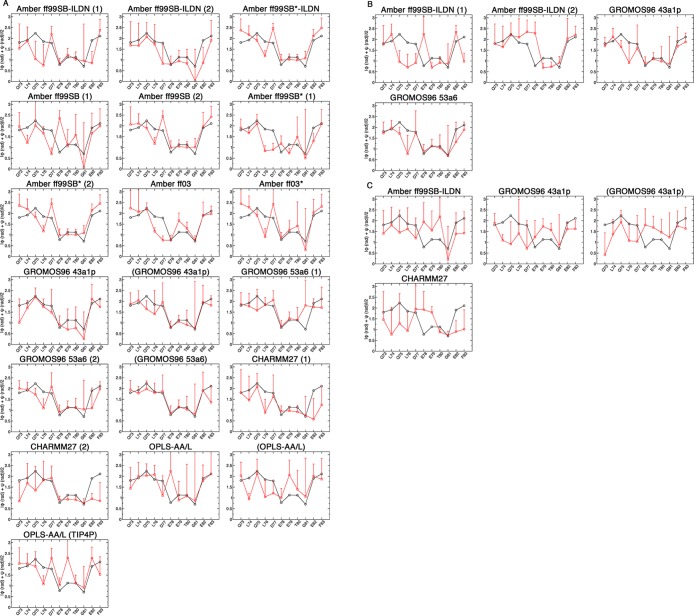
The convergence of the dihedral angles from the trajectories to those from the bound state structure was also assessed (PDB id: 2FLU).³¹ The combined ϕ and ψ angles from the simulations and bound state structure are shown in Figure 7, and the average per-residue deviations are shown in Figure 8. For the uncapped peptides, the GROMOS96 43a1p with charge groups and 53a6 force field simulations had the lowest ϕ and ψ deviations from the bound state structure (Figure 8A). These simulations had combined ϕ and ψ deviations of <7° and <17° per residue from the bound state in their β-turn and hairpin regions, respectively (Figure 8A). The Amber ff99SB-ILDN (1) and CHARMM simulations had combined ϕ and ψ deviations of ∼10° in their β-turns, but deviated >20° per residue when considering the entire hairpin (Figure 8A). For the capped peptides, both GROMOS96 force fields had slightly lower deviations as compared to their uncapped counterparts and had considerably lower deviations than Amber ff99SB-ILDN (Figure 8B). The β-turn and hairpin deviations were higher in all pThr-80 simulations as compared to those of the unphosphorylated peptides (Figure 8B).

Figure 7.

Comparison of the backbone dihedral angles from the bound state structure and MD simulations. The ϕ and ψ angles for residues ⁷³QLQLDEETGEF⁸³ were converted to radians, and the absolute values were summed and averaged. Black circles indicate the values from the bound state crystal structure (PDB id: 2FLU).³¹ Red squares are the values over the last 0.1 μs of the simulations. (A) Uncapped peptide. (B) Capped peptide. (C) pThr-80 peptide.

Figure 8.

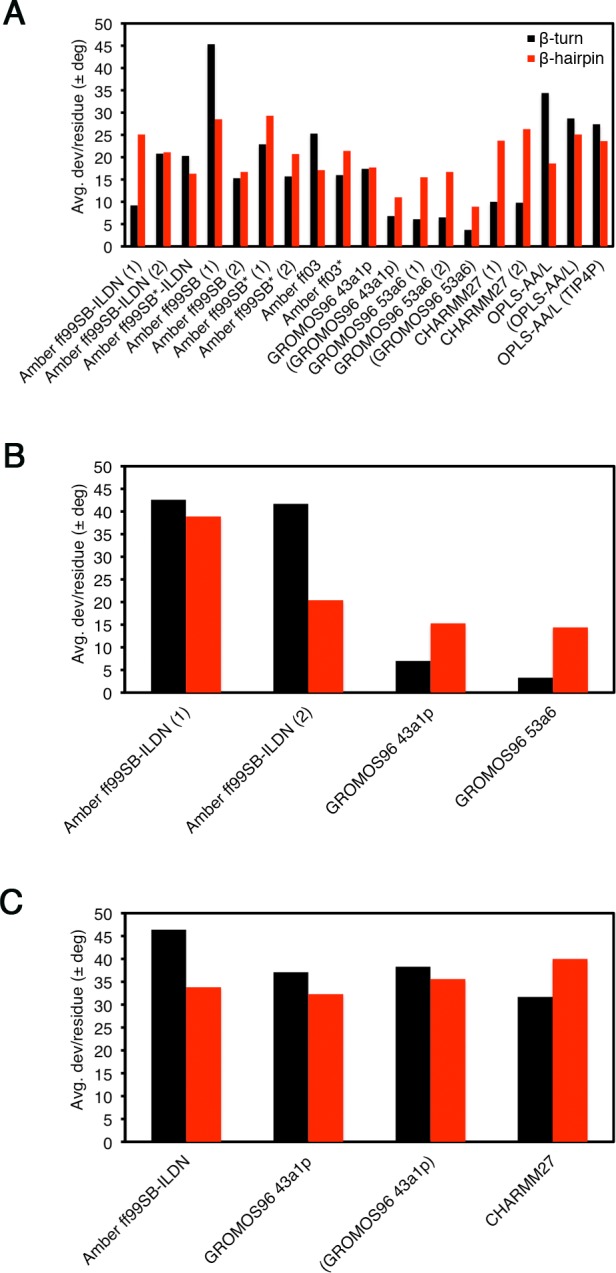
Average combined ϕ and ψ deviations per residue from the bound state crystal structure (PDB id: 2FLU).³¹ Black bars are for the β-turn 4-mer, ⁷⁷DEET⁸⁰, and red bars are for the β-hairpin 13-mer, ⁷²AQLQLDEETGEFL⁸⁴. Data were analyzed over the last 0.1 μs of the simulations. (A) Uncapped peptide. (B) Capped peptide. (C) pThr-80 peptide.

Secondary Structure Formation at Elevated Temperatures

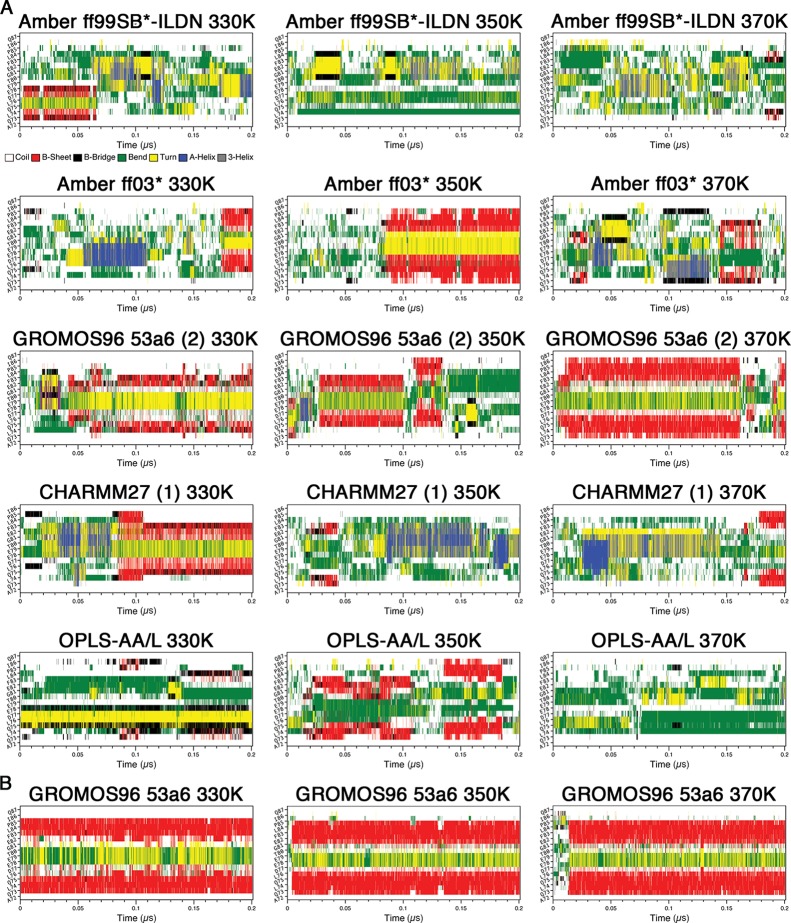
Finally, we have performed MD simulations at elevated temperatures using a subset of force fields, Amber ff99SB*-ILDN and ff03*, GROMOS96 53a6, CHARMM27, and OPLS-AA/L, to identify secondary structure formation of the Neh2 peptide under these conditions. Using elevated temperatures provides an additional test to examine possible metastable states. The simulations were performed at 330, 350, and 370 K from both the initial and the final (after 1 μs) system configurations at 310 K. Again, we used DSSP analysis to illustrate the evolution of secondary structures over the trajectories.

In the simulations starting from the initial (unfolded) system coordinates, hairpin formation, at the expected location, was observed in the Amber ff03*, GROMOS96 53a6 (2), and capped GROMOS96 53a6 simulations at 330 K (Figure 9). β-Hairpin structures were also identified in the MD simulations using these force fields at 310 K as mentioned above (Figure 1). Hairpin conformation, which was not observed in CHARMM27 (1) at 310 K, was significantly populated in the trajectory at 330 K (Figure 9). At 350 K, the Amber ff03*, GROMOS96 53a6 (2), and capped GROMOS96 53a6 simulations still had hairpin signatures at some points in their trajectories, but β-hairpin structure was no longer observed in the CHARMM27 (1) simulation (Figure 9). On the other hand, a low population of hairpin conformation was observed in the 350 K OPLS-AA/L trajectory (Figure 9). Significant population of β-hairpin structure remained even at 370 K in GROMOS96 53a6 (2) and capped GROMOS96 53a6 simulations (Figure 9), while only transiently formed hairpin was observed in CHARMM27 (1). It is noteworthy that rapid hairpin folding and high thermal stability were observed in the capped GROMOS96 53a6 simulations at all elevated temperatures (Figure 9).

Figure 9.

Secondary structure propensity analysis of the elevated temperature simulations from the initial system configurations. Secondary structure content was assessed with the DSSP algorithm:⁷¹ coil (white), β-sheet (red), β-bridge (black), bend (green), turn (yellow), α-helix (blue), and 3₁₀ helix (gray). (A) Uncapped peptide. (B) Capped peptide.

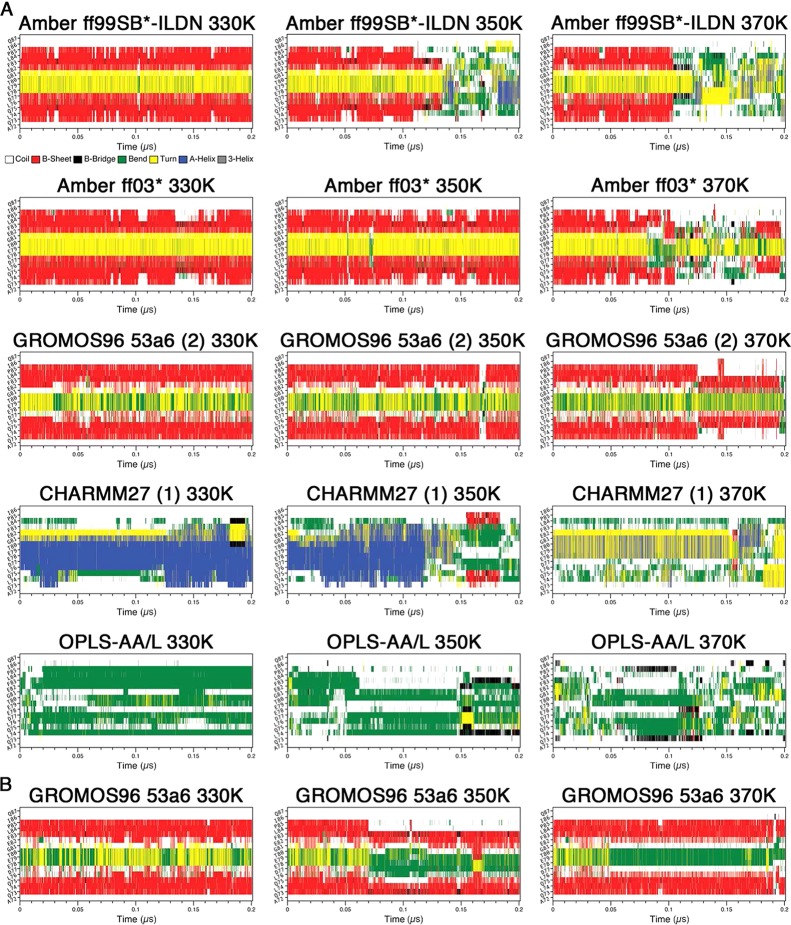
In the simulations starting from the final system coordinates, the Amber ff99SB*-ILDN, Amber ff03*, GROMOS96 53a6 (2), and capped GROMOS96 53a6 trajectories, all of which formed hairpins at 310 K, maintained hairpin signatures at 330 K over 0.2 μs (Figure 10). On the other hand, the CHARMM27 (1) and OPLS-AA/L trajectories at 330 K were heavily biased by α-helical and bend conformations, respectively, similar to what was observed at 310 K (Figure 10). When the temperature was increased to 350 K, the hairpin signature in the Amber ff99SB*-ILDN trajectory disappeared shortly after ∼0.1 μs; however, the Amber ff03*, GROMOS96 53a6 (2), and capped GROMOS96 53a6 trajectories maintained their hairpins over the whole 0.2 μs period (Figure 10). The CHARMM27 (1) simulation at 350 K lost its helical properties after about 0.15 μs and appeared to form a hairpin shortly after (Figure 10). At 370 K, both the Amber ff99SB*-ILDN and the Amber ff03* trajectories lost their hairpin signatures after ∼0.1 μs, but the GROMOS96 53a6 (2) and capped GROMOS96 53a6 simulations still remained in hairpin conformations throughout almost whole trajectories (Figure 10). On the other hand, the CHARMM27 (1) simulation at 370 K lost its helical property almost immediately and a turn conformation was present in the expected location, but a distinct hairpin signature was not observed (Figure 10). The OPLS-AA/L trajectories did not have any clear hairpin signatures at any of the temperatures (Figure 10). Once again, high thermal stability was observed in the GROMOS96 53a6 simulations (Figure 10).

Figure 10.

Secondary structure propensity analysis of the elevated temperature simulations from the final (after 1 μs) system configurations. Secondary structure content was assessed with the DSSP algorithm:⁷¹ coil (white), β-sheet (red), β-bridge (black), bend (green), turn (yellow), α-helix (blue), and 3₁₀ helix (gray). (A) Uncapped peptide. (B) Capped peptide.

Discussion and Conclusions

We have examined the folding of a 16-mer polypeptide with 10 commonly used biomolecular force fields. The peptide used in this study is derived from the Neh2 domain of Nrf2. Despite that Neh2 has been characterized as being intrinsically disordered, the region encoded by the sequence of this peptide has been shown to contain β-hairpin structure.^30,31,72 Various criteria were used to assess β-hairpin formation of this peptide and compare the results to experimental data. Although the simulations all used the same, non-native, starting structure and were performed with identical parameters, clear differences were observed between different force fields used and even between replicate simulations with the same force field.

While no single type of analysis was sufficient to thoroughly assess and compare β-hairpin formation, the DSSP plots were useful for visualizing potential hairpin formation in this work. In addition, these analyses were also useful in identifying other types of secondary structures. For example, DSSP plots of the CHARMM27 simulations showed that the Nrf2 peptide did not fold into hairpins, but had tendencies to form short α-helices (Figure 2A). This finding was not completely unexpected because CHARMM force fields have been known to have a bias toward helical structures, even when simulating the folding of all β proteins.^3,11−13,73 In addition to CHARMM27, the Amber ff03 force field has also been shown to overstabilize helical structures. Lindorff-Larsen et al.⁴⁴ observed that while both CHARMM27 and Amber ff03 could fold the α-helical villin headpiece, proper folding of the β-sheet WW domain could not be achieved even in simulations that were 10 times the experimentally determined folding time in length. On the other hand, they found that the “helix–coil-balanced” Amber ff03* and recently developed CHARMM22* variants could achieve proper folding of both villin and the WW domain.^8,57

The DSSP plots for the OPLS-AA/L force field simulations also were not indicative of hairpins, but showed considerable amounts of “bend” content. This aligns with the finding of Cao et al.⁷⁴ that this force field did not produce the expected β-hairpin structure of the H1 peptide. Interestingly, simulations of the H1 peptide performed with GROMOS96 43a1 yielded a β-hairpin structure consistent with experimental data.⁷⁴ It is difficult to determine why the OPLS-AA/L simulations did not form a native-like hairpin structure in our simulations. It is possible that, in general, longer trajectories may be needed for convergence due to the rugged energy landscape and different barriers in these systems.^75,76 The weak hairpin signature observed in the DSSP plot of the OPLS-AA/L trajectory at 350 K supports this notion. Alternatively, there may be incompatibilities between our peptide sequence and OPLS-AA/L, such as high amounts of exposed hydrophobic content.⁷⁴

The C_α–C_α contacts plots also illustrated β-hairpin formation and helped to identify non-native hairpins. For example, these plots showed that the β-turn in the capped peptide Amber ff99SB-ILDN (2) simulation was slightly displaced from its expected location (Figure 2B). This likely explains the lack of Asp-77 to Thr-80 hydrogen bonding in this simulation (Table 2). Together, our findings from the DSSP and C_α–C_α contact analysis suggested that the uncapped Amber ff99SB-ILDN (1), Amber ff99SB*-ILDN, Amber ff99SB (2), Amber ff99SB* (2), Amber ff03, Amber ff03*, GROMOS96 43a1p, GROMOS96 53a6 (1 and 2), and capped GROMOS96 43a1p and 53a6 simulations formed native-like β-hairpins.

Interestingly, the simulations that formed β-hairpins, as judged by DSSP and C_α–C_α contact analysis, also exhibited experimentally determined native contacts present in the free state of Nrf2. Furthermore, we observed that the presence or absence of native contacts was correlated with the frequency of Asp-77 to Thr-80 hydrogen bonding to some extent. Interactions between these residues are thought to be important for the hairpin structure.^9,31 Most of the simulations of the uncapped and unphosphorylated peptides that had two or more native contacts also had high frequencies of Asp-77 to Thr-80 hydrogen bonding. On the other hand, when one or zero native contacts were present, there was usually less hydrogen bonding. One exception was the Amber ff03 simulation, which had all three native contacts, but lacked hydrogen bonding between Asp-77 to Thr-80. Figure 5 shows that in this simulation, Leu-76 and Asp-77 had large backbone dihedral angle deviations from the bound state structure, which could possibly explain the lower hydrogen bonding with Thr-80. It is possible that alternate hydrogen bonds between Leu-76 and Thr-80 may have compensated. The evident positive correlation between native contact formation and a high frequency of Asp-77 to Thr-80 hydrogen bonding in our simulations supports prior suggestions that these interactions are vital for the hairpin structure.^9,31

We also found that the simulations that formed β-hairpins converged upon conformations that were similar to the structure of Nrf2 bound to Keap1 (PDB id: 2FLU).³¹ It is common for disordered proteins, like Nrf2, to contain preformed structural elements in their binding regions.^9,30,77−79 Indeed, NMR data and our prior MD simulations indicated that Nrf2 adopts a hairpin structure in the free-state, which is in high resemblance to its Keap1 bound form (PDB id: 2FLU).^9,31 Therefore, it was expected that simulations with 2–3 free state native contacts also had low rmsd’s to the bound state structure. The GROMOS96 simulations clearly had the lowest β-turn and hairpin rmsd’s of all of the simulations. These simulations also had very low dihedral angle deviations from the bound state structure.

In general, the simulations that used charge-groups or peptide capping groups were not largely different from their uncapped counterparts with single atom charge-groups. When studying peptides from the interior of a protein sequence, it is common to add capping groups to the ends. This neutralizes the unphysical charges introduced by the free N- and C-termini, which can potentially disrupt the native structure. However, we did not find that the uncapped termini had a detrimental effect on hairpin folding in our current simulations. The GROMOS96 force field simulations employing default charge-groups or peptide capping groups were highly consistent, in all aspects, to their uncapped counterparts. On the other hand, in both capped Amber ff99SB-ILDN replicates, the peptide folded into structures that were moderately different from their uncapped counterparts. It was difficult to determine the cause of this behavior, and it could simply be a convergence issue.

The finding that none of the simulations where Thr-80 was phosphorylated formed β-hairpins was not surprising. Experimental data have shown that phosphorylation of this residue can severely impair binding of Nrf2 to Keap1, likely due to a disruption of β-turn formation.³¹ Our pThr-80 simulations were consistent with this proposition and also suggest that β-turn disruption strongly impairs hairpin formation.

The evident differences between duplicate simulations in this work highlight the importance of replica simulations when performing MD simulations of folding. Even though all duplicate simulations here used identical starting structures and parameters, the assignment of different initial atom velocities led the simulations to follow different pathways. As a result, duplicate simulations did not always converge upon folded structures even with microsecond long trajectories. In this work, we have conducted simulations at elevated temperatures using a subset of force fields to gain insights into the temperature-dependence and metastability of conformational sampling. The results show that with the GROMOS96 53a6 force field, the Neh2 peptide continued to fold into β-hairpin conformation and remained stable even at higher temperatures. This is quite different from what was observed for Amber ff99SB*-ILDN as the hairpin structure becomes less stable under this force field when the temperature increases. Although native-like conformation was not observed in the microsecond long CHARMM27 (1) simulation at 310 K, the peptide quickly folded into a β-hairpin structure at 330 K. Therefore, the lack of conformational convergence at lower temperature may simply be due to insufficient sampling time. However, further increase in temperature (i.e., 350 and 370 K) again led to the disappearance of β-hairpin structure in the CHARMM27 (1) simulations. The results here also show that, although long simulation times are necessary, it is important to have alternative methods of sampling conformations, such as replica-exchange and related methods.⁸³⁻⁸⁵

Finally, this and other recent comparative studies^44,45,86 show the importance of using different criteria for assessing the properties of different force fields. In addition to more reliable simulations, such studies provide invaluable information about the collective nonadditive properties of amino acids that are helpful in interpreting experiments.

Information Available.

Two videos are available: Video 1: The first and last 10 ns of the Amber ff99SB-ILDN (1), Amber ff99SB*-ILDN, Amber ff99SB (2), Amber ff03, Amber ff03* GROMOS96 43a1p, GROMOS96 53a6 (2), CHARMM27 (2), and OPLS-AA/L trajectories (without terminal capping or charge groups). For clarity, water, ions, and hydrogens are not shown, and rotation and translation of the peptide has been removed. Secondary structures were colored as follows in VMD: yellow, β-sheet (arrows indicate chain direction); purple, α helix; blue, 3₁₀ helix; white, coil. Video 2: 0–400 ns of the Amber ff99SB* (2) trajectory. For clarity, water, ions, and hydrogens are not shown, and rotation and translation of the peptide has been removed. Secondary structures were colored as follows in VMD: yellow, β-sheet (arrows indicate chain direction); purple, α helix; blue, 3₁₀ helix; white, coil. This material is available free of charge via the Internet at http://www.flickr.com/photos/softsimu/.

The authors declare no competing financial interest.