iAPBS: a programming interface to Adaptive Poisson-Boltzmann Solver (APBS)

Abstract

The Adaptive Poisson-Boltzmann Solver (APBS) is a state-of-the-art suite for performing Poisson-Boltzmann electrostatic calculations on biomolecules. The iAPBS package provides a modular programmatic interface to the APBS library of electrostatic calculation routines. The iAPBS interface library can be linked with a FORTRAN or C/C++ program thus making all of the APBS functionality available from within the application. Several application modules for popular molecular dynamics simulation packages – Amber, NAMD and CHARMM are distributed with iAPBS allowing users of these packages to perform implicit solvent electrostatic calculations with APBS.

1. Introduction

The important role of solvation in biomolecular systems has led to the development of a variety of computational methods for studying the properties of these interactions [1]. Two of the most popular methods are explicit solvent methods, which treat the solvent in full atomic detail, and implicit solvent methods, which represent the solvent through its average effect on solute. Although explicit solvent methods offer a very detailed description of biomolecular solvation they are computationally demanding due to the large number of degrees of freedom associated with the explicit solvent and ions. Consequently, implicit solvent methods have become popular alternatives to explicit solvent approaches [2–5].

The Adaptive Poisson-Boltzmann Solver (APBS) [6] is a software package for the numerical solution of the Poisson-Boltzmann equation, one of the most popular continuum descriptions of solvation for biomolecular systems. The Poisson-Boltzmann equation (PBE) [7, 8]

$$-\nabla ·\epsilon (x)\nabla \phi (x)+{\overline{\kappa }}^2(x)sinh\phi (x)=f(x),$$ (1)

relates the electrostatic potential (φ) to the dielectric properties of the solute and solvent (ε), the ionic strength of the solution and the accessibility of ions to the solute interior (κ̄²), and the distribution of solute atomic partial charges (f). This nonlinear PBE equation is often simplified to the linearized PBE (LPBE) by assuming sinh φ(x) ≈ φ(x).

APBS was designed to efficiently evaluate electrostatic properties for a wide range of length scales and has been used for calculations on systems from small to very large [6, 9, 10]. APBS is robust and offers state-of-the-art computational algorithms for the finite difference (FD) and finite element (FE) discretization schemes of the Poisson-Boltzmann equation. The iAPBS interface library programmatically abstracts all APBS features and makes them available to 3rd-party applications, like molecular dynamics and Monte Carlo simulation packages. APBS integration augments these 3rd-party packages with an advanced facility for evaluating implicit solvent electrostatic energies and forces. It also adds the ability for 3rd-party software to output spatial distributions of the calculated properties (charge, electrostatic potential, energy density, etc.) for visualization and post-processing.

2. Software Design and Methods

2.1. Implementation

The APBS package^§ is written in an object-oriented form of ANSI C with some parts of the code in FORTRAN^||. The numerical basis of the code is FEtk, a scientific computing toolkit developed by the Holst group [11, 12]. Through FEtk, APBS uses MALOC, a hardware abstraction library for a great portability, PMG (a multigrid solver) [13, 14] and MC (an adaptive finite element solver) [11, 12] for the problem domain discretization routines. The object-oriented nature of the APBS code lends itself to encapsulation and inclusion in other applications. The iAPBS software was written with this goal in mind: encapsulating the APBS functionality for easy integration with biochemical simulation codes which use molecular dynamics, Monte Carlo and other methods where implicit solvent contributions are evaluated.

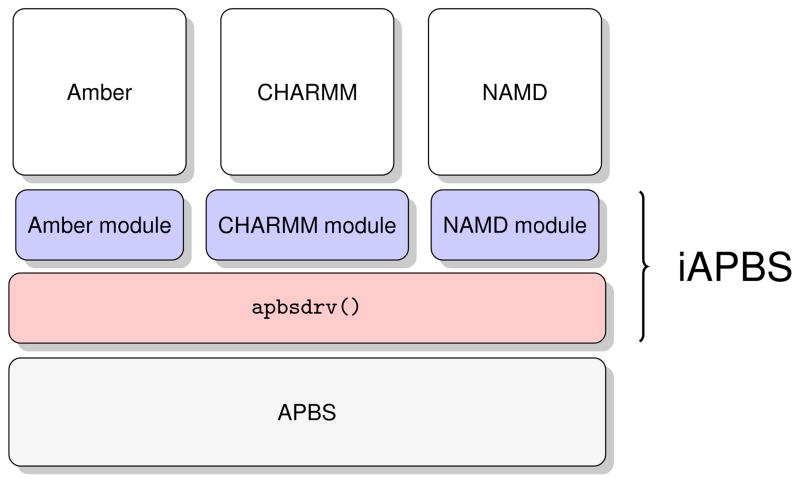
A schematic representation of the iAPBS architecture design is shown in Figure 1. iAPBS consists of two software layers: a low-level APBS library interface function (apbsdrv()) and high level, application-specific modules. The apbsdrv() interface function abstracts all APBS functionality and exposes it through an application programming interface (API) to the higher level application module. The function accepts several input parameters – coordinates of atoms, their charges and radii and APBS calculation parameters. All these input parameters are passed to the APBS routines prior to the electrostatic calculation. The function returns calculated polar and non-polar solvation energies and forces. Various calculated properties like electrostatic potential, solvent accessible surface definition, charge distribution, can also be written to files and subsequently post-processed or visualized by external applications. The interface is written in an object-oriented form of the C programming language and can be transparently called from any C, C++ or FORTRAN code.

Figure 1.

Schematic design of the iAPBS architecture. The low level interface (apbsdrv(), light red) abstracts all the APBS functionality and presents it through an API to higher level, application specific modules (blue).

The calculated electrostatic and non-polar energies and forces are then incorporated into a biochemical simulation program by the application-specific module. This module should also parse the application input files and perform error checking and output printing. Currently, application modules for Amber [15], CHARMM [16] and NAMD [17] molecular dynamics packages are distributed with iAPBS.

The iAPBS distribution also includes, in addition to the extensive testing facilities a reference module implementation in FORTRAN (src/wrapper.f) which reads input data from an external file, calls the apbsdrv() interface function and prints out calculated electrostatic energy. This reference code can be used as a template for writing additional application modules. The iAPBS documentation includes an extensive user guide with practical examples and also a programmer’s guide describing the iAPBS API which should aid in application module development.

2.2. Application Modules

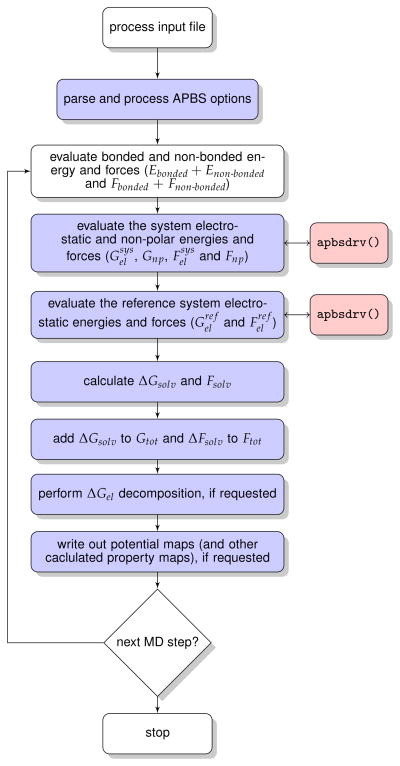
The role of the application modules is to integrate APBS calculated electrostatic properties into the information flow in a molecular dynamics simulation program. When carrying out implicit solvent molecular dynamics simulations, the calculated solvation energies and forces are typically added to the total system free energy (G_tot) and forces (F_tot) in each MD step. A flowchart presented in Figure 2 shows how the iAPBS modules can be incorporated into a molecular dynamics modeling program.

Figure 2.

A symbolic flowchart of the iAPBS module integration to a molecular dynamics simulation program. The white boxes represent data processing and calculation by the MD application. The iAPBS module code (blue blocks) parses and pre-processes APBS calculation parameters, calls the low level apbsdrv() interface (light red), updates the total system forces and energy with the calculated solvation terms (ΔF_el + F_np and ΔG_el + G_np, respectively) and, if requested carries out post-processing of the calculated quantities.

First, the application parses the general MD calculation parameters, reads in the molecule coordinates, bonding information and the necessary force field parameters. Next, the iAPBS module parses input files for the APBS-related calculation parameters; for example, if solution of the nonlinear or linearized Poisson-Boltzmann equation was selected, discretization scheme, type of boundary conditions, size of the grid and its resolution, dielectric constants for the protein and solvent, ionic strength, etc. In addition to the molecular Cartesian coordinates, per-atom charges and radii are also read in. Since calculated continuum solvation properties using a discontinuous dielectric function are very sensitive to the surface definitions, the selection of radius parameters is an important step in any PB calculation [18–20]. iAPBS modules offer several flexible options how the charge and radius set is constructed. These values can be either automatically extracted from the appropriate molecular dynamics force field or they can be read in from an external file. All available modules support reading the charge and radius information from PQR files. The format of PQR files is a modified PDB format with added charge and radius parameters. A PQR file can be generated from a PDB file using the PDB2PQR utility [21] or the PDB2PQR web service [22]. The charge and radius information can also be read from a simply formatted keyword/value list.

The iAPBS interface function then performs the actual electrostatic calculation utilizing the necessary APBS library routines^¶. Upon exit the function returns the calculated electrostatic and non-polar energies and forces which are then added to the total system free energy and forces. This process is described in detail in the following two sections.

2.2.1. Calculating Solvation Energy

The total free energy of the system (G_tot) in implicit solvent stochastic molecular dynamics simulations can be written as a sum of the internal energy of the molecule (bonded and non-bonded) and free energy of solvation

$$G_{\mathit{tot}}=E_{\mathit{bonded}}+E_{\mathit{non}-\mathit{bonded}}+\mathrm{\Delta }{G}_{\mathit{solv}}.$$ (2)

The bonded internal energy E_bonded includes contributions from covalent interactions and the non-bonded internal energy E_non-bonded usually contains the van der Waals and Coulombic electrostatic terms. Both, the bonded and non-bonded energy terms are calculated by the MD application. The total solvation free energy of a molecule ΔG_solv is calculated by the iAPBS module using the APBS electrostatic routines. This term is computed [23] as a sum of the electrostatic energy of the system (ΔG_el) and the non-polar contribution to biomolecular energetics (G_np)

$$\mathrm{\Delta }{G}_{\mathit{solv}}=\mathrm{\Delta }{G}_{el}+G_{np}.$$ (3)

The total electrostatic energy G_el can be obtained by solving the Poisson-Boltzmann equation. However, the calculated electrostatic energy (and force) contains large “self-energy” terms associated with the interaction of a particular charge with itself these terms are highly dependent on the discretization of the problem [24]. Therefore, the self-energy terms are removed by a reference calculation using the same numerical discretization

$$\mathrm{\Delta }{G}_{el}=G_{el}^{\mathit{sys}}-G_{el}^{\mathit{ref}},$$ (4)

where $G_{el}^{\mathit{sys}}$ is the electrostatic free energy of the system with different dielectric constant inside (in the protein, ε_p) and outside (in the solvent, ε_s) of the biomolecule, a fixed charge distribution corresponding to the atom locations and charges, and a varying ion accessibility coefficient (κ̄²(x)) that is zero inside the biomolecule and equal to the bulk ionic strength outside. The reference free energy $G_{el}^{\mathit{ref}}$ uses the same fixed charge distribution but has a constant dielectric coefficient equal to the value in biomolecular interior (ε_s = ε_p) and a constant zero ion accessibility coefficient (κ̄²(x) = 0).

The ΔG_el evaluation is implemented in iAPBS as a two step calculation (see Figure 2). First, the electrostatic energy of the system ( $G_{el}^{\mathit{sys}}$) is computed by calling apbsdrv() with the requested calculation parameters. Then the same calculation is repeated in the reference environment – in homogeneous dielectric ε = ε_p and zero ionic strength (κ̄²(x) = 0). Both calculations use the same discretization (i.e., same FD grid spacing or FE refinement) to ensure cancellation of self-energies in computing ΔG_el.

In iAPBS, the non-polar solvation term G_np in Equation 3 is approximated by a linear function of the solvent-accessible surface area:

$$G_{np}=\gamma A$$ (5)

where A is the solvent-accessible surface area and γ is the energetic coefficient or surface tension. APBS also offers more accurate approximate methods [25] for evaluating G_np; these will be implemented in the future releases of iAPBS.

2.2.2. Calculating Solvation Forces

Similar to the total free energy calculation, the total force on the system in implicit solvent molecular dynamics simulations is evaluated as a sum of bonded forces (F_bonded), non-bonded forces (F_non-bonded) and forces due to the solvent environment (ΔF_solv):

$$F_{\mathit{tot}}=F_{\mathit{bonded}}+F_{\mathit{non}-\mathit{bonded}}+\mathrm{\Delta }{F}_{\mathit{solv}}.$$ (6)

Both F_bonded and F_non-bonded forces are computed by the MD application and the solvation forces ΔF_solv are calculated by the iAPBS interface function. Like their energetic counterparts, solvation force evaluations must also be performed using reference calculation due to the presence of self-interactions in the charge distribution. The total solvation force on the system is calculated as

$$\mathrm{\Delta }{F}_{\mathit{solv}}=F_{el}^{\mathit{sys}}-F_{el}^{\mathit{ref}}+F_{np},$$ (7)

where $F_{el}^{\mathit{sys}}$ is the total electrostatic force on atoms of the system due to all atoms. This is calculated from the numerical solution of the PB equation and the dielectric and ion accessibility coefficients are inhomogeneous. $F_{el}^{\mathit{ref}}$ is the total electrostatic force on atoms in the reference system due to all atoms. This is again calculated from the numerical solution of the PB equation, however the dielectric and ion accessibility coefficients are homogeneous (ε_s = ε_p) and κ̄²(x) = 0. As with the computation of free energies, this calculation is performed using the same discretization as the calculation of $F_{el}^{\mathit{sys}}$. The F_np term represents the non-polar forces.

As shown in Figure 2, the total solvation energy and force (ΔG_solv and ΔF_solv) calculation requires two calls to the low level apbsdrv() function per MD step. During the first call, the system electrostatic energy and forces ( $G_{el}^{\mathit{sys}}$ and $F_{el}^{\mathit{sys}}$) and the non-polar energy and forces (G_np and F_np, respectively) are calculated. During the second call the reference electrostatic energy and force ( $G_{el}^{\mathit{ref}}$ and $F_{el}^{\mathit{ref}}$) are computed. These two calculations must be repeated for each MD step (unless an alternative solvation force update scheme is used, see below). Since the apbsdrv() evaluation is the slowest step in the workflow there are some performance issues to be considered. Although it is possible to implement, with certain assumptions, a solvation energy and force calculation protocol using only one apbsdrv() call per MD step (i.e., skipping the reference system calculation) this comes with a significant accuracy penalty. The current versions of Amber, CHARMM and NAMD modules use the reference system calculation every MD step to ensures cancellation of self energies and, therefore, accurate solvation energies and forces. These modules also reconstruct the numerical grid every MD step instead of re-using it. This improves the PB calculation stability and accuracy due to maintaining the rotational invariability of the PB solution with respect to the grid (at adequate grid spacing) with only a negligible impact on the performance.

The forces and energies due to Coulomb’s law (pairwise Coulombic interactions between all atoms in the molecule) are not calculated by iAPBS and must be supplied by the molecular dynamics application. This is usually not an issue since the calculation of Coulombic energies and forces is implemented as a part of the non-bonded energy and force evaluation in these programs.

2.2.3. Other Features

The currently available iAPBS application modules also contain several features extending the capabilities of these applications:

Adaptive grid size

The Amber, NAMD and CHARMM modules implement an adaptive grid size algorithm for minimization and molecular dynamics calculations. This feature allows the user to specify a target grid resolution (for example 0.5 Å); the grid span and size are then recalculated on the fly during each minimization or MD step, ensuring that the molecule is completely enveloped by the grid of the requested resolution. This adaptive grid resizing increases accuracy of the calculation of both electrostatic energy and electrostatic forces due to the consistent grid discretization parameters between the MD steps. It also prevents the molecule from “falling off” the grid when the volume of the molecule is changed from one MD step to another during the simulation.

On-the-fly electrostatic potential map generation

The Amber module can also write out electrostatic potential maps after each individual step in the molecular dynamics simulation. The maps (one per each MD step or optionally per n-th MD step) can be post-processed to create a dynamic picture of the electrostatic potential during the molecular dynamics (for example as a movie).

Electrostatic energy decomposition

Another feature implemented in the Amber module is the availability of electrostatic energy decomposition – either at per-atom or per-residue levels. This information can be used, for example, to study the changes in the electrostatic potential at active site residues during a MD simulation.

Alternative solvation force update scheme

The Poisson-Boltzmann-based solvation force evaluation is one of the slowest steps in molecular dynamics simulations and there has been a considerable effort to address this performance issue [26]. Since the electrostatic potential distribution varies only slowly with small conformation changes during dynamic simulations, it is reasonable to assume that updating this potential only every n-th step should not compromise the integrity of the calculated thermodynamic and kinetic data. The iAPBS Amber module implements an alternative solvation force update scheme based on the mollified impulse method [27]. Additionally, the solvation update force code is written in a modular way so new update schemes can be easily implemented.

MM-PBSA based post-processing

The availability of very accurate solvation energies via the iAPBS module can also be exploited in MM-PBSA [28] type of calculations. The mmpbsa.py script [29] which is distributed with Amber allows use of the iAPBS-calculated solvation energies (both electrostatic and non-polar parts) in the MM-PBSA protocol.

Visualization and post-processing of volumetric data

Visualization is a very important tool when analyzing biomolecular electrostatics. Some of the most common ways to study the three dimensional distribution of electrostatic potential around the molecule include projection of the calculated potential on the solvent accessible surface area (SASA) of the molecule or construction of electrostatic potential isocontours around the molecule.

APBS features an advanced facility for writing out calculated three-dimensional volumetric data, from electrostatic maps to charge distributions. The iAPBS interface allows for this facility to be used in the molecular dynamics simulation packages thus providing a way to generate “dynamic” electrostatic data. The ability to investigate how the electrostatic spatial data change during the molecular dynamics simulation can offer additional insights to the structure and function of biomolecules. There are many possible applications of this approach for example observing dynamical changes in three-dimensional properties of the electrostatic potential around an active site in a biomolecule, visualizing changes in per-residue (or per-atom) electrostatic properties, monitoring electrostatic interactions between selected residues during the molecular dynamics simulation, etc. The iAPBS distribution includes several PyMOL [30] script templates for generating movies of electrostatic properties from the individual MD simulation frames.

3. Conclusions

The Adaptive Poisson-Boltzmann Solver (APBS) software package is a widely used tool for evaluating electrostatic interactions in biomolecular systems in implicit solvent. The iAPBS interface library offers a straightforward integration of the APBS capabilities into biomolecular simulation programs. Several application modules for popular molecular dynamics applications – Amber, CHARMM and NAMD are distributed with iAPBS. These modules allow incorporation of APBS-calculated electrostatic and solvation energies and forces into simulations. They also add the ability to easily generate time series of spatial distributions for electrostatic data during the molecular dynamics simulation using the advanced APBS volumetric data output facility. The modular design of the iAPBS interface library allows easy extendability and addition of new application modules.

Availability

iAPBS is distributed as part of the APBS source code, in the contrib/iapbs directory. APBS with iAPBS can be downloaded from http://www.poissonboltzmann.org/apbs. Instructions on how to build and install iAPBS can be found at http://mccammon.ucsd.edu/iapbs. The software is being released under the GNU public license.