Abstract
Viral infections involve a complex interplay of the immune response and escape mutation of the virus quasispecies inside a single host. Although fundamental aspects of such a balance of mutation and selection pressure have been established by the quasispecies theory decades ago, its implications have largely remained qualitative. Here, we present a quantitative approach to model the virus evolution under cytotoxic T-lymphocyte immune response. The virus quasispecies dynamics are explicitly represented by mutations in the combined sequence space of a set of epitopes within the viral genome. We stochastically simulated the growth of a viral population originating from a single wild-type founder virus and its recognition and clearance by the immune response, as well as the expansion of its genetic diversity. Applied to the immune escape of a simian immunodeficiency virus epitope, model predictions were quantitatively comparable to the experimental data. Within the model parameter space, we found two qualitatively different regimes of infectious disease pathogenesis, each representing alternative fates of the immune response: It can clear the infection in finite time or eventually be overwhelmed by viral growth and escape mutation. The latter regime exhibits the characteristic disease progression pattern of human immunodeficiency virus, while the former is bounded by maximum mutation rates that can be suppressed by the immune response. Our results demonstrate that, by explicitly representing epitope mutations and thus providing a genotype–phenotype map, the quasispecies theory can form the basis of a detailed sequence-specific model of real-world viral pathogens evolving under immune selection.
Keywords: population dynamics, next-generation sequencing, stochastic simulation, HIV
Viruses with RNA genomes, such as human immunodeficiency virus type 1 (HIV-1), have high rates of mutation and evolve rapidly in response to host immune selection pressure. One of the consequences of such rapid mutations is the error catastrophe (1), where a virus population is driven to extinction when its mutation rate exceeds a threshold. The existence of such a threshold is a central prediction of the quasispecies theory pioneered by Eigen (1) and Swetina and Schuster (2). The recent experimental demonstration of lethal mutagenesis (3–5), in which an error catastrophe transition is caused by mutagens, demonstrates that key features of the balance of mutation and selection in viruses are elegantly captured by the quasispecies theory.
Although insights provided by the quasispecies theory have greatly expanded our understanding of virus behavior, applications so far have been limited to a conceptual level, partially due to the lack of experimental information on the evolutionary dynamics in sequence space. Next-generation sequencing techniques (6) have the potential to change this situation. To build quantitative models implementing the quasispecies dynamics and describe such experimental data, it is important to realistically specify the nature of selection pressure. Viruses in animal hosts evolve under immune pressure, and their capacity for rapid escape mutation underlies many of the difficulties in combating pathogens, including HIV-1. In a typical disease pathogenesis of HIV-1, the acute viremia after an initial infection is curbed by CD8+ cytotoxic T-lymphocyte (CTL) responses as well as subsequent antibody actions, leading to an asymptomatic chronic infection stage that can last up to 10 y (7). However, this apparent control of viremia is never complete, and without antiviral therapy, the chronic infection eventually leads to the onset of disease. This chronic infection stage involves continuous escape mutation-CTL response cycles, whose detailed characteristics are being uncovered by ultradeep sequencing (8–12). CTLs recognize specific viral epitopes (approximately 10 amino acids long) presented on the surface of infected cells by class I human leukocyte antigen (HLA). The epitope recognition depends sensitively on HLA alleles, leading to differential patterns of immune response among patients (13–15), while characteristics of immune response during early infection often shape and influence the overall disease progression (16, 17). Quantitative sequence-based models of virus-CTL dynamics will greatly facilitate the interpretation of experimental data.
In a series of pioneering works (18–20), Nowak and coworkers introduced population dynamics concepts that capture a diverse range of immune response and escape mutation. Similar approaches focused more on escape dynamics have also been proposed (21, 22). These models, however, do not describe mutations in sequence space explicitly. Other mathematical models of sequence evolution focus on sequence divergence during the very early stages of infection, while ignoring or only implicitly including the effect of selection pressure (23, 24). In this paper, we describe a quantitative quasispecies-based model of virus dynamics under T cell-based immune pressure, explicitly mapping genotype–phenotype relationships. Our approach combines the description of virus evolutionary dynamics provided by the quasispecies theory and the population dynamics models of Nowak and coworkers. We show that the model not only captures the salient features observed in sequencing data of simian immunodeficiency virus (SIV) (9) but also reveals general qualitative features of viral infection disease pathogenesis: The immune system can clear the infection within time scales ranging from days to those much longer than patient lifetimes, or be overwhelmed by immune escape. The viral load progression in the latter regime closely matches the observed HIV-1 disease pathogenesis pattern.
Results and Discussion
Stochastic Quasispecies Dynamics.
During acute infection, the founder virus (often a single virion) (7, 11, 17, 25) undergoes replications to produce an exponentially growing population, which may be described by the quasispecies dynamics without degradation,
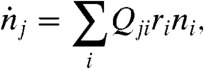 |
[1] |
where ni is the number of virions with genotype i, ri is the replication rate of i, and Qji = (1 - μ)L-d(j,i)(μ/3)d(j,i) is the mutation probability from i to genotype j, with mean mutation rate μ, genome length L (in bp), and Hamming distance (the number of nucleotides that are different) d(j,i) between j and i. A more complete description for early stages of infection, where ni is of the order of 1 and restricted to integer values, is given by the chemical reaction representation
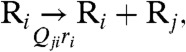 |
[2] |
where Ri is a virion with genotype i. Eq. 2 can be simulated stochastically with the Gillespie algorithm (26). A major advantage of such a stochastic formulation is that it allows us to avoid exhaustive enumerations of all possible genotypes. This is significant even for a single epitope of viral proteins: An amino acid sequence with La = 10, whose genome length is L = 3La = 30 bp, still has 4L ∼ 1018 genotypes. Nowak and Schuster (27) performed Gillespie algorithm simulations of the standard quasispecies model under the single-peak fitness landscape (ri = 1/τ for the wild-type (WT) sequence and ri = 1/Aτ for all other mutants, where A > 1 is the relative fitness of the WT and τ is a characteristic time scale). In this case, distributions of individuals among only two groups (WT and mutants) need to be tracked.
In our numerical simulations, the initial genotype (referred to here as the WT) replicates with mutation rate μ, and the generated mutants are compared with the existing list of sequences, which is updated dynamically when new sequences arise. We verified that this numerical scheme sampled the relevant sequence space sufficiently (SI Text, Figs. S1–S3). The initial condition we used (single WT) and the discreteness of ni imply that ni should be interpreted as the total number of virions within a finite system. The HIV-1 viral load during the acute infection phase can reach up to 104 ∼ 106 RNA copies/mL (7). Accounting for the volume of blood in the body of an average adult (approximately 5 L), the total population size Nv = Σi ni would be up to about 109. We found simulations to slow down significantly as Nv became larger than about 106. For computational efficiency, we therefore regarded the system as a small representative volume (1 mL) of blood, and the viral loads and CTL levels reported refer to RNA copy numbers and cell counts within this volume.
CTL Response.
Within an infected host, the action of the cellular immune response provides the major force countering the acute viremia. In this work, we combine the population dynamics approach of virus-immune system dynamics by Nowak and coworkers (18, 19) with the classic quasispecies theory. Accordingly, Eq. 2 is modified as follows:
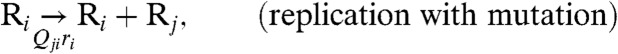 |
[3A] |
 |
[3B] |
 |
[3C] |
 |
[3D] |
where the genotype i is now a member of the combined sequence space of l epitopes. The amino acid sequence (“phenotype”) of epitope k in genotype i is denoted as αik, and C(α) represents a CTL specific to phenotype α. Eq. 3B represents a reaction in which, with a rate b, virions of sequence i stimulate the production of a set of CTLs C(αik) corresponding to the phenotypes of its epitopes. Eq. 3C denotes the reaction where cells infected with viruses with genotype i are cleared by CTLs with phenotypes that match one of its epitopes with a rate p, and Eq. 3D represents the natural decay of T cells with a rate g. Under the alternative deterministic continuum approximation, one may write:
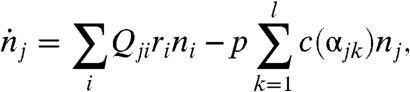 |
[4A] |
| [4B] |
where c(α) is the number of T cells C(α) and nα is the total number of virions containing epitopes with phenotype α.
The qualitative features of the infection-clearance dynamics can be illustrated by setting the mutation rate μ to zero. Numerical integrations of Eq. 4 yield the continuum approximation result (Fig. S4 for μ = 0 and l = 1), which showed reasonable agreement with the stochastic simulation results. For nonvanishing mutation rates, numerical integration rapidly becomes prohibitive with increasing L because of the high dimensionality of the sequence space. The inverse of b is a measure of the time delay of the growth of T cells compared to that of viruses. Here, we adopted b values of approximately 0.01 d-1. The efficiency of CTLs in recognizing cells presenting the epitope and killing them is represented by parameter p, the clearance rate. We found p values of 10-4 ∼ 10-3 d-1 to give good fits to experiments (see below).
Immune Escape Dynamics.
To make comparisons with experiments, it is necessary to consider that fitness is determined by amino acid sequences, and many mutations are synonymous. Therefore, the full immune escape dynamics represented by Eq. 3 distinguishes the amino acid sequence αik corresponding to the nucleotide sequence of epitope k in genotype i. We refer to the set of nucleotide and amino acid sequences as “genotypes” and “phenotypes,” respectively. The fitness ri is a function of phenotypes only. During simulations, each genotype is translated into a phenotype, and a new mutant is checked against the existing phenotype/genotype list, which is updated and expanded. The nature of this genotype–phenotype map plays important roles in evolutionary dynamics, leading to key signatures of selective pressure, such as the ratio of synonymous to nonsynonymous mutations (28). Quantitative insights to the effects of this mapping on molecular evolution have been provided by Manrubia and coworkers (29), who studied short RNA sequences for which fitness can be estimated by secondary structure predictions. In our case, a simplified overview of the genotype–phenotype map can be gleaned from a network representation of the genetic code (Fig. S5): If all mutations were neutral and amino acids within an epitope independent, this map would be sufficient to determine the statistics of evolutionary drifts. The accessibility of certain mutations from a phenotype, in particular, has been shown to affect the evolvability of viruses (30).
Another major ingredient for a realistic model of immune escape is the fitness landscape beyond the level of the single-peak model. Much progress has been made recently in understanding the nature of fitness landscapes (31–34). Explicit fitness measurements of viral clones (35, 36) and biochemical assays of proteins (37) both indicate that single-nucleotide substitutions lead to a broad distribution of fitness changes, most of which are deleterious. Therefore, one may assume that the fitness of a mutant is a random variable centered around a mean fitness value f. We expect this mean fitness to be a decreasing function of distance d to the WT (the number of amino acids that are different), which we assume to be exponential: f(d) = exp(-d/ξ), where ξ denotes a characteristic distance (Methods).
An empirical evidence for this choice can be found from a recent experimental study by Fernández et al. (37), who measured the fitness landscapes of HIV-1 protease quasispecies for three patients. We plotted the distribution of their reported fitness values as a function of distance to the dominant phenotype and found near-exponential dependence for two quasispecies (Fig. S6). Our fitness function therefore models both the decrease of the mean fitness away from WT and the distribution of neutral, deleterious, and beneficial mutants for a given distance. In simulations, these fitness values were assigned dynamically to newly encountered phenotypes. It is important to note, however, that this landscape chosen is still an approximation that ignores many potentially important effects, such as the heterogeneity of the mutational neighborhoods within the phenotype space.
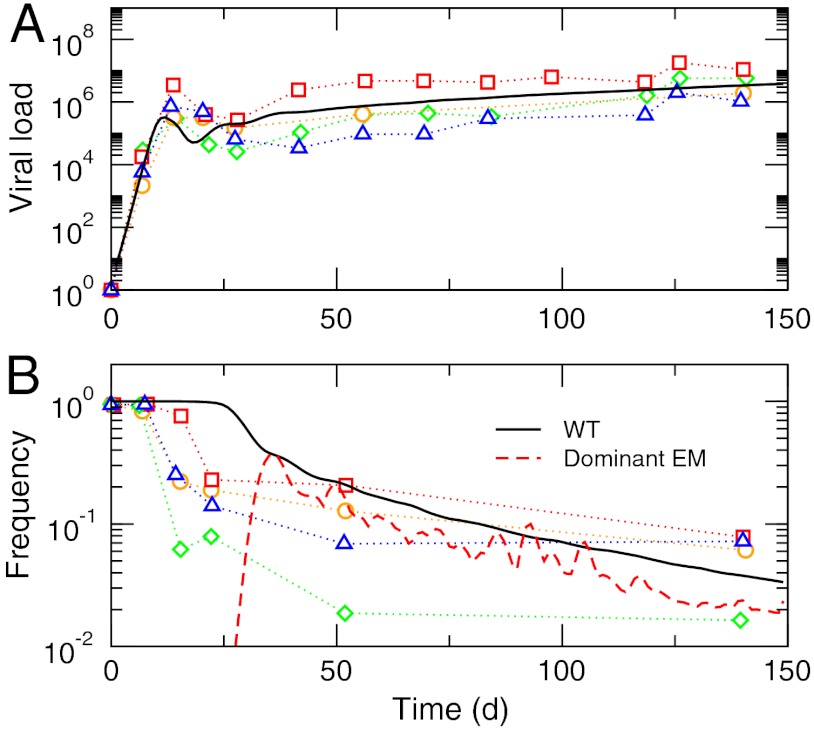
We tested this quasispecies model with the ultradeep sequencing data (9, 22) of the SIV epitope Tat28–35SL8 (38). Fig. 1 shows the time dependence of the viral load and WT frequency from simulations of the single-epitope version of Eq. 3 compared with the experimental data (22). The initial rapid growth of the viral load, its subsequent decrease as CTLs are activated, and the more gradual increase as mutants appear are all captured quantitatively. The WT frequency decrease agrees with experimental trends (Fig. 1B) with signatures of two distinct time scales (22). The mutation rate we used (μ = 2 × 10-7 bp-1) was chosen to obtain the best overall agreement for WT frequency with the single-epitope version of the model. For multiepitope applications, larger mutation rate values close to the experimental estimate for HIV-1 (μ = 3.4 × 10-5 bp-1) (39) gave realistic dynamics (Fig. 2).
Fig. 1.
Simulation of full immune escape dynamics of a single SIV epitope Tat28–35SL8. (A) Viral load. (B) Frequencies of WT and the dominant escape mutants (EM). Symbols represent experimental data from refs. 9 and 22, with each symbol corresponding to one of four different animals. Solid lines are from our stochastic quasispecies model with τ = 0.8 d, μ = 2.0 × 10-7 bp-1, b = 0.01 d-1, g = 0.2 d-1, and p = 2.0 × 10-4 d-1. The fitness function parameters were σ = 0.1 and ξ = 1 (Methods). The EM frequency is for a single trajectory while the rest are averages.
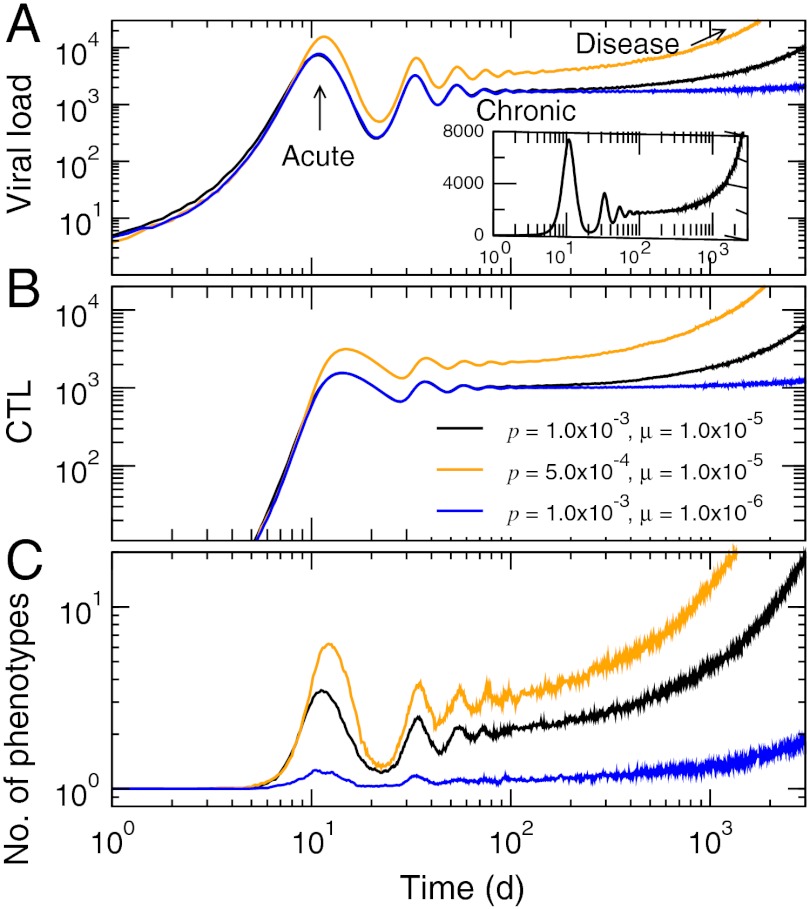
Fig. 2.
Typical disease progression patterns in the runaway regime from the multiepitope quasispecies model. (A) Viral load. (B) Total CTL levels. (C) Number of distinct phenotypes per epitope present in the population. The inset in A shows the viral load in linear scale for p = 1.0 × 10-3 d-1 and μ = 1.0 × 10-5 bp-1. Other parameter values were b = 0.02 d-1, g = 0.1 d-1, τ = 1 d, σ = 0.2, and ξ = 1. The units of p and μ in the legends are d-1 and bp-1, respectively. All data represent averages over trajectories.
Fig. 1B also shows the frequency of the most dominant escape mutant (EM) at each time point. As mutations occur, a new strain proliferates temporarily before being curbed down, and the total number of phenotypes continues to increase. The increase in viability of populations with multiple but lower fitness peaks has been described first by Schuster and Swetina (40) and has later been known as the “survival of the flattest” effect (41). Further insights into the role this expansion in sequence space plays in the growth of viral loads can be gained from the deterministic continuum approximation, Eq. 4, without mutation: The immune response to WT leads to damped oscillations of viral load and CTL level (Fig. S4), reaching a steady state n∗ and c∗. This process is repeated for each new mutant, leading to continued increases in n∗ and c∗ roughly proportional to the number of phenotypes (18). However, the timing, distribution, and the probability of the appearance of mutants are highly nontrivial functions of the characteristics of the system, including genome length, genotype–phenotype map, and fitness landscape. Our quantitative quasispecies-based model, Eq. 3, provides a realistic description of this complex diversification process via the single parameter μ. We note that, for a single epitope, this interpretation ignores the effects of competition among viral strains because each CTL is specific to only one phenotype. In reality, in addition to competing directly for host cells, different viral strains share their vulnerability to CTLs specific to common epitopes within their genomes. By considering multiple epitopes within a strain, our model takes into account this interdependence of viral strains and their indirect competition arising from shared epitope phenotypes (see below).
As a quantitative measure of the relative degree of WT persistence during immune escape, we also examined the time (half-life) required for WT frequency to reach one-half (Fig. 1B) (22) with varying stimulation rate b and clearance rate p (Fig. S7). The SIV epitopes studied by Bimber et al. (9) were estimated to have a WT half-life of about 20 d (22). We found that, within our model, the WT half-life increases with increasing p and b in this range: An increase in the magnitude of selection pressure, rather than accelerating immune escape, suppresses viral population growth more effectively and reduces the chances of escape mutation (Fig. 2). The immune escape thus becomes more pronounced when viral loads in the chronic phase are larger with more frequent mutations.
Disease Progression Under Immune Response.
We examined general trends of viral infection-immune response dynamics within our quasispecies model on multiple-epitope levels (l = 3) with variations of key model parameters. The evolutionary dynamics, in particular, is critically affected by p, the clearance rate representing the effectiveness of immune response, and the mutation rate μ. We identified two qualitatively different behaviors based on the eventual fate of viral load/CTL level: in one regime (“runaway,” Fig. 2), the chronic phase after the resolution of the acute infection is eventually followed by a runaway growth in viral loads (Fig. 2A). The level of CTLs also rises consistently during the chronic phase (Fig. 2B). This disease progression is accompanied by an increase in the diversity of quasispecies, or the “spreading of clouds” (Fig. 2C). The time scale for the duration of the chronic phase, in particular, varied sensitively with p and μ (from a few months to years) (Fig. 2A). We found that the total number of phenotypes per epitope (Fig. 2C) generally goes down as the number of epitopes increases: A new escape mutant has much lower probability for survival with multiple epitopes because it shares WT phenotypes on other parts of its genome with existing strains, and therefore is susceptible to CTLs that are already present.
The disease progression pattern in the runaway regime corresponds to situations where the immune system is overwhelmed by viral growth, either shortly after infection (there is no discernible chronic phase for sufficiently small p) or after a long chronic phase and accumulation of escape mutants. The latter case closely matches the characteristic HIV-1 disease pathogenesis (7), revealing the major role played by the uncontrolled diversification of the quasispecies that overwhelms the CTL response. This feature was first suggested by Nowak and May (19), who coined the term “diversity threshold” based on a model assuming random appearances of mutants. Our results show that the basic quasispecies dynamics under selection pressure provide a realistic description of this phenomenon.
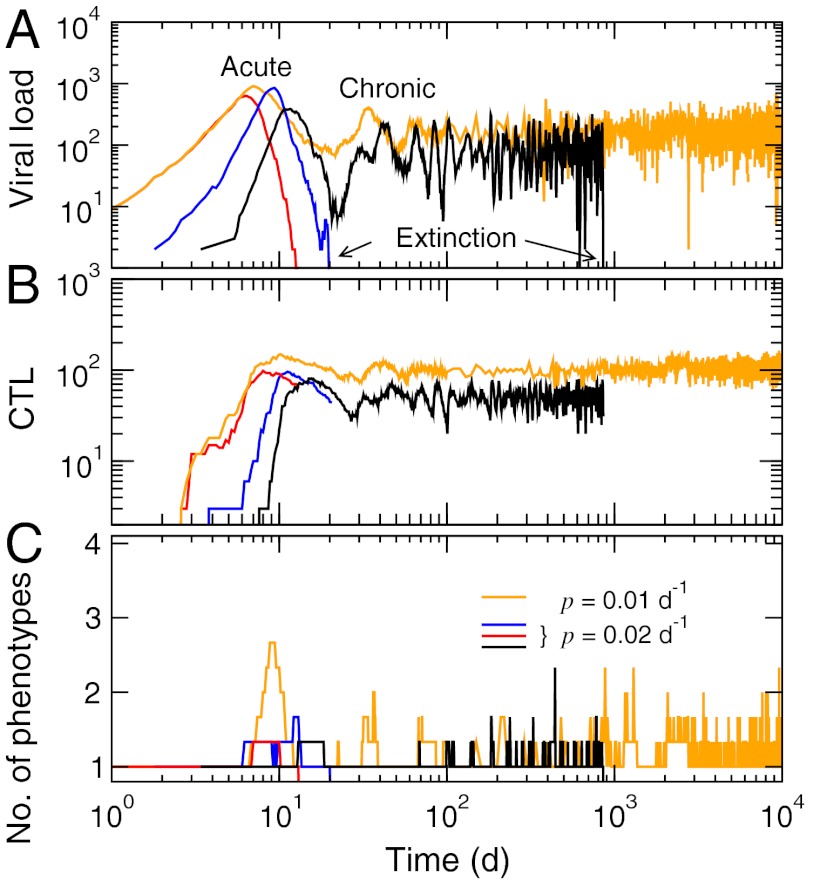
If p is sufficiently large and μ sufficiently small, one enters a different regime (“extinction,” Fig. 3), where the acute and chronic phases lead to viral loads that decrease either rapidly or asymptotically with time. As populations shrink in size, their dynamics become increasingly stochastic, and extinction (a complete clearance of infection) occurs when the viral load reaches zero. This behavior is inherently stochastic and cannot be captured by the deterministic approximation in Eq. 4. The time required for clearing the infection (“extinction time”) typically has a broad distribution, increasing with decreasing p while becoming infinite above a threshold μ (Fig. 4A). The rapid clearance of infection within approximately 10 d corresponds to the normal state of affairs in a healthy immune system against viruses such as influenza. As shown in Fig. 3A (p = 0.01 d-1), however, the extinction time can also reach time scales approaching a patient’s lifetime. This feature may be relevant in understanding the basis for some chronic viral infections with long and stable setpoints (e.g., hepatitis C), although the high variability of extinction times we observed (Fig. 4A) likely may not correspond to actual possible clearances of such chronic infections.
Fig. 3.
Typical disease progression patterns in the extinction regime from the multi-epitope quasispecies model. (A) Viral load. (B) Total CTL levels. (C) Number of distinct phenotypes per epitope present in the population. The parameter values other than p and μ = 1.0 × 10-5 bp-1 were the same as in Fig. 2. The data shown are individual trajectories.
Fig. 4.
Crossover between the runaway and extinction regimes. (A) Variation of extinction time with mutation rate μ for different clearance rates p in the extinction regime. Error bars represent one standard deviation. Near the threshold, the extinction events occur increasingly in the edge of viral load fluctuations (Fig. 3A). (B) The estimated threshold between the runaway and extinction regimes in the p - μ parameter space (defined as the maximum μ for which the extinction time converges for a given p). The arrow illustrates the dynamic deterioration of immune response during HIV-1 infection. Other parameter values were the same as in Fig. 2.
The threshold separating the runaway (Fig. 2) and extinction (Fig. 3) regimes can be identified by the maximum mutation rate for which the extinction time remains finite (Fig. 4A). This error threshold for the immune control of infection is analogous to Eigen’s threshold for genomic stability: The latter is the error rate above which replicators cannot maintain a stable master sequence. The former is a maximum mutation rate the given immune system can suppress. Fig. 4B shows this threshold as a function of p and μ. A given virus would have roughly the same mutation rate, while p would vary with individual patients. The sensitivity of disease progression with p is consistent with the observation that even when the fatality rate of a certain infection is known, the course of infection in a patient is often unpredictable.
The case for HIV-1 is unique in the sense that without treatment, most patients eventually progress to the disease stage. One of the special characteristics of HIV-1 is that it targets CD4+ (helper) T cells, which play critical roles in eliciting and mediating CTL responses. Within the context of our model, the destruction of CD4+ T cells would lead to a gradual decrease in both the stimulation rate b and the clearance rate p. One therefore expects a continual deterioration of any initial effective control of infection, represented by p values that decrease over the course of disease progression. In Fig. 4B, therefore, even though patients with stronger immune systems may have p values initially in the extinction regime, the continued depletion of CD4+ cells would lower p and cause them to cross the threshold.
Conclusions
In this paper, we demonstrated that the classic quasispecies theory can form the basis of a quantitative model of virus evolution under immune selection. One of the apparent challenges in developing such a model is that viral genomes, while relatively small (approximately 104 bp), still constitute a huge sequence space. Here, we showed that a set of epitopes (La ∼ 10 amino acids) can be considered as minimal units of genomic segments on which selection acts. In standard quasispecies theory, competition between different strains arises indirectly from the constraint of fixed total population size. In our model, the degradation and removal of virions occur via immune response, which can be regarded as a concrete specification of the selection forces. In this case, indirect competition occurs because most viral strains share identical phenotypes in a large fraction of their epitopes and are constrained by common groups of CTLs. However, the model does not account for the effects of direct competitions for resources (limited number of host cells available for infection). We have additionally explored an extended model that includes host-cell dynamics (SI Text), whose analysis suggests that the main qualitative results remain valid (Fig. S8).
Our finding that the relative importance of immune escape is mainly determined by the viral load in chronic infection may have implications to vaccine design (42): Strategies aimed at preventing immune escape, such as targeting epitopes with higher fitness costs to mutations, may not confer more benefits than those attempting to boost the overall immune response. We also note, however, that more realistic representations of T-cell stimulation and clearance will have to take their dependence on phenotypes into account (p and b should depend on amino acid sequences), because mutations affect HLA-epitope-CTL binding affinities. Our model also ignores complex epistatic effects coupling mutations on the same and different epitopes (43). The approach presented here likely can provide a foundation for a more comprehensive modeling framework to tackle such global genome-wide effects. In addition, although we interpreted Eqs. 3B–3D strictly as the CTL-mediated immune response, we expect similar approaches to be applicable for antibody-based responses.
Methods
Stochastic Evolutionary Dynamics.
Simulations are carried out by applying the Gillespie algorithm (26) to Eq. 3. At a given time, a dynamic list of genotypes and phenotypes (N and M in total, respectively), starting with a single WT at the initial condition, is kept and updated, instead of enumerating all possible sequences. A genotype consists of the nucleotide sequence of a set of epitopes (l in total), each with the same length L, such that the total length becomes l × L. We define the following quantities
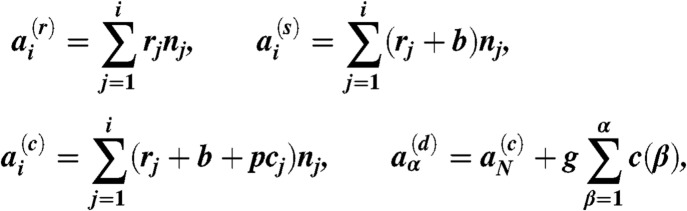 |
each corresponding to the replication, stimulation, clearance, and decay reactions (Eq. 3), respectively, where cj = Σkc(αjk) is the total number of CTLs corresponding to any of the epitope phenotypes belonging to the genotype j. A random number 0 < r < 1 is drawn to determine the time interval Δt = (1/a) ln(1/r) before the next reaction event, where 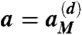 . A second random number r is drawn, and if
. A second random number r is drawn, and if 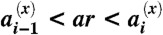 for x = r, s, c, the replication, stimulation, or clearance reaction is chosen for the genotype i, respectively. If
for x = r, s, c, the replication, stimulation, or clearance reaction is chosen for the genotype i, respectively. If 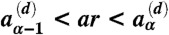 instead, the decay reaction is carried out for the CTL with phenotype α. In this algorithm, therefore, a given CTL contributes equally to the clearance probabilities of all viral strains containing its phenotype. This prescription generates unbiased trajectories of two classes of objects, the viruses with genotype i and phenotype αik and CTLs with phenotype α. For replication reactions, the chosen genotype i is mutated with probability μ per bp. Further details on implementing the genotype-phenotype lists can be found in SI Text.
instead, the decay reaction is carried out for the CTL with phenotype α. In this algorithm, therefore, a given CTL contributes equally to the clearance probabilities of all viral strains containing its phenotype. This prescription generates unbiased trajectories of two classes of objects, the viruses with genotype i and phenotype αik and CTLs with phenotype α. For replication reactions, the chosen genotype i is mutated with probability μ per bp. Further details on implementing the genotype-phenotype lists can be found in SI Text.
Simulation Conditions.
The standard genetic code was used to translate mutant genotypes into phenotypes. The reduced fitness sα = rατ of a phenotype α was taken as follows: sα = 1 for the WT, and for all other phenotypes sα is a random variable with the following Gaussian distribution: P(sα) = exp{-[sα - f(dα)]2]/2σ2}/(2π)1/2σ, where the position of the maximum f(dα) = exp(-dα/ξ) is an exponentially decreasing function of the distance dα≥1 (summed over all epitopes; in units of amino acids) of the phenotype α to the WT. The parameters ξ and σ are the measures of the fitness costs of mutations and of randomness in fitness distributions, respectively. During simulations, a newly encountered phenotype is dynamically assigned a fitness value based on this distribution with negative rα values replaced by zero. Phenotypes containing stop codons were assigned zero fitness. In Fig. 1, the SIV epitope Tat28–35SL8 with the WT sequence of 5′-TCC ACT CCA GAA TCG GCC AAC CTG-3′ (STPESANL) (38) was used (La = 8 and l = 1). In Figs. 2–4, random sequences were used for the WT and simulations were performed with La = 10 and l = 3. Typically, quantities were averaged over 102 ∼ 103 trajectories unless otherwise specified.
Supplementary Material
ACKNOWLEDGMENTS.
This work was sponsored by both the US Army’s Network Science Initiative, managed by the Military Operational Medicine Research Program of the US Army Medical Research and Materiel Command, Fort Detrick, Maryland, and by a competitive In-House Laboratory Independent Research award by the US Army Assistant Secretary of the Army for Acquisition, Logistics, and Technology. The opinions and assertions contained herein are the private views of the authors and are not to be construed as official or as reflecting the views of the US Army or of the US Department of Defense. This paper has been approved for public release with unlimited distribution.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1117201109/-/DCSupplemental.
References
- 1.Eigen M. Selforganization of matter and the evolution of biological macromolecules. Naturwissenschaften. 1971;58:465–523. doi: 10.1007/BF00623322. [DOI] [PubMed] [Google Scholar]
- 2.Swetina J, Schuster P. Self-replication with errors: A model for polynucleotide replication. Biophys Chem. 1982;16:329–345. doi: 10.1016/0301-4622(82)87037-3. [DOI] [PubMed] [Google Scholar]
- 3.Loeb LA, et al. Lethal mutagenesis of HIV with mutagenic nucleoside analogs. Proc Natl Acad Sci USA. 1999;96:1492–1497. doi: 10.1073/pnas.96.4.1492. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Iranzo J, Perales C, Domingo E, Manrubia SC. Tempo and mode of inhibitor-mutagen antiviral therapies: A multidisciplinary approach. Proc Natl Acad Sci USA. 2011;108:16008–16013. doi: 10.1073/pnas.1110489108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Domingo E, Holland JJ. RNA virus mutations and fitness for survival. Annu Rev Microbiol. 1997;51:151–178. doi: 10.1146/annurev.micro.51.1.151. [DOI] [PubMed] [Google Scholar]
- 6.Mardis ER. Next-generation DNA sequencing methods. Annu Rev Genomics Hum Genet. 2008;9:387–402. doi: 10.1146/annurev.genom.9.081307.164359. [DOI] [PubMed] [Google Scholar]
- 7.McMichael AJ, Borrow P, Tomaras GD, Goodnetilleke N, Haynes BF. The immune response during acute HIV-1 infection: Clues for vaccine development. Nat Rev Immunol. 2010;10:11–23. doi: 10.1038/nri2674. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Mild M, Hedskog C, Jernberg J, Albert J. Performance of ultradeep pyrosequencing in analysis of HIV-1 pol gene variation. PLoS One. 2011;6:e22741. doi: 10.1371/journal.pone.0022741. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Bimber BN, et al. Ultradeep pyrosequencing detects complex patterns of CD8+ T-lymphocyte escape in simian immunodeficiency virus-infected macaques. J Virol. 2009;83:8247–8253. doi: 10.1128/JVI.00897-09. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Bimber BN, et al. Whole-genome characterization of human and simian immunodeficiency virus intrahost diversity by ultradeep pyrosequencing. J Virol. 2010;84:12087–12092. doi: 10.1128/JVI.01378-10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Fischer W, et al. Transmission of single HIV-1 genomes and dynamics of early immune escape revealed by ultradeep sequencing. PLoS One. 2010;5:e12303. doi: 10.1371/journal.pone.0012303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Cale EM, et al. Epitope-specific CD8+ T lymphocytes cross-recognize mutant simian immunodefieciency virus (SIV) sequences but fail to contain very early evolution and eventual fixation of epitope escape mutations during SIV infection. J Virol. 2011;85:3746–3757. doi: 10.1128/JVI.02420-10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Moore CB, et al. Evidence of HIV-1 adaptation to HLA-restricted immune responses at a population level. Science. 2002;296:1439–1443. doi: 10.1126/science.1069660. [DOI] [PubMed] [Google Scholar]
- 14.Bhattacharya T, et al. Founder effects in the assessment of HIV polymorphisms and HLA allele associations. Science. 2007;315:1583–1586. doi: 10.1126/science.1131528. [DOI] [PubMed] [Google Scholar]
- 15.Kawashima Y, et al. Adaptation of HIV-1 to human leukocyte antigen class I. Nature. 2009;458:641–645. doi: 10.1038/nature07746. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Addo MM, et al. Comprehensive epitope analysis of human immunodeficiency virus type 1 (HIV-1)-specific T-cell responses directed against the entire expressed HIV-1 genome demonstrate broadly directed responses, but no correlation to viral load. J Virol. 2003;77:2081–2092. doi: 10.1128/JVI.77.3.2081-2092.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Goodnetilleke N, et al. The first T-cell response to transmitted/founder virus contributes to the control of acute viremia in HIV-1 infection. J Exp Med. 2009;206:1253–1272. doi: 10.1084/jem.20090365. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Nowak MA, Bangham CR. Population dynamics of immune responses to persistent viruses. Science. 1996;272:74–79. doi: 10.1126/science.272.5258.74. [DOI] [PubMed] [Google Scholar]
- 19.Nowak MA, May RM. Virus Dynamics: Mathematical Principles of Immunology and Virology. New York: Oxford Univ Press; 2001. [Google Scholar]
- 20.Nowak MA, et al. Antigenic oscillations and shifting immunodominance in HIV-1 infections. Nature. 1995;375:606–611. doi: 10.1038/375606a0. [DOI] [PubMed] [Google Scholar]
- 21.Althaus CL, De Boer RJ. Dynamics of immune escape during HIV/SIV infection. PLoS Comput Biol. 2008;4:e1000103. doi: 10.1371/journal.pcbi.1000103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Love TM, Thurston SW, Keefer MC, Dewhurst S, Lee HY. Mathematical modeling of ultradeep sequencing data reveals that acute CD8+ T-lymphocyte responses exert strong selective pressure in simian immunodeficiency virus-infected macaques but still fail to clear founder epitope sequences. J Virol. 2010;84:5802–5814. doi: 10.1128/JVI.00117-10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Lee HY, et al. Modeling sequence evolution in acute HIV-1 infection. J Theor Biol. 2009;261:341–360. doi: 10.1016/j.jtbi.2009.07.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Lee HY, Perelson AS, Park S-C, Leitner T. Dynamic correlation between intrahost HIV-1 quasispecies evolution and disease progression. PLoS Comput Biol. 2008;4:e1000240. doi: 10.1371/journal.pcbi.1000240. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Keele BF, et al. Identification and characterization of transmitted and early founder virus envelopes in primary HIV-1 infection. Proc Natl Acad Sci USA. 2008;105:7552–7557. doi: 10.1073/pnas.0802203105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Gillespie DT. Exact stochastic simulation of coupled chemical reactions. J Phys Chem. 1977;81:2340–2361. [Google Scholar]
- 27.Nowak M, Schuster P. Error thresholds of replication in finite populations mutation frequencies and the onset of Muller’s ratchet. J Theor Biol. 1989;137:375–395. doi: 10.1016/s0022-5193(89)80036-0. [DOI] [PubMed] [Google Scholar]
- 28.Yang Z, Bielawski JP. Statistical methods for detecting molecular adaptation. Trends Ecol Evol. 2000;15:496–503. doi: 10.1016/S0169-5347(00)01994-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Aguirre J, Buldu JM, Stich M, Manrubia SC. Topological structure of the space of phenotypes: The case of RNA neutral networks. PLoS One. 2011;6:e26324. doi: 10.1371/journal.pone.0026324. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Burch CL, Chao L. Evolvability of an RNA virus is determined by its mutational neighborhood. Nature. 2000;406:625–628. doi: 10.1038/35020564. [DOI] [PubMed] [Google Scholar]
- 31.Schuster P, Fontana W. Chance and necessity in evolution: Lessons from RNA. Physica D. 1999;133:427–452. [Google Scholar]
- 32.Hietpas RT, Jensen JD, Bolon DN. Experimental illumination of a fitness landscape. Proc Natl Acad Sci USA. 2011;108:7896–7901. doi: 10.1073/pnas.1016024108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Stich M, Briones C, Manrubia SC. On the structural repertoire of pools of short, random RNA sequences. J Theor Biol. 2008;252:750–763. doi: 10.1016/j.jtbi.2008.02.018. [DOI] [PubMed] [Google Scholar]
- 34.Pitt JN, Ferre-D’Amare AR. Rapid construction of empirical RNA fitness landscapes. Science. 2010;330:376–379. doi: 10.1126/science.1192001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Duarte EA, et al. Subclonal components of consensus fitness in an RNA virus clone. J Virol. 1994;68:4295–4301. doi: 10.1128/jvi.68.7.4295-4301.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Sanjuan R, Moya A, Elena SF. The distribution of fitness effects caused by single-nucleotide substitutions in an RNA virus. Proc Natl Acad Sci USA. 2004;101:8396–8401. doi: 10.1073/pnas.0400146101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Fernandez G, Clotet B, Martinez MA. Fitness landscape of human immunodeficiency virus type 1 protease quasispecies. J Virol. 2007;81:2485–2496. doi: 10.1128/JVI.01594-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Allen TM, et al. Tat-specific cytotoxic T lymphocytes select for SIV escape variants during resolution of primary viraemia. Nature. 2000;407:386–390. doi: 10.1038/35030124. [DOI] [PubMed] [Google Scholar]
- 39.Mansky LM, Temin HM. Lower in vivo mutation rate of human immunodeficiency virus type 1 than that predicted from the fidelity of purified reverse transcriptase. J Virol. 1995;69:5087–5094. doi: 10.1128/jvi.69.8.5087-5094.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Schuster P, Swetina J. Stationary mutant distributions and evolutionary optimization. Bull Math Biol. 1988;50:635–660. doi: 10.1007/BF02460094. [DOI] [PubMed] [Google Scholar]
- 41.Wilke CO, Wang JL, Ofria C, Lenski RE, Adami C. Evolution of digital organisms at high mutation rates leads to survival of the flattest. Nature. 2001;412:331–333. doi: 10.1038/35085569. [DOI] [PubMed] [Google Scholar]
- 42.Gaschen B, et al. Diversity considerations in HIV-1 vaccine selection. Science. 2002;296:2354–2360. doi: 10.1126/science.1070441. [DOI] [PubMed] [Google Scholar]
- 43.Dahirel V, et al. Coordinate linkage of HIV evolution reveals regions of immunological vulnerability. Proc Natl Acad Sci USA. 2011;108:11530–11535. doi: 10.1073/pnas.1105315108. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.