Abstract
It is not fully understood why we cooperate with strangers on a daily basis. In an increasingly global world, where interaction networks and relationships between individuals are becoming more complex, different hypotheses have been put forward to explain the foundations of human cooperation on a large scale and to account for the true motivations that are behind this phenomenon. In this context, population structure has been suggested to foster cooperation in social dilemmas, but theoretical studies of this mechanism have yielded contradictory results so far; additionally, the issue lacks a proper experimental test in large systems. We have performed the largest experiments to date with humans playing a spatial Prisoner’s Dilemma on a lattice and a scale-free network (1,229 subjects). We observed that the level of cooperation reached in both networks is the same, comparable with the level of cooperation of smaller networks or unstructured populations. We have also found that subjects respond to the cooperation that they observe in a reciprocal manner, being more likely to cooperate if, in the previous round, many of their neighbors and themselves did so, which implies that humans do not consider neighbors’ payoffs when making their decisions in this dilemma but only their actions. Our results, which are in agreement with recent theoretical predictions based on this behavioral rule, suggest that population structure has little relevance as a cooperation promoter or inhibitor among humans.
Keywords: evolutionary game dynamics, network reciprocity, conditional cooperation
The strong cooperative attitude of humans defies the paradigm of Homo economicus and poses an evolutionary conundrum (1, 2). This conundrum is because many of our interactions can be framed as Prisoner’s Dilemmas (3–5) or Public Goods Games (6), famous for bringing about a tragedy of the commons (7). Several mechanisms have been suggested as putative explanations of cooperative behavior (8), among which the existence of an underlying network of contacts constraining who one can interact with has received very much attention. This mechanism was first proposed in the work by Nowak and May (9), where simulations on a square lattice with agents that imitate the behavior of their neighbor with the highest payoff showed high levels of cooperation in the Prisoner’s Dilemma. The ensuing two decades have witnessed a wealth of theoretical studies that have concluded that this so-called network reciprocity (8) is, indeed, possible under a variety of circumstances, but in many other contexts, networks do not promote—or they even inhibit—cooperation (10, 11). The effect of regular and homogeneous networks on cooperation is very sensitive to the details of the model (e.g., dynamics and clustering), whereas theoretical results and simulations indicate that heterogeneous networks should be particularly efficient in fostering cooperation in social dilemmas (11–13). A natural way to shed some light on these partially contradictory results would be to test experimentally the predictions of the different models. Such tests are currently lacking (14), because the few available experimental works only deal—with some exception (15)—with very small networks (16–18). Interestingly, the only theoretical result (19) that takes into account the behavioral information extracted from experiments predicts that neither homogeneous nor heterogeneous networks would influence the cooperative behavior in the Prisoner’s Dilemma (i.e., the observed cooperation level should be the same as if every player interacted with every other player).
Here, we close the cycle by testing the above theoretical predictions (19) and contributing to the current debate on the existence and effects of network reciprocity by performing experiments on large samples of structured populations of individuals who interact through a Prisoner’s Dilemma (PD) game. Specifically, we have designed a setup in which 1,229 human subjects were placed in either a square lattice or a scale-free network, and for more than 50 rounds, they played a 2 × 2 multiplayer PD game with each of their k neighbors, taking only one action [either to cooperate (C) or defect (D)—the action being the same against all opponents]. The experiment was simultaneously carried out on two different virtual networks: a 25 × 25 lattice with k = 4 and periodic boundary conditions (625 subjects) and a heterogeneous network with a fat-tailed degree distribution (604 subjects; the number of neighbors varied between k = 2 and k = 16). Fig. 1 depicts a snapshot of a visual representation of the experiment as well as the two networks; more details on the experimental setup as well as a summary of the actions of the subjects during the experiment can be found in SI Materials and Methods and SI Results and Discussion. Subjects played a repeated (weak) PD with all their neighbors for an initially undetermined number of rounds. Payoffs of the PD were set to be 7 Experimental Currency Units (ECUs) for mutual cooperation, 10 ECUs for a defector facing a cooperator, and 0 ECUs for any player facing a defector (weak PD) (9). We note that this choice of payoffs is like the experiment in the work by Grujić et al. (15) on a smaller regular lattice (Fig. 1), and therefore, cooperation should reach a high level according to the available simulations (9, 11–13). The size of each network was large enough, and therefore, clusters of cooperators could form (the underlying mechanism by which cooperators may thrive) (20, 21).
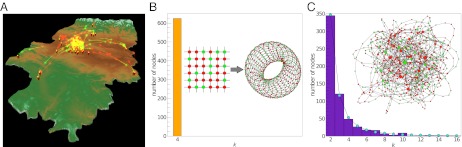
Fig. 1.
Players in the experiment were sitting in different physical locations but played in two virtual networks. A is a snapshot at round 10 of a graphic animation illustrating the activity during the experiment (SI Results and Discussion). On a map of Aragón, the image displays small buildings representing the schools. Arrows (green for cooperate and red for defect) represent actual actions taken by players. They travel to the school, where their randomly assigned neighbors were sitting. Buildings are colored green and red, proportional to the respective number of cooperative and defective actions taken by the subjects in that school. The height of the yellow column on top of each building is proportional to the school’s accumulated payoffs. B and C show snapshots of the two networks at that same round along with their degree distributions (in the case of the heterogeneous network, both the theoretical distribution and the actual realization corresponding to the network of the experiment are represented). Colors indicate the corresponding player’s action (green, cooperate; red, defect). The size of a node is proportional to its degree.
On this general setup, we carried out two treatments, which we will refer to as experiment and control. In the experiment, subjects remained at the same positions in the network with the same neighbors throughout all of the rounds played. In the control treatment, we removed the effect of the network by shuffling the neighbors of each subject in every round. Therefore, in this phase, the players were always connected to the same number of neighbors, but these neighbors changed from round to round. On the screen, subjects saw the actions and normalized payoffs of their neighbors from the previous round, who in the control treatment, were different from their current neighbors with high probability (SI Materials and Methods and SI Results and Discussion). All treatments of the experiment were carried out in sequence with the same subjects. Players were also fully informed of the different setups that they were going to run. The number of rounds in each treatment was randomly chosen between 50 and 70 to avoid subjects knowing in advance when it was going to finish, resulting in 51 and 59 rounds for the experimental and control treatments, respectively. Full details are provided in SI Materials and Methods and SI Results and Discussion.
Results and Discussion
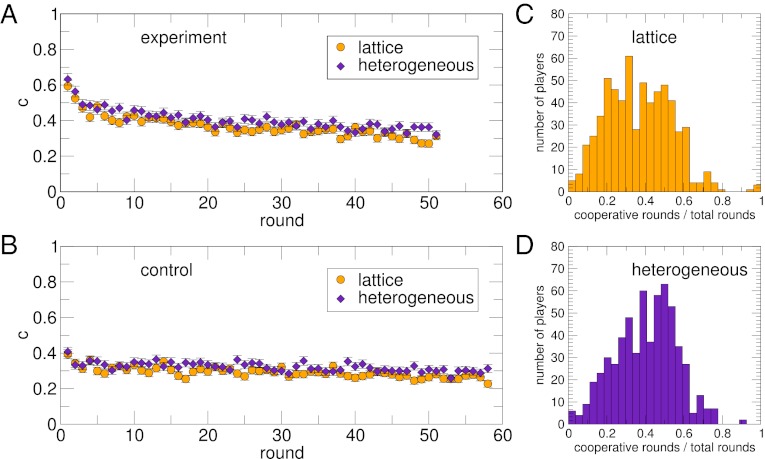
Fig. 2 A and B shows the fraction of cooperative actions, c, in each round for the two networks and both treatments. The first feature worth noticing in Fig. 2 is that, in the experiment phase, the level of cooperation in either network quickly drops from initial values around 60% to values around 40% and finally settles at a slower pace around 30%, much lower than theoretical models predict (9–11). This finding is especially remarkable for the heterogeneous network, on which no previous results are available, and it is in stark contrast with the predictions that this kind of networks should be particularly efficient in promoting cooperation (11–13). In the control, the initial level of cooperation is already at these low values. This behavior is consistent with previous findings in experiments with smaller lattices (15, 18) as well as unstructured populations (22, 23). Regarding the slow decay undergone by these curves after the first quick drop in the level of cooperation, we believe that this finding is associated with a process of learning (see below). However, the most remarkable result that Fig. 2 provides is that, quite unexpectedly, the network does not have any influence in the evolution of the level of cooperation. In fact, both curves are nearly identical—the slightly lower values obtained for the lattice are likely to arise from the small difference in the initial level of cooperation—despite the very different nature of the networks of contacts between the players.
Fig. 2.
The level of cooperation declines and is independent of the network of contacts. Fraction of cooperative actions (level of cooperation) per round during the experiment (A) and the control (B) for both networks and histograms of cooperative actions in the lattice (C) and the heterogeneous network (D). The histograms (C and D) show the number of subjects ranked according to the fraction of cooperative actions that they perform along the experiment in the two networks. A Kolmogorov–Smirnov test shows that the distributions are statistically indistinguishable (SI Results and Discussion). They illustrate the high heterogeneity in subjects’ behavior—their levels of cooperation ranging from nearly zero to almost one in a practically continuous distribution. The corresponding histograms for the control (Fig. S4) show that a sizable group of subjects lowered their levels of cooperation, hence becoming mostly defectors. Actually, the decline in the level of cooperation observed in the experiment (A and B) can be explained as a constant flow of subjects to more defective strategies (evidence supporting this hypothesis in Figs. S5 and S6).
The experimental result that we have just reported is in very good agreement with the theoretical prediction in ref. 19. This finding prompts us to investigate in detail the players’ behavior, because the reason why this prediction was different from earlier ones is the use of the update rule observed in ref. 15. The distributions of subjects by their individual cooperation levels (averaged over the whole experiment) depicted in Fig. 2 C and D show some heterogeneity of behavior: a few subjects have a high level of cooperation (above 70%), and a sizable fraction cooperated in less than 20% of the rounds, whereas the bulk of subjects have intermediate levels of cooperation. Importantly, the comparison of these distributions of actions, which turns out to be statistically indistinguishable (Kolmogorov–Smirnov test data in Table S1), provides additional evidence that the behavior observed in the two networks is the same. This finding, along with the identical behavior of the cooperation level, suggests that subjects use the same strategies in the lattice and the heterogeneous network, regardless of the fact that, in the latter, the number of neighbors of each individual is heterogeneously distributed.
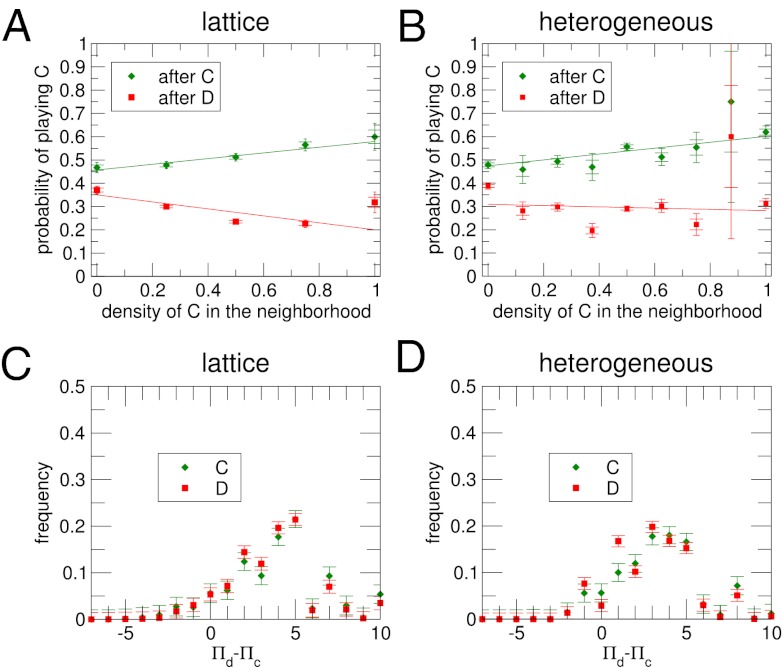
After considering the aggregate distribution of actions, let us now look for deeper insights on the individual behaviors. As in previous experiments on smaller lattices (15, 18) or unstructured populations (22, 23), our results are compatible with a coexistence of at least three basic strategies: cooperators (players who cooperate with a high probability regardless of the context), defectors (players who defect with a high probability regardless of the context), and moody conditional cooperators (15) (players whose action depends on their previous action as well as the level of cooperation in their neighborhood). A search for moody conditional cooperation shows the results depicted in Fig. 3. Fig. 3 A and B shows the fraction of cooperative actions occurred after a cooperation/defection as a function of the level of cooperation in the neighborhood. The plots are the fingerprint of moody conditional cooperation: players are more prone to cooperate the more their neighbors cooperate if they cooperated than if they defected. Furthermore, Fig. 3 also supports the striking finding that the strategic behavior of subjects is remarkably similar whether they are playing on the lattice (Fig. 3A) or the heterogeneous network (Fig. 3B). However, Fig. 3 C and D shows that the next action of a subject cannot be predicted knowing the largest payoff difference that he/she sees in the neighborhood, thus confirming that subjects did not use payoff differences as a guidance to update their actions.
Fig. 3.
Players’ behavior depends both on the level of cooperation in the neighborhood and their previous action. Frequency of cooperative actions after a cooperative/defective action conditioned to the context (fraction of cooperative actions in the neighborhood in the previous round) observed in the lattice (A) and the heterogeneous network (B). Details of the linear fits and comparison with randomizations to prove statistical significance can be found in Table S2 and SI Results and Discussion. The plots show that there is a relevant dependence on the context for subjects who cooperated in the previous round (i.e., were in a cooperative mood): the cooperation probability increased with the fraction of cooperative neighbors, similar to the conditional cooperators found in the work by Fischbacher et al. (24). However, after having defected, this dependence is less clear, and if anything, it suggest an exploiting behavior—subjects who defected are less prone to cooperate the more cooperation that they find. C and D show how subjects who cooperated or defected are distributed according to the largest payoff-per-link difference in their neighborhoods between the two actions. These plots reveal that a player’s decision to cooperate or defect was independent of the payoffs per link that they observed (information that was explicitly provided during the experiment).
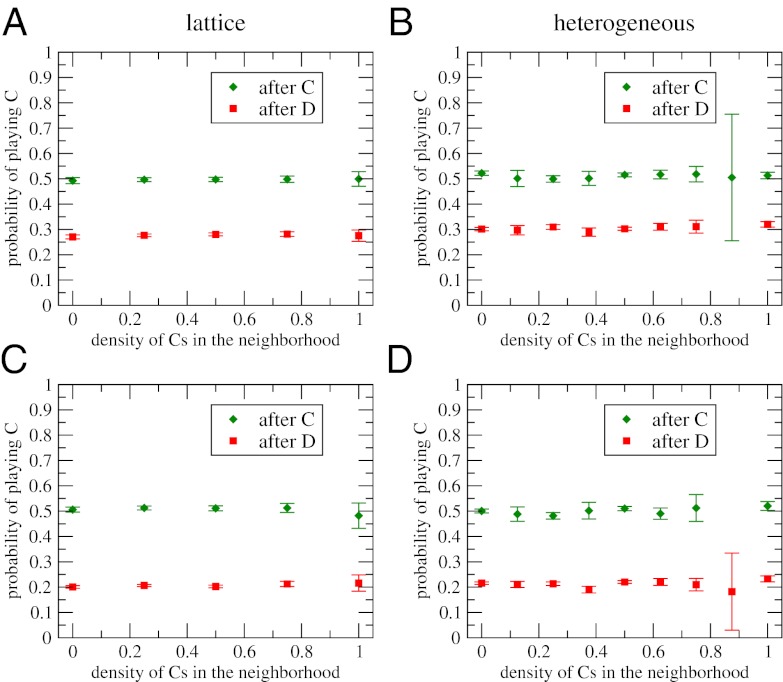
Fig. 4 provides additional evidence of the significance of the moody conditional cooperation by means of a nonparametric bootstrap check. The series of actions taken by every individual is randomly reassigned to other positions in the lattice or the network, and the probability of cooperation is recomputed. This action is done 106 times, and the results show that the two probabilities become independent of the context. Of course, such a reshuffling will not change the dependence on the player’s own previous action, because the order of the actions is not altered; consequently, there are still two distinct lines corresponding to the probability of cooperation after cooperation or defection, but the dependence on the number of cooperators in the previous round is fully removed.
Fig. 4.
Null hypothesis statistical significance test. Probability of cooperating after playing C or D, conditioned to the context (fraction of cooperative actions in the neighborhood in the previous round), averaged over 106 random shuffling of players. A corresponds to the experimental treatment in the lattice, B corresponds to the same treatment for the heterogeneous network, C corresponds to the control phase in the lattice, and D corresponds to the same control treatment for the heterogeneous network. The results show that there is no dependence on the context and hence, that the results of Fig. 3 A and B are statistically relevant. The anomalous variance (or even absence of data) observed at a fraction of Cs in the neighborhood close to 0.9 is not a relevant feature of the experimental results but a consequence of the very low probability of having events contributing to that bin of the histogram in the heterogeneous network. This anomaly can also be noticed in Fig. 3.
The existence of (almost pure) cooperators and defectors aside from moody conditional cooperators can be further supported through a comparison with the same histograms but for the control condition (Fig. S4), because for the latter, a larger number of subjects are in the region that would correspond to defectors. This finding can be interpreted as an indication that a fraction of (probably) moody conditional cooperators changed to a defective strategy, given that retaliation is ineffective in the control condition. Furthermore, performing running averages of the levels of cooperation during the experiment condition (Figs. S5 and S6) shows that the number of subjects with levels of cooperation that are below a given threshold increases with time—irrespective of the precise value of the threshold. Not only does this finding give support to the existence of this kind of players, but it is consistent with a continuous (albeit small) flow of players who change from moody conditional cooperation to defection—a behavior that could be understood as a generalized form of a grim strategy. Notice that this flow can account for the slow decay observed all along the run of the experiment and control observed in Fig. 2 A and B.
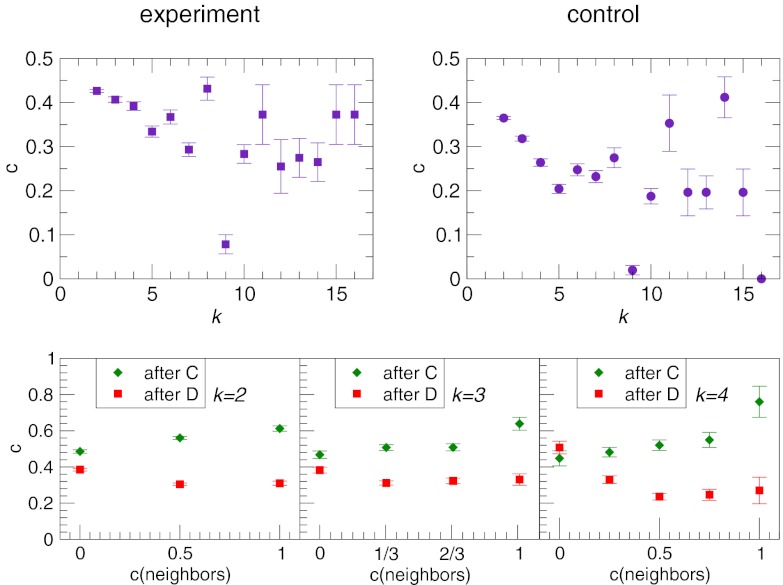
Finally, another important point that our experiment addresses to some extent is the dependence of the actions on the connectivity of the participants for the heterogeneous network. The results are displayed in Fig. 5, where we represent the average cooperation level c as a function of the connectivity of the players k for both treatments: experiment and control. As can be seen from the plots, there might be some trend to lower levels of cooperation with increasing degree for small connectivities, particularly in the control (the levels for the first three values of the degree in the experiment are not statistically different). However, looking at Fig. 5 as a whole, it becomes clear that there does not seem to be any statistically significant trend. It has to be borne in mind that, in this type of network, the number of hubs or large-degree nodes is intrinsically small, and therefore, the statistics for them are not very accurate (notice the size of the error bars). Going beyond these results would require much larger networks (which would still have the same problem for their higher-degree nodes). Additionally, Fig. 5, Lower shows the frequency of cooperative actions of nodes with degree k after playing as C or D with respect to the fraction of their neighbors that cooperated in the previous round. The results are clear evidence that moody conditional cooperation is, indeed, the general behavior, even if one disaggregates the data in terms of their degree. As we have already stated above for the total level of cooperation, for higher degrees, the statistics are poorer, and the analysis does not lead to such clear-cut results.
Fig. 5.
Dependence of the strategies on the connectivity. Upper shows the cooperation level c as a function of the connectivity ki in the heterogeneous network averaged over all rounds of the experiment (Upper Left) and the control (Upper Right) of the experiment. In Lower, we plot the frequency of cooperative actions of players with degree as indicated after they have cooperated or defected as a function of the fraction of cooperative actions in their neighborhood during the previous round; we also plot the experiment treatment in the heterogeneous network. Statistics are restricted to nodes of connectivity: k = 2 (Lower Left), k = 3 (Lower Center), and k = 4 (Lower Right).
Conclusions
To sum up, we have performed a large-scale experimental test of the hypothesis of network reciprocity (i.e., that the existence of a structure in the population may affect cooperation in social dilemmas). Our experiment shows that, when it comes to human behavior, the existence of an underlying network of contacts does not seem to have any influence in the global outcome. We want to stress that this conclusion applies only to human cooperation, and network reciprocity may still be relevant in other contexts (e.g., microbiology) (25). Players seem to act by responding to the level of cooperation in their neighborhood, and this finding renders the network irrelevant. In addition, players behave in a moody manner, being significantly less likely to cooperate after a defection of their own. The levels of cooperation attained in a regular lattice and a highly heterogeneous network (hitherto thought to be a cooperation enhancer) are indistinguishable, and the responsive behavior of subjects seems to be independent of the number of neighbors that they have or the payoff differences that they observe. The results are in full agreement with the theoretical prediction in ref. 19; the fact that the key hypothesis in that model is that people behave in the way that we have just described provides additional support to our finding of moody conditional cooperation in networked PDs.
Our results have implications for policy-making when cooperation is a desired behavior. Although additional experiments with other social dilemmas still need to assess the range of applicability of our conclusions, the present study suggests that imposing a network structure might be a sterile effort. It should be noted, however, that this caveat does not imply that networking is useless to achieve cooperation—results would probably be very different if the network is allowed to be formed by the subjects as part of the game. Recent experiments on groups of up to 20 people (26, 27) strongly suggest this theory, but to the best of our knowledge, no large-scale experiments have been carried out to test this issue. However, the theoretical work in ref. 19 does not predict the slow decay of the cooperation level observed in the experiments, which we have conjectured arises from moody conditional cooperators becoming defectors in a generalized grim behavior. Such a change in the percentage of players using different strategies is not included in the theoretical model, and therefore, a next step would require accounting for such changes and if possible, justifying them within an evolutionary framework. Finally, given that, in our setup, players have to play the same action with all their neighbors, it is clear that our results should be related to Public Goods experiments. In fact, conditional cooperation was first observed in that context (24). Our findings suggest that the moody version that we have found can also arise in Public Goods games. If that is the case, it is likely that network reciprocity does not apply to Public Goods games on networks. Hopefully, our experiment will encourage additional research in all these directions.
Materials and Methods
The experiment was carried out with 1,229 volunteers chosen among last year’s high school students (17–18 y old) of 42 different high schools located throughout the geography of the Autonomous Region of Aragón, Spain. All of the students played through a web interface specifically created for the experiment (see Figs. S1–S3 and SI Materials and Methods) that was accessible through the computers available in the computer rooms of their respective schools. At least one teacher supervised the experiment in each computer room (which at most, had a maximum capacity of 20 students), preventing any interaction among the students. To further guarantee that potential interactions among students seating next to each other in the class did not influence the results of the experiment, the assignment of players to the different topologies was completely random. The colors used to code the two available actions of the game were also selected randomly, also decreasing the likelihood that neighboring participants could influence each other. All participants went through a tutorial (included in SI Materials and Methods) on the screen, including questions to check their understanding of the game. When everybody had gone through the tutorial, the experiment began, lasting for approximately 1 h. The experiment assumed synchronous play; thus, we had to make sure that every round ended in a certain amount of time. This playing time was set to 20 s. At the end of the experiments, volunteers were presented a small questionnaire to fill in. Immediately after, all participants received their earnings and their show-up fee. Total earnings in the experiment ranged from 2.49 to 40.48 Euros.
Supplementary Material
Acknowledgments
We thank E. Cauhé, J. J. Molinero, M. P. Pérez, and C. Viñas for their assistance during several phases of the project and J. Grujić for discussions during the software design phase. Work was supported by Fundación Ibercivis and Projects MOSAICO, PRODIEVO, FIS2008-01240, FIS2011-25167, FIS2009-13364-C02-01, FIS2009-12648-C03-02, and Complexity-NET RESINEE from Ministerio de Ciencia e Innovación (Spain); Project MODELICO-CM from Comunidad de Madrid (Spain); and a project to FENOL from Comunidad de Aragón (Spain).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1206681109/-/DCSupplemental.
See Commentary on page 12846.
References
- 1.Fehr E, Fischbacher U. The nature of human altruism. Nature. 2003;425:785–791. doi: 10.1038/nature02043. [DOI] [PubMed] [Google Scholar]
- 2.Pennisi E. Origins. On the origin of cooperation. Science. 2009;325:1196–1199. doi: 10.1126/science.325_1196. [DOI] [PubMed] [Google Scholar]
- 3.Axelrod R. The Evolution of Cooperation. New York: Basic Books; 1984. [Google Scholar]
- 4.Rapoport A, Chammah AM. Prisoners Dilemma. Ann Arbor, MI: Univ of Michigan Press; 1965. [Google Scholar]
- 5.Axelrod R, Hamilton WD. The evolution of cooperation. Science. 1981;211:1390–1396. doi: 10.1126/science.7466396. [DOI] [PubMed] [Google Scholar]
- 6.Groves T, Ledyard J. Optimal allocation of public goods: A solution to the free rider problem. Econometrica. 1977;45:783–809. [Google Scholar]
- 7.Hardin G. The tragedy of the commons. Science. 1968;162:1243–1248. [PubMed] [Google Scholar]
- 8.Nowak MA. Five rules for the evolution of cooperation. Science. 2006;314:1560–1563. doi: 10.1126/science.1133755. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Nowak MA, May RM. Evolutionary games and spatial chaos. Nature. 1992;359:826–829. [Google Scholar]
- 10.Szabó G, Fáth G. Evolutionary games on graphs. Phys Rep. 2007;446:97–216. [Google Scholar]
- 11.Roca CP, Cuesta JA, Sánchez A. Evolutionary game theory: Temporal and spatial effects beyond replicator dynamics. Phys Life Rev. 2009;6:208–249. doi: 10.1016/j.plrev.2009.08.001. [DOI] [PubMed] [Google Scholar]
- 12.Santos FC, Pacheco JM. Scale-free networks provide a unifying framework for the emergence of cooperation. Phys Rev Lett. 2005;95:098104. doi: 10.1103/PhysRevLett.95.098104. [DOI] [PubMed] [Google Scholar]
- 13.Gómez-Gardeñes J, Campillo M, Floría LM, Moreno Y. Dynamical organization of cooperation in complex topologies. Phys Rev Lett. 2007;98:108103. doi: 10.1103/PhysRevLett.98.108103. [DOI] [PubMed] [Google Scholar]
- 14.Helbing D, Yu W. The future of social experimenting. Proc Natl Acad Sci USA. 2010;107:5265–5266. doi: 10.1073/pnas.1000140107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Grujić J, Fosco C, Araujo L, Cuesta JA, Sánchez A. Social experiments in the mesoscale: Humans playing a spatial prisoner’s dilemma. PLoS One. 2010;5:e13749. doi: 10.1371/journal.pone.0013749. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Cassar A. Coordination and cooperation in local, random and small world networks: Experimental evidence. Games Econ Behav. 2007;58:209–230. [Google Scholar]
- 17.Kirchkamp O, Nagel R. Naive learning and cooperation in network experiments. Games Econ Behav. 2007;58:269–292. [Google Scholar]
- 18.Traulsen A, Semmann D, Sommerfeld RD, Krambeck HJ, Milinski M. Human strategy updating in evolutionary games. Proc Natl Acad Sci USA. 2010;107:2962–2966. doi: 10.1073/pnas.0912515107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Gracia-Lázaro C, Cuesta JA, Sánchez A, Moreno Y. Human behavior in Prisoner’s Dilemma experiments suppresses network reciprocity. Sci Rep. 2012;2:325. doi: 10.1038/srep00325. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Langer P, Nowak MA, Hauert C. Spatial invasion of cooperation. J Theor Biol. 2008;250:634–641. doi: 10.1016/j.jtbi.2007.11.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Roca CP, Cuesta JA, Sánchez A. The effect of population structure on the evolution of cooperation. Phys Rev E. 2009;80:46106. doi: 10.1103/PhysRevE.80.046106. [DOI] [PubMed] [Google Scholar]
- 22.Ledyard JO. In: Public Goods: A Survey of Experimental Research, Handbook of Experimental Economics. Nagel JH, Roth AE, editors. Princeton: Princeton Univ Press; 1995. pp. 111–251. [Google Scholar]
- 23.Camerer CF. Behavioral Game Theory. Princeton: Princeton Univ Press; 2003. [Google Scholar]
- 24.Fischbacher U, Gächter S, Fehr E. Are people conditionally cooperative? Evidence from a public goods experiment. Econ Lett. 2001;71:397–404. [Google Scholar]
- 25.Velicer GJ. Social strife in the microbial world. Trends Microbiol. 2003;11:330–337. doi: 10.1016/s0966-842x(03)00152-5. [DOI] [PubMed] [Google Scholar]
- 26.Fehl K, van der Post DJ, Semmann D. Co-evolution of behaviour and social network structure promotes human cooperation. Ecol Lett. 2011;14:546–551. doi: 10.1111/j.1461-0248.2011.01615.x. [DOI] [PubMed] [Google Scholar]
- 27.Rand DG, Arbesman S, Christakis NA. Dynamic social networks promote cooperation in experiments with humans. Proc Natl Acad Sci USA. 2011;108:19193–19198. doi: 10.1073/pnas.1108243108. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.