Quantum rotation of ortho and para-water encapsulated in a fullerene cage

Abstract

Inelastic neutron scattering, far-infrared spectroscopy, and cryogenic nuclear magnetic resonance are used to investigate the quantized rotation and ortho–para conversion of single water molecules trapped inside closed fullerene cages. The existence of metastable ortho-water molecules is demonstrated, and the interconversion of ortho-and para-water spin isomers is tracked in real time. Our investigation reveals that the ground state of encapsulated ortho water has a lifted degeneracy, associated with symmetry-breaking of the water environment.

The synthetic procedure known as “molecular surgery” (1–3) involves opening an orifice in fullerene (C₆₀) cages by a series of chemical reactions, insertion of small molecules into the cavity, and resealing of the cage by further reactions. This procedure has made available, in macroscopic quantities, a class of pure, stable, substances in which closed fullerene cages encapsulate small molecules. These systems provide “nano-laboratories” in which the small molecules are isolated in a geometrically well-defined, highly symmetrical environment. Confined small molecules such as H₂ behave as quantum rotors, in which the quantized translational and rotational levels are mixed by the confinement, generating a rich energy level structure (4–12).

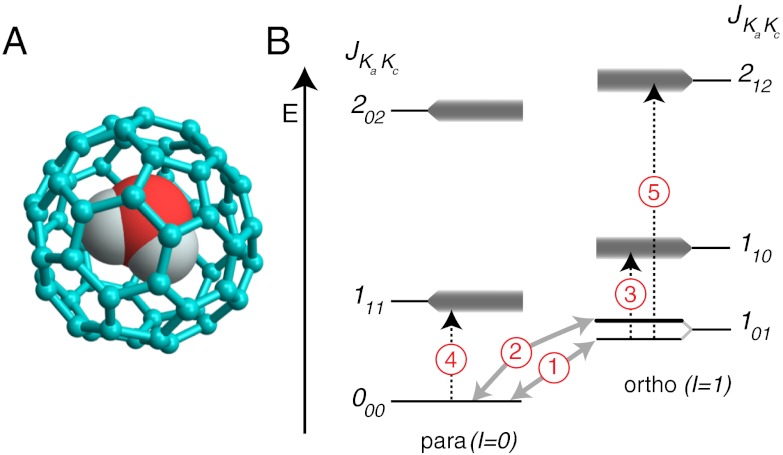
The recently synthesized water-endofullerene H₂O @ C₆₀ (3) is particularly intriguing (see Fig. 1A). Like H₂, water exhibits spin isomerism, with ortho- and para-forms, but unlike H₂, water has an electric dipole moment. Do the electric dipoles of encapsulated water molecules rotate freely, reflecting the absence of hydrogen bonding? Do the ortho- and para-spin isomers interconvert? Can energetic ortho-water molecules be trapped in a metastable state? What is the potential describing the interaction of water with the curved carbon surface? Do the electric dipole moments of water molecules in neighboring cages line up cooperatively, exhibiting ferroelectricity (13)?

Fig. 1.

(A) Molecular structure of the water-endofullerene H₂O @ C₆₀, using a ball-and-stick representation for the C₆₀ cage and space-filling spheres for water; (B) Energy level diagram, showing the principal transitions detected by INS (grey arrows) and IR spectroscopy (dashed arrows). The three-fold rotational degeneracy of the ortho-H₂O ground state is lifted. The upper level of the split 1₀₁ state is doubly degenerate. Unresolved fine structure is indicated by shading.

We study the energy levels, spin isomerism and quantum dynamics of single water molecules enclosed in fullerene cages, using three complementary physical methods: inelastic neutron scattering (INS), far-infrared spectroscopy (FIR), and nuclear magnetic resonance (NMR). In all cases, the homogeneous and symmetric environment provided by the fullerene cages isolates the ortho and para spin isomers, and gives rise to relatively narrow and unambiguous spectral features. We observe the existence of metastable ortho-water molecules, follow the slow conversion of ortho-water into para-water, and detect an energy splitting in the ortho-water rotational ground state, which is a signature of broken symmetry.

A simplified energy level diagram of endohedral water, based on free water in the gas phase, is shown in Fig. 1B. The endohedral water molecule behaves as an asymmetric top, with rotational energy levels indexed by the three numbers J_KaKc where J is the quantum number for the total angular momentum. The indices K_a and K_c refer to the angular momentum quantum numbers in the corresponding prolate and oblate symmetric tops (14). In an environment with tetrahedral symmetry or higher, each J_KaKc level is (2J + 1)-fold degenerate, with an additional quantum number M_J∈{-J,-J + 1…+J} defining the angular momentum projection on an external axis. The rotational states are correlated to the proton spin states through the Pauli principle: ortho-water states have total nuclear spin I = 1, and odd parity for K_a + K_c in the ground vibrational state. The para-water states have total nuclear spin I = 0, and even parity for K_a + K_c in the ground vibrational state.

Results

Inelastic Neutron Scattering.

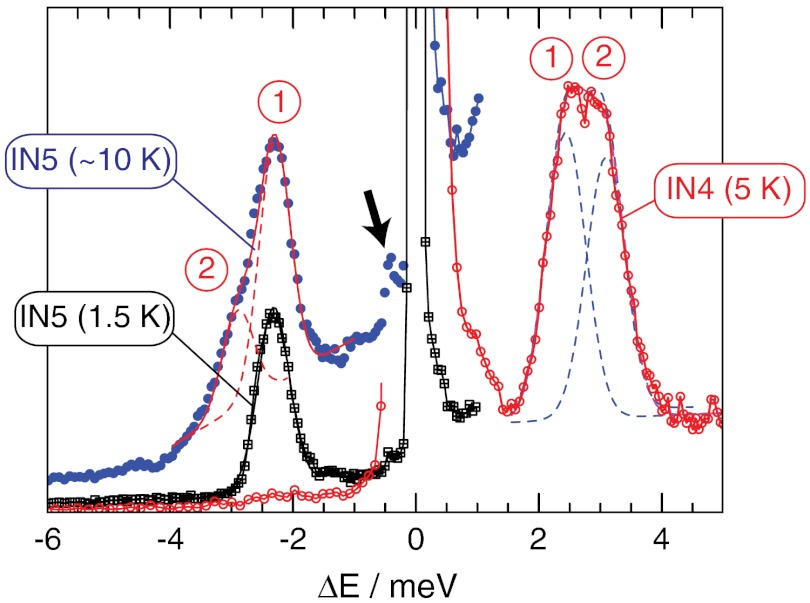
Fig. 2 shows INS spectra of H₂O @ C₆₀ as a function of neutron energy transfer ΔE, at two different sample temperatures. The intense peak centred at ΔE = 0 represents elastically scattered neutrons. The inelastic neutron scattering peaks appear as smaller features on either side, with the sign convention that ΔE represents the energy loss or gain relative to the molecule. Therefore in the scattering event between the neutron and the nuclei of the molecule, negative ΔE corresponds to neutron energy (NE) gain transitions while positive ΔE represents NE loss.

Fig. 2.

INS spectra recorded on the time-of-flight spectrometers IN4 and IN5. The 10 K spectrum is an average over 5, 10, and 15 K data. The dashed lines show the best fit components where the transitions are labeled according to Fig. 1B.

INS transitions are mediated by a spin dependent interaction and are dominated by scattering from ¹H nuclei. This has significant consequences. Firstly, unlike photon spectroscopy, INS can drive transitions between different nuclear spin-isomers of H₂O. Therefore, INS peaks that connect ortho-H₂O and para-H₂O appear with significant intensity. Secondly, since para-water has spin 0, transitions between different states of para-H₂O have negligible intensity. However, since the ortho spin isomer has spin 1, ortho–ortho transitions appear with similar intensity to ortho–para transitions.

Even at the lowest temperature T = 1.5 K, an INS peak (labeled “1”) appears with NE gain at ΔE = -2.4 ± 0.1 meV; this is generated by scattering events in which the sample has undergone a transition from a high energy state to one of lower energy, raising the energy and speed of the scattered neutron. Since the energy of the transition ΔE/k_B = 28 K is much larger than the available thermal energy at 1.5 K, this peak must arise from a meta-stable state that is not at thermal equilibrium. Peak “1” is therefore assigned to the transition from the metastable ground state of ortho-H₂O to the ground state of para-H₂O, 1₀₁ → 0₀₀ (see Fig. 1B). The observation of this peak provides compelling evidence that the ortho-H₂O spin isomer is long-lived inside the fullerene cage and, upon cooling, does not convert completely to para-H₂O, over the timescale of the experiment (6 h).

Increasing the sample temperature to T = 10 K gives rise to a second peak in NE gain at ΔE = -2.9 ± 0.1 meV (labeled “2”). This peak becomes populated at temperatures as low as 5 K and the temperature dependence of the peak amplitude indicates that it corresponds to an excited state of ortho-water that is approximately 0.6 meV above the ortho-H₂O ground state. We postulate that the three-fold degenerate 1₀₁ ortho ground state is split, and assign peak “2” to transitions between the upper sublevel of 1₀₁ and the para ground state 0₀₀, while peak “1” is assigned to transitions between the lower sublevel of 1₀₁ and 0₀₀ (Fig. 1B). The existence of a splitting in the ortho ground state is supported by the NMR data (see below).

We can be confident that the NE gain spectrum arises only from transitions originating in metastable ortho-H₂O molecules. Librational and vibrational modes of C₆₀ and phonon modes above approximately 0.2 meV are not populated in the NE gain spectrum at a temperature of 1.5 K.

More transitions are observed in the NE loss spectrum, including the transitions 1 and 2 in the opposite direction to those observed in NE gain. Transition 3 in Fig. 1B appears in neutron energy loss, but it overlaps with transitions 1 and 2 (see infrared data, below). As indicated above, the para–para transition 4 is absent in INS.

The small feature in the 10 K spectrum at a neutron energy gain of ΔE ≅ -0.6 meV (indicated by the arrow) is provisionally attributed to transitions from the upper to the lower sublevel of 1₀₁.

Far-Infrared Spectroscopy.

Far-infrared (FIR) spectroscopy detects transitions between the rotational levels of H₂O. The absorption coefficient of radiation is proportional to the difference in the populations of the initial and final states. Unlike INS, transitions between ortho and para states are highly forbidden. Since each spin isomer attains internal thermal equilibrium very rapidly, the slow time evolution of the peak intensities is due to ortho–para conversion. This allows us to identify the ortho and para lines unambiguously, and to determine the kinetics of ortho–para conversion.

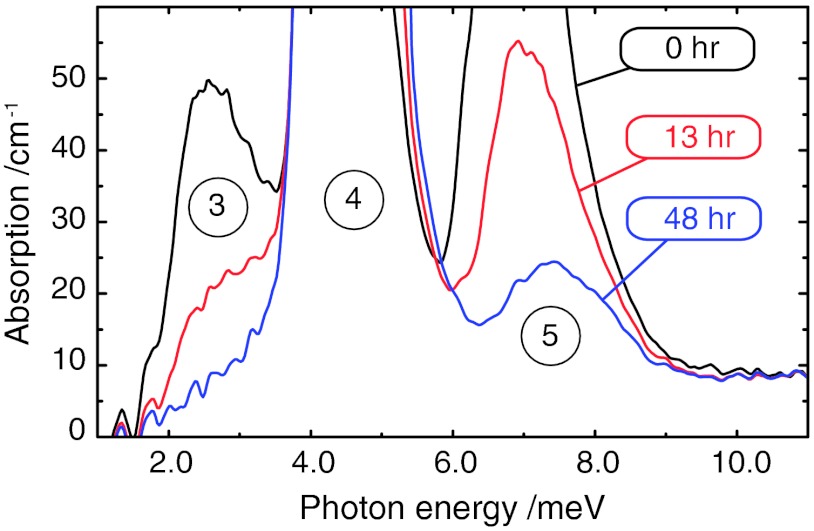
The FIR spectrum of 10 mg of H₂O @ C₆₀ is shown in Fig. 3. The three peaks in the displayed spectral region are assigned to the rotational transitions shown in Fig. 1B. Peak “4” is a rotational transition of para-H₂O (0₀₀ → 1₁₁), while peaks “3” and “5” are rotational transitions of ortho-H₂O (1₀₁ → 1₁₀ and 1₀₁ → 2₁₂, respectively). The assignments are supported by the effect of ortho–para conversion (see below). Peak “4” provides strong absorption of the infrared radiation, which saturates the absorption curve under the experimental conditions. On thinner samples, the absorption maximum is observed at 4.55 ± 0.2 meV. The energy of transition “3” lies between that of “1” and “2”, which explains why it is unresolved in neutron energy gain (see above).

Fig. 3.

Far-infrared spectra of H₂O @ C₆₀ at 3.5 K. The times indicate the elapsed intervals after cooling from 77 K. The circled numbers refer to the transition assignments in Fig. 1B. The time-dependence of the peaks indicates slow ortho-to-para conversion. Peaks 4 and 5 are initially saturated due to the strong absorption and thick sample.

The spectra shown in Fig. 3 were all obtained at a sample temperature of 3.5 K, and were taken after slow cooling from a temperature of 77 K. The spectrum shown in black was obtained immediately after cooling, while the spectra shown by the red and blue curves were obtained after the indicated waiting periods. Peak “5” is initially saturated due to its strong absorption, but the saturation disappears at later times, as the peak becomes less intense. Although the amplitude of peak “4” cannot be measured directly, the movement of the peak edges indicate that peak “4” increases in amplitude as peaks “3” and “5” become weaker.

The changing intensity of the FIR peaks is due to ortho-to-para conversion, which strongly depletes the ortho state in favor of para at the sample temperature of 3.5 K. The time dependence, shown in Fig. S1, is almost mono-exponential with a time constant of 12 ± 1.3 h at the temperature of 3.5 K. This is similar to the ortho–para conversion rate for water in argon matrices at 4.2 K (15).

The splitting in the ortho ground state, which is resolved by INS, is not visible in the FIR, presumably due to unresolved structure in the higher energy levels. The ortho–ortho transition 1₀₁ → 1₁₀ (transition “3” in Fig. 1B) has similar energy to the transition from the para ground state 0₀₀ to the lower sublevel of the ortho ground state 1₀₁(transition “1”). This coincidence explains why transition “3” does not separately show up in NE loss in the INS spectrum (Fig. 2); the NE loss spectrum evidently contains multiple transitions, not all of which are thermally populated in NE gain at the temperatures studied.

Magic-Angle-Spinning NMR.

Magic-angle-spinning (MAS) NMR is used to provide high-resolution spectra of solid samples; rapid spinning of the sample around an axis subtending the angle 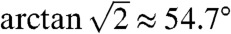averages out many anisotropic nuclear spin interactions, providing narrow spectral lines in the solid state (16). Recent technological advances have made it possible to perform MAS-NMR experiments reliably in the cryogenic temperature regime (4, 17–20).

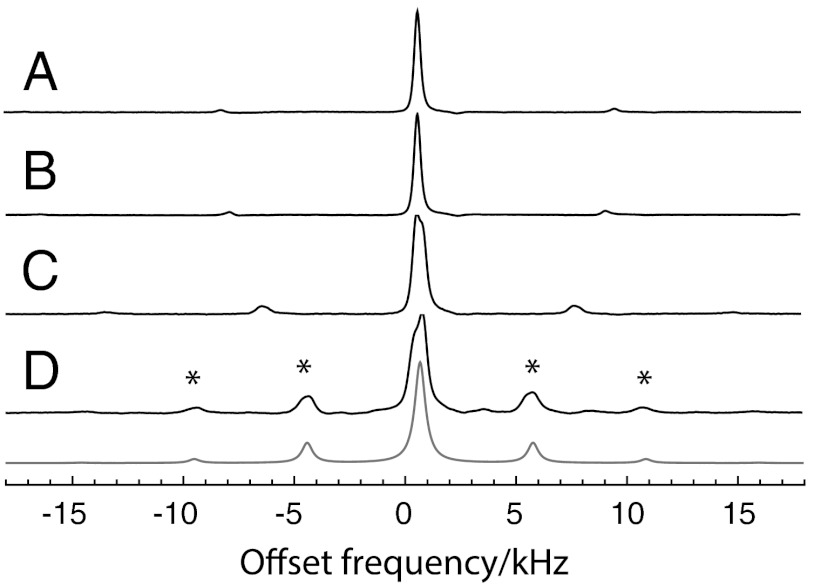
MAS proton NMR spectra of 9 mg of H₂O @ C₆₀ are shown in Fig. 4. These NMR signals come exclusively from the ortho spin isomer: the para spin isomer has zero nuclear spin and does not provide an NMR signal. In the light of the INS and FIR results, the 9.6 K NMR spectra must originate from metastable ortho-H₂O molecules.

Fig. 4.

Magic-angle-spinning proton NMR spectra of H₂O @ C₆₀, taken in a magnetic field of 14.1T (proton precession frequency ≈-600.0 MHz). All spectra were obtained by taking the Fourier transform of a single transient after a 90° excitation pulse and subjecting it to Lorentzian linebroadening with a linewidth of 200 Hz followed by baseline correction. The sample temperatures and spinning frequencies are (A) 22.8 K, 8.86 kHz; (B) 18.5 K, 8.38 kHz; (C) 13.0 K, 7.12 kHz; (D) 9.6 K, 5.04 kHz. The peaks indicated by asterisks are spinning sidebands. The grey line is a simulation for randomly oriented pairs of protons with a magnetic dipole–dipole interaction of -5.5 kHz.

The NMR spectra do not exhibit strong spinning sidebands at temperatures above ∼20 K. This is a signature of rapid isotropic molecular motion, which is consistent with molecular dynamics simulations (21). However, at low temperature, spinning sidebands develop in the MAS NMR spectrum, and an unresolved shoulder appears on the centerband. Apart from the asymmetric centerband, the 9.6 K spectrum is a good match to a simulation for randomly oriented pairs of spins-1/2 experiencing a through-space dipole–dipole coupling of -5.5 kHz (grey curve in Fig. 4). For comparison, no spinning sidebands are observed in the MAS proton spectrum of H₂ @ C₆₀ under similar conditions (5). The slight asymmetry of the centreband at 9.6 K is currently unexplained.

Ortho-to-para transitions are expected to lead to a slow decay in the NMR signal intensity at low temperatures, since para-H₂O provides no NMR signal. We did not observe this decay, presumably because our NMR experiments were performed at the lowest temperature for approximately 90 min, as compared to the approximately 12-h ortho–para conversion time observed in infrared spectroscopy (see above).

Internuclear dipole–dipole couplings must be interpreted by a quantum treatment which takes into account the spatial delocalization of the rotational wavefunctions in rotational quantum states (4, 22). For J = 1 states, the nuclear dipole–dipole coupling is scaled by a factor of 2/5 compared to a classical model, with the same internuclear distance (4, 22). In addition, the nuclear dipole–dipole coupling tensor is averaged over the populated quantum states, with populations governed by the Boltzmann distribution. At high temperature, all 2J + 1 components of a level with rotational quantum number J are equally populated, leading to a vanishing dipole–dipole coupling. This corresponds to the case of isotropic classical rotation. An energy splitting between the sublevels causes unequal populations in thermal equilibrium, and generates a finite dipole–dipole coupling tensor. Conversely, the existence of a finite dipole–dipole coupling is a signature of an energy splitting between the sublevels.

The -5.5 kHz internuclear dipolar coupling at 9.6 K leads to an estimate of the ortho ground state splitting of approximately 0.9 meV. The analysis (see SI Text) makes the following approximations and assumptions: rigid water molecules, with a proton-proton distance of 1.515 Å (see Fig. S2); splitting of the three 1₀₁ sublevels into a nondegenerate lower level with M_J = 0 and a doubly degenerate upper level with M_J =  ± 1; and neglect of higher rotational and translational states of ortho-water. The estimated splittings from cryogenic NMR (approximately 0.9 meV) and INS (approximately 0.6 meV) are reasonably consistent, given the many approximations that are involved. The discrepancy is attributed to contributions from intermolecular couplings, chemical-shift anisotropy, spin-rotation effects, and the influence of higher rotational and translational levels.

The approximately 1 kHz linewidth of the experimental ¹H MAS peaks is greater than that anticipated for isolated water molecules. The origin of the linewidths is currently unknown, but may be associated with the presence of a protonated impurity in the sample, see Fig. S3.

Discussion

The energy level spacings of the lowest rotational sublevels of water in H₂O @ C₆₀, as determined by INS and FIR spectroscopy, are compared with those of gas-phase water vapor (23, 24) in Table 1. The most striking difference between encapsulated water and free water is the 0.6 meV splitting in the ortho-water ground state. Apart from this splitting, the encapsulation in C₆₀ does not change the lower rotational energies of water by more than 0.2 meV (taking the average of the split 1₀₁ levels, and accounting for the double degeneracy of the upper level). Unlike the case of H₂ @ C₆₀ (6, 7), there is no obvious signature of strong translation-rotation coupling.

Table 1.

Rotational transitions of water in H₂O @ C₆₀ and in the gas phase

				H2O @ C60 [meV (cm-1)] (this work)
Transition	Quantum states		Type	IR	INS	Gas phase H2O [meV (cm-1)] (ref. (24))
1	000	101 (lower)	p↔o	—	2.3 ± 0.1 (18.6 ± 0.8)	2.95* (23.8)*
2	000	101 (upper)	p↔o	—	2.9 ± 0.1 (23.4 ± 0.8)
3	101	110	o↔o	2.5 ± 0.6 (20 ± 5)	—	2.30 (18.6)
4	000	011	p↔p	4.6 ± 0.6 (37 ± 5)	—	4.60 (37.1)
5	101	212	o↔o	7.0 ± 0.6 (56 ± 5)	—	6.91 (55.7)

The transition energies are given in meV and in cm^-1 (in parentheses). The gas phase data is from ref. (24), except for the ortho–para transition 0₀₀ → 1₀₁ (marked with an asterisk), which is inferred by modeling the water molecule as a rigid asymmetric rotor.

All three forms of spectroscopy reveal the presence of metastable ortho-water molecules at low temperature which undergo slow transitions to the low-energy para-spin isomer. FIR spectroscopy provides the most detailed picture of ortho–para conversion, allowing the spin isomerization process to be followed in real time on the timescale of hours.

The INS and NMR data are both consistent with a splitting in the triply degenerate ground state of ortho-water by around 0.6 meV. This lifting of degeneracy may be due to crystal packing effects which break the local symmetry, or to a spontaneous distortion of the fullerene cage induced by the rotationally degenerate water molecule, analogous to the Jahn-Teller effect. The observation of this phenomenon in the magic-angle-spinning NMR spectra indicates that the symmetry-breaking distortion must have a lifetime of at least several tens of milliseconds. An intriguing possibility, which requires deeper investigation, is that the breaking of symmetry reflects cooperative electric dipole alignment; i.e., ferroelectricity (13).

Materials and Methods

Synthesis.

H₂O @ C₆₀ was synthesized by the published procedure (3). Solution-state proton NMR spectra of the last open-cage derivative before the final closing reaction indicated that about 60% of the C₆₀ cages are occupied by water molecules. The compound, which was purified by column chromatography eluted with CS₂/pentane = 2/1, was dissolved in CS₂. The solution was dropped into pentane to give a precipitate. The precipitate was collected by centrifuge and then heated at 180 °C under vacuum for 3 d. The resulting powder was used for the measurements. Solid-state NMR measurements indicated the presence of a protonated impurity with a proton concentration of about 3 times the endohedral water molecules (see Fig. S3).

Inelastic Neutron Scattering.

The experiments were conducted using two different time-of-flight INS spectrometers, IN4 and IN5, at the Institut Laue-Langevin. In both instruments, the sample is irradiated by a pulsed beam of monochromatic neutrons. The energy of the scattered neutrons is then determined from the time taken between the arrival of the neutron pulse at the sample and the arrival of a neutron in a detector that is situated a known distance away. The momentum transfer may be inferred from the geometry of the scattering event, and the angular position of the neutron detector. The INS spectra in Fig. 2 are obtained from a sum of detectors covering a momentum transfer range approximately 1.5 Å ≤ Q ≤ 8 Å. On IN4, Bragg diffraction from a curved monochromator is used to select the energy/wavelength of the incident neutrons, with a Fermi chopper being used to provide the pulsed structure of the beam. The flight path between sample and detectors is 2 m. On IN5 the pulsed monochromatic structure is obtained using six pairs of counter-rotating choppers, with their phases and frequencies being set to determine the energy/wavelength of the beam. IN5 has a 4-m flight path between the sample and an array of pixilated position sensitive detectors.

The sample used for the INS experiments was 95 mg of H₂O @ C₆₀ powder packed in an aluminum foil container. The sample was mounted in the cryostat under a reduced pressure of He gas.

Far Infrared Spectroscopy.

The sample was pressed under vacuum from a powder of 60% of H₂O @ C₆₀ and 40% of empty C₆₀ into a d = 0.83 mm thick and 3-mm diameter pellet of mass 10 mg.

The pellet was pumped at room temperature for several hours inside the sample compartment of a liquid He cryostat before cooling and adding the He heat exchange gas to the sample compartment. Light was guided from the Sciencetech SPS Martin-Puplett type spectrometer to the sample cryostat using a light pipe and detected with a 0.3 K bolometer located inside a vacuum chamber in the same liquid He cryostat. A motorized sample changer inside the cryostat was used to change between the sample and a reference hole of 3 mm diameter. The absorption coefficient was calculated by 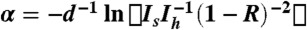, where I_s and I_h are the light intensities transmitted by the sample and by the reference hole. This formula accounts for one back reflection from the pellet front and back face, where the reflection coefficient R = (n - 1)²(n + 1)^-2 and constant index of refraction n = 2 is assumed. The plotted spectra in Fig. 3 are not corrected for the 65% content of H₂O @ C₆₀ in the sample.

Nuclear Magnetic Resonance.

The equipment for cryogenic magic-angle spinning NMR uses three separate cryogenic streams of supercritical He for the bearing system, the turbine system, and for sample cooling. The separate streams of supercritical helium were generated from liquid in a large custom-built cryogenic vessel, and kept below 7 K at a stable controlled pressure of 2.5–4.5 bar. The flow rates and temperatures of all three streams are independently controlled by using cryogenic needle valves and electrical heaters. The temperatures of the three gas streams are measured on entry to the probe cryostat.

The cryogenic spinning system uses a zirconia rotor with an outer diameter of 2 mm and length of 16.2 mm (including the turbine wheel inserts), provided by Revolution NMR. The rotor was packed with 9 mg of H₂O @ C₆₀ powder. The temperature of the gas exiting the spinning assembly was monitored by using a Cernox temperature sensor mounted in the exhaust pipe about 2 cm from the rotor with an accuracy of 0.15 K. The real sample temperature was cross-checked against the exhaust gas temperature in separate experiments using the ¹²⁷I nuclear spin-lattice relaxation in CsI as an internal thermometer (20).

The 9.6 K spectrum shown in Fig. 4 was obtained at the end of a long experimental series involving slow cooling of the magic-angle-spinning sample from room temperature over approximately 10 h. The sample spent approximately 90 min below 20 K during the acquisition of this spectrum. This interval is reasonably short compared to the ortho–para conversion rates measured by infrared spectroscopy.

The chemical shift scale in the proton spectra was calibrated by using the 1.8 ppm proton NMR peak of adamantane as a reference. The endohedral water peak is at -4.6 ppm, which is close to the position observed in room temperature liquid state NMR (3).