Abstract
Coarse-grained (CG) models have proven to be very effective tools in the study of phenomena or systems that involve large time- and length-scales. By decreasing the degrees of freedom in the system and using softer interactions than seen in atomistic models, larger timesteps can be used and much longer simulation times can be studied. CG simulations are widely used to study systems of biological importance that are beyond the reach of atomistic simulation, necessitating a computationally efficient and accurate CG model for water. In this review, we discuss the methods used for developing CG water models and the relative advantages and disadvantages of the resulting models. In general, CG water models differ with regards to how many waters each CG group or bead represents, whether analytical or tabular potentials have been used to describe the interactions, and how the model incorporates electrostatic interactions. Finally, how the models are parameterized depends on their application, so, while some are fitted to experimental properties such as surface tension and density, others are fitted to radial distribution functions extracted from atomistic simulations.
Keywords: molecular simulation, anomalies, mapping, force field development, coarse graining
1. Introduction
Water is, most likely, the most utilized solvent in experimental and computational studies [1–3], particularly for biological systems. However, water has many unique properties, such as a density maximum at 277 K and increased diffusivity upon compression, which complicates its dynamics and physics compared to other solvents [4]. Because of its importance as a solvent in biological systems and its unique properties, developing an accurate computational model for water is an ever-evolving and ongoing quest.
In biological systems and biological processes, the time- and length-scales that need to be studied typically prevent the use of fully atomistic simulations because of the computational cost and coarse-grained (CG) models are instead used to overcome atomistic limitations. In CG models, groups of atoms are represented by single sites or beads to drastically reduce the degrees of freedom in the simulations and allow for larger timesteps (i.e., ~10 – 20 fs, rather than 1 – 2 fs as is commonly used in atomistic simulations) so that molecular dynamics simulations can be run for very long times.
In some cases, a system’s solvent, including water, is modeled implicitly (see for example [5–7]). Essentially, the CG model of the solute is optimized to interact as it would in the presence of a solvent, without explicitly modeling the solvent molecules. While implicit models are computationally efficient, they can easily miss important physical details. For example, although hydrophobic solutes typically have little effect on the solvent with changing concentration, ionic solutes like NaCl affect how the solvent behaves at higher concentrations [8].
While the techniques and practices behind using implicit solvents are interesting, with this review we have chosen to focus on explicit CG models for water, where the emphasis is on the development of accurate models with respect to water’s properties and behaviors rather than the solute (as is the case with implicit solvent models). In particular, we aim to introduce the reader to the most recent and the most popular CG water models developed for use in molecular dynamics or Monte Carlo simulations. First, in Section 2, we will summarize the main coarse-graining methods used to develop CG water models, and also models for lipids, proteins, and polymers, as well as highlighting water specific cases. In section 3, we review water models that map one water to each bead followed by multi-water models in section 4. Finally, in section 5, we discuss models with analytical functions with and without explicit electrostatics.
2. Coarse-graining methods
Although there are many CG methods available with which to develop accurate force fields for solvents and solutes of interest, they all typically share common procedures. The first step involves “mapping” the molecule from the atomistic level to the CG level. Before the mapping begins, the degree of coarse-graining must be determined; in other words, how many atoms should be assigned to each bead. Traditionally, no more than six heavy atoms (non-hydrogen atoms) are represented by a single CG bead, because too much detail is lost beyond that level of coarse-graining and isotropic potentials become inadequate with respect to representing the beads. The other major component of mapping is retaining specific functional groups such as the choline group of certain phospholipids.
In molecules with multiple heavy atoms (e.g., lipids), mapping specific atoms from atomistic simulations to pre-determined sites is somewhat trivial and only requires simple intuition. The difficulty with water is determining which waters should be mapped to which beads since the water molecules move independently, as they are only bound by non-bonded interactions [9]. Because of this, three strategies are currently used to map water to the CG level. The first, and perhaps the simplest method, is to map one water molecule to one CG bead. This strategy is usually implemented with center-of-mass (COM) based techniques, as discussed below, but only saves a marginal amount of simulation time. More commonly, water is implicitly mapped (i.e., each bead is assigned a fixed number of arbitrary water molecules rather than explicitly mapping atomistic waters to the CG level) and beads interact with each other through an analytical potential; the CG bead is meant to represent multiple waters as dictated by its size, interaction strength, and other thermodynamic and structural properties. Finally, as detailed in section 4, clustering algorithms can be used as a way to dynamically determine which waters belong to which beads in COM based CG methods [9, 10].
With a mapping strategy determined, the next step is to define the force field used to dictate the thermodynamics and physics of the CG model. In short, the input parameters of the force field must be optimized in a way to reproduce macroscopic properties of interest (i.e., experimental or simulated surface tension, structure, diffusivity, and density). Unfortunately, the loss of detail prevents matching all properties, with some behaviors being mutually exclusive in relation to fitting. For example, as shown by Izvekov and Voth [11], diffusivity and RDFs cannot be matched simultaneously. Likewise, Toth found total energy and structure could not be fitted simultaneously [12]. As such, the key to this step is deciding what properties need to be retained on the CG level, which, in turn, usually determines the most appropriate coarse-graining method. For example, if the goal of the CG model is to study structural behavior the most appropriate CG method is one that fits the interaction potentials to RDFs, but a different method would be more appropriate if the target were accurate free energies of solvation of dynamical properties.
There are two major types of targets for fitting the CG force field: experimental measurements and measurements taken from atomistic simulations. When atomistic simulations are used as the target, the CG method is usually a COM based method, where the mapping determines which atoms at the atomistic level contribute each bead and the COM of the atoms within a bead is then used to determine the position of the bead on the CG level. When experimental measurements serve as the optimization target, the mapping only serves as a guide to interpret atomistic level information from the CG simulations rather than to enable atomistic data to be extracted to the CG level.
With the mapping and target for the CG model defined, what remains is to parameterize the CG force field. If a numerical (or tabulated), rather than an analytical, potential is to be developed, there are three main approaches and are all COM-based CG methods: force-matching (FM), developed by Voth and co-workers [11, 13–17], inverse Monte Carlo (typically depicted as IMC), first reported by Lyubartsev and coworkers [18–21], and the iterative Boltzmann inversion (IBI) method initially developed by Reith et al. [22]. In contrast, no general methods have been reported to parameterize analytical expressions for CG force fields fitted to target experimental properties. Rather, each CG model developed either uses some kind of iterative approach to achieve the optimization they desire or a fitting procedure unique to their CG model. As such, the methods used to develop the water models with an analytical expression will be discussed separately in the subsequent sections.
In the FM approach, the potential is iterated until the forces between the CG molecules matches the forces between their atomistic counterparts [11, 15–17]. In short, a target atomistic simulation is run and a set of reference forces are collected to which the set of CG forces are subsequently matched by minimizing equation (1):
| (1) |
where N and L are the total number of atoms and atomic configurations, respectively, and gi are the parameters in the force field (e.g., the site diameter of a CG bead) where 1 ≤ i ≤ m,. In cases where the CG model is to be used for Monte Carlo simulation instead of molecular dynamics, Toth has developed an energy-matching algorithm that is analogous to the force-matching strategy [12]. Since the thermodynamic parameters are not inputs or targets, the derived potentials are generally more transferable than other CG potentials.
The IMC method [18–21] works by fitting input parameters to observables taken from the target atomistic simulation using equation (2),
| (2) |
where A* is the target observable, represents the input parameters, and 〈A〉k the CG ensemble average of the observable. From the definition of an ensemble average, the value of the gradient of the observables can be estimated via equation (3):
| (3) |
where H is the total Hamiltonian of the system and β is equal to 1/kT, where k is the Boltzmann’s constant and T is the simulation temperature. By combining equations (2) and (3), the required change in the parameters can be calculated to update the force field in an iterative fashion until the CG observables converge to the target values. An appealing feature of this method is the built-in sensitivity analysis with respect to the observable/input parameter gradient, which can indicate which parameters have the most influence on the observables in question.
Finally, the IBI method works by iteratively optimizing the potential to match radial distribution functions measured in the CG simulation to those from the target atomistic simulation mapped to the CG level using equation (4),
| (4) |
In equation 4 the tabulated potential, Vi (r), is updated at each point, r, by comparing the target RDF, g*(r), with the CG RDF, gi (r). Also shown in equation 4 is a damping factor δ that was not included in the original work as the authors were able to reach convergence without one. However, several groups [9, 23–30] have found adding a damping factor with values less than 1.0 is necessary in ill-defined optimization schemes. Specifically, Hadley and McCabe encountered a diverging oscillatory response when optimizing many different (coupled) CG potentials simultaneously or for systems in a well-structured (crystalline) state [9, 27–29].
While the above three methods are the most common in the literature, many other novel and application specific methods for deriving tabulated CG potentials exist. For example, Wei and Wang [31] have developed a novel way to retain a large degree of atomistic detail in systems solvated by water, but accelerate dynamic processes so coarse-graining is not even necessary. Their damped short-ranged interaction (DSRI) smooths out the potential energy surface by subtracting out a short ranged correction term,
| (5) |
scaled by λ (0.3) from the original Hamiltonian at distances less than 0.40 nm (rsr). With these values, the RDF of pure water is still reproduced, but the diffusion coefficient is drastically increased due to less friction between molecules and softer interactions. The authors considered this change in diffusivity their goal as they wanted to minimize the barrier to diffusion to accelerate processes like self-assembly. Using this methodology, a CG model for dimyristoyl-phosphatidylcholine was shown to self-assemble within 40 ns from a completely random initial configuration, after which, λ can be set to 0.0 and the simulations run without the correction term [31].
3. Single water models
As mentioned previously, CG water models with a one water mapping limit the amount of time that can be saved by using a CG model. However, with COM-based techniques, mapping multiple waters to single beads for force field development is difficult and has only recently been overcome.[9, 10] As such, CG water models from FM [11, 15, 16], IMC [19, 32], and IBI [23, 33, 34] have traditionally been limited to mapping one water to each bead.
While the structuring and dynamics obtained from simulations that use these water models are generally good, they do require longer simulation times than other, more CG water models. Additionally, the work of Wang et al. [34] provides interesting insight into accuracy issues and the isotropic nature of the interactions in single water CG models. In their work, the IBI method was used to fit RDFs for single water beads based on the SPC [35], SPC/E [36], and TIP3P [37] atomistic water models and found that accurate RDFs were mutually exclusive to accurate tetrahedral packing; if RDFs were fitted within line thickness, the tetrahedral packing was much lower than the target, and if the model was modified to fit tetrahedral packing, the output RDF was much more structured. The authors attributed this to the isotropic nature of a CG model derived from the IBI method. Without the directionality of hydrogen-bonding between beads, they could not maintain the tetrahedral organization found in water, and with tetrahedral configuring enforced, the water hydrogen-bonded in an isotropic fashion causing a much higher degree of structure.
In the rest of this section, we aim to review single water CG models that treat water in a novel way, or significantly reduce the simulation times whilst still retaining a level of atomistic detail that is comparable to COM-based CG water models. Borgis and coworkers [38–40] developed the so-called polarizable pseudo-particle (PPP) model for water that retains accurate hydrodynamics and solvation, whilst minimizing simulation time and speed up of diffusion for similar reasons as stated for the DSRI method [31] discussed above. Originally [38], the model used a 12-6 Lennard-Jones (LJ) potential,
| (6) |
with εij equal to the interaction strength and σij equal to the diameter between sites i and j, but many properties, including density and vaporization enthalpy, were inaccurate. To overcome these problems Masella et al. [40], refined the original potential by adding a sum of Gaussian functions,
| (7) |
where ε is an energy term, rk is the Gaussian center, and γk is the width of the Gaussian peak and a density energy term (used to maintain the local solvent density near a particle),
| (8) |
| (9) |
| (10) |
| (11) |
In equations 8 through 11, Rmin corresponds to the first peak of the water RDF, Rmax corresponds to the location of the minimums in the RDF, P5 is a fifth order switching function, and n̅ represents the average number of neighboring particles. were fitted to heat of vaporization and the free energy required to create a cavity in the solvent. The revised PPP model was shown to not only reproduce better pure solvent properties, but also still retain the ability to provide good structuring of biomolecules like polypeptides.
Vlcek and Nezbeda introduced a primitive model for water aimed at simplifying calculations, while retaining hydrogen-bonding features [41, 42]. To achieve this, an attractive square-well potential was implemented between hydrogen-bonding partners (oxygen and hydrogen in water) and a hard sphere potential was used for every other pair-wise interaction. The square-well depth, attractive cutoff and the hard sphere diameters were derived from fully atomistic models (SPC/E, TIP4P and TIP5P) using perturbation theory. The authors were able to show that, despite an absence of long-ranged interactions, these simple models quantitatively describes the PVT behavior and structural properties of water of water in Monte Carlo simulations.
In a similar attempt to capture hydrogen-bonding in a simple manner, Dill and coworkers constructed the Mercedes-Benz water model [43], so named because water is represented as a two-dimensional disk with three symmetrical hydrogen-bonding vectors stemming from the center similar to the Mercedes-Benz® logo. The centers interact through a 12-6 LJ potential and through a Gaussian-based orientation dependent hydrogen-bonding potential, where equal but opposite vectors from different discs have the strongest attraction. A number of the thermodynamic anomalies found within water (such as the density maximum at lower temperatures and large anomalous heat capacity) could be simulated with this model, but its use is limited considering its two-dimensional nature. As a result, Bizjak et al. extended the model to a three-dimensional form with four tetrahedral hydrogen-bonding vectors to enhance its accuracy and realism [44, 45].
One issue with both the primitive and Mercedes-Benz models is their dependence on using Monte Carlo versus molecular dynamics simulations. As such, dynamic properties and phenomena cannot be studied, no matter how accurate or computationally efficient. In order to enforce tetrahedrality in a model compatible with molecular dynamics, Molinero and Moore introduced the so-called monotonic water (mW) model adapted from the Stilinger-Weber silicon potential [46, 47]. In the mW model the water molecules interact through a LJ Gaussian potential and a three body tetrahedral potential, described by,
| (12) |
where rij is the distance between particles i and j, θ is the angle between three waters, and λ is the scales the repulsive tetrahedral term, ϕ3. The tetrahedrality, λ, is fit to vaporization enthalpy, the interaction energy, ε, is fitted to melting temperature, and the site diameter, σ, is fitted to the density of water at room temperature. The remaining model parameters in equation (12) are taken from the original silicon model. While this model is not very coarse-grained, its major source of timesaving stems from the lack of electrostatics and the small non-bonded interation cutoff of 0.432 nm, which is large enough to reproduce the structure of water.
In a further study, the mW model was combined with a CG model of DNA [48] in which the other CG beads interacted with water via the potential from equation (12) with the tetrahedrality parameter equal to zero. The DNA model parameters were fitted to reproduce RDFs, the number of neighbors in the first solvation shell seen in atomistic simulations, and the residence time for solvation. The mW model proved to be very compatible with this CG model to provide accurate results with the use of molecular dynamics. Molinero and co-workers also found the mW model could reproduce the structure and anomalies in liquid and solid water, enabling the study of ice [49] and clathrate hydrate formation [50, 51].
Instead of using exotic geometries to reproduce anomalies, de Oliveira et al. [52, 53] add a Gaussian term to a 12-6 LJ potential as per equation (13),
| (13) |
and found a single water bead could reproduce thermodynamic, dynamic, and structural anomalies in water due to the introduction of a soft shoulder in the potential. Chaimovich and Shell fitted the parameters in equation (14) to minimize the relative entropy,
| (14) |
where p is the probability of configuration i [54]. In essence, when equation (14) is minimized, the configurations the CG model encounters should be identical to the configurations encountered by the atomistic counterpart. While the anomalies and RDFs of water could be reproduced through this optimization scheme, the anomalies are only accurate near the state conditions of the density maximum.
When attempting to model CG water capable of reproducing the unique anomalies found within water, single water models incorporate the necessary features to retain a high level of accuracy whilst minimizing simulation time. If these anomalies are of little interest in the simulation in question (i.e., in biological simulations), a multiple water CG model may be a better choice.
4. COM-based multiple water models
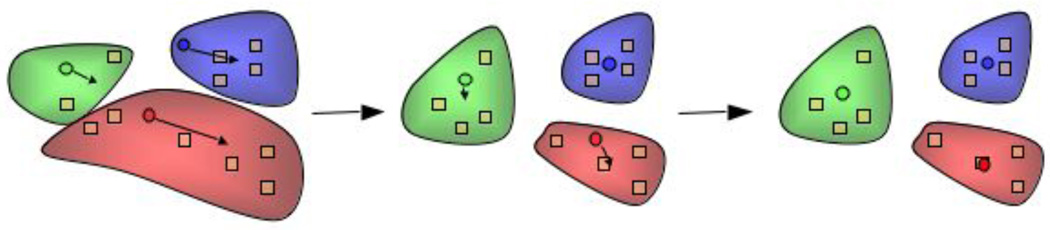
Until only recently, multiple water models compatible with a COM-based coarse-graining methods have been missing from the literature. To the best of our knowledge, the work by Hadley and McCabe was the first to successfully map multiple waters to a single CG bead compatible with a COM-based approach [9]. The motivation behind this work was to develop computationally efficient water model that was compatible with the IBI method [22]. Because an atomistic RDF mapped to the CG level is used as the target of the optimization, a method to identify the different clusters of waters to be mapped to a CG bead as a function of time is needed and the k-means cluster optimization algorithm [55, 56] was used. The k-means algorithm identifies groupings of data points, which when applied to the mapping of multiple atomistic waters to single CG beads, the data points represent the water’s spatial coordinates and the groupings represent the location of the mapped CG bead. Initially, the number of clusters, k, must be chosen and their starting coordinates decided. Normally, deciding the value of k is a major difficulty in proper application of the k-means algorithm, so there exists steps in variations of this algorithm to dynamically change k during the optimization. A graphical representation of a generic application of the algorithm can be seen in Figure 1, where the squares represent waters, the spheres represent the location of the CG beads, the “clouds” represent the allocation of waters to each cluster, and the arrows represent updating of the cluster’s coordinates.
Figure 1.
Schematic illustration of the application of the K-means algorithm to the clustering of water molecules. Circles represent the center of mass of a given cluster, squares represent the center of mass of water molecules, and shaded regions represent the allocation of waters to each cluster in a color-coded fashion. Reprinted with permission of Journal of Physical Chemistry B.9
In the case of mapping water, k represents the number of CG beads, and, therefore, the average amount of waters mapped to each CG bead. In the development of the CG water model, this was varied so that 1, 3, 4, 5, 6, 8, and 9 waters were mapped to each bead (called H2OX, where X equals the number of mapped waters), respectively, to assess the appropriate level of coarse-graining that achieved the best balance between accuracy and computational efficiency. The starting locations of the clusters are chosen randomly from the coordinates of the oxygen atoms in the first frame of the trajectory and the final locations determined from the previous frame (i − 1) served as the starting locations for subsequent frames (i). The authors found that the target RDF had minimal variation with different starting locations in the first frame. In the next step, each data point (coordinates of the water molecule) is allocated to the nearest cluster (employing periodic boundary conditions). The cluster’s coordinates are then updated by finding the COM of each allocated water. With the new coordinates, the allocation is repeated iteratively until the termination criteria,
| (15) |
is satisfied. In equation (5), is the position of bead n at iteration i and tol is the tolerance set by the user (0.001 nm in their case).
Through their analysis, H2O4 was found to have the best balance between accuracy and computational efficiency. Additional insight was gained from comparing H2O4 to H2O1 (the one water mapping) in that H2O4 was found to be approximately 15 times faster than H2O1 in pure water simulations, which highlights the computational time involved in modeling single water beads in a CG simulation, and the RDF between water beads in the mixed system was actually better for the multiple water models than the single water model (H2O1). This was attributed to hydrogen-bonding between beads and within beads similar to the analysis by Wang et al. [34] (discussed in the previous section). Between single water beads, hydrogen-bonding has a large contribution to the interaction energy, but, in a multi-water bead, the majority of hydrogen-bonding occurs within the bead and the hydrogen-bonding across beads is negligible compared to the other non-bonded interactions between the beads as a whole. In other words, because hydrogen-bonding is directional, an isotropic potential is less accurate in a single water model where hydrogen-bonding has such a large contribution. Furthermore, the authors were able to show this water model developed enabled good structuring of a lipid solute (hexadecanoic acid) and was capable of driving self-assembly between hexadecanoic acid and cholesterol in a later publication [29].
Another multiple water mapping method called CUMULUS was reported by van Hoof et al. [10] The motivation behind CUMULUS stems from the desire to map a specific number of waters to each bead, as opposed to an average number of waters as found in the H2O4 model [9]. In addition, the methodology can map ions to the water clusters in a controlled fashion. The CUMULUS method defines a “division energy” through equation (16),
| (16) |
where Q equals the number of bead types, Ni the number of groups of bead type i, Li the number of molecules or atoms in bead type i, and α is a shifting parameter in order to determine their mapping each frame of the trajectory. Furthermore, r0,i is a user-defined threshold for the root of mean squared distances to the center of mass in a CG bead, which, basically controls the sphericity of a bead and the maximum distance between a heavy atom and its mapped site. By minimizing the division energy, the CUMULUS model explicit four-water mapping (or one ion solvated by three waters) and maximizes the sphericity of the CG beads. Using a Monte Carlo framework and simulated annealing to achieve a minimum in the division energy, CUMULUS can be used to determine which waters belong to which beads. The Monte Carlo moves allow the creation of a new bead from unmapped atoms, abandoning an old bead to unmap atoms, switch a free atom to an existent bead, or switch atoms between beads. While this method can restrict the number of heavy atoms to a CG site, by definition of the Monte Carlo moves, some heavy atoms will not be mapped to the CG level. As such, technically each water bead will represent a little more than four waters per bead.
With the mapping from CUMULUS, target RDFs can be measured and fitted to by way of the IBI method. The authors mapped four water beads, three water beads with an ion, and a model for octanol to test their methodology and show how the model was transferable over a range of salt and octanol concentrations and could accurately reproduce the structure in the systems studied.
Although these are the only reports of clustering algorithms used for mapping in a COM-based approach, given the advantages of such models we anticipate their ideas and concepts will be refined and built upon in future publications.
5. Analytical multi-water CG models
Without a doubt, the most used CG water model in the literature is the one developed by Marrink et al. in the MARTINI force field [57–59]. In the MARTINI force field, CG beads interact through a 12-6 LJ potential, with the addition of a Coulombic term for charged beads,
| (17) |
In equation (17), qi is the charge of bead i, ε0 is the permittivity of a vacuum, and the relative dielectric constant εr = 15 for explicit screening.
In general, CG beads in the MARTINI force field are categorized with respect to their interaction type (i.e., polar, non-polar, etc) and the interaction strength is taken from an interaction matrix [59]. The diameter of most MARTINI beads is set to 0.47 nm, while the interaction strength is fitted to free energies of vaporization, hydration, and partitioning. The MARTINI water model is described as a single charge-neutral bead (type P4) mapped to four waters. Due to the use of a 12-6 LJ potential, the high interaction strength, and the lack of explicit charges, the MARTINI water model has poor representation of many important properties (i.e., interfacial tension and compressibility) and actually requires anti-freeze particles [59], to prevent the water beads from solidifying as the water model can freeze at temperatures as high as 300 K under the right simulation conditions [59].
Attempts have been made by several authors to develop an improved water model within the MARTINI framework that does not freeze near room temperature. For example, Chiu et al. used a Morse potential,
| (18) |
instead of a LJ potential because of its softer nature [60]. The three model parameters (ε, a, R0) were fitted to enthalpy of vaporization, density, and surface tension data. While slightly more expensive than a LJ calculation, a much larger timestep can be used due to the increased softness of the potential. In similar work, Shinoda et al. used a 12-4 Mie potential for water instead of a 12-6 LJ or Morse potential [61]. By fitting parameters to density and surface tension, instead of solvation free energies, the water model developed was found to be describe the temperature dependence of these properties well but scarifies structural agreement. They investigated many different forms of Mie potentials, but found 12-4 allowed for the best isothermal compressibility. While the 12-4 Mie potential was fitted for all water cross-interactions, a 9-6 Mie potential was used for all of the solute-solute interactions. In a later publication, Shinoda et al. found that the model could accurately simulate bilayer bending, buckling, and budding, because it was fitted to surface tensions as opposed to free energies [62].
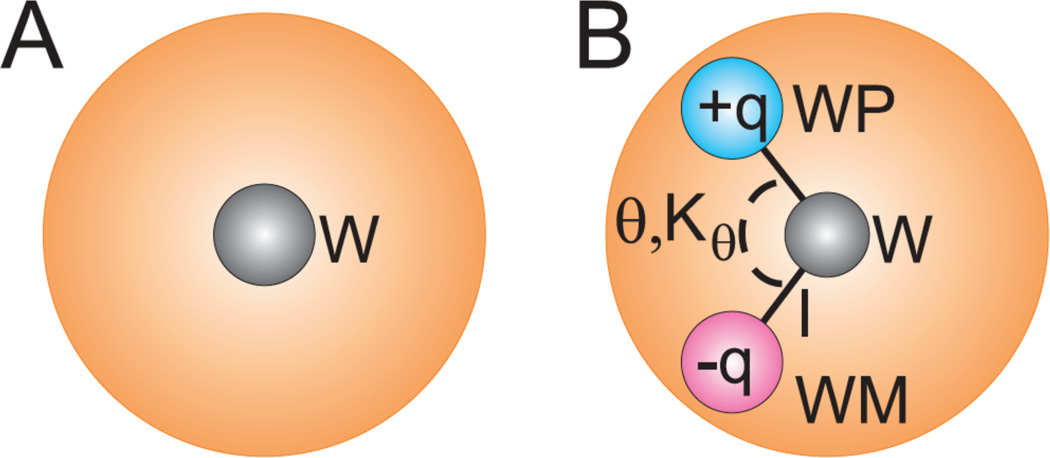
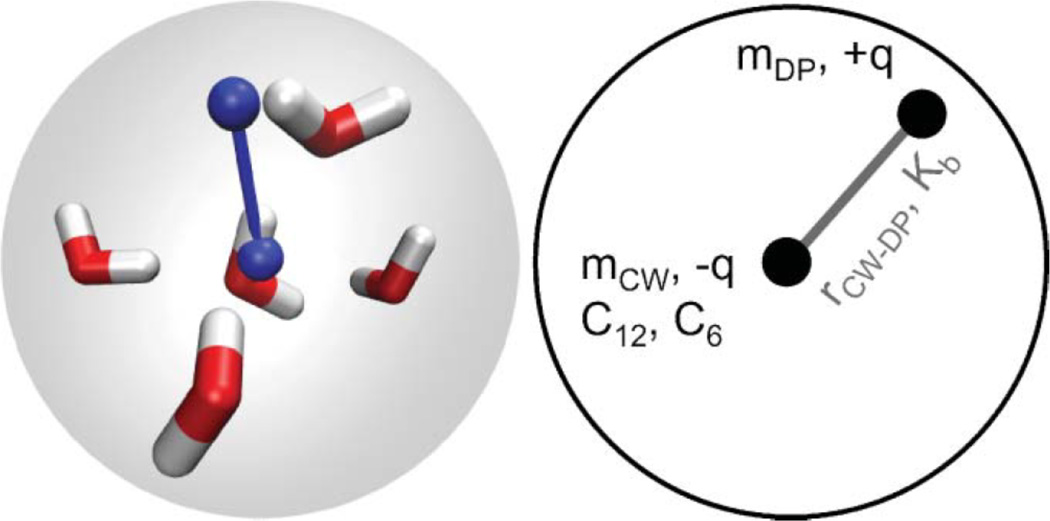
To address issues of charge neutrality (i.e. the high relative dielectric permittivity and inaccuracies associated with charged sites), a polarizable version of the MARTINI water was developed by Yesylevskyy et al. [63]. As shown in Figure 2, three sites represent this polarizable model; WP and WM are charged sites at fixed bond lengths from the center site (W), but only interact via Coloumbic interactions, while the center site interacts only through the LJ potential. Because of the explicit charges involved, the relative dielectric constant can be lowered to a value of 2.5 from the original value of 15. Five variables in this model (θ,Kθ, q, bond length, and interaction strength of W) can be fitted to target properties, though the bond length and θ were fixed at 0.14 nm and 0°, respectively, with the other three being altered systematically until both density and the dielectric constant matched experimental values. With these alterations, the model performs better with respect to reproducing the air/water surface tension and the freezing temperature [63]. In addition, the revised model allows for accurate free energy of ion transport across bilayers and the electroporation process of a bilayer matches the expected behavior [63]. The major issue of the model is the higher computational expense due to the increased degrees of freedom and the inclusion of more electrostatic calculations. As such, the authors suggest reverting to the original model when dielectric screening is not an issue [63].
Figure 2.
Schematics of the A) original and B) polarizable MARTINI water models. The shaded area indicates the van der Waals radii of the central particle W. Reproduced with permission from PLoS Computational Biology [63].
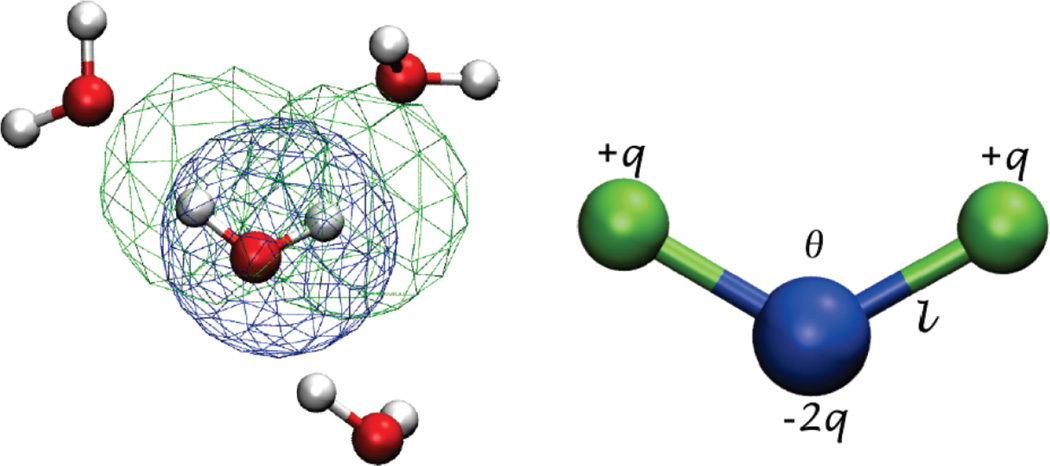
Wu et al. [64] also attempted to incorporate electrostatics into a CG water model compatible with the MARTINI force field through the use of a multipole in a four-water bead that is designed to match the properties of a 4-water cluster as closely as possible. The model, referred to as the big multipole water (BMW) model, is similar to the polarizable model of Yesylevskyy et al. [63] in that, it uses three sites to represent four waters, as shown in Figure 3, where the outer sites only interact through electrostatic forces. However, because the bonds and angles are kept rigid, the model is technically not polarizable. The geometry and charges of the BMW model were optimized to best reproduce both the dipole and the quadrupole moment of a four-water cluster in a COM mapping style. In the target atomistic simulation, a cluster is defined as a water molecule and its three nearest neighbors; the dipole moment and quadrupole moment of that cluster are measured in order to determine the target values on the CG level. In addition to electrostatic forces, the central sites interact through a modified form of the Born-Mayer-Huggins potential (equation (19)), which is much softer than the LJ potential used within the MARTINI force field.
| (19) |
Figure 3.
The 4-water clustering (left) described by the big multipole water model (right). The green beads interact through coloumbic forces, while the center bead (blue) interacts through both coloumbic and van der Waals forces. Reproduced with permission from the Journal of Physical Chemistry B. [64]
In equation (19), ε and rm are the depth and position of the minimum, respectively, while f and a determine the softness of repulsion and shallowness near the minimum. Like MARTINI, a relative dielectric screening must be used, which is fitted to experimental density alongside the four parameters in equation (4) to experimental values for the interfacial tension, interfacial potential at the air-water interface, permittivity in bulk, and isothermal compressibility. Due to the fact that these properties are fitted, BMW performs much better than other MARTINI-based water models, though it is computationally slower. When combined with the MARTINI lipid force field, BMW gives the correct dipole potential of a DPPC bilayer derived without any further optimization. However, it should be noted that the potential was parameterized at 300K and so it is not recommended for use at very different state conditions.
Comparing these models, Bennett and Tieleman found both polarizable MARTINI water and BMW performed similarly in the application of studying pore formation in a lipid membrane.[65] While neither improves structure compared to the original neutral water model, the polarizable MARTINI water model does slightly improve the free energy.
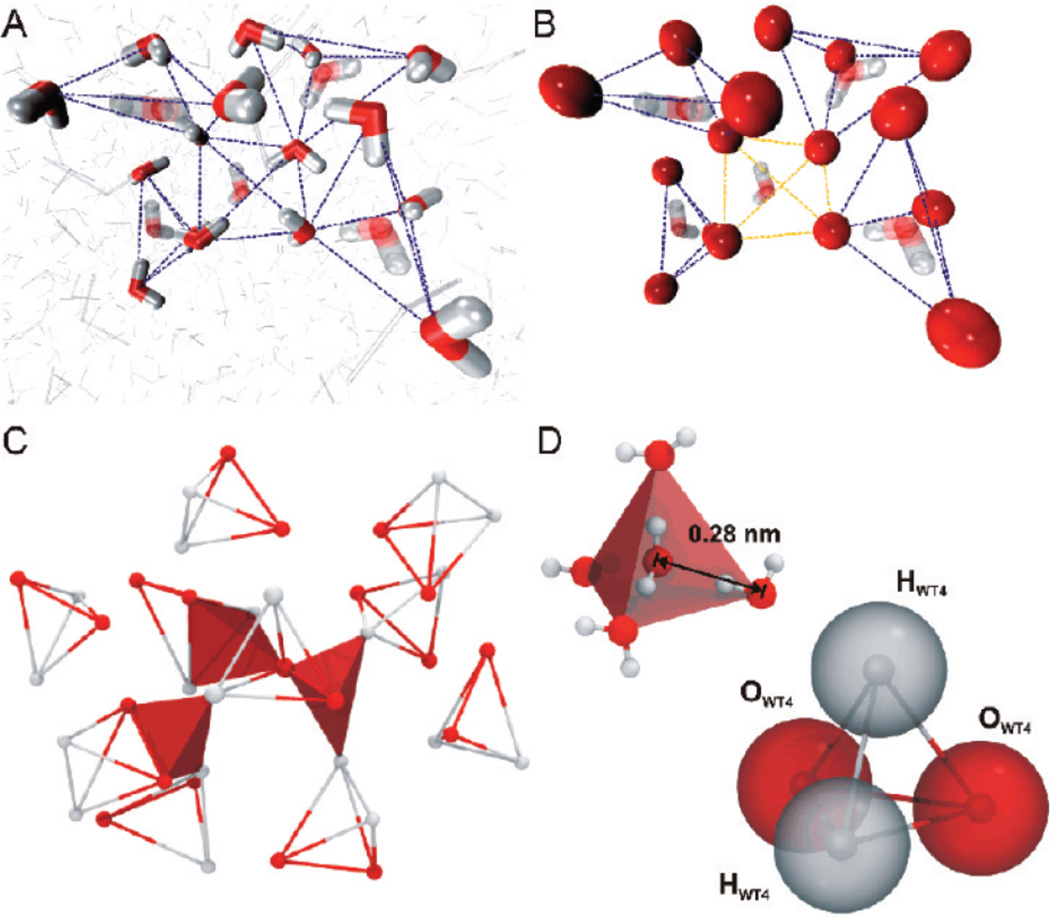
The works of Darré et al. [66] and Riniker and van Gunsteren [67] have tried to extend the degree of coarse-graining of water compared to all of the previously mentioned models, while still incorporating electrostatics and polarizability. Darré et al. proposed the WAT4 model in which four tetrahedral bound beads (Figure 4) collectively represent 11 waters [66]. Fitting the mass of WAT4 to the experimental room temperature density and dividing the final result by the molecular weight of one water molecule determined the degree of coarse-graining. Each bead has a partial charge that is fitted to dielectric permittivity. The bonds between beads are fairly flexible to allow for polarizability and to make the structure more malleable. Because of its tetrahedral topology, WAT4 has a good solvation structure and was shown to solvate DNA well compared to a fully atomistic rendition.
Figure 4.
From atomistic to CG water. (A) Snapshot taken from a MD simulation showing the tetrahedral hydrogen-bonding network of water with hydrogen bonds indicated by dashed lines. (B) The location of CG beads in the model with explicit CG bonds shown as dark dashed lines and non-bonded interactions shown as transparent dashed lines. (C) Structural organization of WT4 in the bulk solution taken from a MD snapshot. Red planes highlight the tetrahedrality between WT4 groups. (D) A single WT4 group in which the grey beads represent the positively charged groups and the red beads represent the negatively charged groups. Reproduced with permission from the Journal of Chemical Theory and Computation [66].
Riniker and van Gunsteren developed a two-site water model designed to represent five atomistic waters [67]. The atomistic properties to be matched and compared against were tracked using a clustering algorithm similar to k-means [55, 56], CUMULUS [10], or the BMW model [64], as discussed earlier. Each water and its four nearest neighbors belong to a separate cluster, but clusters that share waters with another cluster are deleted. To overcome reallocation problems stemming from self-diffusion of individual waters, waters in a cluster are loosely bound through a highly flexible ghost bond. As seen in Figure 5, the central site interacts through a 12-6 LJ potential and Coloumb’s law, while the dipole particle (near the edge) only interacts through electrostatic forces. The mass of the central particle is twice that of the dipole particle to obtain the correct rotation of the dipole. The parameters were fitted to density and relative static dielectric permittivity. The bond was controlled through a harmonic oscillator so the model is polarizable. The model performed better than both BMW and MARTINI with respect to unfitted properties like compressibility or surface tension, does not require anti-freeze particles, and is more computationally efficient.
Figure 5.
Schematic representation of the two-site CG water model representing five water molecules proposed by Riniker and van Gunsteren[67]. Reproduced with permission from the Journal of Chemical Physics [67].
6. Conclusions
While atomistic level models for water have high accuracy and provide a large degree of detail, they can be computationally costly. With the softer interaction and reduced degrees of freedom found in CG models, they allow for longer time- and length-scales to be studied because of their computational savings. Phenomena appropriate for CG modeling typically uses water as a solvent, so the CG model of water must be accurate at the CG level. In addition, a large amount of water is typically applied as a solvent, so really coarse-grained models with maximum accuracy is of greatest utility.
In this review, we covered many degrees of coarse-grained water models, including models with explicit electrostatics and polarizability for accurate treatment of CG ions, and exotic models to reproduce water’s thermodynamic anomalies near their respective state conditions. These models were fitted to many different properties of water including surface tension, RDFs, density, and dielectric permittivity according to what properties were of interest for that simulation. While some are only compatible within their own framework, others are designed to be compatible with CG molecules of interest like lipids or DNA. Most of these developments have been within the last three years, so the field of coarse-graining water is still in its early stages and continues to evolve to enhance accuracy while retaining computational efficiency. Our hope for this review is to introduce readers to what has been developed and inspire them to take the models to the next stage of evolution.
Acknowledgements
The project described was partially supported by Grant Number R01 AR057886-01 from the National Institute of Arthritis and Muscoskeletal and Skin Diseases. Resources were also provided by the National Energy Research Scientific Computing Center, supported by the Office of Science of the Department of Energy under Contract No. DE-AC02-05CH11231, and the National Science Foundation through TeraGrid grant number MCB080117N.
References
- 1.Guillot B. A reappraisal of what we have learnt during three decades of computer simulations on water. J. Mol. Liq. 2002;101:219–260. [Google Scholar]
- 2.Holt JK. Methods for probing water at the nanoscale. Microfluidics and Nanofluidics. 2008;5:425–442. [Google Scholar]
- 3.Malenkov G. Liquid water and ices: understanding the structure and physical properties. Journal of Physics-Condensed Matter. 2009;21:35. doi: 10.1088/0953-8984/21/28/283101. [DOI] [PubMed] [Google Scholar]
- 4.Guillot B, Guissani Y. How to build a better pair potential for water. J. Chem. Phys. 2001;114:6720–6733. [Google Scholar]
- 5.Chen J, Brooks CL., III Implicit modeling of nonpolar solvation for simulating protein folding and conformational transitions. PCCP. 2008;10:471–481. doi: 10.1039/b714141f. [DOI] [PubMed] [Google Scholar]
- 6.Fennell CJ, Dill KA. Physical Modeling of Aqueous Solvation. Journal of Statistical Physics. 2011;145:209–226. doi: 10.1007/s10955-011-0232-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Vorobjev YN. Advances in Implicit Models of Water Solvent to Compute Conformational Free Energy and Molecular Dynamics of Proteins at Constant PH. In: Christov C, editor. Advances in Protein Chemistry and Structural Biology, Vol 85: Computational Chemistry Methods in Structural Biology. 2011. pp. 281–322. [DOI] [PubMed] [Google Scholar]
- 8.Shen JW, Li CL, van der Vegt NFA, Peter C. Transferability of Coarse Grained Potentials: Implicit Solvent Models for Hydrated Ions. Journal of Chemical Theory and Computation. 2011;7:1916–1927. doi: 10.1021/ct2001396. [DOI] [PubMed] [Google Scholar]
- 9.Hadley KR, McCabe C. Developing a Coarse-Grained Water Model: Efficient Mapping of Multiple Waters to a Single Site. J. Phys. Chem. B. 2010;114:4590–4599. doi: 10.1021/jp911894a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.van Hoof B, Markvoort AJ, van Santen RA, Hilbers PAJ. The CUMULUS Coarse Graining Method: Transferable Potentials for Water and Solutes. J. Phys. Chem. B. 2011;115:10001–10012. doi: 10.1021/jp201975m. [DOI] [PubMed] [Google Scholar]
- 11.Izvekov S, Voth GA. A multiscale coarse-graining method for biomolecular systems. J. Phys. Chem. B. 2005;109:2469–2473. doi: 10.1021/jp044629q. [DOI] [PubMed] [Google Scholar]
- 12.Toth G. Effective potentials from complex simulations: a potential-matching algorithm and remarks on coarse-grained potentials. Journal of Physics-Condensed Matter. 2007;19 doi: 10.1088/0953-8984/19/33/335222. [DOI] [PubMed] [Google Scholar]
- 13.Hone TD, Izvekov S, Voth GA. Fast centroid molecular dynamics: A force-matching approach for the predetermination of the effective centroid forces. J. Chem. Phys. 2005;122 doi: 10.1063/1.1836731. [DOI] [PubMed] [Google Scholar]
- 14.Izvekov S, Parrinello M, Burnham CJ, Voth GA. Effective force fields for condensed phase systems from ab initio molecular dynamics simulation: A new method for force-matching. J. Chem. Phys. 2004;120:10896–10913. doi: 10.1063/1.1739396. [DOI] [PubMed] [Google Scholar]
- 15.Izvekov S, Violi A, Voth GA. Systematic coarse-graining of nanoparticle interactions in molecular dynamics simulation. J. Phys. Chem. B. 2005;109:17019–17024. doi: 10.1021/jp0530496. [DOI] [PubMed] [Google Scholar]
- 16.Izvekov S, Voth GA. Effective force field for liquid hydrogen fluoride from ab initio molecular dynamics simulation using the force-matching method. J. Phys. Chem. B. 2005;109:6573–6586. doi: 10.1021/jp0456685. [DOI] [PubMed] [Google Scholar]
- 17.Izvekov S, Voth GA. Multiscale coarse graining of liquid-state systems. J. Chem. Phys. 2005;123:13. doi: 10.1063/1.2038787. [DOI] [PubMed] [Google Scholar]
- 18.Lyubartsev AP, Laaksonen A. Calculation of Effective Interaction Potentials from Radial-Distribution Functions - a Reverse Monte-Carlo Approach. Phys. Rev. E. 1995;52:3730–3737. doi: 10.1103/physreve.52.3730. [DOI] [PubMed] [Google Scholar]
- 19.Lyubartsev AP. Multiscale modeling of lipids and lipid bilayers. European Biophysics Journal with Biophysics Letters. 2005;35:53–61. doi: 10.1007/s00249-005-0005-y. [DOI] [PubMed] [Google Scholar]
- 20.Lyubartsev A, Tu YQ, Laaksonen A. Hierarchical Multiscale Modelling Scheme from First Principles to Mesoscale. Journal of Computational and Theoretical Nanoscience. 2009;6:951–959. [Google Scholar]
- 21.Lyubartsev A, Mirzoev A, Chen LJ, Laaksonen A. Systematic coarse-graining of molecular models by the Newton inversion method. Faraday Discussions. 2010;144:43–56. doi: 10.1039/b901511f. [DOI] [PubMed] [Google Scholar]
- 22.Reith D, Putz M, Muller-Plathe F. Deriving effective mesoscale potentials from atomistic simulations. J. Comput. Chem. 2003;24:1624–1636. doi: 10.1002/jcc.10307. [DOI] [PubMed] [Google Scholar]
- 23.Elezgaray J, Laguerre M. A systematic method to derive force fields for coarse-grained simulations of phospholipids. Computer Physics Communications. 2006;175:264–268. [Google Scholar]
- 24.Chen LJ, Qian HJ, Lu ZY, Li ZS, Sun CC. An automatic coarse-graining and fine-graining simulation method: Application on polyethylene. J. Phys. Chem. B. 2006;110:24093–24100. doi: 10.1021/jp0644558. [DOI] [PubMed] [Google Scholar]
- 25.Chan ER, Striolo A, McCabe C, Cummings PT, Glotzer SC. Coarse-grained force field for simulating polymer-tethered silsesquioxane self-assembly in solution. J. Chem. Phys. 2007;127:4102. doi: 10.1063/1.2753493. [DOI] [PubMed] [Google Scholar]
- 26.Peter C, Delle Site L, Kremer K. Classical simulations from the atomistic to the mesoscale and back: coarse graining an azobenzene liquid crystal. Soft Matter. 2008;4:859–869. doi: 10.1039/b717324e. [DOI] [PubMed] [Google Scholar]
- 27.Hadley KR, McCabe C. Coarse-grained Models for Amorphous and Crystalline Fatty Acids. J. Chem. Phys. 2010;132:134505. doi: 10.1063/1.3360146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Hadley KR, McCabe C. A Structurally Relevant Coarse-Grained Model of Cholesterol. Biophysical Journal. 2010;99:2896–2905. doi: 10.1016/j.bpj.2010.08.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Hadley KR, McCabe C. Self-Assembly of Coarse-Grained Skin Lipids into an Experimentally Observed Bilayer. Soft Matter. 2011 doi: 10.1039/C2SM07204A. submitted, [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Chan ER, Striolo A, McCabe C, Glotzer SC, Cummings PT. A Coarse-Grained Force Field for Simulating Polymer-Tethered Nanoparticle Self-Assembly in Solution. In: Voth GA, editor. Coarse-Graining of Condensed Phase and Biomolecular Systems. Taylor & Francis; 2008. [Google Scholar]
- 31.Wei D, Wang F. Mimicking coarse-grained simulations without coarse-graining: Enhanced sampling by damping short-range interactions. J. Chem. Phys. 2010;133 doi: 10.1063/1.3478526. [DOI] [PubMed] [Google Scholar]
- 32.Lyubartsev AP, Laaksonen A. Novel Methods in Soft Matter Simulations. Springer-Verlag; 2004. On the Reduction of Molecular Degrees of Freedom in Computer Simulations; pp. 219–244. [Google Scholar]
- 33.Bedrov D, Ayyagari C, Smith GD. Multiscale modeling of poly(ethylene oxide)-poly(propylene oxide)-poly(ethylene oxide) triblock copolymer micelles in aqueous solution. Journal of Chemical Theory and Computation. 2006;2:598–606. doi: 10.1021/ct050334k. [DOI] [PubMed] [Google Scholar]
- 34.Wang H, Junghans C, Kremer K. Comparative atomistic and coarse-grained study of water: What do we lose by coarse-graining? European Physical Journal E. 2009;28:221–229. doi: 10.1140/epje/i2008-10413-5. [DOI] [PubMed] [Google Scholar]
- 35.Berendsen HJC, Postma JPM, von Gunsteren WF, Hermans J. Interaction Models for Water in Relation to Protein Hydration. In: Pullman B, editor. Intermolecular Forces: Proceedings of the Fourteenth Jerusalem Symposium on Quantum Chemistry and Biochemistry. Reidel: Dordrecht; 1981. p. 331. [Google Scholar]
- 36.Berendsen HJC, Grigera JR, Straatsma TP. The Missing Term in Effective Pair Potentials. J. Phys. Chem. B. 1987;91:6269–6271. [Google Scholar]
- 37.Jorgensen WL, Chandrasekhar J, Madura JD, Impey RW, Klein ML. Comparison of Simple Potential Functions for Simulating Liquid Water. J. Chem. Phys. 1983;79:926–935. [Google Scholar]
- 38.Basdevant N, Borgis D, Ha-Duong T. A semi-implicit solvent model for the simulation of peptides and proteins. J. Comput. Chem. 2004;25:1015–1029. doi: 10.1002/jcc.20031. [DOI] [PubMed] [Google Scholar]
- 39.Basdevant N, Ha-Duong T, Borgis D. Particle-based implicit solvent model for biosimulations: Application to proteins and nucleic acids hydration. Journal of Chemical Theory and Computation. 2006;2:1646–1656. doi: 10.1021/ct0600417. [DOI] [PubMed] [Google Scholar]
- 40.Masella M, Borgis D, Cuniasse P. Combining a Polarizable Force-Field and a Coarse-Grained Polarizable Solvent Model. II. Accounting for Hydrophobic Effects. J. Comput. Chem. 2011;32:2664–2678. doi: 10.1002/jcc.21846. [DOI] [PubMed] [Google Scholar]
- 41.Vlcek L, Nezbeda I. Thermodynamics of simple models of associating fluids: primitive models of ammonia, methanol, ethanol and water. Mol. Phys. 2004;102:771–781. [Google Scholar]
- 42.Vlcek L, Nezbeda I. From realistic to simple models of associating fluids. II. Primitive models of ammonia, ethanol and models of water revisited. Mol. Phys. 2004;102:485–497. [Google Scholar]
- 43.Silverstein KAT, Haymet ADJ, Dill KA. A simple model of water and the hydrophobic effect. J. Am. Chem. Soc. 1998;120:3166–3175. [Google Scholar]
- 44.Bizjak A, Urbi T, Vlachy V, Dill KA. The three-dimensional "Mercedes Benz" model of water. Acta Chim. Slov. 2007;54:532–537. [Google Scholar]
- 45.Bizjak A, Urbic T, Vlachy V, Dill KA. Theory for the three-dimensional Mercedes-Benz model of water. J. Chem. Phys. 2009;131 doi: 10.1063/1.3259970. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Stillinger FH, Weber TA. COMPUTER-SIMULATION OF LOCAL ORDER IN CONDENSED PHASES OF SILICON. Phys. Rev. B. 1985;31:5262–5271. doi: 10.1103/physrevb.31.5262. [DOI] [PubMed] [Google Scholar]
- 47.Molinero V, Moore EB. Water Modeled As an Intermediate Element between Carbon, Silicon. J. Phys. Chem. B. 2009;113:4008–4016. doi: 10.1021/jp805227c. [DOI] [PubMed] [Google Scholar]
- 48.DeMille RC, Cheatham TE, Molinero V. A Coarse-Grained Model of DNA with Explicit Solvation by Water and Ions. J. Phys. Chem. B. 2011;115:132–142. doi: 10.1021/jp107028n. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Moore EB, Molinero V. Structural transformation in supercooled water controls the crystallization rate of ice. Nature. 2011;479 doi: 10.1038/nature10586. 506-U226. [DOI] [PubMed] [Google Scholar]
- 50.Jacobson LC, Hujo W, Molinero V. Thermodynamic Stability and Growth of Guest-Free Clathrate Hydrates: A Low-Density Crystal Phase of Water. J. Phys. Chem. B. 2009;113:10298–10307. doi: 10.1021/jp903439a. [DOI] [PubMed] [Google Scholar]
- 51.Jacobson LC, Molinero V. A Methane-Water Model for Coarse-Grained Simulations of Solutions and Clathrate Hydrates. J. Phys. Chem. B. 2010;114:7302–7311. doi: 10.1021/jp1013576. [DOI] [PubMed] [Google Scholar]
- 52.de Oliveira AB, Netz PA, Colla T, Barbosa MC. Structural anomalies for a three dimensional isotropic core-softened potential. J. Chem. Phys. 2006;125 doi: 10.1063/1.2357119. [DOI] [PubMed] [Google Scholar]
- 53.de Oliveira AB, Netz PA, Colla T, Barbosa MC. Thermodynamic and dynamic anomalies for a three-dimensional isotropic core-softened potential. J. Chem. Phys. 2006;124 doi: 10.1063/1.2168458. [DOI] [PubMed] [Google Scholar]
- 54.Chaimovich A, Shell MS. Anomalous waterlike behavior in spherically-symmetric water models optimized with the relative entropy. PCCP. 2009;11:1901–1915. doi: 10.1039/b818512c. [DOI] [PubMed] [Google Scholar]
- 55.MacQueen JB. 5th Berkeley Symposium on Mathematical Statistics and Probability. Berkeley, CA: University of California Press; 1967. Some Methods for Classification and Analysis of Multivariate Observations. [Google Scholar]
- 56.Steinley D. K-means clustering: A half-century synthesis. British Journal of Mathematical & Statistical Psychology. 2006;59:1–34. doi: 10.1348/000711005X48266. [DOI] [PubMed] [Google Scholar]
- 57.Marrink SJ, de Vries AH, Mark AE. Coarse grained model for semiquantitative lipid simulations. J. Phys. Chem. B. 2004;108:750–760. [Google Scholar]
- 58.Marrink SJ, Risselada J, Mark AE. Simulation of gel phase formation and melting in lipid bilayers using a coarse grained model. Chemistry And Physics Of Lipids. 2005;135:223–244. doi: 10.1016/j.chemphyslip.2005.03.001. [DOI] [PubMed] [Google Scholar]
- 59.Marrink SJ, Risselada HJ, Yefimov S, Tieleman DP, de Vries AH. The MARTINI force field: Coarse grained model for biomolecular simulations. J. Phys. Chem. B. 2007;111:7812–7824. doi: 10.1021/jp071097f. [DOI] [PubMed] [Google Scholar]
- 60.Chiu S-W, Scott HL, Jakobsson E. A Coarse-Grained Model Based on Morse Potential for Water and n-Alkanes. Journal of Chemical Theory and Computation. 2010;6:851–863. doi: 10.1021/ct900475p. [DOI] [PubMed] [Google Scholar]
- 61.Shinoda W, Devane R, Klein ML. Multi-property fitting and parameterization of a coarse grained model for aqueous surfactants. Mol. Simul. 2007;33:27–36. [Google Scholar]
- 62.Shinoda W, DeVane R, Klein ML. Zwitterionic Lipid Assemblies: Molecular Dynamics Studies of Monolayers, Bilayers, and Vesicles Using a New Coarse Grain Force Field. J. Phys. Chem. B. 2010;114:6836–6849. doi: 10.1021/jp9107206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Yesylevskyy SO, Schafer LV, Sengupta D, Marrink SJ. Polarizable Water Model for the Coarse-Grained MARTINI Force Field. PLoS Comput. Biol. 2010;6 doi: 10.1371/journal.pcbi.1000810. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Wu Z, Cui Q, Yethiraj A. A New Coarse-Grained Model for Water: The Importance of Electrostatic Interactions. J. Phys. Chem. B. 2010;114:10524–10529. doi: 10.1021/jp1019763. [DOI] [PubMed] [Google Scholar]
- 65.Bennett WFD, Tieleman DP. Water Defect and Pore Formation in Atomistic and Coarse-Grained Lipid Membranes: Pushing the Limits of Coarse Graining. Journal of Chemical Theory and Computation. 2011;7:2981–2988. doi: 10.1021/ct200291v. [DOI] [PubMed] [Google Scholar]
- 66.Darre L, Machado MR, Dans PD, Herrera FE, Pantano S. Another Coarse Grain Model for Aqueous Solvation: WAT FOUR? Journal of Chemical Theory and Computation. 2010;6:3793–3807. [Google Scholar]
- 67.Riniker S, van Gunsteren WF. A simple, efficient polarizable coarse-grained water model for molecular dynamics simulations. J. Chem. Phys. 2011;134 doi: 10.1063/1.3553378. [DOI] [PubMed] [Google Scholar]