SMALL WORLD NETWORK MEASURES PREDICT WHITE MATTER DEGENERATION IN PATIENTS WITH EARLY-STAGE MILD COGNITIVE IMPAIRMENT

Abstract

Alzheimer’s Disease (AD) has long been considered a cortical degenerative disease, but impaired brain connectivity, due to white matter injury, may exacerbate cognitive problems. Predicting brain changes is critically important for early treatment. In a longitudinal diffusion tensor imaging study, we investigated white matter fiber integrity in 19 patients (mean age: 74.7 +/− 8.4 yrs at baseline) displaying early signs of mild cognitive impairment (eMCI). We first examined whether baseline average fractional anisotropy (FA) measures in the corpus callosum (CC) predicted changes in white matter integrity over the following 6 months. We then examined whether “small world” architecture measures - calculated from baseline connectivity maps - predicted white matter changes over the next 6 months. While average CC FA measures at baseline were not associated with future changes in FA, network measures were a sensitive biomarker for predicting white matter changes during this critical time before AD strikes.

1. INTRODUCTION

Alzheimer’s disease (AD) is the most common type of dementia, affecting 1 in 8 people (13%) aged 65 or older. AD is a neurodegenerative disease characterized by memory loss in its early stages, followed by a progressive decline in other behavioral and cognitive functions. Recent therapeutic efforts have focused on early mild cognitive impairment (eMCI) to enable earlier treatment of individuals with heightened risk of developing AD. Identifying biomarkers in these patients that might predict brain tissue loss is vital for drug trial enrichment, and to help identify those most likely to decline. Image-based predictors of decline may also offer new leads for understanding the development and pathogenesis of AD.

The Alzheimer’s Disease Neuroimaging Initiative (ADNI) is a large multi-site longitudinal study to evaluate measures that may help to track or predict disease progression in AD. In addition to the more widely-accepted measures from anatomical MRI, PET, and CSF measures of pathology, ADNI recently added additional neuroimaging measures including diffusion tensor imaging (DTI), arterial spin labeling, and resting state functional MRI. The primary goal of ADNI is to identify sensitive biomarkers of very early AD progression to help monitor disease progression and treatment efficacy with greater precision.

MRI-based image analysis methods have long been used to track structural atrophy of the brain. Diffusion tensor imaging (DTI) is sensitive to microscopic white matter (WM) injury not always detectable with standard anatomical MRI [1]. Diffusion imaging can be used to track the highly anisotropic diffusion of water along axons, revealing microstructural fiber bundles connecting cortical and subcortical regions. In diseases such as AD, and even in MCI subjects at risk for AD, these connections progressively deteriorate.

By combining DTI with standard MRI, we can measure the integrity and connectivity of white matter tracts. Connectivity mapping is a relatively recent direction in neuroimaging, and variations in the degree and extent of connections may be useful as measures of disease burden. Recent models of AD suggest that cognitive deficits arise from the progressive disconnection of cortical and subcortical regions, promoted by neuronal loss and white matter injury [2]. The two accepted pathological markers of AD, amyloid plaques and neurofibrillary tangles, tend to affect association cortices early in the disease. From these cortical regions, long pathways of association fibers are linked to many other brain regions, made up of large populations of pyramidal neurons that support connections within and between hemispheres [3, 4]. AD patients also show a decrease in the volume and integrity of WM commissures such as the corpus callosum, as well as pathways such as the cingulum and superior longitudinal fasciculus [5, 6], suggesting an ongoing disruption of connectivity.

Recently, graph theory has been used to describe anatomical networks and characterize connectivity patterns based on signals in brain images. Structural brain networks are modeled as graphs where nodes designate elements (i.e., brain regions) linked by edges representing physical connections. A recent study found that AD patients have abnormal “small-world” architecture in large-scale brain networks, with increased clustering and longer shortest paths linking individual regions, implying a less optimal network topology [8]. However, as far as we know, small-world global network measures, such as characteristic path length (CPL) and mean clustering coefficient (MCC), have not yet been used to predict future WM disruption in AD.

Here we assessed a group of 19 patients with early signs of cognitive impairment (also termed “early MCI”). We first examined whether baseline average fractional anisotropy (FA) measures in the corpus callosum (CC) were predictive of changes in white matter integrity, as measured by changes in FA, after a 6-month follow-up interval. When we found that this was not the case, we further examined whether small-world architecture measures calculated from baseline connectivity maps, derived from both MRI and DTI data, were able to predict changes in white matter integrity after 6 months. We found that global network measures may offer a potentially useful biomarker in predicting white matter changes at this critical time before the onslaught of AD.

2. METHODS

2.1. Subjects and Image Acquisition

At the time of writing (November 2011), data collection for the ADNI2 project is still in its early stages. Here we performed an initial analysis of 32 eMCI adults (mean age: 73.2 yrs, SD: 8.7; 18 men/14 women). Of those, 19 had returned for a 6-month follow up scan (mean age: 74.7 yrs, SD: 8.4 at baseline; 11 men/8 women).

All 19 subjects underwent whole-brain MRI scanning on 3-Tesla GE Medical Systems scanners, on at least two occasions: once at baseline and again 6 months later. T1-weighted SPGR sequences (256×256 matrix; voxel size = 1.2×1.0×1.0 mm³; TI=400 ms; TR = 6.984 ms; TE = 2.848 ms; flip angle=11°), T2*-weighted sequences, and diffusion-weighted images (DWI; 256×256 matrix; voxel size: 1.4×1.4×2.7 mm³; scan time = 9 min) were collected. 46 separate images were acquired for each DTI scan: 5 T2-weighted images with no diffusion sensitization (b₀ images) and 41 diffusion-weighted images (b=1000 s/mm²).

2.2. Image Analysis

2.2.1 Preprocessing of Baseline & 6-Month Follow-up T2 Scans

Extra-cerebral tissue was removed from all T2-weighted scans using the Brain Extraction Tool (BET) from FSL [9]. Anatomical scans subsequently underwent intensity inhomogeneity normalization using the MNI “nu_correct” tool (www.bic.mni.mcgill.ca/software/). To align data from different subjects into the same 3D coordinate space, each anatomical image was linearly aligned to a standard brain template (the Colin27; [10]) using FSL FLIRT [11] with 9 degrees of freedom to allow translations, rotations and scaling in 3D.

2.2.2 DWI Preprocessing for Baseline & 6 Month Follow-up

For each subject, raw DWI volumes were eddy corrected using FSL (www.fmrib.ox.ac.uk/fsl). Non-brain tissue was removed using BET [9]. To correct for echo-planar induced (EPI) susceptibility artifacts, which can cause distortions at tissue/fluid interfaces, each subject’s 5 skull-stripped b₀ images were averaged, linearly aligned and elastically registered to their respective T2-weighted scans by inverse consistent elastic registration with a mutual information cost function [12]. The resulting 3D deformation fields were applied to the remaining 41 DWI volumes prior to mapping diffusion parameters. A single diffusion tensor [13] was fitted at each voxel in the brain from the eddy- and EPI-corrected DWI scans using FSL, and scalar anisotropy maps were obtained from the resulting diffusion tensor eigenvalues (λ₁, λ₂, λ₃). Fractional anisotropy (FA) was defined as:

$$\begin{array}{c}FA=\sqrt{\frac{3}{2}}\frac{\sqrt{{({\lambda }_1-<\lambda >)}^2+{({\lambda }_2-<\lambda >)}^2+{({\lambda }_3-<\lambda >)}^2}}{\sqrt{{\lambda }_1^2+{\lambda }_2^2+{\lambda }_3^2}}\in [0,1]\\ <\lambda >=\frac{{\lambda }_1+{\lambda }_2+{\lambda }_3}{3}\end{array}$$

2.2.3 Template Creation & Spatial Normalization

A study-specific minimal deformation template (MDT) was created from a randomly selected subset of spatially aligned baseline FA maps (n=24). A customized template based on subjects in the study can reduce bias in the registrations [14]. The MDT template deviates least from the anatomy of the subjects, and can improve statistical power [15]. The MDT was generated by creating an initial affine mean template from all subjects, then elastically registering all the aligned individual scans to that mean [12] while regularizing the Jacobians [16]. A new mean was created from the registered scans; this process was iterated several times. Each subject’s initial baseline FA map was elastically registered to the final MDT. To ensure white matter alignment across subjects, registered FA maps were thresholded at FA > 0.2 to include only highly anisotropic anatomy and the thresholded maps were elastically registered to the thresholded MDT (FA > 0.2).

We then elastically registered [12] each subject’s 6 month follow up FA map to their registered baseline FA. To ensure white matter alignment, registered 6 month FA maps were thresholded at FA > 0.2 and again elastically registered to their respective thresholded baseline FA (FA > 0.2). The resulting registered baseline and 6 month follow-up FA images where then spatially smoothed with a Gaussian kernel (5mm FWHM). We then subtracted the 6 month scan from the baseline scan to calculate change in FA.

2.2.4 Probabilistic White Matter Tract Atlas ROI Definition

We elastically registered [12] the FA image from the JHU DTI atlas [17] to each subject’s baseline FA image, as previously described in section 2.2.3. We then applied the outcome deformations to the stereotaxic WM atlas labels, using nearest neighbor interpolation to avoid intermixing of labels. This placed the atlas ROIs in the same coordinate space as each subject. We were then able to calculate the baseline average FA within the corpus callosum for each subject.

2.2.5 Tractography

Tractography was performed using the Diffusion Toolkit (http://trackvis.org/) to calculate fiber pathways from the corrected DWI images using the interpolated streamline method with a 0.5 voxel fixed step length. To limit small noisy tracts, we filtered out fibers with less than 15 points. Elastic deformations, from the EPI distortion correction, were then applied to each tract’s 3D coordinates. Previously, we found this makes a significant difference in connectivity analysis [18].

2.2.6 Automated Cortical ROI Segmentation

35 cortical labels (Table 1) were automatically extracted in each hemisphere from the raw T1-weighted structural MRI scans using FreeSurfer (http://surfer.nmr.mgh.harvard.edu/) [19]. As a linear registration is performed within the software, the resulting T1 weighted images and cortical models were aligned to the corrected T2 images using nearest neighbor interpolation (to avoid intermixing of labels) as the DWIs were elastically registered to the T2 space. To ensure tracts would intersect cortical labeled boundaries, labels were dilated with an isotropic box kernel of 5×5×5 voxels.

Table 1.

Index of the cortical labels extracted from FreeSurfer [19]

1	Bank of the superior temporal sulcus
2	Caudal anterior cingulate
3	Caudal middle frontal
4	Corpus callosum
5	Cuneus
6	Entorhinal
7	Fusiform
8	Inferior parietal
9	Inferior temporal
10	Isthmus of the cingulate
11	Lateral occipital
12	Lateral orbitofrontal
13	Lingual
14	Medial orbitofrontal
15	Middle temporal
16	Parahippocampal
17	Paracentral
18	Pars opercularis
19	Pars orbitalis
20	Pars triangularis
21	Peri-calcarine
22	Postcentral
23	Posterior cingulate
24	Pre-central
25	Precuneus
26	Rostral anterior cingulate
27	Rostral middle frontal
28	Superior frontal
29	Superior pariental
30	Superior temporal
31	Supra-marginal
32	Frontal pole
33	Temporal pole
34	Transverse temporal
35	Insula

2.2.7 NxN Matrices Representing Structural Connectivity

As in [20], for each subject, a ba aseline 70×70 (35 right hemisphere ROIs and 35 left) connectivity matrix was created. Each element described the estimated proportion of the total number of fibers, in that subject, connecting each of the labels to each of the other labels. Figure 1 shows, in a single subject, how tracts connecting two cortical regions, the precuneus and the superior-parietal cortex are represented in the N×N matrix.

Figure 1.

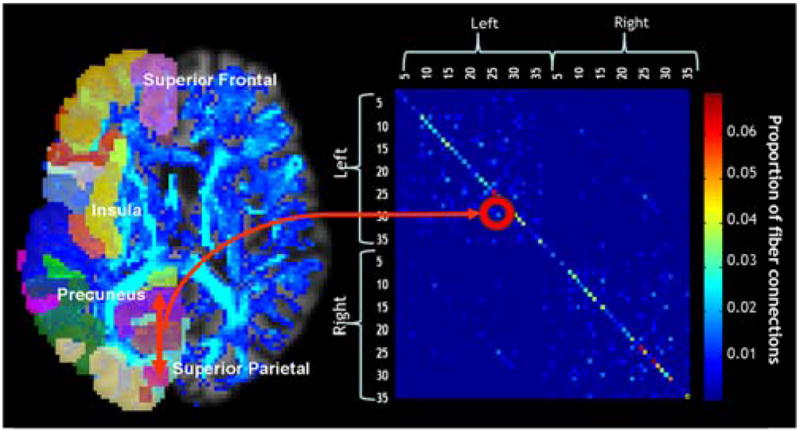
Each colored element of the 70×70 connectivity matrix (right) for each subject was calculated based on the proportion of fibers (shown on the left as a blue fiber density map) connecting each of the colored labels in each hemisphere to each of the other colored labels (left).

2.2.8 Network Analysis Based on Graph Theory

On the baseline 70×70 matrices generated above, we used the Brain Connectivity Toolbox (https://sites.google.com/a/brain-connectivity-toolbox.net/bct/Home) to compute the two measures whose values contribute to small world architecture, characteristic path length (CPL), and mean clustering coefficient (MCC). CPL is an average measure of the minimum number of edges necessary to travel from one node to another in a network (i.e., average minimum path length); MCC measures how many neighbors of a given node are also connected to each other, relative to the total possible number of connections in the network [7].

2.3 Statistics

We first ran a voxel-wise linear regression, controlling for age and sex, to predict changes in FA between baseline and 6 months. To predict the changes in FA, we used the most logical measure – namely the average FA calculated in the corpus callosum (CC) at baseline. To broaden the range of predictors, we also used a voxel-wise multiple linear regression, and a partial F test, using both baseline CPL and MCC as predictors – both jointly and independently – of the FA difference maps over the 6-month interval. To limit statistical testing to highly anisotropic white matter, where the power is greater to detect differences, statistics were run only on voxels within the boundaries of the MDT mask thresholded at FA > 0.2.

Computing thousands of association tests at a voxel-wise level can introduce a high false positive error rate in neuroimaging studies, if not corrected. To correct for these errors, we used the searchlight method for false discovery rate correction (FDR) [21]. All statistical maps were thresholded at a corrected p-value to show regression coefficients only in regions that controlled the false disc covery rate.

3. RESULTS

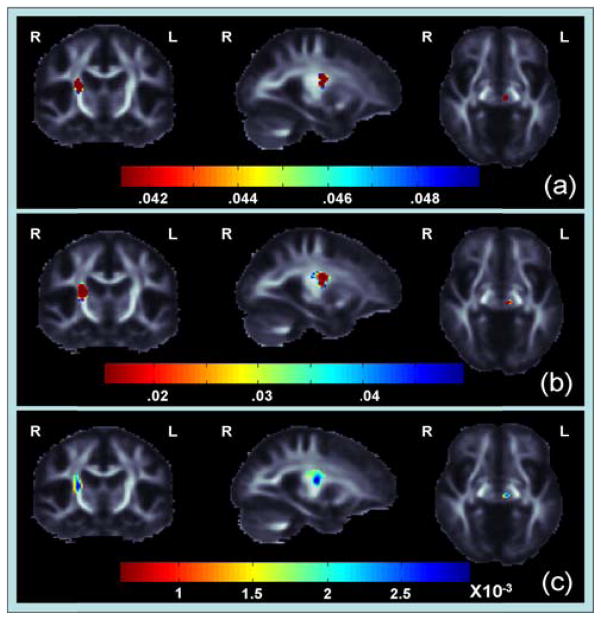
We found no significant differences in FA maps between baseline and 6 months. We also found no significant association between the baseline average FA CC measures and the FA difference maps. However, we did find a significant association between baseline CPL an nd MCC measures - used together as predictors - and FA differen nce maps in the right internal capsule and left thalamus (Figure 2; corrected p<0.05 [21]). We assessed the average change in FA across all 19 subjects in these significant regions to identify the directionality of FA difference and found decreases in FA in the internal capsule and FA increases in the thalamus. When we assessed CPL and MCC separately we found no significant associattion between ch hanges in FA and CPL, suggesting that the MCC measure was driving our findings. We found a significant positive association with MCC (corrected p<0.05 [21]). This suggests that a lower mean clustering coefficient at baseline is associatted with a larger decrease in FA in the right internal capsule and changes in FA in the left thalamus.

Figure 2.

(a) These p-maps show regions where CPL and MCC are joint pr redictors of FA differences (corrected p<0.05 [21]) (b) These p-maps show regions where MCC is significantly associated with change in FA (c) These maps show Beta-values (non-normalized slope of regression coefficient in units of imaging measure per unit of predictor) within regions where MCC has a significant positive correlation with changes in FA.

4. DISCUSSION

Cerebral atrophy and cognitive impairment are known consequences of AD. Whether or not such deficits can be predicted in early MCI subjects is of great interest for identifying candidates for early treatment, and in pre-selecting groups for clinical trials. In this study we found no significant differences in FA maps between baseline and 6 months in eMCI subjects. We also found no significant association between the baseline average FA corpus callosum measures and FA difference maps. However, we did find an association between baseline small world global network measures and changes in FA after just 6 months.

Networks with higher levels of clustering are more densely connected and may indicate a more functionally coherent neural system [7]. We found that lower mean clustering coefficient at baseline was associated with larger decreases in FA in the right internal capsule. The fibers from the corona radiata, including the thalamocortical and long corticofugal tracts, all converge into the internal capsule. These systems are likely part of the overall network that becomes disconnected in AD.

DTI has some limitations in gauging fiber integrity in regions with extensive fiber crossing and mixing. The simplistic single-tensor model assumes diffusion is Gaussian, with a dominant direction in 3D that can be inferred. For example, we found MCC associations with increases in FA in the thalamus, but the thalamus is known to have reciprocal connections to a large portion of the cortex potentially making it prone to fiber crossing. Such patterns have also been found in other studies of elderly patients [22]. Using high angular diffusion imaging (HARDI) in future studies, along with FA analogs derived to accommodate multimodal ODFs, may better characterize the integrity of complex intra-voxel structures. FA from the tensor distribution function (TDF) can better characterized the anisotropy where fibers cross [23]. Resolving the multi-fiber microstructure of WM in these regions may provide a better understanding of why we found increases in FA in the thalamus.

This study only examined eMCI subjects. As ADNI is a longitudinal study, we will later investigate which of these subjects eventually develop AD. If these early aberrations in connectivity accurately predict a patient’s conversion to AD, there may also be certain connectivity patterns that reflect a cognitive reserve.

This study offers initial evidence that DTI-based network measures may be a novel predictor of AD progression. Corroboration of this finding in a larger cohort and with other imaging methods is needed and may help in understanding the symptoms and prognosis for patients.