Oscillating and Pulsed Gradient Diffusion Magnetic Resonance Microscopy Over an Extended b-value Range: Implications for the Characterization of Tissue Microstructure

Abstract

Oscillating gradient spin-echo (OGSE) pulse sequences have been proposed for acquiring diffusion data with very short diffusion times, which probe tissue structure at the subcellular scale. OGSE sequences are an alternative to pulsed gradient (PGSE) measurements, which typically probe longer diffusion times due to gradient limitations. In this investigation, a high-strength (6600 G/cm) gradient designed for small-sample microscopy was used to acquire OGSE and PGSE data in a rat hippocampal specimen at microscopic resolution. Measurements covered a broad range of diffusion times (TD_eff=1.2–15.0 ms), frequencies (ω=67–1000 Hz) and b-values (b=0–3.2 ms/μm²). Variations in ADC with frequency and diffusion time provided microstructural information at a scale much smaller than the imaging resolution.

For a more direct comparison of the techniques, OGSE and PGSE data were acquired with similar effective diffusion times. Measurements with similar TD_eff were consistent at low b-value (b<1 ms/um²), but diverged at higher b-values. Experimental observations suggest that the effective diffusion time can be helpful in the interpretation of low b-value OGSE data. However, caution is required at higher b, where enhanced sensitivity to restriction and exchange render the effective diffusion time an unsuitable representation. Oscillating and pulsed gradient diffusion techniques offer unique, complementary information. In combination, the two methods provide a powerful tool for characterizing complex diffusion within biological tissues.

Introduction

In biological systems, molecular motion is influenced by interactions with tissue components such as cell membranes, macromolecules and fibers. The diffusion coefficient measured by magnetic resonance imaging (MRI) (i.e. of water) is typically referred to as the apparent diffusion coefficient (ADC), to account for the presence of different tissue micro-environments and interactions with barriers which restrict or hinder motion. The measured diffusion coefficient, or ADC, thus deviates from the intrinsic self-diffusion coefficient and provides valuable information about tissue microstructure and integrity. Furthermore, the ADC exhibits dependence on experimental parameters, including the shape of the diffusion sensitizing gradient pulse.

The restricted movement of water molecules within tissue forms the basis for the contrast observed in diffusion MRI and the changes observed with disease. Barriers to water mobility such as cell membranes and myelin are believed to be the primary mechanisms behind diffusion anisotropy in the brain (1). The formation of these barriers explains the decreases in diffusivity which are known to occur during brain development (2). In tumors, reductions in the ADC are likely related to increased tissue disorganization and extracellular space tortuosity (3). In stroke, reduced ADC values are commonly attributed to the movement of water from the extracellular to the intracellular space, where intracellular organelles and macromolecules slow movement (4,5). ADC reductions have also been associated with a drop in the intracellular diffusion coefficient (6), which may be caused by increased restriction due to beading (i.e. focal enlargements separated by constrictions) of axons and dendrites (7).

Given the complexity of biological tissues, it is not surprising that obstructions to free diffusion exist at multiple length scales: from cell membranes down to intracellular structures and organelles and even further down to individual macromolecules (1). Sensitivity to a particular restrictive scale depends primarily on the time interval over which diffusion is probed, known as the diffusion time, TD. As diffusion times become longer, the likelihood for water molecules to encounter multiple barriers or larger scale barriers increases. Experiments conducted with long TD are therefore sensitive to larger obstructions. With short diffusion times, only those barriers at the shortest length scales, if any, are encountered. Short TD experiments are thus more sensitive to smaller scale obstructions. Due to reflection at barriers or slow diffusion through permeable membranes, the ADC obtained from a long TD measurement will typically be slower than that obtained with a short TD. This time dependent behaviour of the ADC has been observed in a variety of systems including packed microbeads and cells, as well as intact neurological tissues (8–12).

The length scale probed by a particular TD can be judged using the Einstein relationship for the root-mean-square displacement of a freely diffusing molecule:

$$r_{\mathit{rms}}=\sqrt{6·D·TD},$$ [1]

where D is the diffusion coefficient. The ‘length’ of the diffusion time is established by comparing r_rms to the typical restricted size (or cell dimension), a. If a ≫r_rms, TD is short, as very few molecules will encounter the cell membrane and the motion of water is unrestricted. Conversely, if a≪;r_rms, TD is considered long and diffusion is fully restricted.

To characterize diffusion behaviour and gain insight into tissue microstructure, it is necessary to collect a series of measurements with a variety of diffusion times, thus probing a wide range of restrictive scales. Typically, diffusion measurements are acquired using a pulsed gradient spin echo (PGSE) sequence, where a pair of gradients (of equal amplitude, G and duration, δ) are centered around a refocusing radiofrequency (RF) pulse and separated by time, Δ (13). For a PGSE experiment, the effective diffusion time, including a correction for dephasing during the finite-length gradient pulse, is TD_eff= Δ−δ/3 (13). The diffusion-decayed signal, S, is typically plotted as a function of the diffusion-weighting parameter b=(γGδ)²TD_eff.

Typical PGSE measurements are limited to diffusion times on the order of ~10 ms due primarily to gradient strength and switching time limitations. In addition, the gradient spacing, Δ, must be long enough to accommodate the refocusing pulse and any gradient spoilers. To overcome these limitations, oscillating gradient spin echo (OGSE) pulse sequences have been proposed (9,14). In an OGSE sequence, the pulsed gradients are replaced with periodic, sinusoidal gradient waveforms. The effective diffusion time of the OGSE experiment is related to the period of the oscillation. The diffusion weighting (b-value) can be increased by lengthening the waveform duration (i.e. playing out multiple periods), rather than increasing the gradient amplitude. The experiment thus consists of a series of concatenated diffusion weighting periods. In this manner, short diffusion time measurements can be obtained by systems with moderate gradient strengths.

OGSE experiments have been reported in various model, cell and animal systems, showing an increase in ADC with the gradient oscillation frequency (15). There have also been reports of novel OGSE-based contrast, which can distinguish microscopic structures in regions that appear otherwise homogenous on conventional PGSE scans (12,16). While these are promising findings, the vast majority of OGSE studies report ADC values calculated from two diffusion weighted acquisitions with b<1 ms/μm² (10–12,16). In systems where diffusion signal attenuation is not mono-exponential, additional insight might be obtained from a more complete characterization of the diffusion decay curve, which includes multiple acquisitions spanning a broader range in b.

Interpretations of OGSE data commonly assume that an OGSE measurement is essentially equivalent to a PGSE measurement with a very short diffusion time (11,16). The simplicity of this interpretation, along with the implication that OGSE can be used to infer structural changes on subcellular scales, has attracted a lot of recent interest in this method. However, the obvious differences between these two techniques (e.g. pulsed vs. sinusoidal gradients, single vs. multiple diffusion weighting periods), suggest that their comparison could be complicated by other factors (e.g. sensitivity to exchange and restriction).

In this work, we address these issues by using a strong and rapidly switching, compact gradient system developed for magnetic resonance microscopy (MRM) applications. The 6600 G/cm triple-axis gradient allows measurements to be made with a combination of high b-value and short diffusion time. Specifically, PGSE experiments were conducted with diffusion times as low as 1.2 ms and OGSE experiments were conducted with frequencies as high as 1 kHz. For both PGSE and OGSE measurements, the maximum b-value was 3.2 ms/μm². To our knowledge, such combinations of short diffusion time/high frequency and high b-value have never been applied to the study of a biological tissue. Combined with microscopic imaging resolution, these diffusion parameters can provide information on tissue microstructure that may not be obtainable by other means. Furthermore, by conducting OGSE and PGSE experiments with similar effective diffusion times, we were able to compare these two types of measurement in a manner, which, until now, was limited to simulation (17,18).

Theory

OGSE vs. PGSE

The interpretation of an OGSE experiment is somewhat more complex than that of its PGSE counterpart. Although it is tempting to describe OGSE and PGSE experiments in a similar manner (i.e. in terms of a specific diffusion time), in the case of restricted diffusion this does not offer a complete description of the OGSE technique (11,15). Nevertheless, an effective diffusion time, TD_eff, can still be defined for an OGSE experiment, by comparison to the b-value calculation for PGSE (11). For a cosine-shaped oscillating gradient with period τ, TD_eff=τ/4. For a sine shaped gradient, TD_eff=3τ/8.

OGSE measurements may be better suited to a frequency domain interpretation. Spin motion within the system is described by the diffusion spectrum, $\underset{\_}{\underset{\_}{\mathit{D}}}(\omega )$, which is the Fourier transform of the spin velocity autocorrelation function (19). Assuming a Gaussian distribution of particle phases (i.e. Gaussian phase approximation), the signal attenuation is given by (14,19):

$$S=S_{0}exp\left(-\frac{1}{2\pi }\underset{-\infty }{\overset{\infty }{\int }}\mathit{F}(\omega )\underset{\_}{\underset{\_}{\mathit{D}}}(\omega )\mathit{F}(-\omega )d\omega \right),$$ [2]

where S₀ is the signal magnitude in the absence of diffusion gradients. The gradient spectrum, F(ω), is the Fourier transform of the time integral of the gradient waveform, g(t):

$$\mathit{F}(\omega )=\underset{0}{\overset{\infty }{\int }}\mathit{dt}exp(i\omega t)\underset{0}{\overset{t}{\int }}{dt}^{\prime }\gamma \mathit{g}(t^{\prime }),$$ [3]

where γ refers to the gyromagnetic ratio. In a typical diffusion experiment (OGSE or PGSE), the signal attenuation is related to D(ω), the projection of the tensor $\underset{\_}{\underset{\_}{\mathit{D}}}(\omega )$ onto a unit vector in the direction of the diffusion gradient pulse (9). Under these conditions, eq. [2] simplifies to:

$$S=S_{0}exp\left(\frac{-1}{2\pi }\underset{-\infty }{\overset{\infty }{\int }}{\mid \mathit{F}(\omega )\mid }^2\mathit{D}(\omega )d\omega \right).$$ [4]

Assuming mono-exponential diffusion decay, the ADC is given by:

$$\mathit{ADC}=\frac{-log(S/S_0)}{b}.$$ [5]

Applying Parseval’s relation:

$$b=\underset{0}{\overset{t}{\int }}{\mid \mathit{F}(t)\mid }^{2}dt=\frac{1}{2\pi }\underset{-\infty }{\overset{\infty }{\int }}{\mid \mathit{F}(\omega )\mid }^{2}d\omega .$$ [6]

Combining equations [4–6], the ADC can be expressed in terms of the spectrum of the diffusion sensitizing gradient, F(ω), and the diffusion spectrum, D(ω):

$$\mathit{ADC}=\frac{\underset{-\infty }{\overset{\infty }{\int }}{\mid \mathit{F}(\omega )\mid }^2\mathit{D}(\omega )d\omega }{\underset{-\infty }{\overset{\infty }{\int }}{\mid \mathit{F}(\omega )\mid }^{2}d\omega }.$$ [7]

Equations [2–7] can be applied to both OGSE and PGSE measurements. A more detailed description of these principles can be found in (9,15).

While it may extend the measurable range of diffusion times, the OGSE technique is not free from limitations. The maximum frequency of gradient modulation is limited by the rise time of the gradient system. Furthermore, to maintain the same b-value, increases in frequency, ω=1/τ, must be accompanied by increases in the waveform amplitude or duration (i.e. number of periods, N). Due to gradient amplitude limitations, increasing N may be the only option, but lengthening the oscillating gradient waveform results in longer echo times, which reduces SNR. OGSE measurements are therefore rarely conducted with both high frequency (ω >500 Hz.) and high b-value (b>1 ms/μm²) (10–12,16).

In MR microscopy, the small sample size warrants the use of specialized hardware – in particular, a high-strength, compact gradient system (20). Strong and fast-switching gradients are necessary for micro-imaging at resolutions finer than ~10 μm, as they reduce the effects of diffusion during spatial encoding (14,20). An added benefit of this hardware is the ability to perform diffusion measurements with combinations of high b-value and short diffusion time.

Modeling the Diffusion Spectrum

Analytical expressions for the diffusion spectrum, D(ω), have been derived for simple geometries, such as planar layers and cylindrical and spherical boundaries (19). For the interpretation of diffusion measurements, this study uses the simplest of these models: diffusion between infinitely large parallel planes. The diffusion spectrum, D(ω), for the parallel plane model (PPM) can be expressed as (19):

$$\mathit{D}(\omega )=\sum _k{B}_k\frac{a_k{\mathit{D}}_{\mathit{free}}{\omega }^2}{a_k^2{{\mathit{D}}_{\mathit{free}}}^2+{\omega }^2},$$ [8]

where D_free=D(ω=∞) refers to the self-diffusion coefficient of the free liquid. Summation terms B_k and a_k are given by:

$$B_k=\frac{8d^2}{{(2k-1)}^4{\pi }^4},a_k=\frac{{\pi }^2{(2k-1)}^2}{d^2},$$ [9]

where d is the distance between the parallel planes.

In eq. [8], which was derived for impermeable planes, the diffusion coefficient drops to zero at low frequencies or long diffusion times (i.e. D(ω=0)=0). However, if barriers to diffusion are permeable (as in biological tissues), the diffusion coefficient will not vanish at ω=0 (19). An additive term, D_rest, which specifies the zero-frequency diffusion coefficient, was therefore incorporated into eq. [8]. Re-formulating eq. [8] in terms of D_rest=D(ω=0) and D_free=D(ω=∞), provides:

$$\mathit{D}(\omega )={\mathit{D}}_{\mathit{rest}}+\sum _k{B}_k\frac{a_k\left({\mathit{D}}_{\mathit{free}}-{\mathit{D}}_{\mathit{rest}}\right){\omega }^2}{a_k^2{\left({\mathit{D}}_{\mathit{free}}-{\mathit{D}}_{\mathit{rest}}\right)}^2+{\omega }^2}$$ [10]

This formulation is desirable, as it makes specific reference to the diffusion coefficient in the long and short diffusion time limits, which can be determined by data fitting techniques.

Modeling Diffusion Decay Curves

Signal decay due to diffusion can be described in a number of ways. The most basic of these is based on a Taylor series expansion of the logarithm of the diffusion-decayed signal:

$$ln(S(b))=ln(S_0)+C_{1}b+C_2{b}^2+C_3{b}^3+\dots$$ [11]

The simplicity of Eq. [11] arises from the fact that it is a purely mathematical representation of the signal, which makes no physical assumptions about the underlying tissue structure (21).

For low b-values (b<1 ms/μm²) in neural tissue, the Gaussian phase approximation is valid and the b² term in eq. [11] is negligible. The Taylor series can thus be truncated after the linear term, yielding the well known mono-exponential representation of the signal:

$$S(b)=S_{0}exp(-b·\mathit{ADC}).$$ [12]

Combining eq. [12] with eq. [7], which relates the ADC to the diffusion gradient spectrum, provides an expression for the mono-exponential signal decay, which incorporates the effects of gradient pulse shape:

$$S(b)=S_{0}exp\left(-b·\frac{\underset{-\infty }{\overset{\infty }{\int }}{\mid \mathit{F}(\omega )\mid }^2\mathit{D}(\omega )d\omega }{\underset{-\infty }{\overset{\infty }{\int }}{\mid \mathit{F}(\omega )\mid }^{2}d\omega }\right).$$ [13]

With an intermediate range of b-values (b<3 ms/um²), non-Gaussian diffusion is observed in neural tissue. The b² term is therefore no longer negligible and must be included in the Taylor expansion:

$$S(b)=S_{0}exp\left(-b·\mathit{ADC}+\frac{1}{6}{b}^2·{\mathit{ADC}}^2·K_{\mathit{app}}\right).$$ [14]

The K_app term in eq. [14] refers to the apparent kurtosis, which is a dimensionless measure of the deviation of the diffusion probability distribution from a Gaussian (22). The diffusion probability distribution describes the probability for a water molecule to displace by a given distance during the diffusion time, TD. Within biological tissues, structural barriers and multiple diffusing compartments cause this distribution to deviate substantially from a Gaussian.

While it may not offer direct biophysical insight, the kurtosis is an indicator of structural complexity and the diversity of diffusing populations (i.e. “diffusional heterogeneity” (23)) within the tissue (24). Much like the ADC, the apparent kurtosis is affected by experimental parameters, particularly the shape of the diffusion sensitizing gradient. In this study, diffusion decay data was fit to eq. [14], which was chosen because it fit the data well and is well suited to the range of b-values explored.

Methods

Sample Preparation and Positioning

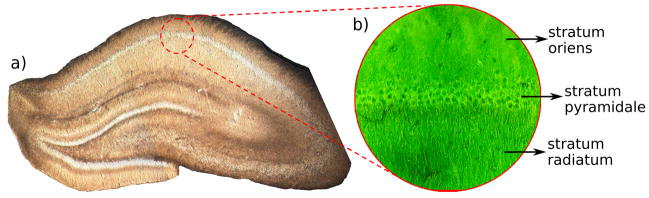
Imaging was conducted on a 600 MHz Bruker spectrometer using 100 μm diameter RF micro-surface coils developed by Bruker Biospin (25). Hippocampal sections (100 μm thick) were cut from a perfusion-fixed (4% formaldehyde) rat brain specimen using a vibratome. Prior to imaging, samples were washed overnight in phosphate buffered saline (PBS). PBS washing has been shown to reverse some of the fixation effects on MR parameters, particularly the shortening of the T₂ relaxation time constant (26). Sections were positioned so that the pyramidal cell layer in the CA1 region ran across the centre of the coil face. Three distinct tissue layers were thus captured in the images: the stratum pyramidale (i.e. cell layer), the stratum oriens, and the stratum radiatum (Figure 1). More details on the RF micro-surface coil and the tissue positioning and retention scheme can be found in (27).

Figure 1.

Illustration of relevant anatomy. a) Real-colour light-microscope image of a perfusion-fixed rat hippocampal slice (300 μm thick). The red circle indicates the area captured within the field-of-view of the micro-surface coil. b) False-colour microscope image showing a magnified view of the 3 tissue components visible in the MR images: (top) stratum oriens, (middle) stratum pyramidale, (bottom), stratum radiatum.

Gradient System

The short diffusion time/high frequency and high b-value acquisitions used in this study were facilitated by a high-strength triple-axis planar gradient system. The planar design accommodates Bruker’s slide-mounted RF micro-surface coils, which are inserted into the gap between the two halves of the gradient coil. More information on the gradient hardware, including a detailed diagram can be found in (20).

The maximum gradient strength was 6600 G/cm in a linearity range of ~1 mm. This was determined by calibration with a phantom consisting of a piece of nylon mesh with 50 μm square pores and 40 μm threads (Small Parts Inc.) immersed in water doped with 1g/L copper sulfate.

Additional gradient calibration was performed by measuring the diffusion coefficient in a doped water sample using both OGSE and PGSE pulse sequences (see below). Across all measurements (7 PGSE, 8 OGSE), the diffusion coefficient was measured as: 1.98±0.02 μm²/ms.

Image Acquisition

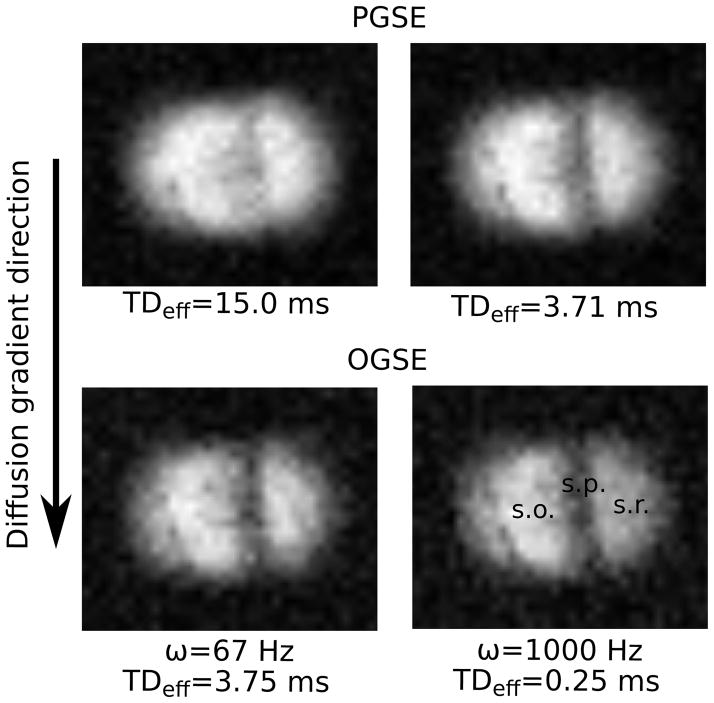
Diffusion-weighted images were acquired using both OGSE and PGSE pulse sequences. Diffusion sensitizing gradients were applied in the readout direction. Representative images are shown in Figure 2, which also indicates the direction of diffusion gradients relative to the anatomy. All images had a 0.8 × 0.8 × 0.4 mm³ field-of-view and a 64 × 64 × 8 data matrix, providing a resolution of 12.5 × 12.5 × 50 μm³. With a repetition time of 2 s and 2 averages, the acquisition time for each image was approximately 34 minutes. Temperature was maintained at 23°C throughout scanning.

Figure 2.

PGSE (top row) and OGSE (bottom row) images. Images were acquired with b=1.6 ms/μm². Three distinct anatomical regions are visible. The low signal intensity band near the center is the stratum pyramidale (s.p.). Based on the curvature of the cell layer, the tissue regions on the left and right are identified as the stratum oriens (s.o.) and stratum radiatum (s.r.), respectively. Note that relative to Figure 1b, the anatomy within the images is rotated 90° counter-clockwise.

PGSE Measurements

To minimize the diffusion time, a 3D spin echo sequence with hard excitation and refocusing pulses was used. To eliminate unwanted echoes, crusher gradients were applied on either side of the refocusing pulse, in the lowest resolution dimension. This added some diffusion weighting in this direction (b=0.074 ms/μm²).

Data was acquired at 9 different diffusion times, TD_eff=Δ−δ/3, ranging from 1.2–15.0 ms. TD_eff was varied by changing the spacing, Δ, between diffusion gradients. The duration of the diffusion gradient pulses, δ, was constant at 110 μs. Although the diffusion time was varied, the echo time, TE, of PGSE acquisitions was always 17 ms (the minimum TE to accommodate the maximum diffusion time of 15 ms). The constant echo time ensures that T₂ effects are equal across all PGSE measurements.

For each diffusion time, the diffusion gradient amplitude, G, was varied to provide b-values ranging from 0–3.2 ms/μm², in increments of 0.4 ms/μm².

OGSE Measurements

For consistency, the same 3D spin echo sequence was adapted for OGSE measurements. The pulsed gradients were replaced with a pair of apodized, cosine-modulated diffusion gradients, in which the first and last quarter periods of the cosine function were replaced with a sine function of twice the frequency (9).

OGSE acquisitions were performed at 10 different frequencies between 67 Hz and 1 kHz. This range of frequencies was achieved by varying both the duration of the oscillating gradient waveform, T (10 – 15 ms) and the number of periods, N (1–12). The effective diffusion time, TD_eff, for the OGSE acquisitions ranged from 0.25–3.75 ms. To accommodate the long, oscillating gradients, all OGSE measurements were conducted with TE=35 ms.

As with the PGSE measurements, the gradient amplitude, G, was varied and data was acquired at b-values from 0–3.2 msec/μm². For an apodized cosine waveform, the relationship between gradient strength and b-value is (9):

$$b=\frac{1}{8}{\left(\frac{\gamma G}{\pi N}\right)}^2{T}^3\left(1-\frac{1}{8N}\right)$$ [15]

Data Processing

The mean signal intensity was measured in manually selected, homogenous regions of interest (ROIs) in each of the three anatomical regions (stratum oriens, stratum radiatum, and stratum pyramidale). For each diffusion time/frequency and ROI, the mean signal, S(b), was fit, using least squares minimization, to eq. [14]. Fitted parameters included S₀, the signal in the absence of diffusion weighting, the apparent diffusion coefficient (ADC), and the apparent diffusional kurtosis K_app.

Although data was collected up to b=3.2 ms/μm², some fits did not include all b-values. The maximum b-value included in the fit was determined by the first point where the signal was less than 2·S_out, where S_out refers to the mean pixel intensity in a noise ROI. That point, and all points at higher b-value were excluded from the fit. Assuming that the noise on the two quadrature channels is independent and Gaussian distributed (with zero mean), measurement of an average ROI intensity, S≥ 2·S_out implies a noise contribution of, on average, less than 10% (28). The threshold thus prevents the inclusion of noise-dominated data points in the fit.

To obtain more information about underlying tissue microstructure, ADC estimates obtained from data fitting were subsequently fit to the infinite parallel plane model. For each acquisition, F(ω) was calculated from equation [3]. Knowledge of F(ω) and the ADC then allowed us to fit for the diffusion spectrum parameters using equations [7] and [10]. These parameters include: d (distance between parallel planes), D_rest (long time or ‘restricted’ diffusion coefficient), and D_free (the intrinsic, ‘free’ diffusion coefficient). To calculate D(ω), it was not necessary for the summation in eq. [10] to go beyond 200 terms. Since the diffusion spectrum is a reflection of spin motion, it is tissue specific and should not depend on the experiment. Therefore, for each anatomical region, fits were performed globally on OGSE and PGSE data. These fits were performed using weighted least squares minimization to account for the variable uncertainty in ADC estimates.

Uncertainties in fitted parameters were expressed in terms of confidence regions. The confidence bounds for each parameter were determined by finding the maximum and minimum value of the parameter while optimizing all remaining parameters, such that the sum of squares, SSQ₀, increased by a factor:

$$\frac{\mathit{SSQ}}{{\mathit{SSQ}}_0}=\left[1+\frac{np}{N-np}F(np,N-np,0.68)\right],$$ [16]

where np is the number of fitted parameters, N is the number of data points included in the fit, 0.68 refers to the confidence level, and F is the F-distribution. This method assumes that the measurement error for each data point is independently random and Gaussian distributed (29).

Results

To demonstrate the image quality and anatomical features, a set of four images acquired with b=1.6 ms/μm² and different diffusion times/frequencies is shown in Figure 2. The diffusion gradient direction is shown alongside the images. Three distinct anatomical regions are visible. The band near the center of the image with low signal intensity is the pyramidal cell layer. Based on the curvature of the cell layer, the regions on the left and right are identified as the stratum oriens and stratum radiatum, respectively.

As indicated by the sample images, increased contrast was observed between anatomical regions when measurements were conducted with shorter TD_eff and higher ω. Another feature is the reduced SNR of OGSE scans relative to PGSE. This is due to the longer echo time (35 vs. 17 ms), which was necessary to accommodate the long, oscillating gradient waveforms. In the absence of diffusion gradients, the average SNR for OGSE was 44, compared to an average SNR of 65 for PGSE.

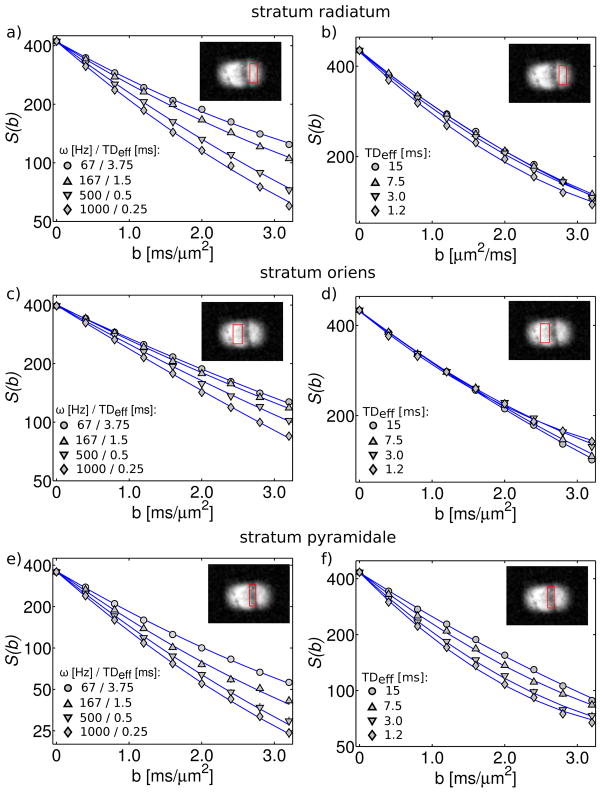
For a subset of the frequencies/diffusion times tested, Figure 3 shows the mean signal intensity as a function of b-value for ROIs within the 3 anatomical areas. Figure 3 demonstrates the quality of the fits, for which the average reduced χ² was 0.9. Depending on the anatomical area and the diffusion time/frequency, the data exhibited varying degrees of deviation from a mono-exponential. Non mono-exponential behaviour can be observed from the non-linear relationship between log(signal) and b-value. In general, OGSE data more closely resembled a mono-exponential than PGSE. Within the PGSE data, greater deviation from a mono-exponential was observed at shorter TD_eff.

Figure 3.

Mean signal intensity (in log scale) vs. b-value. The left-hand column (a,c,e) shows OGSE data and the right-hand column (b,d,f) shows PGSE data. Data points correspond to the mean signal within the ROI shown in the inset. Solid lines represent fits to the kurtosis model, which were performed individually for each diffusion time/frequency.

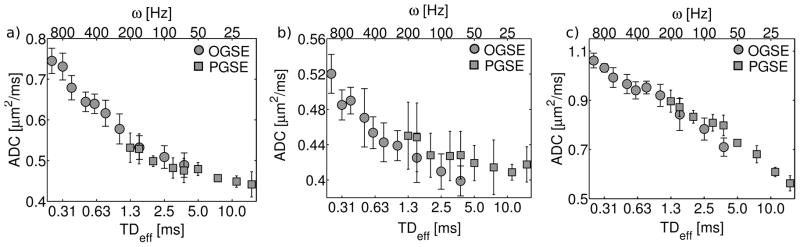
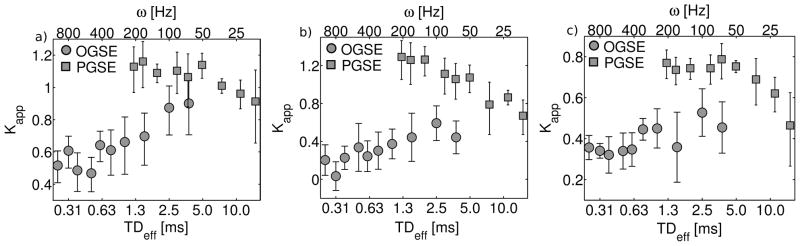
The best-fit ADC and K_app values, determined by fitting the data to eq. [14], are plotted in Figures 4 and 5, respectively. Note the consistency of OGSE and PGSE derived ADC measurements, which results in a continuous trend in ADC vs. diffusion time. In contrast, not only do OGSE and PGSE measurements of K_app exhibit opposite trends with respect to diffusion time, PGSE K_app values are significantly higher than their OGSE counterparts.

Figure 4.

Fitted ADC values obtained from OGSE (circles) and PGSE (squares). The 3 plots correspond to different hippocampal subregions [a) stratum radiatum, b) stratum oriens, c) stratum pyramidale]. Errorbars refer to the 68% confidence interval. The diffusion time, TD_eff, is shown on the lower x-axis. Frequency, ω, is shown on the upper x-axis and applies only to OGSE measurements. Due to the inverse proportionality between time and frequency, the upper and lower axes are displayed in opposite directions.

Figure 5.

Fitted apparent kurtosis, K_app, values. PGSE and OGSE measurements are plotted together (PGSE-squares, OGSE-circles) for each ROI [a) stratum radiatum, b) stratum oriens, c) stratum pyramidale]. Errorbars correspond to the 68% confidence interval.

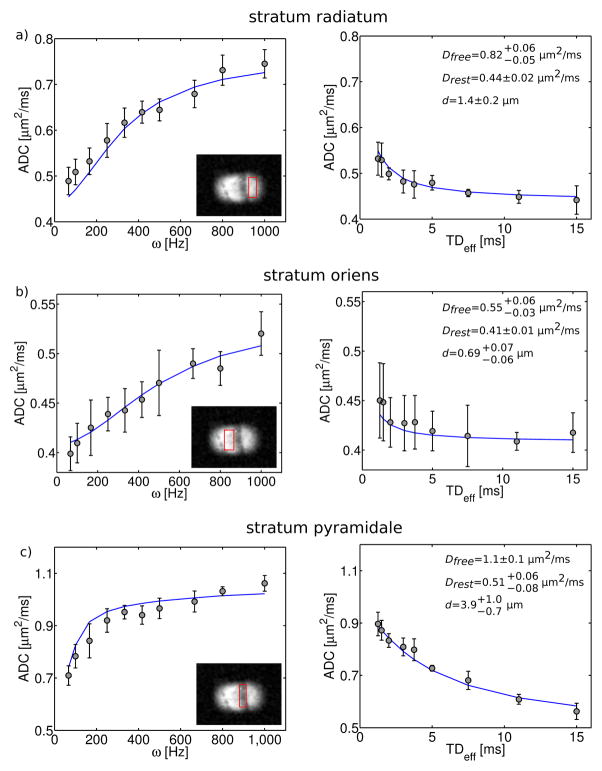
Results of fitting the ADC data to the parallel plane model are shown in Figure 6. The fits generally describe the data well, but there are regions of systematic deviation between the data and the fit (e.g. OGSE data in Figure 6c). Estimates of PPM parameters, including the long time diffusion coefficient, D_rest, the intrinsic ‘free’ diffusion coefficient, D_free, and the distance between parallel planes, d, are summarized in Table 1. These parameters varied significantly across the different ROIs. Both diffusion coefficients and the plane separation were highest in the cell layer, intermediate in the stratum radiatum, and lowest in the stratum oriens.

Figure 6.

PPM fits to ADC measurements. OGSE data is plotted vs. frequency (left-hand column) and PGSE data is plotted vs. diffusion time (right-hand column). Results are shown for all 3 hippocampal subregions, which are indicated in the insets. Solid lines represent the PPM model fit. For each anatomical region (row), the fit was performed simultaneously on OGSE and PGSE measurements. Best fit parameters are shown in the upper right corner of PGSE data plots. These include: 1) the intrinsic, ‘free’ self-diffusion coefficient, D_free, 2) the long-time, or ‘restricted’ diffusion coefficient, D_rest, and 3) the distance, d, between parallel planes. Reported uncertainties correspond to the 68% confidence interval.

Table 1.

Summary of best-fit parallel plane model (PPM) parameters. Reported uncertainties correspond to the 68% confidence interval.

	Dfree [μm2/ms]	Drest [μm2/ms]	d [μm]
stratum radiatum	$0.82{\pm }_{0.05}^{0.06}$	0.44±0.02	1.4±0.2
stratum oriens	$0.55{\pm }_{0.03}^{0.06}$	0.41±0.01	$0.69{\pm }_{0.06}^{0.07}$
stratum pyramidale	1.1±0.1	$0.51{\pm }_{0.08}^{0.06}$	$3.9{\pm }_{0.7}^{1.0}$

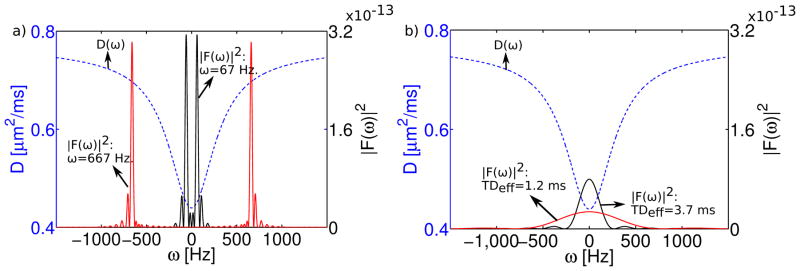
Figure 7 shows a plot of the fitted PPM diffusion spectrum, D(ω), for the region-of-interest in the stratum radiatum. Overlaid on D(ω) are plots of the gradient spectrum, F(ω), for an OGSE acquisition with a frequency of 67 Hz (TD_eff=3.75 ms, Figure 7a) and a PGSE acquisition with TD_eff= 3.71 ms (Figure 7b). This particular pair of gradient spectra is shown because of their similarity in effective diffusion time. To demonstrate the effect of increasing the oscillation frequency, Figure 7a also shows the spectrum for an OGSE experiment with ω=667 Hz (TD_eff=0.38 ms). Similarly, Figure 7b includes the spectrum for a PGSE measurement with TD_eff=1.2 ms.

Figure 7.

Combined plots of the diffusion spectrum, D(ω), and the square of the gradient spectrum, |F(ω)|². D(ω) was obtained from the PPM fit to the stratum radiatum. a) Gradient spectra correspond to apodized cosine waveforms with frequency, ω=67 Hz (TD_eff=3.75 ms) and ω=667 Hz (TD_eff=0.375 ms). b) Gradient spectra correspond to PGSE waveforms with TD_eff=3.7 ms and TD_eff=1.2 ms.

Plots of F(ω) overlaid on D(ω) are helpful in the interpretation of the measurement, because F(ω) is essentially an experimental sampling function, which determines the weightings of different components of the diffusion spectrum (15). Spectra for the OGSE and PGSE waveforms differ markedly. The gradient spectrum for PGSE approximates a rectified sinc function. The spectrum for the apodized cosine OGSE waveform has peaks at the oscillation frequency, ±ω, in addition to significant sidelobes, which arise from the finite waveform duration.

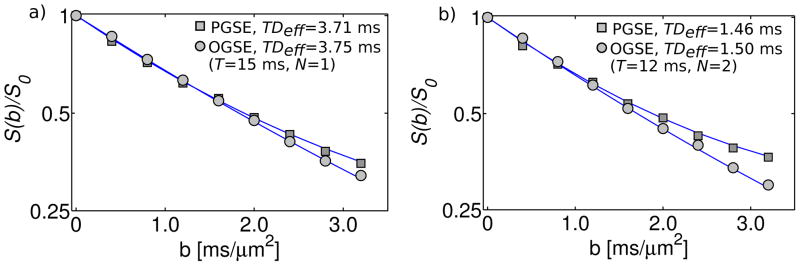
To demonstrate differences between the two techniques, Figure 8 compares PGSE and OGSE measurements with very similar diffusion times. Figure 8a shows the mean signal intensity in the stratum oriens vs. b-value, for OGSE and PGSE acquisitions with diffusion times of 3.75 and 3.71 ms, respectively. Figure 8b shows similar data, but with OGSE/PGSE diffusion times of 1.5/1.46 ms. For easier comparison, data has been normalized to the signal intensity in the absence of diffusion gradients. For b<1 ms/μm², the PGSE and OGSE data are quite similar – the initial slopes of the diffusion curves are almost identical. With increased b-value, they begin to diverge, as the PGSE data exhibits slower decay and greater deviation from a mono-exponential (i.e. greater apparent kurtosis). This divergence is more significant at the shorter (~1.5 ms) diffusion time. The results shown in Figure 8 are for the ROI in the stratum oriens, but similar trends were observed in all three anatomical areas.

Figure 8.

Comparison of OGSE (circles) and PGSE (squares) measurements with similar effective diffusion time. a) Mean signal intensity (in log scale) in the stratum oriens for PGSE/OGSE acquisitions with TD_eff=3.71/3.75 ms. b) Same as (a), but with TD_eff=1.46/1.50 ms.

Discussion

In this investigation, a high-strength, compact gradient system allowed us to extend the boundaries of typical OGSE and PGSE experiments towards higher frequencies and shorter diffusion times with higher b-values. PGSE and OGSE data were acquired with TD_eff ranging from 1.2–15.0 ms and 0.25–3.75 ms, respectively. There was thus a range of diffusion times from 1.2–3.75 ms, where PGSE and OGSE measurements overlapped. This provided an opportunity for a more direct comparison of these two experimental techniques.

Comparison of PGSE and OGSE data must account for the difference in echo time between the measurements (17 ms for PGSE and 35 ms for OGSE). The long OGSE echo time is a fundamental limitation of the technique, which decreases the SNR. Although the diffusion times are longer, the echo time of PGSE measurements can be comparatively short (since there is only a single diffusion weighting period). To maintain this characteristic difference between the two techniques, the PGSE echo time was not extended to match that of OGSE. However, diffusion behaviour can vary with TE, as the sensitivity of the measurement to different tissue components changes (30). For instance, the contribution of a slowly diffusing, short T₂ component to the measured signal would be smaller at TE=35 ms, resulting in a faster apparent diffusion coefficient. To determine if this was the source of the difference between OGSE and PGSE, a subset of PGSE experiments were repeated with TE=35 ms. The results did not change in the follow-up analysis: ADC estimates were consistent, while the apparent kurtosis was significantly higher for PGSE.

Further interpretation of experimental results is divided into 3 sections. The first section discusses the ADC measurements obtained from fits to the kurtosis model. The second section examines the fits of ADC data to the infinite parallel plane model for restricted diffusion. The final section discusses measurements of the apparent kurtosis, K_app.

ADC Measurements

OGSE- and PGSE-derived ADC measurements with similar TD_eff (see Figure 4) were consistent within the estimated uncertainties. This observation was true for all three of the distinct anatomical regions identified within the hippocampus, suggesting that it might apply to other neural tissues. The consistency in ADC values can be inferred from the low b-value (b<1 ms/μm²) agreement of OGSE and PGSE diffusion decay curves (see Figure 8). In the kurtosis model, the best-fit ADC is constrained primarily by low b-value data, where the b² term is still negligible (eq. [14]). The particular range this corresponds to depends on the tissue under study; for brain, b<1 ms/μm² is typical (22). OGSE measurements performed on systems with moderate gradient strengths rarely achieve b-values above 1 ms/μm².

Considering the differences in the gradient spectra for the two experiments (see Figure 7), the agreement of PGSE and OGSE ADC measurements is somewhat surprising. However, it is possible that the intrinsic ADC differences were too subtle to observe under experimental conditions with limited SNR. To assess the effect of differences in F(ω) on ADC values, eq. [7] was applied to the fitted parallel-plane model diffusion spectra. Based on this calculation, ADC differences between OGSE and PGSE experiments (with TD_eff ranging from 0.25–3.75 ms) do not exceed 9% in all three ROIs. For the experimental range of OGSE/PGSE overlap (1.2 ms<TD_eff<3.75 ms), the differences are less than 6%. The measurement uncertainty may have obscured these small variations in the diffusion coefficient.

Experimental results suggest that, although they may not be equivalent, OGSE- and PGSE-derived ADCs are similar. In many cases, the ADC differences may be too small to observe experimentally, particularly with the reduced SNR of long echo time OGSE acquisitions. This simplifies the interpretation of these two types of measurement. It suggests that typical, low b-value OGSE acquisitions are comparable to PGSE measurements with equivalent effective diffusion times.

Parallel Plane Model (PPM)

Although the PPM fit the ADC data reasonably well, it has significant shortcomings. Most obviously, it is a gross oversimplification of the structural complexity of biological tissues. In addition, the fit was based on eq. [7], which describes the relationship between the ADC, the diffusion spectrum, D(ω), and the gradient spectrum, F(ω). This relationship is based on the Gaussian phase approximation and therefore results in mono-exponential signal decay as a function of b (where b-variation was achieved by changing only the gradient amplitude, G). As a result, this method of fitting for the diffusion spectrum, regardless of the chosen structural model (e.g. parallel planes, packed spheres/cylinders), could not be used to describe data at b>1 ms/um², where the decay deviates from a mono-exponential. One way to characterize the data across the entire range of experimental b-values is to develop a more complex model, which consists of multiple exchanging tissue compartments with their own respective diffusion spectra (and Gaussian diffusion). Similar multi-compartment models have been developed and successfully applied to blood and white matter (30,31).

In spite of its shortcomings and inherent assumptions, the fit to the PPM model may be helpful in interpreting the variation in ADC estimates with diffusion time and frequency. In a multi-compartment system, such as a biological tissue, the ADC at low b-value approaches the mean decay rate, weighted by the compartment sizes and relaxation times (5). Tracer diffusion measurements indicate that the extracellular volume fraction is approximately 20% in all three hippocampal subregions (strata oriens, radiatum and pyramidale) (32). Assuming that spin densities are similar in the intra- and extracellular space, PPM parameter estimates are therefore heavily weighted towards the intracellular compartment (which comprises 80% of the volume fraction). This weighting is not likely to be affected by the choice of TR/TE, as the hippocampus is primarily a grey matter structure. In grey matter, longitudinal and transverse relaxation have been observed to be mono-exponential (11).

The variation in extracted PPM parameters across the different ROIs is a result of the unique microstructure within these hippocampal subregions. The hippocampal cell layer consists of large, densely-packed neuronal cell bodies, which are roughly 20 μm in diameter (16). Basal and apical dendrites, which range in diameter from ~0.5 to several micrometers, extend from these cell bodies into the adjacent layers: the strata oriens and radiatum, respectively. These two layers are classified as neuropil, which is a complex web of dendrites and axonal projections interspersed with glia and relatively few neuronal cell bodies (33). The straight, smooth structure of the apical dendritic shafts gives the stratum radiatum an ordered, striped appearance (Figure 1). In our MR scans, the diffusion gradients were oriented roughly perpendicular to the dendritic shafts (Figure 2).

It is not surprising that the plane distance, d, was largest in the cell layer (3.9 μm). While this is substantially smaller than the typical cell body diameter, it might be explained by the presence of sub-cellular structures such as nuclear membranes, which decrease the distance between restricting barriers. The significantly smaller estimates of d in the strata oriens and radiatum (0.79 and 1.4 μm, respectively) are also justifiable, given the dendrite diameters and the fine, complex structure of neuropil. The factor of 2 difference in d between the stratum oriens and radiatum is slightly more difficult to interpret. A possible explanation may be the larger diameter of the apical dendritic shafts (~2–3 μm) relative to the basal dendrites (~1 μm) (34).

Previously published hippocampal ADC values show trends similar to those observed in our measurements. In a diffusion tensor study of fixed rat hippocampus the reported mean diffusivity was significantly lower in the strata oriens and radiatum (0.238 and 0.227 μm²/ms, respectively) than in the stratum pyramidale (0.308 μm²/ms) (33). Since these published values were obtained from PGSE acquisitions with a 17 ms diffusion time, they are much closer to our estimates of D_rest than to D_free. In a similar study of human hippocampal autopsy specimens, mean water diffusivities were lowest in the stratum oriens, intermediate in the stratum radiatum, and highest in the pyramidal cell layer (35). In no instance did our estimates of the ‘restricted’ diffusion coefficient, D_rest, approach zero. This is consistent with the tortuous, hindered diffusion, which is expected in a biological tissue. Only in systems with perfectly impermeable membranes should the diffusion coefficient tend to zero at long diffusion times.

Kurtosis Measurements

Estimates of the apparent kurtosis were positive and higher for PGSE measurements than OGSE. PGSE-derived values of K_app were consistent with previously reported neural tissue measurements (22,23). The apparent kurtosis was estimated with greater fractional uncertainty, based on the 68% confidence interval, than the ADC.

OGSE and PGSE kurtosis estimates exhibited opposite trends with respect to TD_eff. With PGSE, K_app decreased with diffusion time. This behaviour has been predicted (22,36) and stems from a loss of diffusional heterogeneity, which occurs when all water molecules have had time to explore the full space. In contrast, OGSE kurtosis measurements increased with diffusion time. The growth of K_app with TD_eff has also been predicted, but only for short diffusion times (22). In the limit of very short diffusion time, few, if any barriers are encountered and the diffusion probability distribution approximates a Gaussian, resulting in zero kurtosis. Just above this limit, restrictive barriers cause the diffusion PDF to deviate from a Gaussian, causing increased apparent kurtosis. Decreases in kurtosis at long TD_eff have been observed previously (36), but increases at very short TD_eff have, until now, only been predicted by mathematical models and simulations (22,37).

Combining the short time growth and long time reduction in kurtosis suggests that K_app should have a maximum at some intermediate value of the diffusion time (22). In this study, this observation was not confirmed due to disagreement between OGSE and PGSE kurtosis measurements with similar effective diffusion times. This inconsistency could be inferred from the divergence of the decay curves shown in Figure 8 at high b-values (b>1 ms/μm²).

A potential explanation for this discrepancy is the difference between the gradient spectra, F(ω), of OGSE and PGSE measurements. For apodized cosine OGSE acquisitions, F(ω) consists of peaks positioned roughly at the waveform oscillation frequency, ±ω (Figure 7a). For PGSE, the spectrum approximates a sinc function centered at ω=0, which broadens with decreasing diffusion time (Figure 7b). The peak of the PGSE spectrum always coincides with the minimum in the restricted diffusion spectrum, D(ω). This suggests that, no matter how short the diffusion time, PGSE measurements always retain some sensitivity to restriction, which could lead to increased apparent kurtosis.

The Gaussian phase approximation may be more valid for OGSE than for PGSE. OGSE acquisitions use an oscillating gradient with many periods, over which the b-value accumulates. Individual periods thus induce a small loss of phase coherence and these accumulate to generate the overall signal attenuation (38). As noted by Callaghan: “it is precisely under these cumulatively averaging conditions that the central limit theorem suggests the likelihood of a Gaussian phase distribution” (38). In contrast, the signal attenuation in a PGSE experiment is induced by a single pair of gradient pulses which are often high in amplitude, particularly when the diffusion time is short. This may result in greater sensitivity to non-Gaussian diffusion, which can contribute to the increased kurtosis of PGSE measurements.

To test the effects of non-Gaussian diffusion on OGSE and PGSE measurements, we ran a Monte-Carlo simulation of particles restricted between infinite, impermeable parallel planes. It is well known that simple barriers cause the diffusion probability distribution to deviate from a Gaussian and can lead to non mono-exponential diffusion decay (39). In the simulation, the free self-diffusion coefficient was set to D_free=1.0 μm²/ms and the plane spacing, d, was varied from 1–10 μm. The simulation was used to calculate the diffusion-decayed signal for all of the diffusion gradient waveforms used in this study (PGSE/OGSE, b=0–3.2 ms/μm² - see methods section). To determine the kurtosis and the ADC, the simulated, diffusion-decayed signal (as a function of b-value) for each diffusion time, frequency and plane spacing was fit to eq. [14].

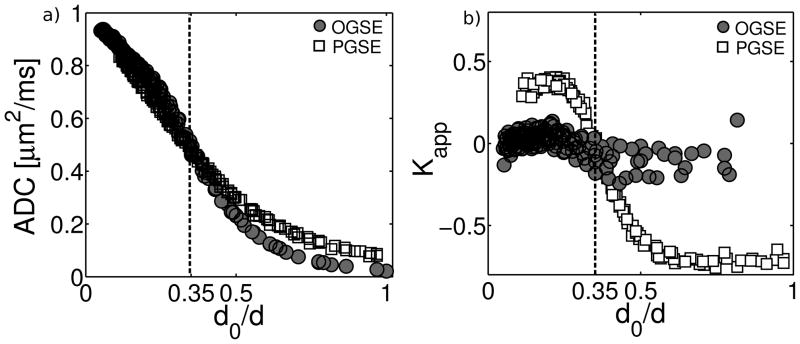
The results of the Monte-Carlo simulation are shown in Figure 9. The ADC (Fig. 9a) and apparent kurtosis (Fig 9b) values are plotted as a function of the quantity d₀/d, a ratio of the characteristic diffusion distance, d₀=(D_free·TD_eff)^1/2 to the plane spacing, d (39). Across the entire range of d₀/d, the kurtosis values for OGSE simulations were much closer to zero than their PGSE counterparts. This confirms that the Gaussian phase approximation is more appropriate for OGSE experiments than for PGSE.

Figure 9.

ADC (a) and kurtosis (b) estimates obtained from Monte-Carlo simulations of diffusion between infinite, impermeable parallel planes. The free diffusion coefficient was set to D_free=1.0 μm²/ms and the plane spacing, d, was varied from 1–10 μm. Simulations were conducted for all the experimental diffusion gradient waveforms used in this study (see methods section).

Each data point represents a simulation with a unique combination of d and gradient waveform. OGSE and PGSE simulations are indicated by circles and squares, respectively. Data are plotted vs. d₀/d: the ratio of the characteristic diffusion distance, d₀=(D_free· TD_eff)^1/2,to the plane spacing. For d₀/d<0.35 (dashed line), simulations predict results similar to experimental observations (i.e. similar ADC values, but kurtosis is positive and higher for PGSE).

The Monte-Carlo simulation predicted results similar to our experimental observations when the effective diffusion time was sufficiently short that d₀ was less than ~1/3 of the plane distance (i.e. d₀/d<0.35). Under these conditions, PGSE- and OGSE-derived ADC estimates are similar, but PGSE kurtosis estimates are positive and higher than their OGSE counterparts. To investigate how this relates to the experimental circumstances, the condition, d₀/d<0.35 was tested on the fitted PPM parameters (see Table 1). Based on the estimates of D_free and d in the stratum radiatum, stratum oriens, and stratum pyramidale, the condition was fulfilled for TD_eff < 0.3 ms, 0.1 ms, and 1.7 ms, respectively. Comparing these values to the experimental PGSE diffusion times suggests that the condition applied only to measurements in the stratum pyramidale at the two shortest values of TD_eff (1.46 ms, 1.2 ms).

According to the comparison above, the vast majority of experimental PGSE measurements were in the regime where simulations predict negative kurtosis, indicating that the diffusion probability distribution was more sharply peaked than a Gaussian (23). However, negative kurtosis was not observed experimentally. This may be because, unlike the parallel plane model, biological tissues contain a broad distribution of restricted sizes and scales, for which estimates of D_free and d represent only a weighted average. In less restricted tissue compartments, the condition d₀/d<0.35 may have been fulfilled. Therefore, we cannot rule out the contribution of simple restriction (and its distinct effects on OGSE and PGSE measurements) to the observed discrepancy in kurtosis.

The presence of exchange between different tissue compartments may also contribute to the kurtosis differences. Unlike a PGSE sequence, OGSE acquisitions consist of several concatenated diffusion weighting periods. Although the diffusion time for each individual period is short, spins can migrate between compartments over multiple periods. In the fast exchange limit, where spins spend each period within a different compartment, the diffusion curve will decay mono-exponentially at a rate equal to the average short-time diffusion coefficient, weighted by compartment size (5).

While the OGSE and PGSE experiments shown in Figure 8 had similar diffusion times, they may have probed different exchange regimes. The exchange regime (i.e. fast or slow) probed by OGSE depends on the rate of spin migration between compartments (exchange rate) and the number and duration of OGSE diffusion weighting periods. To test this hypothesis, we simulated the effects of exchange during multiple diffusion weighting periods (with short TD_eff) using the modified Bloch equations proposed by Karger (40). Following Karger’s method, the effects of diffusion were modeled by a diffusion decay rate constant, R_diff:

$$R_{\mathit{diff}}=\frac{b}{{TD}_{\mathit{eff}}}·\mathit{ADC}$$ [17]

For OGSE experiments with a pair of oscillating gradients (each of duration T and period N), the gradient strength is reduced by a factor N_total= 2N and the overall b-value accumulates over N_total weighting periods. The decay rate for a single period is thus given by R_diff/N_total. Assuming two compartments (A and B) coupled by the exchange rate k_AB, the magnetization during each period is described by the following pair of differential equations:

$$\frac{{dM}_A}{dt}=-\left(R_{\mathit{diff}}/N_{\mathit{total}}-k_{AB}\right)M_A+k_{BA}{M}_B$$ [18]

$$\frac{{dM}_B}{dt}=-\left(R_{\mathit{diff}}/N_{\mathit{total}}-k_{BA}\right)M_B+k_{AB}{M}_A$$ [19]

with the equilibrium condition:

$$k_{AB}{M}_A(0)=k_{BA}{M}_B(0)$$ [20]

To propagate through multiple periods, the differential equations were solved with the final conditions for one period serving as initial conditions for the subsequent one. The measured signal, S(b), is the sum of the magnetizations M_A and M_B. Before proceeding, it should be noted that this description may be helpful in interpretation, but is oversimplified: it only considers two compartments, neglects relaxation effects, and does not account for the broadening of F(ω) which occurs when N_total is reduced. Furthermore, the Karger does not account for the geometric organization of the tissue (37), as it allows particles to change compartments without consideration of the boundaries or interfaces between them and how these can affect diffusion.

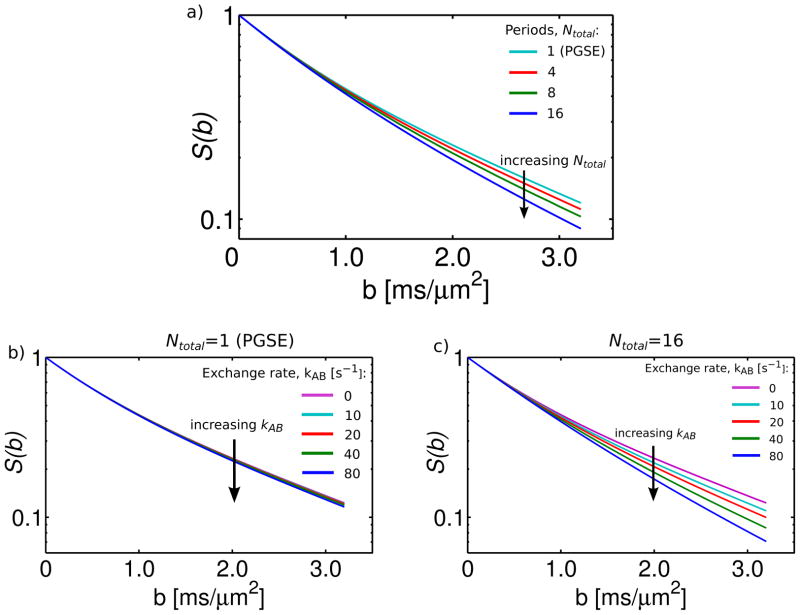
Simulation parameters were similar to those obtained for in-vitro bovine optic nerve (31). Compartments A and B refer to the intra- and extracellular spaces, respectively: ADC_A=0.5 μm²/ms, ADC_B=1.7 μm²/ms, M_A(0)/M_B(0)=0.6/0.4, k_AB=33 s⁻¹. The effective diffusion time was 1.5 ms (c.f. Figure 8b). The value for the intracellular ADC is considerably lower than the free diffusion coefficient of 1.3 um²/ms, which was reported in (31). This value was reduced to simulate the restrictive effects of the ~2 μm axon diameter at TD_eff=1.5 ms.

The results of the simulation are shown in Figure 10. Figure 10a plots the normalized signal, S(b)/S₀, vs. b-value for a variable number of diffusion weighting periods (N_total=1,4,8,16). The curve labeled N_total=1 is comparable (in terms of exchange) to a PGSE sequence, which has only a single diffusion weighting period. The curve labeled N_total=4 corresponds to the OGSE experiment in Figure 8b, which included a pair of cosine waveforms with 2 periods each. The results of the simulation are similar to our experimental observations. In particular, increases in N_total did not affect the initial slope of the diffusion decay curve, but resulted in visible signal decreases at high b-value and reduced kurtosis.

Figure 10.

Simulation of the effect of exchange between two compartments (A and B) during multiple diffusion weighting periods. a) Normalized signal vs. b-value for a variable number of diffusion weighting periods (N_total=1,4,8,16). Simulation parameters included: ADC_A/ADC_B=0.5/1.7 μm²/ms, M_A(0)/M_B(0)=0.6/0.4, k_AB=33 s⁻¹. (b,c) Normalized signal vs. b-value for N_total=1 (b) and N_total=16 (c) and variable exchange rate (k_AB=0, 10, 20, 40, 80 s⁻¹). Note that simulations with N_total=1 are comparable (in terms of exchange) to PGSE, as it only has a single diffusion weighting period.

The effects of exchange in our study were likely even more significant than Figure 9a suggests, as it was performed on fixed tissue. In a study which used a two-compartment tissue model to describe diffusion in cortical tissue specimens, tissue fixation was shown to increase the inter-compartmental exchange rate by over 200% (26). Figure 10b-c simulates the effect of varying the exchange rate (k_AB=0, 10, 20, 40, 80 s⁻¹) on data acquired with N_total=1(Fig. 9b) and N_total=16 (Fig. 9c). With N_total=1 (PGSE), varying the exchange rate had little effect on the decay curves. With N_total=16, increasing the exchange rate resulted in faster decay with reduced kurtosis, as the experiment approached the fast exchange regime.

Conclusion

This work presents the results of pulsed and oscillating gradient diffusion measurements with combinations of short effective diffusion time/high frequency and high b-value. In addition to confirming previously published results, this study provides new insight into the comparability of these distinct measurement techniques. The observed temporal (and frequency) dependence of the ADC is similar to that reported in previous studies (11,18). Like in other investigations (10–12,16), the variation in ADC with diffusion time provided important information about tissue microstructure at a scale far smaller than the image resolution.

Novel findings include the differences in OGSE and PGSE estimates of the apparent kurtosis, K_app. Measurements of K_app obtained from OGSE were consistently lower than those obtained from PGSE experiments with similar diffusion times. As confirmed by Monte-Carlo simulations, this may be caused by heightened sensitivity of PGSE measurements to non-Gaussian diffusion. Unlike PGSE, OGSE methods use oscillating gradient waveforms with low amplitudes and long durations, making them better suited to the Gaussian Phase Approximation. The kurtosis discrepancy may also be attributed to exchange between tissue compartments, which occurs over multiple OGSE diffusion weighting periods. This makes it possible for short-time OGSE and PGSE measurements to probe different exchange regimes. These fundamental distinctions between oscillating and pulsed gradient techniques should be recognized and accounted for in the interpretation of experimental data and the development of mathematical models.

The consistency of OGSE and PGSE data with similar effective diffusion time at low b-value (b<1 ms/um²) is encouraging. This greatly simplifies the comparison of conventional ADC measurements obtained using these two methods. At low b, OGSE and PGSE can be viewed as complementary techniques; OGSE measurements at short, sub-millisecond diffusion times and PGSE measurements at intermediate and long diffusion times can be combined to probe a broad range of restrictive scales. At higher b-values, where sensitivity to restriction and exchange increases, the situation becomes more complex: OGSE and PGSE measurements with similar TD_eff do not agree, as the effective diffusion time is no longer an adequate description for the measurement.