Cerebral blood volume changes during brain activation

Abstract

Cerebral blood volume (CBV) changes significantly with brain activation, whether measured using positron emission tomography, functional magnetic resonance imaging (fMRI), or optical microscopy. If cerebral vessels are considered to be impermeable, the contents of the skull incompressible, and the skull itself inextensible, task- and hypercapnia-related changes of CBV could produce intolerable changes of intracranial pressure. Because it is becoming clear that CBV may be useful as a well-localized marker of neural activity changes, a resolution of this apparent paradox is needed. We have explored the idea that much of the change in CBV is facilitated by exchange of water between capillaries and surrounding tissue. To this end, we developed a novel hemodynamic boundary-value model and found approximate solutions using a numerical algorithm. We also constructed a macroscopic experimental model of a single capillary to provide biophysical insight. Both experiment and theory model capillary membranes as elastic and permeable. For a realistic change of input pressure, a relative pipe volume change of 21±5% was observed when using the experimental setup, compared with the value of approximately 17±1% when this quantity was calculated from the mathematical model. Volume, axial flow, and pressure changes are in the expected range.

Introduction

Recently, magnetic resonance imaging (MRI) studies of human brain function have begun to investigate changes in cerebral blood volume (CBV) (Herman et al, 2009; Kim and Kim, 2005; Lu et al, 2003; Stefanovic and Pike, 2005) in addition to the well-accepted blood oxygen level-dependent (BOLD) contrast methods. Cerebral blood volume has been measured as blood plasma volume via blood pool contrast agents (Leite et al, 2002; Zhao et al, 2001), total volume of intravascular blood via the vascular space occupancy method (Lu et al, 2003; Poser and Norris, 2011), or volume of hemoglobin via optical techniques (Devor et al, 2008; Hudetz, 1997; Kennerley et al, 2005). In addition, there are techniques that focus on volume measurement of the arterial (Donahue et al, 2010; Kim and Kim, 2005; Kim and Kim, 2011) or the venous (Stefanovic and Pike, 2005) compartment of cerebral blood vessels. Although such techniques show arterial or venous volume weighting in estimating CBV, some partial volume effects with the other compartment cannot be excluded. Activation-related time-course changes in CBV, determined using each method, have been compared with the corresponding BOLD time courses that have led to an improved understanding of the latter (Buxton et al, 1998; Frahm et al, 2008; Mandeville et al, 1999). However, the concept of CBV itself has received surprisingly little analysis. Because of inconsistent and partly incomparable results from the methods outlined above (Berwick et al, 2005; Hoge et al, 2005), this lack of understanding has become a matter of increasing concern.

The methods outlined above measure different blood components (total blood volume, hemoglobin volume, blood plasma volume) or show a compartmental weighting (venules, capillaries, arterioles). Thus, each technique could in principle show a different time course during brain activation (Pawlik et al, 1981). However, experiments typically show parallel volume changes in total blood volume, hemoglobin volume, and plasma volume. There is an ongoing debate about the exact compartmental distribution of blood volume and its changes during neuronal stimulation or vasoactive modulation. Classic hemodynamic models have assumed that changes of CBV are dominated by the venous side (Mandeville et al, 1999). In contrast, recent studies attribute the largest fractional response to arterial CBV (Chen and Pike, 2009; Griffeth and Buxton, 2011; Hillman et al, 2007; Kim et al, 2007; Lee et al, 2001; Zhao et al, 2007). It should be noted that oxygen extraction also takes place in arterioles (Buxton, 2010; Vazquez et al, 2010) and is thus an additional source of BOLD signal. However, capillary contributions to CBV changes are often disregarded (Buxton et al, 1998; Hoge et al, 1999; Kong et al, 2004; Lee et al, 2001; Lorthois et al, 2011a, 2011b; Zheng et al, 2005), although there is evidence that cerebral capillaries expand significantly during functional stimulation (Piechnik et al, 2008). Optical studies support these findings (Devor et al, 2007, 2008; Duelli and Kuschinsky, 1993; Fernandez-Klett et al, 2010; Hillman et al, 2007; Hudetz, 1997; Kleinfeld et al, 1998; Peppiatt et al, 2006; Tian et al, 2010) and quantify typical capillary volume changes during neuronal stimulation as approximately 20% (Stefanovic et al, 2008). Hypercapnia-related capillary volume changes under physiologic conditions show similar findings (Villringer et al, 1994). Although most results are based on animal studies using high CO₂ content (Chiarelli et al, 2007), even higher CO₂ content has been used in human studies (Feihl and Perret, 1994; Gauthier et al, 2011). The optically observed time courses of capillary volume changes (Hillman et al, 2007; Tian et al, 2010) are comparable to those measured via MRI (Kim et al, 2007; Lu et al, 2003). Consequently, capillary volume changes might have a larger contribution to blood volume changes than usually assumed, especially since expansion of larger arteries has little effect on BOLD MR signal, and the diameter of pial veins appears to be affected very little by state of activation of underlying neural tissue (Berwick et al, 2005; Drew et al, 2011; Hillman et al, 2007).

Now, the key question is: How can cerebral capillaries expand to this presumed extent inside the rigid cranium, without dangerously increasing the intracranial pressure (ICP)? According to the Monro–Kellie doctrine, the sum of CBV, cerebrospinal fluid volume, and brain tissue volume must remain constant over time, to minimize changes of ICP (Mokri, 2001). This statement is based on the inextensibility of the skull. An increase of one compartment can only occur by the decrease of another (Knapp, 2005; Ursino and Lodi, 1997). To take a specific example, a typical visual stimulation might lead to CBV changes of 3 mL per 100 mL tissue (Ito et al, 2001; Lu et al, 2003; Pears et al, 2003; Wu et al, 2007). Under the assumption that at least one-third of this CBV change is based on capillary volume changes (Piechnik et al, 2008; Stefanovic et al, 2008) room for an additional 1 ml of blood must be found within the cerebrospinal cavity. The spinal canal is a potential candidate, but realistic modeling shows that it cannot easily accommodate such a volume change (Ursino and Lodi, 1997). The change in ICP when 1 mL cerebrospinal fluid substitute is injected into the brain has been modeled. The results suggest that even such a small volume increase can lead to an increase in ICP by 15%. Such a change could initiate a positive feedback loop of intracranial volume increase, leading eventually to cerebral ischemia (Girouard and Iadecola, 2006). If the Ursino injection experiment fairly represents the mechanism of blood volume change during functional brain activation, the existing models for activation-related changes in CBV (Buxton et al, 1998; Mandeville et al, 1999) would be implausible.

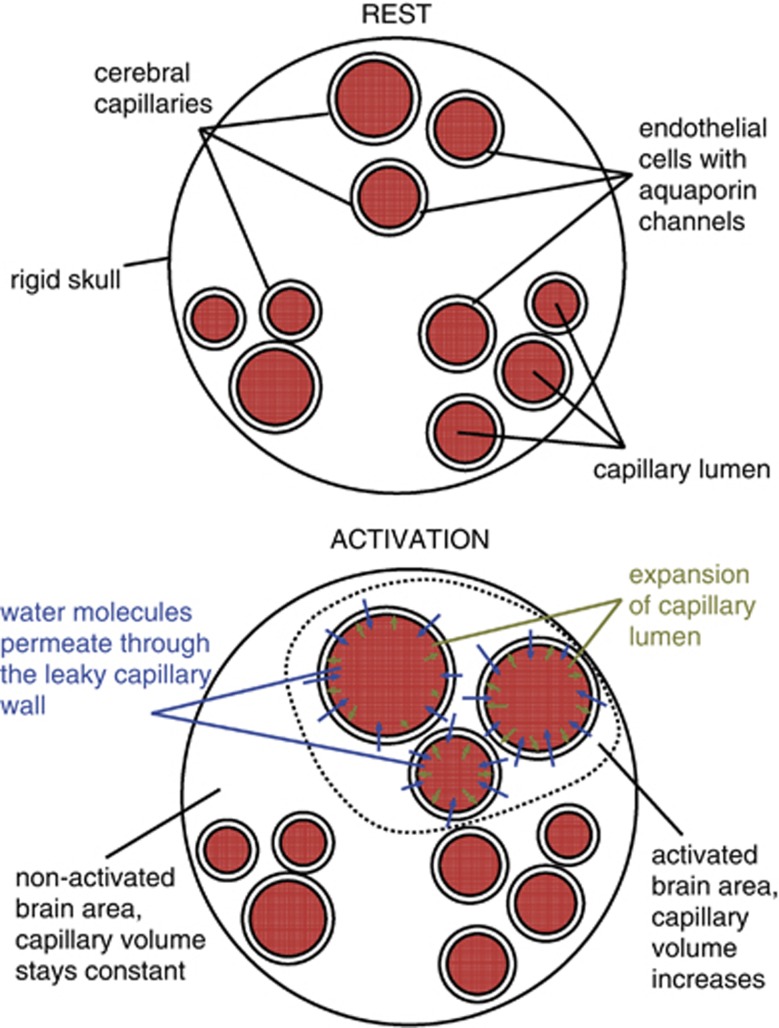
A fundamental property of the smallest blood vessels, particularly capillaries, may play an important role in avoiding undesirable changes in ICP. Cerebral capillary walls form the blood–brain barrier, which protects brain tissue from harmful substances inside the blood. However, the blood–brain barrier consists of elastic endothelial cells that, because of aquaporin channels, are known to be very leaky to water (Lennon et al, 2005). Approximately 80% of the water entering the capillary bed is extracted into the tissue (Ginsberg et al, 1985) before it enters a draining venule. Could capillary porosity (see Figure 1) account for the smallness of changes in ICP that have been measured (Asgari et al, 2010) in hypercapnia? Although this concept has already been introduced in recent years (Buxton, 2009; Turner and Thomas, 2006), it has yet to receive a thorough biophysical analysis.

Figure 1.

During neuronal activation, water permeates through the capillary wall to keep the total brain volume constant.

To explore the biophysics of changes in CBV, we have developed a new hemodynamic boundary-value model, which takes into account the elastic as well as the permeability properties of a capillary wall. The Monro–Kellie doctrine is respected, that is to say, there is no change in total volume during capillary volume changes. The model is solved via a numerical compartmental method. It uses Darcy's law, describing the filtration process through the capillary membrane and takes account of pressure changes in the cavity and the tube. As a physical counterpart, we have constructed a simple macroscopic model that simulates several of the known features of capillaries in the tissue. It consists of a water-filled cylindrical cavity with rigid walls, which represents the cranium. Water is guided through this cavity through an elastic tube. This tube is perforated to simulate water permeability of the blood–brain barrier. Water exchange through the tube wall is studied, as well as pressure and volume effects during activation processes. New insights into the processes taking place during blood flow in cerebral capillaries are provided.

Materials and methods

The Boundary-Value Model

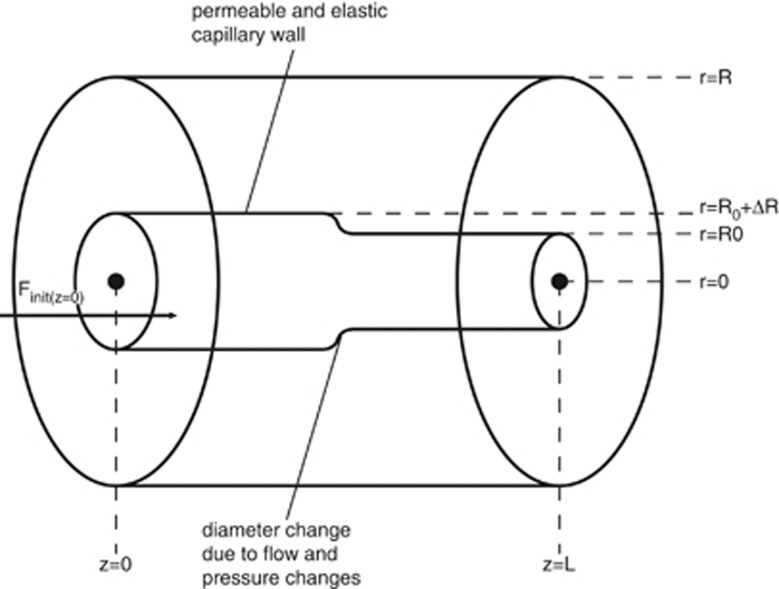
The model presented relies on the fundamental hydrodynamical equations, namely the Navier–Stokes equations and the continuity equation. In addition, an elastic differential equation models the motion of the capillary wall. Because a general solution of these coupled nonlinear partial differential equations has not yet been found, we have formulated a numerical approximation. A diagram of the theoretical as well as the experimental setup can be found in Figure 2.

Figure 2.

Diagram of the theoretical and experimental setup. Flow direction is from left to right.

Blood is modeled as an incompressible homogeneous fluid and described using the incompressible Navier–Stokes equations in cylindrical coordinates (equations (1) and (2)). We assume the flow to be irrotational, and consequently to have no tangential velocity. In addition, no change of velocity in this direction is expected. Gravity effects are neglected because of the small capillary length and diameter

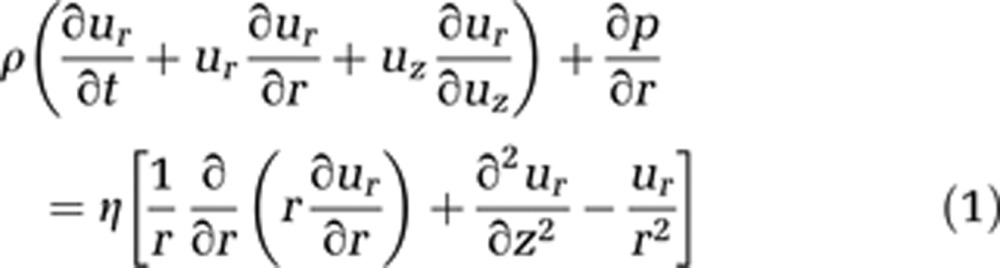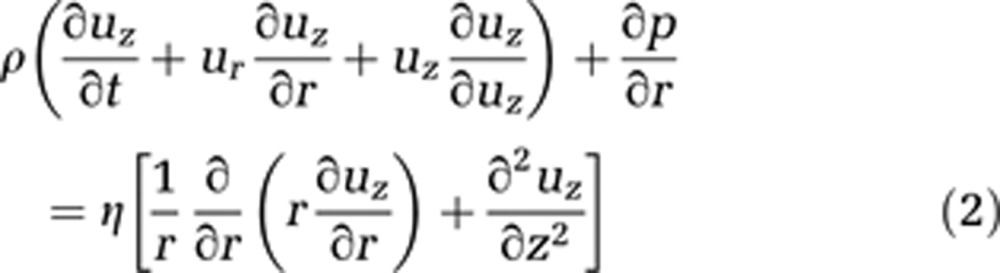where u_r stands for the radial and u_z for the axial velocity component. Both depend on time t, z, and r, where r is the radius and z the flow axis, η represents the dynamic viscosity, and p is the pressure.

In addition, the continuity equation must be used in cylindrical coordinates  

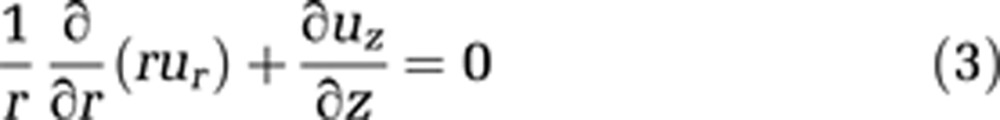To make use of the cylindrical coordinate system, the cranium is also modeled as a cylinder. This geometry as well as capillary wall permeability is defined via boundary conditions 4, 5, and 6:

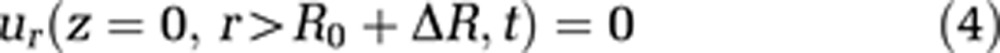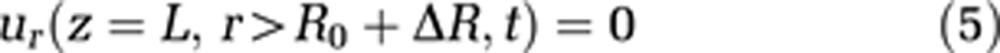where L stands for the total length of the capillary and the cavity, and R represents the radius of the external cavity. R₀ is a reference radius and ΔR the radius change of the capillary, and consequently R₀+ΔR is the capillary radius. We assume the velocity component parallel to the cavity wall at the cavity wall to be zero (no-slip condition, equation (7))

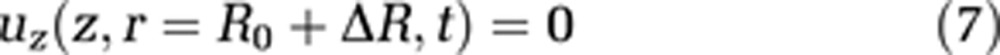To quantify the permeation through the capillary wall, we use Darcy's law, extended by inclusion of the difference of internal osmotic pressure π_i and external osmotic pressure π_e (see equation (8)). k is the permeability constant and s represents the capillary wall thickness; p_i is the pressure inside the capillary and p_e is the extravascular pressure

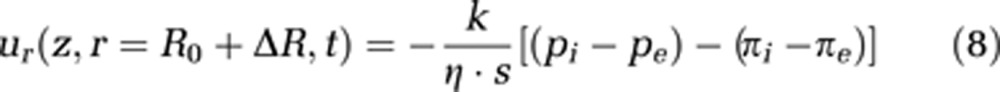Blood movement through capillaries is slow, which implies a low Reynolds number. To a first approximation, we assume the flow to be laminar (see equations (9) and (10)). In reality, the unusual rheological properties of blood result largely in plug flow, in capillaries, which are often slightly smaller than the diameter of a red cell. Red blood cells squeeze through the capillary, sometimes as rouleaux of adjacent red cells, but in general red cells are separated from each other by plasma. Within these plasma volumes, we may assume the flow to be laminar

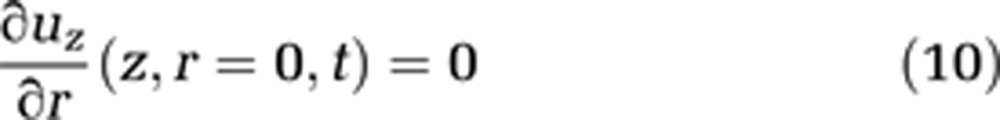In addition, a specific value for the pressure at the arterial part of the capillary end has to be set (see equation (11)). The pressure at the venous end of the capillary can then be calculated by the pressure loss because of the capillary length

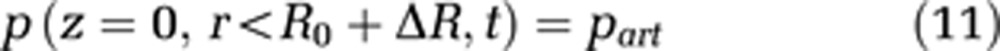The displacement of the capillary wall is described via a Newtonian ansatz, which leads to the following equation of motion for the capillary wall

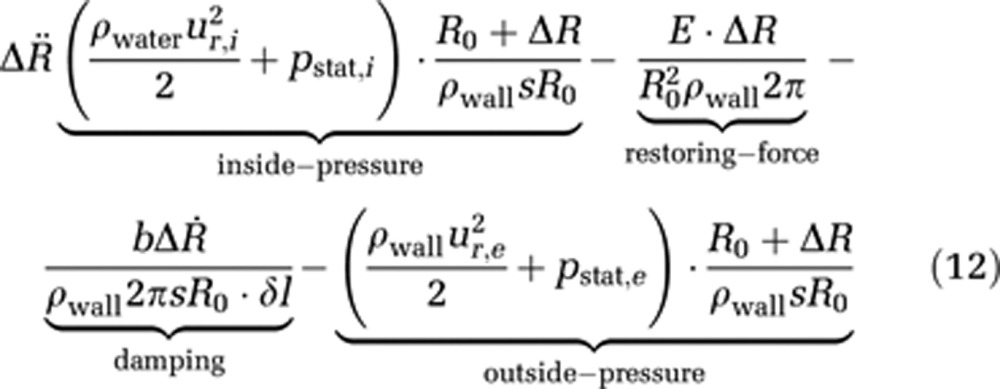where ρ_water and ρ_wall represent the water and wall mass density, u_r,i the radial velocity at (r=R₀+ΔR) within the capillary and u_r,e the radial velocity at (r=R₀+ΔR) outside of the capillary, p_stat,i and p_stat,e are the hydrostatic pressures within and outside the capillary, respectively, R₀ is the reference radius at t=0, ΔR represents the radius change and Δl stands for an infinitesimal length, for which the force is calculated; s is the wall thickness and E is Young's modulus, which describes the elastic properties of a material. Finally, b is a damping constant.

This equation of wall motion consists of four parts: the hydrostatic and hydrodynamic pressure inside and outside of the capillary, which produce a force acting perpendicular to the capillary wall; a restoring force because of the wall's elasticity, described via Hooke's law; and finally damping of the wall movement is implemented via the damping constant b.

The set of coupled equations (1), (2), (3) and (12) together with the boundary conditions from 4 to 11 models permeable elastic tube flow within an external rigid cavity and can thus lead to a better understanding of changes in cerebral capillary volume.

Approximation: The Compartment Model

To obtain easily interpretable results that allow a qualitative and quantitative evaluation of the inclusion of capillary wall permeability within a physiologic model, the boundary-value model is transformed into a compartment model. The capillary length is divided into 100 compartments, for which the descriptive equations are solved separately. This number of compartments was estimated as the best compromise between calculation time and spatial resolution. The flow and pressure values of the preceding compartment (i−1) are used to feed the next one (i). The radius change and its derivatives and the pressure expressions are thus replaced by its discretized equivalents

When assuming an average capillary flow velocity of u_r,i=1 mm/second, we obtain a hydrodynamic pressure of p_dyn=ρ_water × u²_r,e/2=5 × 10⁻⁴ Pa, which is about seven orders of magnitude smaller than a reasonable hydrostatic capillary pressure of p_stat=30 mm Hg=4,000 Pa. Together with the assumption of nonchanging ICP during activation processes, the internal and external pressure can be expressed as a resulting pressure p_res(i,t). The discretized equation of wall motion becomes

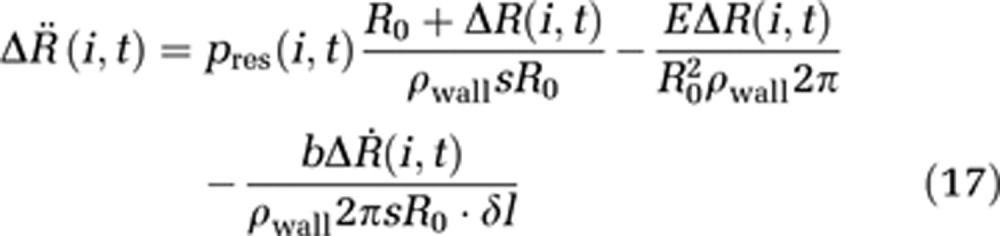Note that δl is now the length of one compartment instead of an infinitesimal length in the boundary-value model. Conservation of energy is obtained by defining the additional boundary condition

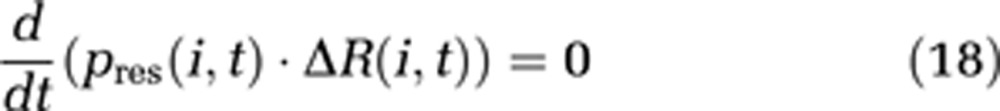This condition replaces the continuity equation (3) in our model.

For solving equations for each compartment, appropriate initial values for t=0 are required. p_init(i) for each compartment is estimated via Hagen–Poisseuille's law, which is applicable because of the small compartment diameter compared with the capillary length.

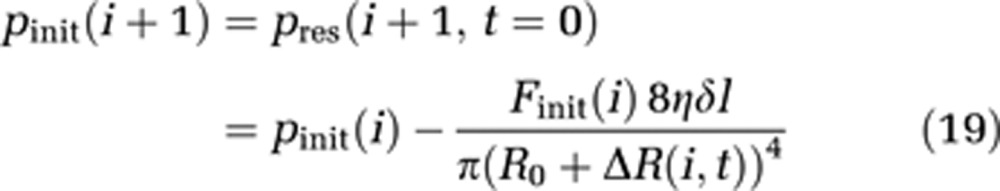Furthermore, the initial flow F_init(i) of each compartment is estimated by equation (20), which is the discretized expression of equation (8). L_p is the hydraulic conductivity, a measure of the capillary wall permeability.

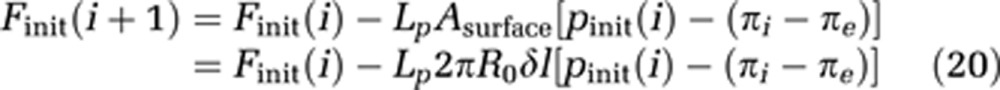The starting values for the radius displacement and its first derivative in time are 10⁻⁷ m and 0. The reference radius R₀=3.5 × 10⁻⁶ m (Hauck et al, 2004).

With the set of equations (17), (18), (19), (20), two different levels of brain activation have been simulated. Each compartment is calculated separately, while the preceding compartment feeds the next. Mathworks Matlab algorithm ode15 (Mathworks, Natick, MA, USA) was used to solve the coupled differential equations (17) and (18). The parameters assumed for the calculations are listed in Table 1. The capillary wall includes a single layer of endothelial cells (Farkas et al, 2001), and thus its thickness is assumed to be in the range of the typical thickness of a cerebral endothelial cell (Mathur et al, 2001). In the absence of literature values, we assumed that the capillary wall mass density is similar to that of water and the damping constant has a value typical for a damped oscillator. The flow parameters for the activation levels were estimated via the Hagen–Poiseuille law relating the pressure decrements (Schmidt and Thews, 1997), dynamic viscosity (Karbowski, 2011; Schmidt and Thews, 1997), typical capillary length, and the typical capillary radius (Duelli and Kuschinsky, 1993; Hudetz, 1997; Vetterlein et al, 1990; Villringer et al, 1994). The capillary length assumed in our work is based on typical transit times of 0.5 to 1.5 seconds (Hudetz et al, 1994; Hudetz, 1997) and capillary flow velocities of 0.5 to 1.5 mm/second (Hauck et al, 2004; Hudetz, 1997; Kleinfeld et al, 1998; Stefanovic et al, 2008; Villringer et al, 1994). Such a total length generally comprises several much shorter connected capillary segments, but for the sake of modeling we have assumed that the pressure drops and flow rates will be similar in a single equivalent capillary. The calculated flow increase from levels 1 to 2 of approximately 50% is comparable to CBF measurements based on ASL functional (fMRI) techniques (Ances et al, 2008; Donahue et al, 2009; Hernandez-Garcia, 2004; Hoge et al, 2005; Pike, 2011). Activation level 1 is chosen such that it matches commonly measured CBF changes during mild hypercapnia or low-intensity neuronal stimulation. Activation level 2 is therefore related to high-intensity stimulation, such as visual stimuli via flickering checkerboards (Pike, 2011).

Table 1. Parameters used by the compartment model.

Parameter	Description	Value
s	Capillary wall thickness	0.5 × 10−6 m
E	Young's modulus	3 × 105 N/m2
ρwall	Capillary wall mass density	1,000 kg/m3
R0	Capillary reference radius	3.5 × 10−6 m
Lp	Hydraulic conductivity	1.5 × 10−7 cm/s/cmH2O
η	Dynamic viscosity	5 kg/m/s
δl	Compartment length	10−5 m
b	Damping constant	0.5 kg/m2/s
πi	Internal osmotic pressure	25 mm Hg
πe	External osmotic pressure	5 mm Hg
Finit(i=1)	Initial inflow of 1st and 2nd activation level	8.4 × 10−17 m3/s; 12.5 × 10−17 m3/s
pinit(i=1)	Initial pressure of 1st and 2nd activation level	30 mm Hg; 35 mm Hg

The Experimental Setup

A thin elastic cylindrical balloon made of rubber was used to simulate a single capillary. The balloon, running between two rigid nozzles, was mounted inside a water-tight rigid cylindrical cavity constructed of Perspex, which represents the rigid skull. Connection of one of the nozzles to a reservoir allowed water to flow through the balloon with a well-defined pressure head. The cylindrical cavity is watertight, and its Perspex construction means that very little expansion can take place, even at high internal pressures. Only the ring gaskets at the inlets provide a possibility for volume expansion. This possible volume change is relevant when calculating the balloon volume changes of the different experiments. The rigid nozzles on which the balloon is mounted can be regarded as the arterioles and venules, which define the pressure difference and axial flow velocity. For simplicity, we assume that the flow behavior of a capillary depends on the boundary conditions defined by the supplying arteries, although in reality the effect of pericytes, which surround the capillary membrane, should also be considered. For all experiments, two activation stages with different arterial pressures and volumetric inflow were applied. Recordings were performed by a video camera (Canon Legria HF S10, 8 Megapixel, 0.3 lx min. lux rating). The balloon diameter was plotted for each position z to obtain a diameter profile of the balloon. When the diameter profiles from two activation stages were subtracted from each other, a profile of diameter change could be calculated (compare Figure 5). Three experiments and two test cases were performed. Standard deviations were obtained by repeating each experiment 10 times. Experimental details and parameters can be found in Tables 2 and 3. A brief description of the test cases can be found in the next paragraph.

Table 2. Balloon experiments performed.

Experiment	Cavity	Balloon	Fluid
1	Empty	Non-permeable	Water
2	Water	Non-permeable	Water
3a	Water	Permeable	Water
3b	Water	Permeable	Ink

Table 3. Experimental parameters.

Parameter	Description	Value
Lb	Balloon length	250 mm
R0	Undistended balloon radius	2.0 mm
Lc	Rigid cavity length	250 mm
Rc	Rigid cavity internal radius	140 mm
q	Balloon permeability	10 holes/cm2
pinit(z=0)	Arterial pressure of 1st and 2nd activation level	30±5 cmH2O; 60±5 cmH2O
Finit(z=0)	Arterial inflow of 1st and 2nd activation level	400±50 mL/min; 700±50 mL/min

Similar to aquaporin channels in capillary walls, the balloon perforations provide a fast water exchange between the intracapillary and extracapillary space. For the experiment to match the physiologic relationship between the size of aquaporin channels and typical capillary dimensions, an elastic permeable tube with a length of several hundred meters would be required. Thus, this experiment can provide primarily a qualitative insight into the mechanisms of blood volume changes within a constant bulk volume.

To quantify the effect of water compressibility, an initial experiment was performed with a balloon that had no outlet. The balloon was filled with water, driven by an inlet pressure of 60 cmH₂O. Expansion of the balloon could only occur by (1) water compression, (2) compression of the bubbles inside the water, or (3) cavity expansion. This experiment tested possibilities (2) and (3). The second test case was performed with the same arrangement as in the first test case, but with an additional air-filled balloon inside the cavity. The diameter of this balloon indicates pressure changes within the cavity. Size changes in both balloons are observed during pressure changes to the balloon connected to the water reservoir.

Results

Theoretical Compartment Model

Figures 3 and 4 show the results derived from the compartment model for activation level 1 with F_init(i=1)=8.4 × 10⁻¹⁷ m³/second and p_init(i=1)=30 mm Hg and activation level 2 with F_init(i=1)=12.5 × 10⁻¹⁷ m³/second and p_init(i=1)=35 mm Hg. The initial radius was defined as 3.6 μm.

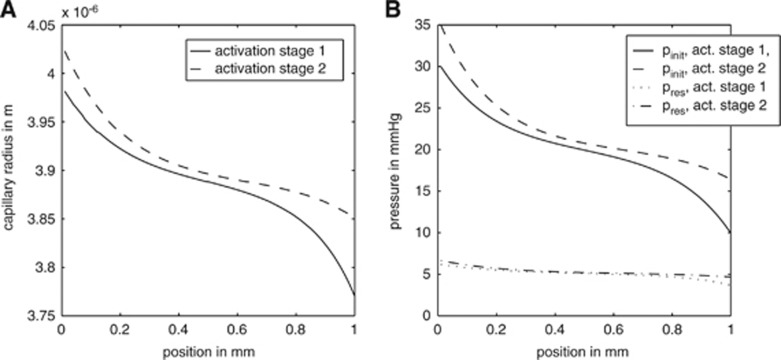
Figure 3.

The capillary radius (A) and pressure (B) distribution along the z axis based on the compartment model. Activation stage I: F_init(i=1)=8.9 × 10⁻¹⁷ m³/second and p_init(i=1)=30 mm Hg; activation stage II: F_init(i=1)=12.5 × 10⁻¹⁷ m³/second and p_init(i=1)=35 mm Hg. p_init(i) and F_init(i) stand for the initial pressure and flow, whereas p_res represents the resulting pressure.

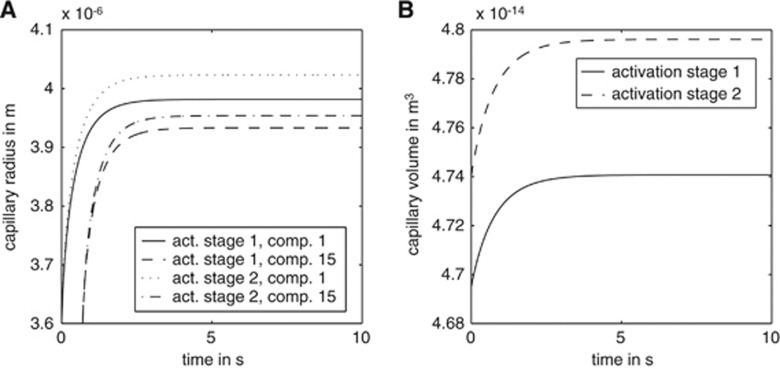
Figure 4.

The time courses of capillary radius changes (A) and capillary volume changes (B) based on the compartment model. Panel A shows plots for different compartments (comp.). Activation stage I: F_init(i=1)=8.9 × 10⁻¹⁷ m³/second and p_init(i=1)=30 mm Hg; activation stage II: F_init(i=1)=12.5 × 10⁻¹⁷ m³/second and p_init(i=1)=35 mm Hg. p_init(i) and F_init(i) stand for the initial pressure and flow.

Capillary radius and volume during activation: The radius change resembles a damped oscillator with an external force. For both activation levels, the time constant is approximately 3 seconds (compare Figure 4A). Once equilibrium is reached, the radius decreases continuously along the length of the capillary, so that for both activation levels the radius at the venous end (z=L) of the capillary is smaller than that at the arterial end (z=0). For p_init(i=1)=30 mm Hg, the radius at z=0 is 3.98 μm, decreasing to 3.77 μm at z=L. This is an absolute decrease of 0.21 μm, a relative decrease of 5.2%. The difference in radius from the arterial end of the capillary to its middle is 0.11 μm, and the radius difference between compartment number 50 and the venous end is 0.10 μm (Figure 3A). In the second activation scenario, where p_init(i=1)=35 mm Hg, the capillary radius decreases from 4.02 μm at z=0 to 3.85 μm at z=L in equilibrium. This absolute radius difference of 0.17 μm implies a relative change of 4.2%. The radius difference between compartment number one and compartment number 50 is 0.12 μm, while the difference between number 50 and number 100 is 0.05 μm. This is a relative radius change from the arterial end to the middle of the capillary of 2.9%. The relative radius change from the middle to the venous end of the capillary is 1.2% (Figure 3A). Blood volume changes because of higher pressure and flow are shown in Figure 4B. The capillary volume changes from a value of 4.07 × 10⁻¹⁴ to 4.74 × 10⁻¹⁴ m³ for the first activation level, and to 4.795 × 10⁻¹⁴ m³ for the second activation level. This represents relative volume changes of 16% and 18%, respectively. The capillary expansion takes approximately 4 seconds to reach equilibrium.

Pressure distribution inside the capillary: A comparison of the initial pressure p_init(i) and the equilibrium state during constant flow p_res(i,t) is displayed in Figure 3B. At the beginning of the capillary, the pressure declines rapidly, while further down the capillary the pressure gradient is considerably smaller. The pressure gradient also decreases over time. In the first activation scenario, the arterial pressure decreases from 30 down to 7 mm Hg and the venous pressure from 10 down to 3 mm Hg. This leads to an overall equilibrium pressure gradient of 4 mm Hg. The absolute initial pressure difference from the arterial to the venous end of the capillary was 20 mm Hg. The pressure change from the arterial to the venous end of the capillary changed to 2.5 mm Hg for the second activation scenario with p_init(i=1)=35 mm Hg (Figure 3B). The pressure at z=0 decreases from p_init(i=1)=35 mm Hg at t=0 to 7 mm Hg in equilibrium. At z=L the pressure declines from 16 mm Hg at t=0 to 4.5 mm Hg. The absolute initial pressure difference was 19 mm Hg.

The Balloon Experiment

In each of the three cases studied, the capillary radius increases with initial pressure at z=0. This effect appears over the total length, so that at both z=0 and 25 cm the balloon radius increases when the arterial pressure is increased at the capillary entrance. The increase is distributed over the capillary length. The pressure change is accompanied by an axial flow change from 400±50 to 700±50 mL/minute, a relative change of 75% from lower to higher pressure.

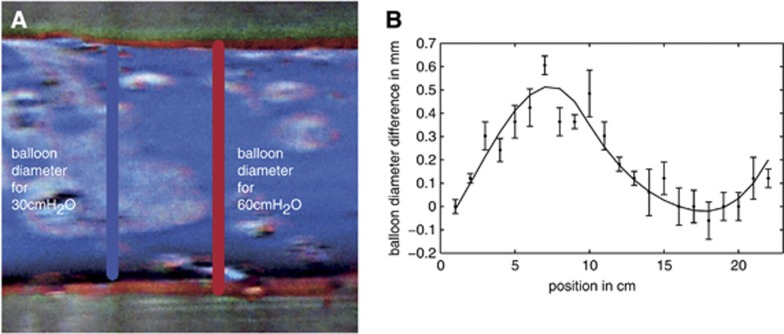
Balloon volume changes: With an impermeable balloon and an air-filled cavity, the average radius difference between 30 and 60 cmH₂O is 0.75±0.2 mm, a relative radius change of 37%, and thus a relative volume change of 88%. The average radius change over the capillary length for the impermeable water-filled cavity case is roughly 0.3 mm, a relative change of 14%. The standard deviation is estimated as 0.1 mm. The average change of volume is 30%. In the permeable water-filled cavity case, a small average expansion of approximately 0.2 mm was observed and a relative diameter change of 10%, giving an average volume change of 21%. The standard deviation of the measurements was 0.05 mm (Figure 5).

Figure 5.

Diameter change of a permeable balloon within the water-filled cavity induced by an initial pressure change from 30 to 60 cmH₂O. False colors are used in A to highlight the balloon expansion in the range from L=5 to 8 cm. The diameter change of the whole balloon is shown in B.

Ink experiment: When ink was used instead of water, with the perforated balloon, permeation becomes visible. We observed the ink moving radially out of the ‘capillary' along its first half (until z∼15 cm) (Figure 6). After leaving the balloon, the ink gained an axial velocity component, and so moved slowly to the venous end. There, some of the ink permeated back into the balloon.

Figure 6.

Permeation through the balloon wall can be observed by using ink instead of water; the ink moves out of the permeable balloon over the first half of its length, and in over its second half. (A) The ink experiment at t=0.5 seconds, (B) at t=3 seconds, and (C) at t=10 seconds.

Test cases: The test cases with the impermeable balloon reveal a slight movement of the cavity covers during periods of increased arterial pressure. This movement is related to the ring gaskets, squeezed by the elevated pressure inside the cavity. In addition, a volume change of the air bubbles within the cavity can be seen. This enables the balloon volume to change. A significant pressure increase can also be observed within the cavity. When the pressure inside the balloon increases, it reduces the volume of the air-filled balloon monitoring the pressure inside the cavity, indicating a pressure increase inside the cavity itself.

Discussion

Recently, CBV has become recognized as a well-localized marker of neural activity (Herman et al, 2009; Kim et al, 2007; Lu et al, 2003; Stefanovic and Pike, 2005). However, the concept of CBV itself is still poorly understood. How can capillaries expand without changing the bulk volume of the cranium, and without dangerously increasing the ICP? We have addressed this problem by presenting a new mathematical model for flow and volume changes during neural activation processes. Our model involves capillary wall permeability as well as elasticity, and respects the Monro–Kellie doctrine. The results based on this theoretical approach are compared and supplemented with an experimental counterpart that simulates a single capillary inside a rigid cavity.

Changes of cerebral blood volume during activation processes: Both the experimental data and the simulation show a volume change of the permeable capillary when pressure changes at the arterial end, accompanied by a flow change through the capillary. The volume change arising from a pressure change of 30 to 60 cmH₂O in the experimental balloon model, ΔCBV_balloon=21±5% (Figure 5B), is comparable to the changes calculated by the numerical compartment model ΔCBV_compartment=17±1% (Figure 4B). These values are in the same range as earlier in-vivo measurements of capillary expansion during neuronal activation and hypercapnia (Lee et al, 2001; Stefanovic et al, 2008; Villringer et al, 1994). It is reasonable to assume that a typical blood volume fraction of 4.5% to 5.5% of the total gray matter volume (Gu et al, 2006; Ito et al, 2004; Lu et al, 2005). Thus in 100 mL of blood, more careful measurements indicate an arterial volume of 0.8 to 1.2 mL (An and Lin, 2002a; Donahue et al, 2009; Kim and Kim, 2005), a capillary blood volume of 1.8to 2.1 mL (Pawlik et al, 1981), and a venous blood volume of 2.0 to 2.5 mL (An and Lin, 2002a, 2002b). Total blood volume changes during activation processes have been measured to be typically around 30% (∼1.5 mL). Of this, arterial blood volume change has been estimated as 1.0 mL (∼80% change of arterial volume) (Lee et al, 2001) and venous blood volume change is no larger than 0.1 mL (∼5% change of venous volume) (Berwick et al, 2005; Chen and Pike, 2009; Drew et al, 2011; Hillman et al, 2007). Our results suggest a capillary expansion of approximately 20%, which would give a volume change of approximately 0.4 mL. On the basis of these values, changes in arterial, capillary, and venous volume contribute approximately 60%, 30%, and 10%, respectively, to the total volume change and confirm the important contribution of capillary volume changes to the total change in CBV.

We observed no significant pressure changes in the external cavity, in the theoretical model, or in the experimental simulation. Our results are supported by ICP measurements during hypercapnia by Asgari et al (2010), who state that ICP changes over the day are much larger than those induced by hypercapnia. Among other factors, during hypercapnia, hydrogen concentration in cerebral blood vessels is believed to be a major driver of vasodilation. By contrast, during neuronal activity, the release of nitric oxide plays an important role in vasodilation. Although nitric oxide may have a minor role in hypercapnia-induced vasodilation, it is commonly more associated with vasodilation during neuronal activity (Iadecola, 1993; Iadecola and Zhang, 1994; Piechnik et al, 2009). Hypercapnia produces global vasodilation, often resulting in larger total blood volume change within the skull than neuronal activity, which produces only local changes of CBV. Consequently, neuronal stimulation is expected to produce lower ICP changes than hypercapnia. Volume changes are also observable in the experiment when using the impermeable balloon in an air-filled cavity (88±10% average volume change) and in a water-filled cavity (30±5% average volume change). However, in contrast with the experiment with the permeable balloon, a large increase of pressure inside the cavity is observable with an impermeable balloon inside the water-filled cavity. The shrinkage of an additional air-filled balloon inside the cavity indicated a pressure increase inside the cavity during impermeable balloon expansion. In the absence of the additional balloon, such an expansion could only be explained by (1) the expansion of the external cavity (and/or its inlet gasket), (2) by water compression, or (3) size changes of the air bubbles inside the cavity. Our results suggest that the end-plates of the cavity, although constructed of rigid plastic, can move slightly as a result of the pressure increase associated with balloon expansion. The gasket rings sealing the cavity ends become slightly compressed during the simulated activation (p_init=60 cmH₂O). The gaskets have an initial thickness of approximately 2 mm, and shrink to approximately 1 mm with higher pressure. As the diameter of the end-plate is 40 mm, the total volume change because of gasket compression yields 2.5 × 10⁻⁶ m³. This value is comparable with the calculated balloon volume change of 2.9 × 10⁻⁶ m³ obtained by the activation scenario with a water-filled cavity and an impermeable balloon. In addition, our test cases reveal shrinkage of air bubble sizes during higher pressures. Thus, the balloon volume change observed in the impermeable balloon in the water-filled cavity is consistent with a change in the cavity volume combined with compression of air bubbles. For the physiologic counterpart, this implies that if capillaries were impermeable to water, cerebral volume changes could not take place without significant increases in ICP. The crucial capillary property of permeability must be considered in modeling CBV changes during brain activation processes.

In contrast to cavity expansion, water compression can have only a minor influence on the capillary radius. The water temperature used in the balloon experiments was approximately 10°C, which means a compressibility of κ=2.8 × 10⁹ Pa. equation (21) defines the change of volume for a given pressure p and initial volume V₀:

Assuming a pressure of p_init(z=0)=60 cmH₂O and an initial volume of V₀=3 L, the volume change because of compression of water turns out to be ΔV=1.4 × 10⁻⁹ m³=1.4 × 10⁻⁶ L. An average balloon volume change of 30±5% inside the water-filled cavity means a total change of approximately 2.9±0.5 × 10⁻⁶ m³=2.9±0.5 × 10⁻³ L. Thus, possible volume change because of the compression of water is negligible.

Capillary radius distribution along the flow axis: The compartment model suggests that the radial expansion of the capillary decreases along its length, in the flow direction (Figure 3A). The difference in radii between the arterial and venous ends is approximately 4% to 5%. This value cannot be compared with experimental data as there is no published literature available regarding this finding. The minimum pixel size that can be imaged in vivo with high-resolution optical techniques is approximately 0.5 μm. A 5% radius change from the arterial to the venous side of the capillary would mean 0.25 μm even for very large capillaries with 5 μm in diameter at the arterial end. Therefore, such small diameter changes cannot be detected, especially since the point spread function of those techniques leads to somewhat poorer actual resolutions than the minimum pixel size. However, according to the Hagen–Poiseuille law, the hydrostatic pressure within the capillary must decrease along its length. This is supported by the ink tracer experiment, which shows that water perfuses out at the arterial end of the capillary (Figure 6) and in at the venous end. Both of these effects indicate a radial wall force decreasing along the capillary length, in agreement with our simulations.

The second activation level results in a faster decrease of the balloon radius over the capillary's first half than its second half, in equilibrium (Figure 3A). This is consistent with the pressure distribution over the capillary length for this activation stage (Figure 3B). p_init(i) decreases faster over the first half of the capillary than the second. Consequently, a stronger radial force acts over the first half. In contrast, the radius change for the lower activation level is about the same for the first and the second half. However, the radius decreases faster close to the arterial and the venous ends. In the middle of the capillary, one can observe a moderate slope of radius decrease. Significant changes of the dependence of radius on the length of a vessel during neural activation would cause dramatic physiologic changes. Thus, our results reflect the behavior of physiologic environments.

Figure 5B, which shows the experimentally measured balloon diameter change between 30 and 60 cmH₂O input pressure, reveals a balloon diameter change of zero at the arterial end, which increases until z=7 cm, drops again to zero at z=18 cm, and grows again until the venous end. This curve can be qualitatively compared with the theoretically calculated capillary radius change, which is large at the arterial and the venous end and shows minor changes in the middle of the capillary (compare Figure 3A). Note that Figure 3A shows radius changes, while Figure 5B shows changes in diameter. It is at the arterial end where the largest discrepancy between the experimental results and the theoretical model are largest. This arises from the fact that the balloon is mounted on a rigid tube at the arterial end, which fixes its radius at that point, an additional boundary condition absent from the theoretical model. However, diameter changes further down the tube are qualitatively comparable between experiment and theory.

Temporal dimensions of capillary radius changes: The time constants for radius changes because of activation processes obtained by the compartment model are closely comparable with those measured via in-vivo and in-vitro fMRI (Frank et al, 1994; Hua et al, 2009; Kennerley et al, 2010; Lu et al, 2003) and optical techniques (Hillman et al, 2007; Hudetz, 1997; Tian et al, 2010). Even under changing physiologic conditions (changing axial flow and capillary pressures), the time constant remains in the same range (several seconds) (Figures 4A and B). Our calculations are consistent with a direct relationship between neural activity and blood volume changes, and help to justify the use of blood volume as marker of activation processes in the brain. The time course of the radius change could not be observed experimentally with our equipment. This took place very rapidly after the initial pressure was changed, and our camera was too slow to resolve this process accurately.

Pressure and flow distribution inside the capillary: The compartmental solution uses two different pressure expressions: p_init(i) and p_res(i,t) (Figure 3B). p_init(i) is the initial pressure for each compartment i, and is calculated via Darcy's equation. The inflow for each compartment is also based on this expression. p_init(i) is held constant over time to obtain a well-defined pressure gradient along the z axis, which feeds the compartments. In contrast, p_res(i,t) is time-dependent. p_res(i,t=0) equals p_init(i), but because of the effects of equations (17) and (18) it changes over time. Use of p_res(i,t) is required to ensure energy conservation (equation (18)).

The axial flow is assumed to be constant over time (for one theoretical activation stage), but varies along the capillary length. It is calculated via Darcy's law (equation (20)) to take capillary wall permeability into account. About half way along the capillary, the difference between the resulting osmotic and hydrostatic pressure becomes negative. The permeation also becomes negative, which in turn leads to a decreasing axial flow from for the first half of the tube and an increasing axial flow for the second half.

Effects of capillary wall permeability to water: The major effect of capillary permeability to water was observed using ink instead of water in the experimental approach (Figure 6). Some of the ink that moves from the nozzle into the permeable balloon perfuses into the outside cavity (Figure 6A). Because the overall volume stays approximately constant, water flow begins within the cavity. The ink leaves the balloon perpendicular to its walls (Figures 6A and B). After a few seconds this radial movement becomes axial, indicating that at the venous end of the balloon, water must have left the cavity (Figure 6C). The outflow over the first half of the capillary is matched by inflow over its second half. This observation is related to the Starling hypothesis (Starling, 1896), suggesting that nutrient and oxygen supply for the surrounding tissue, and clearance of waste products, is based on this effect (Schmidt and Thews, 1997). Beside that capillary permeability to water offers a reasonable mechanism of water exchange between the intra- and extravascular space while simultaneously providing a possibility of balancing out the intravascular and extravascular pressure. This prevents from increased ICPs during changes of vascular diameter even in large activated areas.

Implications for calibrated-blood oxygen level-dependent functional magnetic resonance imaging and oxygen metabolism: Blood oxygen level-dependent calibration based on hypercapnia has become a widely used fMRI technique (Davis et al, 1998) and hyperoxic BOLD calibration has recently been introduced as an alternative approach (Blockley et al, 2012a; Chiarelli et al, 2007; Mark et al, 2011; Mark and Pike, 2011). A combination of both techniques is believed to give more robust results than one technique alone (Blockley et al, 2012b; Gauthier et al, 2011). In each technique, carbon dioxide and oxygen breathing are used as physiologic reference standards to enable calculation of the cerebral metabolic rate of oxygen (CMRO₂). In such models, the Grubb equation is classically used to approximate total CBV in terms of CBF, whereas CBF is classically measured in combination with BOLD experiments (Hoge et al, 1999). Calibrated BOLD models thus rely ultimately on estimates of total volume changes, including arterial, capillary, and venous vessels, although these estimates derive only indirectly from changes in CBF. Such models have usually overestimated the contribution of venous compartments to the BOLD signal and underestimated arterial contributions (Vazquez et al, 2010). However, some recent models have included these indications of reduced venous contribution through the use of a reduced CBF–CBV relationship (Griffeth and Buxton, 2011; Mark and Pike, 2011).

Our theoretical and experimental results suggest that capillary wall permeability to water should be included when BOLD signal responses to neural activation are modeled. Up to now, this crucial property of capillary vessels has been widely disregarded (Buxton et al, 1998; Lorthois et al, 2011a, 2011b; Mandeville et al, 1999) and has led to improbable or at least incomplete models. These models commonly assume blood flow and the related mass conservation only in one direction, and fail to consider exchange of blood water through the capillary wall (Buxton, 2010). Inclusion of a radial velocity component in such models leads to an at least two-dimensional set of equations describing water movement in radial and axial directions. The physiologic properties of arterial, venous, and capillary vessels are quite different, as outlined above, and the importance of radial water movement will vary accordingly. It is likely that this water movement is well correlated with oxygen transfer across the vascular wall, which is also a passive process. Models of BOLD signal have mainly focused on oxygenation changes in the venous vasculature because of its largest changes in blood oxygenation during activation (Buxton et al, 1998; Hoge et al, 1999; Kong et al, 2004; Lee et al, 2001; Lorthois et al, 2011a, 2011b; Zheng et al, 2005). Arteriolar and especially capillary changes of blood volume and oxygenation have tended to be regarded as minor contributions, although capillaries are the major source of oxygen extraction, and consequently are closer to the site of neuronal activation than veins and arteries. A large contribution of the capillary compartment to total CBV changes could explain observations suggesting much better localization of CBV changes to neural activity than BOLD signal (Zhao et al, 2007). In addition, a fuller accounting for capillary CBV changes may lead to much better estimates of the relative contributions to BOLD signal of these different vascular compartments, and explain the large range of results found in the literature (Kim et al, 2007; Lee et al, 2001; Mandeville et al, 1999; van Zijl et al, 1998; Zhao et al, 2007).

Limitations to the current model: The Reynolds numbers of the balloon model Re_balloon≈1 and the compartmental model Re_compartment≈10⁻⁷ differ by seven orders of magnitude. The Reynolds number represents the relationship between inertia and viscosity. Fluids with similar Reynolds numbers have similar behaviors with regard to turbulence. However, the Reynolds number in the experiment and the theoretical model are both very low (Re≤1), so that turbulence can be neglected and the results may be reasonably compared.

Although these results are encouraging, it needs to be stressed that both the compartment model and the experimental approach are highly simplified. The most important variables neglected are the fluid–wall interaction, turbulence, and rheological effects associated with the discreteness of red blood cells. To obtain a full physiologic description of blood volume changes during brain activation, the boundary-value model itself would have to be solved, at least numerically. However, this is the first qualitative and quantitative study of this problem. Both experimental and theoretical models highlight the importance of the blood–brain barrier permeability to water.

The authors declare no conflict of interest.