Gyrotropic response in the absence of a bias field

Abstract

Electromagnetic materials lacking local time-reversal symmetry, such as gyrotropic materials, are of keen interest and importance both scientifically and technologically. Scientifically, topologically nontrivial phenomena, such as photonic chiral edge states, allow for reflection-free transport even in the presence of large disorder. Technologically, nonreciprocal photonic devices, such as optical isolators and circulators, play critical roles in optical communication and computing technologies because of their ability to eliminate cross-talk and feedback. Nevertheless, most known natural materials that lack local time-reversal symmetry require strong external fields and function only in a limited range of the electromagnetic spectrum. By taking advantage of metamaterials capable of translating the property of unidirectional active electronic circuits into effective dielectric response, we introduce a microwave gyrotropic metamaterial that does not require an external magnetic bias. Strong bulk Faraday-like effects, observed in both simulations and experiments, confirm nonreciprocity of the effective medium. This approach is scalable to many other wavelengths, and it also illustrates an opportunity to synthesize exotic electromagnetic materials.

Among natural mechanisms leading to gyrotropy, ferromagnetic resonance (1) is one of the strongest gyrotropic effects requiring a bias magnetic field at sub-Tesla levels, but is limited to the GHz frequency range. Magnetized plasma (2) and Zeeman splitting of optical dipole transitions do provide gyrotropy at optical frequencies, but at a very weak level even with a biasing field of several Tesla. These constraints, together with associated large absorption, have so far prevented large-scale application of nonreciprocal photonic systems. However, the recent advent of photonic crystals (3–6) and metamaterials enabled synthesis of artificial composite materials (7–14), possessing previously nonexistent electromagnetic properties, such as negative indices of refraction. Extending the concept of metamaterials to gyrotropic effects is thus an attractive venue to circumvent the limits of natural gyrotropic materials, especially if this could be done without using external magnetic fields. An important feature of gyrotropic materials is their nonreciprocal behavior, which cannot be created from dielectric or metallic structures alone even in the presence of loss or gain, according to the Rayleigh-Carson reciprocity theorem (15). Therefore, realizing gyrotropic metamaterials requires exploiting the inherent unidirectional property in the underlying electronic circuits, which has so far remained largely unexplored. In this paper, we intentionally combine unidirectional lumped electronic circuit elements with small subwavelength antennas oriented to change the polarization states: We introduce a bulk gyrotropic metamaterial with large Faraday-like rotation in the absence of an external magnetic bias; highly nonreciprocal propagation is observed in both simulations and experiments, where up to 14.4 degrees of Faraday-like rotation occurs over a 0.1 wavelength-thick metamaterial layer.

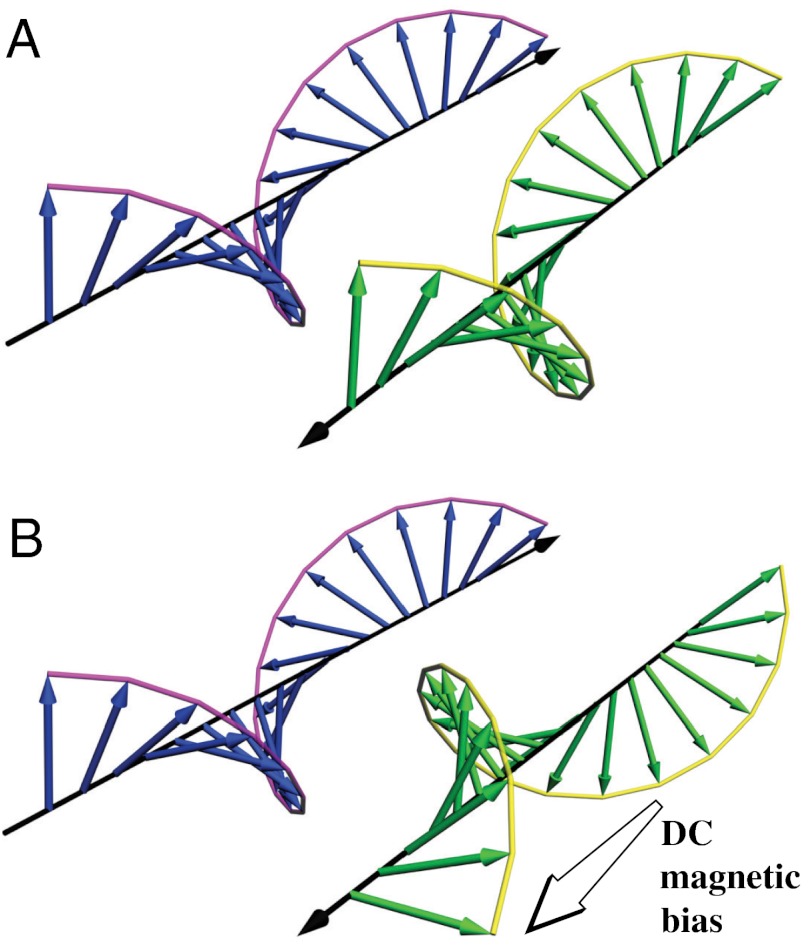
We start by reviewing the Faraday effect (1), which not only is a quintessential manifestation of both the broken local time-reversal symmetry and the nonreciprocity of a gyrotropic medium, but also reveals important clues on the conditions necessary for construction of gyrotropic metamaterials. The Faraday rotation clearly differentiates gyrotropic materials from the closely related chiral materials (16–22), which, in contrast, are locally time-reversal symmetric and reciprocal. In a chiral medium, a linearly polarized traveling wave experiences a rotation of its polarization vector, with the direction of rotation determined by the wavevector k (23). Consequently, a backward-propagating wave unwinds the polarization vector (Fig. 1A) of a forward-propagating wave. The net change of the polarization angle of the reflected wave is zero, and the local time-reversal symmetry is preserved. On the other hand, an external dc magnetic field B dictates the rotation direction of the polarization in a gyrotropic medium (Fig. 1B). For instance, one can set up a magnetic field parallel to the optical axis such that a linearly polarized incident wave experiences a clockwise rotation for its polarization angle from φ₀ to φ₀ + Δφ. However, the backward wave, traveling along the direction antiparallel to the magnetic field, experiences a counterclockwise rotation, and the polarization angle of the exiting wave increases to φ₀ + 2Δφ. In other words, waves reflected in a gyrotropic medium do not revert to their initial incident polarization states; this implies broken local time-reversal symmetry and nonreciprocal propagation. In slightly more complicated geometries, Faraday rotation can also enable nonreciprocal amplitude and phase response (24), or even more exotic disorder-immune one-way waveguides (2, 25–27). Nevertheless, in this paper we focus on the essential feature of the Faraday rotation: the change in the polarization angle of the transmitted wave, which is conventionally determined by the external dc magnetic field in naturally occurring gyrotropic materials.

Fig. 1.

Spatial evolution of the polarization vector (blue and green arrows) of a linearly polarized electromagnetic incident wave traveling through (A) a chiral medium and (B) a gyrotropic medium with its dc magnetization parallel to the optical axis. The propagation directions are indicated with black arrows.

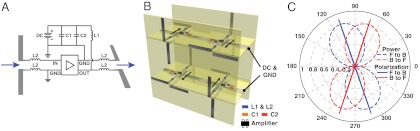
Although breaking local time-reversal symmetry in photonic systems is generally hard, in electronic systems it occurs quite commonly. Instead of employing an external magnetic field, our metamaterials take advantage of the directionality inherent in electronic amplifiers and transistors. By strongly coupling such electronic systems to incident electromagnetic radiation, we break the local time-reversal symmetry for E and M waves also. The input and output terminals are physically fixed by the circuit layouts and the underlying geometries of transistor channels (28). Signals travel only in one direction: Input voltages determine output voltages, but not the other way around. This circuit-level directionality is translated into a directional effective medium where, in each basis assembly, a unit-gain amplifier is driven by an input dipole antenna, and controls an output dipole antenna. The output polarization can be positioned along an arbitrary angle by the orientation of the antenna. To enable Faraday-like rotation, we implement four such assemblies per unit cell, as illustrated in Fig. 2A and explained in detail in SI Text.

Fig. 2.

Fully polarized gyrotropic metamaterial and its Faraday-like rotation. (A) Schematic of a unit cell of a single-layer fully polarized gyrotropic metamaterial. Each unit cell contains four basis assemblies, two with +z and two with -z directed signal flow (white arrows). Each assembly consists of four staggered wire elements, creating antennas in the x and y directions. The wire elements are color coded to depict the four combinations of polarization and current direction possible. The amplifiers (detailed in Fig. 3B), located between the circuit board substrates (yellow), designate the direction of the signal flow. At 805 MHz, the simulated single-pass polarizations (solid curves, defined in SI Text) and power patterns (dashed curves) are shown for (B) horizontally polarized incidence and (C) vertically polarized incidence, respectively. The polarization angles are defined with respect to the propagation direction. “F to B” indicates the direction from front side to back side, as viewed from the front. “B to F” refers to the opposite direction, as viewed from the back. The opposite sign of the rotation as viewed along the propagation direction indicates nonreciprocity.

Principles of operation of our class of designs are first tested with a full-wave numerical simulation using CST Microwave Studio and CST Design Studio. The dimension of the metamaterial unit cell is 60 mm by 60 mm by 30 mm, and each dipole spans a 29-mm length with a 1-mm gap at the middle. The front and back dielectric boards are made of 1 mm-thick FR4 with a rated relative permittivity 4.6. Simulating properties of a high-linearity surface-mount amplifier Avago MGA53543, we numerically calculated the polarization state of the transmitted wave at 805 MHz, as shown in Fig. 2 B and C. Along the direction from the source to the receiver, the polarization angle changes by -5.4 degrees and +5.4 degrees for waves incident from the front side and the back side, respectively. Fig. 2B shows the simulated polarizations (solid) and power patterns (dashed) at the receiver for a horizontally polarized wave at 805-MHz incident in different directions. Fig. 2C shows the simulated results for a vertically polarized wave at 805-MHz incident in different directions. The simulation was performed with the spice model of MGA53543 at a preset dc voltage (0.67 V) neglecting the impact on the propagation of the uncoupled waves from the finite dimension of the amplifier and the other circuit elements. Comparing the 373-mm wavelength at 805 MHz with the dimension of the unit cell, the metamaterial can be regarded as an effective medium. In the sense of the Maxwell-Garnett effective medium theory (29), the medium possesses an effective constitutive permittivity tensor describing a naturally occurring dc-biased gyrotropic medium. Utilizing an optimization algorithm, both effective permittivity and permeability tensors can be reconstructed from calculated S-parameters. The calculated S-matrix (SI Text) is found to be nonsymmetric, which is consistent with the nonreciprocal nature of the system. The effective permittivity and permeability tensors so obtained (except for the inconsequential ε_rz and μ_rz, described in detail in SI Text) take the form below:

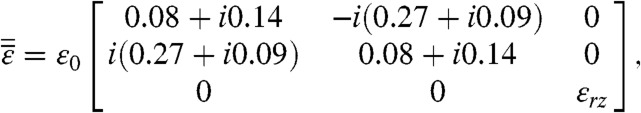[1]

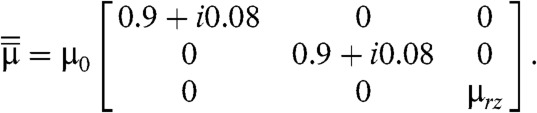[2]

Note the imaginary parts (0.14 and 0.08) along the diagonals arise from the losses of the effective medium. Such losses are also reflected in the 0.09 terms of the off-diagonal elements of the permittivity. The imaginary parts (0.27) of the off-diagonal elements clearly describe a gyrotropic effective material. Traditionally, in natural materials, these off-diagonal imaginary parts arise from an applied symmetry-breaking magnetic field.

To account fully for the finite dimension of the lumped circuit elements and as a preparation for the experiments, we next performed simulations incorporating the physical sizes and the phase retardation from the circuit elements. To simplify the experimental setup while demonstrating all the essential physics, we only included half of the orthogonal dipole pairs in each basis assembly to create a simplified metamaterial that acts only on the vertically polarized incidence, as shown in Fig. 3. The schematic of the amplifier circuit is shown in Fig. 3A. C1 and C2 are capacitors for decoupling. L1 is an inductor for ac blocking. L2s are inductors for impedance matching. The vertically polarized model uses horizontal wires for dc supply through the center of the amplifier circuit board, as can be seen in Fig. 3B. The dimension of this model remains 60 mm by 60 mm by 30 mm and the length of each dipole remains 29 mm with a 0.5-mm gap in the middle. The substrates for the front, back, and circuit boards are 1 mm-thick FR4 with relative permittivity 4.6 and loss tangent 0.02. The directions of the amplifier MGA53543 are marked by the black arrows. The lumped elements mounted on the circuit board are marked in different colors. C1 = 100 pF, C2 = 10 nF, and L1 = L2 = 27 nH. Simulation performed at 885.45 MHz for a vertically polarized incident wave is shown in Fig. 3C. Along the direction from the source to the receiver, the polarization angle rotates by +16.75 degrees and -16.75 degrees for front-side incidence and back-side incidence, respectively. The dc voltage of the amplifiers for these results is 0.533 V.

Fig. 3.

Gyrotropic metamaterial for vertical polarization and its simulation results. (A) The circuit schematic of a basis assembly. (B) The structure schematic of a unit cell. (C) The simulated polarizations (solid) and power patterns (dashed) at the receiver when a vertically polarized wave at 885.45 MHz is incident in two opposite directions.

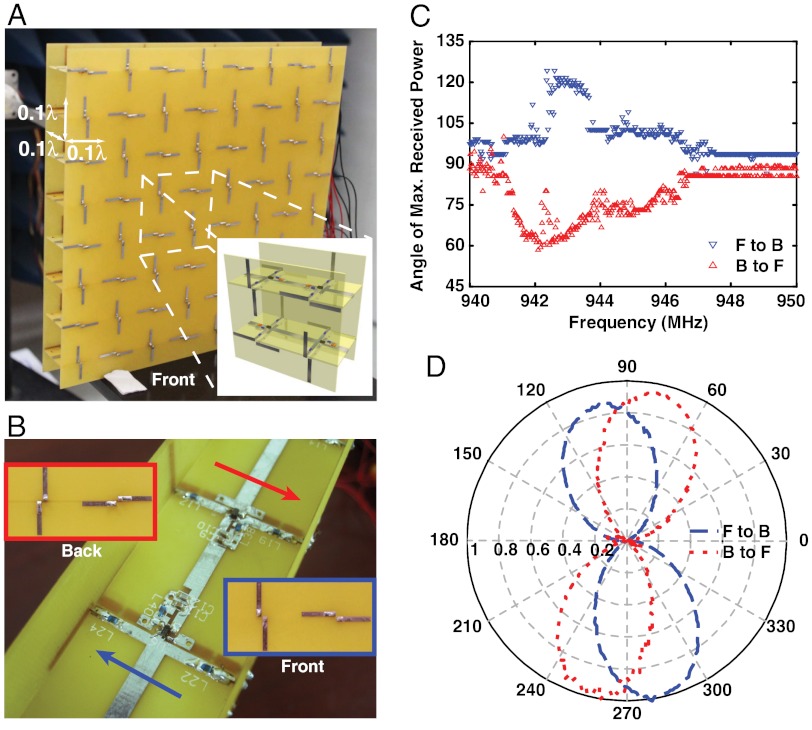
Finally, the Faraday-like rotation of the proposed gyrotropic metamaterial is confirmed in a transmission measurement experiment. The photo of a metamaterial sample is shown in Fig. 4A, with the top-layer circuit board seen in Fig. 4B. Blue and red arrows indicate the directions of the amplifiers. A two-ridge horn antenna, serving as the source, is polarized along the vertical direction and driven with power at 10 dBm by a Hewlett-Packard 8350B Sweep Oscillator. A 133 mm-length printed dipole antenna on a 1 mm-thick FR4 substrate serves as a detector on the other side of the sample and is rotated to measure the polarization of the field through a Hewlett-Packard 8756A Scalar Network Analyzer. We first measured the polarization change with the wave incident from the front side to the back side of the sample, then flipped the sample horizontally and measured the polarization change with the wave incident from the back side to the front side. Along the direction from the source to the detector, we identify the change in the polarization angles, at a dc voltage of 0.8 V and a dc current of 0.19 A. Using a motorized stage, we stepped the detector angle 0.9 degrees at a time. The measured results are shown in Fig. 4 C and D. Fig. 4C shows the angles of the maximum received power at each frequency, and Fig. 4D shows the calibrated measured power patterns by using the free space-measured data when vertically polarized wave at 946 MHz is incident. From these results we can see that the polarization changes through the sample with different incident directions are opposite: The polarization angle changes are +14.4 degrees and -14.4 degrees with incident directions from the front side to the back side and from the back side to the front side, respectively. Considering the thickness of the metamaterial is only around one-tenth wavelength of the incident wave, such a Faraday-like rotation angle corresponds to an unprecedented Voigt parameter of 3. Such a large ratio of the off-diagonal imaginary part over the diagonal real part far exceeds typical values of 0.1–1 at microwave frequencies and 0.03 and below at optical frequencies.

Fig. 4.

Photos of the single-polarization gyrotropic metamaterial sample and its experimental results. (A) The photo of a single-layer gyrotropic metamaterial for vertical polarization. (B) The photo of the circuit board in the sample. (B, Inset) Photos of the metallic pattern on the front and the back board of the sample. (C) Angles at which the received power is maximized for a given incident frequency. (D) Measured power patterns calibrated from the free-space measurement with a vertically polarized wave incident at 946 MHz.

Several improvements could improve the performance of the presented gyrotropic metamaterial in the future. With further optimization on the structure and the circuit, one could reduce the dimensions of the unit cell to improve the homogenization, raise the upper-frequency limit, and obtain better antenna-coupling efficiency. One could also engineer the near-field coupling between the adjacent layers of the metamaterial in order to scale linearly the Faraday rotation angle with respect to the overall thickness of the metamaterial. Using integrated antennas and circuits in high-mobility semiconductor platforms (30), operational frequencies as high as 500 GHz should be theoretically obtainable, which is two orders of magnitude larger than with naturally occurring ferromagnetic materials. The current operational bandwidth is limited by the phase-matching circuits, which interface the two orthogonally polarized components of the output wave. It should be possible to improve the circuit phase response to match the phase in a substantially larger bandwidth so as to construct a very broadband gyrotropic medium. In addition, the directionality of our gyrotropic medium could be controlled readily by changing the polarity of the external dc voltage.

In conclusion, we introduce a systematic approach to synthesize bulk gyrotropic metamaterials from directional circuit elements, and demonstrate strong Faraday-like rotation at microwave frequencies. We envision this approach could contribute to exploration of nonreciprocal phenomena and devices in frequency ranges previously inaccessible to gyrotropic materials. More importantly, this work is an illustration of how additional control of the electromagnetic response in metamaterials incorporating active electronic circuit elements can be exploited to enable exotic phenomena.