Cytotoxic T-Lymphocyte Escape Mutations Identified by HLA Association Favor Those Which Escape and Revert Rapidly

Abstract

Identifying human immunodeficiency virus (HIV) immune escape mutations has implications for understanding the impact of host immunity on pathogen evolution and guiding the choice of vaccine antigens. One means of identifying cytotoxic-T-lymphocyte (CTL) escape mutations is to search for statistical associations between mutations and host human leukocyte antigen (HLA) class I alleles at the population level. The impact of evolutionary rates on the strength of such associations is not well defined. Here, we address this topic using a mathematical model of within-host evolution and between-host transmission of CTL escape mutants that predicts the prevalence of escape mutants at the population level. We ask how the rates at which an escape mutation emerges in a host who bears the restricting HLA and reverts when transmitted to a host who does not bear the HLA affect the strength of an association. We consider the impact of these factors when using a standard statistical method to test for an association and when using an adaptation of that method that corrects for phylogenetic relationships. We show that with both methods, the average sample size required to identify an escape mutation is smaller if the mutation escapes and reverts quickly. Thus, escape mutations identified as HLA associated systematically favor those that escape and revert rapidly. We also present expressions that can be used to infer escape and reversion rates from cross-sectional escape prevalence data.

INTRODUCTION

The human leukocyte antigen (HLA)-restricted cytotoxic T-lymphocyte (CTL) immune response is thought to make a significant contribution to the control of human immunodeficiency virus (HIV) (4, 5, 13, 27). A deeper understanding of the CTL response is important to the development of an HIV vaccine. One way to study the CTL response is by investigating the way in which HIV is evolving escape mutants—viral strains that evade recognition by CTLs. Evidence to support the evolution of CTL escape mutants has been observed both within individuals (4, 21, 28, 36, 39) and at the population level (3, 9, 17, 23, 25, 33, 38). At the population level, evidence has been found in the form of statistical associations between certain HLA class I alleles—the human genetic determinants of CTL responses—and certain mutations away from the sample/subtype consensus in the HIV genome (3, 9, 33). The patterns emerge because of heterogeneity in HLA alleles among the population. Individuals who share HLA alleles tend to target the same viral antigens (called CTL epitopes) and therefore drive the same escape mutations. Escape mutations have been shown to revert to the wild-type form (e.g., back to the subtype consensus) following transmission to hosts who do not bear the selecting HLA (28, 29). The combination of these two factors—escape in “HLA-matched” hosts and reversion in “HLA-mismatched” hosts—means that although viral mutants can be transmitted between individuals, any particular escape mutation should be more prevalent in HLA-matched than in HLA-mismatched hosts. Simple statistical tests involving a contingency table or logistic regression were originally used to find sites where this difference in the prevalence of a mutation is greater than can be expected by chance (6, 33).

In recent years, lists of HLA-associated mutations have been compiled and compared to data such as epitope maps, epitope-targeting potency (enzyme-linked immunospot [ELISPOT] data), in vitro viral fitness measurements, epitope binding assays, epitope anchor residue sites, viral loads, CD4 counts, escape rates, and reversion rates (9, 12, 20, 22, 31, 32, 40). These comparisons are helping to elucidate the sites, pathways, and consequences of CTL escape while also providing insights into the characteristics of different immunogens. To correctly interpret the results of such analyses, however, it is important to understand the nature of the errors that can be incurred in the identification of CTL escape mutations. Errors can be classified into two kinds. One kind occurs when a mutation that is not an escape mutation is identified as an escape mutation. Factors that can lead to this kind of error include linkage disequilibrium among HLA alleles, codon covariation, and founder effects, whereby if a particular HLA allele and a particular viral lineage (e.g., HIV subtype) are both more common among a subgroup of the population (e.g., a racial group), mutations unique to that lineage (founder virus) could appear to be associated with the HLA allele. Exposure to antiretrovirals (ARVs) may also differ (in type and/or coverage) between different subgroups of a population, and this could similarly lead to erroneous associations between ARV-resistant mutations and HLAs common in a subgroup. Finally, the stochastic nature of the within- and between-host evolution of HIV and the fact that observations are taken from only a sample of the population can also lead to misidentification of an escape mutation. Such errors that result from random sampling are classified as type I errors. Escape mutations are identified when the null hypothesis of the statistical hypothesis test is rejected according to a fixed bound, called the significance level or the critical P value, on the type I error probability.

A second kind of error occurs when a genuine escape mutation is not identified. Random sampling contributes to this type of error, as do factors that affect the strength of the signal of escape in the population (i.e., the signal that would be observed if everyone in the population was sampled). Signal strength is influenced by stochasticity in the evolution of escape mutations and by the presence of additional variation or “noise” in the genome, arising randomly or because of additional selective pressures. Escape and reversion rates influence the distribution of escape mutations among HLA-matched and -mismatched hosts and are therefore also likely to influence the underlying strength of the signal. Technically, if a signal of escape that is present in the whole population is not picked up because of random sampling, a type II error occurs. More loosely, failure to identify a true escape mutation can be regarded as a type II error. The probability of not making a type II error is called the power of the test.

Rapid progress has been made in recent years in the development of mathematical techniques to reduce errors incurred in the identification of CTL escape mutations through HLA association. Notably, phylogenetic models, used to infer the evolutionary relatedness of different viral strains, have now been incorporated into HLA association techniques (2, 3, 7, 8, 9, 10, 11, 12, 22, 31, 40). In 2007, Bhattacharya et al. (3) showed how such methods can reduce misidentification “founder effect” errors, as well as lack of signal “noise-related” type II errors. Phylogenetically informed methods to reduce misidentification stemming from codon covariation (12) and linkage disequilibrium among HLA alleles (12) have also been developed. No studies, however, have yet explored the relationship between escape and reversion rates on the strength of statistical associations achieved using either traditional or phylogenetically corrected techniques. That is, none have explored how escape and reversion rates are linked to type II errors or (equivalently) the power of the test.

In this study, we use a mathematical model to address this gap. We also explain how the model can be used to infer escape and reversion rates of different escape mutations from data detailing the prevalence of those mutations in HLA-matched and -mismatched hosts. In summary, we address the following two sets of questions on the relationship between rates of escape and reversion and the prevalence of an escape mutation in HLA-matched and -mismatched hosts. (i) How do escape rates in HLA-matched hosts and reversion rates in HLA-mismatched hosts affect the strength of statistical associations between escape mutations and HLA alleles? At a fixed sample size, will mutations identified through HLA association favor those with higher or lower escape and reversion rates? (ii) How can the escape and reversion rates of an escape mutation be estimated from measurements of its prevalence in HLA-matched and -mismatched hosts?

To address these questions, we used a mathematical model that describes how within-host evolution and between-host transmission of CTL escape mutants affect the prevalence of escape mutants in the population (16). Crucially, this model accounts for heterogeneity with respect to host HLA type and incorporates three processes relating to a particular mutation: escape in HLA-matched hosts, transmission of the escape mutant (the strain containing the escape mutation) between hosts, and reversion of the escape mutation in HLA-mismatched hosts.

We first investigate how escape and reversion rates affect the strength of associations measured using a standard contingency table statistical technique (with Fisher's exact test) (33) in which phylogenetic relationships between sequences are not corrected for. We show that with this method, higher rates of escape in HLA-matched hosts and higher rates of reversion in HLA-mismatched hosts both lead to stronger associations between the mutation and the restricting HLA. Thus, mutations identified through such associations systematically favor those with higher escape and reversion rates.

Secondly we investigate how escape and reversion rates affect the strength of associations measured using a method that accounts for phylogenies (3). We show that with this method also, identified mutations favor those that escape rapidly in HLA-matched hosts and those that revert rapidly in HLA-mismatched hosts.

Finally, we provide a description of how to infer rates of escape and reversion from HLA-typed cross-sectional escape prevalence data. While the methods we describe have roots in a mathematical model, they are widely accessible, as they do not require the user to run model simulations. We demonstrate the use of this technique in identifying escape mutations that could be missed using HLA association tests but that are contained in epitopes that could nevertheless be robust vaccine antigens.

MATERIALS AND METHODS

Mathematical model.

In this study, we use a mathematical model that describes how within-host evolution and between-host transmission of CTL escape mutants affect the prevalence of escape at the population level. The basic dynamics of the model have been explored elsewhere (17). The underlying framework of the model is one in which there is frequency-dependent transmission of an infectious disease with no recovery throughout a population in which there are births and deaths. This is commonly known as the susceptible-infected (SI) model with host turnover. The model represents the dynamics of escape at a single CTL epitope or at a single site within an epitope, incorporating host heterogeneity (with respect to the presence or absence of the HLA that restricts the epitope) and viral heterogeneity (with respect to the presence or absence of an escape mutation at the epitope). In mathematical terms, a proportion, π, of the population are HLA matched for the epitope (host type [h] = 1), and the remainder are HLA mismatched for the epitope (h = 0). Each infected host is infected and infectious with the wild-type (i.e., subtype consensus) strain (virus type [v] = 0) or the escape mutant (v = 1). Depending upon the host type, within-host evolution takes two forms. HLA-matched hosts who are infected with the wild-type strain have the potential to make an immune response to the epitope and drive the emergence of an escape mutant at rate ϕ. In contrast, HLA-mismatched hosts do not have the potential to make an immune response to the epitope, and thus, in these individuals, an escape mutation at the epitope does not confer any benefit on the virus. Escape mutations may impose a fitness cost on the virus, so in HLA-mismatched hosts infected with an escape mutant, reversion to the wild type occurs at rate ψ. At any time, t, the number of susceptible hosts of host type h is denoted X^h(t) and the number of infected hosts of host type h and virus type v is denoted Y_v^h(t). The per capita rate at which susceptible hosts become infected with each virus type, λ_v(t), is proportional to the portion of the population who are infected with virus type v. Thus, λ_v(t) is equal to βc(Y_v¹(t) plus Y_v⁰(t))/N(t), where β is the transmission probability per partnership, c is the rate of partner change, and

$$N\left(t\right)={\displaystyle \sum _{h=0,1}(X^h\left(t\right)+{\displaystyle \sum _{v=0,1}{Y}_v^h\left(t\right))}}$$

is the total population size at time t. The product of the transmission probability per partnership and the rate of partner exchange, βc, is traditionally referred to as the transmission coefficient. Host turnover is modeled by people being born into the susceptible population at a constant rate B. A proportion, π, of newborns are HLA matched for the epitope; thus, the fraction of the population who are HLA matched for the epitope remains constant over time. The death rate of susceptible hosts is μ, and infected hosts die at the higher rate of μ + α. The average life expectancies of susceptible and infected hosts are therefore 1/μ and 1/(μ + α), respectively. This system can be represented using a set of six coupled ordinary differential equations (equations 1 to 6).

Model equations.

The six model equations are as follows: susceptible, HLA mismatched,

$$\frac{d{X}^0\left(t\right)}{dt}=\left(1-\pi \right)B-\left({\lambda }_0\left(t\right)+{\lambda }_1\left(t\right)+\mu \right)X^0\left(t\right)$$ (1)

susceptible, HLA matched,

$$\frac{d{X}^1\left(t\right)}{dt}=B\pi -\left({\lambda }_0\left(t\right)+{\lambda }_1\left(t\right)+\mu \right)X^1\left(t\right)$$ (2)

infected, wild type, HLA mismatched,

$$\frac{d{Y}_0^0\left(t\right)}{dt}={\lambda }_0\left(t\right)X^0\left(t\right)+\psi Y_1^0\left(t\right)-\left(\mu +\alpha \right)Y_0^0\left(t\right)$$ (3)

infected, escape, HLA mismatched,

$$\frac{d{Y}_1^0\left(t\right)}{dt}={\lambda }_1\left(t\right)X^0\left(t\right)-\psi Y_1^0\left(t\right)-\left(\mu +\alpha \right)Y_1^0\left(t\right)$$ (4)

infected, wild type, HLA matched,

$$\frac{d{Y}_0^1\left(t\right)}{dt}={\lambda }_0\left(t\right)X^1\left(t\right)-\phi Y_0^1\left(t\right)-\left(\mu +\alpha \right)Y_0^1\left(t\right)$$ (5)

and infected, escape, HLA matched,

$$\frac{d{Y}_1^1\left(t\right)}{dt}={\lambda }_1\left(t\right)X^1\left(t\right)+\phi Y_0^1\left(t\right)-\left(\mu +\alpha \right)Y_1^1\left(t\right)$$ (6)

Patient cohorts. (i) Short-course treatment in acute-infection cohort.

Escape and reversion rates were measured at the within-host level (Table 1) from a cohort—described in detail elsewhere (14)—of 189 predominantly Caucasian male acute seroconverters recruited within a median of 60 days from their estimated date of seroconversion. Each of these patients was recruited from London, United Kingdom, into one of two studies into the effects of short-course antiretroviral treatment during acute infection. One hundred one of these individuals were part of an initial nonrandomized study, 88 of whom received a short course of treatment (0.5 to 6 months; median, 3.0 months) at seroconversion and then remained drug naïve until either viral-load, CD4 cell count, or clinical parameters were met to require formal institution of highly active antiretroviral therapy (HAART). The remaining 88 patients were part of a randomized trial that remained blinded at the time of this study. At seroconversion, patients received either no therapy, 12 weeks of HAART, or 48 weeks of HAART and then remained off therapy according to clinical need. The median time between the estimated date of seroconversion and enrollment was 60 days (interquartile range, 39 to 86 days). The criteria used for acute HIV-1 infection have been described previously (14). Plasma samples were taken at baseline and various times thereafter so that across the two studies, patients were followed for a mean further 1.9 years (range, 0.5 to 5 years). Viral RNA was extracted from patient plasma. The majority (87%) of patients were found to be infected with a subtype B strain. Where possible, sequences were obtained for the gag, reverse transcriptase (RT), and nef genes. Only patients with sequences at two or more time points were included in our analysis. This resulted in gag, RT, and nef sequences from 166, 79, and 116 individuals, respectively. For each individual, four-digit human leukocyte antigen (HLA) class I A, B, and C genotypes were determined by PCR using sequence-specific primers.

Table 1.

Demonstration, using known escape mutations, of how escape and reversion rates affect the sample size required to identify escape mutations through statistical association^a

Epitope for which the mutation confers escape (HXB2 location)	HLA restriction (prevalence [π]) in Caucasians	Epitope amino acid sequence and escape site (underlined)	Avg time (yr) to escape (1/ϕ) (HLA matched with the subtype consensus at first sample)	Avg time (yr) to reversion (1/ψ) (HLA mismatched with mutant at first sample)	Predicted escape prevalence in HLA-matched hosts (Λ1)	Predicted escape prevalence in HLA-mismatched hosts (Λ0)	Avg sample size required to find a statistical association
RT (128–135)	B*51 (0.126)	TAFTIPSI	0.5 (n = 1)	25 (n = 28)	0.94	0.04	158
p24 gag (15–23)	B*57 (0.057)	ISPRTLNAW	4.3 (n = 8)	64 (n = 58)	0.58	0.24	596
p24 gag (131–140)	B*27 (0.073)	KRWILGLNK	11 (n = 17)	15 (n = 9)	0.30	0.07	587
p24 gag (108–117)	B*57/58 (0.096)	TSTLQEQIGW	1.6 (n = 6)	2.5 (n = 12)	0.71	0.05	83
nef (116–125)	B*57 (0.057)	HTQGYFPDW	2.3 (n = 5)	No reversion (n = 32)	0.78	0.44	649
nef (134–143)	A*24 (0.196)	RYPLTFGW	1.9 (n = 11)	6.7 (n = 18)	0.75	0.21	91

^aThe escape mutations presented here have previously been described in the literature as conferring escape and demonstrated as such in vitro (18, 19, 24, 28, 37). For each mutation, the average time between infection and escape in HLA-matched hosts (the reciprocal of the escape rate) and the average time between infection and reversion in HLA-mismatched hosts are provided. These rates are measured from a longitudinal cohort of acute seroconverters (14). Parameterized with these rates and with the estimated prevalence of the restricting HLA in Caucasians), the deterministic model is used to predict the escape prevalence in HLA-matched and -mismatched hosts 58 years into an epidemic that has a basic reproductive number of 3 (1). Based upon these escape prevalences, the average sample size required to identify the mutation using a 1-tailed Fisher's exact test with a critical P value of 0.0001 is presented. This demonstrates that realistic differences in escape and reversion rates between mutations correspond to noticeable differences in the sample sizes required to identify those mutations by statistical association. In calculating escape and reversion rates from the longitudinal cohort study, we defined an escape mutation as being any mutation away from the B-clade consensus amino acid at the identified escape site. The proportion of Caucasians with each HLA type is estimated from allele frequencies among Caucasians (30), assuming Mendelian genetics. This calculation ignores linkage between alleles.

(ii) Treatment interruption cohort.

The cross-sectional escape prevalence data used in Table 2, Fig. 3) and Fig. S3 (see supplemental material) were gathered from 96 patients from Switzerland recruited into the Swiss-Spanish Intermittent Therapy Trial (SSITT). This study was devised to assess the outcome of structured treatment interruptions in individuals with chronic HIV infection. These individuals have been described and studied in detail elsewhere (16, 35, 41). Patients were included in the study only if their CD4 counts were above 300 cells per mm³ at the time of enrollment and if they had been on continuous antiretroviral therapy (ART) with a plasma viral load of less than 50 copies per ml for at least 6 months. Although these patients were followed for an average of 14 months, for the present study, only data from a sample taken toward the end of the study (i.e., while the patients remained off treatment) were analyzed. Proviral DNA from 88 of the Swiss patients was sequenced. Sixty-seven of them were infected with a subtype B strain, and the remainder were excluded from our analysis. Ultimately, gene sequences for the following numbers of individuals were analyzed: p17 gag, n = 41; p24 gag, n = 60; RT HXB2 18 to 252, n = 55; RT HXB2 309 to 448, n = 60; and nef, n = 50. For each individual, four-digit HLA class I A and B genotypes were also determined by PCR using sequence-specific primers.

Table 2.

Identification of CTL escape mutations using different techniques^a

Mutation characteristics	Gene (HXB2 amino acid sites) of CTL epitope	HLA restriction (prevalence [π]) in Caucasians	Sample consensus amino acids of the CTL epitope (escape site underlined)	Inferred avg time (yr) to escape (1/ϕ)	Inferred avg time (yr) to reversion (1/ψ)	HLA association P values (q values)
						Using a contingency table	With phylogenetic correction
Escape rapidly (<10 yr) and revert rapidly (<10 yr)	p24 gag (108–117)	B*57/58 (0.096)	TSTLQEQIGW	0.5	3.4	1.6 × 10−6 (0.0014)	0.0070
	nef (134–141)	A*24 (0.196)	RYPLTFGW	0.9	5.0	2.6 × 10−5 (0.0074)	0.033
	p24 gag (174–184)	B*44 (0.211)	AEQASQEVKNW	3.2	5.9	0.0015 (0.26)	0.36
	p17 gag (20–28)	A*03 (0.224)	RLRPGGKKK	4.1	4.8	0.0078 (0.95)	0.036
	nef (84–92)	A*02 (0.438)	AALDLSHFL	4.4	7.8	0.020	0.046
	nef (90–97)	B*08 (0.143)	FLKEKGGL	5.4	9.4	0.041	0.316
	RT (392–401)	A*32 (0.077)	PIQKETWEAW	6.4	2.4	0.0064 (0.92)	0.0064
	nef (68–76)	B*07 (0.166)	FPVRPQVPL	7.2	4.0	0.072	0.025
	p24 gag (131–140)	B*27 (0.073)	KRWIILGLNK	8.7	9.9	0.038	0.010
	nef (135–143)	B*18/53 (0.140)	YPLTFGWCY	9.1	4.1	0.035	0.068
	RT (156–166)	A*11 (0.133)	AIFQSSMTK	9.4	5.6	0.086	0.031
Escape slightly more slowly (10–15 yr) and revert rapidly (<10 yr)	RT (128–135)	B*51 (0.129)	TAFTIPSI	12	0.0	0.019	1.0
	nef (74–81)	B*35 (0.196)	VPLRPMTY	12	3.3	0.089	0.089
	RT (137–146)	B*18 (0.122)	NETPGIRYQY	13	2.6	0.052	0.052
	p24 gag (84–92)	B*07 (0.166)	HPVHAGPIA	13	1.7	0.044	0.044
	RT (244–252)	B*57 (0.057)	IVLPEKDSW	14	0.1	0.093	0.093
	RT (173–181)	A*30 (0.067)	KQNPDIVIY	14	0.0	0.091	0.091
	p24 gag (197–205)	B*08 (0.143)	DCKTILKAL	15	2.2	0.056	0.056
HLA association P value of <0.05 using either technique	p24 gag (131–140)	B*27 (0.073)	KRWIILGLNK	3.8	16	0.012	0.013
	nef (116–124)	B*57 (0.057)	HTQGYFPDW	0.0	18	5.0 × 10−4 (0.11)	0.0012
	RT (128–135)	B*51 (0.129)	TAFTIPSI	0.9	19	0.0094	0.015
	nef (128–137)	B*07 (0.166)	TPGPGIRYPL	0.0	22	0.046	0.077

^aThis table shows how our method for estimating escape and reversion rates from cross-sectional data can be used alongside HLA association studies to give a broader overview of how to classify epitopes of potential benefit in a CTL-inducing vaccine. For this analysis, multiple comparisons were made between sites in optimally defined CTL epitopes in gag, RT, and nef and their restricting HLAs. For each comparison (n = 862), the strength of the association between the HLA and the mutation at the site was measured using a standard contingency table approach and an approach that corrects for phylogenies. Fisher's exact P values are provided and highlighted (boldface) where less than 0.05. As a measure of association strength under multiple comparison correction, q values estimated using the Benjamini and Hochberg method are provided where available. These can be used as a rough guide for the relationship between q values and P values using this type of data. Two escape mutations (underlined) remained significant at a value of 0.05 after correction for multiple comparisons using either the Bonferroni correction (P < 5.8 × 10⁻⁵ = 0.05/862) or false-discovery rate control (q value < 0.05). For each comparison, escape rates and reversion rates were inferred by fitting the escape prevalence data to the model under the assumption of exponential growth of the epidemic, making use of equations S1 and S2 in the supplemental material. Mutations—and their corresponding CTL epitopes—were listed if they escape rapidly (average time to escape < 10 years) and revert rapidly (<10 years). Mutations are also listed if they escape slightly more slowly (10 to 15 years) but revert rapidly (<10 years). Finally, additional mutations with an HLA association P value of less than 0.05 using either method are listed. More details of the methods and model parameters used for the analysis are provided in Materials and Methods. Note that mutation away from threonine (T; underlined) in TSTLQEQIGW was also found to be strongly associated with B*57 alone. A standard contingency table approach returns a P value of 1.5 × 10⁻⁵ and a q value of 0.0065. With phylogenetic correction, the P value is 0.0069, but no q value is returned using the Benjamini and Hochberg method.

Fig 3.

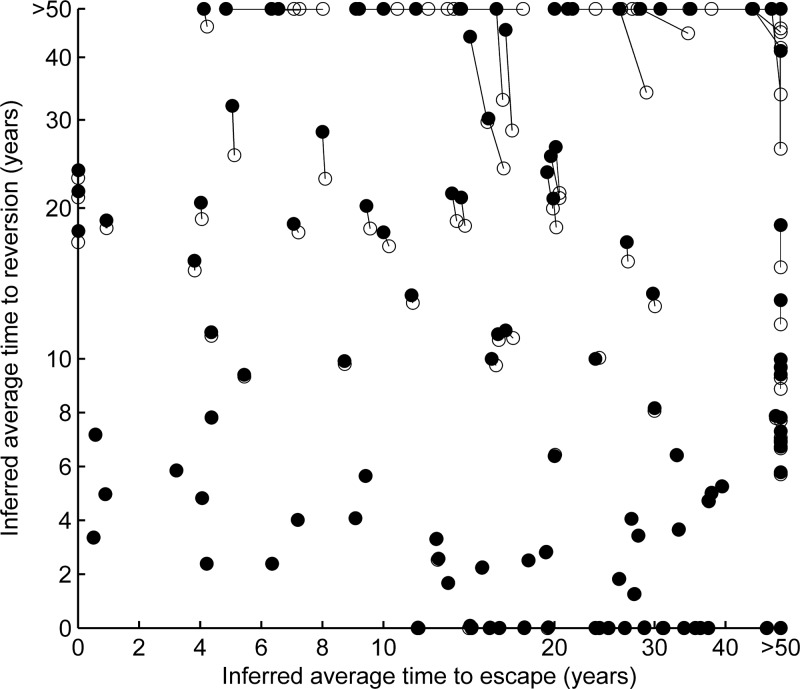
Escape and reversion rates inferred from escape prevalence data using expressions 7 and 8 are broadly consistent with the rates inferred by fitting the model to the data. Escape and reversion rates for possible escape mutations inferred using two methods derived from our model are compared. The rates, inferred from cross-sectional escape prevalence data, are provided for all comparisons between sites in optimally defined epitopes in gag, RT, and nef and their restricting HLA alleles (see Materials and Methods for more details). Both sets of estimates assume exponential growth of the infection prevalence. For each HLA-site comparison, the filled circles represent the rates—presented in terms of their reciprocals and the average times to escape and reversion—inferred by fitting our model to the escape prevalence data using equations S1 and S2 in the supplemental material. The same results would be achieved by fitting the model, under the assumption of exponential growth, to the data (17). The data are presented on a linear scale from 0 to 10 years and on a log scale beyond 10 years. The open circles represent the rates inferred using direct expressions 7 and 8. Lines connect the rates inferred using both methods. Where the inferred rates are the same using both methods, only the filled symbol is visible. This representation shows that both methods yield broadly consistent results. For HLA comparisons yielding reversion rates measured in years (or faster), the inferred rates are entirely consistent. Only for HLA comparisons yielding very low reversion rates (average time to reversion, >20 years) are the inferred rates less consistent. Thus, overall, both expressions accurately differentiate between rates measured in years or decades, as well as accurately demonstrating the relative rates at which different mutations escape and revert. The parameter assumptions used for these estimates are discussed in Materials and Methods.

(iii) Analysis of the treatment interruption cohort data.

We analyzed the data from the Swiss treatment interruption cohort by first comparing the HIV gene sequence from each patient to the sample consensus sequence and identifying where mutations away from the consensus appeared. We considered all optimal CTL epitopes, as defined by the Los Alamos Database (http://www.hiv.lanl.gov), that were contained within the gene regions under study (gag, RT, and nef genes). We then performed multiple comparisons between all the sites in an optimally defined epitope and all HLA alleles restricting those epitopes present in four or more individuals. Some epitopes were restricted by more than one HLA allele, and in these cases, we also considered combinations of restrictions. HLA allele restrictions were considered according to their two-digit specifications. For each site-HLA comparison, we used a standard contingency table approach to evaluate the strength of the association between the HLA and the mutation at the site. For this analysis, Fisher's exact test was used to generate P values for the test of whether mutation at the site was more common in HLA-matched than in HLA-mismatched hosts.

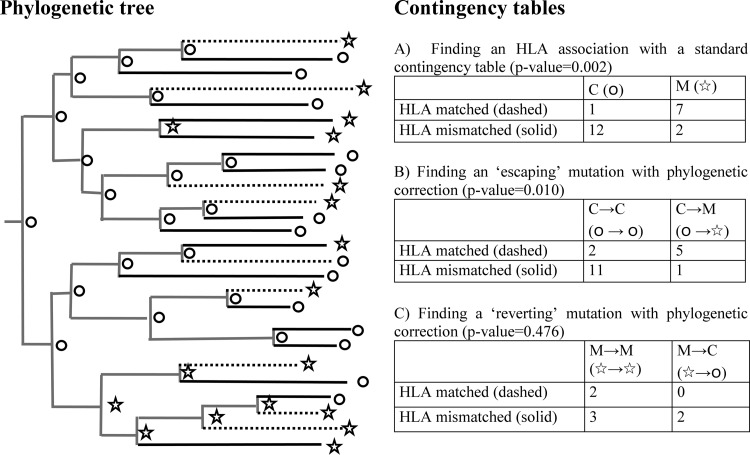
For each site-HLA comparison, we also evaluated the strength of the association using a method that accounts for phylogenies, as described by Bhattacharya et al. (3). To do this, for each of our five gene segments, we created a maximum-likelihood tree under the assumption that nucleotide sites evolve independently according to the generalized time reversible model (42). Genes were not stitched because the sample size for each gene was already relatively small and not all patients had sequences available for each segment. An algorithm called dnaml (15) that is part of the downloadable PHYLIP package (http://evolution.genetics.washington.edu/phylip) was used for this analysis. It assumes no recombination and a constant rate of mutation across all sites. The input order of sequences was jumbled 20 times for each segment. As well as producing a maximum-likelihood tree, this program also infers the expected sequences at internal nodes. We then identified mutations away from the sample consensus at the leaves and the internal nodes. For each site-HLA comparison, we used a contingency table approach (with Fisher's exact test) to test evidence for “escaping” and “reverting” mutations, as shown in Fig. 1.

Fig 1.

Techniques used to identify HLA-associated mutations. These methods are demonstrated on a hypothetical phylogenetic tree with node data. (A) The first method is a standard contingency table approach whereby, for each HLA-site comparison, patients are grouped according to whether they are matched or mismatched for the HLA allele and whether they exhibit mutation away from the subtype consensus at that site in their viral sequence. Although a phylogenetic tree is not required for this analysis, these data are represented on the left as dashed (HLA matched) and solid (HLA mismatched) end branches of the tree and circles (consensus amino acid [C]) and stars (mutation [M]) at the leaves of the tree. Typically, Fisher's exact test can be used to determine an association using this method. When sample sizes are equal, the association is stronger if the difference in the proportions of HLA-matched and HLA-mismatched hosts with the mutation is greater. (B and C) The second method is an adaptation of the standard approach whereby a consensus phylogenetic tree is first estimated to describe the evolutionary relationships between the viral sequences isolated from the individuals in the study. Sequences at each of the internal nodes are also inferred. A contingency table is then used to consider only the mutational changes that occurred over the most recent generation of the tree, i.e., the end branches. (B) To search for so-called escaping mutations, patients are grouped in a contingency table according to whether they are HLA matched or mismatched and whether the mutation emerged (○→☆) or there was no change from the wild-type state (○→○) during the most recent generation of the tree. Any sample patient (a patient at the leaves of the tree) whose evolutionary “parent” has the mutation (☆) is excluded from the analysis. Escaping mutations are defined when escape is statistically more prevalent in HLA-matched hosts. (C) To search for so-called reverting mutations, patients are grouped according to whether they are HLA matched or mismatched and, secondly, whether the mutation reverted (☆→○) or there was no change from the mutant state (☆→☆) during the most recent generation of the tree. Any sample patients whose evolutionary parent has the consensus strain (○) is excluded from the analysis. Reverting mutations are defined when reversion is statistically more likely in HLA-mismatched than in HLA-matched hosts.

Finally, for each site-HLA comparison, we also measured the fraction of HLA-matched hosts with mutation at the site (Λ¹) and the fraction of HLA-mismatched hosts with mutation at the site (Λ⁰). Only comparisons where the prevalence of escape was greater in HLA-matched than in HLA-mismatched hosts (ϕ1 < ϕ0) (n = 142) were considered further. For each HLA type, the prevalence of the HLA allele in a Caucasian population (π) was then estimated from Caucasian allele frequencies (28), assuming Mendelian genetics. This calculation ignores linkage between HLA alleles. For each comparison, escape and reversion rates were then estimated using two methods that assume that the epidemic is growing exponentially. The first was by fitting (using least squares) the mutation prevalences in the two host types to model predictions of those prevalences computed using equations S1 and S2 in the supplemental material. These predictions assume an epidemic duration (i.e., the time to the ancestor of the sample sequences) of 46 years (t = 46). This was based upon an estimate that the ancestor of U.S. B-clade strains date to 1954 (26) and the fact that our samples date to 2000. Finally, the transmission coefficient (βc) was assumed to equal 0.3 year⁻¹. This was calculated from an assumption that the basic reproductive number (R₀) of HIV is 3 (1) and that the life expectancy [1/(μ + α)] of infected hosts is 10 years (34) [for this model, R₀ is equal to βc/(μ + α)]. Escape and reversion rates estimated using this “fitting” method appear in Fig. S3 (see supplemental material), Fig. 3 (filled symbols), and Table 2. In Fig. 3 (unfilled symbols) we also present escape and reversion rates inferred directly using expressions S1 and S2 (see supplemental material). For these estimates, we also used a transmission coefficient of 0.3 year⁻¹.

RESULTS

Escape and reversion rates affect the strength of statistical associations.

Previous studies have identified CTL escape mutations by scanning population level HIV sequence data for statistical associations between mutations and HLA class I alleles (3, 9, 33). Traditionally, an escape mutation is declared when, for any given HLA allele, mutation away from the subtype/sample consensus at a particular site is markedly more prevalent in HLA-matched than HLA-mismatched hosts (6, 33). This can be tested using a contingency table (using, e.g., Fisher's exact test) in which patients are grouped first according to whether they are matched or mismatched for the HLA allele and second according to whether they have the mutation (Fig. 1, contingency table A). Roughly speaking, for any fixed sample size, the contingency table approach yields stronger associations when the difference in escape prevalence between HLA-matched and -mismatched hosts is greater. Recently it has been shown how this method can be adapted to consider phylogenetic relationships between sequences, and we evaluate one such method (3) below. However, to begin, we use a mathematical model to investigate how the rate of escape and the rate of reversion affect our ability to identify an escape mutation using a standard contingency table approach.

The model we use here has formerly been used to understand how within-host evolution and between-host transmission of CTL escape mutants affects the evolution of escape mutants at the population level (17). In brief, it models the dynamics of escape at a single CTL epitope or a single amino acid site within an epitope. For the purposes of this study, however, we focus on escape at a single site. The backbone of the model is a standard model of the frequency-dependent transmission of an infectious disease from which there is no recovery. In addition, the model includes viral heterogeneity (wild type/consensus or escape mutation), host heterogeneity (HLA matched or mismatched for the epitope), and two within-host evolutionary processes (escape in HLA-matched hosts and reversion in HLA-mismatched hosts). The model is described in more detail in Materials and Methods and in our previous publication (17). In that study, we used the model to show that if an escape mutation reverts in HLA-mismatched hosts, then throughout the epidemic it will be more prevalent in HLA-matched than in HLA-mismatched hosts. Furthermore, we showed how the difference in prevalence between the two host types is larger when escape in HLA-matched hosts and reversion in HLA-mismatched hosts are faster. Only mutations that do not revert in HLA-mismatched hosts continue to increase in prevalence and reach fixation in both host types, and this can take a long time (e.g., it could take over a century for a mutation that appears an average of 1 month postinfection in HLA-matched hosts, who make up 10% of the host population, to reach a prevalence greater than 95% in the whole population).

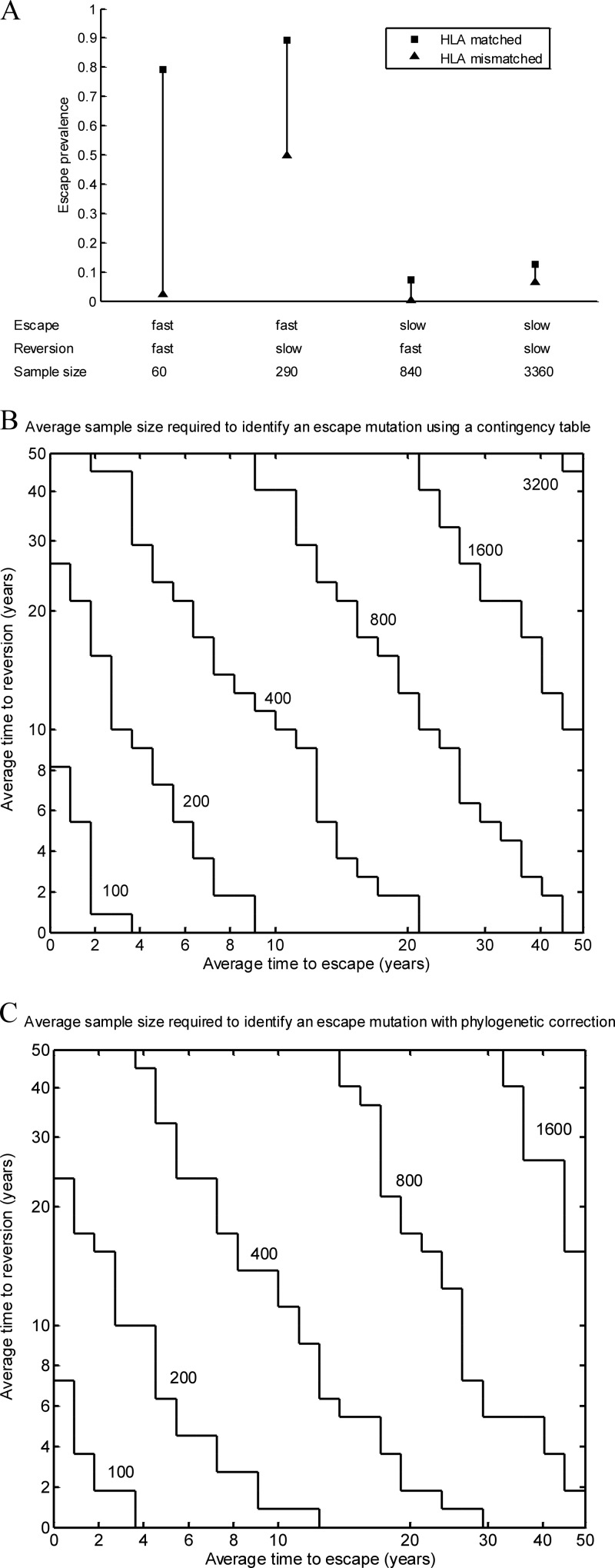
According to the model, for the foreseeable future, any particular escape mutation should therefore be more prevalent in HLA-matched than in HLA-mismatched hosts (see Fig. S1 in the supplemental material), and provided the sample size is large enough, it should be possible to identify the mutation by statistical association. In reality, sample sizes are bounded, and therefore, only those escape mutations with a large enough disparity in escape prevalence between HLA-matched and HLA-mismatched hosts will be identified. The model shows that this disparity is smaller when escape and reversion are slower (Fig. 2A and Figure S1). In the case of slowly escaping mutations, this is because the escape prevalence in both host types is low and thus the difference will also be small. In the case of slowly reverting mutants, it is because they persist in HLA-mismatched hosts and will be relatively prevalent in these hosts compared to HLA-matched hosts. The sample size required to find an association therefore increases as the rate of escape and the rate of reversion decrease. Equivalently, with a limited sample size, mutations that escape slowly and/or revert slowly can fail to be identified using a standard contingency table approach.

Fig 2.

CTL escape mutations identified through HLA associations favor those that escape rapidly in HLA-matched hosts and those that revert rapidly in HLA-mismatched hosts. (A) Model predictions show that the difference between the fractions of HLA-matched (squares) and -mismatched (triangles) hosts with an escape mutation 58 years into an epidemic (t = 58) is larger when the mutation escapes rapidly in HLA-matched hosts and when it reverts rapidly in HLA-mismatched hosts. Different escape and reversion rates are considered (fast escape, ϕ = 1 year⁻¹; slow escape, ϕ = 1/50 year⁻¹; fast reversion, ψ = 1 year⁻¹; and slow reversion, ψ = 1/50 year⁻¹). (B) Model predictions of the impact of escape and reversion rates on the average sample size required to identify an HLA-associated mutation using a traditional contingency table approach (1-tailed Fisher's exact test with a critical P value of 0.0001). Mutations with escape rates and reversion rates that fall below each contour line would, on average (with 50% power), be identified at that sample size. This representation shows that the average required sample size decreases as the escape and reversion rates increase. At a fixed sample size, identified mutations therefore favor those with higher escape and reversion rates. (C) Model predictions of the impacts of escape and reversion rates on the sample size required to identify so-called escaping mutations with a critical P value of 0.0001 using a method that corrects for phylogenies. These predictions show that, with phylogenetic correction, the average sample size required to identify an association is smaller when escape and reversion are faster. Identified mutations therefore favor those with higher escape and reversion rates. For each of these panels, we made the following additional assumptions: 10% of the population are HLA matched for the epitope (π = 0.1); the average life expectancy of infected hosts is 10 years (μ + α = 1/10 year⁻¹) (34); the average life expectancy of uninfected hosts is 80 years (μ = 1/80 year⁻¹); the transmission coefficient (βc) is 0.3, and thus, R₀ is equal to βc/(μ + α) is equal to 3 (1); the population size is 10⁷, and at the start of the epidemic, one individual is infected with the unmutated strain.

This is exemplified in Fig. 2B, a contour plot showing, for different sample sizes, the mutations, defined according to their escape and reversion rates, that will on average (i.e., with 50% power) be identified using a 1-tailed Fisher's exact test with a critical P value of 0.0001. These estimates derive from our model predictions of the prevalence of escape in HLA-matched and -mismatched hosts 58 years into an epidemic. This epidemic duration parameter assumes sampling from a U.S. B-clade-infected population and is estimated from a time-measured phylogeny showing that the ancestor of the U.S. B-clade epidemic dates back 58 years to 1954 (26). Other important model assumptions that we make for this analysis are as follows: 10% of the population are HLA matched for the epitope, the average life expectancy of infected hosts is 10 years (34), and the basic reproductive number of HIV is 3 (1). The basic reproductive number can be defined as the average number of secondary infections caused by one primary infection in a wholly susceptible population.

Figure 2B shows contour lines representing different sample sizes. Mutations with escape and reversion rates that fall below and to the left of a particular contour line would, on average, be identified at that sample size. Mutations with escape and reversion rates that fall above and to the right of that contour would not be identified. For example, for a sample size of 100, the mutations identified will, on average, take less than 4 years to escape and less than 8 years to revert. Thus, even rapidly escaping mutations can be missed if they revert slowly. Likewise, rapidly reverting mutations can be missed if they escape slowly. A corollary of this is that identified mutations favor those with higher escape and reversion rates. This is revealed by the observation that as the sample size increases, the contours expand, showing that mutations with a greater range of escape and reversion rates (i.e., including those that escape and/or revert more slowly) will be identified.

There are several points to note about these estimates. The first is that the stepwise appearance of the contours occurs because the contingency table requires the input of whole numbers of hosts in each of the four categories. Estimates of these values are first derived from the model and are then rounded. This compounds the approximations and results in contours that are not smooth. The second is that the estimates presented in Fig. 2A predict the sample size required to identify mutations with a critical P value of 0.0001 and a bounded type II error probability of 0.5 (power of 50%). Sample sizes required to identify escape mutations assuming different error bounds (critical P value, 0.00001, and type II error probability, 0.2 [80% power]) are explored further in Fig. S2 in the supplemental material. Inevitably, the required sample sizes are larger if the imposed bounds on these errors are smaller. A third important point is that the critical P values quoted here relate to the type I error rate of a single (or “uncorrected”) hypothesis test, yet HLA association studies typically involve multiple comparisons between different HLAs and mutations at different sites. According to the Bonferroni correction, critical P values of 0.0001 and 0.00001 are equivalent to specifying an overall critical value of 0.05 while correcting for 500 and 5,000 multiple comparisons, respectively. Finally, we note that our estimates assume that evolution is governed by the mean field dynamics of our simple model, and we do not account for stochasticity in the evolution of escape mutations or “noise” in the genome arising randomly or because of additional selective pressures. The type II error rates that we quote, therefore, do not account for all sources of type II error.

Our finding that escape and reversion rates affect the sample sizes required to identify a mutation is further explored in Table 1, where examples of six known escape sites are provided. Mutations at each of these sites have previously been shown to confer escape in vitro (18, 19, 24, 28, 37). The rates at which they escape in HLA-matched hosts and revert in HLA-mismatched hosts, as measured from a longitudinal cohort of 189 acute seroconverters, are presented in Table 1. These patients, described in detail elsewhere (14, 17), were first sampled a median of 60 days following their estimated dates of seroconversion and were then followed for a mean further 1.9 years (range, 0.5 to 5 years). In calculating the escape and reversion rates at each of the six identified amino acid sites, we assumed that any mutation away from the B-clade consensus at that site confers escape. By parameterizing the model with these rates and the relevant population HLA prevalences (Table 1) (30), we estimated the fractions of HLA-matched and -mismatched hosts with escape 58 years into an epidemic and the corresponding average sample size required to identify the escape site using a standard contingency table approach with a critical P value of 0.0001. One escape mutation that we consider is in the B*57-restricted p24 gag (HXB2 15 to 23) epitope, ISPRTLNAW (37). In HLA-matched patients, mutation away from isoleucine (I) at HXB2 15 appeared rapidly in HLA-matched hosts (average time to escape, 4.3 years), but reversion took 64 years averaged across the 58 patients who had a mutation at that site at their first sample. Parameterized by these rates, the model predicts that the escape mutant requires a sample size of 596 individuals to be identified. In contrast, mutation away from the threonine (T) at HXB2 110 in the B*57/58-restricted p24 gag epitope TSTLQEQIGW (HXB2 108 to 117) (28) both appears and reverts rapidly, and the escape mutation is estimated to be identifiable with 50% power in a sample size as small as 83 hosts.

In Fig. S3A in the supplemental material, we demonstrate further how mutations identified by HLA association favor those with higher escape and reversion rates by demonstrating the effect on cross-sectional data. For this figure, we analyze HIV-1 gag, RT, and nef sequences from 67 chronically (B-clade) infected participants of a Swiss treatment interruption study (35). Using these cross-sectional data, we performed multiple Fisher's exact HLA association tests, comparing each site (subtype consensus amino acid versus nonconsensus sites) in each optimal CTL epitope to each HLA allele restricting that epitope. For each comparison, we also calculated the fraction of HLA-matched and -mismatched hosts with and without the consensus amino acid. By employing a method—derived from our model—that we describe below, we then inferred escape and reversion rates that would yield the mutation prevalence at each site. More details of this analysis and the assumed model parameters are provided in Materials and Methods. Figure S3A in the supplemental material plots the inferred escape and reversion rates corresponding to each site-HLA comparison. Furthermore, different symbols are used to distinguish the strength of the HLA association (filled circles, P value < 0.05; open circles, P value ≥ 0.05) measured using Fisher's exact test. Note that, as throughout this analysis, these P values are related to a single-hypothesis test. In the context of multiple-hypothesis testing, it is more typical to bound the false-discovery rate (e.g., at 0.05) or to fix a much lower critical P value than was used here. In our analysis (with 862 comparisons), a critical P value of 5.8 × 10⁻⁵ (equal to 0.05/862) would be appropriate for an overall significance level of 0.05 using the Bonferroni correction. Using either of these criteria, only two escape mutations would be identified (see Table 2 for details) as significant. As the intention of this study was to demonstrate the impact of escape and reversion rates on association strength rather than to identify mutations through HLA association, we chose a critical P value that, given the relatively small sample sizes in our study, would be large enough to show the spread of escape mutations that would be identified at a fixed sample size. However, we found that irrespective of the critical P value used, mutations identified through HLA association favor those that escape and revert more rapidly.

In summary, we found that an escape mutation will appear more strongly associated with its restricting HLA if it escapes more rapidly in HLA-matched hosts and reverts more rapidly in HLA-mismatched hosts. A corollary of this is that escape mutations identified through statistical association favor those with higher escape and reversion rates.

Escape mutations identified by phylocorrective methods as escaping also favor those that escape and revert rapidly.

Statistical methods to locate sites under HLA-mediated selection have recently been adapted to account for evolutionary (phylogenetic) relationships between viral strains, thereby reducing subtype-related errors, as well as type II “noise” errors. Phylogenetic correction was not designed to reduce the impact of escape and reversion rates on type II “inherent lack of signal” errors, and no studies have yet explored the link between evolutionary rates and type II error rates (or the power of the study) using this method.

Bhattacharya et al. (3) were the first to correct for phylogenies. They described a method that first uses a maximum-likelihood algorithm, in which nucleotide sites were assumed to evolve independently according to the general reversible model, to infer a phylogenetic tree of the evolutionary relationships between the viruses isolated from each of the patients in the study. For each HLA type and each amino acid at a particular site under consideration, the presence or absence of that amino acid in each patient was noted and marked against its respective position at one of the leaves of the tree (Fig. 1). Similarly, the inferred presence or absence of that amino acid at each internal node was also marked on the tree. Whether each patient was HLA matched or mismatched for the HLA under consideration was also noted. The tree and the amino acid states were then used to infer the probable changes that have occurred over the most recent generation of the tree and to assess whether those changes are indicative of HLA-mediated selection. More specifically, the technique was used to identify so-called escaping and reverting HLA-associated mutations. Here, we discuss the definitions of escaping and reverting mutations used in that study and explore how escape and reversion rates affect the mutations identified.

The phylocorrective approach identifies the most likely amino acid state at each of the nodes preceding the leaves of the tree (i.e., prior to the most recent branching event). To identify HLA-associated escaping mutations, mutational changes that occurred over the most recent generation on the tree were compared statistically. A contingency table was used to group the sample hosts (those at the leaves of the tree) according to whether they were matched or mismatched for the HLA allele under consideration and whether during the most recent generation of the tree the mutation escaped (○→☆) (i.e., mutated away from the subtype consensus) or whether there was no change from the consensus at that site (○→○). This method, illustrated on a hypothetical tree in Fig. 1 (contingency table B), is employed to reduce potentially confounding signals caused by mutational changes that occur during earlier generations of the phylogenetic tree. However, because population studies normally sample only a portion of the hosts from the population, even the most recent generation of the inferred tree will, on average, represent more than one true transmission generation (i.e., the passage of the virus between several individuals). Over this shorter time period, escape and reversion rates influence the distribution of an escape mutation among HLA-matched and -mismatched hosts—and thus the average sample size required to identify an association—in the same manner we have described for the whole epidemic duration. The precise extent of their influence, however, varies because the period over which they can influence the distribution of the mutation between the two host types is shorter and because the phylocorrective method inherently reduces the data in the contingency to only those patients linked in the previous generation to a consensus strain.

This is shown in Fig. 2C, in which we used the model to assess how escape and reversion rates affect the sample size required to identify an HLA-associated escaping mutation using this method. As for the analysis in Fig. 2B, we assumed that the duration of the epidemic among the population is 58 years. Based upon measurements from the same phylogeny, we also assumed that the average duration of the most recent generation of the tree is 25 years (26). We first used the model to estimate the fraction of HLA-matched and -mismatched hosts who have a strain with the consensus amino acid (○) after 33 years of an epidemic to represent all but the most recent generation of the tree. We then used the model to consider the fraction of HLA-matched and -mismatched hosts with the escape mutation 25 years later (year 58), whose infection would have descended from a strain with the consensus amino acid at year 33. This gave an estimate of the fraction of HLA-matched and -mismatched hosts displaying a change from the consensus amino acid to the escape mutant (○→☆) or no change from the consensus (○→○) over the last generation of the tree. We then used a contingency table (Fig. 1, contingency table B) to test whether a change from consensus to escape occurred more frequently than no change from the consensus in HLA-matched compared to HLA-mismatched hosts.

Figure 2C shows that the average sample size required to identify an escaping mutation under phylogenetic correction remains smaller for mutations that not only escape faster, but also revert faster. Mutations identified as escaping, therefore, also favor those with higher escape and reversion rates. For mutations that escape and revert rapidly, the average required sample size is approximately the same using both methods. For mutations that escape and revert more slowly, the required sample sizes are a little smaller using the phylocorrective method. This is because, in effect, we are comparing the footprints of HLA-mediated selection that emerge over a 25-year period to those over a 58-year period. Over a 58-year period, there is more time for the signal of escape to become blurred by the spread of mutants between hosts.

To demonstrate these findings on data, we repeated the analysis shown in Fig. S3A in the supplemental material, but for each of the site-HLA comparisons, we measured the strength of the HLA association according to the phylocorrective method employed by Bhattacharya et al. (3) (see Materials and Methods for details). The results, shown in Fig. S3B in the supplemental material, confirm that mutations identified as escaping using phylogenetically corrected HLA association tests favor those that escape and revert more rapidly.

Bhattacharya et al. (3) also described a complementary technique to use phylogenetic correction to identify so-called reverting mutations. With this method (Fig. 1, contingency table C), a contingency table was used to group the sample hosts according to whether they were matched or mismatched for the HLA allele under consideration and whether during the most recent generation of the tree the amino acid under consideration reverted toward consensus (☆→○) or whether there was no change at that site (☆→☆). A reverting mutation was defined as when reversion was statistically more common in HLA-mismatched than HLA-matched hosts. We performed this technique on the cross-sectional data from the Swiss treatment interruption cohort to explore the impacts of escape and reversion rates on the strength of reverting HLA associations (see Fig. S3C in the supplemental material). The relatively small sample sizes in the Swiss data set yield large P values across all comparisons, but irrespective of the critical P value chosen, we found that this technique would miss some rapidly reverting mutations and identify some mutations that revert more slowly. This effect, which occurs because internal node sequences inferred using the maximum-likelihood method inevitably do not precisely match the true internal sequences, is also seen when we do not restrict comparisons only to sites in optimally defined epitopes (see Fig. S3D in the supplemental material). Incorrect inference of internal sequences particularly confuses the signals of reversion (more so than escape) because the models used to infer internal nodes do not explicitly model reversion. This finding reveals that using association techniques to identify so-called reverting mutations may yield misleading results, identifying some escape mutations that revert slowly while missing others that revert rapidly.

How to estimate escape and reversion rates from cross-sectional escape prevalence data.

Estimating escape and reversion rates of mutations could prove a useful tool in understanding more about CTL responses. Previously, we have demonstrated how the model used in this study can also be used to estimate the rates at which CTL escape mutations appear in HLA-matched hosts and revert in HLA-mismatched hosts using HLA-typed cross-sectional escape prevalence data (17). In that study, we estimated escape and reversion rates for previously defined escape mutants in gag, RT, and nef using data from the Swiss treatment interruption cohort described here. We found these estimates to be in close agreement with the rates measured directly from longitudinal data gathered from the London cohort of acute seroconverters (also described here). We also showed how model predictions of changes in the prevalences of escape mutants among the population are in close agreement with the changes that have been observed. These results support the estimation of escape and reversion rates from cross-sectional data as a means for understanding more about CTL antigens. Understanding the rates at which different sites escape and revert might be directly relevant to the choice of vaccine antigens. It might also prove useful for testing hypotheses (31).

The method for estimating rates that we described previously requires model simulations to be run. The model is used to predict the prevalence of escape in HLA-matched and -mismatched hosts at a specific time in the epidemic for different escape and reversion rates. The observed prevalence of the escape mutation in HLA-matched and -mismatched hosts is then compared to the different model predictions. The paired escape and reversion rates that best match the observations are then identified. Here, we present details of how model-derived analytic expressions defining the escape prevalences in HLA-matched and -mismatched hosts can be used to simplify the estimation process, thus making the method broadly accessible. The trade-off using these simplifications is that they require additional assumptions and that some level of error is incurred when these assumptions are not upheld. We investigate the extent of these errors by applying our methods to data. In the supplemental material, we provide the derivation of these expressions and discuss more theoretically the reasons for the associated errors.

To estimate escape and reversion rates using the methods discussed here, one must first consider whether the underlying epidemic can approximate a growing epidemic (technically, one growing exponentially). In our previous study, where we showed our escape and reversion rate estimates to be in good agreement with independent longitudinal data, we made this assumption implicitly through our parameter assumptions. As we demonstrate, however, whether or not this assumption is upheld will, at most, change the magnitude of the inferred rates. Importantly, it will not affect the relative rates at which different sites are estimated to escape and revert.

Under the assumption that the epidemic is growing, expressions S1 and S2 (provided in the supplemental material and in the supplemental material of our previous publication [17]) can be used to estimate the escape and reversion rates of different escape mutations. Respectively, these expressions predict the escape prevalence in HLA-matched (Λ¹) and -mismatched (Λ⁰) hosts under assumptions about the rate at which the mutation escapes in HLA-matched hosts (ϕ) and reverts in HLA-mismatched hosts (ψ). The term “escape prevalence” is used here to mean the fraction of hosts who are infected with a strain containing the escape mutation. For estimation of the escape and reversion rates of a particular mutation, observations of the prevalence of the mutation among HLA-matched and HLA-mismatched hosts in the population at a specific point in time measured in a cross-section of the population are required. In addition, three parameters must be provided: the prevalence of the restricting HLA in the population (π), the duration of the epidemic in the population (t), and the transmission coefficient (βc), a parameter defining the transmissibility of the virus. More precisely, it can be defined as the multiple of the average rate of partner exchange (c) and the transmission probability per partnership (β). Neither of these parameters is simple to estimate directly, but their combined value (βc) can be inferred from two quantities about which more is known. First, the death rate of infected hosts (μ + α)—or the reciprocal of the average life expectancy of infected hosts—and, second, the basic reproductive number (R₀), since for our model, βc is equal to (μ + α)R₀ (17). We discuss the estimation of these parameters in more detail in Materials and Methods, where we demonstrate the use of this method Table 2, Fig. 3, and Fig. S3 in the supplemental material.

With these three parameters (π, t, and βc) fixed, expressions S1 and S2 (see the supplemental material) reveal that escape prevalences in HLA-matched and -mismatched hosts both strictly increase with higher escape rates and lower reversion rates; thus, any unique pair of escape and reversion rates correspond to a unique pair of escape prevalences in the two host types. In order to estimate escape and reversion rates, expressions S1 and S2 in the supplemental material can be used to calculate pairs of escape prevalences that correspond to different pairs of escape and reversion rates spanning the nonnegative real numbers. Least squares can then be used to find the unique pair of escape and reversion rates that minimizes the difference between the observed and expected escape prevalences. If necessary, this calculation can be performed using a standard spreadsheet program, making it accessible to a broad range of users.

In Table 2, we demonstrate the use of this method in identifying escape mutations in HIV. We show how escape and reversion rate estimation can be used alongside HLA association measurements to provide a broader understanding of the characteristics of different epitopes. Such knowledge may inform the identification of epitopes that could prove to be useful components of a CTL-inducing vaccine. Although the ideal characteristics of a vaccine epitope remain unclear, we speculate that epitopes with escape mutations that revert rapidly may be preferable because they could robustly induce CTL responses over many generations. Whether high escape rates are also an indication of a good vaccine epitope is uncertain. Rapid escape indicates that an epitope induces a strong response but that the response may be short-lived. Epitopes that escape at a slower pace may induce weaker but longer-lived responses and may therefore also be important, yet they may not typically be identified as being of interest by HLA association methods. To demonstrate this, in Table 2 we identify two groups of epitopes (and their corresponding escape mutations) in gag, RT, and nef that could prove to be robust components of an HIV vaccine. These escape mutations were identified by first performing multiple comparisons between sites in optimally defined epitopes and their restricting HLA alleles and, for each comparison, inferring escape and reversion rates as described previously (see Fig. S3 in the supplemental material). Escape mutations were then classified according to two criteria: (i) those that escape rapidly (average time to escape, <10 years) and revert rapidly (average time to reversion, <10 years) and (ii) those that escape at a slightly slower pace (average time to escape, 10 to 15 years) and revert rapidly (average time to reversion, <10 years). For comparison, we also list additional escape mutations that would be identified using standard or phylocorrective association tests with a critical P value of 0.05. P values of less than 0.05 are highlighted in Table 2. Using this approach, we found 11 mutations that escape and revert rapidly and a further 7 mutations that escape at a slower pace but revert rapidly. We speculate that these epitopes could be important for the development of a robust CTL-based vaccine, yet most of those in the slower-escape bracket (10 to 15 years) would not be identified by HLA association techniques with a critical P value of 0.05. Four additional mutations (in two additional epitopes), however, would be identified by HLA association techniques. Most of them escape very rapidly but revert comparatively slowly, and their corresponding epitopes may be less robust in the context of a vaccine. We note once again that in the context of multiple-hypothesis tests, a critical P value lower than 0.05 would typically be used for association tests, but given the relatively small sample sizes of our study, we use this higher bound to demonstrate, by comparison, the application of our method. Nevertheless, for completeness, we also highlight two escape mutations that remain significant at a level of 0.05 after correction for multiple comparisons, using either the Bonferroni correction (P < 5.8 × 10⁻⁵ = 0.05/862) or false-discovery rate control (q value < 0.05). q values (the false discovery rate analogue of P values) estimated using the Benjamini and Hochberg algorithm are provided where they exist and can be used as a rough guide for the relationship between q values and P values using this type of data.

A further simplification for estimating escape and reversion rates under the assumption of an exponentially growing epidemic is to estimate them directly using analytic expressions 7 and 8. The derivation of these formulae is provided in the supplemental material. Fortunately, the use of these expressions requires estimation and substitution of the HLA prevalence (π) and only one epidemic parameter (the transmission coefficient, βc). Moreover, these expressions show that the inferred escape and reversion rates are proportional to the transmission coefficient. Thus, even acknowledging the uncertainty surrounding estimation of the transmission coefficient, this method is useful for ranking the escape and reversion rates of different epitopes. The trade-off using these simple analytic formulae is that they are an approximation to the rates yielded by fitting the data to the model during the exponential growth phase of the epidemic. In Fig. 3, however, we show that, broadly speaking, both methods yield the same results. In the figure, cross-sectional sequence data from HLA-typed participants of a Swiss treatment interruption cohort were analyzed. As described more fully in Materials and Methods and Table 2 and in Fig. S3 in the supplemental material, comparisons were made between all sites in optimally defined epitopes and their restricting HLAs. For each site-HLA comparison where the prevalence of mutation away from the sample consensus was greater in HLA-matched than HLA-mismatched hosts, we inferred the rates of escape and reversion using both of these methods. This representation shows that most escape rates and reversion rates measured in years are consistent using both methods. Reversion rates measured in decades, however, are slightly underestimated. Nevertheless, both expressions differentiate between rates measured in years and decades and consistently estimate the relative rates at which different mutations escape and revert. All of the rapidly reverting escape mutations that we show in Table 2 (average time to escape, <15 years, and average time to reversion, <10 years) have the same inferred rates irrespective of the method used. Put in the context of other potential sources of error in the estimation of escape and reversion rates, e.g., from sampling errors, estimation of the transmission coefficient, and more complex dynamics underpinning the evolution of escape mutations than are included in our model, we expect that errors incurred through the use of these direct formulae are unlikely to be significant. The formulae are as follows: inferred escape rate,

$$\phi =\beta c\left(1-\pi \right)\left(\frac{{\Lambda }^1-{\Lambda }^0}{1-{\Lambda }^1}\right)$$ (7)

inferred reversion rate,

$$\psi =\beta c\pi \left(\frac{{\Lambda }^1-{\Lambda }^0}{{\Lambda }^0}\right)$$ (8)

Depending upon the population under study, the assumption that we have made thus far that the epidemic is growing exponentially may or may not be valid. We note, however, that at most this assumption would affect the magnitude of the estimated rates. It would not influence the rank estimates corresponding to different escape mutations. This is apparent from expressions 9 and 10 for estimating escape and reversion rates under the assumption that the entire system—the escape prevalence as well as the epidemic dynamics—has reached equilibrium. These expressions are identical to expressions 7 and 8 except that they have the death rate of infected hosts, μ + α (equal to 0.1 year⁻¹ in our calculations) as a multiplying factor in place of the transmission coefficient, βc (equal to 0.3 year⁻¹ in our calculations). Irrespective of the underlying epidemic dynamics, the value of this multiplying factor is therefore the primary assumption that needs to made about the epidemic for these calculations. In our previous publication, we used assumed a value of 0.3 year⁻¹ and found this to yield results consistent with independent data sets. If a smaller parameter value was used, the inferred rates would be lower. For example, if 0.1 year⁻¹ was used, as might be appropriate under the assumption that the system has reached equilibrium, the inferred rates would be a third of the size: inferred escape rate,

$$\phi =\left(\mu +\alpha \right)\left(1-\pi \right)\left(\frac{{\Lambda }^1-{\Lambda }^0}{1-{\Lambda }^1}\right)$$ (9)

inferred reversion rate,

$$\psi =\left(\mu +\alpha \right)\pi \left(\frac{{\Lambda }^1-{\Lambda }^0}{{\Lambda }^0}\right)$$ (10)

In summary, we provide analytic expressions that can be used to estimate escape and reversion rates from HLA-typed cross-sectional escape prevalence data without the need to run model simulations. These expressions yield results broadly similar to the rates inferred by fitting the model to the data. Estimation using these expressions requires only one assumption about the epidemic in the form of a single parameter. Furthermore, irrespective of the assumed parameter, the relative rates inferred for different escape mutations will remain fixed.

DISCUSSION

In this study, we first asked how different factors affect our ability to detect HIV CTL escape mutations by looking for sites under HLA-mediated positive selection. We first considered a traditional contingency table approach to find associations. We have shown that the average sample size required to find an association is smaller when the mutation escapes rapidly in HLA-matched hosts and when it reverts rapidly in HLA-mismatched hosts. As a result, escape mutations identified by statistical association systematically favor those with higher escape and reversion rates. Recently, association studies have accounted for phylogenies. While these new techniques have been used to separately identify so-called escaping mutations and reverting mutations, they do not account for escape and reversion occurring simultaneously in the population. As a result, identified escaping mutations also favor those with higher escape and reversion rates. Our analysis also indicates that phylocorrective methods to identify reverting mutations are likely to miss some rapidly reverting mutations while identifying others that revert more slowly. This effect, which stems from imperfect estimation of sequences at internal nodes, could yield misleading results.

It is worth noting that the approach for identifying escaping and reverting mutations investigated here was not the only phylocorrective approach described by Bhattacharya et al. (3). In a second approach, for each association tested, two models were formally compared. The null model, in which the observations are generated by the phylogenetic tree alone, and the alternative model, in which an additional selective pressure acts at the leaves of the trees. This technique has been described in other publications (12, 31), where it has also been used to separately identify escaping and reverting mutations. The models used do not ordinarily account for escape and reversion occurring simultaneously in the population. Instead, they use different models to assess evidence for each process separately. Any such approach will, by definition, be unable to disentangle the signals of escape and reversion within the data. We therefore expect that escape and reversion rates influence the mutations identified through this second approach in a manner similar to that described for the first approach, but further analysis would be required to test this formally.

We have described how expressions derived from our model can be used to estimate escape and reversion rates of different mutations using cross-sectional escape prevalence data from HLA-typed individuals. Escape and reversion rate estimates are useful for understanding the characteristics of different epitopes. We demonstrate the use of this method by identifying immunogenic epitopes that are more likely to remain robust in the context of a CTL-based vaccine. Escape and reversion rate estimates could also be used in testing hypothesis by, for example, comparing them with other immunological and virological markers. As our model simultaneously accounts for escape in HLA-matched hosts, reversion in HLA-mismatched hosts, and the transmission of escape mutants between hosts, our estimates therefore inherently also account for these processes. Nonetheless, our model is still a simplified representation of the way in which escape mutations evolve and spread through the population. For example, it assumes that escape mutations cannot revert in HLA-matched hosts, that escape and reversion rates are homogeneous throughout the duration of infection, that individuals are equally infectious throughout their infection, that individuals are infected with a single viral strain, and that epitopes are independent entities that do not overlap each other. We have intentionally used this simple representation to allow a transparent explanation of the assumptions that we have made. As we have discussed in detail previously (17), although these factors could affect the pace at which escape mutations are changing in prevalence in the population, they would not change our qualitative predictions about how their prevalence is influenced by escape and reversion rates, indicating that additional factors are unlikely to significantly affect our escape and reversion rate estimates. Parameter estimates (notably the transmission coefficient, βc) also influence the inferred escape and reversion rates but also do not affect the relative inferred rates of different mutations. Furthermore, comparisons between within-host data and population level data using the model yield consistent results from both quantitative and qualitative perspectives (17), suggesting that our estimates are largely robust to the assumptions of the model. However, our mean field approach does not explicitly make use of all the information about the evolutionary history of the virus embedded throughout the sequences, and we therefore advocate the development of new methods that can exploit such information.

Our qualitative inferences about how escape and reversion rates affect the strength of HLA associations are also likely to be robust to the model assumptions. We note, however, that our methods for estimating the sample sizes required to identify HLA associations require additional assumptions that could affect our quantitative predictions. Our method for investigating phylocorrective techniques assumes that the inferred tree is an accurate representation of the evolutionary relationships and that across the tree, the most recent generation is 25 years. If this period was, on average, longer than 25 years, it would yield results closer to those observed without phylocorrection—the required sample sizes for slowly reverting mutations would be larger. If the period was shorter (i.e., the population was more heavily sampled), the required sample sizes would be smaller.