Abstract
It is increasingly clear that bacteria manage to evade killing by antibiotics and antimicrobials in a variety of ways, including mutation, phenotypic variations, and formation of biofilms. With recent advances in understanding the dynamics of the tolerance mechanisms, there have been subsequent advances in understanding how to manipulate the bacterial environments to eradicate the bacteria. This study focuses on using mathematical techniques to find the optimal disinfection strategy to eliminate the bacteria while managing the load of antibiotic that is applied. In this model, the bacterial population is separated into those that are tolerant to the antibiotic and those that are susceptible to disinfection. There are transitions between the two populations whose rates depend on the chemical environment. Our results extend previous mathematical studies to include more realistic methods of applying the disinfectant. The goal is to provide experimentally testable predictions that have been lacking in previous mathematical studies. In particular, we provide the optimal disinfection protocol under a variety of assumptions within the model that can be used to validate or invalidate our simplifying assumptions and the experimental hypotheses that we used to develop the model. We find that constant dosing is not the optimal method for disinfection. Rather, cycling between application and withdrawal of the antibiotic yields the fastest killing of the bacteria.
INTRODUCTION
The difficulties in treating bacterial infections are becoming increasingly more understood. Evidently, bacteria exploit a host of mechanisms to avoid eradication (7, 10, 11). In this study, we do not include mutation or genotypic variation but focus on other tolerance mechanisms that depend more explicitly on the environment. Several of these mechanisms, such as growth-rate-dependent disinfection, depend on the replication stage of the bacteria (8). Others, such as physical protection, depend on whether the bacteria are planktonic or buried within a biofilm (10, 20).
We study the disinfection of bacteria mathematically in a general chemostat setting that has implications for both planktonic and biofilm-bound bacteria. We use the term “chemostat” to refer to a continuously stirred tank reactor (22), which is a generalization of the concept first described elsewhere (19). We focus on the dynamics of a protected subpopulation of bacteria referred to as “persisters.” There is increasing evidence that persisters are found in both planktonic and biofilm settings (8, 13, 17). We also consider how the transient or permanent attachment of bacteria affects the dynamics of disinfection. This complements a series of studies that consider optimal disinfection in batch, chemostat, and biofilm settings (2–4). The novel aspect of this study is that rather than proposing a disinfection protocol and determining whether this is effective, the goal is to determine the optimal protocol. Moreover, we include methods for applying the antibiotic in experiments more realistic than those that have been studied in previous mathematical models.
We remark that one of the reasons for introducing the chemostat model is to untangle the effect of the persister population on the dynamics of the population. In a standard MIC test, one looks for the minimum concentration of antibiotic that suppresses the growth of the bacteria. Since the persister cells do not reproduce measurably, the presence of this subpopulation does not alter the observed MIC. Likewise, if one tests for the minimum bactericidal concentration, the persisters are present at such low concentrations that the results for a mixed population are likely to be quite similar to those for a population of only susceptible bacteria. However, one way to understand the effect of the persister population is to consider the optimal disinfection protocol (i.e., the method that eliminates all bacteria the fastest). Although this can be studied theoretically in batch culture, it is not immediately obvious how to implement this experimentally. We argue here that a chemostat is a natural framework where the persister population plays a role in the rate of elimination and a framework that is feasible to implement in bench experiments. Our hope is that these observations may inspire novel testing to understand the persister dynamics.
In the next few sections, we review the relevant biological observations that motivate the particular model that is developed. We then describe previous mathematical models to provide a contrast with the current analysis. The method for determining the optimal disinfection protocol is determined using Pontryagin's principle (14). Pontryagin's principle is a method to optimize the behavior of a dynamic system relative to some goal (the objective) and adjust a control parameter. This is mathematically similar to finding the location of maxima (or minima) of a function by finding zeros of the derivative. Unfortunately, it is quite difficult to determine the optimal conditions explicitly, so we approximate the solution numerically. This is described in some detail in the Appendix. The results of a sequence of numerical studies indicating how this method extends previous results and suggests particular treatment protocols are outlined. These numerical studies also explore the role of attachment of the bacteria, although we do not include biofilm-specific concepts (e.g., exopolymeric substances [EPSs], spatial variations, and fluid dynamics).
Biological background.
It has been established that it is much more difficult to kill bacteria within a biofilm than similar numbers of planktonic bacteria (6). There is evidence that bacteria from disrupted biofilms have similar killing rates as planktonic bacteria, so the source of tolerance may not be intrinsic to the biofilm itself (8, 23). However, the biofilm structure offers additional, layered protection against diffusible antimicrobials. The protective mechanisms are often separated into physical, physiological, and phenotypic protection.
Physical protection stems from the polymeric gel that surrounds the bacteria. The EPS hinders the diffusion of antimicrobials into the biofilm both passively (by obstructing the space where molecules are diffusing) and actively (by reacting with the antimicrobial agents) (24). Although biocide penetration may be delayed, it is typically not completely prevented (26). Therefore, there are several other tolerance mechanisms that must play a role in the failure of disinfection of biofilms. Here we are not modeling biofilm dynamics. Many of the observation data that our model addresses come from either planktonic cultures or disrupted biofilms, where delayed biocide penetration does not play a role. We do include other mechanisms that are relevant to both biofilm and planktonic bacteria.
Most biocides and antibiotics are more effective at killing actively reproducing bacteria, so heterogeneous growth rates within the biofilm imply spatial variation in killing. Typical observations indicate that bacteria in the outer layers of the biofilm are more easily killed than those deeper within the biofilm (8, 27). This is presumably because the deeper regions of the biofilm are less active than those nearer the nutrient source. The growth-stage-dependent disinfection also plays a role in the reactor studies, since the nutrient may be dynamic in time as the population grows or is killed by the antibiotic. In a well-mixed system, such as a chemostat, there may be variations in growth stage if the bacteria and other constituents are not at their steady-state values. We account for this in our model of bacterial disinfection.
These tolerance mechanisms offer transient protection in biofilm settings since long-term application of a biocide will force the biocide concentration to equilibrate within the biofilm (at least in the case of a stoichiometric reaction, where the EPS/antimicrobial reaction destroys the reactive ability of the EPS). Moreover, long-term application will eventually remove the bacteria that form nutrient gradients through consumption. It is not completely clear what role these defense mechanisms play in a chemostat setting, especially if the source of nutrient and antibiotic is not constant.
One might assume that the way to eliminate bacteria is to apply sufficient antimicrobial long enough to overwhelm the tolerance mechanisms. Unfortunately, this is not what is observed. Even without the EPS network, there are subpopulations that resist the antimicrobial challenge (1, 8, 13, 17). There is some debate about the mechanisms that govern the dynamics of the persistent subpopulations, but it seems clear that some bacteria within a population forgo reproduction to evade microbial challenges. These bacteria have been termed “persisters” and allow the biofilm to be repopulated once the challenge is gone. We refer the readers to previously published reports (1, 8, 17) for reviews of possible biological mechanisms.
Here, we follow the assumptions made in previous studies (2, 3, 16) that pose the persister dynamics in relatively simple terms. This model is compatible with others that bring different biological details into the model, such as the one described in reference 1. However, this model assumes a very simple transition into the persister state, one that may not be the only transformational process. The arguments and methods described below are quite robust in terms of the qualitative results, but we focus on one concrete model to clarify the mathematical methods and comparisons. The present analysis provides an experimentally testable hypothesis for a generic model of persister formation.
We also note that the persister hypothesis is different from an adaptive response, such as the one proposed in reference 28. An adaptive response requires low levels of antimicrobials to trigger the change in phenotype, where persister formation seems to depend on growth stage (13, 17). The low-level signal for an adaptive response can be a consequence of the diffusion through the biofilm; however, persisters seem to exist even in the absence of the physical biofilm (8, 13).
Mathematical background.
In this section, we briefly review a sequence of studies that motivates the current investigation. This study focuses on planktonic cultures, so we do not include biofilm processes such as diffusion of antibiotic or production of EPS. This has been done previously (4) (although without attempting to optimize the disinfection). There are models similar to the current model developed in reference 1, which focused on persister formation coupled with experimental studies; references 4 and 21, which focused on the effect of spatial variations in persisters; reference 18, which focused on potential molecular mechanisms for persister formation; reference 28, which focused on adaptive response; and reference 15, which focused on senescence. A thorough review of these studies is beyond the scope of this paper. Instead, we focus the background on one particular model of persister formation that is consistent with many experimental observations and sets the stage for the optimal control study presented here.
A simple model of persister dynamics was proposed (2) and extended to a chemostat (3, 16). Spatial variations were neglected, and the bacterial densities were separated into susceptible bacteria, Bs, and persister bacteria, Bp. A single growth-limiting substrate, S, was also incorporated. Each of the dependent variables is measured in units of mg liter−1. Further parameters, units, and values used throughout this report are shown in Table 1.
Table 1.
Parameter values used in the simulations
| Definition | Symbol | Units | Value |
|---|---|---|---|
| Susceptible bacterial density | Bs | mg liter−1 | Variable |
| Persister bacterial density | Bp | mg liter−1 | Variable |
| Substrate density | S | mg liter−1 | Variable |
| Antibiotic density | A | mg liter−1 | Variable |
| Time | t | h | Variable |
| Nutrient dependence | f(S) | Nondimensional | S/(ks + s) |
| Antibiotic reservoir density | Ar | mg liter−1 | 3.0 |
| Nutrient reservoir density | Sr | mg liter−1 | 1.0 |
| Dilution rate (basic chemostat) | D | h−1 | 0–50 |
| Dilution rate for antibiotic | DA | h−1 | 0–50 |
| Dilution rate for nutrient | DS | h−1 | 0–50 |
| Dilution rate for persister | DBp | h−1 | 0–50 |
| Dilution rate for susceptible population | DBs | h−1 | 0–50 |
| Transition rate to persister | kl | h−1 | 0.1 |
| Transition rate from persistera | kg | h−1 | |
| Maximum transition rate from persister | kg,max | h−1 | 0.5 |
| Maximum death rate of susceptible population | kd | h−1 | 3.0 |
| Width of transition ratea | ϵ | mg liter−1 | 0.01 |
| Yield | Y | Nondimensional | 0.1 |
| Maximal growth rate | μ | h−1 | 0.417 |
| Half-saturation | ks | mg liter−1 | 0.2 |
| Threshold for persister reversiona | Athresh | mg liter−1 | 0.05 |
| Antibiotic sensitivitya | K | Nondimensional | 0.05 |
| Final susceptible population sensitivitya | Ks | liter mg−1 | 100 |
| Final persister sensitivitya | Kp | liter mg−1 | 100 |
Parameters specific to this study. The other parameters are the same as described elsewhere (16), and the dilution rates are specified in the simulations.
The dynamics of the system are represented as ordinary differential equations governing the rates of change of the densities in time. Susceptible bacteria consume nutrient, reproduce, and are killed by the antibiotic. Persisters consume a negligible amount of nutrient and do not reproduce. The persisters are not reproducing, and we are explicitly assuming that persisters are insensitive to the antibiotic.
The two populations are also coupled. Susceptible bacteria can transition into the persister population at a rate that is independent of the antibiotic concentration but depends on the nutrient availability. Persister bacteria can transition back to susceptible bacteria at a rate that depends on the antibiotic concentration. It was previously shown (17) that persisters either do not revert or revert very slowly, unless the antibiotic concentration is zero (or possibly close to zero). It was further demonstrated that the reversion rate (in the absence of antibiotic) is much lower than the transition rate from susceptible to persister bacteria. There is some debate in the literature concerning the reversion process. We have not attempted to include observations such as those included elsewhere (9) that indicate that persisters may revert to susceptible bacteria even in the presence of certain antibiotics; however, preliminary testing of our model (data not shown) indicates that this mainly affects the time scales but not the qualitative results of our model.
The nutrient concentration changes as nutrient is added to the system and consumed by the bacteria. Additionally, all the densities are washed out of the system at a rate D (h−1), termed the dilution rate. For the chemostat system described previously (3, 16), the particular model that was derived was
| (1) |
| (2) |
| (3) |
The assumptions described above are captured in the particular forms of the disinfection and transition processes. The term (μ − kd − kl)f(S)Bs represents the growth, death, and transition processes that all depend on the function f(S) that denotes the dependence on nutrient. Typical Monod kinetics are used to handle growth, where the growth rate is μS/(ks + S). The maximal specific growth rate, in units of h−1, is denoted μ. The function f(S) = S/(ks + S) is dimensionless, and ks is the half-saturation constant, that is, the substrate density at which the bacterial population is reproducing at half the maximal rate. Thus, ks has the same units as nutrient and scales the saturation scale for the system.
The disinfection rate for the population depends on the metabolic processes of the bacteria. Since observations for some antibiotics conclude that more bacteria are killed in the exponential phase than in the stationary phase, we assume that disinfection is proportional to growth rate (29). In this form of the model, the killing of bacteria by the antibiotic is proportional to the product of f(S) and the parameter kd (h−1), which denotes the maximal rate of killing of the population by the antibiotic.
The transition from susceptible to persister bacteria depends on the available nutrient; specifically, the transition is proportional to f(S) with rate constant kl (h−1). The reversion from persister to susceptible bacteria is represented by the term kg(A)Bp, where kg(A) (h−1) denotes the transition rate, which depends on the antibiotic density.
Details regarding the form of the reversion rate are given below, but we note that we are incorporating observations from previous reports (13, 17). In several papers (13, 17), the authors argue that the antibiotic attacks a target somewhere on the replication operon. The attachment does not harm the bacteria until they begin DNA replication; however, it blocks the bacteria from transitioning away from the nonreproductive persister state. It is not at all clear how correct this picture is, but it is clear that if persisters transition back to susceptible bacteria in the presence of antibiotics, constant application of antibiotic should be successful (which it is not). Therefore, it is likely that the presence of antibiotic hinders the transition from persisters to susceptible bacteria.
Equation 3 governs the dynamics of the nutrient concentration. The right-hand side represents the change in concentration due to nutrient introduced into the system at source concentration Sr. Nutrient is also lost due to dilution at a rate proportional to the dilution rate, D, and the nutrient concentration, S. The first term on the right-hand side of Equation 3 collects these as the change due to the difference between the reservoir and chemostat densities. If S is larger than Sr, the nutrient density within the chemostat decreases. Nutrient is consumed by susceptible bacteria at a rate proportional to the growth rate of the bacteria (represented by the last term in Equation 3). The constant Y refers to the yield fraction and indicates how much nutrient must be consumed to produce a change in bacterial density. This parameter is nondimensional because it is measured in mg liter−1 of bacteria per mg liter−1 of nutrient.
When D is equal to zero, which is equivalent to batch culture, there are some outcomes that can be easily determined. Constant application of antibiotic kills all susceptible bacteria, leaving persisters to repopulate once the challenge is removed. It can be shown that by cycling between biocide challenge and biocide withdrawal, both susceptible bacteria and persisters can be eliminated (2). The optimal dose/withdrawal protocol (i.e., the one that kills the entire population the fastest) can also be determined numerically. A more sophisticated version that incorporates one mechanism that might regulate the formation of persisters (toxin-antitoxin interaction) has also been proposed (3), and the predictions are similar to those developed here and elsewhere (1).
When the dilution rate D is nonzero (as in previous studies) at the same time that the antibiotic is applied as a piecewise constant (i.e., a step function that is locally constant but might have jumps in the value), the optimization can be determined analytically. We previously showed (16) that there is an optimal piecewise constant treatment that was consistent with the dose/withdrawal protocol proposed elsewhere (2).
There are several practical limitations in these studies. First, it is quite unrealistic to assume a piecewise constant treatment in a chemostat setting. In an experimental setup, the antibiotic is typically fed into the system in the same way that the nutrient is introduced (i.e., at a constant rate). This is not the discontinuous application used previously (2, 3, 16). It is not clear that there is a feasible experiment that corresponds to discontinuous disinfection. Another limitation is on the bacterial dilution, which was previously assumed to be constant (16) and zero (2). Neither of these corresponds to experimental observations. Planktonic bacteria have increased residence time, since they tend to transiently attach to the surface of the chemostat (25). However, if the attachment becomes permanent and a biofilm forms, the population is no longer spatially homogeneous.
A related study (12) compared experimental data with modeling predictions for a similar model (i.e., disinfection within a chemostat, where bacteria can transiently attach). In that study, the processes were constant in time, which makes the model completely solvable (unlike the model developed below).
The case of spatially varying bacterial density (as opposed to a well-mixed density) with piecewise constant treatment has been studied elsewhere (4); however, the structure of the model makes it extremely difficult to predict the optimal treatment. The model that includes spatial variation inherently depends on both time and space, and the model is a set of nonlinear partial differential equations set in multiple spatial dimensions. This leads to equations that are difficult to solve numerically, and there is no general theory for the optimal control problem for these sorts of equations. Both successful and unsuccessful piecewise constant treatment protocols were previously determined (16), but the precise cutoff depended nontrivially on the initial conditions and parameters (like bulk flow rates).
In this study, we assume spatial homogeneity but allow an increased residence time, even to infinite residence times. We also compare the case where the biocide is fed into the reactor at a rate that is discontinuous in time (even though the biocide concentration within the reactor is continuous) to the case where the biocide concentration is discontinuous in time, focusing on the case when the dilution rate of the antibiotic is several orders of magnitude greater than that of the nutrient. The main aim in this line of inquiry is to connect the current model with our previous results where the antibiotic dilution rate was essentially infinite. Moreover, we develop the optimal strategy of disinfection in a more experimentally realistic setting, where the control parameter is the source concentration of disinfectant. The results are comparable to those found previously but with more physical realism and different disinfection protocols predicted.
MATERIALS AND METHODS
Optimal control begins with a model for the interchange between persister and susceptible subpopulations and disinfection. This model is essentially the model described previously (16). As above, we define Bs and Bp to be the susceptible and persister bacterial densities inside a chemostat, respectively. Antibiotic and nutrient, with concentrations A and S, respectively, are introduced into the chemostat at concentrations Aru(t) and Sr, respectively. The maximal concentration of antibiotic that can be fed into the system (i.e., the reservoir density) is denoted Ar. This is different from the earlier model, where A was treated as a parameter rather than a dependent variable. That is, earlier A was treated as a known constant (i.e., parameter), while here A depends explicitly on time (i.e., a variable).
The function u(t) takes values between 0 and 1 and represents the proportion of the maximum concentration that is introduced into the reactor. This is easily viewed mathematically with u(t) as a dimensionless function that scales the concentration of antibiotic source. An intuitive interpretation would be to think of a valve that controls the release of antibiotic into the source feed from a reservoir of antibiotic. The valve can be completely open (corresponding to u = 1), shut (corresponding to u = 0), or partially open (corresponding to 0 < u < 1). In this way, u(t) controls the antibiotic concentration in the reactor. This control is indirect, since turning the valve off does not instantaneously remove the antibiotic from the reactor; in previous studies, this control is direct: when u is equal to 0, there is no antibiotic in the reactor.
The goal of the present analysis is to determine u(t), to eliminate the entire bacterial population as quickly as possible. In optimal control language, u(t) is the control. Meanwhile, nutrient is fed into the system at a constant concentration. The dynamics of the system are governed by
| (4) |
| (5) |
| (6) |
| (7) |
This system is very similar to the system described previously (16); however, there are several differences.
We allow different dilution rates for each component (denoted DB, DBp, Ds, and DA for the variables Bs, Bp, S, and A, respectively). It is important to note that the motivation for varying the dilution rates for all variables separately is multifaceted. Because no bacteria are fed into the system, DB, DBp represents the rate at which bacteria exit the chemostat. This rate may be different from the dilution rate of the chemostat, as the bacteria attach to the walls of the chemostat. Therefore, both DB and DBp are at most the same as the dilution rate of the chemical species but may be much smaller (in the case of high levels of attachment). Because bacterial attachment is a very important process in bacterial infections (especially in biofilms), the response to the system as DB and DBp are varied from the dilution rate of the chemical species is an important biological line of inquiry.
The reason to investigate how the system responds to a varying antibiotic dilution rate, DA, is to connect this investigation mathematically with our earlier studies, where DA was infinite. It is difficult to envisage an experiment that would be consistent with this (which is part of the motivation for this study), but one might imagine an antibiotic that was very susceptible to light. In the dark, the antibiotic works well, but if light is shined on the reactor, the antibiotic is completely reduced. Infinite dilution, periodic disinfection corresponds to programming the light to be on or off discontinuously in time. So, again, our earlier models assumed that the experimentalist had complete control over the antibiotic in the chamber (which is mathematically equivalent to DA being equal to infinity).
We aim to show that the updated model, given by Equations 4 to 7, is consistent with our previous results. Namely, we show that for a large DA the optimal disinfection regime is consistent with our earlier analysis. This argues that the model proposed here is a consistent extension of our previous studies.
Rather than treat the antibiotic concentration as a known and controllable parameter (as was done previously [16]), we treat the source of antibiotic as the control parameter and calculate the antibiotic concentration. This provides an experimentally viable method for testing our predictions. Again, as DA tends to infinity, the model proposed here is consistent with our earlier results; however, this model shows a natural way to incorporate our observations into an experimental design.
We do not treat the reversion rate, kg, as a piecewise constant. The reason for this is primarily mathematical but also reflects some experimental observations. From a mathematical standpoint, the procedure that we use to determine the optimal protocol requires differentiation of kg (with respect to the antibiotic concentration). Piecewise constant functions are not differentiable, so we chose to replace the piecewise functions with differentiable functions that have similar characteristics (namely, constant for most of the range of A with a rapid transition between the constant values). Biologically, it is likely that persisters do not sense the antibiotic concentration perfectly. So, for small but nonzero antibiotic concentrations, persister bacteria have the potential to revert to susceptible bacteria. We use
| (8) |
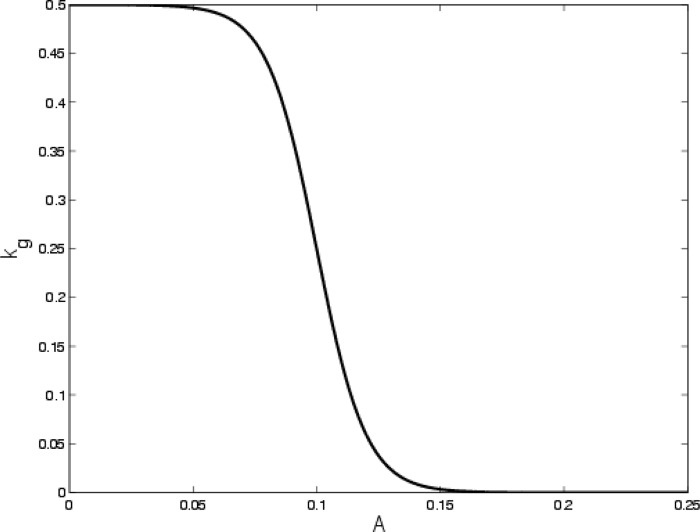
where kg,max and Athresh denote the maximal reversion rate (h−1) and sensing threshold (i.e., the minimal antibiotic concentration that prevents the reversion from persister to susceptible bacteria), respectively. The parameter ε adjusts the sensitivity of the persisters. Large values of ε indicate persisters that tend to transition back, even though the antibiotic is not small. Figure 1 shows a graph of kg(A) for the parameters that we assume.
Fig 1.
Sketch of the reversion rate as a function of A. The threshold sensing level is Athresh equal to 0.1, and the width of the transition is fixed by ε equal to 0.01.
The basic idea of optimal control is similar to finding the value of a variable that optimizes a function in calculus. There one learns that maxima or minima of functions occur where the derivative is zero (or at endpoints in the domain). This provides a method for finding a list of candidates for extreme values. In a similar manner, optimal control seeks to find the value of a control function that optimizes an objective functional. The objective functional reflects the tension between increasing and decreasing the value of the control function. This is discussed more fully in the Appendix. A functional is a mapping that takes inputs that are functions and provides outputs that are numbers. In our current situation, the goal is to determine u(t) so that the bacterial population is eliminated. We do this in several iterations by minimizing the total population (analogous to minimizing a function) at the end of a disinfection cycle. Unfortunately, our situation is a bit more complex and restrictions that are an extension of the idea of constrained optimization in calculus must be placed on the minimization problem. Details of our methods are given in the Appendix, but the thrust of the method is to minimize the functional
| (9) |
The first term of the functional describes the total antibiotic applied between time zero and time tf (the period of the application cycle). The last terms represent the population density at the end of disinfection in the same time interval. Minimizing J(u) minimizes the bacteria at the end of the disinfection cycle while using the smallest amount of antibiotic. The integral term is often referred to as a penalization term since the functional gets larger as K increases. The functional J(u) is nondimensional, so K is nondimensional, while Ks and Kp are measured in units of inverse density. We note that the predictions described below depend on the choices of the parameters K, Ks, and Kp.
Intuitively, J(u) describes the cost of the outcome. That is, when J(u) is large for a given u(t), the interpretation is that the particular disinfection regime, controlled by u(t), either requires too much antibiotic (if the integral term is large) or does not successfully kill the bacteria (if the second and/or third term is large). Similarly, if J(u) is small, the bacteria must be being removed.
Since J(u) depends on the sensitivity parameters K, Ks, and Kp, we explore the dependences on K below. The results (not shown) do not change measurably for variations of Ks and Kp over 1 order of magnitude. This is widely observed in optimal control problems (for example, see reference 14) and reflects a qualitative description of the penalization that often depends on the application under consideration. Here we note only that if K is too small, constant dosing is predicted. If it is too large, the bacterial population does not tend toward zero. In this report, we do not pursue this further than these observations.
Again, the goal is to minimize the total antibiotic applied and the bacterial populations at the end of the application cycle. The discontinuous protocol assumes periodic application of the same treatment. The optimal disinfection, for a given set of parameters and a 10-hour base period, was constant application for between 6 and 6.5 h and withdrawal of the antibiotic for the remaining time. This will provide our base comparison, although we will calculate the optimal control for each of the periods rather than periodically apply the initial treatment.
The next section provides results for three variations on the theme of optimizing the disinfection. The first set considers varying the weight of the penalization term within the optimal control problem. This is useful, since the predictions depend on these weights. This dependence is intuitive: if you penalize the use of antibiotics (if the side effects of taking the antibiotic are quite severe), you should limit the amount of antibiotic that is used; but this might not be an effective treatment.
The second set compares the optimal control method described in this report with the discontinuous control studied previously (2, 3, 16). We find that the two methods agree, which argues that the current method and numerical procedures are correct. We also demonstrate that although the protocol proposed previously (16) is successful, it is not optimal. In particular, the value of J(u) can be made smaller using a different (successful) treatment.
We then explore the effect of bacterial adhesion to the reactor. While still not modeling the bacteria as a biofilm proper, attachment is certainly one of the important steps toward establishing a biofilm and plays a significant role in the analysis within a bioreactor. As bacteria attach (possibly transiently), the residence time increases. We include attachment and detachment processes by allowing the dilution rate of the bacteria to differ from that of the chemical species.
RESULTS
Case 1: varying K.
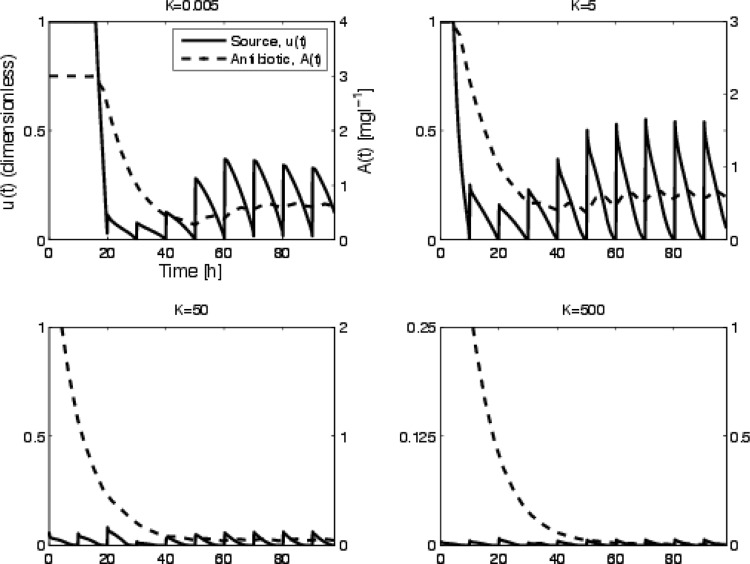
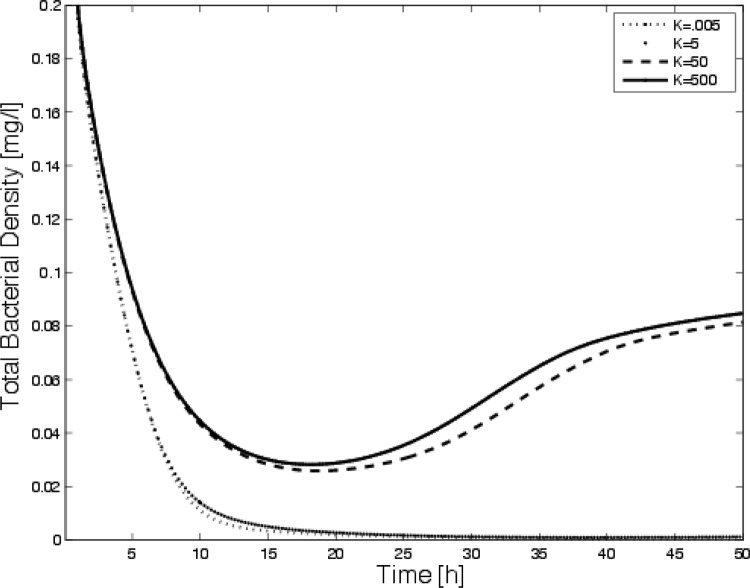
The optimal disinfection protocol and the response to periodic applications that is predicted are shown for various values of K in Fig. 2. The resulting survival curves are shown in Fig. 3. We assume that there is initially antibiotic in the reactor. The antibiotic source concentration is then altered according to the control prediction. There is a distinction between protocols that successfully eliminate the bacteria and those that fail. As K decreases, there is less of a penalty for a higher concentration of antibiotic, so the method allows more antibiotic to enter the reactor. For sufficiently high K, the treatment is penalization of it too high and the treatment fails. It is also evident that there is a difference in the time when the population goes to zero, which is more relevant for this study. We note that solutions to the equation governing the antibiotic density (Equation 7) are continuous; even if u(t) is discontinuous (this is a very basic result from differential equations), as DA increases there are sharper transitions in the antibiotic density. Thus, even if the control function, u(t), is discontinuous, the antibiotic density, A(t), is continuous. This can be observed in Fig. 2 by comparing the solid curve for u(t) and the dashed curve for A(t).
Fig 2.
Optimal control function and corresponding antibiotic time course for various values of K. The left-hand axis corresponds to the control function, u(t), while the right-hand axis corresponds to the antibiotic density in the chemostat, A(t). Higher values of K imply more penalty for antibiotic application so u decreases. For K equal to 500, the source is quite small (note the axis range), and we see the dilution of the initial concentration of antibiotic. The corresponding survival curves are shown in Fig. 3, where the concentrations for high K values do not clear the bacteria.
Fig 3.
Time-dependent disinfection for periodic application of the optimal source shown Fig. 2. Note that for sufficiently high values of K, the dose is too minimal to clear the bacteria and the system approaches a steady state.
Case 2: comparisons.
The goal of this section is to compare the optimal control method outlined above with results presented previously (16), where the disinfectant was discontinuous in time. To do this, we temporarily assume that the dilution rates for the antibiotic and the nutrient are different. As DA approaches infinity, the solution of the antibiotic equation, Equation 7, approaches A = A0u(t). This is easily seen by dividing both sides of Equation 7 by the dilution rate and taking the limit DA → ∞. In that case, discontinuous u(t) is equivalent to the discontinuous treatment described previously (3, 16).
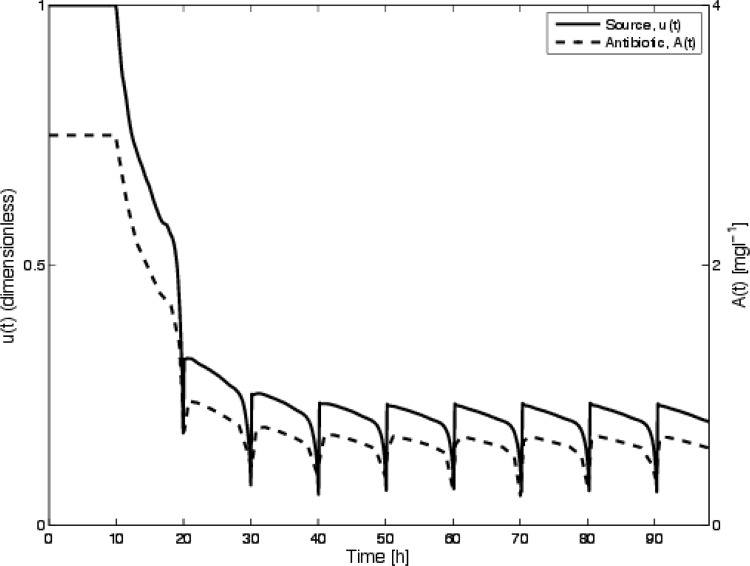
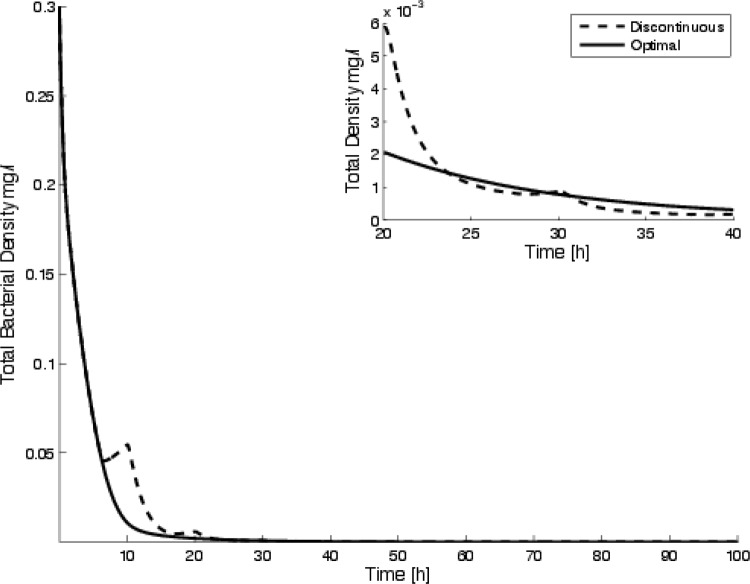
The optimal control strategy and subsequent antibiotic concentration are shown in Fig. 4. The survival curves for the discontinuous treatment determined previously (16) along with a comparison of the periodic application for the protocol determined using the optimal control theory are shown in Fig. 4. The results compare favorably, with the new method of calculating the optimal disinfection regime being similar to the prediction derived previously.
Fig 4.
Optimal control, u(t), and calculated antibiotic density, A(t), for a large value of DA (50 h−1) so that the current model is consistent with the model used previously (16). The survival curve corresponding to this simulation is shown in Fig. 5, along with the survival curve for the protocol used previously (16).
Results comparing the periodic application for this protocol with the optimal discontinuous treatment predicted previously (16) are shown in Fig. 5. Notice that these are essentially indistinguishable at the end of the run. The current method minimizes the application of the biocide and is equally successful in clearing the bacteria. In fact, the objective function is substantially lower for the optimal control prediction (with J equal to 5.15) than the objective function for the discontinuous protocol (with J equal to 9.8). We see that while the discontinuous protocol developed previously (16) is the optimal of all piecewise constant protocols, it is not, in fact, the optimal one (at least the approach that minimizes our objective functional).
Fig 5.
Time-dependent clearance of bacteria (sum of susceptible and persister bacteria) using a periodic application of biocide. The inset shows the same curves for times between 20 and 40 h to emphasize the difference in the survival curves. Notice that the discontinuous approach has a lower total bacterial concentration at various times, even though the value of the objective functional is higher. Each method clears the bacteria; however, the optimal control has a lower value of the objective functional, J (namely, 5.09 compared with 9.83).
Case 3: varying attachment.
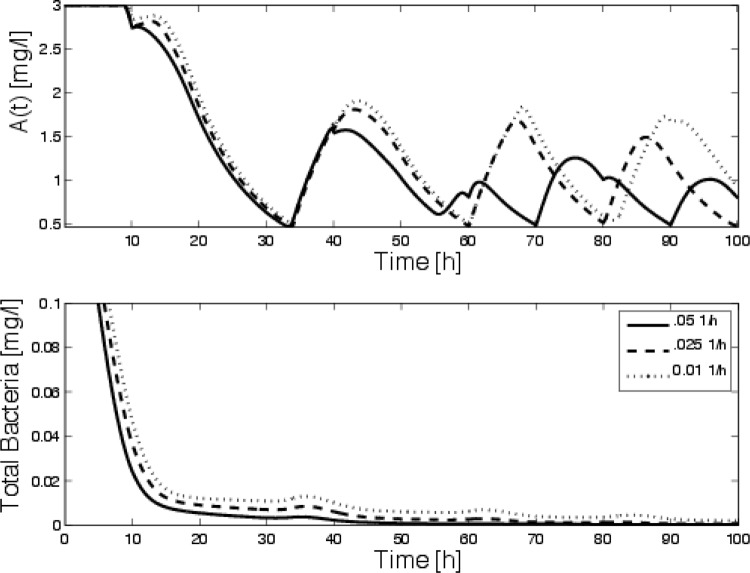
Bacteria tend to adhere to solid surfaces, while our previous models neglected this. It is clear that bacteria tend to move from planktonic to attached states in a quite complicated manner. Rather than focus on detailed modeling, we will assume that the bacteria attach to and detach from the walls of the reactor at constant rates. In this case, the bacterial dilution rate is reduced depending on the rates of attachment/detachment. Assuming that persisters and susceptible bacteria attach and detach at the same rates, we vary the bacterial dilution (DBs = DBp = Ds) between 0 and 50% of the nominal dilution rate of the chemical species. We assume that the antibiotic and nutrient are diluted at the same rate and that all other parameters are kept the same as in case 2. Figure 6 shows the optimal control and survival curves for cases where the detachment rate is not zero and the bacteria wash out of the chemostat at different rates. We see that the survival rates increase as the dilution rate decreases, as would be expected. We also see that as the dilution rate decreases, the optimal disinfection begins to be more cyclical and higher concentrations of antibiotic are needed to kill the bacteria.
Fig 6.
(Top) Optimal source of antibiotic for various bacterial dilution rates. Each of the curves corresponds to predictions with all parameters held constant except the bacterial dilution, which changes from 0.5Ds = 0.05 h−1 to 0.1Ds = 0.01 h−1. (Bottom) Corresponding survival curves, indicating that lower bacterial dilution delays the clearance of the bacteria.
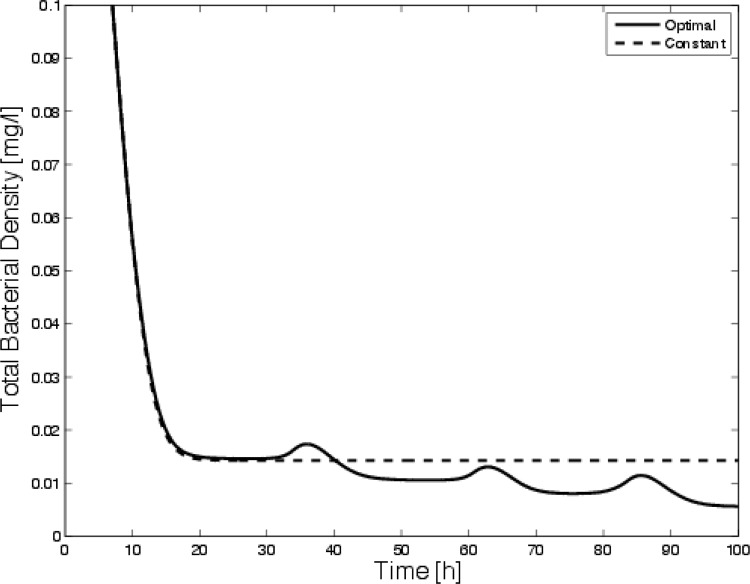
It is also interesting to note that if the bacterial dilution rate is low (i.e., if the bacteria are more strongly attached), constant dosing is essentially ineffective. This has been argued previously for biofilm models (2, 5). Figure 7 shows a comparison of survival curves for constant disinfection and optimal disinfection for zero bacterial dilution. Although constant application prevents the bacteria from growing to their carrying capacity, the population is never eliminated (as our intuitional argument suggested); however, the optimal procedure clears the bacteria.
Fig 7.
Comparison of survival curves for constant dosing and optimal dosing in the case where the bacteria are permanently attached.
DISCUSSION
We have described a method for determining the optimal disinfection method for bacteria within a biological reactor. This model extends the results of previous studies that have determined the optimal discontinuous protocol by numerical and analytic methods. In particular, we have considered a more realistic model of the application of biocide through the influent source rather than by discontinuously being changed. This is an important step in making predictions that are experimentally verifiable. The broad interpretation of this model of persisters remains: constant dosing is not as effective as transiently withdrawing the antibiotic to allow the persisters time to revert to susceptible bacteria. This is especially important in the case where the bacteria attach either transiently or permanently to the chemostat walls.
This leads to the second extension that was considered in this study. It is well-known that bacteria tend to attach to most surfaces and that this attachment becomes irreversible in the case of a biofilm colony. We have included transient attachment of the bacteria to the walls of the chemostat to incorporate this process. As the attachment rate increases, the time that it takes to eliminate the bacteria increases, which accords with intuition (since fewer bacteria are being washed out per unit time). Our results indicate that this makes constant dosing less effective since preventing growth (or keeping the bacteria in the persister state by never withdrawing the antibiotic) can eliminate the bacteria if they are washed out of the system.
Although the model presented here is relatively simple, it has several advantages. First, it has been studied in several settings (well mixed [2], chemostat [3, 16], and spatially extended [4]). This helps put our current results into perspective. More importantly, by using the source concentration as our optimal control, we have also moved much closer to an analysis that may be practically implemented. Discontinuous disinfection is relatively simple to analyze but is not easily implemented experimentally. The qualitative results (e.g., that alternating dose/withdrawal is a successful strategy) do not depend very much on the details of the model. From our experience, changing the bacterial growth, death, and disinfection kinetics changes the details, but not the overall picture of success. More importantly, the only requirement on the transition processes between susceptible and persister bacteria is that susceptible bacteria turn into persisters (the manner can be quite arbitrary) and that persister reversion is delayed in the presence of antibiotic. This is a crucial observation, since we are assuming particular mechanisms that may not be accurate. We hope our results help encourage experimental validation and exploration of disinfection protocols.
ACKNOWLEDGMENT
This work was supported by NSF grant DMS-1122378.
APPENDIX
Our model is an example of constrained optimization. We assume a particular goal, such as minimize the value of the functional J(u) with respect to the function u, subject to constraints on u. These problems are extensions of those that arise in calculus, where the goal might be to maximize the function f(x, y) subject to the constraint that g(x, y) = k. In calculus, the function f(x, y) might represent the profit from manufacturing and sale of boxes, while g(x, y) = k might denote the amount of material that is available. In calculus, one learns that there is a geometric interpretation to the optimization problem that implies that the gradients of f(x, y) and g(x, y) point in the same direction. Here we wish to determine the value of a control function [u(t), the time-varying parameter in the system] that yields the minimum of the functional J(u, Bs, Bp) subject to the constraint that Bs and Bp satisfy the differential equations. In fact, this defines the optimal control problem: the objective of the problem is to choose u(t) to minimize a functional (the objective functional) that describes the goal. Here the objective functional includes a contribution from the total amount of antibiotic that is applied to the system as well as contributions for surviving susceptible and persister bacteria. This is given in Equation 9.
The integral term is proportional to the total applied antibiotic over the time interval [0, tf], and the next terms define the contribution from the surviving bacteria at the end of the application cycle. The parameter K denotes the antibiotic sensitivity, while Ks and Kp denote the sensitivity to the remaining bacteria. Below we show that this affects the scale of the optimal value of the control function, u(t).
Pontryagin's maximum principle (14) gives a method to do this by constructing a Lagrangian:
that incorporates the Lagrange multipliers, λi. These are often called the adjoint variables. Geometrically the adjoint variables (λi) and the state variables (Bs, Bp, etc.) are related similarly to f(x, y) and g(x, y) above.
Pontryagin's principle states that the geometric concept implies that the Lagrange multipliers satisfy the equations (dλ1/dt) = −(∂L/∂Bs), (dλ2/dt) = −(∂L/∂Bp), (dλ3/dt) = −(∂L/∂S), and (dλ1/dt) = −(∂L/∂A), where L is the Lagrangian.
There are additional constraints imposed on the Lagrange multipliers, λi, similar to initial conditions; however, the geometric interpretation argues that the condition should be applied at the end of the integration time. The transversality conditions (those that make the adjoint variables agree smoothly with the state variables) are λ1(tf) = Ks, λ2(tf) = Kp, λ1(tf) = 0, and λ1(tf) = 0.
Notice that these conditions also incorporate the weights Ks and Kp, in the objective functional.
At the optimal value of the control, denoted u*, the derivative of the Lagrangian, L, with respect to the control variable, u, must vanish (just as the derivative of a function must vanish at extreme points). Hence, we require that (∂L/∂u)(u*) equal 0 at the optimal value of u(t). We denote the optimal value of the control function as u* and find that there is a relationship between the optimal value of the control variable, u*(t), and the Lagrange multiplier, λ4. The optimal value of the control function satisfies the algebraic equation Ku* = λ4kdDA = 0.
The scale of the optimal value of the control variable also depends on the antibiotic sensitivity parameter, K (which is dimensionless, since J carries no dimensions); the maximum death rate, kd (h−1); and the dilution rate of the antibiotic, DA (h−1).
Equations for the adjoint variables (λi) and the state variables (Bs, Bp, etc.) are typically nonlinear and cannot be solved analytically and so are solved numerically. There are several methods for solving this system, which can be considered a two-point boundary value system since the variables (λi) satisfy transversality conditions at the final time. We use the simplest method here, termed the forward/backward sweep method. The basic idea is to make a guess for λ1(t), λ2(t), λ3(t), and λ4(t) and proceed with a forward (in time) sweep for the variables Bs, Bp, S, and A using Equations 4 to 7. The calculated solutions are then used to solve for the variables λ1, λ2, λ3, and λ4 backward in time (backward sweep). We iterate the process until the solutions converge (14). In this study, we used MATLAB's Runga-Kutta algorithm to approximate the solutions to the differential equations.
The parameters are listed in Table 1. Each of the disinfection studies is initialized with an initialization time of 10 h with no dosing. This gives initial conditions that are chosen to be Bs(0) = 0.3, Bp(0) = 0, S(0) = 0.4, and A(0) = Ar, consistent with previous results (16).
Footnotes
Published ahead of print 2 July 2012
REFERENCES
- 1. Balaban NQ, Merrin J, Chait R, Kowalik L, Leibler S. 2005. Bacterial persistence as a phenotypic switch. Science 305:1622–1625 [DOI] [PubMed] [Google Scholar]
- 2. Cogan NG. 2006. Effects of persister formation on bacterial response to dosing. J. Theor. Biol. 238:694–703 [DOI] [PubMed] [Google Scholar]
- 3. Cogan NG. 2007. Incorporating toxin hypothesis into a mathematical model of persister formation and dynamics. J. Theor. Biol. 248:340–349 [DOI] [PubMed] [Google Scholar]
- 4. Cogan NG. 2010. An extension of the boundary integral method applied to periodic disinfection of a dynamic biofilm. SIAM J. Appl. Math. 70:2281–2307 [Google Scholar]
- 5. Cogan NG, Cortez R, Fauci LJ. 2005. Modeling physiological resistance in bacterial biofilms. Bull. Math. Biol. 67:831–853 [DOI] [PubMed] [Google Scholar]
- 6. Costerton JW, Lewandowski Z, Caldwell DE, Korber DR, Lappin-Scott HM. 1995. Microbial biofilms. Annu. Rev. Microbiol. 49:711–745 [DOI] [PubMed] [Google Scholar]
- 7. Davies D. 2003. Understanding biofilm resistance to antibacterial agents. Nat. Rev. Drug Discov. 2:114–122 [DOI] [PubMed] [Google Scholar]
- 8. Desai M, Buhler T, Weller PH, Brown MRW. 1998. Increasing resistance of planktonic and biofilm cultures of Burkholderia cepacia to ciprofloxacin and ceftazidime during exponential growth. J. Antimicrob. Chemother. 42:153–160 [DOI] [PubMed] [Google Scholar]
- 9. Drusano GL, et al. 2010. The combination of rifampin plus moxifloxacin is synergistic for suppression of resistance but antagonistic for cell kill of Mycobacterium tuberculosis as determined in a hollow-fiber infection model. mBio 1(3):e00139–10 doi:10.1128/mBio.00139-10 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Fux CA, Costerton JW, Stewart PS, Stoodley P. 2005. Survival strategies of infectious biofilms. Trends Microbiol. 13:34–40 [DOI] [PubMed] [Google Scholar]
- 11. Grobe KJ, Zahler J, Stewart PS. 2002. Role of dose concentration in biocide efficacy against Pseudomonas aeruginosa biofilms. J. Ind. Microbiol. Biotechnol. 29:10–15 [DOI] [PubMed] [Google Scholar]
- 12. Haag R, Lexa P, Werkhäuser I. 1986. Artifacts in dilution pharmacokinetic models caused by adherent bacteria. Antimicrob. Agents Chemother. 29:765. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Keren I, Kaldalu N, Spoering A, Wang Y, Lewis K. 2004. Persister cells and tolerance to antimicrobials. FEMS Microbiol. Lett. 230:13–18 [DOI] [PubMed] [Google Scholar]
- 14. Kirschner D, Lenhart S, Serbin S. 1997. Optimal control of the chemotherapy of HIV. J. Math. Biol. 35:775. [DOI] [PubMed] [Google Scholar]
- 15. Klapper I, Gilbert P, Ayati BP, Dockery J, Stewart PS. 2007. Senescence can explain microbial persistence. Microbiology 153:3623–3630 [DOI] [PubMed] [Google Scholar]
- 16. Leenheer PD, Cogan NG. 2009. Failure of antibiotic treatment in microbial populations. J. Math. Biol. 59:563–579 [DOI] [PubMed] [Google Scholar]
- 17. Lewis K. 2001. Riddle of biofilm resistance. Antimicrob. Agents Chemother. 45:999–1007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Lou C, Li Z, Ouyang Q. 2008. A molecular model for persister in E. coli. J. Theor. Biol. 255:205–209 [DOI] [PubMed] [Google Scholar]
- 19. Novick A, Szilard L. 1950. Description of the chemostat. Science 112:715–716 [DOI] [PubMed] [Google Scholar]
- 20. Prakash B, Veeregowda BM, Krishnappa G. 2003. Biofilms: a survival strategy of bacteria. Curr. Sci. India 85:1299–1307 [Google Scholar]
- 21. Roberts ME, Stewart PS. 2004. Modeling antibiotic tolerance in biofilms by accounting for nutrient limitation. Antimicrob. Agents Chemother. 48:48–52 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Smith H. 1981. Competitive coexistence in an oscillating chemostat. SIAM J. Appl. Math. 40:498–522 [Google Scholar]
- 23. Spoering AL, Lewis K. 2001. Biofilms and planktonic cells of Pseudomonas aeruginosa have similar resistance to killing by antimicrobials. J. Bacteriol. 183:6746–6751 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Stewart PS. 2003. Diffusion in biofilms. J. Bacteriol. 185:1485–1491 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Stoodley P, Sauer K, Davies DG, Costerton JW. 2002. Biofilms as complex differentiated communities. Annu. Rev. Microbiol. 56:187–209 [DOI] [PubMed] [Google Scholar]
- 26. Suci PA, Mittelman MW, Yu FP, Geesey GG. 1994. Investigation of ciprofloxacin penetration into Pseudomonas aeruginosa biofilms. Antimicrob. Agents Chemother. 38:2125–2133 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Sufya N, Allison DG, Gilbert P. 2003. Clonal variation in maximum specific growth rate and susceptibility towards antimicrobials. J. Appl. Microbiol. 95:1261–1267 [DOI] [PubMed] [Google Scholar]
- 28. Szomolay B, Klapper I, Dockery J, Stewart PS. 2005. Adaptive responses to antimicrobial agents in biofilms. Environ. Microbiol. 7:1186–1191 [DOI] [PubMed] [Google Scholar]
- 29. Tuomanen E, Cozens R, Tosch W, Zak O, Tomasz A. 1986. The rate of killing of Escherichia coli by β-lactam antibiotics is strictly proportional to the rate of bacterial growth. J. Gen. Microbiol. 132:1297–1304 [DOI] [PubMed] [Google Scholar]