Exact Green's function of the reversible diffusion-influenced reaction for an isolated pair in two dimensions

Abstract

We derive an exact Green's function of the diffusion equation for a pair of disk-shaped interacting particles in two dimensions subject to a backreaction boundary condition. Furthermore, we use the obtained function to calculate exact expressions for the survival probability and the time-dependent rate coefficient for the initially unbound pair and the survival probability of the bound state. The derived expressions will be of particular utility for the description of reversible membrane-bound reactions in cell biology.

Diffusion, or Brownian motion, and its microscopic basis, random walks, are key concepts of non-equilibrium statistical mechanics and the theory of stochastic processes. Their ubiquity renders them applicable in numerous areas of physics and beyond, for instance, engineering, chemistry, biology, and mathematical finance, see, for example, Refs. ¹ and ² and references therein.

In the theory of diffusion-influenced reactions,³ solutions of the diffusion equation which satisfy certain boundary conditions can be used to investigate different types of chemical reactions. Among those solutions, Green's functions (GF) enjoy a privileged role because they permit calculating the solution for any given initial distribution and can be used to derive important other quantities, for instance survival probabilities and time-dependent reaction rate coefficients.^{4, 5, 6} In this sense, knowledge of the GF is tantamount to a “completely solved” problem. However, in most cases, an analytical representation of the GF remains elusive, a notable exception being the case of an isolated pair. Here, GFs and derived quantities have not only been important from a conceptual point of view but have also been used to fit experimental data for a diffusion model with reversible reactions⁷ and to investigate how the reduced parameter set could be determined from experimental data describing geminate recombination.⁸

Motivated by the desire to understand the influence of stochastic fluctuations and spatial heterogeneities on the behavior of biochemical networks, the last decade has witnessed an increased interest in theoretical approaches describing diffusion-influenced reactions at the molecular level. Analytical representations of GFs describing an isolated pair figure prominently in a number of proposed particle-based stochastic simulation algorithms, because a reaction network may be thought of as composed of unimolecular and bimolecular reactions A + B → products. In this context, GFs can be used to enhance the efficiency of Brownian dynamics simulations.^{9, 10, 11} Moreover, the knowledge of exact analytical expressions permits to validate newly devised stochastic simulation algorithms.¹²

Exact analytic expressions for the GF of an isolated pair that can undergo a reversible reaction have been derived for the one and three dimensional cases,^{4, 6} whereas a corresponding expression in the time domain for the two dimensional case has been lacking and analytical approaches were limited to approximations^{13, 14} in spite of its broad applicability to surface phenomena. The two dimensional case is of particular importance in cell biological applications, providing the basis for a better understanding of processes such as signal-induced inhomogeneities and receptor clustering on cell membranes¹⁵ where small diffusion constants govern the lateral motion of receptors and diffusion represents a less efficient mixing mechanism than in the three dimensional cytoplasm. Finally, diffusion in two dimensions (2D) is special because the steady-state solution of the diffusion equation is inconsistent with the boundary condition at infinity¹⁶ and because 2D is the critical dimension with regard to the recurrence and transience of random walks.¹⁷

To derive the GF in 2D, we consider an isolated pair of two disklike particles A and B with diffusion constants D_A and D_B, respectively. The particles may associate when their separation equals the encounter distance a to form a bound molecule AB. When bound, the molecules may dissociate again to form an unbound pair A + B. Such a system may be described as the diffusion of a point-like particle with diffusion constant D = D_A + D_B around a static disk with radius a. In this picture, reactions are introduced by imposing boundary conditions at the disk's “surface.” The irreversible association reaction is described by the radiation boundary condition (BC) that is characterized by an intrinsic association constant κ_a. To take into account reversible reactions, i.e., to allow for dissociations, the radiation BC has to be generalized to the backreaction BC that involves an additional intrinsic dissociation constant κ_d.^{4, 5, 6} We consider the probability density function (PDF) g(r, t|r₀), which gives the probability to find the particles at a distance equal to r at time t, given that the distance was initially r₀ at time t = 0. The time evolution of g(r, t|r₀) is governed by the 2D diffusion equation⁵

$$\frac{\partial }{\partial t}g(r,t|r_0)=D\left(\frac{{\partial }^2}{\partial r^2}+\frac{1}{r}\frac{\partial }{\partial r}\right)g(r,t|r_0),r\ge a.$$ (1)

The diffusion equation has to be completed by specifying boundary conditions. Together with the following initial:

$$2\pi r_{0}g(r,0|r_0)=\delta (r-r_0),$$ (2)

and boundary condition

$$\underset{r\to \infty }{\lim }g(r,t|r_0)=0,$$ (3)

Eq. 1 is equivalent to the free-space diffusion equation in 2D (if a = 0, r > 0) with the familiar solution¹⁸ (Ch. 14.8, Eq. 1)

$$g_{\text{free}}(r,t|r_0)=\frac{1}{4\pi Dt}{e}^{-(r^2+r_0^2)/4Dt}{I}_0\left(\frac{r{r}_0}{2Dt}\right),$$ (4)

which is also known as the free-space GF. I₀(x) denotes the modified Bessel function of first kind and zero order¹⁹ (Sec. 9.6).

The PDF we are interested in is only defined for r ⩾ a > 0 and one has to impose a BC for r = a specifying the behavior at the encounter distance. To incorporate association and dissociation on the surface of the “interaction disc,” we thus require^{4, 5, 6}

$$\begin{array}{c}\hfill 2\pi aD\frac{\partial }{\partial r}g(r,t|r_0){|}_{r=a}={\kappa }_{a}g(a,t|r_0)-{\kappa }_d[1-S\left(t\right|r_0)].\end{array}$$ (5)

Here, S(t|r₀) denotes the survival probability that a pair of molecules with initial distance r₀ survives until time t

$$\begin{array}{ccc}\hfill S\left(t\right|r_0)& =& 2\pi {\int }_a^{\infty }g(r,t|r_0)rdr,\hfill \end{array}$$ (6)

$$\begin{array}{ccc}& =& 1-2\pi aD{\int }_0^t\frac{\partial }{\partial r}g(r,t^{\prime }|r_0){|}_{r=a}d{t}^{\prime }.\hfill \end{array}$$ (7)

Note that, strictly speaking, the notion of a “survival probability” is somewhat misleading in the case we consider here. For the irreversible reaction, a non-vanishing likelihood to find a separated isolated pair at a time t necessarily implies that no association has occurred before. For the reversible reaction, association and subsequent dissociation events that took place possibly many times before t also contribute to the probability of finding an isolated pair unbound at a time t. Therefore, more precisely, one could refer to the quantity S(t|r₀) as a separation probability.⁵ Nevertheless, in the following we will use survival probability interchangeably with separation probability.⁶ Furthermore, we would like to point out that the possibility of an initial bound state (henceforth denoted by *) requires to consider two different survival probabilities: S(t|r₀) and S(t|*), corresponding to the initially unbound and bound state, respectively. Similarly, the reversible GF has four components: besides g(r, t|r₀), one has to consider g(r, t|*), g(*, t|r₀), and g(*, t|*) for the initial and final bound states.^{5, 6} For all these quantities, we will derive exact analytical expressions in the time domain.

Following the general strategy of Ref. 18, [Ch. 14.8, p. 368], we make the following ansatz for the Laplace transform of the Green's function that satisfies the backreaction BC

$$\tilde{g}(r,q|r_0)={\tilde{g}}_{\text{free}}(r,q|r_0)+{\tilde{g}}_{\text{br}}(r,q|r_0).$$ (8)

Here,

$${\tilde{g}}_{\text{free}}(r,q|r_0)=\frac{1}{2\pi D}\left\{\begin{array}{cc}{I}_0\left(q{r}_0\right)K_0\left(qr\right),\hfill & \hfill r>r_0\\ I_0\left(qr\right)K_0\left(q{r}_0\right),\hfill & \hfill r<r_0\end{array}\right.,$$ (9)

is the Laplace transform of the free-space GF Eq. 4, cp.¹⁸ (Ch. 14.8, Eq. 2). K₀(x) refers to the modified Bessel function of second kind and zero order¹⁹ (Sec. 9.6). The variable q is defined by $q:=\sqrt{p/D}$, where p denotes the Laplace domain variable.

Alternatively, one could also seek a solution in the form^{4, 6}

$$\tilde{g}(r,q|r_0)={\tilde{g}}_{\text{ref}}(r,q|r_0)+{\tilde{g}}_{\text{ref,br}}(r,q|r_0),$$ (10)

where ${\tilde{g}}_{\text{ref}}(r,q|r_0)$ denotes the Laplace transform of the GF that obeys reflecting BCs.

The part ${\tilde{g}}_{\text{br}}$ in Eq. 8 that takes into account the BC is a solution of the Laplace transformed 2D diffusion equation¹⁸ (Ch. 14.8, Eq. 3)

$$\frac{d^2{\tilde{g}}_{\text{br}}}{d{r}^2}+\frac{1}{r}\frac{d{\tilde{g}}_{\text{br}}}{dr}-q^2{\tilde{g}}_{\text{br}}=0.$$ (11)

The general solution to Eq. 11 is AK₀(qr) + BI₀(qr). Because we require ${\lim }_{r\to \infty }{\tilde{g}}_{\text{br}}\to 0$, and lim_{x → ∞}I₀(x) → ∞, the coefficient B has to vanish and hence,

$${\tilde{g}}_{\text{br}}(r,q|r_0)=A(q,r_0)K_0\left(qr\right).$$ (12)

A(q, r₀) is determined by the requirement that the complete GF Eq. 8 satisfies the Laplace transformed backreaction BC, cp. Eq. 5,

$$\begin{array}{c}\hfill \frac{\partial }{\partial r}\tilde{g}(r,q|r_0){{|}_{r=a}=h\tilde{g}(a,q|r_0)-{\kappa }_d{p}^{-1}\frac{\partial }{\partial r}\tilde{g}(r,q|r_0)|}_{r=a},\end{array}$$ (13)

where we have defined h ≔ κ_a/(2πaD). Using Eqs. 8, 9, 12, 13, and $I_0^{\prime }\left(x\right)=I_1\left(x\right),K_0^{\prime }\left(x\right)=-K_1\left(x\right)$¹⁹ (Eq. (9.6.27)) and defining κ_D ≔ κ_d/D, we obtain

$$\begin{array}{ccc}\hfill {\tilde{g}}_{\text{br}}(r,q|r_0)& =& \frac{1}{2\pi D}{K}_0\left(qr\right)K_0\left(q{r}_0\right)\hfill \\ & & \times \frac{(q^2+{\kappa }_D)I_1\left(qa\right)-hq{I}_0\left(qa\right)}{(q^2+{\kappa }_D)K_1\left(qa\right)+hq{K}_0\left(qa\right)}.\hfill \end{array}$$ (14)

We would like to point out that for the irreversible case, the GF that takes into account the reaction by satisfying the radiation BC can be rewritten in terms of the GF that corresponds to nonreactive diffusion and satisfies a reflective BC (Ref. ²⁰)

$$\begin{array}{ccc}\hfill {\tilde{g}}_{\text{rad}}(r,q|r_0)& =& {\tilde{g}}_{\text{ref}}(r,q|r_0)\hfill \\ & & -{\kappa }_a\frac{{\tilde{g}}_{\text{ref}}(r,q|a){\tilde{g}}_{\text{ref}}(a,q|r_0)}{1+{\kappa }_a{\tilde{g}}_{\text{ref}}(a,q|a)}.\hfill \end{array}$$ (15)

It was also shown that Eq. 15 relating the GFs for reactive and nonreactive diffusion takes the form of a Dyson integral equation in the time domain.²⁰ Furthermore, in Ref. 21, Eq. 15 was extended to the reversible case in 3D. This relationship is valid for the reversible case in 2D also. To obtain the GF satisfying reflective BCs, we set h = κ_D = 0 in Eq. 14 and find

$$\begin{array}{ccc}\hfill {\tilde{g}}_{\text{ref,bc}}(r,q|r_0)& :=& {\tilde{g}}_{\text{ref}}(r,q|r_0)-{\tilde{g}}_{\text{free}}(r,q|r_0),\hfill \\ & =& \frac{1}{2\pi D}{K}_0\left(qr\right)K_0\left(q{r}_0\right)\frac{I_1\left(qa\right)}{K_1\left(qa\right)}.\hfill \end{array}$$ (16)

Using I₀(x)K₁(x) + I₁(x)K₀(x) = x⁻¹, cp.¹⁹ (Eq. (9.6.15)) it follows that

$$\begin{array}{ccc}\hfill {\tilde{g}}_{\text{br}}(r,q|r_0)& =& {\tilde{g}}_{\text{ref,bc}}(r,q|r_0)\hfill \\ & & -{\kappa }_a{q}^2\frac{{\tilde{g}}_{\text{ref}}(r,q|a){\tilde{g}}_{\text{ref}}(a,q|r_0)}{q^2+{\kappa }_D+{\kappa }_a{q}^2{\tilde{g}}_{\text{ref}}(a,q|a)}.\hfill \end{array}$$ (17)

The inversion theorem for the Laplace transformation can be applied to find the corresponding expression of ${\tilde{g}}_{\text{br}}$ in the time domain

$$g_{\text{br}}(r,t|r_0)=\frac{1}{2\pi i}{\int }_{\gamma -i\infty }^{\gamma +i\infty }{e}^{pt}{\tilde{g}}_{\text{br}}(r,q|r_0)dp.$$ (18)

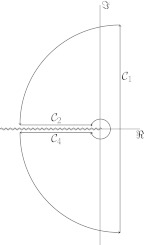
To calculate the Bromwich contour integral, we first note that ${\tilde{g}}_{\text{br}}$ has a branch point at p = 0. Therefore, we use the contour of Fig. 1 with a branch cut along the negative real axis, cp.¹⁸ (Ch. 12.3, Fig. 40). Furthermore, we note that the integrand has no poles within and on the contour²² and that the contribution from the small circle around the origin vanishes, which can be seen by the limiting forms of the modified Bessel functions for small arguments¹⁹ (Eqs. (9.6.7)–(9.6.9)). Therefore, we obtain

$$\begin{array}{ccc}\hfill 0& =& \oint e^{pt}{\tilde{g}}_{\text{br}}(r,q|r_0)dp={\int }_{\gamma -i\infty }^{\gamma +i\infty }{e}^{pt}{\tilde{g}}_{\text{br}}(r,q|r_0)dp\hfill \\ & & +{\int }_{{\mathcal{C}}_2}{e}^{pt}{\tilde{g}}_{\text{br}}(r,q|r_0)dp+{\int }_{{\mathcal{C}}_4}{e}^{pt}{\tilde{g}}_{\text{br}}(r,q|r_0)dp.\hfill \end{array}$$ (19)

Thus, it remains to calculate the integrals ${\int }_{{\mathcal{C}}_2},{\int }_{{\mathcal{C}}_4}$. To this end, we choose p = Dx²e^iπ and use¹⁸ (Append. 3, Eqs. 25, 26)

$$\begin{array}{ccc}\hfill I_n\left(x{e}^{\pm \pi i/2}\right)& =& e^{\pm n\pi i/2}{J}_n\left(x\right),\hfill \end{array}$$ (20)

$$\begin{array}{ccc}\hfill K_n\left(x{e}^{\pm \pi i/2}\right)& =& \pm \frac{1}{2}\pi i{e}^{\mp n\pi i/2}[-J_n\left(x\right)\pm i{Y}_n\left(x\right)].\hfill \end{array}$$ (21)

J_n(x), Y_n(x) denote the Bessel functions of first and second kind, respectively¹⁹ (Sec. 9.1). It follows that

$$\begin{array}{ccc}\hfill {\int }_{{\mathcal{C}}_2}{e}^{pt}{\tilde{g}}_{\text{br}}(r,q|r_0)dp& =& \frac{i}{2}{\int }_0^{\infty }{e}^{-D{x}^{2}t}{H}_0^{\left(2\right)}\left(xr\right)H_0^{\left(2\right)}\left(x{r}_0\right)\hfill \\ & & \times \frac{\alpha \left(x\right)\left[\alpha \right(x)+i\beta (x\left)\right]}{\alpha {\left(x\right)}^2+\beta {\left(x\right)}^2}xdx.\hfill \end{array}$$ (22)

Here, $H_n^{\left(2\right)}\left(x\right):=J_n\left(x\right)-i{Y}_n\left(x\right)$ denotes the Bessel function of third kind (also referred to as Hankel function)¹⁹ (Eq. 9.1.4) and we have defined

$$\begin{array}{ccc}\hfill \alpha :=\alpha \left(x\right)& :=& (x^2-{\kappa }_D)J_1\left(xa\right)+hx{J}_0\left(xa\right),\hfill \end{array}$$ (23)

$$\begin{array}{ccc}\hfill \beta :=\beta \left(x\right)& :=& (x^2-{\kappa }_D)Y_1\left(xa\right)+hx{Y}_0\left(xa\right).\hfill \end{array}$$ (24)

To evaluate the integral along the contour ${\mathcal{C}}_4$, we choose p = Dx²e^−iπ and after an analogous calculation, one finds that ${\int }_{{\mathcal{C}}_2}{e}^{pt}{\tilde{g}}_{\text{br}}(r,q|r_0)dp=-{\left({\int }_{{\mathcal{C}}_4}{e}^{pt}{\tilde{g}}_{\text{br}}(r,q|r_0)dp\right)}^{*},$ where * means complex conjugation. Thus, one arrives at

$$\begin{array}{ccc}\hfill g_{\text{br}}(r,t|r_0)& =& -\frac{1}{\pi }\Im \left({\int }_{{\mathcal{C}}_2}{e}^{pt}{\tilde{g}}_{\text{br}}(r,q|r_0)dp\right),\hfill \\ & =& -\frac{1}{2\pi }{\int }_0^{\infty }{e}^{-D{x}^{2}t}\alpha \frac{\alpha \Omega +\beta \Pi }{{\alpha }^2+{\beta }^2}xdx,\hfill \end{array}$$ (25)

where we have defined

$$\begin{array}{c}\hfill \Omega :=\Omega (x,r,r_0):=J_0\left(xr\right)J_0\left(x{r}_0\right)-Y_0\left(xr\right)Y_0\left(x{r}_0\right),\\ \hfill \Pi :=\Pi (x,r,r_0):=Y_0\left(xr\right)J_0\left(x{r}_0\right)+J_0\left(xr\right)Y_0\left(x{r}_0\right).\end{array}$$

Next, we use the fact that the free-space Green's function may be written as

$$g_{\text{free}}(r,t|r_0)=\frac{1}{2\pi }{\int }_0^{\infty }{e}^{-D{x}^{2}t}{J}_0\left(xr\right)J_0\left(x{r}_0\right)xdx$$

to arrive at the exact Green's function in the time domain

$$g(r,t|r_0)=\frac{1}{2\pi }{\int }_0^{\infty }{e}^{-D{x}^{2}t}T(x,r)T(x,r_0)xdx,$$ (26)

where we introduced the function²³

$$T(x,r):=\frac{J_0\left(rx\right)\beta \left(x\right)-Y_0\left(rx\right)\alpha \left(x\right)}{{[\alpha {\left(x\right)}^2+\beta {\left(x\right)}^2]}^{1/2}}.$$ (27)

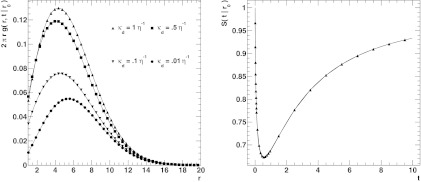
Note that in the limit κ_d → 0, one recovers the known GF for the irreversible case with radiation BC¹⁸ (Chap. 14.8, Eqs. 12, 13). We compared the obtained analytical expression for the GF to solutions that were numerically constructed using the Spherically Symmetric Diffusion Problem (SSDP) software,²⁴ version 2.66. Results are shown in the left panel of Fig. 2. We find excellent agreement.

Figure 1.

Integration contour used in Eq. 19.

Figure 2.

The reversible Green's function and survival probability for an initially unbound isolated pair in 2D. The parameters are: a = 1, D = 2, r₀ = 1.1, κ_a = 2πD. The left panel shows the r dependence of the reversible GF 2πrg(r, t|r₀) at time t = 10η for various values of the dissociation constant κ_d = 1 η⁻¹, 0.5 η⁻¹, 0.1 η⁻¹, 0.01 η⁻¹, where η = a²D⁻¹ denotes the natural time scale of the system. The solid lines correspond to the analytical expression Eq. 26. The various markers refer to numerical solutions that were obtained using the SSDP software, ver. 2.66. The right panel shows the time dependence of the survival probability S(t|r₀). The dissociation constant is κ_d = 0.5 η⁻¹. The solid line refers to the analytical expression in Eq. 29. The markers indicate the SSDP results.

With the exact GF at our disposal, further important quantities can be derived.²⁵ Notably, the survival probability can be calculated using Eq. 7. To this end, we first introduce the function

$$\begin{array}{c}\hfill P(x,r):=-\frac{1}{x}\frac{\partial }{\partial r}T(x,r)=\frac{J_1\left(xr\right)\beta -Y_1\left(xr\right)\alpha }{{[{\alpha }^2+{\beta }^2]}^{1/2}},\end{array}$$ (28)

where we used $J_0^{\prime }\left(x\right)=-J_1\left(x\right)$ and $Y_0^{\prime }\left(x\right)=-Y_1\left(x\right)$¹⁹ (Eq. 9.1.28). Then the survival probability can be written as

$$S\left(t\right|r_0)=1-a{\int }_0^{\infty }{e}^{-Dt{x}^2}P(x,a)T(x,r_0)dx.$$ (29)

To obtain this result, we note that, as discussed in Appendix A, the integral ${\int }_0^{\infty }P(x,a)T(x,r_0)dx$ has to vanish. Clearly, the reversible survival probability approaches unity for large times, lim_{t → ∞}S(t|r₀) = 1. Therefore, it can explicitly be shown that the fate of an isolated pair for the reversible reaction is always dissociation in 2D, as in the 1D and 3D cases.^{4, 6}

Let g(*, t|r₀) and g(r, t|*), g(*, t|*) denote the Green's functions for the final and initial bound states, respectively.^{5, 6} Note that g(*, t|r₀) and g(*, t|*) are probabilities instead of probability densities and that g(*, t|r₀) = 1 − S(t|r₀). Because of the detailed balance condition^{5, 6}

$${\kappa }_{d}g(*,t|r)={\kappa }_{a}g(r,t|*),$$ (30)

the GF of the initial bound state becomes

$$g(r,t|*)=\frac{{\kappa }_d}{{\kappa }_a}a{\int }_0^{\infty }{e}^{-Dt{x}^2}P(x,a)T(x,r)dx.$$ (31)

Thus, the probability that an initially bound pair is unbound at time t > 0 becomes

$$S\left(t\right|*)=1-2\pi \frac{{\kappa }_d}{{\kappa }_a}{a}^2{\int }_0^{\infty }{e}^{-Dt{x}^2}{P}^2(x,a)\frac{1}{x}dx.$$ (32)

Note that S(0|*) = 0, due to Eq. 38. In Ref. 5, it was demonstrated that S(t|*) relates to S(t|r₀) in the time domain as

$$S\left(t\right|*)={\kappa }_d{\int }_0^t{e}^{-{\kappa }_d{t}^{\prime }}S(t-t^{\prime }|a)d{t}^{\prime }.$$ (33)

Using the obtained expression for the GF, Eqs. 26, 27, and the survival probabilities, Eq. 29, 32, as well as

$$Y_0^{\prime }\left(x\right)J_0\left(x\right)-J_0^{\prime }\left(x\right)Y_0\left(x\right)=2/\left(\pi x\right),$$ (34)

Ref. ¹⁹ (Eq. (9.1.16)) and Eq. 38, we can explicitly verify that Eq. 33 is satisfied in 2D. Finally, we obtain for g(*, t|*) = 1 − S(t|*),

$$\begin{array}{c}\hfill g(*,t|*)=2\pi \frac{{\kappa }_d}{{\kappa }_a}{a}^2{\int }_0^{\infty }{e}^{-Dt{x}^2}{P}^2(x,a)\frac{1}{x}dx,\end{array}$$ (35)

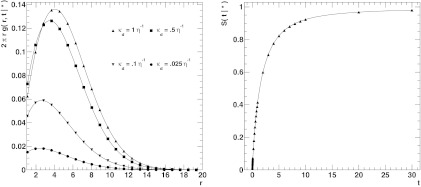
and g(*, 0|*) = 1. Using the SSDP software, we compared the numerically calculated survival probability S(t|r₀) of the initially unbound as well as the GF and survival probability S(t|*) of the initially bound state to our analytical expressions Eq. 29, Eq. 31, and Eq. 32. The right panel of Fig. 2 and both panels of Fig. 3 show the results. Again, we find excellent agreement.

Figure 3.

The reversible Green's function and survival probability for an initially bound isolated pair in 2D. The parameters are: a = 1, D = 2, κ_a = 2πD. The left panel shows the r dependence of the reversible GF 2πrg(r, t|*) at time t = 10 η for various values of the dissociation constant κ_d = 1 η⁻¹, 0.5 η⁻¹, 0.1 η⁻¹, 0.025 η⁻¹, where η = a²D⁻¹ denotes the natural time scale of the system. The solid lines are obtained from the analytical expression Eq. 31. The various markers indicate the corresponding numerical solutions generated by the SSDP software. The right panel shows the time dependence of the survival probability S(t|*). The dissociation constant is κ_d = 0.5 η⁻¹. The solid line refers to the analytical expression Eq. 32. The markers indicate the SSDP results.

Finally, the time-dependent reaction rate coefficient can be defined as^{5, 6}

$$k\left(t\right):=2\pi aD\frac{\partial }{\partial r_0}S\left(t\right|r_0){|}_{r_0=a}.$$ (36)

The resulting exact expression is

$$k\left(t\right)=2\pi a^{2}D{\int }_0^{\infty }{e}^{-Dt{x}^2}{P}^2(x,a)xdx.$$ (37)

As explained in Appendix A, one can show that

$${\int }_0^{\infty }{P}^2(x,a)\frac{1}{x}dx=\frac{{\kappa }_a}{{\kappa }_{d}2\pi a^2}.$$ (38)

We thus recover the correct expression for the equilibrium constant K_eq,

$${\int }_0^{\infty }k\left(t\right)dt=\frac{{\kappa }_a}{{\kappa }_d}=:K_{\text{eq}}.$$ (39)

Alternatively, Eq. 39 may be deduced in the following way. According to Ref. 5, the time-dependent reaction rate can also be calculated by using the survival probability S(t|*),

$$k\left(t\right)=K_{\text{eq}}\frac{\partial S\left(t\right|*)}{\partial t}.$$ (40)

Now, given Eqs. 29, 32, one can explicitly show that Eqs. 36, 40 yield the same result. Then, taking into account that S(∞|*) = 1 and S(0|*) = 0, Eq. 39 is immediately implied by Eq. 40.

APPENDIX A: INTEGRAL IDENTITIES

In this appendix, we will show how the derived GF Eq. 26 and the backreaction BC Eq. 5 can be used to calculate seemingly intractable integrals that are needed in the main text. Substituting the found expression of the GF into the backreaction BC and taking the limit t → ∞ or, alternatively, using T(x, a) = −(x² − κ_D)/(hx)P(x, a), yields

$${\int }_0^{\infty }P(x,a)T(x,r_0)dx=0.$$ (A1)

By definition, the Green' s function has to satisfy the initial condition Eq. 2, i.e., in the case considered here we have

$$\frac{1}{2\pi }{\int }_0^{\infty }T(x,r)T(x,r_0)xdx=\frac{\delta (r-r_0)}{2\pi r_0}.$$ (A2)

It follows by direct integration over ${\int }_a^{r}d{r}^{\prime }{r}^{\prime }$

$${\int }_0^{\infty }P(x,r)T(x,r_0)dx=\{\begin{array}{cc}0,\hfill & \hfill r<r_0,\\ r^{-1},\hfill & \hfill r>r_0\text{,}\end{array}$$ (A3)

where we have used Eq. A1. Note also that to perform the integral, we used d/dx[x^νJ_ν(x)] = x^νJ_ν−1 and d/dx[x^νY_ν(x)] = x^νY_{ν − 1}¹⁹ (Eq. (9.1.30)). Next, we apply the derivative ∂/∂r₀ to the BC Eq. 5 and subsequently integrate from 0 to t. Finally, we again consider the limit t → ∞ and find

$$\begin{array}{ccc}\hfill {\int }_0^{\infty }P(x,a)P(x,r_0)xdx& =& -\frac{{\kappa }_a}{2\pi aD}{\int }_0^{\infty }T(x,a)P(x,r_0)dx\hfill \\ & & +\frac{{\kappa }_d}{D}{\int }_0^{\infty }P(x,a)P(x,r_0)\frac{dx}{x}.\hfill \end{array}$$ (A4)

The integral on the lhs has to vanish, as can be seen by taking into account Eq. A1 and

$${\int }_0^{\infty }P(x,a)P(x,r_0)xdx=-\frac{\partial }{\partial r_0}{\int }_0^{\infty }P(x,a)T(x,r_0)dx.$$ (A5)

Furthermore, we just calculated the first integral on the rhs, cp. Eq. A3. Hence, we arrive at

$${\int }_0^{\infty }P(x,a)P(x,r_0)\frac{dx}{x}=\frac{{\kappa }_a}{{\kappa }_{d}2\pi a{r}_0}.$$ (A6)

APPENDIX B: ASYMPTOTIC AND APPROXIMATE EXPRESSIONS

In the following, we present some approximate solutions for small and long times. Note that approximate solutions have been discussed before⁵, ¹³, ¹⁴ and at least for the survival probabilities, we re-derive already known results.

Generally, two alternative ways exist to obtain approximate solutions for long times. One method starts in the Laplace domain and is described in Ref. 18 (Ch. 13.6). One starts from the expressions Eq. 9 and Eq. 14 in the Laplace domain and expands them in the ascending powers of q. The obtained series can be integrated term by term using the integrals given in Ref. 18 (Ch. 13.6, Eqs. 4, 5, 6, 7, 8, 9). Alternatively, one might use the exact expressions in the time domain to generate approximations. To demonstrate the general idea, we start with the survival probability S(t|r₀). First, we note that

$$\text{numerator}\text{of}P(x,a)=\frac{2h}{\pi a},$$ (B1)

because of Eqs. 28, 34. We make a variable substitution $\sqrt{Dt}x\to u$ to obtain

$$\begin{array}{ccc}& & {\int }_0^{\infty }{e}^{-Dt{x}^2}P(x,a)T(x,r_0)dx\hfill \\ & & \to \frac{1}{\sqrt{Dt}}{\int }_0^{\infty }{e}^{-u^2}P(u{\sqrt{Dt}}^{-1},a)T(u{\sqrt{Dt}}^{-1},r_0)du.\hfill \end{array}$$ (B2)

Because we are interested in long times, we use the expansions¹⁸ (Append. 3, Eqs. 1, 5) of the Bessel functions suitable for small arguments to expand the integrand in ascending powers of $\xi :=u{\sqrt{Dt}}^{-1}$. To leading order, we find

$$\frac{1}{\alpha {\left(\xi \right)}^2+\beta {\left(\xi \right)}^2}=\frac{{\xi }^2}{{\left[2{\left(\pi a\right)}^{-1}{\kappa }_D\right]}^2{[1+\mathcal{O}\left({\xi }^2\ln \xi \right)]}^2}.$$ (B3)

Similarly, we arrive at

$$\text{numerator}\text{of}\xi T(\xi ,r_0)=\frac{2{\kappa }_D}{\pi a}(1+\mathcal{O}\left({\xi }^2\ln \xi \right)).$$ (B4)

Combining Eqs. 29, B1, B2, B3, B4, we arrive at

$$S\left(t\right|r_0)\underset{t\to \infty }{\to }1-\frac{K_{eq}}{4\pi Dt}+\cdots$$ (B5)

In the same way, we can find an approximate expression for S(t|*). Again performing the variable substitution $\sqrt{Dt}x\to u$ and using Eqs. 32, B1, B3, we obtain

$$S\left(t\right|*)\underset{t\to \infty }{\to }1-\frac{K_{eq}}{4\pi Dt}+\cdots ,$$ (B6)

so we find that the survival probabilities S(t|r₀) and S(t|*) show the same long time behavior. This is what one expects, because the long time characteristics should be independent of the initial state. Finally, to derive a long time expansion for the GF Eq. 26, we first expand the free GF Eq. 4 as follows:

$$g_{\text{free}}(r,t|r_0)=\frac{1}{4\pi Dt}\left(1-\frac{r^2+r_0^2}{4Dt}+\mathcal{O}\left(t^{-2}\right)\right),$$ (B7)

where we have used the expansion of I₀(x) suitable for small arguments¹⁸ (Append. 3, Eqs. 7). We obtain for Eq. 25

$$g_{\text{br}}(r,t|r_0)=\frac{a^2}{4\pi D^2{t}^2}\left(\frac{1}{2}-\frac{K_{eq}}{2\pi a^2}\right)\ln \left(C\frac{r{r}_0}{Dt}\right)+\mathcal{O}\left(t^{-3}\right),$$ (B8)

where C ≔ 1/4e^{γ + 1} and γ = .5772156649… denotes Euler's constant¹⁹ (Eq. (6.1.3)). To derive Eq. B8, we used

$${\int }_0^{\infty }{e}^{-mx}\ln \left(x\right)xdx=\frac{1}{m^2}(1-\gamma -\ln \left(m\right)),$$ (B9)

which follows from Ref. 26 (Eq. (4.331.1))

$${\int }_0^{\infty }{e}^{-mx}\ln \left(x\right)dx=-\frac{\gamma +\ln \left(m\right)}{m},$$ (B10)

by differentiation with respect to the parameter m.

To obtain a small time expansion, it is convenient to start from the Laplace domain and to use the expressions for the free GF and the boundary component, given by Eq. 9 and Eq. 14, respectively. Furthermore, we switch to dimensionless variables $R=r/a,R_0=r_0/a,\tilde{h}=ha,{\tilde{\kappa }}_D={\kappa }_D{a}^2,\tilde{q}=qa,$ and τ = tDa⁻². To obtain expansions in powers of ${\tilde{q}}^{-1}$, we exploit the asymptotic expansions of the modified Bessel functions for large arguments¹⁹ (Eqs. (9.7.1), (9.7.2)),

$$\begin{array}{c}\hfill I_{\nu }\left(x\right)\sim \frac{e^x}{\sqrt{2\pi x}}\sum _{k=0}^{\infty }{(-1)}^k\frac{a_k\left(\nu \right)}{x^k},\end{array}$$ (B11)

$$\begin{array}{c}\hfill K_{\nu }\left(x\right)\sim \sqrt{\frac{\pi }{2x}}{e}^{-x}\sum _{k=0}^{\infty }\frac{a_k\left(\nu \right)}{x^k},\end{array}$$ (B12)

where the coefficients are defined by

$$a_k\left(\nu \right)=\frac{(4{\nu }^2-1^2)(4{\nu }^2-3^2)\cdots (4{\nu }^2-{(2k-1)}^2)}{k!8^k}$$ (B13)

to arrive at the following asymptotic expansion in powers of q⁻¹:

$$\begin{array}{ccc}\hfill {\tilde{g}}_{\text{free}}(R,\tilde{q}|R_0)& \sim & \frac{e^{-\tilde{q}(R-R_0)}}{4\pi D\sqrt{R{R}_0}\tilde{q}}\sum _{k=0}^{\infty }\frac{{\psi }_k(R,R_0)}{{\tilde{q}}^k},\hfill \end{array}$$ (B14)

$$\begin{array}{ccc}\hfill {\tilde{g}}_{\text{br}}(R,\tilde{q}|R_0)& \sim & \frac{e^{-\tilde{q}(R+R_0-2)}}{4\pi D\sqrt{R{R}_0}\tilde{q}}\sum _{k=0}^{\infty }\frac{{\varphi }_k(R,R_0)}{{\tilde{q}}^k}.\hfill \end{array}$$ (B15)

Note that Eq. B14 assumes R > R₀. For convenience, we give the first expansion coefficients (ψ₀ = ϕ₀ = 1),

$$\begin{array}{ccc}\hfill {\psi }_1& =& -\frac{1}{8}(R^{-1}-R_0^{-1}),\hfill \end{array}$$ (B16)

$$\begin{array}{ccc}\hfill {\varphi }_1& =& -\frac{1}{8}(R^{-1}+R_0^{-1})-\frac{3}{4}-2\tilde{h}.\hfill \end{array}$$ (B17)

The explicit form of the coefficients quickly becomes cumbersome, so that for instance in a simulation that uses small time expansions of the GF, all the required coefficients should be calculated by iterative use of B13. To proceed, we use the (inverse) Laplace transforms¹⁸ (Append. 5, Eqs. 7, 11)

$$\begin{array}{ccc}\hfill {\mathcal{L}}^{-1}\left(\frac{e^{-qx}}{q}\right)& =& {\left(\frac{D}{\pi t}\right)}^{1/2}{e}^{-\frac{x^2}{4Dt}},\hfill \end{array}$$ (B18)

$$\begin{array}{ccc}\hfill {\mathcal{L}}^{-1}\left(\frac{e^{-qx}}{p^{1+n/2}}\right)& =& {\left(4t\right)}^{n/2}{\text{i}}^{\text{n}}\text{erfc}\left(\frac{x}{2\sqrt{Dt}}\right).\hfill \end{array}$$ (B19)

The functions iⁿerfc(x) are defined by¹⁸ (Append. 2, Eqs. 9, 10, 11)

$${\text{i}}^{\text{n}}\text{erfc}\left(x\right):={\int }_x^{\infty }{\text{i}}^{\text{n-1}}\text{erfc}\left(\xi \right)d\xi ,$$ (B20)

and i⁰erfc(x) ≔ erfc(x). None of the integrals in Eq. B20 has to be calculated, because the iⁿerfc(x) functions satisfy the recursion relation¹⁸ (Append. 2, Eq. 14)

$$2n{\text{i}}^{\text{n}}\text{erfc}\left(x\right)={\text{i}}^{\text{n-2}}\text{erfc}\left(x\right)-2x{\text{i}}^{\text{n-1}}\text{erfc}\left(x\right),$$ (B21)

which allows to calculate Eq. B20 swiftly.

We finally arrive at the expressions for small times in the time domain

$$\begin{array}{ccc}\hfill g(R,\tau |R_0)& \sim & \frac{1}{4\pi a^2\sqrt{\tau R{R}_0}}\{{\pi }^{-1/2}\left[e^{-\frac{{(R-R_0)}^2}{4\tau }}+e^{-\frac{{(R+R_0-2)}^2}{4\tau }}\right]\hfill \\ & & +\frac{1}{2}\sum _{n=1}^{\infty }[{\psi }_n{\text{i}}^{\text{n-1}}\text{erfc}\left(\frac{R-R_0}{2\sqrt{\tau }}\right)\hfill \\ & & +{\varphi }_n{\text{i}}^{\text{n-1}}\text{erfc}\left(\frac{R+R_0-2}{2\sqrt{\tau }}\right)\left]{\left(2\sqrt{\tau }\right)}^n\right\}.\hfill \end{array}$$ (B22)

Note that again R > R₀ is assumed.

Small-time expansions for the other quantities considered here can be derived in a similar way. The survival probability becomes

$$\begin{array}{c}\hfill S\left(t\right|r_0)\sim 1-\frac{{\sum }_{n=2}^{\infty }{\phi }_n{\text{i}}^{\text{n-1}}\text{erfc}\left(\frac{R_0-1}{2\sqrt{\tau }}\right){\left(2\sqrt{\tau }\right)}^n}{4\sqrt{R_0\tau }}.\end{array}$$ (B23)

The first two coefficients are ${\phi }_2=2\tilde{h}$ and ${\phi }_3=-\tilde{h}(3/4+2\tilde{h}+1/\left(4R_0\right)).$

Using the Laplace transform¹⁸ (Append. 5, Eq. 2) ${\mathcal{L}}^{-1}\left(p^{\nu +1}\right)=t^{\nu }\Gamma {(\nu +1)}^{-1}$, we finally obtain

$$\begin{array}{c}\hfill S\left(t\right|*)\sim {\tilde{\kappa }}_D\tau \sum _{n=0}^{\infty }{\omega }_n{\tau }^{n/2},\end{array}$$ (B24)

where ${\omega }_0=1,{\omega }_1=-4/\left(3\sqrt{\pi }\right)\tilde{h}.$

Finally, we would like to comment on how to numerically evaluate the analytical expressions for the GF Eq. 26 and the derived quantities. The time dependence of all the quantities is generically given by ${\int }_0^{\infty }{e}^{-Dt{x}^2}...dx$. The quadratic exponential strongly dampens the value of the whole integrand and limits the infinite integration range to a finite range in the sense that contributions to the integral coming from x values larger than a cut-off can be neglected. For the actual integration, we used the Quadrature Adaptive General integrand (QAG) integration algorithm of the GNU Scientific Library (GSL),²⁷ which employs the Gauss-Kronrod scheme²⁸ (Ch. 2.7.1.1). If the accuracy is still not satisfactory, one might divide the integration range in three intervals corresponding to small, intermediate, and large x values. Then the integrand can be approximated corresponding to the x range using the expansions of the Bessel functions that are suitable for small and large arguments,¹⁸ (Append. 3, Eqs. 1, 5) and¹⁹ (Eqs. (9.2.5), (9.2.6)). Alternatively, for small and large times one may directly use the expressions Eqs. B22, B7, B8, respectively.