Multiple barriers in forced rupture of protein complexes

Abstract

Curvatures in the most probable rupture force (f^*) versus log-loading rate (log r_f) observed in dynamic force spectroscopy (DFS) on biomolecular complexes are interpreted using a one-dimensional free energy profile with multiple barriers or a single barrier with force-dependent transition state. Here, we provide a criterion to select one scenario over another. If the rupture dynamics occurs by crossing a single barrier in a physical free energy profile describing unbinding, the exponent ν, from (1 − f^*/f_c)^1/ν ∼ (log r_f) with f_c being a critical force in the absence of force, is restricted to 0.5 ⩽ ν ⩽ 1. For biotin-ligand complexes and leukocyte-associated antigen-1 bound to intercellular adhesion molecules, which display large curvature in the DFS data, fits to experimental data yield ν < 0.5, suggesting that if ligand unbinding is assumed to proceed along one-dimensional pulling coordinate, the dynamics should occur in a energy landscape with multiple-barriers.

INTRODUCTION

Single molecule pulling experiments have generated a wealth of data, which can be used to probe aspects of folding that were not previously possible.^{1, 2, 3} In addition, dynamic force spectroscopy (DFS) has been used to decipher the energy landscape of molecular complexes by measuring the rupture force (f) by linearly increasing load at a rate r_f (=df/dt). Because of the stochastic nature of the unbinding events, f varies from one complex (or realization) to another, giving rise to an r_f-dependent rupture force distribution (P(f)). For a molecular complex obeying Bell's formula, k(f) = k_offexp (fx^‡/k_BT), Evans and Ritchie showed that the most probable force is f^* = (k_BT/x^‡)log (r_fx^‡/k_offk_BT),⁴ where x^‡(= x_ts − x_b) is the location of the transition state (x_ts) from the bound state (x_b) projected along the pulling coordinate and k_off is the unbinding rate in the absence of force. However, Bell-Evans formulae are applicable only if the molecular complexes are mechanically brittle or if the applied tension is sufficiently small that x^‡ does not shift upon application of force.⁵ More generally, f^* follows a (log r_f)^ν dependence, where ν depends on the details of the assumed one-dimensional (1D) model potential.^{6, 7, 8, 9, 10, 11, 12, 13} The basic assumption in all these works is that a single free energy barrier along the pulling coordinate is sufficient to describe force-driven rupture of the bound complex.

Sometime ago Merkel et al. used DFS to probe load dependent strength of biotin bound to ligands, streptavidin and avidin,¹⁴ showing that over six orders of variation in r_f (from about 10⁻² to r_f in excess of 10⁴ pN/s) the plot of f^* versus log r_f ([f^*, log r_f] plot) varies nonlinearly for both ligands. We note parenthetically that it is also common to observe curvature in unfolding rates of proteins when the r_f is varied.¹⁵ By careful data analysis combined with molecular dynamics simulations, they proposed an energy landscape for the complex, with multiple energy barriers.¹⁴ A similar picture emerges in the rupture of intercellular adhesion molecules (ICAM-1 and ICAM-2) bound to leukocyte function-associated antigen-1 (LFA-1) upon application of force.¹⁶

In principle, however, nonlinearity in [f^*, log r_f] plot could also arise from load dependent variation in x^‡ (Ref. ¹⁷) in a 1D energy landscape with a single barrier.^{5, 6, 7, 8, 9, 10, 12, 13, 17} A theoretical model describing force-induced escape from a bound state with a single barrier in a cubic potential (ν = 2/3) has been used to rationalize the biotin-ligand data by identifying various linear regimes demarcated by r_f.⁹ However, in the absence of easily discernible changes in the slopes in [f^*, log r_f] plot, it is difficult to justify such an analysis. Here, we show by analyzing experimental data that the observed nonlinearity in the DFS data of several protein complexes can be better accounted for with an energy landscape containing multiple sequential barriers, as originally demonstrated.^{14, 16}

THEORY

To illustrate how steep curvatures in DFS data can arise naturally from a 1D free energy profile, we calculated P(f) and [f^*, log r_f] of forced-escape kinetics of a quasiparticle from a potential with two barriers, U(x) = Ax(x − 1)[(x − 2) (x − 3)(x − 4)(x − 5) + 1] with A > 0 (Fig. 1). The distributions P(f) are typical of what is observed in experiments (Fig. 1b). For all values of A, [f^*, log r_f] plots are curved although one could discern a modest change in slope (Fig. 1c). The loading rate dependent x^‡(r_f), calculated from the slope of the data k_BT/x^‡(r_f) at each r_f in Fig. 1c, changes from ∼3 nm to <1 nm. The precipitous change in x^‡ at r_f ≈ (e⁻³ − e⁰) pN/s reflects the transition of the confining barrier from the outer to inner barrier with an increasing force (see Fig. 1a). In contrast, gradual change of x^‡ in the range 0 < log r_f < 10 is most likely due to the movement of the inner transition state (see Fig. 5(c) in Ref. 5). For an underlying potential given as the one in Fig. 1a, it is straightforward to interpret that the two discrete slopes in Fig. 1c (or the precipitous transition of x^‡ in Fig. 1d) are due to crossing the two barriers. In contrast, it is nontrivial to solve the inverse problem, i.e., to unambiguously decide from [f^*, log r_f] plots whether the underlying free energy profile has a single barrier with a moving transition state or multiple barriers.

Figure 1.

Rupture characteristics obtained numerically using a potential with two barriers at constant loading rates. (a) U(x) (magenta) and U(x) − f · x (cyan) with A = 5 pN nm and f = 50 pN. Reflecting and absorbing boundary conditions are set at x = a and x = b, respectively. (b) Rupture force distributions, $P\left(f\right)=k\left(f\right)/r_f·\exp [-{\int }_0^{f}d{f}^{\prime }k\left(f^{\prime }\right)/r_f]$, at varying r_f were computed by using mean first passage time (MFPT), $k^{-1}\left(f\right)=D^{-1}{\int }_a^{b}dy{e}^{\beta \left(U\right(y)-f·y)}{\int }_a^{y}dz{e}^{-\beta \left(U\right(z)-f·z)}$, starting from the first bound state at a(=0 nm) to reach an absorbing boundary at b(=5 nm). MFPT expression is valid in the force regime where stationary flux approximation holds.⁴ The length was scaled by nm, and D = 1.0 × 10⁷ nm²/s was used for the diffusion constant. (c) [f^*, log r_f] plots at three A values. Fits of [f^*, log r_f] to Eq. 5 yield ν ≪ 0.5 for all A values (ν = 0.064, 0.075, 0.046 for A = 4, 5, 6 pN nm, respectively). In this case, the data should be divided into two regions and analyzed by the two linear fits as depicted using green lines on the curve with A = 6 pN nm. (d) Loading rate dependent x^‡(r_f) (= x_ts − x_b), extracted from the slope of plot at each r_f in (c) with A = 5 pN nm, shows a sharp decrease from ∼3 nm to <1 nm around r_f ≈ (e⁻³ − e⁰) pN/s.

To establish a criterion for ascertaining whether the energy landscapes for forced-ligand rupture from biotin and LFA-1 have multiple barriers, we study the range of applicability of DFS formalism based on a model potential with a single barrier. Consider a Kramers’ problem of barrier crossing in a free energy profile G(x) in which a single barrier separates the bound and unbound states of a quasi-particle as in ligand bound in a pocket of a receptor

$$G\left(x\right)=G\left(x_c\right)+f_c(x-x_c)+\frac{{(-1)}^{n+1}M}{(n+1)!}{(x-x_c)}^{n+1},$$ (1)

with M > 0. In G(x), a 1D-free energy profile with a single barrier, the shape of barrier and energy well is approximated using n-th order polynomial with n = 1, 2, 3, …. For odd n, we assume that G(x) = −∞ for x > x_c, so that the transition state of G(x) is cusped. In the absence of tension, the barrier height, G^‡, and the location of transition state, x^‡, are $G^{‡}=\chi \frac{n}{n+1}{f}_c{(n!f_c/M)}^{1/n}$ and x^‡ = χ(n!f_c/M)^1/n, respectively, where χ = 1 (for odd n), 2 (for even n). Thus, the critical force (f_c) at which the transition barrier vanishes is given by $f_c=\frac{n+1}{n}{G}^{‡}/x^{‡}$. The form of G(x), an extension of the so-called microscopic models using harmonic-cusp or linear-cubic potential, accounts for the degree of plasticity (or ductility) or brittleness of the energy landscape⁴ by changing n (Fig. 2).⁵ Under tension, the effective free profile is given by G_eff(x) = G(x) − f · x, and f_c should be replaced with f_c(1 − f/f_c) = f_cɛ. Therefore, the force dependent free energy barrier and transition state are G^‡(f) = G^‡ɛ^{1 + 1/n} and x^‡(f) = x^‡ɛ^1/n. Although Eq. 1 looks similar to the one Lin et al. used to discuss rupture dynamics for ɛ ≪ 1, where the barrier height is almost negligible,¹² we did not impose any specific force condition on G(x). Instead of attributing the movement of transition state to a large external tension,^{7, 8, 9, 10, 12, 13} we mapped the nonlinearity in DFS data onto G(x) that has the n-dependent shape of transition barrier and bound state. In G(x), increasing brittleness makes x^‡(f) insensitive to applied tension, which is dictated by n; x^‡(f)/x^‡ = ɛ^1/n → 1. For a generic free energy profile F(x) with high curvatures at both x = x_ts and x_b, x^‡(f)/x^‡ = 1 − f/x^‡ × (|F^″(x_ts)|⁻¹ + |F^″(x_b)|⁻¹) → 1.⁵ When free energy profile is associated with a brittle barrier, Bell's formula can be used to extract the feature of the underlying 1D profile from DFS data.⁵

Figure 2.

The n-dependent shape of G(x) (Eq. 1). The potential with increasing n is associated with more brittle molecular complexes. The yellow circle (x = x_c) denotes an inflection point and a cusp in each even and odd n potential, respectively.

For general n, the Kramers’ rate equation based on the Eq. 1 under tension can be derived as

$$k\left(\varepsilon \right)=\kappa {\varepsilon }^{\alpha \left(n\right)}\exp (-\beta G^{‡}{\varepsilon }^{(n+1)/n}),$$ (2)

where κ is the prefactor in Kramers’ theory and α(n) = χ (1 − 1/n) with χ = 1, 2 for odd and even n, respectively. For a given k(f), the most probable unbinding force is determined by ${dP\left(f\right)/df|}_{f=f^{*}}=0$, resulting in a general equation for f^*

$$k^{\prime }\left(f^{*}\right)=\frac{1}{r_f}{\left[k\left(f^{*}\right)\right]}^2,$$ (3)

where k′(f) = dk(f)/df. This equation leads to

$$\begin{array}{c}\hfill {\varepsilon }^{\frac{n+1}{n}}=\frac{-1}{\beta G^{‡}}\log \left[\frac{r_f{x}^{‡}}{\kappa k_{B}T}{\varepsilon }^{1/n-\alpha \left(n\right)}\left(1-\frac{1}{\beta G^{‡}}\frac{n\alpha \left(n\right)}{n+1}{\varepsilon }^{-\frac{n+1}{n}}\right)\right].\end{array}$$ (4)

Under the typical condition that rupture occurs by thermal activation, i.e., f ≪ f_c(ɛ ≈ 1) and βG^‡ ≫ 1, the most probable unbinding force is approximated as

$$f^{*}\approx f_c\left[1-{\left(-\frac{k_{B}T}{G^{‡}}\log \frac{r_f{x}^{‡}}{\kappa k_{B}T}\right)}^{\nu }\right],$$ (5)

where $\nu =\frac{n}{n+1}$. In deriving Eq. 5 using G(x), the large force ɛ(= 1 − f/f_c) ≪ 1 or fast loading condition, an assumption made in obtaining the mean unbinding force expression similar to Eq. 5,^{6, 12, 13} is not needed. Only the shape of the energy potential matters in deriving Eq. 5 from Eq. 1. The DFS data will have a larger curvature for smaller n, for example, when the energy landscape associated with a protein complex is more ductile (Fig. 2). Because n = 1 (harmonic cusp), 2 (linear cubic), …, ∞ (Bell), ν must satisfy the bound

$$1/2\le \nu \le 1,$$ (6)

for an arbitrary 1D profile that suffices to describe rupture kinetics.

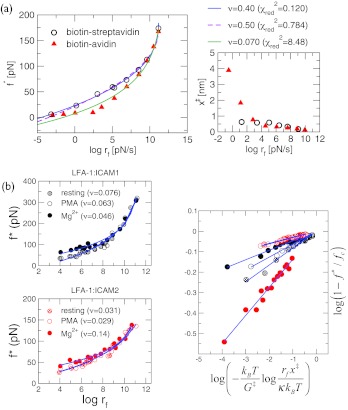
For forced-rupture of biotin-ligand complex, fits to the entire range of the data using Eq. 5 give ν in the disallowed range; ν = 0.40 (biotin-streptavidin) and ν = 0.070 (biotin-avidin) (see Fig. 3a). Even in biotin-streptavidin case, the parameters extracted from the fits with ν = 0.40 and ν = 0.5 (fixed) are comparable; however, the fit with ν = 0.40 is superior yielding both smaller relative error and reduced chi-square value, ${\chi }_{red}^2$, than with ν = 0.5, the lower bound of Eq. 6, that gives the maximal curvature in the single-barrier picture (see Figs. 3a, 4). For both the biotin-ligand complexes, our criterion consistently suggests that the unbinding landscapes for the complexes involve more than one barrier, as was emphasized by Merkel et al.¹⁴ Next, we analyzed the extensive data on LFA-1 expressed in Jurkat T cells whose binding affinity to ICAM-1 and ICAM-2 can be enhanced by treating the cells with phorbol myristate acetate (PMA) and the divalent counterion, Mg^{2 +}. Under all conditions, the exponents that best fit the DFS data are ν < 0.5 (Fig. 3 (b)). As originally argued by entirely different method¹⁶ rupture of ICAM-1 and ICAM-2 from LFA-1 is best described using a free energy profile with at least two barriers. Taken together we arrive at a consistent conclusion that ν < 0.5 implies that the underlying free energy landscape in protein-ligand complexes has multiple barriers.

Figure 3.

Analysis of DFS data with large curvatures. (a) The data obtained using biomembrane force probe (BFP) with force constant in the range 0.1–3 pN/nm (Ref. ¹⁴) were fitted to Eq. 5 (solid lines) with ν = 0.40 for biotin-streptavidin (circle) and ν = 0.070 for biotin-avidin (triangle). The x^‡(r_f) at each r_f is calculated on the right using the slope of four successive data points of [f^*, log r_f] plot. Analyses of data using restricted ν values (ν = 0.5 fit is in dashed line in Fig. 4a). (b) Analysis of DFS data of LFA-1 and its ligands, ICAM-1 and ICAM-2 in Ref. 16. The fits in log-log scale are shown on the right. In all cases, ν < 1/2 suggests that for these complexes as well the underlying free energy profiles must contain at least two barriers; thus multi-state fits are required by dividing the DFS data into multiple regions as was already surmised in Ref. 16.

Figure 4.

Analysis of DFS data using Eq. 5 for (a) biotin-streptavidin and (b) biotin-avidin. For each ν, the fits, residuals ($|f_{fit}^{*}-f_{exp}^{*}|/f_{exp}^{*}\times 100$), and extracted parameters were summarized in the table on the right. We can draw some general conclusions from the fits. For the biotin-streptavidin complex, fit with ν = 0.397 produces the smallest errors although at high loading rates the relative errors for ν = 0.397 and ν = 0.5 are comparable. There are variations in other parameters (x^‡, G^‡, and κ) for all ν. For the biotin-avidin complex, the situation is far worse. In particular, the relative errors in the fits are large even when ν is varied. Similarly, the parameters extracted from the fits are not totally consistent. Taken together, the fits using a 1D free energy profile with a single barrier is not appropriate to describe the rupture kinetics of these two complexes.

DISCUSSION

Mathematically the inequality (Eq. 6) is not strict because it is possible to construct 1D profiles with ν < 0.5 for which [f^*, log r_f] plots exhibit curvature like those observed in experiments. However, such free energy profiles are physically pathological with non-existing first derivatives in the vicinity of the bound complex and fits to the data give manifestly unrealistic parameters (see the Appendix for detailed calculations and analysis). For the physical free energy profiles with a single barrier, Eq. 6 is rigorously satisfied. In addition, there is no compelling reason to choose a special n value even if 1D profile is deemed adequate, and thus ν ought to be treated as a parameter. Although Ref. 11 used ν as a free parameter, the validity range for ν was not discussed. If a global fit of [f^*, log r_f] data using Eq. 5 yields ν < 0.5 and the effect of probe stiffness¹⁸ is absent in the DFS data (see below), we can conclude that a single barrier description of the energy landscape is inadequate.

In principle, curvature in the DFS data could also arise due to probe stiffness. Simple procedure of tiling free energy profile by the amount −f · x under tension is widely used in analyzing single molecule force experiment. However, more rigorous formulation for the effective free energy profile under load using a transducer with stiffness k should read $G_{tot}(x,X_{tr})=G\left(x\right)+\frac{1}{2}{k}_{eff}{(x-X_{tr})}^2$, where x is the position of the end of molecule, X_tr is the position of transducer, and k_eff is the effective stiffness of molecular construct combining the stiffness of the transducer (k_tr) and that of the molecular complex (k_m) ($k_{eff}^{-1}=k_{tr}^{-1}+k_m^{-1}$). In fact, $\frac{1}{2}{k}_{eff}{(x-X_{tr})}^2=-f·x+\frac{1}{2}{k}_{eff}{x}^2+\frac{1}{2}{k}_{eff}{X}_{tr}^2$ with f = k_effX_tr. Therefore, the effective free energy for the complex under tension should be written in general as $G_{eff}\left(x\right)=G\left(x\right)-[f-\frac{1}{2}{k}_{eff}x]·x$.¹⁹ As long as $f\gg \frac{1}{2}{k}_{eff}x$ (or X_tr ≫ x/2) especially when k_eff is small as in optical tweezers or biomembrane force probe (BFP), one can approximate G_eff(x) ≈ G(x) − f · x. Otherwise, rebinding from transient capture well created by a large probe stiffness at near-equilibrium loading condition could give rise to the nonlinearity in the DFS data.¹⁸ Therefore, the rupture force being measured should be replaced by $f^{*}\to f^{*}-\frac{1}{2}{k}_{eff}{x}^{‡}{\varepsilon }^{1/n}$, and at low forces (f ≪ f_c) the most probable force measured by using a transducer with high stiffness such as AFM could be approximated as

$$f^{*}\approx \underset{=f_{pl}}{\underbrace{\frac{1}{2}{k}_{eff}{x}^{‡}}}+\underset{=f_{\mathrm{DFS}}}{\underbrace{f_c\left[1-{\left(-\frac{k_{B}T}{G^{‡}}\log \frac{r_f{x}^{‡}}{\kappa k_{B}T}\right)}^{\nu }\right]}}.$$ (7)

The effect of probe stiffness manifests itself as a non-vanishing plateau force, which could be as large as f_pl ≈ (10 − 100) pN, when k_eff ≈ 100 pN/nm and x^‡ = 0.1 − 1 nm, even when r_f is small enough that f_DFS = 0.¹⁸

The biotin-ligand complexes data preclude the possibility of curvature arising due to probe stiffness because the probe stiffness of BFP is k_eff = 0.01 − 0.3 pN/nm,¹⁴ which is 1–2 orders of magnitude smaller than the k_eff value discussed in the literature.^{20, 21} As a result f_pl ≪ f_DFS, and hence the probe stiffness has no effect on the dependence of f^* on r_f. The value of k_eff is 0.5 − 2.0 pN/nm in the experiments involving LFA-1.¹⁶ Even the largest estimated x^‡ value for the outmost barrier (x^‡ ≈ 3 nm) only yields f_pl < 1 pN. Furthermore, if the nonlinear curvature of DFS data is suspected to be due to the stiffness effect, this ought to be discerned from the curvature due to multiple barriers by producing DFS data at a smaller probe stiffness. The curvature due to multiple barrier should persist in the DFS data even with a small k_eff. Thus, the curvature in the data in¹⁴ can only be attributed to the presence of multiple barriers.

CONCLUSION

The variable that is conjugate to the applied mechanical force in single molecule force spectroscopy is the molecular extension. Thus, it is natural to extract the underlying free energy profiles in terms of extension from measurements such as unbinding force versus loading rate or unfolding rates as a function of force. With the exception of the theory introduced to obtain the roughness of the energy landscape,²² the experimental data are analyzed using theories by assuming that a suitable one-dimensional energy landscape profile captures the unbinding process. The single barrier based 1D force theories,^{7, 8, 9, 10, 11, 12, 13} which are sometimes termed microscopic models, have been applied to many different systems to extract the characteristics of free energy profile,^{11, 23, 24} such as the free energy barrier between the bound and unbound states and location of the transition state. The validity of the extracted parameters can only be assessed using theoretical methods as has been demonstrated for the location of the transition state.²⁵ However, for a class of systems for which force data displays a large curvature as the loading rate is varied, it is not clear if the microscopic models, based on a single barrier picture with moving transition state, can still be used. The condition (Eq. 6), which we showed, should be strictly satisfied for single-barrier based 1D force theories,^{7, 8, 9, 10, 11, 12, 13} provides a guideline that can be used to assess whether the curvature in DFS data is due to multiple barriers or single barrier with a ductile transition state. The presence of multiple barriers in the pulling coordinate can only be discerned by globally fitting the DFS data using Eq. 5 over a broad range of log r_f with ν as a fitting parameter. While a more complex scenario that considers a dynamics on a multidimensional landscape could also produce a large curvature in DFS data,^{26, 27} we did not consider further complication beyond one-dimension because the extracted parameters from the data for the protein complexes with ligands using 1D profile with multiple barriers are physically reasonable.^{14, 16} When two different models produce results of a similar quality but the knowledge on molecular structure associated with force-induced dynamics is absent, it is reasonable to choose a simpler model. It is still to be noted that additional justification for the use of particular energy landscapes can only be made by studying the structures of the protein complexes in molecular detail.

APPENDIX: DFS THEORY FOR A FREE ENERGY PROFILE WITH NON-INTEGER n

It could be argued that the inequality 1/2 ⩽ ν ⩽ 1 (valid rigorously for integer n) that accounts for the curvature of DFS data is not mathematically required. Here, we show that it is possible to construct 1D free energy profiles for which ν is clearly less than 0.5. Indeed, these free energy profiles can even have nearly vanishing ν. However, such profiles are unphysical because near the bound state, they have incorrect curvatures compared to the physical profiles discussed in the text and in the references cited therein. More importantly, the first derivatives of these free energy profiles, which yield ν < 0.5, do not exist near the bound state, i.e, they have a singularity. For these and other reasons (see below), we reject these free energy profiles as plausible models for explaining the curvatures in the observed [f^*, log r_f] plots in a number of protein complexes discussed in the main text, which have all been explained using a two-barrier model.

A free energy profile with 0 < n < 1 (see Eq. 1) can lead to 0 < ν < 1/2 since $\nu =\frac{n}{n+1}$. To explore this possibility, we consider a free energy profile

$$\begin{array}{c}\hfill G\left(x\right)=\sigma a{x}^{1/\sigma }-bx,\end{array}$$ (A1)

with σ > 1. Here, we may regard n = 1/σ and hence n < 1. The term −bx is required for the potential to have a barrier at a finite value of x^‡, the location of the transition state (TS). The TS location and the associated barrier height are

$$\begin{array}{cc}\hfill x^{‡}& ={\left(\frac{a}{b}\right)}^{\frac{\sigma }{\sigma -1}},\hfill \\ \hfill G^{‡}& =(\sigma -1)a{\left(\frac{a}{b}\right)}^{\frac{1}{\sigma -1}}.\hfill \end{array}$$ (A2)

Under tension f, the potential becomes G_eff = G(x) − fx = σax^1/σ − (b + f)x. The f-dependent TS location and the barrier height are

$$\begin{array}{cc}\hfill \frac{x^{‡}\left(f\right)}{x^{‡}}& ={\left(\frac{b}{b+f}\right)}^{\frac{\sigma }{\sigma -1}}={\left(\frac{\frac{G^{‡}/x^{‡}}{\sigma -1}}{\frac{G^{‡}/x^{‡}}{\sigma -1}+f}\right)}^{\frac{\sigma }{\sigma -1}}={\eta }^{\frac{\sigma }{1-\sigma }},\hfill \\ \hfill \frac{G^{‡}\left(f\right)}{G^{‡}}& ={\left(\frac{b}{b+f}\right)}^{\frac{1}{\sigma -1}}={\left(\frac{\frac{G^{‡}/x^{‡}}{\sigma -1}}{\frac{G^{‡}/x^{‡}}{\sigma -1}+f}\right)}^{\frac{1}{\sigma -1}}={\eta }^{\frac{1}{1-\sigma }},\hfill \end{array}$$ (A3)

where η ≡ (1 + f/f_1/σ) with $f_{1/\sigma }\equiv \frac{1}{\sigma -1}\frac{G^{‡}}{x^{‡}}$. Therefore, one can rewrite Eq. A1, (G(x)) and an effective free energy (G_eff(x)) under tension as

$$\begin{array}{cc}\hfill G\left(x\right)& =\frac{\sigma G^{‡}}{\sigma -1}{\left(\frac{x}{x^{‡}}\right)}^{1/\sigma }-\frac{G^{‡}}{\sigma -1}\left(\frac{x}{x^{‡}}\right),\hfill \\ \hfill G_{eff}\left(x\right)& =\frac{\sigma G^{‡}}{\sigma -1}{\left(\frac{x}{x^{‡}}\right)}^{1/\sigma }-(\frac{G^{‡}}{\sigma -1}+f{x}^{‡})\left(\frac{x}{x^{‡}}\right).\hfill \end{array}$$ (A4)

Given G_eff(x), it is possible to obtain the mean first passage time expression corresponding to the lifetime of the complex that can be measured in single molecule experiments. It is given by,

$$k{\left(f\right)}^{-1}=\frac{1}{D}{\int }_0^{\infty }dx{e}^{\beta G_{eff}\left(x\right)}{\int }_0^{x}dy{e}^{-\beta G_{eff}\left(y\right)}.$$ (A5)

The saddle-point approximation, $k\left(f\right)\approx D{\left({\int }_{bound}dy{e}^{-\beta G_{eff}^{\prime }\left(0\right)y}\right)}^{-1}\sqrt{\frac{G_{eff}^{\prime \prime }\left(x^{‡}\left(f\right)\right)}{2\pi k_{B}T}}{e}^{-\beta G^{‡}\left(f\right)}$ with Eq. A3, yields Kramers’ equation for the escape rate

$$\begin{array}{c}\hfill k\left(f\right)=\kappa {\eta }^{\alpha \left(\sigma \right)}\exp \left[-\beta G^{‡}{\eta }^{\frac{1}{1-\sigma }}\right],\end{array}$$ (A6)

with $\alpha \left(\sigma \right)\equiv \frac{2\sigma -1}{2(\sigma -1)}$. Here, note that the κ, defined as the prefactor, contains the singular integral ${\left({\int }_{bound}dy{e}^{-\beta G_{eff}^{\prime }\left(0\right)y}\right)}^{-1}$. By using the relationship k^′(f^*) = [k(f^*)]²/r_f to derive the most probable force, we get

$$\begin{array}{c}\hfill {\eta }^{\frac{1}{1-\sigma }}=-\frac{1}{\beta G^{‡}}\log \frac{r_f{x}^{‡}}{\kappa k_{B}T}\left[\frac{(\sigma -1)\alpha \left(\sigma \right)}{{\eta }^{\alpha \left(\sigma \right)+1}\beta G^{‡}}+{\eta }^{\frac{\sigma }{1-\sigma }}\right].\end{array}$$ (A7)

By assuming βG^‡ ≫ 1 and f ≪ f_1/σ, we can simplify the above equation into

$$\begin{array}{c}\hfill {\eta }^{\frac{1}{1-\sigma }}\approx -\frac{1}{\beta G^{‡}}\log \frac{r_f{x}^{‡}}{\kappa k_{B}T}.\end{array}$$ (A8)

Therefore, the most probable force (f^*) for the fractional potential (Eq. A1) is

$$\begin{array}{cc}\hfill f^{*}& \approx f_{1/\sigma }\left[{\left(-\frac{1}{\beta G^{‡}}\log \frac{r_f{x}^{‡}}{\kappa k_{B}T}\right)}^{1-\sigma }-1\right]\hfill \\ & =f_{1/\sigma }\left[{\left(-\frac{1}{\beta G^{‡}}\log \frac{r_f{x}^{‡}}{\kappa k_{B}T}\right)}^{2-1/\nu }-1\right],\hfill \end{array}$$ (A9)

where $\sigma =\frac{1-\nu }{\nu }$ was employed in the last line.

There are a few important comments about Eq. A9 that need to be made. (i) Note that the form of Eq. A9 is very different from Eq. 5. The difference is related to the aforementioned difficulties associated with G_eff(x). Nevertheless, it is possible mathematically to construct model free energy profiles, without regard to physical considerations, for which [f^*, log r_f] plot has a curvature that is reminiscent of what is observed in experiments. (ii) Although Eq. A9 can be used to obtain excellent fits to DFS data on protein complexes, it turns out that the extracted value of κ is extremely large and is clearly unphysical (see Fig. 5). The unphysical values are a consequence of the singularity of G(x) (or G_eff(x)) at x = 0. We conclude that the free energy profiles with a fractional power of n, which mathematically creates singularity at bound state, is not suitable to be used to analyze experimental data. Thus, the bound 1/2 ⩽ ν ⩽ 1 in Eq. 6 must hold for physical 1D free energy profiles with a single barrier.

Figure 5.

(a) The blue curve is the bare (f = 0) free energy profile of the form given in Eq. A1 and the green curve is the tilted form of G(x) in the presence of force. By fitting the numerically computed (black circles) f^* as a function of r_f to Eq. 5 (red curve), we obtain the parameters shown below. Although the features of original potential G(x) = 100x^1/3 − 10x are reasonably recovered (σ is larger than the value in G(x)) by using Eq. 5, the extracted value of κ is unrealistically large. (b) Equation 5 was used to fit the DFS data of biotin-strepavidin (circles) and biotin-avidin (triangles). Although the quality of fit is excellent, the unrealistically large value of κ, due to the singularity of the hypothesized fractional potential at x = 0, suggests that the potential with a fractional power should not be used for the analysis. In fact, the κ values are comparable to or much greater than the TST estimate k_BT/h (≈6.2 × 10¹²s⁻¹), which of course makes no sense. Hence, we can rule out the free energy profiles of the form given in Eq. A1 to analyze DFS data on protein complexes.