Network-based Empirical Bayes Methods for Linear Models with Applications to Genomic Data

Abstract

Empirical Bayes methods are widely used in the analysis of microarray gene expression data in order to identify the differentially expressed genes or genes that are associated with other general phenotypes. Available methods often assume that genes are independent. However, genes are expected to function interactively and to form molecular modules to affect the phenotypes. In order to account for regulatory dependency among genes, we propose in this paper a network-based empirical Bayes method for analyzing genomic data in the framework of linear models, where the dependency of genes is modeled by a discrete Markov random field defined on a pre-defined biological network. This method provides a statistical framework for integrating the known biological network information into the analysis of genomic data. We present an iterated conditional mode algorithm for parameter estimation and for estimating the posterior probabilities using Gibbs sampling. We demonstrate the application of the proposed methods using simulations and analysis of a human brain aging microarray gene expression data set.

1 Introduction

Empirical Bayes-based methods are one of the most popular statistical approaches for analysis of microarray gene expression data in order to account for the parallel nature of the inference in microarrays and to borrow information from the ensemble of genes that can enhance the inference about each gene individually. Efron et al. (2001) used a non-parametric empirical Bayes approach for analyzing the factorial microarray gene expression data. Lonnstedt and Speed (2002) took a parametric empirical Bayes approach using a simple mixture of normal models and a conjugate prior and derived the closed-formed posterior odds of differential expression for each gene. Smyth (2004) developed the hierarchical model of Lonnstedt and Speed (2002) into a practical approach for general microarray experiments in the framework of linear models with arbitrary coefficients and contrasts of interests. Smyth (2004) also derived the posterior odds statistic in terms of a moderated t-statistic in which posterior residual standard deviations are used in place of ordinary standard deviations. While these empirical Bayes methods have proved to be very useful for identifying the differentially expressed genes or genes that are related to certain covariates, they make a key assumption that genes are independent. However, since many biological processes are involved in activation of multiple pathways of correlated genes, the genes with regulatory relationships are expected to be dependent. These dependent genes often interact with each other to form molecular modules that affect the cellular and clinical phenotypes (Ideker and Sharan, 2008).

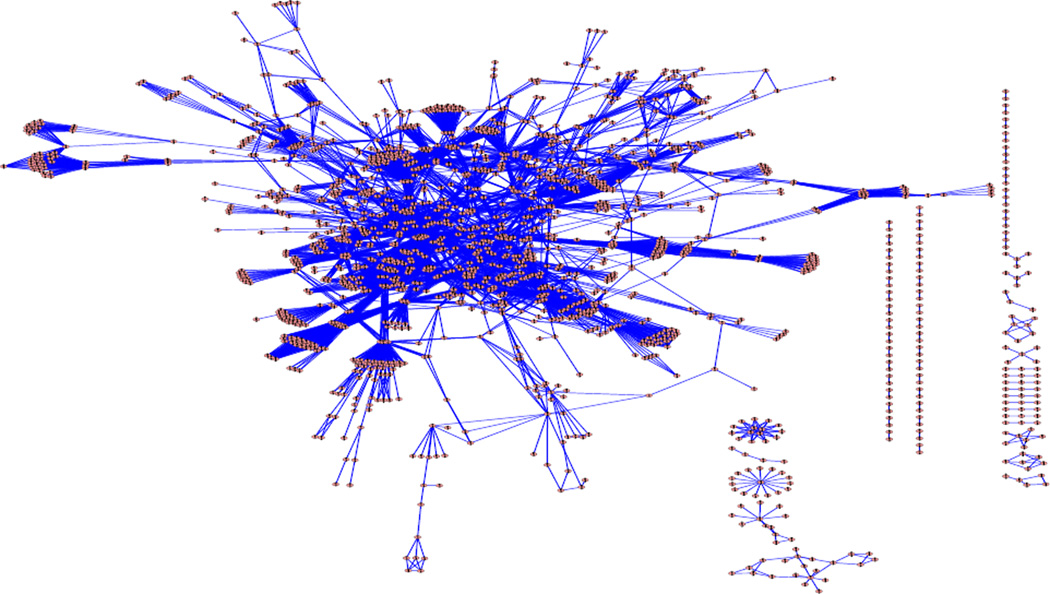
The goal of this paper is to develop a network-based empirical Bayes methods for linear models for the analysis of genomic data where we utilize the prior genetic regulatory network information to model the regulatory dependency among genes. Information about gene regulatory dependence has been accumulated from many years of biomedical experiments and is summarized in the form of pathways and networks and assembled into pathway databases. Some well-known pathway databases include KEGG, BioCarta (www.biocarta.com) and Bio-Cyc (www.biocyc.org). As an exmaple, Figure 1 shows the KEGG human regulatory network (Kanehisa and Goto, 2002), consisting of 33 interconnected regulatory pathways. There has been great interest in developing statistical and computational methods that can integrate the prior biological network information into the analysis of genomic data, especially into the analysis of microarray gene expression data (see Ideker and Sharan (2008) for a review). Representing the known genetic regulatory network as an undirected graph, Wei and Li (2007; 2008) and Wei and Pan (2008) have recently developed hidden Markov random field (HMRF)-based models for identifying the subnetworks that show differential expression patterns between two conditions, and have demonstrated using both simulations and applications to real data sets that the procedure is more sensitive in identifying the differentially expressed genes than those procedures that do not utilize pathway structure information. Alternatively, regression analysis methods have also been developed when the gene expression data are linked on pathways and are treated as independent variables. Li and Li (2008) developed a network-constrained regularization for linear regression analysis where a graph-constrained penalty function was introduced. Zhu, Pan and Shen (2009) developed support vector machines with disease-gene-centric network penalty for high dimensional microarray data. Tai and Pan (2009) developed Bayesian variable selection in regression with networked predictors where a Markov random field prior is introduced for the latent inclusion variables. While the methods of Wei and Li (2007; 2008) and Wei and Pan (2008) mainly focus on identifying differentially expressed genes between two conditions and the network-constrained regression analysis treats the gene expression levels as covariates and aims to identify those genes that are predictive to the responses, in this paper, we develop a network-based empirical Bayes method for linear models, which can handle more general covariates for the analysis of microarray gene expression data, including multiple continuous covariates or covariates from complex experimental designs that can potentially be associated with the gene expression levels. Different from the network-constrained regression approaches, our approach treats the gene expression levels as responses and aims to identify the genes that are affected by the covariates. This approach is especially useful when the sample size is to small to perform any meaningful regression analysis with gene expression levels as covariates.

Figure 1.

Undirected graph of the KEGG regulatory network, consisting of 33 interconnected regulatory pathways. There are a total of 1663 genes (nodes) and 8011 regulatory relationships (edges).

As a motivating example of our proposed methods, we consider the problem of identifying age-dependent molecular modules or subnetworks in human brains using the microarray gene expression data of Lu et al. (2004), where they conducted a microarray gene expression study of the postmortem human frontal cortex from 30 individuals ranging from 26 to 106 years of age. To identity the aging-regulated genes, they performed simple linear regression analysis for each gene with age as a covariate. In our approach, we re-analyze this data set by combining the KEGG regulatory network information (Kanehisa and Goto, 2002) with the gene expression data in order to identify the molecular modules that are aging-regulated. Here we can treat age as a continuous covariate for the analysis of gene expression levels.

The rest of the paper is organized as follows. We first present a network-based empirical Bayes method for linear models and present the iterative conditional mode (ICM) algorithm (Besag, 1974; 1986) for parameter estimation. We then present results from simulation studies and analysis of the human brain aging gene expression data to evaluate the proposed method. Finally, we give a brief discussion of the methods and results.

2 Network-based Empirical Bayes Methods for Linear Models

2.1 General linear models for gene expression data

We assume that we have a set of n microarrays (samples), we want to determine how the experimental conditions affect the expression levels of genes and which genes or subnetworks of genes are affected. Let Y = (Y₁, …, Y_g, …, Y_p) denote the microarray gene expression profiling data matrix (n × p) of p genes over n samples, where Y_g is the mRNA expression level of gene g for the n samples. Let X = (x₁, …, x_n)^T be the n × q covariate matrix of the n samples, where x_i represent the q-dimensional covariate vector for the ith sample. Depending on designs of the experiments, this vector could correspond to the design matrix or other general covariates (see Smyth (2004) for specification of the design matrices for various microarray experiments). We assume the following linear model for gene expression level for the gth gene:

$$Y_g={\mu }_g+X{\alpha }_g+{\epsilon }_{g,}$$

$$\mathit{\text{var}}({\epsilon }_g)={\sigma }_g^2\mathit{I},g=1,\dots ,p,$$ (1)

where α_g a coefficient vector and ε_g is the vector of random errors. Let α̂_g be the least square estimate of α_g and ${\mathrm{\sigma ̂}}_g^2$ be the estimate of ${\sigma }_g^2$ based on this model. Further let $\mathit{\text{Var}}({\mathrm{\sigma ̂}}_g)=V_g{\mathrm{\sigma ̂}}_g^2$ be the estimated covariance matrix, where V_g is a positive definite matrix based on the design matrix X.

Certain contrasts of the coefficients are assumed to be of biological interest and these are defined by β_g = C^T α_g, where C is a contrast vector. The β_g can then be estimated by β̂_g = C^T α̂_g with its variance estimated by $\mathit{\text{Var}}({\mathrm{\beta ̂}}_g)=C^T{V}_{g}C{\mathrm{\sigma ̂}}_g^2={\upsilon }_g{\mathrm{\sigma ̂}}_g^2$. Based on model (1), we have

$${\mathrm{\beta ̂}}_g|{\beta }_g,{\sigma }_g^2\sim N({\beta }_g,{\upsilon }_g{\sigma }_g^2),$$

$${{\mathrm{\sigma ̂}}_g}^2|{\sigma }_g^2\sim \frac{{\sigma }_g^2}{d_g}{\chi }_{d_g}^2,$$

where d_g = n − q is the residual degrees of freedom.

2.2 Network-based Markov random field prior

We are interested in testing whether individual contrast value β_g to be zero. To achieve this goal, we introduce a random vector z = (z₁, …, z_g, …, z_p)^T, representing the gene states, where

$$z_g=\{\begin{array}{cc}1\hfill & \text{if }{\beta }_g\ne 0\hfill \\ 0\hfill & \text{if }{\beta }_g=0.\hfill \end{array}$$

Besides the gene expression data, suppose that we have a network of known pathways that can be represented as an undirected graph G = (V, E), where V is the set of nodes that represent genes or proteins coded by genes and E is the set of edges linking two genes with a regulatory relationship. Let p = |V| be the number of genes that this network contains. Note the gene set V is often a subset of all the genes that are probed on the gene expression arrays. If we want to include all the genes that are probed on the expression arrays, we can expand the network graph G to include isolated nodes, which are those genes that are probed on the arrays but are not part of the known biological network. For two genes g and g′, if there is a known regulatory relationship, we write g ~ g′. For a given gene g, let N_g = {g′ : g ~ g′ ∈ E} be the set of genes that have a regulatory relationship with gene g and m_g = |N_g| be the degree for gene g.

The key to our approach is that instead of assuming that z₁, …, z_p are independently, identically distributed Bernoulli random variables, we assume that they are dependent on the network, whose dependency can be modeled as a simple discrete Markov random field. Specifically, following Wei and Li (2007), we model the dependency of z = (z₁, …, z_g, …, z_p)^T using a discrete Markov random field model with the following distribution:

$$p(z;\mathrm{\Phi })\propto \text{exp}(\gamma n_1-\eta n_{01}),$$ (2)

where Φ = (γ, η), $n_1={\displaystyle {\sum }_{g=1}^p{z}_g}$ is the number of genes at state 1 and n₀₁ = ∑_g~g′ I{z_g = z_g′} is the number of neighboring genes with different states. The parameters γ and η are arbitrary and we require η to be non-negative to discourage neighboring genes with different states. Given the states of all other genes, the conditional probability of gene i with state z_g can be easily derived as

$$p_g(z_g|z_{{\partial }_g};\mathrm{\Phi })\propto \text{exp}(\gamma z_g-\eta {\mu }_g(1-z_g)),$$ (3)

where ∂_g represents all the other genes except the gth gene on the network and u_g(1 − z_g) denotes the number of neighbors of gene g having state (1 − z_g) (Besag, 1974; 1986). In order to account for different degrees of the nodes (i.e., different numbers of neighboring genes on the network), we propose to modify the conditional probability (3) as

$$p_g(z_g|z_{{\partial }_g;}\mathrm{\Phi })\propto \text{exp}(\gamma z_g-\eta {\mu }_g(1-z_g)/m_g),$$ (4)

where m_g is the number of neighbors of the gth gene. This conditional probability is used in this paper.

We then make the following modeling assumptions:

Assumption 1. Given any particular realization z = (z₁, …, z_g, …, z_p)^T, the random variables Y = (Y₁, …, Y_g, …, Y_p) are conditionally independent, i.e., the distribution of random variable Y_g only depends on z_g. The conditional density of the observed gene expression Y , given z, is simply,

$$l(Y|z)={\displaystyle \prod _{i=1}^{p}f(Y_g|z_g),}$$

where f(Y_g|z_g) will be specified in next section (see equation 6).

Assumption 2. The true state z* is a realization of a discrete MRF with a specified distribution p(z) defined by equation (2).

2.3 Empirical Bayes methods for linear models

Given the large number of gene-wise linear model fits from the same genotype, an empirical Bayesian approach is commonly used to take advantage of the parallel structure. In this section, we first briefly review the hierarchical model introduced by Smyth (2004) and present the key probability distributions that are used in the specification of the empirical Bayes methods for linear models. Smyth (2004) introduced an inverse-gamma prior distribution to describe the variation of ${\sigma }_g^2$ across genes with hyper-parameters $s_0^2$ and d₀:

$$\frac{1}{{\sigma }_g^2}\sim \frac{1}{d_0{s}_0^2}{\chi }_{d_0}^2.$$

Prior distribution on the non-zero coefficient β_g is assumed to be a normal distribution,

$${\beta }_g|{\sigma }_g^2,z_g=1\sim N(0,{\upsilon }_0{\sigma }_g^2).$$

Under the above prior information, the posterior mean of ${\sigma }_g^2$ can be written as

$${\tilde{\sigma }}_g^2=E({\sigma }_g^2|{\mathrm{\sigma ̂}}_g^2)=\frac{d_0{s}_0^2+d_g{\mathrm{\sigma ̂}}_g^2}{d_0+d_g}.$$

Smyth (2004) further defined a moderated t-statistic based on the posterior mean of the variance estimation by

$${\tilde{t}}_g=\frac{{\mathrm{\beta ̂}}_g}{{\tilde{\sigma }}_g\sqrt{{\upsilon }_g}}.$$

Smyth (2004) showed that the moderated t-statistic and residual sample variance are independent, with the following distributions:

$${\mathrm{\sigma ̂}}_g^2\sim s_0^2{F}_{d_g,d_0},$$

$${\tilde{t}}_g|z_g=0\sim t_{d_0+d_g},$$

$${\tilde{t}}_g|z_g=1\sim {(1+{\upsilon }_0/{\upsilon }_g)}^{1/2}{t}_{d_0+d_g},$$ (5)

where F(.) and t(.) are the central F and t distributions.

Note that given z_g, the probability density function of the data observed Y_g from the linear model (1) is a function of ${\mathrm{\sigma ̂}}_g^2$ and t̃_g only. Based on Assumption 1, we can write the conditional density of the observed gene expression Y using the sufficient statistics t̃_g and ${\mathrm{\sigma ̂}}_g^2$ as

$$l(Y|z;\mathrm{\Theta })={\displaystyle {\prod }_{g=1}^{p}f(Y_g|z_g;\mathrm{\Theta })\propto {\displaystyle {\prod }_{g=1}^{p}f({\mathrm{\sigma ̂}}_g^2;\mathrm{\Theta })f({\tilde{t}}_g|z_g;\mathrm{\Theta }),}}$$ (6)

where Θ = (d₀, $s_0^2$, υ₀) is the vector of the parameters associated with the conditional density function of the observed Y.

2.4 ICM algorithm for parameter estimation and Gibbs sampling

While inferring the true gene state z* for all p genes, we carry out the parameter estimation simultaneously. We propose the following algorithm based on the method of moments estimates of Smyth (2004) and the ICM algorithm by Besag (1986) to estimate the parameter Θ in the hierarchical model for the linear regression and the parameter Φ in the network-based empirical Bayes models. The following iterative steps are involved in the algorithm:

• (1). Use the method of moments of Smyth (2004) to obtain estimates of the hyper-parameters d₀ and $s_0^2$, denoted by d̂₀ and ${ŝ}_0^2$. The estimates only depend on the observed samples variances ${\mathrm{\sigma ̂}}_g^2$and its distribution given in (5).

• (2). Obtain an initial estimate ẑ of the true states z* based on the p-values for testing β_g = 0 using the moderated t-statistic t̃. For a given gene g, if the p-value is less than 0.01, we let ẑ_g = 1.

• (3). Estimate υ₀ by the value υ̂₀, which maximizes the likelihood

  $$l(Y|ẑ;{\mathrm{d̂}}_0,{ŝ}_0^2,{\upsilon }_0)\propto {\displaystyle {\prod }_{g=1}^{p}f({\tilde{t}}_g|z_g;ẑ;{\mathrm{d̂}}_0,{ŝ}_0^2,{\upsilon }_0)}$$

  (see Equation 6). Note that this is different from Smyth (2004) in that our estimate of υ₀ depends on the values of the latent vector z.
• (4). Estimate Φ by the value Φ̂, which maximizes the pseudolikelihood pl(ẑ; Φ) based on the current states ẑ, where

  $$pl(z;\mathrm{\Phi })={\displaystyle \sum _{g=1}^p{p}_g(z_g|z_{{\partial }_g};\mathrm{\Phi })}={\displaystyle \sum _{g=1}^p\frac{\text{exp}\{\gamma z_g-\eta {\mu }_g(1-z_g)/m_g\}}{\text{exp}\{\gamma -\eta {\mu }_g(0)/m_g\}+\text{exp}\{-\eta {\mu }_g(1)/m_g\}}.}$$
• (5). Carry out a single cycle of ICM based on the current ẑ, Θ̂, and Φ̂ to obtain a new ẑ. Specifically, for g = 1, …, p, update z_g, which maximizes

  $$P(z_g|Y,{ẑ}_{{\partial }_g})\propto f({\tilde{t}}_g|z_g;\mathrm{\Theta ̂})p_g(z_g|{ẑ}_{{\partial }_g};\mathrm{\Phi ̂}),$$ (7)

  subject to z_g = 1 or z_g = 0.

• (6). Go to step (3) until approximate convergence of all the parameters. In particular, we stop the iterations when the maximum of the relative changes of the parameter estimates is smaller than a small value ε.

After obtaining the parameter estimates Θ̂ and Φ̂ based on the algorithm outlined above, we then carry out a Gibbs sampling procedure to sample z_g, g = 1, …, p given the data using the conditional probability defined in Equation (7) and obtain posterior probabilities of q_g = Pr(z_g = 0|Y; Θ̂, Φ̂), g = 1, …, p. The resulting posterior probabilities are then used to determine which genes are affected by the phenotype and those relevant genes can be mapped back to the network to identify the subnetworks. In addition, we can estimate the false discovery rate (FDR) based on these posterior probabilities (Sun and Cai, 2009). Specifically, consider p null hypotheses, H_0g : β_g = 0, g = 1, …, p and let q₍₁₎, …, q_(p) be the order values of the posterior probabiities and H₍₀₁₎, …, H_(0p) be the corresponding null hypotheses. The data-driven FDR procedure can defined as:

$$\text{let }l=\text{max }\left\{i:\frac{1}{i}{\displaystyle \sum _{g=1}^i{q}_g\le \alpha }\right\},\text{then we reject all }{H}_{(0i)},i=1,\dots ,l.$$

If all the parameters are known, using the same argument as in Sun and Cai (2009), we can show that this procedure can indeed control the FDR at α or smaller. It is however unclear whether this still holds for the data-driven procedure due to fact that the theoretical properties of the parameter estimates are unknown.

3 Simulation Studies

To demonstrate the performance of our proposed procedure, we conducted simulation studies and simulated data based on two real regulatory networks: the KEGG human regulatory network (see Figure 1) and the yeast transcription network used in Milo et al. (2002). For the KEGG network, we first obtained the network of 33 human regulatory pathways from the KEGG database (December 2006 version) and excluded those non-gene-gene interactions, e.g., compound-gene relations, compound-compound relations. The resulting data are represented as an undirected graph where each node is a gene and an edge is drawn to connect two nodes if there is a regulatory relation between them. The KEGG network is represented as an undirected graph with 1668 nodes and 8011 edges (see Figure 1).

To simulate the vector of gene states z, we first chose K pathways among the 33 regulatory pathways and initialized those genes in the K pathways to be relevant genes with z_g = 1 and the rest of the genes to be irrelevant, which gave us the initial z₀. Then starting with z₀, we performed sampling five times based on the discrete MRF model (3) with γ = 0, η = 2. In this simulation study, we chose K = 5, 9 and 17 to obtain about 11.5%, 18.9% and 48.7% of relevant genes, respectively. For a given vector of gene states z, we then simulated those non-zero coefficients β in the linear models based on the following hierarchical model,

$${\beta }_g|{\sigma }_g^2,z_g=1\sim N(0,{\upsilon }_0{\sigma }_g^2),$$

where ${\sigma }_g^2$ follows an inverse Gamma distribution:

$$\frac{1}{{\sigma }_g^2}\sim \frac{1}{d_0{s}_0^2}{\chi }_{d_0}^2.$$

The tuning parameters were set as d₀/(d₀ + d_g) = 0.5 and s₀ = 8, υ₀ = 2, similar to those used by Smyth (2004). Finally, for a sample size of 10, the gene expression level Y was simulated from the following linear model,

$$Y_g=X{\beta }_g+{\epsilon }_g,$$

where X = (4.0, 4.2, 4.5, 4.8, 5.2, 5.3, 5.6, 6.1, 6.6, 7.0)^T is fixed and the error terms for the 10 independent samples were simulated from N (0, ${\sigma }_g^2$), where ${\sigma }_g^2$s range from 27.87 to 194.20 with a mean of 69.24 (sd=20.33).

The yeast regulatory network is also represented as an undirected graph with 688 genes and 1079 edges. Note that the yeast regulatory network is expected to be more reliable than the KEGG network (Ideker and Sharan, 2008). A similar simulation procedure was used to simulate data on the yeast regulatory network. We chose K = 2, 4 and 14 transcriptional modules as initially relevant and iterated to get about 7.88%, 11.5% and 47.3% of relevant genes, respectively.

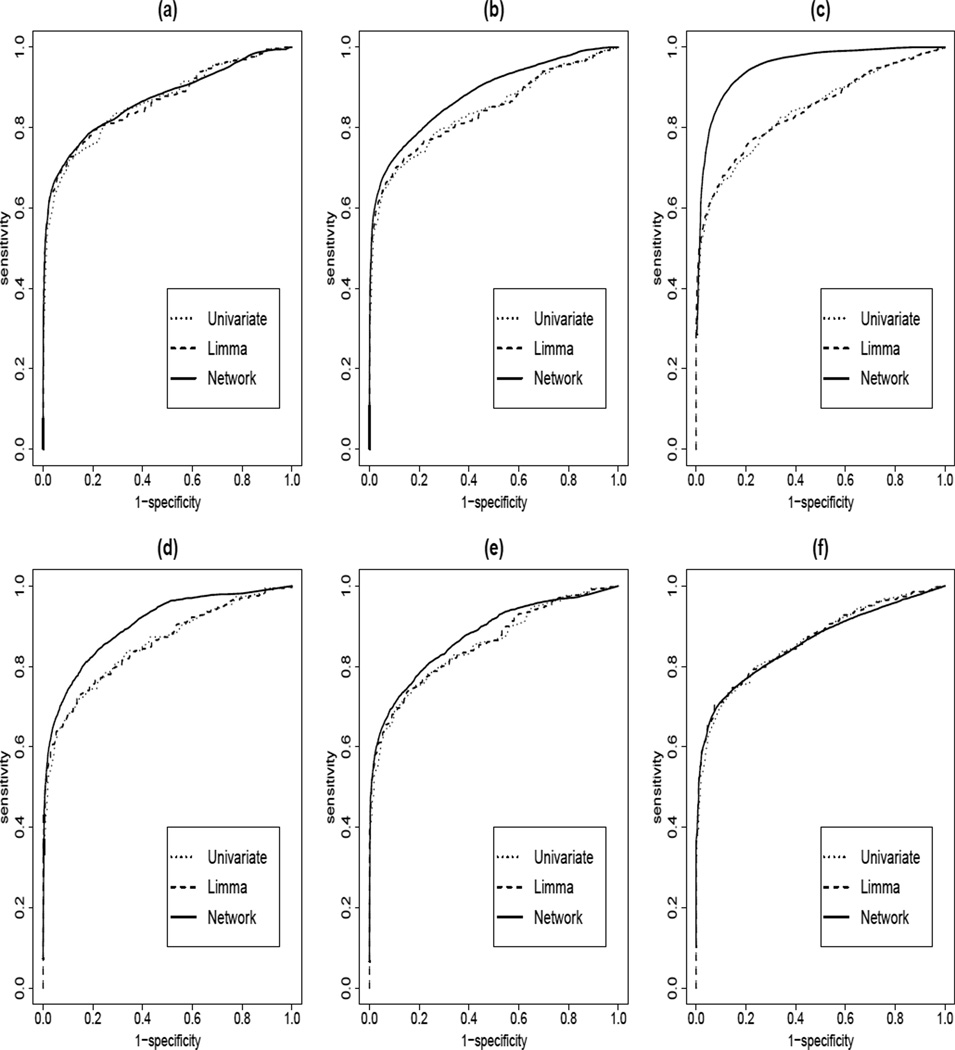
Simulations were repeated 50 times to assess the sensitivity, specificity of our proposed network-based empirical Bayes procedure (NetEB). We compared our proposed procedure with the results from the ordinary t–statistics, which does not consider any prior information and the moderated t–statistics, which borrows information across genes based on the empirical Bayesian modeling (Smyth, 2004). Figure 2 shows the simulation results, where the sensitivity is the average over 50 replications of the percentage of correctly identified relevant genes; specificity is calculated as the average of the fraction of irrelevant genes correctly identified. The ordinary t-statistics and the moderated t-statistics performed almost identically in all six models we considered. Our proposed NetEB methods showed certain gains in sensitivities over the moderated t-statistics, indicating that the gain in sensitivities indeed were indeed resulted from using the network information. For simulations using the the KEGG network, the improvement is bigger than there are more relevant genes. However, for simulations using the yeast regulatory network, we observed bigger improvement when the number of relevant genes is small. The improvement of the NetEB procedure over the moderated t-statistics or the standard t-statistics seems to depend on the network structures and where the relevant subnetworks are related to each other.

Figure 2.

Average areas under the curves over 50 replications for comparing the network-based empirical methods, ordinary t-statistics and the moderated t-statistics of Smyth as implemented in Limma. (a)–(c): KEGG regulatory network is used in simulation with average of 11.5%, 18.9% and 48.7% of relevant genes; (d)–(f): Yeast regulatory network is used in simulation with average of 7.88%, 11.5% and 47.3$ of relevant genes.

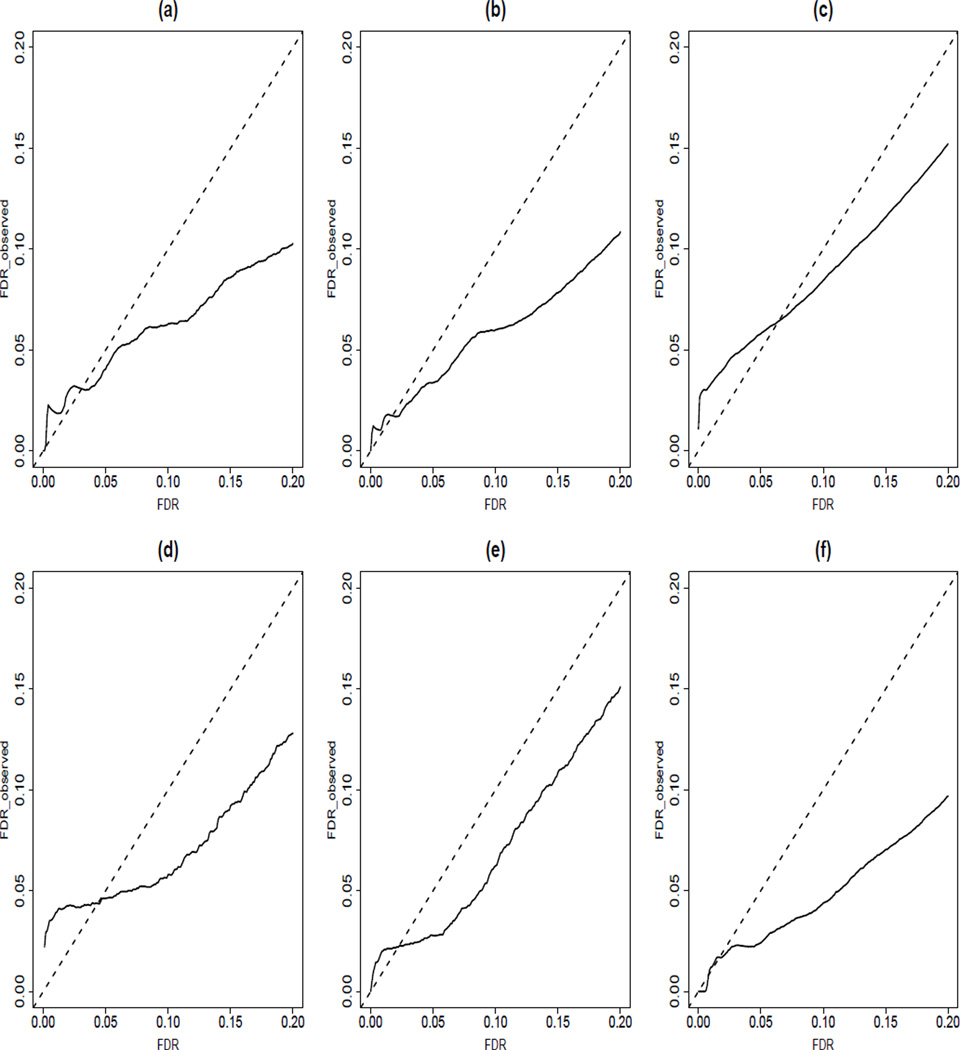
We also checked whether the posterior-probability based data-adaptive FDR procedure indeed controls the FDR at the desired levels. Figure 3 presents the observed FDRs versus the specified levels of α for the six different models we considered. We observed that unless α is very small, the observed FDRs are always smaller than the specified α levels, indicating that the posterior probability-based procedure can approximately controls the FDRs but is somewhat conservative. When α is very small, the numbers of the identified genes were very small and varied a lot over the 50 replications.

Figure 3.

Average observed FDRs (solid lines) over 50 replications for posterior probability-based FDR controlling procedure for different levels of α (x-axis). (a)–(c): KEGG regulatory network is used in simulation with average of 11.5%, 18.9% and 48.7% of relevant genes; (d)–(f ): Yeast regulatory network is used in simulation with average of 7.88%, 11.5% and 47.3% of relevant genes.

4 Application to Microarray Gene Expression Study of Human Aging Brain

To demonstrate the proposed methods, we consider the problem of identifying age-dependent molecular modules based on the gene expression data measured in human brains of individuals of different ages published in Lu et al. (2004). In this study, the gene expression levels in the postmortem human frontal cortex were measured using the Affymetrix arrays for 30 individuals ranging from 26 to 106 years of age. The R RMA procedure (Irizarry et al., 2003) was used to normalize the gene expression data. To identity the aging-regulated genes, Lu et al. (2004) performed simple linear regression analysis for each gene with age as a covariate. We analyzed this data set by combining the KEGG regulatory network information with the gene expression data. In particular, we limited our analysis to the genes that can be mapped to the KEGG regulatory work and focused on the problem of identifying the subnetworks of the KEGG regulatory network that are perturbed during the human aging process. The final KEGG network includes 1305 genes.

Using our proposed network-based empirical Bayes method, we estimated γ̂ = −2.15 and η̂ = 0.35 in the Markov random field model, with a positive estimate of the dependency parameter η indicating some regulatory dependency of the genes on the KEGG network. The negative value of the γ estimate indicates that there are fewer genes that are associated with brain ageing and the positive value of the η estimate indicates that whether a gene is related the covariate depends on the states of the neighboring genes. For example, for a gene with five neighbors, based on the parameter estimates, the odds for this gene to be associated with the covariate is increased by about 2 folds if all its five neighbors are associated as compared to none of its neighbors being associated with the covariates. After the convergence of the ICM algorithm, we ran Gibbs sampling 20,000 times to estimate the posterior probabilities of genes on the KEGG network being associated with aging. We identified 61, 46 and 31 genes related to aging using cutoff values of 0.80, 0.90 and 0.95 of the posterior probability, with estimated false discovery rates of 0.063, 0.033 and 0.016, respectively. Using a cutoff of 0.80 of the posterior probability, 39 of the 61 genes identified are connected on the KEGG network with a total of 31 edges.

Figure 4 shows the subnetworks identified by our proposed network-based empirical Bayes methods. It is interesting to note that one subnetwork includes fibroblast growth factors (FGF1, FGF2, FGF12, FGF13) and their receptor (FGFR3). It has been demonstrated that fibroblast growth factors are associated with many developmental processes including neural induction (Bottcher and Niehrs, 2005) and are involved in multiple functions including cell proliferation, differentiation, survival and aging (Yeoh and de Haan, 2007). Another interesting subnetwork includes the mitogen-activated protein kinase (MAPK) (MAPK1 and MAPK9) and the specific MAPK kinase (MAP2K) also appeared in several subnetworks. The MAPKs play important roles in induction of apoptosis. MAPK1 is also linked to the insulin receptor gene (INSR) on the KEGG pathway. INSR binds insulin (INS) and regulates energy metabolism. Evidence from model organisms, including results from fruit flies (Tatar et al, 2001) and roundworms (Kimura et al., 1997), relates INSR homologues to aging, most likely as part of the GH1/IGF1 axis. MAPK1 is also linked to MAPT gene, which was observed to decrease in expression with increased age (Hayesmoore et al., 2008). The third interesting subnetwork includes a few genes related to α-calcium/calmodulin-dependent protein kinase (CALM1, CALM3 and CAMK4). Study by Hinds et al. (2003) suggested that these genes serve as a negative activity-dependent regulator of neurotransmitter release at hippocampal synapses and maintains synapses in an optimal range of release probabilities necessary for normal synaptic operation.

Figure 4.

Subnetworks identified by the proposed network-based empirical Bayes method for the human brain aging gene expression data of Lu et al. (2004). These subnetworks include 39 of the 61 aging-associated genes with posterior probability of greater than 0.80 estimated by the proposed method.

Other interesting genes include RAS protein-specific guanine nucleotide-releasing factor 1 (RASGRF1), the functionality of which is highly significant in various contexts of the central nervous system. In the hippocampus, RASGRF2 has been shown to interact with the NR2A subunits of NMDARs, triggering Ras-ERK activation and induction of long-term potentiation, a form of neuronal plasticity that contributes to memory storage in the brain (Tian et al., 2004). A subnetwork of seven genes including Caveolin-1 (CAV1) gene was also identified. A study by Park et al. (2003) demonstrated that loss of Cav-1 gene expression and caveolae organelles dramatically affects the long-term survival of an organism. These results indicate that our method can indeed recover some biologically interesting molecular modules or KEGG subnetworks that are related to brain aging in human.

5 Conclusion and Discussion

With the increase in availability of human regulatory networks and protein interaction networks, the focus of bioinformatics research has shifted from understanding networks encoded by model species to understanding the pathways and networks underlying human diseases (Ideker and Sharan, 2008). In order to incorporate the prior biological network information into the analysis of gene expression data related to human diseases, we have presented in this paper a network-based empirical Bayes method for general linear models for analysis of genomic data. Different from the commonly used empirical Bayes methods for analysis of microarray gene expression data that assume independence among the genes (e.g., Limma), our proposed method imposes dependency among the latent indicator variables using a simple discrete Markov random field model defined on a known regulatory network. We demonstrated the application of the proposed methods in the analysis of human brain aging microarray gene expression data and identified several aging related molecular modules, some with solid biological supports.

We analyzed the aging data set using the KEGG regulatory pathways. However, it should be noted that the proposed methods can be applied to other relevant pathways such as human protein-protein interaction networks. Since our current knowledge of the genetic pathways of humans is still very limited, our proposed method depends on the validity of the regulatory networks used. One limitation of the proposed method is that the gene dependency provided by these prior networks may not be reflected at the gene expression levels. If this is the case, we should expect that the estimate of the dependency parameter η in the MRF model to be small, then the network information will not contribute too much and the results should be similar to the standard empirical Bayes analysis. It would be interesting to test the ideas in this paper on other types of biological networks such as protein-protein interaction networks. Finally, since most of the KEGG pathways are signaling pathways with a path of interactions through protein-protein or protein-DNA interaction networks, the KEGG network is often directed with a direction of information flow and a regulatory influence (activating or repressing). It would be interesting to develop methods that can account for these directions.