Three-Dimensional RNA Structure Refinement by Hydroxyl Radical Probing

Abstract

Molecular modeling guided by experimentally-derived structural information is an attractive approach for three-dimensional structure determination of complex RNAs that are not amenable to study by high-resolution methods. Hydroxyl radical probing (HRP), performed routinely in many laboratories, provides a measure of solvent accessibility at individual nucleotides. HRP measurements have, to date, only been used to evaluate RNA models qualitatively. Here, we report development of a quantitative structure refinement approach using HRP measurements to drive discrete molecular dynamics simulations for RNAs ranging in size from 80 to 230 nucleotides. HRP reactivities were first used to identify RNAs that form extensive helical packing interactions. For these RNAs, we achieved highly significant structure predictions, given inputs of RNA sequence and base pairing. This HRP-directed tertiary structure refinement approach generates robust structural hypotheses useful for guiding explorations of structure-function interrelationships in RNA.

Introduction

RNA molecules play central roles in gene expression, splicing, and translation¹. Knowledge of the underlying three-dimensional structure is a fundamental prerequisite to a complete understanding of most RNA functions. High-resolution methods such as X-ray crystallography and NMR spectroscopy offer unparalleled atomic-level insight into RNA structure. However, many RNAs are not amenable to structural characterization by these methods because of their conformational flexibility or large size. Recent advances^2–5 in molecular modeling yield accurate structure predictions of small RNAs but, due to the vast RNA conformational space and inaccuracies in available force fields describing atomic interactions, structure prediction for large RNA molecules with complex topologies is beyond the reach of current ab initio approaches. Incorporation of experimentally-derived structural information with computational modeling can dramatically reduce the allowed conformational space and thereby facilitate prediction of native RNA ensembles^6–11.

One can often establish the pattern of base pairing in an RNA, or secondary structure, with high accuracy by sequence covariation analysis^12,13 or by experimentally-constrained secondary structure prediction, especially with information obtained from selective 2′-hydroxyl acylation analyzed by primer extension (SHAPE) experiments^14,15. Accurate knowledge of the RNA secondary structure greatly restrains the possible tertiary folds^16,17, but the size of the conformational space is still large¹⁶. Through-space distance constraints derived from biochemical experiments or bioinformatics analyses can provide information crucial for refining the fold of an RNA molecule. Critically, a small number of long-range, through-space distance constraints are often sufficient to limit the conformational space to allow accurate RNA structure prediction^10,12. Experimental methods used to probe through-space distances, including site-directed hydroxyl radical footprinting, cross-linking, and fluorescence resonance energy transfer, can give high-quality distance information. However, these approaches often require synthesis of specialized RNA constructs, careful controls for unintended structural perturbations, and complex approaches for data interpretationr¹⁵. In contrast, HRP, which reports the approximate backbone solvent accessibility^18–20 (Fig. 1a), is relatively straightforward to implement. HRP measurements have been used to evaluate or filter RNA structural ensembles^9,18,21,22 but not to drive three-dimensional RNA structure determination in a quantitative and systematic way. Here we describe a framework for biasing discrete molecular dynamics (DMD)²³ simulations of RNA to generate structural ensembles consistent with experimental HRP measurements.

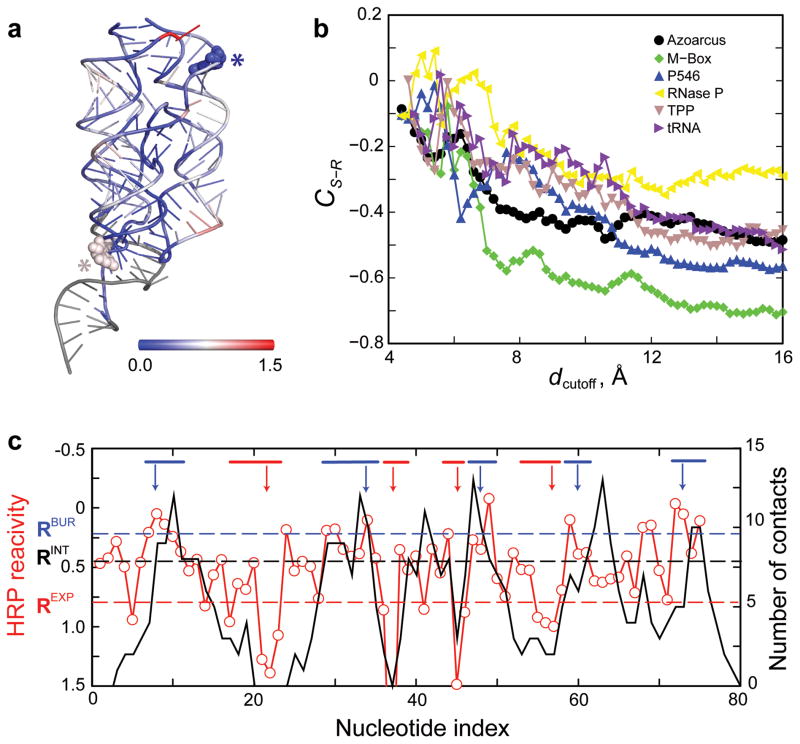
Figure 1. Relationship between RNA structure and HRP reactivity.

(a) Structure of the M-Box riboswitch shown in cartoon representation. Nucleotides are colored according to HRP reactivity (blue to red); nucleotides without HRP data are gray. A solvent exposed nucleotide with low HRP reactivity (blue) and a buried nucleotide with high HRP reactivity (red) are emphasized with all-atom representations (asterisks). (b) Structure-reactivity correlation coefficient, C_S-R, as a function of d_cutoff for the six training RNAs using HRP data smoothed over a three-nucleotide window (Online Methods). (c) Comparison of experimentally measured HRP reactivities (red) with the number of through-space contacts (black) for the TPP riboswitch RNA using a d_cutoff of 14.0 Å. Buried and exposed nucleotide segments are denoted with blue and red lines, respectively (top); arrows indicate the representative nucleotides characteristic of each nucleotide segment. Dashed horizontal lines represent the exposed (R^EXP), buried (R^BUR), and intermediate (R^INT) threshold values.

Results

We used a coarse-grained approach to model RNA molecules in which each RNA nucleotide is represented by three pseudo-atoms corresponding to the base, sugar, and phosphate groups. Three beads are sufficient to correctly recapitulate major features of RNA structure, including excluded volume, base pairing and stacking, and loop entropy, and sufficiently simple to allow efficient computational sampling³. This three-bead modeling approach has been used successfully to fold small RNAs with simple topologies from sequence alone³ and to refine larger RNA structures using distance constraints^8,10. This delineation into base, sugar, and phosphate groups is also compatible with HRP chemistry, where the hydroxyl radical reacts primarily at the ribose sugar¹⁸.

We first optimized HRP-directed refinement with a training set of six structurally diverse RNAs ranging from 75 to 214 nucleotides in length (Table 1). Prediction accuracy was evaluated by comparison with available high-resolution structures. After optimization with the training set, HRP-directed refinement was applied to an independent set of four RNAs (from 152 to 412 nucleotides in length; Table 1). Structures in the test set were not used to optimize the method, and therefore the significance of the resulting models is expect to be indicative of the predictive capability of the HRP-directed structure refinement method.

Table 1. Summary of HRP-directed RNA fold refinement for the studied RNAs.

The first six RNAs comprise the training set used for algorithm optimization and applicability determination: yeast tRNA^Asp (ref 27), thiamine pyrophosphate (TPP) riboswitch²⁸, specificity domain of ribonuclease P²⁹), P546 domain of the Tetrahymena thermophila group I intron¹⁹, M-Box riboswitch²⁴, and Azoarcus group I intron³⁰. The last four RNAs were used for testing the performance: glmS ribozyme³¹, lysine riboswitch³², catalytic domain of ribonuclease P³³, and Oceanobacillus iheyensis group II intron³⁴. The fraction of highly protected nucleotides, f_0.25, was computed using only the experimental HRP data; f_0.25 values above 0.25 are in bold. The structure-reactivity correlation, C_S-R, was calculated with reference to the accepted experimental structure. One hundred selected structures were clustered by pairwise RMSD (Online Methods). Small clusters (1 or 2 structures) were excluded. For each cluster, P-values were calculated based on the average RMSD with respect to the accepted experimental structure¹⁶; highly significant predictions (P < 0.01) are in bold.

RNA	Length (nts)	f0.25	CS-R	Number of clusters	Large Clusters
					n (out of 100)	RMSD (Å)	P-value
Azoarcus group I intron	214	0.43	−0.45	1	100	16.8±2.1	<10−6
M-Box riboswitch	161	0.35	−0.68	1	100	11.6±2.3	<10−6
P546 domain	158	0.37	−0.57	3	66	19.8±1.4	3.0 × 10−3
					32	15.1±1.9	<10−6
RNase P specificity domain	152	0.25	−0.30	3	93	24.9±1.2	0.67
					4	24.1±3.2	0.50
					3	22.7±0.5	0.22
TPP riboswitch	80	0.21	−0.50	4	44	12.6±1.3	0.10
					42	14.6±1.9	0.44
					12	9.9±1.8	2.9 × 10−3
tRNAAsp	75	0.25	−0.45	8	29	14.1±1.3	0.50
					23	17.5±1.5	0.97
					18	16.4±0.8	0.90
					8	18.9±0.8	0.99
					6	12.3±1.5	0.17
					6	15.7±0.4	0.82
					5	18.9±0.8	0.99
Group II intron	412	0.21	−0.30	-	-	-	-
RNase P catalytic domain	231	0.28	−0.50	4	46	19.2±1.6	<10−6
					41	21.6±2.1	<10−6
					8	25.0±0.7	1.3 × 10−4
					5	24.4±2.0	3.5 × 10−5
Lysine riboswitch	174	0.36	−0.57	3	57	12.0±1.6	<1.0−6
					42	18.1±1.0	1.6 × 10−6
glmS ribozyme	152	0.35	−0.55	2	74	16.6±1.7	1.5 × 10−5
					26	8.5±1.3	<10−6

We used a widely employed approach for the HRP experiment²⁴. Our data are consistent with protection patterns described in previously reported HRP experiments (Online Methods). In order to incorporate experimentally measured HRP reactivities into DMD simulations, we needed to define a structural parameter reflective of the information obtained in an HRP measurement that could also be readily implemented as a constraint to drive the folding simulations. Hydroxyl radical reactivity is correlated with backbone solvent accessibility^19,25; however, it is not straightforward to incorporate solvent accessibility as a constraint in a molecular dynamics simulation. We found that solvent accessibility is inversely proportional to the number of through-space neighbor atoms. In the example of the M-Box riboswitch, despite some outliers (Fig. 1a, asterisks), nucleotides with low HRP reactivities are generally buried and have many through-space contacts, whereas nucleotides with high reactivities have fewer through-space contacts and are more exposed (Fig. 1a). The number of through-space contacts can be readily incorporated as a constraint in DMD and other simulation methods, and we used it here to bias our simulations (Online Methods).

We defined through-space contacts based on the sugar pseudo-atoms in our three-bead model for RNA³. We computed the number of contacts as the number of sugar beads within a cutoff distance, d_cutoff, of a given nucleotide sugar bead. We excluded immediate neighbors in the linear sequence and base-pairing partners in helical elements because these neighbors reflect primary and secondary structure rather than higher-order tertiary interactions. To find the optimal d_cutoff, we calculated the structure-reactivity correlation, C_S-R, the Pearson correlation coefficient between the number of contacts and the corresponding HRP reactivity for each nucleotide (Fig. 1b). Data obtained using the six RNAs from the training set were used in determining the optimal d_cutoff value. In these calculations, C_S-R was negative because a lower HRP reactivity corresponds to a more buried nucleotide with a larger number of through-space neighbors. The absolute magnitude of C_S-R was largest when the cutoff range was 13–15 Å (Fig. 1b). With an intermediate cutoff value of 14 Å, the correlation coefficients for the six training RNAs ranged from −0.5 to −0.7, with the exception of RNase P, for which C_S-R was smaller (~−0.30).

To incorporate HRP data in DMD simulations, we assigned two bias interaction potentials (Online Methods)). The first included pair-wise attractive potentials for all nucleotides to encourage collapse of the RNA and general nucleotide packing. The second was an over-burial repulsion potential incurred when a given nucleotide exceeded the assigned threshold number of contacts (N_max) derived from its experimental HRP reactivity (Fig. 2a). To assign N_max values, we defined high and low HRP cutoff values corresponding to the highest and lowest mean HRP reactivities, respectively. Based on analysis of single chain RNAs in the RCSB database²⁶ and on exploratory simulations with the six training set RNAs, the largest and smallest N_max values were assigned as 11 and 0.5, respectively (Fig. 2b). Nucleotides with HRP values above and below HRP threshold values were assigned N_max values of 11 and 0.5, respectively. For nucleotides with intermediate HRP values, N_max was assigned by linear interpolation (Online Methods).

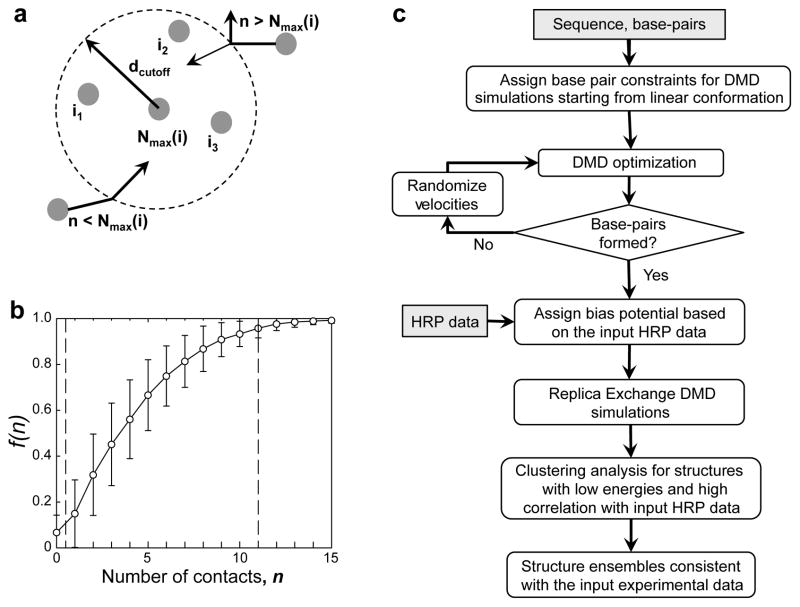
Figure 2. Assignment of potentials for incorporating HRP reactivities into DMD simulations.

(a) Scheme for modeling the number of allowed contacts. Each nucleotide is assigned a threshold number of contacts (N_max) within the cutoff distance (d_cutoff = 14 Å). For a given nucleotide i, its n through-space neighbors are denoted as i₁, i₂, i₃ … An approaching nucleotide can form a new contact (indicated by the inward arrow) if the number of total contacts is smaller than N_max. If n is larger than N_max, the approaching nucleotide can form a contact only if the total DMD kinetic energy is sufficient to overcome the energy penalty for over-packing (Online Methods). Otherwise, the nucleotide reflects back without forming a new contact (denoted by the outward arrow). (b) Fraction of nucleotides, f(n), forming at most a given number of contacts, n. Mean (open circles) and standard deviations (error bars) were computed over all single-chain RNA structures in the RCSB database. Adjacent and same-helix nucleotide neighbors were excluded from the number of contacts calculation. Vertical dashed lines correspond to the minimal and maximal number of contacts, 0.5 and 11, respectively. (c) HRP-directed DMD simulation algorithm.

HRP experiments are intrinsically noisy (Fig. 1c and Supplementary Fig. 1), making assignment of interaction potentials challenging, especially in regions with moderate HRP reactivities. To reduce the effects of noise on structure prediction, we incorporated stronger biasing interactions for RNA nucleotides that could be designated as exposed or buried with high confidence. We identified RNA segments (≥3 nts) with high or low HRP reactivities and selected the central nucleotide in each segment as the representative exposed or buried nucleotide, respectively (Online Methods and Fig. 1c, red and blue bars). These central representative nucleotides have a high probability of being buried or exposed in the native structure because the impact of the noise associated with HRP measurements is less significant when measured over several consecutive highly buried or solvent-exposed nucleotides. A strong pair-wise attraction was included between nucleotides identified as highly buried and the rest of the RNA molecule, while a strong over-burial repulsion was assigned for the nucleotides identified as either highly buried or highly exposed (Online Methods).

We used DMD simulations to obtain structural ensembles consistent with experimental HRP data, in three steps (Fig. 2c, Online Methods). First, we performed serial DMD simulations with inputs of RNA sequence and canonical base pairing taken from high-resolution structures. Following the formation of native secondary structures, we performed replica exchange DMD simulations with HRP-derived potentials. We then selected top 100 structures based on low energy and high C_S-R values and identified representative structures through clustering analysis. Our goal was to define the RNA conformations that best represent clusters (sub-states) of low energy conformational ensembles that have strong correlations with experimental HRP reactivities.

The training set for the initial DMD refinements were the yeast tRNA^Asp (75 nts), the TPP riboswitch (80 nts), the RNase P specificity domain (152 nts), the P546 domain (158 nts), the M-Box riboswitch (161 nts), and the Azoarcus group I intron (214 nts). These six RNAs have diverse folds and exhibit different levels of higher-order packing interactions. The Azoarcus group I intron, M-box riboswitch, and P546 domain RNAs have folds defined by close helical packing (Fig. 3); in contrast, folds for the RNase P domain, the TPP riboswitch, and tRNA^Asp are characterized by local interactions between coaxially stacked helices (Supplementary Fig. 2). HRP is appropriate for de novo RNA structure refinement for the subset of RNAs with extensive helical packing. The extent of higher-order RNA packing can be estimated a priori from the fraction of nucleotides, f(r), with HRP reactivities smaller than a given reactivity, r (Supplementary Fig. 3 and Online Methods). At r = 0.25 the RNAs with extensive helix packing interactions – the Azoarcus group I intron, M-box riboswitch, and P546 domain – have significantly larger f(r) than the other RNAs (Table 1 and Supplementary Fig. 3).

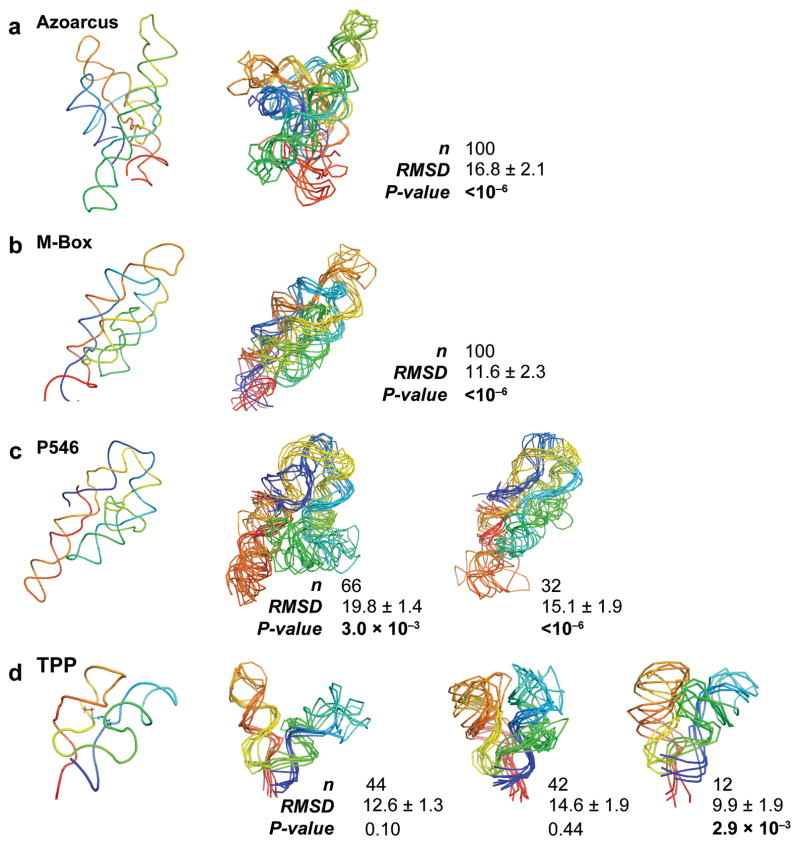
Figure 3. HRP-directed RNA fold refinement for the training set.

RNAs are shown with backbone traces. The left-most panel shows the accepted structure for each RNA. Right-hand panels show representative structures for each highly populated cluster. Small clusters (with 1 or 2 structures) are not shown. Backbones are colored from blue to red in the 5′ to 3′ direction. For each cluster, the number of structures, mean RMSD, and P-value are shown. Significant P-values¹⁶ are emphasized in bold.

We characterized the predicted structural ensembles for each RNA in terms of the number and population of clusters in the 100 final structures. For each cluster, we also computed the mean RMSD relative to the accepted structure and the prediction significance or P-value¹⁶ (Table 1). The RMSD value corresponding to a significant prediction varies with RNA size, and it is not appropriate to apply a single cutoff for all RNAs¹⁶. For example, an RMSD of 7–10 Å is not significant for a small RNA but is highly significant for a 100-nt RNA¹⁶. The P-value quantifies the statistical significance of the RNA fold prediction as the probability of observing a given conformation in an unbiased simulation with a pre-constrained base pairing arrangement. P-values less than 0.01 correspond to predictions with high statistical significance¹⁶.

We obtained highly significant predictions for each of the three largest RNAs in the training set. For the Azoarcus group I intron and the M-Box riboswitch, all predicted structures fell into a single cluster with a low average RMSD and low P-value and were thus native-like (Fig. 3a,b). For the P546 domain, refined structures formed two highly populated clusters; both had low P-values and differed primarily in the location of a single helix (Fig. 3c). Simulations of the TPP riboswitch yielded three clusters of structures. P-values for two of these clusters were poor (P > 0.01), although the third cluster had a significant P-value (0.003) and correctly recapitulated the TPP ligand-binding pocket (Fig. 3d). For tRNA^Asp and RNase P, HRP-directed structure refinement did not generate native-like structures (P > 0.01; Table 1 and Supplementary Fig. 2).

For the six training RNAs, we observed a strong correlation between the fraction of nucleotides protected from HRP cleavage, f_0.25, and the prediction significance (Table 1). tRNA^Asp, RNase P, and the TPP riboswitch had f_0.25 values less than 0.25 and yielded inaccurate predictions; whereas, we obtained statistically significant fold predictions for the three RNAs with higher f_0.25 values (Fig. 3). The f_0.25 values are calculated based on the HRP data alone, without reference to the accepted structure. Thus, we conclude that the HRP-directed structure refinement is appropriate for RNAs with extensive close packing of helices, corresponding to f_0.25 > 0.25.

We next applied HRP-directed structure refinement to the test set of four additional RNA molecules: the glmS ribozyme (152 nts), the lysine riboswitch (174 nts), the catalytic domain of RNase P (231 nts), and a group II intron (412 nts). Based on f_0.25 values (Table 1), three of these RNAs – the glmS ribozyme, the lysine riboswitch, and the catalytic domain of RNase P – were appropriate candidates for structure refinement. In contrast, with an f_0.25 value of 0.21, the group II intron was not a suitable candidate for refinement using HRP-derived constraints. The three RNAs with appropriate f_0.25 values all refined to native-like folds with significant P-values (Table 1 and Supplementary Fig. 4). The major structural variations between different clusters for a given RNA corresponded to regions without well-defined HRP data (for example, the 3′ end of RNase P catalytic domain) (Supplementary Fig. 4 and Supplementary Dataset 1).

HRP-directed structure predictions often resulted in multiple clusters with distinct structures (Fig. 3 and Supplementary Fig. 4), suggesting that all experimental constraints cannot be satisfied simultaneously. Predictions that yielded multiple clusters reflect either the intrinsic structural heterogeneity of an RNA molecule or non-ideal experimental data. To explore the relationship between prediction accuracy and experimental HRP data quality, we generated idealized datasets by assuming perfect structure-reactivity correlations (C_S-R = 1) for the M-Box, P546 domain, and TPP riboswitch RNAs (Online Methods and Supplementary Table 1). Additional simulated datasets with decreasing C_S-R values were generated by introducing random noise into the idealized data. Larger C_S-R values generally yielded significant increases in the RNA prediction significance (Supplementary Table 1).

Discussion

HRP-directed structure refinement is unique among RNA structure refinement methods as prediction quality is highest for larger and more complex RNA folds with extensive helical packing and a significant fraction of nucleotides occluded from solvent. (Table 1, Fig. 3 and Supplementary Fig. 4). The HRP-directed fold prediction is also highly tolerant of the noise intrinsic to the RNA HRP experiment. Although the overall correlations between structure and HRP reactivity, as illustrated by C_S-R, were modest (Fig. 1b), highly significant refinements were obtained because our algorithm reduces the impact of noise by identifying subsets of nucleotides with high probability of being buried or exposed (Fig. 1c) and imposes strong energy terms on these nucleotides to drive RNA folding.

Previous RNA tertiary structure prediction studies have shown that a relatively small number of long-range constraints are often sufficient to reduce allowable conformational space and to make possible prediction of diverse native-like structures^8,10. In three of the RNAs studied here, the Azoarcus group I intron, the lysine riboswitch, and the glmS ribozyme, long-range pseudoknot base-pairing constraints were included in structure prediction. Even for these partially pre-constrained RNAs, the HRP-directed structural refinement improved prediction beyond what is possible by including the pseudoknot base-pairing constraints alone (see Methods). One can thus use HRP-directed structural refinement in conjunction with other classes of information. Moreover, the correlation between the structure prediction accuracy and the quality of the input HRP data (Supplementary Table 1) suggests that if it becomes possible to improve the HRP approach or if experiments that better measure the solvent accessibility of RNA molecules are developed, it will be possible to refine RNA folds with an even higher level of accuracy.

The goal of the method is to reconstruct structural models for challenging RNA molecules not amendable to high-resolution methods. These structural models are especially useful for developing experimentally-testable hypotheses and for guiding the exploration of structure-function relationships for RNA.

Methods and any associated references are available in the online version. All software packages developed in this work for analyzing hydroxyl radical data and for predicting RNA structural models are available at http://troll.med.unc.edu/ifoldrna/HRP-1.0-openmpi.tgz.

Online Methods

Hydroxyl radical probing (HRP) measurements

RNA Preparation

RNAs were synthesized by T7 RNA polymerase-mediated in vitro transcription³⁵ using double-stranded PCR-generated templates. Sequences were transcribed in the context of 5′ and 3′ structure cassette sequences to facilitate analysis by primer extension³⁶. Transcribed RNAs were purified on 10% denaturing polyacrylamide gels (7 M urea, 1× TBE). Bands containing full-length product were excised; RNA was recovered by passive elution in 1× TE (10 mM Tris, pH 8.0; 1 mM EDTA) and precipitation with ethanol. Samples were resuspended in 1× TE and quantified by absorbance measurements at 260 nm.

Hydroxyl Radical Cleavage

HRP datasets for the Azoarcus group I intron and the RNase P specificity domain were taken from a previous study, which used essentially the same approach as outlined below³⁷. Hydroxyl radical cleavage experiments for the other RNAs were performed as described²⁴. RNAs were first refolded by heat denaturation, snap-cooling on ice, and incubation at 37 °C. The HRP data reported here are consistent with previously reported experiments.^24,29,38,39

For the ligand-binding RNAs, 1 μL of a 5 μM RNA solution of RNA was combined with 2μL sterile water and 3 μL folding mix (333 mM HEPES, pH 8.0, 333 mM NaCl, 33 mM MgCl₂ for the TPP riboswitch; 333 mM HEPES, pH 8.0, 333 mM KCl, 33 mM MgCl₂ for the lysine riboswitch; 167 mM HEPES, pH 7.5, 6.7 mM MgCl₂ for the glmS ribozyme). RNAs were heated at 95 °C for 2 min, cooled on ice, and then incubated at 37 °C for 10 min. 1 μL of ligand solution (10 μM thiamine pyrophosphate, 50 μM lysine, or 1 mM glucoasamine-6-phosphate for the TPP riboswitch, the lysine riboswitch, and the glmS ribozyme, respectively) was added, and the RNA was incubated in the presence of ligand at 37 °C for 20 min.

To fold the other RNAs, 1 μL of a 5 μM RNA solution was combined with 3 μL sterile water and 3 μL folding mix (46.6 mM HEPES, pH 7.5, 23.3 mM MgCl₂ for tRNA^Asp; 333 mM HEPES, pH 7.5, 333 mM NaCl, 33 mM MgCl₂ for the P546 domain; 46.6 mM HEPES, pH 7.5, 23.3 mM MgCl₂ for the M-Box riboswitch; 33 mM HEPES, pH 7.5, 333 mM NaCl, 33 mM MgCl₂ for the RNase P catalytic domain; 333 mM HEPES, pH 8.0, 333 mM KCl, 416 mM MgCl₂ for the group I intron; 300 mM HEPES, pH 8.0, 300 mM KCl, 375 mM MgCl₂ for the group II intron). These RNAs were then heated at 95 °C for 2 min, cooled on ice, and then incubated at 37 °C for 20 min.

The glmS ribozyme construct contained a point mutation (G40A) to prevent autolytic RNA cleavage during the HRP experiment; this mutant induces minimal structural disruption to the RNA⁴⁰.

Hydroxyl radical cleavage was initiated by addition of Fe(II)-EDTA, sodium ascorbate, and hydrogen peroxide to the folded RNA. Fresh Fe(II)-EDTA [10 mM ammonium iron (II) sulfate and 20 mM EDTA, pH 8.0] and 50 mM sodium ascorbate solutions were made prior to each experiment. The Fe(II)-EDTA and ascorbate solutions were combined in a 1:1 ratio, and 2 μL of this 1:1 solution and 1 μL of 0.03% hydrogen peroxide were spotted in separate areas of the reaction lid. Hydroxyl radical cleavage was initiated by brief centrifugation. After incubation at 37 °C for 2 min, reactions were quenched by addition of a solution containing 169 μL water, 20 μL 3 M sodium acetate (pH 5.5), and 1 μL 20 μg/μL glycogen, followed by addition of 500 μL ethanol. Modified RNA was recovered by precipitation with ethanol and washed with 70% ethanol. For each reaction, a no-reaction control without Fe(II)-EDTA and ascorbate was performed in parallel.

Primer Extension

Sites of hydroxyl radical-mediated cleavages were analyzed by primer extension using fluorescently labeled primers^37,41, labeled with fluorophores from the Applied Biosystems G5 dye set: (+) reaction, FAM; (−) reaction, VIC; sequencing ladder, NED. For each primer extension reaction, 3 μL 0.3 μM fluorescently-labeled DNA primer was added to 1 pmol RNA in 10 μL 0.5× TE. This solution was incubated at 65 °C for 5 min, then cooled on ice for 1 min. To this solution, 6 μL Superscript III enzyme mix (250 mM KCl, 167 mM Tris, pH 8.3, 1.67 mM each dNTP, 17 mM DTT, 10 mM MgCl₂) and 1 μL Superscript III (Invitrogen) were added. For sequencing reactions, 1.67 mM of a ddNTP was included in the Superscript III enzyme mix. The solution was incubated at 45 °C for 1 min, 52 °C for 25 min, and 65 °C for five min. The (+) and (−) reagent and sequencing reactions were then combined in 1 mL ethanol to quench extension and to precipitate the cDNA. Recovered cDNAs were washed with 70% ethanol and resuspended in 10 μL dry formamide (Applied Biosystems).

cDNAs were resolved on Applied Biosystems 3130 or 3500 Genetic Analyzer capillary electrophoresis instruments. Signal processing, sequencing alignment, and peak integration of raw traces were performed using ShapeFinder⁴² and custom signal processing software. A representative processed electropherogram is provided in Supplementary Fig. 5. Net reactivity at each nucleotide was defined as the area of the (+) reaction peak after subtracting the area of the corresponding (−) reaction peak. Nucleotides with high (−) signal were excluded from further analysis as high-background regions; the number of these high-background regions was small in the analyzed RNAs. Net reactivities were normalized by dividing reactivities by the average reactivity of the top 10% of nucleotides, excluding the top 2%. HRP reactivities for each of the ten RNAs are provided in Supplementary Dataset 1.

Computational modeling using HRP reactivities

Overview of the DMD Refinement Approach

We used a coarse-grained RNA model for DMD simulations³ in which each nucleotide is represented by three pseudo-atoms, representing the phosphate, sugar, and base groups. Bonded terms, including covalent bond lengths, angles, and dihedrals, were used to model local RNA geometry. Non-bonded interactions included base pairing, base stacking, phosphate-phosphate repulsion, and hydrophobic interactions. We explicitly modeled the entropy loss for loop formation. To bias the DMD simulation toward the structural ensemble consistent with experimental measurements, we added additional potential terms based on the experimental hydroxyl radical probing data.

DMD simulations and analysis were performed in three steps. First, serial DMD simulations were performed with inputs of RNA sequence and canonical base pairing, including pseudoknotted pairs, as obtained from high-resolution structures. Although the base-pairing arrangements were taken from X-ray crystallographic analyses, this information can be obtained with high accuracy from sequence covariation analysis^12,13 or SHAPE-directed secondary structure prediction^14,15. The result of these simulations was the formation of native secondary structures. Second, replica exchange DMD simulations with the HRP-derived potentials were applied to enrich for conformations consistent with the experimental HRP data. Third, top 100 structures were selected with the lowest energies and highest correlations between HRP reactivities and numbers of contacts (C_S-R). Clustering analysis based on pairwise root-mean-square deviation (RMSD) was then performed to identify representative structures consistent with the predicted structural ensemble.

HRP Bias Potential

For each nucleotide, we assigned a favorable energy increment, E_attr(i) for forming a contact; a threshold number of contacts, N_max(i); and a repulsive energy, dE_rep(i), for exceeding the threshold. The HRP E_bias potential equals:

$$E_{\mathit{bias}}=\sum _{i<j}{E}_{ij}^{\mathit{attr}}+\sum _i{E}_i^{\mathit{over}-\mathit{bury}}.$$ (1)

The first term is the pairwise attraction, $E_{ij}^{\mathit{attr}}(r_{ij})=min\{E_{\mathit{attr}}(i),E_{\mathit{attr}}(j)\}F(r_{ij})$, where F(x) is a step function,

$$F(x)=\{\begin{array}{ll}0\hfill & IR<r\hfill \\ 1\hfill & R_{hc}<r\le IR\hfill \\ \infty \hfill & r\le R_{hc}\hfill \end{array}.$$ (2)

IR is the interaction range of 14 Å, and R_hc is the hard core diameter, 3.0 Å. The second term prevents over-burying by exceeding the threshold number of contacts:

$$E^{\mathit{over}-\mathit{bury}}(i)={dE}_{\mathit{rep}}(i)(n_c(i)-N_{max}(i))\mathrm{\Theta }(n_c(i)-N_{max}(i)),$$ (3)

where n_c(i) is the number of contacts for each nucleotide i, dE_rep(i) is the penalty energy for over-burying, and Θ(x) is the unit step function, which equals 1 if x is positive and zero otherwise. The number of contacts for each nucleotide was computed as the number of non-local sugar beads within the 14 Å cutoff. For each nucleotide i, we excluded contacts with nucleotides that were adjacent (within 4 nucleotides) to i or were adjacent to a nucleotide to which i base pairs (for i pairing with I, these nucleotides are |i-j| > 4, or |I-j| > 4).

Assignment of Interaction Parameters

The energy parameters, N_max(i), E_attr(i), and dE_rep(i) were assigned using HRP reactivities for each nucleotide in the following three steps:

1. Assignment of the threshold number of contacts

Threshold number of contacts, N_max, were assigned according to reactivities, R, smoothed over a sliding window of three nucleotides. Smoothing reduced the influence of the noise intrinsic to HRP experiments performed with RNA and increased the correlations to the accepted structure, C_S-R. We defined two threshold values, R_min and R_max, corresponding to the maximally buried and exposed nucleotides. R_min and R_max were the average of the subsets from 2% to 20% and from 80% to 98% of the rank-ordered R. The top and bottom 2% R values were discarded to reduce the influence of extreme R values observed in typical HRP experiments. For nucleotides with R smaller than R_min or higher than R_max, the threshold number of contacts was defined as NC_max = 11 and NC_min = 0.5, respectively (Fig. 2b). For a nucleotide i with intermediate reactivity, the threshold number of contacts was assigned by linear interpolation,

$$N_{\mathit{max}}(i)={NC}_{\mathit{max}}+({NC}_{\mathit{min}}-{NC}_{\mathit{max}})(R(i)-\langle R_{\mathit{min}}\rangle )/(\langle R_{\mathit{max}}\rangle -\langle R_{\mathit{min}}\rangle ).$$ (4)

2. Assignment of representative buried and exposed nucleotides

We first identified segments of strongly buried and exposed nucleotides. We defined three values, R^EXP, R^INT, and R^BUR, corresponding to the threshold values of exposed, intermediate, and buried residues (Fig. 1c). The buried threshold R^BUR and exposed threshold R^EXP correspond to lowest 20% and highest 80% of the rank-ordered reactivities R, respectively. There are two types of intermediate R values, the average value of all the reactivities 〈R〉 and the median value of the rank-ordered reactivities R₅₀. For simplicity, we chose the mean of these two values as R^INT.

We defined buried segments as those with more than three consecutive nucleotides having R smaller than R^INT and at least one with R smaller than R^BUR. For each buried segment, we selected the one with the lowest reactivity as the buried representative, excluding the first and last residues in the segment. Similarly, we defined exposed segments as those with more than three consecutive nucleotides having R larger than R^INT and at least one nucleotide having R larger than R^EXP and, for two-nucleotide segments, with both nucleotides having R values larger than R^EXP. For each exposed segment, we defined the nucleotide with largest R value as the exposed representative.

3. Assignment of attractions and repulsions

Two attractive energy scales were used, E_low = −0.10 kcal/mol and E_high = −0.05 kcal/ml, based on the simulation temperature (see below). We assigned a strong attractive energy, E_low, to the buried representative nucleotides identified in Step 2 and the median value of (E_high+E_low)/2 to their nearest neighbors. For all remaining nucleotides, we assigned the weak attractive energy of E_high. We defined a strong repulsive over-burial energy, dE_rep(i) = 0.3 kcal/mol, for both the buried and exposed representative positions. We assigned the repulsive energy dE_rep(i) = −E_attr(i) to all other nucleotides, where E_attr(i) equals E_low or E_high. By making over-burial repulsion potentials equal to those for attractions, these nucleotides were allowed to make additional contacts (>N_max) without a net energy penalty. This approach reduced the impact of noise in HRP experiments on RNA structure refinement by promoting compaction while imposing strong energy terms correlated with solvent accessibility for the subset of nucleotides identified as having a high probability of being buried or exposed. The HRP-derived values – threshold number of contacts (N_max), attractive (E_attr), and repulsive (dE_rep(i)) energies – are listed for all tested RNAs in Supplementary Dataset 1.

Replica Exchange DMD Simulations

Because the HRP-directed potential is non-specific with respect to any two nucleotides (in contrast to the distance and bonded constraints between specific nucleotides^8,10) we performed replica exchange DMD simulations to obtain sufficient sampling of conformational space. We used eight replicas with temperatures of 0.200, 0.225, 0.250, 0.270, 0.300, 0.333, 0.367, and 0.400 kcal/(mol·k_B). Every 1000 DMD time units, we exchanged replicas with neighboring temperatures according to a Metropolis-based Monte Carlo algorithm using instantaneous potential energies³. For each replica, we performed simulations over 5 × 10⁵ DMD time units. Replica exchange DMD simulations were performed in parallel on 2.27 GHz Intel Xeon computing nodes. Representative running times for the TPP riboswitch (80 nts), M-Box (160 nts), and Azoarcus RNAs (214 nts) were 60, 170 and 264 CPU hours, respectively. The wall-clock time is one-eighth of the total CPU time.

Identifying Structure Ensembles Consistent with Experiments

To identify structural ensembles consistent with the experimentally measured HRP data, we computed structure-reactivity correlation coefficients, C_S-R, for snapshot structures, computed every 100 time units, yielding 4 × 10⁴ snapshots for each refinement. We rank-ordered these snapshots by C_S-R and selected the 2000 structures with the lowest (negative) correlation coefficients. From these, we selected 100 structures with the lowest energies. We also selected structures applying these rules in the reverse order: from the 4× 10⁴ structures, we selected 2000 structures by energy from which we then selected the 100 structures with the lowest C_S-R.

For the combined 200 structures, we removed duplicates and selected top 100 structures to represent the predicted structural ensemble. The structures were ranked according to the combined rank-order using both energy and C_S-R. We clustered these 100 structures according to pairwise RMSD using a hierarchical clustering algorithm and grouped similar structures into clusters using a cutoff RMSD. For simplicity, we used a cutoff value of 4 Å (roughly two standard deviations) below the average RMSD for a given RNA length¹⁶ (see below), or three quarters of the average RMSD, whichever is smaller:

$$\{\begin{array}{cc}R(n)-4,& R(n)-4<0.75R(n)\\ 0.75R(n),& 0.75R(n)\le R(n)-4\end{array}.$$ (5)

Here, n is the RNA length, and R(n) is the average RMSD as the function of RNA length.

P-Value Calculation

A recent study of a large set of RNA decoy structures derived from both simulations and from threading suggests that the RMSD between two random RNA structures of the same length follows a Gaussian distribution with a length-dependent average RMSD and a length-independent standard deviation (~1.8 Å)¹⁶. For an RNA with known secondary structure, the average RMSD between two random decoy structures is smaller relative to a decoy set generated without knowledge of the secondary structure. We computed the statistical significance, or P-value, corresponding to the probability that an HRP-constrained structure prediction, evaluated by its RMSD from the accepted structure, is significantly better than that expected by chance. The P-value calculation is available online at http://ifoldrna.dokhlab.org¹⁶.

The question of how to interpret the significance of a structure model with a given RMSD value has been a major challenge in the RNA folding field. Some groups have suggested that RMSDs should correspond in some qualitative way with the physical dimensions of RNA. For example, the RMSDs should be less than 7 Å (the average distance between two nucleotides) or within with width of an RNA helix (~20 Å). In fact, the average RMSD between any two structural models is strongly dependent on RNA length and on whether the secondary structure is used as a constraint¹⁶. Thus, we argue that an appropriate way to understand the significance of a structure prediction is in terms of a P-value. Prior work using the 7 or 20 Å heuristic rules tended to overestimate the quality of predictions for short RNAs and to underestimate the significance of predictions for large RNAs. For large RNAs, seemingly large RMSD values with low P-values correspond to native-like folds with high significance (see Fig. 3).

Generation of Ideal and Randomized Reactivity Profiles

We generated idealized HRP reactivities based on the number of contacts in the native structure, R^ideal(i) = 1 − N_c(i)/N_max. We added noise to these idealized reactivities to generate randomized reactivities, R^rand(i) = R^ideal(i)(1+ σx), where x is a random number from −1 to 1, and σ is the amplitude of the noise, determined by the relative error:

$$1/N\sum _{i=1}^N\mid (R^{\mathit{Rand}}(i)-R^{\mathit{ideal}}(i))/R^{\mathit{ideal}}(i)\mid =1/N\sum _{i=1}^N\sigma \mid x\mid ~\sigma /2$$ (6)

where the sum is over all nucleotides in a RNA. By varying σ, we generated randomized reactivity profiles with different levels of noise and, thus, different structure-reactivity correlations (Supplementary Fig. 6a). Notably, the M-Box riboswitch had the least noise-induced decrease in the structure-reactivity correlation C_S-R, while tRNA^Asp had the greatest decrease in C_S-R, which correlates with their respective prediction significances (Supplemental Fig. 6b).

For the M-box, the P546 domain, the TPP riboswitch, and tRNA^Asp RNAs, we selected seven sets of computationally generated HRP data with C_S-R values ranging from −0.4 to −1.0 (Supplementary Table 1). Using the generated HRP reactivities as the input, we applied our structure refinement protocol to generate structural ensembles (Supplementary Table 1). For all tested RNAs, except tRNA^Asp, we found that HRP reactivities with high C_S-R resulted in low RMSDs and highly significant predictions. As the C_S-R of input HRP reactivities decreased, the RMSDs of the predicted structures and the corresponding P-values increased, indicating less accurate predictions.

There are two critical implications of this analysis. First, the high P-value predictions for tRNA^Asp using both experimental and computationally generated HRP reactivities suggest that RNAs like tRNA, with few buried nucleotides, are not good candidates for HRP-directedrefinement. Importantly, these RNAs can be identified (and excluded) in advance using the f_0.25 metric (Supplementary Fig. 3). Second, our simulations indicate that the level of noise and resulting structure-reactivity correlation for the input HRP data play a determining role in the accuracy of HRP-directed structure prediction. If a better experimental method with reduced noise in HRP (or solvent accessibility) reactivities were developed, our approach would immediately lead to significantly more accurate RNA structure refinements.

Structural refinement for RNAs with pseudoknot base pairs

In our study, we assumed that all base pairs, including pseudoknots, were known. A relatively small number of constraints based on long-range contacts, such as pseudoknots, are sufficient to direct the prediction of highly significant RNA structures¹⁰. The Azoarcus group I intron, the lysine riboswitch, and the glmS ribozyme RNA contain long-range pseudoknots that likely reduce available conformational space and may themselves lead to significant structure predictions. To examine the effects of incorporating HRP data for RNA refinements in which long-range pseudoknot constraints were included, we compared the results of RNA structure prediction with and without HRP data.

First, we evaluated whether incorporation of HRP data as constraints drives the conformational sampling toward native states during the course of simulations for the pseudoknot-containing RNAs. We calculated the RMSD for all RNA conformations sampled during DMD simulations both with and without HRP data as constraints. For both the lysine riboswitch and glmS ribozyme, incorporation of HRP data in the DMD simulations significantly enhanced sampling of native-like conformations (Supplementary Fig. 7). Second, we applied the structure selection approach to reconstruct conformational ensembles for simulations that did not incorporate HRP data. Critically, for these large RNAs, if the HRP data were not used to drive refinement, the resulting structural ensembles fell into multiple small clusters with a wide range of RMSD values (Supplementary Table 2); in contrast, using the HRP data to drive refinement yielded only a few clusters, each with well-defined structures and highly significant RMSD values (Table 1). Therefore, although the pseudoknotted base pairs reduced the available conformational space, the HRP-directed structural refinement drove RNA folding to native-like states.

Supplementary Material

1

Supplementary Figure 1. Correlation between HRP reactivity and number of contacts

Supplementary Figure 2. Structure ensembles generated by HRP-directed RNA refinement for RNase P and tRNA^Asp

Supplementary Figure 3. Fraction of nucleotides, f(r), with HRP reactivities below a given value r.

Supplementary Figure 4. HRP-directed RNA fold refinement for the test set

Supplementary Figure 5. Representative HRP data.

Supplementary Figure 6. Simulated HRP reactivities.

Supplementary Figure 7. RMSD histograms for pseudoknot-containing RNA conformations sampled during DMD simulation.

2

Supplementary Table 1. Predicted structural ensembles using simulated HRP reactivities

Supplementary Table 2. Predicted structural ensembles for the RNAs with pseudoknotted base pairs

Supplementary Data Set. The HRP reactivities and interaction parameters for all RNAs