Computer Modeling of Nitroxide Spin Labels on Proteins

Abstract

Electron paramagnetic resonance (EPR) using site-directed spin-labeling (SDSL) can be used as an approach for determination of protein structures that are difficult to solve by other methods. One important aspect of this approach is the measurement of inter-label distances using the double electron-electron resonance (DEER) method. Interpretation of experimental data could be facilitated by a computational approach to calculation of inter-label distances. We describe an algorithm, PRONOX, for rapid computation of inter-label distances based on calculation of spin label conformer distributions at any site of a protein. The program incorporates features of the label distribution established experimentally, including weighting of favorable conformers of the label. Distances calculated by PRONOX were compared with new DEER distances for amphiphysin and annexin B12, and with published data for FCHo2 (F-BAR), endophilin, and α-synuclein; a total of 44 inter-label distances. The program reproduced these distances accurately (r²=0.94, slope=0.98). For 9 of the 11 distances for amphiphysin, PRONOX reproduced the experimental data to within 2.5 Å. The speed and accuracy of PRONOX suggests that the algorithm can be used for fitting to DEER data for determination of protein tertiary structure.

Introduction

Structural analysis of proteins using X-ray crystallography and NMR spectroscopy is well established, with over 50,000 structures deposited in the Protein Data Bank.¹ However, the structures of some classes of proteins, including lipid-bound proteins and protein assemblies, are often difficult to solve using these methods. Site-directed spin labeling (SDSL) and the double electron-electron resonance (DEER) technique using pulse EPR spectroscopy² is a promising method for determination of the structure and motion of proteins in a lipid environment,^3–7 and has also been used for proteins in solution.^8,9 Comparisons with X-ray data have shown the accuracy of DEER distances for the cytoplasmic domain of the anion exchange protein⁹ and the membrane curvature-sensing FCHo2 (F-BAR) domain.¹⁰

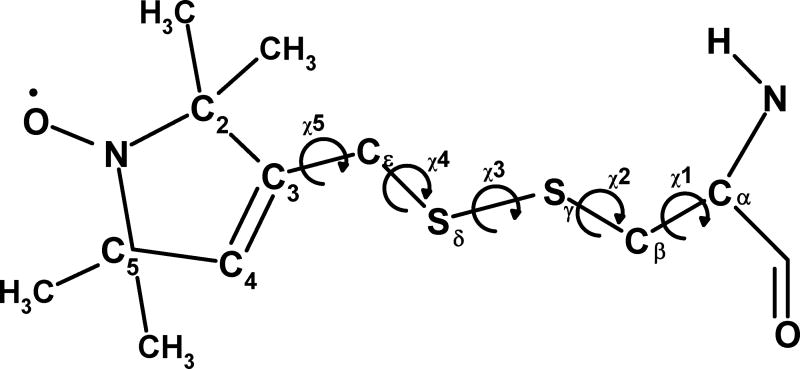
In SDSL of proteins, the common labeling scheme is to attach a stable nitroxide radical, 1-oxyl-2,2,5,5-tetramethylpyrroline, to the backbone of an engineered cysteine via a -C_ε-S_δ-S_γ-C_β linkage, giving the R1 label shown in Figure 1. Each nitroxide spin label is attached to a cysteine residue via a disulfide (S-S) bond, creating a species with five variable torsional angles (Figure 1, χ1 to χ5). The complexity of the torsional motion of the label is reduced by the C_ε-S_δ-S_γ-C_β region (torsion angles χ1, χ2 and χ3) adopting preferential conformations.¹¹ X-ray structures of lysozyme^12,13 with nitroxide labels at different sites show preferred dihedral values for χ1 and χ2, with particularly frequent occurrences of gauche(−), gauche(−) (m,m in the nomenclature in Guo et al.¹¹) and trans, gauche(+) (t,p) conformers due to a favorable interaction between H_α and S_δ in the label.^11–13 The torsional angle around the S-S bond (χ3) adopt values of approximately ±90° based on quantum chemical calculations¹⁴ and observations for S-S bridges in proteins, although with some deviations from these values in X-ray data.^11–13

Figure 1.

Structure and atom names of the R1 nitroxide label with definitions of torsions χ1 to χ5.

DEER distances can be used to probe structural features of proteins. Distances from 15 to 50 Å can be measured between R1 spin labels at any two positions, although distances over 70 Å have been determined.¹⁵ However, establishing a correlation between EPR-measured inter-label distances (i.e., between the nitrogen atoms of the respective nitroxides) and the macromolecular structure requires a method to predict the ensemble of label conformers at a specific site. For this purpose, solution ensembles of linker-nitroxide conformations have been studied using simulation techniques.^16–18 Thus, a combination of Monte Carlo conformational searching and molecular dynamics (MD) simulations on identified low energy conformers can be used to compute theoretical distances in good agreement with experimental data.^16,17 MD simulations can also be used to determine conformational preferences of the label that can be reduced to simple representations of the favored label conformers for subsequent computation of inter-label distances.¹⁸ Comparison of spin label distance distributions from MD simulations with DEER data has been used to draw conclusions on the conformational state of HIV protease upon ligand binding.^19,20 Similar approaches have been used for other proteins.^21,22 By including simulated annealing in the MD simulation, we have determined a model for the vesicle-bound form of α-synuclein using DEER and other EPR-based constraints,⁶ and we have also defined the position of two lipid-bound helices of endophilin.²³

These results show that simulation can be used to study spin label motion and to relate inter-label distances to protein structure. However, these methods are relatively complex and time-consuming. Therefore, the goal of the current work was to produce a simple algorithm that can build spin labels on proteins, generate conformer distributions for each label, and calculate inter-label distances for comparison with DEER data. We show that this algorithm, which we refer to as PRONOX, can be used to compute label distributions and inter-label distances with speed and accuracy. Based on these findings, we suggest that the algorithm will be useful for interpretation of experimental data.

Methods

Computational Spin Labeling of Proteins

PRONOX can be used to build spin-labeled proteins through modification of a structure in PDB format. Each R1 spin label is added at a defined site using the Cβ atom of the original amino acid, followed by determination of the Sγ, Sδ, Cε, C3 and C2 atoms based on torsions χ1 to χ5, respectively (Figure 1) and subsequent addition of other atoms in standard geometry.²⁴ For modification of glycine, the position and geometry of the correct Hα atom is used as the basis for placement of Cβ of the label, with alteration of the resulting Cα-Cβ bond length and a check to ensure that the correct label chirality is produced. The bond lengths and angles for the spin label for the C_ε-S_δ-S_γ-C_β region were based on crystallographic data¹³ and values from the AMBER (parm98) force field for a cysteine-cysteine bridge.²⁵ For the nitroxide ring, we have described a set of bond lengths and angles for an identical nitroxide ring connected via a methylene linkage to a DNA phosphorothioate in the NASNOX program²⁴ and we used this ring geometry unchanged in PRONOX.

Label Conformer Distribution

To calculate inter-label distances for comparison with DEER data, it is necessary to generate multiple conformers at each label position. In PRONOX, variation of each of the five torsion angles (χ1 to χ5, Figure 1) is allowed based on a user-defined starting position and angle increment, with the only restriction being that the increment must divide exactly into 360°. Allowable conformations are generated based on the absence of a clash between the label conformer and the protein. We define a clash as a distance between an atom of the label and an atom of the protein that is less than 75% of the sum of the van der Waals radii of the two atoms. This percentage is adjustable in the program input, but we use 75% as a default based on preliminary runs and successful use of this value for labeling of DNA and RNA.²⁴ The code also contains a “fine search” option, which can be activated for a conformer that does not meet the van der Waals contact. In this approach, a fine search over the local conformational space is performed, with each torsion angle adopting five positions: the original torsion angle (t) − 0.2*increment (I); t − 0.1×I; t; t + 0.1×I; and t + 0.2×I, where the increment (I) is defined based on user input. If any conformer in the fine search meets the above criterion for acceptance, the original conformer is used in the inter-label distance calculation. The goal of the fine search is to introduce some flexibility into the discovery of sterically allowable label conformers.

Evidence from X-ray crystallography^11–13 shows that the χ1 and χ2 torsions are well defined. The χ1, χ2 gauche(−), gauche(−) (m,m); trans, gauche(+) (t,p); and trans, gauche(−) (t,m) conformers have a non-bonded interaction of S_δ with H_α ((m,m) and (t,p)) or other backbone atoms ((t,m)) and this is sufficient to make these conformations favorable. To reflect the favorable conformational space, PRONOX can be run in a mode in which labels with ‘favored’ torsional values for χ1 and χ2 are included in the distribution with a biased weighting (see next section). These labels are identified directly from the χ1, χ2 values, with (m,m), (t,p), and (t,m) identified based on ranges of 60±30°, 180±30° and 300±30° for p, t and m, respectively. The torsional angle around the S-S bond (χ3) is approximately ±90°. The positions of χ4 and χ5 may also be somewhat restricted,¹⁸ but in using PRONOX we assume that all chosen conformers at χ4 and χ5 are isoenergetic.

Calculation of Inter-Label Distances

In PRONOX, inter-label distances can be calculated between different atoms of two nitroxide labels, including N to N and O to O in the respective nitroxide groups. In this work, all distances are those for N to N atoms. With no weighting of favored conformers, the calculated N to N distance is an average of the distances between all pairs of label conformers using the distributions at the two labeled positions. However, the program can account for the favorable conformers described above. Based on preliminary trials, we use a weighting of 90% for each favorable conformer and 10% for each unfavorable conformer. The choice of 90% arises from the observation that the favored label conformation can be altered by interaction with local protein structure,^11–13 which suggests that the energy difference between the favored and unfavored conformers is relatively small. In the calculation of the overall inter-label distance, the distance between a pair of conformers is weighted based on the favorable or unfavorable definition of each conformer. The weighting is the product of two factors (0.9 for favorable and 0.1 for unfavorable conformations). Thus, weighting factors of 0.81, 0.09 and 0.01 are applied for distances between two favorable conformations, between favorable and unfavorable conformations, and between two unfavorable conformations, respectively.

Running the Algorithm

In its simplest mode, PRONOX can be used to compute one inter-spin label distance between conformer distributions at two sites. This mode of PRONOX can be used at: http://rockscluster.hsc.usc.edu/research/software/pronox/pronox.html. It is also possible to generate label distributions at more than 2 sites in the same run, and then calculate all pairwise inter-spin label distances between these sites. The results of these two approaches are the same, since the labels do not “see” each other during the calculation.

Evaluation of the Algorithm

A total of 44 experimental DEER distances from 5 proteins were used for assessment of the algorithm. Structures for the amphiphysin dimer,²⁶ FCHo2 (F-BAR) dimer¹⁰ and annexin B12²⁷ were obtained from the Protein Data Bank (1URU, 2V0O, and 1AEI, respectively). Hydrogen atoms were added to these proteins in standard AMBER geometry²⁵ and the resulting structures were used as input to PRONOX. For endophilin, the family of 60 structures obtained in our recent determination (using DEER distances and simulated annealing) of the lipid-bound positions of the central helix and loop (residues 63–86)²³ were used as input. The BAR domain of this structure is identical to the X-ray structure of the rat endophilin A1 dimer²⁸ (PDB ID: 2C08). For α-synuclein, PRONOX calculations were performed on all 10 structures from the family obtained from simulated annealing based on DEER data.⁶ Distances averaged over all structures in each family were calculated for all label pairs in endophilin and α-synuclein.

PRONOX distances were calculated using the following standard conditions: systematic torsional angle searches with χ1=60,180,300° χ2=60,180,300°, χ3=±90°, χ4=60,180,300°, and χ5=0 to 330 in steps of 30°, with clashes defined as 75% of the sum of the van der Waals radii. Data collected under these conditions were used as the primary results for establishing a correlation with experimental data. For a few labels, it was necessary to use the fine search option for χ1 and χ2, and also to soften the clash criteria to 40% of the sum of the van der Waals radii. Gaussian fits for PRONOX distance distributions were performed in Matlab using code obtained from Matlab Central <http://www.mathworks.com/matlabcentral/fileexchange/11733-gaussian-curve-fit> (accessed 12/17/2010) and modified for data input only.

Molecular Dynamics Simulations

Force field atom types and atomic charges for the spin label are shown in Supplementary Table S1. The charges and atom types for the backbone atoms and the side chain atoms up to Sδ (Figure 1) are standard AMBER parameters for a Cys-Cys bridge (residue CYX).²⁵ Derivation of atom types and charges for the nitroxide ring has been described in detail for a related spin label for DNA²⁴ and these are used unchanged. Charges for the atoms of the methylene group at Cε are averages of those for CYX and the charge set for the DNAnitroxide label²⁴ with minor adjustments to make the sum of charges for the entire label equal to zero. AMBER input files will be made available on request.

A 15 ns simulation was performed on the F-BAR dimer with labels at position 86 of each monomer. The labels were added in an initial conformation with χ1=300° χ2=300°, χ3=90°, χ4=180°, and χ5=180°. The protein was solvated in a periodic box containing TIP3P water molecules, with the box extending 12 Å from the extremes of the solute in the ±x, ±y and ±z directions. This gave a box of approximate dimensions 60×60×75 Å that contained 6000 to 6500 water molecules. Following minimization of the system for 1000 steps (500 steps of steepest decent, followed by 500 steps of conjugate gradient minimization), molecular dynamics simulations were run on a Verari Systems computer with a Red Hat Linux 9.0 operating system, using the parallelized version of AMBER8.0 operating on 4 processors. Simulations were run with a time step of 0.002 ps, a residue-based cut-off of 8 Å, and the particle-mesh Ewald method for electrostatic interactions. SHAKE was applied to all hydrogen atoms and the target pressure was 1 atm. Equilibration of the solvent molecules was achieved in an initial simulation of 100 ps. This was followed by a 15 ns simulation for data collection, during which structures were collected every 0.2 ps.

DEER Data

The PRONOX algorithm was evaluated using published DEER data for α-synuclein (14 inter-label distances),⁶ endophilin (17 distances),²³ and FCHo2 (1 distance);¹⁰ and newly obtained data for amphiphysin (11 distances) and annexin B12 (1 distance). Single cysteine mutants of Drosophila melanogaster amphiphysin (containing a spin label in each subunit of the dimer) and a double cysteine mutant annexin B12 were expressed and purified as described previously.^29,30 Dithiothreitol was removed using a PD10 column (GE Healthcare) immediately before spin labeling of amphiphysin (in a buffer of 20 mM HEPES, pH 7.4, 500 mM NaCl) or annexin B12 (in a buffer of 20 mM HEPES, pH 7.4, 150 mM NaCl). The protein was then reacted with 10× molar excess of the spin label MTSL (1-oxy-2,2,5,5-tetramethyl-d-pyrroline-3-methyl)-methanethiosulfonate) for 1 h at room temperature. Excess spin label was separated by gel filtration using a PD10 column. Labeled proteins (~100 μM) were mixed with sucrose to give a final sucrose concentration of 20% for cryoprotection. Samples were flash frozen using liquid nitrogen and data were collected at 78 K. Four-pulse DEER³¹ experiments were performed using a Bruker (Billerica, MA) Elexsys E580 X-band pulse EPR spectrometer fitted with a 3 mm split ring (MS-3) resonator, a continuous flow helium cryostat (CF935; Oxford Instruments), and a temperature controller (ITC503S; Oxford Instruments). Data were fitted to a Gaussian distribution (a single Gaussian function was used unless otherwise indicated) and using Tikhonov regularization, as implemented in the DEERAnalysis2010 package.³²

Results

This section includes the results for PRONOX calculations for 44 spin label pairs in 5 proteins. Each protein is used to illustrate different aspects of the algorithm. Beginning with amphiphysin, we describe a simple method to obtain inter-label distances based on a standard approach and default input, with subsequent alterations to input parameters in cases in which the label distribution cannot be obtained using the standard approach. Using amphiphysin and annexin, we fitted the PRONOX data to a Gaussian function for comparison with similar fits to experimental data. Next, using our published data for α-synuclein and endophilin, we tested the agreement of the PRONOX distances with experimental data in structures that were obtained using DEER restraints, with the goal of determining if PRONOX can be used to check DEER-derived structures and to predict distances in these structures for further experimental evaluation. Finally, we compare the results of PRONOX calculations with those for a MD simulation for the F-BAR dimer.

Amphiphysin

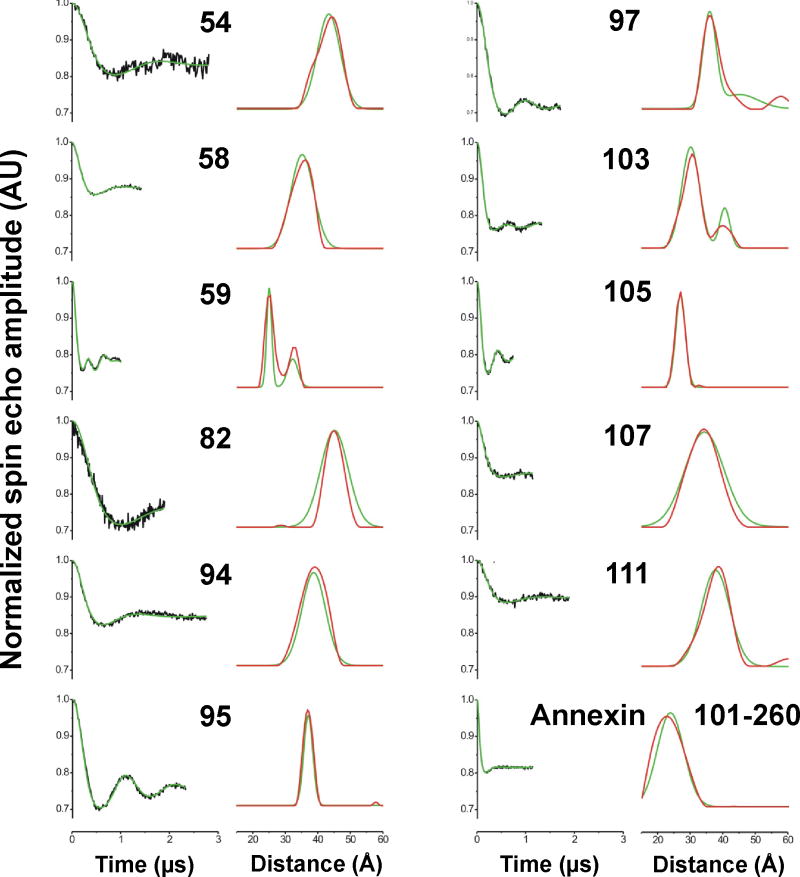
4-pulse DEER experiments were performed to determine the inter label distances for 11 doubly labeled amphiphysin dimers (Figure 2A). For each pair the label is positioned on the same amino acid in each subunit of the dimer, with the respective sites positioned on opposite surfaces of the dimer (Figure 2). The experimental distances were determined from the 4-pulse DEER data, which were fitted using Gaussian functions or Tikhonov regularization (Figure 3). Data that did not fit satisfactorily to a single Gaussian were refitted using two Gaussian functions (positions 59, 97 and 103). The consistency between the Gaussian and Tikhonov results is apparent in Figure 3. The reported experimental distances were taken from the means of the fitted Gaussian functions.

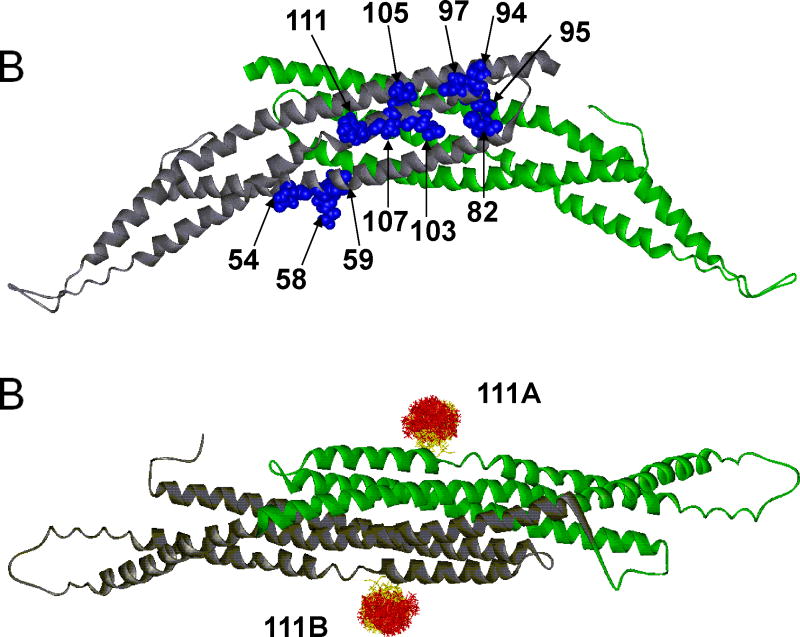
Figure 2.

(A) The 11 labeled sites for the amphiphysin homodimer are indicated in blue in one subunit (which is colored in gray). The second subunit (colored in green) contains the identical sites on the opposite surface of the dimer. The sites are positioned in a region that is largely α-helical. (B) The structure of the amphiphysin dimer is rotated 90° from the position shown in A. An example of spin label distributions calculated by PRONOX is shown for site 111 on each subunit of the dimer (sites 111A and 111B). The label distribution at each site is separated into energetically favorable (yellow) and unfavorable (red) label conformers.

Figure 3.

Intra-dimer distances from 4-pulse DEER experiments for 11 sites on the amphiphysin dimer (referred to by the residue number) and one distance from annexin B12. The left panel for each site shows the background-corrected dipolar evolution time (black) and the results of fits using a Gaussian distribution (green). The right panels show the resulting distance distributions using a Gaussian model (green). These results are summarized in Table 1. The distribution obtained from Tikhonov regularization (red) is shown for comparison. A single Gaussian distribution was used for all sites except 59, 97 and 103, for which bimodal Gaussian distributions were used to improve the fit to the experimental data.

The results for PRONOX calculations of inter-label distances for the 11 label pairs on the amphiphysin dimer are compared with the experimental data in Table 1. The calculated distance was within 2.5 Å of the experimental value for 7 of the 9 label pairs for which conformers were located using PRONOX in standard mode (Table 1). Use of standard conditions failed to locate any label conformers at positions 59 and 82 due to clashes with the protein structure, but switching to the fine search option for χ1 and χ2 solved this problem and resulted in distances close to the experimental values (Table 1). For position 95, a reduced clash criterion was required to obtain conformers, but under these conditions good agreement with experimental data was obtained (Table 1).

Table 1.

Experimental inter-label distances (R_exp, Å), and theoretical distances (R_calc, Å) and size of the distribution (n) calculated by PRONOX for the amphiphysin dimer.

Site	Rexp	Standard a		Fine Search b		Low Clash c
		Rcalc	n	Rcalc	n	Rcalc	n
54	43	43.5	12321	44.2	65536	43.1	144400
58	35	31.5	18632	31.8	64516	30.7	149769
59	25/31 d		0	25.7	49	26.1	8281
82	45		0	46.5	6162	47.2	38025
94	39	40.0	3969	40.6	39204	39.7	110224
95	37		0		0	34.7	361
97	36/45 d	43.6	26244	43.4	95481	41.3	184900
103	30/41 d	37.9	3136	36.5	36284	32.8	126025
105	27	28.4	4	27.8	899	24.8	18906
107	34	34.7	14400	34.6	73441	31.8	171810
111	38	38.2	17424	37.4	77284	36.5	169744

^aχ1=60,180,300°, χ2=60,180,300°, χ3=±90°, χ4=60,180,300°, χ5=0–330 in steps of 30°, clashes defined as 75% of sum of van der Waals radii

^b,cAs for Standard conditions, with ^b the fine search option for χ1 and χ2; and ^c clashes defined as 40% of the sum of van der Waals radii

^dTwo values are given based on a bimodal Gaussian fit of the DEER data. See Figure 3 for details.

PRONOX calculates a distribution of label conformers, as illustrated for the label at position 111 on each amphiphysin subunit in Figure 2B. Site 111 is located on an alpha helix in a solvent-exposed location with the label extended away from the protein. Thus, the label distribution should be unaffected by clashes with the protein and is expected to follow the general rules for favorable conformational space based on the H_α-S_δ interaction. The distribution of favorable and unfavorable label conformers is shown in Figure 2B, with these conformers shown in yellow and red, respectively. It is apparent in Figure 2B that the yellow conformers tend to be closer to the α-helix, and this label-protein interaction (mediated by the H_α-S_δ contact) is the basis for the energetic favorability of these conformers. Standard PRONOX conditions gave 17424 pairwise distances (Table 1) between 132 label conformers at site 111A and the same 132 conformers at site 111B (Figure 2B).

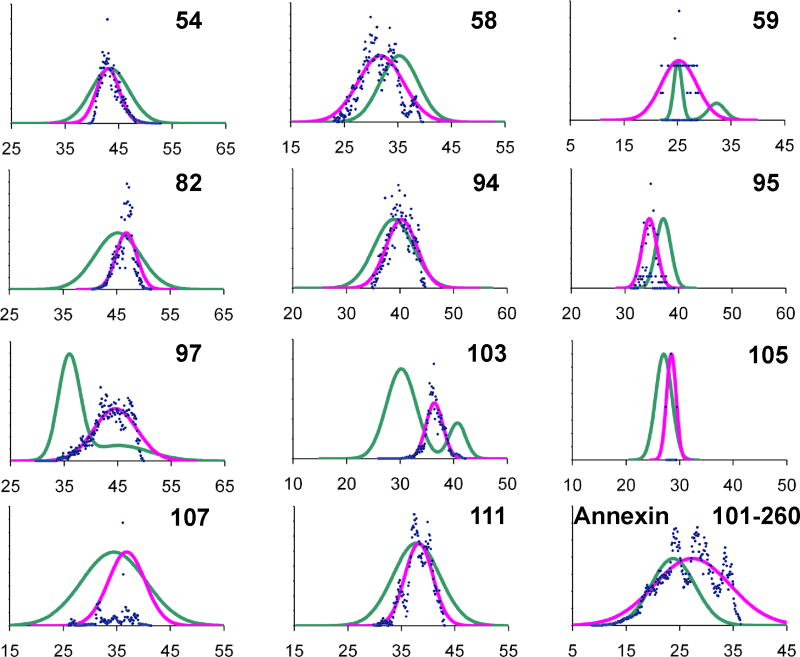
Using the label distributions for each site, PRONOX calculates a distribution of inter-label distances between a pair of labels. These distances can be fitted to a Gaussian function for comparison with similar fits to the DEER data (Figure 4). The Gaussian fits were calculated with biasing of the distances between favored conformers, as explained in the Methods. Of the 8 label pairs with experimental data fitted to a single Gaussian (Figure 3), the mean and width of the PRONOX Gaussian fits showed good agreement for 6 sites (54, 82, 94, 105, 107 and 111) (Figure 4). The mean of the PRONOX Gaussian fits were also in good agreement with the inter-label distance calculated directly by PRONOX (Table 1). These results suggest that the PRONOX distance can be used in lieu of obtaining a mean by fitting the calculated distance data to a Gaussian function.

Figure 4.

Gaussian fits of distance distributions calculated by PRONOX for eleven spin label pairs in amphiphysin (indicated by number only) and between spin labels at sites 101 and 260 of a subunit of the annexin B12 trimer. Pairwise distances were binned using steps of 0.1 Å and the number of distances in each bin is plotted (blue points). Gaussian fits to the PRONOX data (pink) are compared with similar fits to the DEER data (green).

For positions 59, 97 and 103, the experimental data were fitted to bimodal Gaussian distributions, which were in agreement with the Tikhonov distributions (Figure 3). For site 103, the PRONOX distance (Table 1) fits well with the mean of the two Gaussian functions fitted to the experimental data, and the PRONOX distance distribution (Figure 4) is positioned between the two experimental peaks. For position 59, the PRONOX data fit well with the major peak of the bimodal experimental Gaussian distribution. Thus, one of the conformer regions was inaccessible in PRONOX, again probably due to the protein rigidity. This label is in a spatially restricted position in the protein and a more sophisticated calculation may be required to improve the agreement of the experimental and PRONOX Gaussian fits. For position 97, the PRONOX data fit better with the minor peak of the bimodal experimental Gaussian distribution (Table 1, Figure 4). Thus, we were unable to predict the inter-label distance accurately for site 97, despite this label being solvent exposed. This may be due to a local conformational change in solution that is not reflected in the X-ray structure.

Annexin B12

A Gaussian fit of DEER data gave a distance of 23 Å between R1 labels at sites 101 and 260 in annexin B12. These sites are located at solvent exposed surfaces in the same monomer.²⁷ PRONOX was used in the standard mode to calculate the inter-label distance, and gave a value of 26.3 Å, which is higher than the experimental distance. The distribution of distances fitted to a Gaussian function (Figure 4) showed good agreement with the width of the experimental distribution, but also had a higher mean than the experimental value. We note that a distance of 23 Å was calculated with PRONOX without weighting the distance distribution. The label sites at 101 and 260 in annexin are located in loops and the weighting of favored conformers may be less important in these regions.

α-Synuclein

In contrast to amphiphysin and annexin B12, the α-synuclein structure used as the PRONOX input was not determined by X-ray crystallography. Instead, this structure was obtained using DEER data and computational work-up of these data using simulated annealing.⁶ Calculation of the inter-spin label distances was performed using PRONOX in the standard mode and showed very good agreement with the experimental data (Table 2). We note that PRONOX was not used in the original derivation of the structure, other than for simple addition of spin labels prior to simulated annealing.⁶

Table 2.

DEER distances (R_exp, Å)⁶ and distances calculated by PRONOX (R_calc, Å) for pairs of spin labels at different sites in α-synuclein.

Site 1	Site 2	Rexp	Rcalca
11	26	25	24.3
11	41	48	45.9
22	52	49	45.2
26	41	23	22.8
26	56	44	44.4
37	67	42	45.8
41	56	23	22.9
41	67	37	39.6
41	70	41	43.5
44	67	36	36.0
48	67	29	29.8
56	70	22	22.9
56	85	42	44.5
63	81	26	28.9

^aAverage over 10 structures of α-synuclein. See Supplementary Table S2.

Endophilin

The structure of the rat endophilin A1 dimer includes a BAR domain, which has been determined by X-ray crystallography,²⁸ and several helices that are thought to be emersed in the lipid bilayer. We have determined the conformation of the central helix and loop (positions 63 to 86) using DEER data in combination with simulated annealing.²³ In these calculations, a family of structures emerged with the helices in each subunit oriented at approximately 40° (similar to the X-ray structure for human endophilin³³), 90°, or 140° with respect to the long axis of the BAR domain²³.

We used PRONOX to calculate inter-label distances for each of the three central helix conformations of endophilin. The results are separated into two categories of label pairs (Table 3). The first five pairs reflect distances within the BAR domain (Table 3) and do not vary (except slightly for 96A/96B) in the 40°, 90°, or 140° central helix conformers. The agreement between the experimental and calculated distances is reasonable for these pairs. We also note that the DEER distances were obtained in a lipid-bound endophilin dimer,²³ while the PRONOX distances are based on the X-ray structure²⁸ of the BAR domain, and these structures may be slightly different.

Table 3.

DEER distances (R_exp, Å)²³ and distances calculated by PRONOX (R_calc, Å) for pairs of spin labels in three conformers (40°, 90°, 140°) of endophilin.

	Site 1	Site 2	Rexp	Rcalc 40°	Rcalc 90°	Rcalc 140°	Rcalc Average
BAR Domain	96A	96B	38	37.8	37.9	38.0	37.9
	166A	210A	43	40.7	40.7	40.7	40.7
	178A	200A	31	37.4	37.4	37.4	37.4
	216A	216B	37	40.8	40.8	40.8	40.8 d
	227A	227B	9 c	10.9	10.9	10.9	10.9
Central Region	63A a	63B	9 c	14.2	14.6	9.8	12.9
	64A b	64B	18	16.7	19.6	18.4	18.2
	65A b	65B	24	24.3	33.1	27.7	28.4
	66A a	66B	19	21.0	25.6	16.6	21.1
	67A b	67B	23	24.4	17.4	17.7	19.8
	70A a	70B	28	31.2	29.3	25.7	28.7
	71A b	71B	37	37.3	29.0	33.2	33.2
	73A a	73B	41	44.1	45.4	39.1	42.9
	74A a	74B	44	47.3	42.7	42.2	44.1
	75A a	75B	42	52.6	42.9	49.4	48.3
	77A a	77B	49	55.0	51.6	55.8	54.1
	78A a	78B	44	43.4	44.3	45.5	44.4

^aData from labels at these positions were used in simulated annealing calculations in the original derivation of the structure²³

^bData from labels at these positions were not used in derivation of the structure²³

^cDistance from continuous-wave EPR

^dObtained using the fine search approach. Standard conditions only gave one conformer at each site (inter-label distance 44.6 Å)

The other 12 label pairs (Table 3) are within the endophilin central region, which forms a helix (63 to 75) and a loop.²³ Eight of these pairs were used in derivation of the structure, while the other 4 were omitted due to their potential clash with the BAR domain.²³ For many of the 12 pairs, the average PRONOX distances calculated over the 40°, 90°, or 140° conformers are in good agreement with the DEER distances (Table 3). These results show the value of PRONOX in evaluating distances in a structure determined using DEER data, with inclusion of averaging over multiple protein conformers.

FCHo2 (F-BAR)

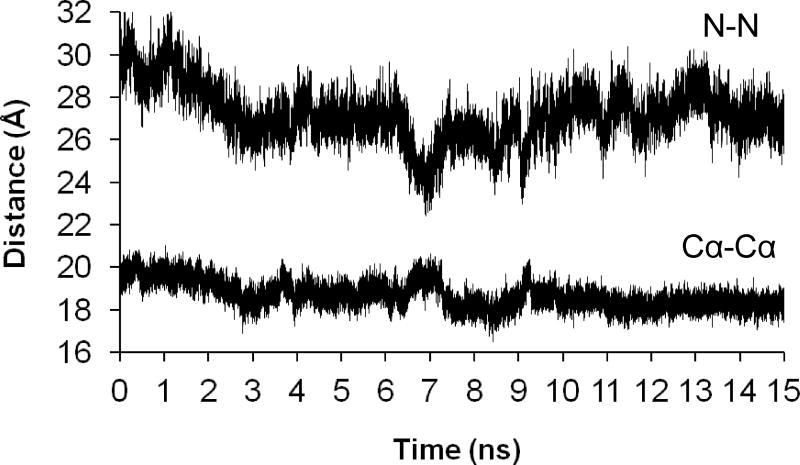
To investigate the effect of protein motion on inter-label distances, we performed a solvated 15-ns molecular dynamics simulation of the F-BAR dimer with labels at position 86 of each subunit. Experimentally, the distance between these labels has been determined to be 29 Å.¹⁰ In the MD simulation, χ1 and χ2 also remained in the (m,m) conformation for the entire simulation, with variation of ±30° around 300°, and t3 essentially remained at 90°. Torsions t4 and t5 showed relatively rapid motion, reflecting the mobility of the label in the simulation. Averaging over 75,000 structures (collected every 0.2 ps) gave an interlabel N-N distance of 27.2 ± 1.3 Å, which was somewhat lower than the experimental value. This distance ranged from 22.4 to 32.3 Å over the simulation (Figure 5A). The Cα(86A)-Cα(86B) distance ranged from 16.5 to 21.0 Å (mean 18.9 ± 0.6 Å) (Figure 5B) and accounted for less than half of the variation in the inter-label N-N distance.

Figure 5.

Distances between the nitroxide N atoms of spin labels at position 86 of each subunit of the FCHo2 (F-BAR) dimer and the Cα atoms of these positions over a molecular dynamics simulation of 15 ns.

The PRONOX calculation for the labels at position 86 of each F-BAR subunit gave an inter-label distance of 30.1 Å, using the fine search approach for χ1 and χ2. Almost all of these conformers had χ1,χ2 = (m,m), in good agreement with the MD simulation. The computed inter-label distance in PRONOX is close to the experimental value, but the MD data give a broader distribution of distances that is closer to the experimental distribution. Thus, the MD data better reproduce the width of the distribution, but at a computational cost, whereas PRONOX was able to calculate an accurate inter-label distance rapidly.

Correlation of PRONOX Distances with Experimental Data

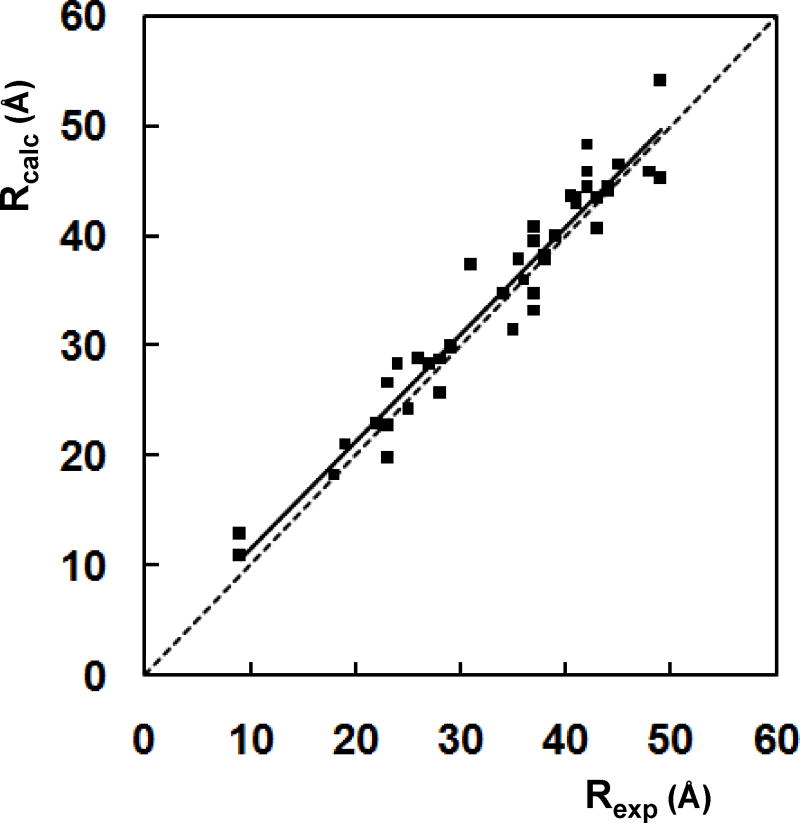
The 44 inter-spin label distances calculated by PRONOX for the five proteins discussed above were compared with the experimental data using linear regression analysis (Figure 6). This comparison gave a correlation coefficient of 0.94 and a slope of 0.98.

Figure 6.

Correlation of experimental (R_exp) and PRONOX (R_calc) distances for 44 inter-label distances in 5 proteins. The correlation coefficient is 0.94 and the slope is 0.98. The dotted line has a slope of 1 and is shown for comparison. For sites 59, 97 and 103 of amphiphysin, the experimental distance in the plot is the mean of the two values given in Table 1.

Discussion

Our results show that PRONOX can be used for accurate calculation of distances between spin labels at two sites on a protein, with good correlation with experimental data. Weighting of the contribution of energetically favored conformers based on crystallographic evidence^11–13 was important in determining these distances. The favorable (m,m) conformation for a spin label attached to an α-helix was supported by results from a molecular dynamics simulation. Fitting of the weighted inter-label distance distribution obtained from PRONOX to a Gaussian function is a useful extension of the program and allows a comparison of the mean and width of the distance distribution with those obtained experimentally. However, the average distance calculated in PRONOX with automatic weighting of favored conformers is similar to the mean of the Gaussian fit and can be used directly as a measure of the inter-label distance. Thus, the appropriate weighting of conformers in PRONOX is an important aspect of the program that improves the fit with experimental data.

PRONOX provides an alternative to simulation methods for computation of interspin label distances. Force field calculations require parameter development and computational resources for determination of multiple inter-spin label distances, since each label pair has to be examined in a separate simulation. To search for a more rapid MD method for determination of inter-label distances, we tried an alternative approach for the amphiphysin dimer, in which multiple pairs of labels at different positions were simultaneously included in a shorter simulation of 2 ns. We ensured that the labels were not interacting with each other directly, but still obtained a poor correlation with the DEER distances (results not shown).

We note that simulations have shown that inclusion of protein motion is important in computing inter-label distances,²⁰ and we also found a contribution of protein motion to the inter-label distance distribution in the MD simulation of the labeled F-BAR dimer. This motion tends to broaden the distance distribution, but has less effect on the mean. In the MD simulation, local backbone motions were the main contributor to broadening of the inter-label distance distribution, based on monitoring of the Cα-Cα distance between the two labeled sites. The distribution could also be influenced by relative motions of protein domains on a longer time scale. Thus, protein rigidity is a limitation in PRONOX, but one that is offset by the benefits of the simplicity of the approach. The lack of rigidity can be addressed to some extent by including the fine search option or reducing the van der Waals cutoff, and these changes to the standard approach can be used to compute label distributions in confined spaces.

There are similarities of the approach in PRONOX with that taken for calculation of inter-spin label distances in the MMM program (http://www.epr.ethz.ch/software/). In a recent paper, Polyhach et al.¹⁸ showed that simplification of conformer distributions for spin-labeled cysteines obtained from MD simulations could be used as a basis for computation of inter-label distances. The rotameric states for χ1, χ2 and χ3 were similar to those assumed in our standard PRONOX input, but we note that there were some differences and generally more restriction on the states for χ4 and particularly for χ5, compared to our standard PRONOX approach. The results with these more restricted distributions still gave good agreement with experiment¹⁸ and exclusion of some conformers for χ4 and χ5 should further increase the speed of PRONOX without apparent loss of accuracy.

Using the standard approach described here, PRONOX calculates the label distributions and inter-label distances in less than a minute on a desktop PC, and with only a few required input parameters. The efficiency and simplicity of PRONOX may permit global searches of elements of protein tertiary structure, with evaluation of the fit of distances computed for a particular conformation with experimental data. Alternatively, with initial knowledge of secondary structure, PRONOX can be used to calculate label distributions at various sites in these structures. These distributions can be reduced to single-point representations, which can be used to determine the relative orientations of regions of secondary structure. Further planned refinements include the introduction of limited motion of protein side chains and options for conformational search through movement of protein secondary structures. This should allow better reproduction of the fine details of distance distributions, and may permit distributions predicted by PRONOX to be used as a means of validating fits to experimental data. The increasing use of DEER for proteins will provide a rich set of experimental data for further evaluation of PRONOX.