New advances in understanding decisions among multiple alternatives

Abstract

Experimental studies of decision-making have put a strong emphasis on choices between two alternatives. However, real-life decisions often involve multiple alternatives. This article provides an overview of theoretical frameworks that have been proposed to account for behavioral data from both economic and perceptual multi-alternative decision-making. We further review recent neurophysiological data collected in conjunction with decision-making behavior. These neural recordings provide constraints on putative models of the decision mechanism. For example, the time course of inhibition provides insight into how the competition between alternatives is mediated. Furthermore, whereas decision-related neural activity seems to reach a common threshold at the end of the decision period, the starting point tends to depend systematically on the number of alternatives. We discuss candidate mechanisms that could drive the reduction in firing rates on decisions among multiple alternatives.

Most behavioral paradigms that have been developed to understand decision-making have employed decision tasks with only two alternatives. In the real world, however, organisms are frequently faced with decisions among many more choices: which of three cars to buy, which of eight potential mates to acquire, or which of one hundred possible animals in a herd to attack. If current frameworks for understanding decision-making are to be relevant for real-world decisions, it is essential that they can explain decisions among more than two alternatives.

What has been learned from studying decisions between two alternatives?

Behavioral, neurophysiological, and theoretical studies of binary choices have led to similar conclusions: decisions that require the evaluation of continuously inflowing information can frequently be described by accumulation-to-threshold mechanisms. Influential models include the drift-diffusion model [1] and the leaky competing accumulator (LCA) model [2], which have both been shown to account for a variety of behavioral datasets. Neural recordings from animals performing a perceptual decision task, in particular from parietal association cortex, are consistent with the view that sensory evidence is accumulated for each alternative until the integrated net sensory evidence for one of them reaches a decision threshold [3]. Computational models based on the integration-to-threshold idea can account for both the choice behavior and the neural activity [4,5]. It can be demonstrated that, under some assumptions, the proposed decision mechanisms provide an approximation of the sequential probability ratio test (SPRT), an optimal decision algorithm that minimizes the average decision time for any desired level of accuracy [6–8]. According to SPRT, a decision-maker should keep collecting evidence until the likelihood ratio for the two alternatives crosses a predefined upper or lower boundary. These boundaries depend on the desired accuracy and on the prior probabilities of the two alternatives.

Models of decisions between multiple alternatives

In contrast to binary choices, studies of the neural mechanisms of decisions between more than two alternatives have, so far, received much less attention. This is surprising, given that decisions between multiple alternatives offer some unique characteristics. For example, when studying decisions that are based on at least two different attributes, it has been observed that adding choice alternatives can lead to interesting preference reversals [9]. Assume that a subject is asked to make a choice between alternatives A and B and ends up preferring A. After adding a third alternative, C, it can sometimes be observed that the subject now prefers alternative B over A. This is surprising and indicates that how desirable a particular alternative is does not only depend on the properties of this alternative, but also on the context. Furthermore, unlike SPRT in the two-choice case, no optimal sequential sampling algorithm for decisions between multiple alternatives with any desired accuracy is currently known.

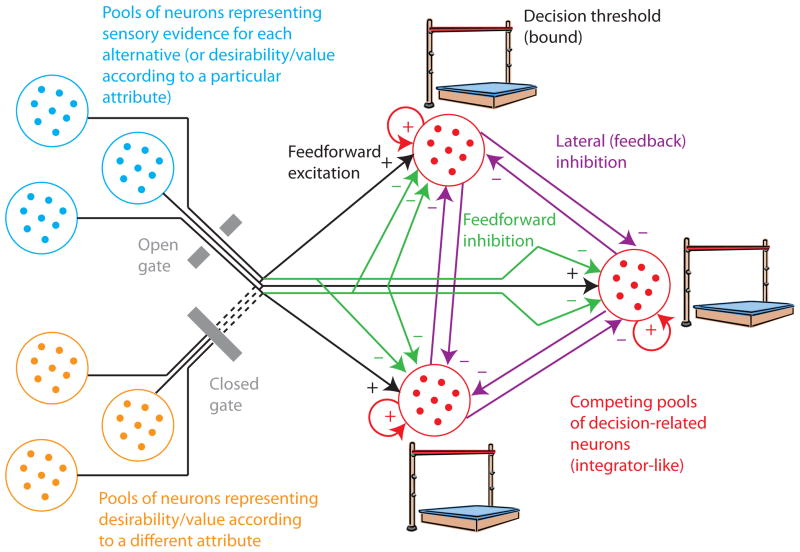
Roe et al. [9] have proposed Multialternative Decision Field Theory (MDFT), a sequential sampling framework for decisions between multiple alternatives. MDFT can capture change-in-preference phenomena like the similarity, attraction, and compromise effects. In this framework, sensory (or attribute) signals do not only provide evidence for a particular choice (black arrows in Fig. 1), but also against the alternatives. This feedforward inhibition mechanism (green arrows in Fig. 1), which calculates the difference between one particular sensory/attribute signal and the average of the remaining signals, is referred to as “contrast”. The resulting net evidence signals are accumulated over time with a definable integration time constant (“leakiness”). The integrators interact via lateral inhibition, the strength of which depends on the similarity of pairs of choice options in terms of “desirability” (purple arrows in Fig. 1). This distance-dependent strength of lateral inhibition is an essential component of MDFT. Preference reversal effects could not be explained without it. Finally, the decision process terminates as soon as one integrator reaches a decision threshold. If a decision is to be based on more than one attribute, only one of the attributes is evaluated at any time, but MDFT switches randomly between attributes (gates in Fig. 1). LCA [2,10] easily generalizes from two to multiple alternatives. In its basic form, each sensory/attribute signal provides excitatory evidence for a particular choice. In contrast to the linear integrators used by MDFT, these evidence signals are accumulated by nonlinear integrators, which have a reflecting lower bound. The lateral inhibition between integrators is not distance-dependent and has a fixed strength. To be able to explain the compromise, attraction, and similarity effects, Usher & McClelland [11] proposed a version of LCA that relies on pairwise comparisons of the sensory or attribute signals (not shown in Fig. 1) and applies a nonlinear “advantage” function to them. This nonlinear function is the critical mechanism that allows LCA to explain the preference reversals.

Figure 1. Structure of multi-alternative decision mechanisms.

Using an example of a decision between three alternatives, the structure of the majority of decision models is illustrated. The decision is based on a competition between three pools of decision-related neurons, one for each alternative (red). These pools of neurons exhibit integrator-like behavior, symbolized as recurrent excitatory feedback. Different models make different assumptions about the integration time constant (leakiness), the existence of a lower reflecting bound, and how the integrator is implemented (attractor dynamics). The simplest decision rule, which has been adopted by most of the models and is consistent with recordings from monkey LIP, is to terminate the decision process when the activity of the most active pool exceeds a decision threshold or bound (represented by high jump bar). More complicated decision rules, like a comparison between the most active and the second-most active pools, are possible. The blue pools of neurons provide sensory evidence for each alternative (in the case of perceptual decision-making) or the desirability or value of each alternative according to a particular attribute (in the case of economic or value-based decision-making). Multiple such representations might exist in the case of multi-attribute decision-making (orange pools). The proposed models for multi-attribute decision-making assume that only a single attribute can influence the decision at any time (open gate) and that the decision mechanism switches randomly between attributes over time. In all of the models, these evidence signals provide feedforward excitation to the decision pools (black arrows). The green arrows indicate feedforward inhibition, meaning that a particular evidence signal cannot only excite one decision pool, but also inhibit other decision pools. These connections are essential in diffusion-like models, present in MDFT, but absent in the standard version of LCA. Recent recordings from monkey LIP [18] suggest that they are present. The purple arrows indicate lateral or feedback inhibition, meaning that the decision pools directly compete with each other by suppressing each other’s activity. Such connections are absent in diffusion-like models, but essential for MDFT and LCA. In the case of MDFT the strength of these inhibitory connections depends on the similarity of choice options, in the case of LCA all inhibitory connections have the same strength. The depicted structure is highly simplified. For example, no interneurons for mediating inhibitory connections are shown.

Relatively complex data patterns can sometimes be consistent with surprisingly simple heuristics. Brown et al. [12] had subjects watch a varying number of columns of bricks that would build up stochastically over time. One of them was building up at a higher rate than the remaining columns. The subjects had to decide which of the columns was building up fastest and could stop the process at any time. The mean response time was a linear function of the logarithm of the available number of alternatives (Hick’s law [13], a regularity that is commonly observed when studying decisions between a varying number of alternatives) and accuracy dropped with an increasing number of alternatives. These and other aspects of the data were consistent with a surprisingly simple decision rule: pick the tallest column when it has a fixed number of bricks more than the second-tallest column.

Several biophysically inspired models have been proposed in response to a combined behavioral and electrophysiological 4-choice dataset from a random-dot motion discrimination task, which will be discussed in more detail later [14]. The first two are exemplary of a class of dynamical attractor models. Furman & Wang [15] provided a model that was based on a continuous representation of the direction of motion, local recurrent excitation, and global recurrent inhibition. Slow, NMDA-mediated reverberation made it possible for the network to replicate the long integration time constants that are evident in real neural systems. A closely-related model based on four discrete competing pools of decision-related neurons was proposed by Albantakis & Deco [16]. This model was able to accurately predict behavior on a version of the task that dissociated the number of choices with the angle of separation between the targets. The model, like the data, showed a decrease in accuracy without much change in reaction time for a 2-choice task where the choice targets were separated by 90° compared to 180°. An alternative approach used a model that was designed to perform optimal probabilistic inference [17]. At each moment, the model represents a probability distribution over motion direction given the accumulated evidence. Evidence is accumulated without loss of information via linear integration of neural activity.

Neural activity associated with decisions among more than two alternatives

i. Neural data begins to constrain possible models

Bollimunta & Ditterich [18] recorded spiking activity and local field potentials (LFPs) from the lateral intraparietal area (LIP) in monkeys making decisions between three alternatives based on a multi-component random-dot stimulus that provided simultaneous control over the amount of sensory evidence for each alternative. Human choice behavior in this task is well-explained by linear accumulation-to-threshold mechanisms that either rely only on feedforward or only on feedback inhibition [19,20]. While these mechanisms do not implement the Multihypothesis Sequential Probability Ratio Test (MSPRT) [21], a generalization of SPRT that can be shown to be asymptotically optimal if the error rate is negligible, they provide no major disadvantage when the error rate is clearly not negligible [19,22]. An implementation of MSPRT would require some nonlinear operations, which have been proposed to be provided by the basal ganglia [23]. Bogacz & Gurney’s feedforward model makes the interesting prediction that cortical activity should no longer reach a stereotyped level at the time when the decision threshold in the basal ganglia is crossed. This seems to be at odds with the LIP recordings. A possible solution would be a decision mechanism that integrates the basal ganglia as part of a cortico-cortical feedback loop [19]. Bollimunta & Ditterich’s recordings were consistent with an accumulation-to-threshold mechanism as the activity of the winning pool of decision-related neurons always reached a stereotyped level at the end of the decision interval. Furthermore, LIP neurons were faster inhibited by sensory evidence against their preferred alternative than excited by sensory evidence in favor of it, suggesting that the inhibition cannot only be provided by the competing decision pools. This suggests the presence of feedforward inhibition, but does not rule out feedback inhibition. In fact, most likely the decision mechanism relies on a combination of feedforward and feedback inhibition for mediating the competition between alternatives. In contrast to the spiking activity, which reflected accumulated net evidence, the LFP reflected the total amount of sensory evidence for and against a particular alternative. Thus, different evidence components seem to be combined at the level of parietal association cortex.

ii. A reduction in neural activity with increased number of alternatives

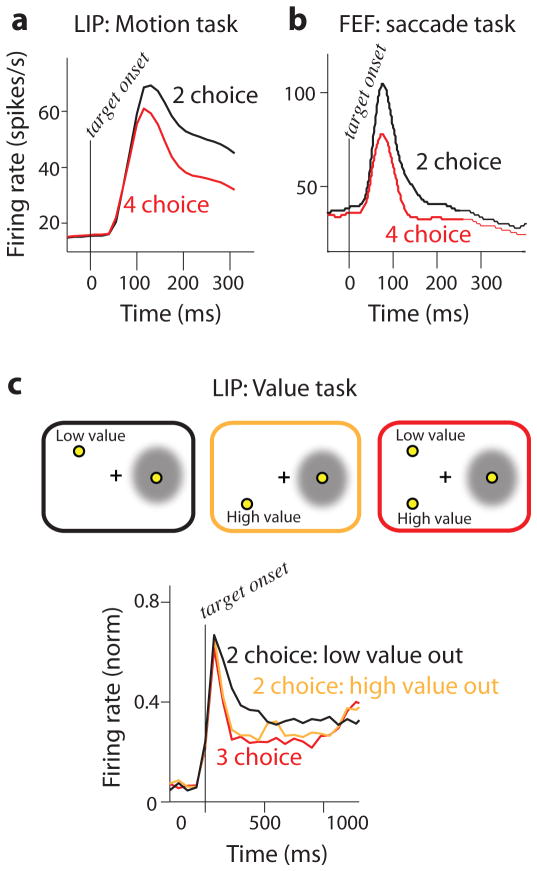
Churchland et al. [14,24] reported on responses of neurons in area LIP of monkeys that had to make decisions between either two or four alternatives based on a random-dot motion stimulus. The results were again consistent with an integration-to-threshold mechanism. Analysis of both the mean firing rate and its variance suggested that the accumulated quantity was very similar for the two tasks. Interestingly, however, neural responses were reduced at the start of 4-choice trials compared to 2-choice trials. The reduction was observed during a brief epoch in which the monkeys knew whether they would be making a decision among 2 or 4 alternatives, but had not yet begun accumulating evidence (Fig. 2a). A lower starting point for accumulation means that more evidence is required to reach threshold, assuming that evidence scales the same way into a spike rate change in LIP on 2- and 4-choice versions of the task, an assumption that other analyses proved likely. This strategy, requiring more evidence before committing to a choice, is a suitable adjustment to the increased uncertainty that accompanies decisions with more alternatives and can explain why response times increase with more alternatives.

Figure 2. The addition of more choice alternatives reduces firing rates in LIP and the FEF.

a. Mean firing rates of LIP neurons (N=70) recorded while monkeys were engaged in a 2- or 4-choice decision task. Responses are aligned to the onset of the choice targets and end before the onset of the stimulus motion about which the decision is eventually made. Re-plotted with permission from [24]. b. Mean firing rates of FEF neurons (N=71) recorded while monkeys were engaged in a color-to-location choice saccade task. Responses are aligned to the onset of the choice targets and end well before the saccade. Re-plotted with permission from [29]. c. Top: Three target configurations presented to monkeys on a computer monitor during LIP recording. For each configuration, monkeys fixated a central target (cross) and were shown 1–3 peripheral choice targets. A choice target with a fixed value was presented in the response field (RF, schematized by the gray circle) of the neuron under study. Left: 2-choice condition, low value target outside the RF. Middle: 2-choice condition, high value target outside the RF. Right: 3-choice condition; values of the targets outside the RF are as indicated in other panels. Bottom: Mean firing rates of LIP neurons (N=62) for each condition. Responses are aligned to the onset of the choice targets and end well before the saccade. Firing rates depended both on the number of targets and on their value. Responses are consistent with a divisive normalization scheme that is based on response value. Re-plotted with permission from [32].

The Churchland et al. study is one of several that have observed that reduced firing rates accompany an increase in the number of choice alternatives. This perhaps counterintuitive observation was first made some time ago in the superior colliculus by Basso & Wurtz [25,26]. Three more recent studies have reported the same. Balan et al. reported on LIP responses during a visual search task among 2, 4 or 8 objects [27]. As in the Churchland et al. study, firing rates were inversely related to the number of targets. Cohen et al. [28] recorded from neurons in the frontal eye field (FEF) during visual search to explore the role of attention in the long reaction times that accompany visual search among multiple targets. They observed lower activity in FEF neurons when the target object was amid 3 distractors instead of 1 distractor. Responses were further suppressed when the target object was amid 7 distractors. Lee et al. [29] likewise observed reduced firing in the FEF (Fig. 2b). They used a challenging color-to-location choice saccade task and observed reduced firing rates for a 4-choice compared to a 2-choice task. Interestingly, the reduction in firing rates was reversed around the time of the saccade: neurons fired the most on 4-choice trials.

What might be the mechanism by which firing rates are reduced for more choice alternatives? One potential explanation is that the additional visual targets are in a suppressive surround that has a subtractive effect on the neurons’ responses, something that has been observed frequently in primary visual cortex [30,31]. This possibility was refuted by Basso & Wurtz [25,26]: after they observed reduced responses on an 8-choice compared to a 2-choice saccade task, they compared responses on two versions of the 8-choice task. On the first, a different target was cued as a saccade endpoint on each trial; on the second, the same target was cued as a saccade endpoint on each trial (blocked task). The monkeys picked up on the manipulation: their reaction times were faster on the blocked task. If the additional visual targets were in a suppressive surround, they should have suppressed responses whether they were potential saccade targets or not. However, Basso & Wurtz found that responses on the blocked 8-choice task looked more like the 2-choice task; the suppression had gone away despite the presence of so many choice targets. This argues that, at least in the colliculus, the suppressed responses during multiple-alternative decisions can’t simply be accounted for by the change in spatial configuration that accompanies those decisions.

An appealing possibility is that the reduced firing rates on multiple-choice decisions reflect the mixture of a greater number of attentional states. Recent reward history might tend to make the monkey slightly biased towards one target or the other on a given trial. On the 2-choice task, this means he can be in one of two states: attending to the target in the response field, or to the other target. On trials with more alternatives, his attention can be to any of a number of targets, most of which are outside the response field. In keeping, Churchland et al. [24] reported that responses on 4-choice trials were more variable compared to those on 2-choice trials. This is consistent with the idea that mean responses on a 4-choice task reflect the mixture of a greater number of states.

Value-based decisions among more than two alternatives

Studies of value-based decisions have likewise observed multiple-choice decisions lead to reduced firing rates. Louie and colleagues [32] presented 1, 2 or 3 targets to monkeys during recording from LIP (Fig. 2c; top). As in previous studies, they observed the lowest firing rates on the trials with the most targets (Fig. 2c, bottom, red line below black, orange lines). The key manipulation was of the targets’ values: choosing the target in the neuron’s response field always resulted in a drop of water of the same size; choosing other targets resulted in drops of water that were either smaller (Figure. 2c, top, left) or larger (Figure 2c, top, middle). By varying the value of targets outside the response field while keeping the target number constant, the authors aimed to dissociate the effects of target number and possible reward value. They reported that firing rates were reduced on trials where the value of an outside target was high compared to trials where the value of an outside target was low (Figure 2c, bottom, orange line below black line). The observations were best captured by a model where excitatory inputs were suppressed by the total value of targets outside the response field; the best fit model used divisive normalization, a mechanism that has been shown to account for suppression elsewhere in the visual system [33] and in the olfactory system as well [34].

The observation that targets of greater value are more suppressive than targets of lower value could be in keeping with Basso & Wurtz’s findings in the superior colliculus: in their blocked task, the non-rewarded targets were known to the monkey to have very low value. Taken together, these findings suggest that suppression may be driven not only by the spatial position of targets, but by their value as well.

Electrophysiological studies in nonhuman primates have been complemented with human fMRI studies. Daw et al. used multiple-choice decision-making to understand how humans trade off the tendency to exploit a preferred alternative versus exploring new alternatives [35]. The authors observed subjects’ decisions as they participated in a “4-armed bandit” slot machine game. The reward associated with each slot changed dynamically over the course of the experimental session. The authors identified a number of brain areas where responses differed between trials that were classified as exploratory and trials that were classified as exploitative. These areas, which included the anterior frontopolar cortex and the anterior intraparietal sulcus, showed increased activity during exploratory decisions. This suggests that exploration of new choice alternatives occurs only when a more automatic exploitative tendency can be overridden.

At first glance, a bounded accumulation framework might seem ill-suited for value-based decisions where the evidence is not stochastic in nature. However, recent work has found that decision outcomes and times are modeled well by an accumulation framework. The success of the framework suggests that the relative value of several decision outcomes might take time to estimate, perhaps because the value is successively sampled from a broad distribution [36]. In a recent paper, Krajbich and colleagues extended their binary model of value-based decision-making to a trinary model [37]. The authors assumed that the brain computes a relative decision value that reflects the difference between the item with the most value and the item with the next-most value (“best versus next”). Such a best-vs-next strategy is one possible way to implement the already mentioned MSPRT algorithm. The authors found that this approach provided a nearly seamless extension of their binary model; in fact, parameters fit to the binary dataset accurately described behavior on the trinary task. The authors point out a caveat, however: for large numbers of choices, it might not be feasible for the brain to track all the alternatives. This caveat probably applies to perceptual decisions as well. Possible solutions are the use of the simpler best-vs-average framework (most of the mechanisms that have been discussed so far belong to this class [19,22]) or the successive elimination of options that cannot compete with the strongest alternatives.

Conclusions

Behavioral, neurophysiological, and modeling studies of both perceptual and value-based decision making all seem consistent with a sequential sampling, accumulation-to-threshold mechanism. This mechanism is probably not an exact implementation of MSPRT, but MSPRT-like. The exact details of this mechanism and its neural implementation are outstanding issues. It has recently been suggested that decision experiments with non-stationary evidence might be a useful tool for discriminating between different decision mechanisms [38]. An obvious question is how a decision mechanism would deal with an ever increasing number of alternatives. Are binary choices and continuous parameter estimation just two extremes on a single continuum? And what is it, if anything, that the brain tries to optimize with its implementation of the decision process?

Highlights.

• Decisions among more than two alternatives can be explained by accumulation to bound frameworks.

• These frameworks can be linked to statistical considerations on optimal decision-making.

• Lower firing rates are often observed as the number of choice alternatives increases.

• The lower firing rates, in some cases, are consistent with divisive normalization.