Abstract
Neurons in area MT are sensitive to the direction of motion of gratings and of plaids made by summing 2 gratings moving in different directions. MT component direction-selective (CDS) neurons respond to the individual gratings of a plaid. Pattern direction-selective (PDS) neurons on the other hand, combine component information and respond selectively to the resulting pattern motion. Adding a third grating creates a “triplaid,” which contains 3 grating and 3 plaid motions and is perceptually multistable. To examine how direction-selective mechanisms parse the motion signals in triplaids, we recorded MT responses of anesthetized and awake macaques to stimuli in which 3 identical moving gratings whose directions were separated by 120° were introduced in 3 successive epochs, going from grating to plaid to triplaid. CDS and PDS neurons—selected based on their responses to gratings and plaids—had strikingly different tuning properties in the triplaid epoch. CDS neurons were strongly tuned for the direction of motion of individual gratings, but PDS neurons nearly lost their selectivity for either the gratings or the plaids in the stimulus. We explain this reduced motion selectivity with a model that relates pattern selectivity of PDS neurons to a broad pooling of V1 afferents with a near-cosine weighting profile. Because PDS neurons signal both component and pattern motion in gratings and plaids, their reduced selectivity for motion in triplaids may be what makes these stimuli perceptually multistable.
Introduction
The cortical computation of motion begins at the level of the primary visual cortex (V1) where direction-selective neurons act as space-time filters to extract the direction of motion of simple visual stimuli such as gratings and oriented bars (Hubel and Wiesel, 1962; Emerson et al., 1992; DeAngelis et al., 1993). To compute the motion of more complex patterns, areas downstream of V1 must integrate local motion signals in the stimulus. Our most refined characterization of this integration comes from comparing neural responses in V1 and area MT (V5) to single versus two superimposed drifting gratings. When two gratings that move in different directions are superimposed, they form a moving plaid whose direction of motion differs from its component gratings (Movshon et al., 1985). Unlike V1 neurons that only represent component motion, MT neurons' direction selectivity ranges from pure component selectivity—selective for the direction of the component gratings—to complete pattern selectivity—selective for the overall motion of the plaid (Zeki, 1974; Albright, 1984; Movshon et al., 1985; Rodman and Albright, 1989; Rust et al., 2006).
For MT neurons to support motion perception (Stoner and Albright, 1992a, 1996; Born and Bradley, 2005; Smith et al., 2005; Majaj et al., 2007), their direction tuning properties must be invariant with respect to the details of the stimulus (Priebe et al., 2003; Jazayeri, 2008). To test whether MT neurons maintain their direction tuning properties in the presence of other moving stimuli, we recorded from individual MT neurons in response to 3 superimposed moving gratings whose directions were 120° apart. These “triplaids” are particularly suited for studying the invariance of direction selectivity because they contain 3 component motions (from the 3 moving gratings) and 3 pattern motions (from the 3 pairs the gratings) simultaneously.
Triplaids are also interesting because they evoke multistable percepts (Movie 1) that fluctuate spontaneously among various combinations of plaid and grating motion in the stimulus (Adelson and Movshon, 1983; Andrews and Schluppeck, 2000). Our experiment bears on the question of how signals in MT might relate to this multistability. For example, neurons that exhibit a stable and robust direction preference in response to triplaids would not be good candidates to support fluctuations of the perceptual state. We were thus interested to see whether triplaid stimuli influence the stability of direction selectivity in MT neurons.
Movie 1.
Demonstration of the perceptual multistability of triplaids. The movie shows three drifting gratings, first separately, and then superimposed. The multistability of the resulting triplaid can be readily verified by fixating a point somewhere outside the stimulus (e.g., edge of the screen) while monitoring the direction of motion in the triplaid. Typically, 2 of the 3 gratings form a plaid that transparently moves oppositely to the remaining grating. Multistability arises from fluctuations among different groupings of the gratings and plaids.
We found that MT responses to triplaids depended on their level of pattern selectivity. Component direction-selective (CDS) neurons were mostly “blind” to the pattern motion in triplaids, and their responses could be related straightforwardly to their tuning for individual gratings. In contrast, the response modulation of pattern direction-selective (PDS) neurons declined steadily, resulting in only weak selectivity for the motion in the triplaid stimulus. In other words, unlike CDS cells, whose preference for component motion did not depend on the presence of other gratings and plaids, PDS cells' ability to signal coherent pattern motion in plaids was remarkably compromised in the presence of a third grating. These observations are consistent with the predictions of a model of MT that explains pattern direction selectivity in terms of pooling V1 afferents with broad excitation and strong opponent inhibition (Rust et al., 2006).
Materials and Methods
Electrophysiology.
We recorded extracellularly from well isolated direction-selective single units in area MT of 2 adult anesthetized paralyzed macaque monkeys (Macaca fascicularis) of either sex, and one adult awake, actively fixating rhesus monkey (Macaca mulatta) of female sex. General procedures for the surgical preparation of animals and single-unit recording in these 2 preparations have been reported in detail previously (Cavanaugh et al., 2002b; Chukoskie and Movshon, 2009). All procedures complied with the National Institute of Health Guide for the Care and Use of Laboratory Animals and the New York University Animal Welfare Committee as well as U.S. Department of Agriculture guidelines.
Visual stimulus.
Stimuli were generated and controlled by an Apple Macintosh G5, and presented on a gamma-corrected Eizo T966 monitor with a refresh rate of 120 Hz at a mean luminance of 33 cd/m2. We first mapped receptive field location. Across our population, receptive fields were centered at eccentricities ranging from 2° to 33°. Afterward, we presented sinusoidal grating stimuli to determine each cell's preference for stimulus direction, spatial and temporal frequency, and size. In the anesthetized experiments, we determined each cell's preferred eye and covered the other.
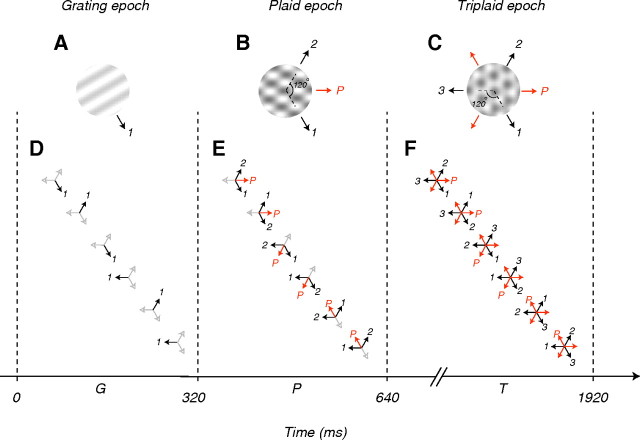
Triplaid stimuli used in the main experiment consisted of 3 successive epochs (see Fig. 1). In the first epoch (Grating epoch), a drifting grating whose direction was randomly chosen from 12 evenly spaced directions was presented (see Fig. 1A, black arrow enumerated 1). In the second epoch (Plaid epoch), a second grating separated by 120° from the first one was added (see Fig. 1B, black arrow enumerated 2) to form a plaid that moved 60° away from the 2 gratings (see Fig. 1B, red arrow labeled P). In the last epoch (Triplaid epoch), a third grating 120° away from those in the 2 preceding epochs was added (see Fig. 1C, black arrow enumerated 3) to form a triplaid that contained 3 grating and 3 plaids moving simultaneously in 6 different directions (see Fig. 1C). The grating, plaid and triplaid epochs followed one another with no gap and lasted 320, 320, and 1280 ms, respectively. Gratings were presented at 33% contrast with the optimal spatial and temporal frequency within a circular aperture confined to the cell's receptive field. Stimuli were presented in random order and were repeated 20–100 times for each cell.
Figure 1.
Visual stimulus. The stimulus consisted of 3 successive epochs, which were referred to as the Grating epoch (G), the Plaid epoch (P), and the Triplaid epoch (T), respectively (separated by vertical dashed lines). A, In the grating epoch, which lasted 320 ms, a single moving grating was presented. B, In the succeeding plaid epoch, which also lasted 320 ms, the addition of a second grating moving 120° away from the first grating created a moving plaid. C, In the triplaid epoch, which lasted 1280 ms, a third grating was added that moved 120° away from the other 2 gratings. The addition of the third grating created 2 additional plaids. Black and red arrows correspond to the component and patterns motions associated with gratings and plaids, respectively. Black arrows were enumerated by 1, 2, or 3 to signify the epoch in which the corresponding grating was first presented, and the red arrows labeled P correspond to the direction of pattern motion in the plaid epoch. Each triplaid could be created from 6 possible permutations of the order of the presentation of the 3 gratings. D–F, Configuration icons showing the 6 possible permutations associated with triplaid shown in C. For each permutation, D shows the grating presented in the grating epoch (black arrow, enumerated 1) along with the other 2 gratings that will follow in the subsequent epochs (gray arrows). E shows the second grating added in the plaid epoch (black arrow, enumerated 2), the plaid motion created from the superposition of the first and second grating (red arrow labeled P) and the third grating that will be presented in the third epoch (gray arrow). In F, the third and last grating (black arrow, enumerated 3) is presented to create the triplaid. Addition of the third grating, which moves opposite to the preceding plaid motion, creates 2 more plaids, which are shown by the additional red arrows.
Behavior.
In the awake-recording preparation, the animal was seated 57 cm in front of the display screen, while her eye movements were monitored using a scleral search coil (Judge et al., 1980). The stimulus was presented in a sequence of trials separated by a 500 ms intertrial interval. Each trial began with the presentation of a central white spot (diameter 0.2°) that the animal had to fixate. The grating–plaid–triplaid sequence was presented 320 ms after fixation. The animal was required to fixate the central spot throughout the presentation of the stimulus and maintain fixation for an additional 320 ms after stimulus offset to complete the trial and receive liquid reward. If the animal failed to fixate within 4 s of the appearance of the central spot, or broke fixation before the end of the trial (gaze shift of >1° away from fixation spot), the trial was aborted and no reward was delivered. The activity during the 320 ms of fixation before and after stimulus presentation was used to estimate each cell's baseline firing rate.
Data analysis.
We used responses in the first 2 epochs (grating and plaid) to compute a pattern index for each cell. The pattern index was computed as the difference between the Z-score of the partial correlation between cell's response to plaid stimuli and the idealized pattern and component predictions (Zp and Zc, respectively) as described previously (Smith et al., 2005; Rust et al., 2006). To take response latencies into account, we estimated firing rate in the first epoch from 70 ms after the onset of the first grating to 40 ms after the onset of the second grating. For the second epoch, because of the longer latencies associated with the development of pattern selectivity (Smith et al., 2005), we estimated average firing rates from 200 ms after the onset of the second grating to 40 ms after the onset of the third grating.
For each cell, we computed a measure of response modulation, which quantified response strength across different stimulus conditions and/or within different time bins divided by the firing rate associated with the grating moving in the preferred direction (see Fig. 5). Response modulation was also used to perform population analyses. Population analyses on cells with positive and negative Zpc were performed separately. Throughout the paper, we refer to cells with positive and negative Zpc as pattern direction-selective (PDS), and component direction-selective (CDS), respectively. For each group, we computed average PSTHs by smoothing each cell's response to each stimulus condition by a 60-ms-long Gaussian kernel (SD = 10 ms). The resulting PSTHs were then used to compare responses across stimulus conditions (see Figs. 3, 7) and to analyze direction-tuning dynamics (see Figs. 4, 6, 10). The analysis of direction tuning in the triplaid epoch (see Figs. 6, 10) was performed on three groups of cell, (1) cells with Zc significantly larger than Zp (Zpc < −1.28), (2) cells with Zp significantly larger than Zc (Zpc > 1.28), and (3) cells with no significant difference between Zp and Zc (−1.28 < Zpc < 1.28). The criterion value of 1.28 corresponds to p = 0.90.
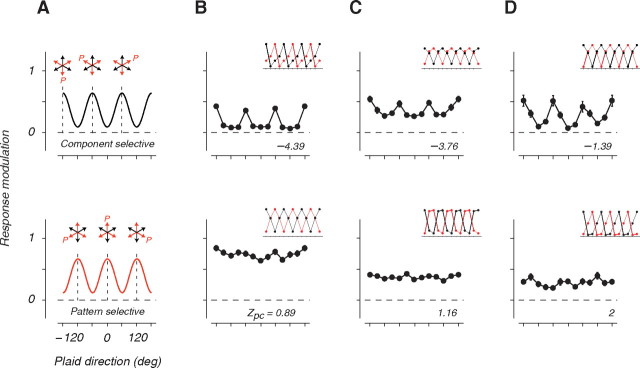
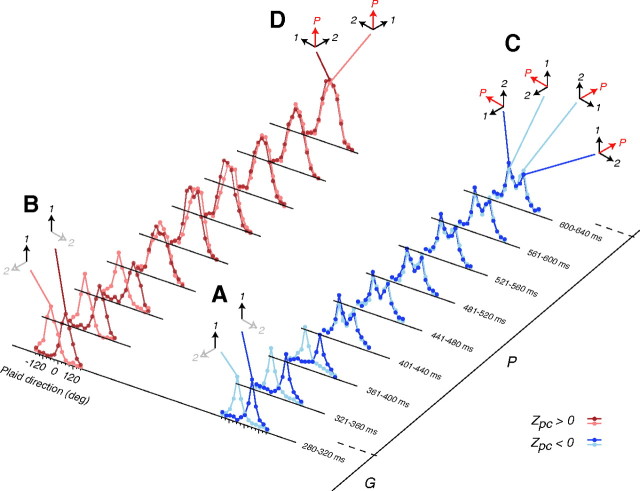
Figure 5.
Direction tuning of MT neurons for triplaid stimuli. A, Triplaid tuning functions for an ideal CDS (top) and an ideal PDS (bottom) neuron tuned for upward motion. To plot the tuning function, different triplaid configurations were ordered with respect to the direction pattern motion during the preceding plaid epoch (red arrow labeled P). By convention, 0° corresponds to the triplaid in which the pattern motion in the plaid epoch moves in the preferred direction (upward red arrow labeled P). The peaks of the ideal CDS tuning function (top, vertical dashed lines) correspond to the triplaid configurations that contain the preferred grating (upward black arrow). In contrast, the ideal PDS tuning function (bottom, vertical dashed lines) is tuned for triplaid configurations with the preferred pattern motion (upward red arrow). B–D, Triplaid tuning function (filled circle) ± SEM (error bars) for 3 randomly picked CDS cells (top) and 3 PDS cells (bottom) plotted with the same conventions as in A, with the value of the corresponding pattern index shown near the abscissa. Tuning functions were computed by normalizing average responses during the triplaid epoch by the response to the preferred grating (see Materials and Methods). The tuning functions for the 3 example CDS cells (B–D, top row) have peaks at −60, 60, and 180°, which correspond to triplaid configurations that contain an upward moving grating. The tuning functions for the 3 example PDS cells (B–D, bottom row), on the other hand, show little selectivity for the grating or plaid motion signals.
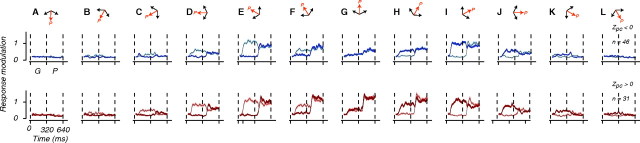
Figure 3.
MT response modulation during the transition from gratings to plaids. Different panels show average response modulation as a function of time during the grating (G) and plaid (P) epochs for different stimulus conditions, as shown by the corresponding configuration icon (black and red arrows) on top. We computed average response modulation (black trace) and SEs (shaded area) for CDS and PDS cells by normalizing each cell's response to each stimulus condition by the response to the preferred grating and averaging across cells in each group (see Materials and Methods). Results for CDS and PDS cells are shown in the top and bottom rows, respectively. The 2 traces in each panel show response modulations for the same plaid (red arrow labeled P) grouped by the order in which the 2 gratings were presented (Fig. 1D,E). By convention, the preferred direction of all the cells is represented by upward motion. Configuration icons (A–L) show the direction of motion of the gratings presented in the first two epochs (black arrows) and the direction of motion of the resulting plaid (red arrow). For example, E and I correspond to stimuli in which one of the gratings (black arrow) moved in the cells' preferred direction; G shows the condition in which the plaid (red arrow) moved in the cells' preferred direction. Early after the onset of the second grating, the responses depended on the order in which the 2 gratings were presented. This was particularly evident in cases in which one of the 2 gratings was drifting near the cells' preferred direction (E, I). Dashed vertical lines delimit the grating (G) and plaid (P) epochs.
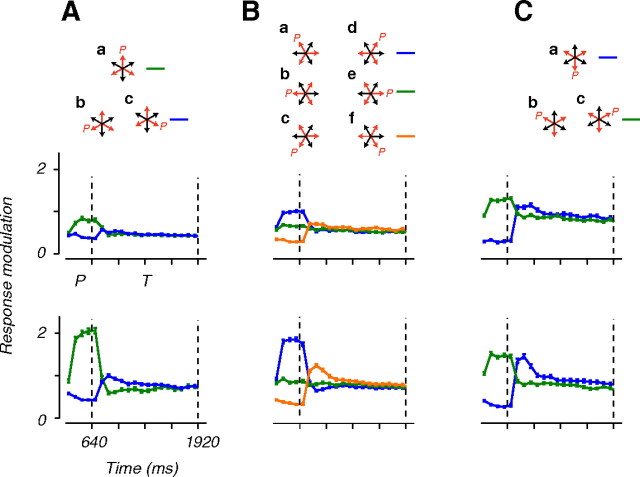
Figure 7.
Order effects in the response of MT neurons during the transition from plaids to triplaids. Top and bottom rows show average responses (mean ± SEM) from late in the plaid epoch (P) to the end of the triplaid epoch (T) for the CDS and PDS population, respectively. Average responses for the CDS and PDS cells were computed from responses of individual cells to each stimulus condition normalized by the response to the preferred grating (see Materials and Methods). To analyze the order effects, for each triplaid configuration, we compared average responses for groups of trials that were associated with different pattern motion in the plaid epoch. To improve our estimate of group PSTHs, we combined trials in which the direction of pattern motion were symmetric with respect to the preferred direction (upward, by convention). Aa–Ac, Responses associated with the triplaid configuration that contained an upward plaid motion (upward red arrow). Aa corresponds to the conditions in which the plaid motion was upward (upward red arrow labeled P), and Ab and Ac correspond to conditions in which the plaid motion moved 120° away from upward. To plot the results, we combined the Ab and Ac conditions because they correspond to conditions that are symmetric with respect to the preferred direction. Ba–Bf, Responses associated with 2 symmetric triplaid configurations, one containing plaids moving −30, −90 and −150° away from the preferred direction (Ba–Bc), and another with plaids moving 30, 90, and 150° away from the preferred direction (Bd–Bf). Again, responses to conditions that were symmetrical with respect to the preferred direction were analyzed together (Ba with Bd, Bb with Be, and Bc with Be). C, Responses associated with the triplaid that contained the preferred grating. Across different triplaid configurations, the order effect was relatively stronger in PDS cells, and lasted up to ∼1 s after the onset of the third grating. For CDS cells, on the other hand, the order effects were transitory and relatively short-lived. For configurations that contained the preferred grating (upward black arrow). PDS cells showed a strong order effect that persisted until the end of the triplaid epoch, 1280 ms after the plaid to triplaid transition. A weaker order effect was evident in CDS cells.
Figure 4.
Direction tuning dynamics during the transition from gratings to plaids. We analyzed the dynamics of direction selectivity for the CDS and PDS cells by computing average direction tuning in contiguous 40 ms time bins starting from the last 40 ms of the grating epoch (G) to the end of the plaid epoch (P). We first normalized each cell's tuning function in each bin by the average response to the preferred grating and then computed averages across CDS and PDS neurons separately (see Materials and Methods). We aligned the preferred direction of all cells before averaging so that the 0° would correspond to the plaid stimulus that moved in cell's preferred direction. Tuning functions for CDS and PDS cells are plotted in shades of blue and red, respectively. Configuration icons (A–D) show a few of the stimulus conditions. As shown by the configuration icons in A and B, during the grating epoch (G), before the second grating (gray arrow) was presented, the direction tuning functions have a single peak that corresponds to the upward moving grating (black arrow in A and B). During the plaid epoch (P), CDS cells develop a characteristic bimodal direction tuning with peaks associated with the 2 upward-moving gratings (black arrows in C). In contrast, PDS cells develop a single peak that corresponds to the pattern motion of the upward moving plaid (red arrow labeled P in D). The bright and the dark shades show the tuning function for the 2 different orders of presentation of the 2 gratings.
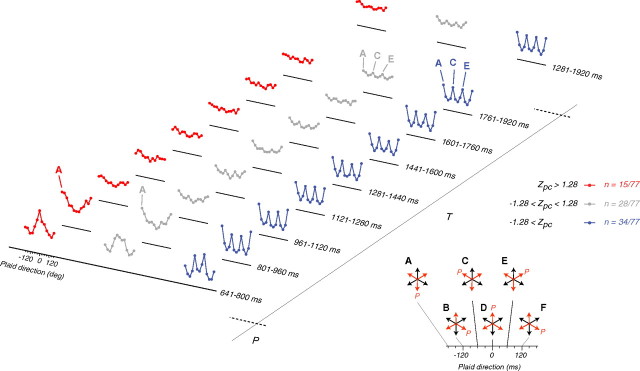
Figure 6.
Direction tuning dynamics of MT neurons for triplaid stimuli. Direction tuning functions were computed in contiguous 160 ms time bins during the triplaid epoch (T) across 3 groups of cells, cells that were strongly component selective (−1.28 > Zpc, red, n = 34), cells that were strongly pattern selective (Zpc > 1.28, blue, n = 15), and cells with intermediate pattern index (−1.28 < Zpc < 1.28, gray, n = 28). For each group and each bin, average tuning functions were computed from responses of individual neurons to different triplaid configurations normalized by the response to the preferred grating (see Materials and Methods). As shown by the figure key (A–F, black), the abscissa shows different triplaid configurations with respect to the direction of pattern motion in the plaid epoch (red arrow labeled P). For example, the configuration labeled D (at 0°) corresponds to the condition in which the pattern motion in the plaid epoch (red arrow labeled P) moved in the cells' preferred direction (upward, by convention). Strongly component-selective cells (blue) were tuned for the triplaid configuration that contained an upward moving grating (A, C, E, blue). The other 2 groups (red and gray) were initially tuned for pattern motion, but soon after the presentation of the third grating (801–960 ms), cells' responded most strongly to triplaids in which the third grating moved in the preferred direction (A, red and gray). Late in the triplaid epoch (1761–1920 ms), cells with intermediate pattern index values (gray) were more strongly activated by the triplaid configuration that contained the preferred grating (A–C, gray). The three top panels show the average tuning functions based on the second portion of the triplaid epoch (1281–1920 ms).
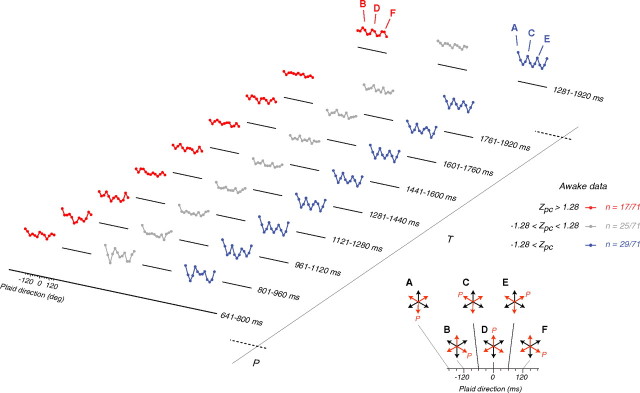
Figure 10.
Direction tuning dynamics of MT neurons for triplaid stimuli in the awake setup. The format of the figure and the corresponding labels (A–F) are similar to Figure 6.
We used the average time derivative of response modulations across cells and stimulus conditions to compare response transients between the awake and anesthetized recording conditions (see Fig. 11). We computed this in four steps: (1) determine the response modulation for each cell and stimulus condition; (2) smooth each response with a 60-ms-long Gaussian kernel (SD = 10 ms); (3) use a 1 ms finite difference approximation to estimate the time derivative; (4) average across individual cells and stimulus conditions to compare the overall strength and dynamics of transient responses between the 2 recording conditions (see Fig. 11).
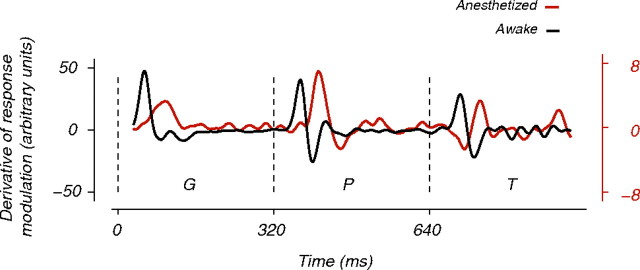
Figure 11.
MT response transients in the awake and anesthetized recording conditions. We quantified response transients throughout the stimulus presentation by the average time derivative of the response modulation across all cells and all stimulus conditions. We first computed the response modulation associated with each cell and each stimulus condition and then estimated the corresponding time derivative using a 1 ms finite difference approximation (see Materials and Methods). The average derivative of the response modulation for cells recorded in the awake and anesthetized recording conditions are plotted in black and red, respectively. The ordinate for the black and red traces are shown in the same colors and placed to the left and right of the abscissa, respectively. Dashed vertical lines delimit the grating (G), the plaid (P), and the triplaid (T) epochs.
To derive population direction tuning functions across cells in each group, for each cell, we assigned a direction of 0° to the pattern motion that moved in that cell's preferred direction. Consequently, the direction tuning for the grating in the first epoch was shifted to 60 or −60° depending on which of the 2 gratings in the plaid appeared first (see Figs. 2, 4, 8). Similarly, component direction selectivity in the triplaid stimuli was associated with response peaks at the −60, 60, and ±180°, and pattern direction selectivity was associated with peaks at −120, 0, and 120° (see Figs. 5, 6, 10).
Figure 2.
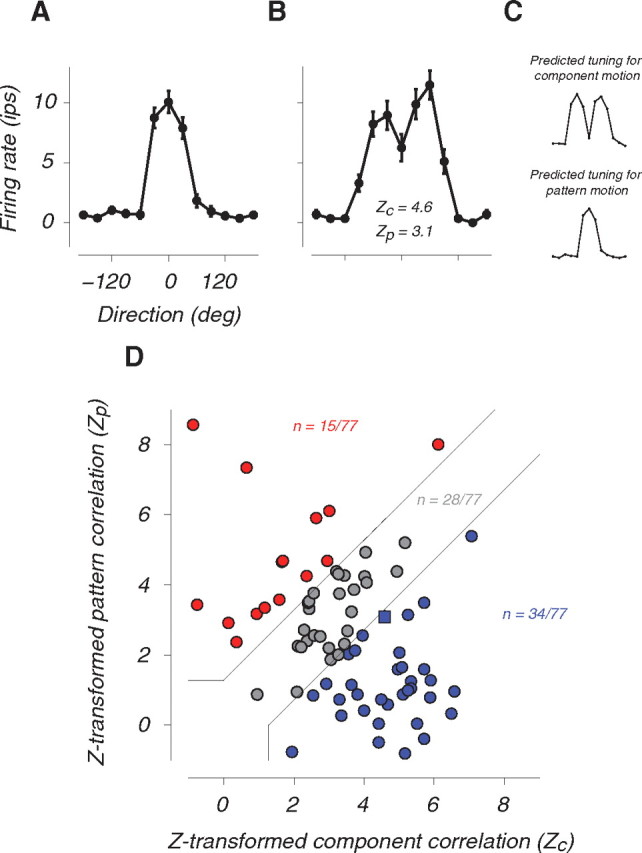
Direction selectivity of MT neurons for grating and plaid stimuli. A, Direction tuning for grating stimuli. Average firing rate (filled circle) ± SEM (error bars) as a function of direction of moving grating with respect to the preferred direction for an example MT cell in the first epoch. B, Direction tuning for the same neurons as in A as a function of the direction of pattern motion during the second epoch. C, Predictions for idealized component (top) and pattern (bottom) selectivity for the neuron shown in A and B. Component prediction is the linear sum of 2 grating tuning curves (after subtracting baseline firing rate), one shifted 60° clockwise and the other 60° counterclockwise with respect to the cell's preferred direction. Pattern prediction is the direction tuning measured for grating stimuli (first epoch). D, Degree of pattern versus component selectivity across MT neurons. To quantify component versus pattern selectivity, we computed the Z-score of the partial correlation between the actual response in the second epoch and the component and pattern predictions, which we denoted by Zc and Zp, respectively. For 34/77 cells, Zc was significantly larger than Zp (blue circles); for 15/77 cells Zp was significantly larger than Zc (red circles) and for the remaining 28/77, the difference between Zc and Zp was not significant (gray circles). The example in A and B is singled out by a blue square.
Figure 8.
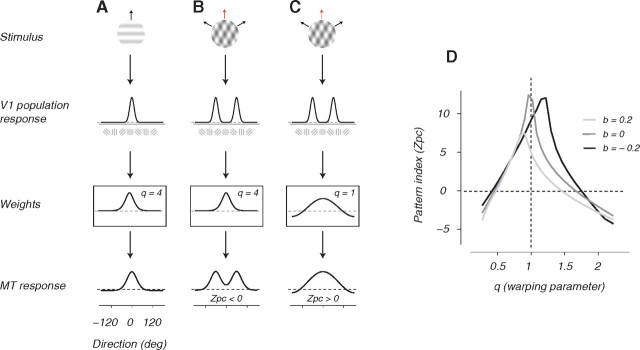
A model of MT direction selectivity. A, Presentation of a grating activates V1 direction-selective neurons. Normalized V1 responses (see Materials and Methods) are then combined linearly using a V1 to MT linear weighting function that confers direction selectivity on the recipient model MT neuron. The V1 to MT weighting function, which has both excitatory and inhibitory components, is characterized by a shape parameter, q, that controls the width of excitations compared with inhibition, and an offset parameter, b, that controls the mean drive (see Materials and Methods). B, C, Presentation of a plaid stimulus activates V1 neurons according to their preference for the plaid's constituent gratings. The MT direction tuning for plaid stimuli depends on the shape of the weighting function. When q = 1 (A), the weighting function is cosinusoidal (see Materials and Methods), and the MT neuron develops pattern direction selectivity (positive pattern index). Larger values of q (B) make the excitatory portion of the weighting function narrower, and make the MT neuron component direction selective (negative pattern index). D, Pattern index reaches its maximum positive value when q is close to 1 (vertical hashed line), and drops sharply for both larger and smaller values of q. The exact location of the maximum pattern index changes somewhat, depending on the value of b, as shown by the 3 different curves in black, dark gray and light gray.
Model.
We constructed a simplified model of direction selectivity based on a previous study that explained direction selectivity in area MT by a linear combination of normalized V1 direction-tuned signals (Rust et al., 2006). In our model, the stimulus activated a population of 360 V1 direction-tuned cells with evenly distributed direction preferences. The response of the ith V1 cell to a single moving grating, g1 was modeled by a von Mises function centered at the cell's preferred direction, θi (expressed in degrees), with a tuning bandwidth (at half-height) of ∼40° (corresponding to a von Mises k value of 10), which is consistent with the direction tuning of MT-projecting V1 cells (Movshon and Newsome, 1996). In our model, V1 tuning functions were scaled to a total area of 1.
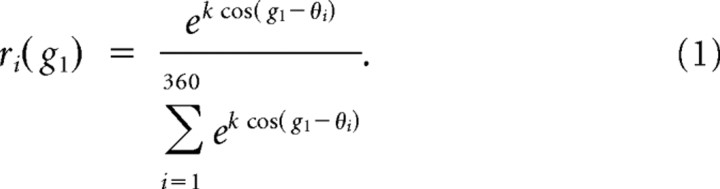 |
Each V1 cell's response to plaids made of 2 gratings, g1,2, and triplaids made of 3 gratings, g1,2,3 was modeled as the arithmetic sum of responses to the corresponding component gratings:
Linear responses determined by the von Mises tuning function were then squared and subjected to untuned and tuned normalization. Our formulation follows from Rust et al. (2006):
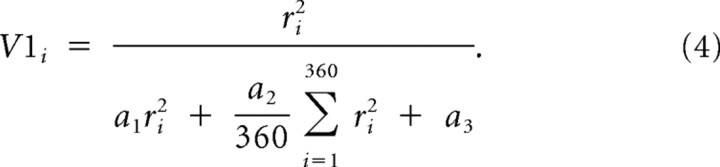 |
The response of a model MT neuron, MTj, tuned for direction θj (expressed in degrees), was then computed from a linear combination of V1 responses using weighting function wji:
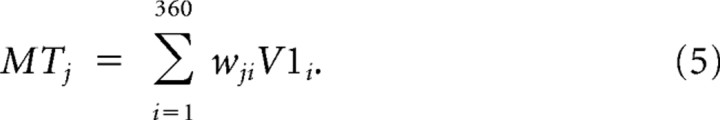 |
We formulated the weighting function as a warped cosinusoidal function and parameterized it with a shape parameter, q, and an offset parameter b:
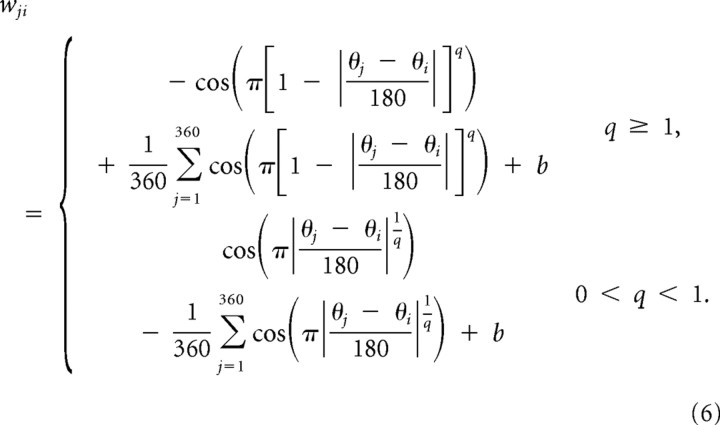 |
The shape parameter q controls the amount of warping with respect to the cosinusoidal function and the offset parameter b controls the mean of the weighting function. For q = 1, the weighting function is an exact cosine. Larger and smaller values of q broaden the relative negative and positive sides of the cosine function, respectively (see Figs. 8, 9).
Figure 9.
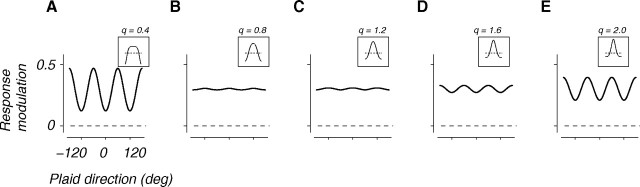
Model prediction for MT direction selectivity for triplaids stimuli. We used the model (Fig. 8A–C) to compute a response modulation index (same as Fig. 5) for MT direction tuning in response to triplaid stimuli using weighting functions with different values of q. For q values < 1 (A), MT responses to triplaid stimuli exhibit direction selectivity for the component gratings. As q gets close to 1, response modulation around mean becomes small with weak preference for the direction of the component gratings (B), or the component plaids (C). For larger values of q, once again, responses exhibit selectivity for the component gratings (D, E). Insets show the weighting function corresponding to the different q values. The horizontal dashed line shows when the weighting function crosses zero.
The normalization parameters, a1, a2, and a3, changed the response amplitude of MT neurons but had little effect on their tuning. The values we used for the simulations (see Figs. 8, 9) were a1 = 0.8, a2 = 0.2 and a3 = 0, which are consistent with the range reported previously (Rust et al., 2006).
Results
We recorded from 77 isolated units in area MT of 2 anesthetized monkeys, and 70 units in area MT of a single awake monkey. We first determined each cell's receptive field and its preferred spatial and temporal frequency for sinusoidal gratings drifting in the cell's preferred direction of motion, and then measured its response to gratings, plaids and triplaids constructed from these optimal stimulation parameters.
The stimulus in the main experiment consisted of a sequence of 3 uninterrupted epochs in which a succession of 3 superimposed gratings moving 120° apart was presented (Fig. 1A–C). In the first epoch, the first drifting grating was presented (Fig. 1A, black arrow enumerated 1). In the second epoch, a second drifting grating whose direction was 120° away from the first grating was added to the stimulus (Fig. 1B, black arrow enumerated 2). The 2 drifting gratings created 3 motion signals, 2 associated with the 2 drifting gratings and a third that was created from the coherent motion of the resulting plaid (Fig. 1B, red arrow labeled P). In the third epoch, the stimulus was superimposed by a third drifting grating whose direction was 120° away from the other 2 gratings (Fig. 1C, black arrow enumerated 3). The addition of a third grating created a triplaid with 6 simultaneous motion signals, 3 from the constituent drifting gratings and another 3 from the plaids created by pairs of gratings (Fig. 1C). For example, in the sequence shown in Figure 1A–C, the first grating moves down and to the right (Fig. 1A). The second grating moves up and to the right, and together with the first grating, creates a plaid with a rightward motion (Fig. 1B). The third grating moves leftward exactly opposite to the direction of the plaid motion, and together with the other 2 gratings creates 2 additional plaid motions, one moving up and to the left and another moving down and to the left (Fig. 1C).
Any triplaid could be created from 6 possible permutations of the order of the presentation of the 3 constituent gratings. Figure 1D–F shows the 6 permutations that correspond to the triplaid configuration shown in Figure 1C. The first row is the exact same sequence shown in Figure 1A–C; the second row is a sequence in which the order of presentation of the first 2 grating is reversed; the third to sixth rows show the remaining possible permutations that create the same triplaid. In all panels, black arrows correspond to the direction of motion of gratings already presented, and gray arrows mark the directions of gratings that will be shown in subsequent epochs.
The sequential design of the stimulus and the large number of conditions tested make the presentations of the results challenging. We will refer to the first, second and third epochs of the stimulus as the grating epoch (G), plaid epoch (P), and triplaid epoch (T), respectively (Fig. 1). Moreover, we will use the configuration icons shown in Figure 1 to refer to different stimulus conditions throughout the manuscript. In each icon, the black and red arrows mark the direction of component (grating) and pattern (plaid) motions, respectively. The number associated with the black arrows (1, 2, or 3) signify the epoch in which the corresponding grating was first presented, and the red arrow with the label P shows the direction of pattern motion in the plaid epoch.
MT responses to gratings and plaids
We used the responses during the first 2 epochs (gratings then plaids) to measure each cell's direction tuning for gratings (Fig. 2A) and plaids (Fig. 2B) and to characterize its pattern motion selectivity. An ideal PDS cell has identical direction tuning for gratings and plaids (Fig. 2C, bottom); an ideal CDS cell's response to plaids, however, is simply the sum of the response to its constituent gratings (Fig. 2C, top). We evaluated pattern selectivity by computing Z-scores for the correlation between the observed plaid tuning and those predicted from an ideal pattern- and component-selective response, Zp and Zc, respectively (Smith et al., 2005). Figure 2D shows Zp versus Zc across our dataset. As in previous reports (Rodman and Albright, 1989; Rust et al., 2006), the distribution of Z-scores in our MT population formed a continuum between significantly component selective (Fig. 2D, blue) to cells with significant pattern selectivity (Fig. 2D, red). We quantified the degree of pattern selectivity by the difference between Zp and Zc. We will refer to this measure as the pattern index and will denote it by Zpc. Throughout the paper cells with positive and negative Zpc will be referred to as PDS and CDS, respectively.
We recorded the responses of each cell to 12 evenly spaced directions for both gratings and plaids. Figure 3 shows normalized averages of MT responses during the grating and plaid epochs. The top and bottom panels with traces in shades of blue and red show average responses across the CDS and PDS cells, respectively. Before averaging, we rotated stimulus conditions and the corresponding responses such that every cell's preferred direction (based on responses in the grating epoch) was aligned to upward motion. The 2 traces in each panel correspond to the 2 possible orderings of the plaid's 2 gratings.
As expected, the CDS neurons (top) were most responsive when one of the gratings moved in the cells' preferred direction (Fig. 3E,I, top), but not so much when the pattern motion moved in the preferred direction (Fig. 3G, top). The PDS neurons (bottom), on the other hand, were strongly modulated when the pattern motion in the plaid epoch (red arrow labeled P) was in the neurons' preferred direction (Fig. 3G, bottom). PDS cells also responded strongly to the preferred grating in the grating epoch (Fig. 3E,I, bottom).
To characterize the response dynamics, we measured the direction tuning of our population at different time bins during the transition from grating to plaid epoch (Fig. 4). We plotted the stimuli such that 0° corresponded to the plaid moving in the cells' preferred direction (upward by convention). As evident by the peaks of the tuning function at −60 and 60°, near the end of the grating epoch, both the CDS and PDS neurons responded maximally to the preferred grating (Fig. 4A,B). After the onset of the second grating, the CDS cells developed a characteristic bimodal plaid tuning and maintained their tuning throughout the second epoch (Fig. 4, blue). The peak response near the end of the plaid epoch corresponded to plaids that contained the preferred grating (Fig. 4C). The PDS cells, on the other hand, were tuned for pattern motion (Fig. 4, red), as evidenced by the peak response to the pattern motion moving in the preferred direction (Fig. 4D). Responses near the end of the plaid epoch did not depend on the order of presentation of the 2 gratings (Fig. 4C,D).
MT responses to triplaids
Previous work on plaids suggests that CDS cells respond selectively to grating motion even when they are presented with two superimposed gratings. Accordingly, we hypothesized that the tuning function of a CDS cell for triplaid stimuli will have three peaks that correspond to conditions in which one of the 3 gratings move in the cells' preferred direction (Fig. 5A, top). In contrast, PDS direction tuning for plaids is characterized by a preference for the pattern motion with no peaks associated with the motion of the two constituent gratings. By extension, we hypothesized that the tuning function of PDS cells for triplaid stimuli will have 3 peaks that correspond to the conditions in which one of the 3 plaids move in the cells' preferred direction (Fig. 5A, bottom).
To formalize these hypotheses, we used each cell's direction tuning in the grating epoch to generate predictions for the shape of the tuning function in response to triplaids. For an ideal CDS cell, the tuning should be the sum of the three tuning functions associated with the three gratings in the triplaid. For an ideal PDS cell, on the other hand, the peak responses should correspond to the three pattern motions in the triplaid.
We tested these predictions against the observed tuning functions during the triplaid epoch of individual CDS and PDS cells, ranging from strongly component direction selective (large negative Zpc) to strongly pattern direction selective (large positive Zpc). Figure 5B–D shows 6 sample neurons from our data, 3 from the CDS population (Fig. 5B–D, top; Zpc < 0), and 3 from the PDS population (Fig. 5B–D, bottom; Zpc > 0). In each panel, the inset shows the tuning of the corresponding ideal CDS and PDS cell in black and red, respectively.
As predicted, CDS cells continued to selectively respond to component motions in the triplaid stimuli and had their peak responses to the preferred gratings (Fig. 5B–D, top). PDS cells, in contrast to our prediction, did not continue to signal pattern motion; instead, their tuning functions became nearly flat with little selectivity for any of the component or pattern motions in the triplaid (Fig. 5B–D, bottom).
To analyze direction selectivity across our population of cells and across time, we examined the dynamics of direction tuning across 3 groups of cells, strongly component-selective cells (Fig. 2B, blue, Zpc < −1.28, n = 34/77), strongly pattern-selective cells (Fig. 2B, red, Zpc > 1.28, n = 15/77), and cells with intermediate pattern index (Fig. 2B, gray, −1.28 < Zpc < 1.28, n = 28/77). For each group, we normalized responses of each cell (see Materials and Methods) and computed average direction tuning functions from nonoverlapping 160 ms bins throughout the triplaid epoch (Fig. 6). As shown by the configuration icons in Figure 6 (A–F, black letters), triplaids along the abscissa were ordered with respect to the direction of pattern motion in the plaid epoch (red arrow labeled P) with upward representing preferred direction. For example, 0° corresponds to the triplaid that was preceded by the upward moving plaid (Fig. 6D, upward red arrow labeled P), and −180° corresponds to the triplaid with an upward moving grating (Fig. 6A, upward black arrow). Because of the circular symmetry of triplaids, the configurations that are 120° apart contain the same combination of component and pattern motions (Fig. 6A,C,E). What differentiates these similar configurations is the direction of pattern motion in the preceding plaid epoch (red arrow labeled P).
Consistent with our observation in the three example neurons (Fig. 5B–D), direction tuning in the triplaid epoch depended on the degree of pattern selectivity. For strongly component direction-selective cells, the maximum response modulation was associated with the preferred grating (Fig. 6, blue traces) as indicated by the peaks at −180, −60 and 60° (Fig. 6, blue A,C,E). This was true both at different time bins as well as for the average tuning across the second part of the triplaid epoch (1281–1920 ms) after the initial transient (Fig. 6, top, blue trace). In contrast, the direction tuning of the strongly pattern direction-selective neurons was not stable and exhibited no consistent tuning (Fig. 6, red traces). For these cells, the strongest response at the 801–960 ms time bin was to the triplaid configuration that included the preferred grating (Fig. 6, red A). The average tuning curve after the initial transient responses (1281–1920 ms), however, was nearly flat (Fig. 6, top, red trace). Cells with intermediate pattern index also had reduced response selectivity (Fig. 6, gray). After the initial transient, the average tuning function in these cells exhibited a weak preference for the configurations with an upward-moving grating (Fig. 6, top, gray trace).
History dependence of MT responses
We exploited the sequential nature of our stimulus design to ask whether MT responses were influenced by the order in which the 3 gratings were presented, a property that we refer to as the “order-effect.” We analyzed order-effects both during the grating to plaid transition and during the plaid to triplaid condition. Our analysis of responses during the grating to plaid transition showed that, early in that epoch, response depended on the order in which the first 2 gratings were presented (Figs. 3, 4). This order-effect, however, diminished rapidly and responses were not significantly different by the time the third grating was presented (p > 0.05). Therefore, for the plaid to triplaid transition, we analyzed order effects regardless of the order of presentation of the first 2 gratings. Specifically, we asked whether responses to a given triplaid configuration depended on the direction of the pattern motion in the preceding plaid epoch (Fig. 7, red arrow labeled P).
Figure 7A corresponds to the triplaid configuration that contained a plaid moving in the cells' preferred direction (upward, by convention). Three possible plaids could have preceded this triplaid configuration (Fig. 7Aa–Ac). In one of these conditions, the preceding plaid moved in the cells' preferred direction (Fig. 7Aa), and in the two other conditions, the preceding plaid moved either 120 or −120° away from the preferred direction (Fig. 7Aa,Ab). We exploited the symmetry of the two latter conditions with respect to the preferred direction and combined their responses to improve the statistical power of our analysis. For the CDS cells, shortly after the triplaid epoch, responses did not depend on whether the preceding plaid moved in the preferred direction (Fig. 7A, top, green), or 120° away from it (Fig. 7A, top, blue). For PDS cells, on the other hand, the marked difference between the corresponding PSTHs (Fig. 7A, bottom) created a strong order effect that lasted for a few hundred milliseconds.
Figure 7B corresponds to 2 other triplaid configurations, one containing plaids moving −30, −90, and −150° away from the preferred direction (Fig. 7Ba–Bc), and another with plaids moving 30, 90, and 150° away from the preferred direction (Fig. 7Bd–Bf). Similar to Figure 7A, we combined responses for conditions that were symmetrical with respect to the preferred direction (Fig. 7B). As evidenced by the comparison of response dynamics in Figure 7B, order effect were stronger for PDS cells (Fig. 7B, bottom) than for CDS cells (Fig. 7B, top). Finally, we examined responses to the triplaid configuration that contained the preferred grating (Fig. 7C), and, again, found that order effects were stronger for PDS cells (Fig. 7C, bottom) than for CDS cells (Fig. 7C, top).
Relationship between selectivity for plaids and triplaids
To examine whether the weak tuning of PDS cells for motion signals in the triplaid stimulus was related to their selectivity for pattern motion in plaid stimuli, we constructed a simple linear model of MT (Fig. 8A–C) based on a more elaborate linear-nonlinear cascade model that captures the range of pattern motion selectivity observed across MT cells (Rust et al., 2006). The first stage of the model was an array of V1 direction-selective neurons whose responses had undergone both untuned (Geisler and Albrecht, 1992; Heeger, 1992; Carandini et al., 1997) and tuned (Sceniak et al., 2001; Cavanaugh et al., 2002a,b; Ringach et al., 2003) normalization. These V1 responses were then combined using a smooth linear weighting with both excitatory and inhibitory components to determine the input to a model MT neuron. The weighting function was parameterized by a shape parameter, q, which controls the width of excitation compared with inhibition, and an offset parameter, b, which controls the overall excitatory drive. In our formulation, when q = 1 the weighting function is a cosine function (see Materials and Methods) whose baseline is determined by the b parameter. Larger values of q make the excitatory portion of the profile narrower and smaller values make it broader.
In this model, the response of an MT neuron to gratings and plaids is derived from pooling V1 responses with a suitable weighting function (Fig. 8A–C). When the weighting function has a relatively narrow excitatory lobe (Fig. 8A,B), the corresponding MT responses become component direction selective (Fig. 8B). In contrast, a cosine pooling weighting function (q = 1) with broad excitatory and inhibitory lobes makes the resulting MT model neuron pattern direction selective (Fig. 8C). More generally, Zpc is largest when q is close to 1 and drops for both larger and smaller values of q for a range of values of the offset parameter (Fig. 8D). This result indicated that a cosine-like weighting function played an important role in conferring MT cells with pattern motion selectivity.
We examined whether this model could account for the different tuning properties of the CDS and PDS neurons to triplaid stimuli. Somewhat surprisingly, we found that for q values close to 1 (near-cosine weighting function) cells lost the strong tuning for pattern and component motion signals in the triplaid stimulus (Fig. 9B,C). As q was made progressively larger or smaller, the tuning function became CDS-like and developed strong peaks for the 3 moving gratings (Fig. 9A,D,E). That is, the same pooling profile that confers pattern motion selectivity on PDS neurons seems to be the key factor in explaining their reduced selectivity to triplaid stimuli.
MT responses to triplaids in awake, fixating monkey
To ensure that our observations with respect to MT responses to triplaid stimuli were not specific to recordings in anesthetized monkeys, we repeated our analyses in 70 MT cells recorded in one awake behaving monkey trained to perform a fixation task. Responses were generally similar across the 2 recording conditions. The distributions of Zpc were roughly comparable (positive for 31/77 and 28/70 of cells in anesthetized and awake, respectively).
Responses to the triplaid stimuli were also similar in the 2 recording conditions. Strongly component-selective neurons (Fig. 10, blue) were tuned for triplaids configurations that contained an upward moving grating (Fig. 10A,C,E). Strongly pattern-selective neurons (Fig. 10, red) had a more variable tuning function with an overall weak selectivity for pattern motion (Fig. 10B,D,F). Cells with intermediate pattern index also had reduced response selectivity (Fig. 10, gray). These observations were in good agreement with the tuning dynamics of MT cells recorded under anesthesia (Fig. 6). The only notable differences between the 2 recording conditions were that responses in the awake monkey had shorter in latency, and were more transient than in the anesthetized monkey. This is evident from a comparison of responses early during the triplaid epoch. In the anesthetized setup, tuning function derived from the first 320 ms after the onset of the third grating (Fig. 6; 641–800 ms time-bin) was largely characterized by the plaid stimulus. In the awake setup, in contrast, response modulations in the same time bin, response modulations were rapidly diminished by the addition of the third grating (Fig. 10; 641–800 ms time-bin). This sluggishness of the responses in the anesthetized data was evident during all transitions in the stimulus (Fig. 11).
Discussion
To learn whether component and pattern direction selectivity in area MT are invariant to the presence of other motion signals, we measured MT responses to triplaid stimuli, which contain 3 component and 3 pattern motions simultaneously. We found that, unlike component selectivity, pattern selectivity is highly susceptible to the presence of other competing motion signals. We explained this reduced selectivity by an MT model in which pattern selectivity emerged from integrating V1 direction-selective signals with a near-cosine weighting function.
Our stimulus consisted of 3 successive epochs going from a single grating to a plaid to a triplaid (Fig. 1A–C). We used responses during the first 2 epochs to characterize cells as CDS or PDS (Fig. 2), and then used responses during the triplaid epoch to assess whether these characterizations were robust when the stimulus contained other competing motion signals. The direction tuning of the CDS cells during the triplaid epoch had 3 peaks that corresponded to the 3 constituent gratings (Fig. 5B–D, top). This result is compatible with the behavior of an ideal CDS cell that maintains its selectivity for component motion even in the presence of other motion signals (Fig. 5B–D, top, black inset). The same logic however, failed to predict the behavior of the PDS cells. The triplaid tuning function for PDS cells did not have clear peaks for the 3 pattern motions; instead, tuning functions became nearly flat with no strong preference for either the component or pattern motion signals (Fig. 5B–D, bottom). A flat tuning is incompatible with predictions based on the behavior of either an ideal CDS or an ideal PDS cell (Fig. 5B–D, bottom, inset). These findings indicate that pattern selectivity, unlike component selectivity, is not robust in the presence of other motion signals. Pattern selectivity in MT is thought to depend, in part, on the presence of a strong opponent mechanism (Rust et al., 2006). The reason why PDS cells do not respond to the preferred plaid in the triplaid stimulus might be due to the activation of this opponent mechanism by the third grating that moves opposite to the preferred plaid.
To ensure that the reduced selectivity of PDS neurons was not a consequence of recording under anesthesia, we repeated our experiment in an awake, fixating monkey. We found that the behavior of MT neurons was generally similar across recording conditions (Movshon et al., 1985; Stoner and Albright, 1992b). Most importantly, the PDS neurons in the awake monkey were also highly sensitive to the presence of other motion signals such that the response modulation during the triplaid epoch was sharply weakened (Fig. 10). The only reliable difference between the 2 recording conditions was that, under anesthesia, transient responses evoked by changes in the stimulus were weaker and slower (Fig. 11). This sluggishness may be due to the effect of anesthesia on subcortical visual processing (Alitto et al., 2011).
We used a model of MT to understand the circuit mechanisms that produced the CDS and PDS tuning properties during the triplaid epoch. Previously, it was shown that an MT cell that receives excitatory input from a broad range of direction-selective V1 neurons, and also received broad inhibitory signal from V1 cells preferring opposite directions would exhibit pattern direction selectivity (Rust et al., 2006). Motivated by this finding, we developed a simplified model in which MT cells pooled V1 responses with a weighting profile that had both positive and negative lobes (Fig. 8). We formulated the weighting profile based on a cosine function, which we could warp parametrically to adjust the relative width of the excitatory and inhibitory lobes (Fig. 9, insets). In simulations, we found that Pattern direction selectivity was critically dependent on the balance between the excitatory and inhibitory lobes of the weighting function. In our formulation, this balance meant that the weighting function had to be nearly a cosine function. Deviations from this profile by increasing the extent of either the excitation or the inhibition caused the responses to lose pattern selectivity and become CDS-like (Fig. 8D).
Remarkably, the same balance of excitation and inhibition predicted the tuning function for the triplaid stimulus. When the weighting function deviated from a cosine function, tuning functions had 3 peaks that corresponded to the component motion signals in the triplaid, similar to the CDS population in our data (Fig. 9A,D,E). However, a near-cosine weighting function—which is what our simulations deemed necessary for pattern selectivity—strongly reduced the selectivity of model MT neurons for component and pattern motion in the triplaid stimuli (Fig. 9B,C), and mimicked the behavior of our PDS population. This reduced selectivity may be related to the balance that the near-cosine weighting function creates between excitation and inhibition of responses by oppositely moving plaids and gratings. These results suggest that the motion opponency that is thought to be important for pattern selectivity (Rust et al., 2006) may be a key factor behind the flattening of direction tuning for triplaids.
We exploited the sequential design of our stimulus to ask whether MT responses depend on the order with which different motion signals are presented. We found a transient effect of the order of the presentation of the first 2 gratings in the responses during the plaid epoch (Fig. 3, 4). When the order of presentation was such that the first grating evoked a relatively stronger response in the first epoch, the response in the ensuing plaid epoch was generally weaker. This effect however, was short-lived and was extinguished by the end of the plaid epoch. This finding is consistent with fast adaptation reported in early visual cortex (Müller et al., 1999).
We also found an order effect in the responses of MT neurons after the onset of the third grating in the triplaid epoch. The general pattern of this effect was consistent with a response adaptation in that, high firing rates were followed by relatively lower excitability and vice versa (Fig. 7). One unexpected aspect of this result was that the order effect in the PDS cells was more pronounced and longer lasting than the CDS cells. This observation suggests that PDS cells are subject to adaptation mechanisms that operate on a longer time scale than those that influence CDS cells.
One remarkable feature of triplaids is that they are perceptually multistable (Movie 1). To establish a direct link between percept and neural substrate, one would need to record from neurons while obtaining a simultaneous report of the percept, which we have not done. Therefore, we can only speculate about the role of MT responses in triplaid perception. Converging evidence from the analysis of MT responses to gratings and plaids suggest that the peak of the PDS population activity corresponds to the perceived direction of both component and pattern motion. For two reasons, we think that PDS cells might also play a role in the perception of triplaids. First, because PDS responses to triplaids are nearly untuned (Fig. 5), small fluctuations could change the location of the peak (Fig. 6, 10) and the corresponding perceptual state. Second, the order-effects during the plaid to triplaid transition (Fig. 7) suggest that PDS cells are subject to slow adaptive mechanisms that have long been associated with perceptual multistability (Blake et al., 1990; Suzuki and Grabowecky, 2002). More sophisticated psychophysical paradigms like those used in the study of binocular rivalry in monkeys (Logothetis and Schall, 1989; Leopold and Logothetis, 1996) could establish a more direct link between the activity of PDS neurons and the perceptual state they support. But this link might be imperfect, because the subjective percept of direction of motion may not be derived from MT responses alone (Williams et al., 2003; Jazayeri and Movshon, 2007). We have noticed that multiple simultaneously presented triplaids tend to adopt the same perceptual state, even when they are widely separated in the visual field, or in opposite hemifields. It seems unlikely that the individual MT responses with far apart receptive fields would interact directly to harmonize percepts. Multistability therefore may emerge from the action of a larger network of neurons in the visual cortex (Logothetis and Schall, 1989).
Models that seek to characterize the mechanisms of pattern selectivity often neglect the fact that afferent signals from which an MT cell derives its response properties are highly variable (Rust et al., 2006). As such, it is conceivable that the transformation of signals from V1 to MT has to satisfy multiple constraints (Born and Bradley, 2005). On the one hand, it is desirable to produce pattern selectivity so that coherent motion can be perceived, and on the other, the pooling strategy must recode signals so as to reduce uncertainty (Jazayeri, 2008). For example, opponent suppression (Majaj et al., 2007), which is thought to be critical for pattern selectivity (Rust et al., 2006), is also thought to play an important role in filtering noise (Snowden et al., 1991; Qian and Andersen, 1994; Qian et al., 1994). Similarly, pooling V1 afferents with a suitable weighting function is both important for computing pattern motion (Simoncelli and Heeger, 1998; Rust et al., 2006) and for reducing variability (Sanger, 2003; Jazayeri and Movshon, 2006; Graf et al., 2011). Interestingly, the near-cosine weighting profile that we suggest is important for pattern selectivity is also a particularly efficient pooling strategy for reducing variability of signals carried by direction-selective cells in both MT and V1 (Jazayeri and Movshon, 2006; Graf et al., 2011). We speculate that pooling signals with a cosine weighting profile may be how raw direction-selective signals are transformed to representations of perceived direction of motion. It remains to be seen how such pooling could be realized at the level of circuits and synapses in extrastriate cortex.
Footnotes
The authors declare no competing financial interests.
This work was supported by research Grants EY02017, EY04440 and F32-EY019833 from the NIH. We thank Nicole Rust, Adam Kohn, Arnulf Graf and Michael Gorman for their help with recording preparation. Requests for materials should be addressed to J.A.M. (E-mail: movshon@nyu.edu).
References
- Adelson EH, Movshon JA. ACM Siggraph and Sigart interdisciplinary workshop on motion: representation and perception. Toronto, Ontario, Canada: 1983. The perception of coherent motion in two-dimensional patterns; pp. 11–16. [Google Scholar]
- Albright TD. Direction and orientation selectivity of neurons in visual area MT of the macaque. J Neurophysiol. 1984;52:1106–1130. doi: 10.1152/jn.1984.52.6.1106. [DOI] [PubMed] [Google Scholar]
- Alitto HJ, Moore BD, 4th, Rathbun DL, Usrey WM. A comparison of visual responses in the lateral geniculate nucleus of alert and anaesthetized macaque monkeys. J Physiol. 2011;589:87–99. doi: 10.1113/jphysiol.2010.190538. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andrews TJ, Schluppeck D. Ambiguity in the perception of moving stimuli is resolved in favour of the cardinal axes. Vision Res. 2000;40:3485–3493. doi: 10.1016/s0042-6989(00)00188-7. [DOI] [PubMed] [Google Scholar]
- Blake R, Westendorf D, Fox R. Temporal perturbations of binocular rivalry. Percept Psychophys. 1990;48:593–602. doi: 10.3758/bf03211605. [DOI] [PubMed] [Google Scholar]
- Born RT, Bradley DC. Structure and function of visual area MT. Annu Rev Neurosci. 2005;28:157–189. doi: 10.1146/annurev.neuro.26.041002.131052. [DOI] [PubMed] [Google Scholar]
- Carandini M, Heeger DJ, Movshon JA. Linearity and normalization in simple cells of the macaque primary visual cortex. J Neurosci. 1997;17:8621–8644. doi: 10.1523/JNEUROSCI.17-21-08621.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cavanaugh JR, Bair W, Movshon JA. Selectivity and spatial distribution of signals from the receptive field surround in macaque V1 neurons. J Neurophysiol. 2002a;88:2547–2556. doi: 10.1152/jn.00693.2001. [DOI] [PubMed] [Google Scholar]
- Cavanaugh JR, Bair W, Movshon JA. Nature and interaction of signals from the receptive field center and surround in macaque V1 neurons. J Neurophysiol. 2002b;88:2530–2546. doi: 10.1152/jn.00692.2001. [DOI] [PubMed] [Google Scholar]
- Chukoskie L, Movshon JA. Modulation of visual signals in macaque MT and MST neurons during pursuit eye movement. J Neurophysiol. 2009;102:3225–3233. doi: 10.1152/jn.90692.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DeAngelis GC, Ohzawa I, Freeman RD. Spatiotemporal organization of simple-cell receptive fields in the cat's striate cortex. II. Linearity of temporal and spatial summation. J Neurophysiol. 1993;69:1118–1135. doi: 10.1152/jn.1993.69.4.1118. [DOI] [PubMed] [Google Scholar]
- Emerson RC, Bergen JR, Adelson EH. Directionally selective complex cells and the computation of motion energy in cat visual cortex. Vision Res. 1992;32:203–218. doi: 10.1016/0042-6989(92)90130-b. [DOI] [PubMed] [Google Scholar]
- Geisler WS, Albrecht DG. Cortical neurons: isolation of contrast gain control. Vision Res. 1992;32:1409–1410. doi: 10.1016/0042-6989(92)90196-p. [DOI] [PubMed] [Google Scholar]
- Graf AB, Kohn A, Jazayeri M, Movshon JA. Decoding the activity of neuronal populations in macaque primary visual cortex. Nat Neurosci. 2011;14:239–245. doi: 10.1038/nn.2733. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heeger DJ. Normalization of cell responses in cat striate cortex. Vis Neurosci. 1992;9:181–197. doi: 10.1017/s0952523800009640. [DOI] [PubMed] [Google Scholar]
- Hubel DH, Wiesel TN. Receptive fields, binocular interaction and functional architecture in the cat's visual cortex. J Physiol. 1962;160:106–154. doi: 10.1113/jphysiol.1962.sp006837. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jazayeri M. Probabilistic sensory recoding. Curr Opin Neurobiol. 2008;18:431–437. doi: 10.1016/j.conb.2008.09.004. [DOI] [PubMed] [Google Scholar]
- Jazayeri M, Movshon JA. Optimal representation of sensory information by neural populations. Nat Neurosci. 2006;9:690–696. doi: 10.1038/nn1691. [DOI] [PubMed] [Google Scholar]
- Jazayeri M, Movshon JA. A new perceptual illusion reveals mechanisms of sensory decoding. Nature. 2007;446:912–915. doi: 10.1038/nature05739. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Judge SJ, Richmond BJ, Chu FC. Implantation of magnetic search coils for measurement of eye position: an improved method. Vision Res. 1980;20:535–538. doi: 10.1016/0042-6989(80)90128-5. [DOI] [PubMed] [Google Scholar]
- Leopold DA, Logothetis NK. Activity changes in early visual cortex reflect monkeys' percepts during binocular rivalry. Nature. 1996;379:549–553. doi: 10.1038/379549a0. [DOI] [PubMed] [Google Scholar]
- Logothetis NK, Schall JD. Neuronal correlates of subjective visual perception. Science. 1989;245:761–763. doi: 10.1126/science.2772635. [DOI] [PubMed] [Google Scholar]
- Majaj NJ, Carandini M, Movshon JA. Motion integration by neurons in macaque MT is local, not global. J Neurosci. 2007;27:366–370. doi: 10.1523/JNEUROSCI.3183-06.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Movshon JA, Newsome WT. Visual response properties of striate cortical neurons projecting to area MT in macaque monkeys. J Neurosci. 1996;16:7733–7741. doi: 10.1523/JNEUROSCI.16-23-07733.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Movshon JA, Adelson EH, Gizzi MS, Newsome WT. The analysis of moving visual patterns. In: Chagas C, Gattass R, Gross C, editors. Pattern recognition mechanisms. Rome: Vatican; 1985. (Pontificiae Academiae Scientiarum Scripta Varia 54, 117–151) [Google Scholar]
- Müller JR, Metha AB, Krauskopf J, Lennie P. Rapid adaptation in visual cortex to the structure of images. Science. 1999;285:1405–1408. doi: 10.1126/science.285.5432.1405. [DOI] [PubMed] [Google Scholar]
- Priebe NJ, Cassanello CR, Lisberger SG. The neural representation of speed in macaque area MT/V5. J Neurosci. 2003;23:5650–5661. doi: 10.1523/JNEUROSCI.23-13-05650.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qian N, Andersen RA. Transparent motion perception as detection of unbalanced motion signals. II. Physiology. J Neurosci. 1994;14:7367–7380. doi: 10.1523/JNEUROSCI.14-12-07367.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qian N, Andersen RA, Adelson EH. Transparent motion perception as detection of unbalanced motion signals. III. Modeling. J Neurosci. 1994;14:7381–7392. doi: 10.1523/JNEUROSCI.14-12-07381.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ringach DL, Hawken MJ, Shapley R. Dynamics of orientation tuning in macaque V1: the role of global and tuned suppression. J Neurophysiol. 2003;90:342–352. doi: 10.1152/jn.01018.2002. [DOI] [PubMed] [Google Scholar]
- Rodman HR, Albright TD. Single-unit analysis of pattern-motion selective properties in the middle temporal visual area (MT) Exp Brain Res. 1989;75:53–64. doi: 10.1007/BF00248530. [DOI] [PubMed] [Google Scholar]
- Rust NC, Mante V, Simoncelli EP, Movshon JA. How MT cells analyze the motion of visual patterns. Nat Neurosci. 2006;9:1421–1431. doi: 10.1038/nn1786. [DOI] [PubMed] [Google Scholar]
- Sanger TD. Neural population codes. Curr Opin Neurobiol. 2003;13:238–249. doi: 10.1016/s0959-4388(03)00034-5. [DOI] [PubMed] [Google Scholar]
- Sceniak MP, Hawken MJ, Shapley R. Visual spatial characterization of macaque V1 neurons. J Neurophysiol. 2001;85:1873–1887. doi: 10.1152/jn.2001.85.5.1873. [DOI] [PubMed] [Google Scholar]
- Simoncelli EP, Heeger DJ. A model of neuronal responses in visual area MT. Vision Res. 1998;38:743–761. doi: 10.1016/s0042-6989(97)00183-1. [DOI] [PubMed] [Google Scholar]
- Smith MA, Majaj NJ, Movshon JA. Dynamics of motion signaling by neurons in macaque area MT. Nat Neurosci. 2005;8:220–228. doi: 10.1038/nn1382. [DOI] [PubMed] [Google Scholar]
- Snowden RJ, Treue S, Erickson RG, Andersen RA. The response of area MT and V1 neurons to transparent motion. J Neurosci. 1991;11:2768–2785. doi: 10.1523/JNEUROSCI.11-09-02768.1991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stoner GR, Albright TD. Motion coherency rules are form-cue invariant. Vision Res. 1992a;32:465–475. doi: 10.1016/0042-6989(92)90238-e. [DOI] [PubMed] [Google Scholar]
- Stoner GR, Albright TD. Neural correlates of perceptual motion coherence. Nature. 1992b;358:412–414. doi: 10.1038/358412a0. [DOI] [PubMed] [Google Scholar]
- Stoner GR, Albright TD. The interpretation of visual motion: evidence for surface segmentation mechanisms. Vision Res. 1996;36:1291–1310. doi: 10.1016/0042-6989(95)00195-6. [DOI] [PubMed] [Google Scholar]
- Suzuki S, Grabowecky M. Evidence for perceptual “trapping” and adaptation in multistable binocular rivalry. Neuron. 2002;36:143–157. doi: 10.1016/s0896-6273(02)00934-0. [DOI] [PubMed] [Google Scholar]
- Williams ZM, Elfar JC, Eskandar EN, Toth LJ, Assad JA. Parietal activity and the perceived direction of ambiguous apparent motion. Nat Neurosci. 2003;6:616–623. doi: 10.1038/nn1055. [DOI] [PubMed] [Google Scholar]
- Zeki SM. Functional organization of a visual area in the posterior bank of the superior temporal sulcus of the rhesus monkey. J Physiol. 1974;236:549–573. doi: 10.1113/jphysiol.1974.sp010452. [DOI] [PMC free article] [PubMed] [Google Scholar]