A dynamical systems analysis of afferent control in a neuromechanical model of locomotion. I. Rhythm generation

Abstract

Locomotion in mammals is controlled by a spinal central pattern generator (CPG) coupled to a biomechanical limb system, with afferent feedback to the spinal circuits and CPG closing the control loop. We have considered a simplified model of this system, in which the CPG establishes a rhythm when a supra-spinal activating drive is present and afferent signals from a single-joint limb feed back to affect CPG operation. Using dynamical systems methods, in a series of two papers, we analyze the mechanisms by which this model produces oscillations, and the characteristics of these oscillations, in the closed and open loop regimes. In this first paper, we analyze the phase transition mechanisms operating within the CPG and use the results to explain how afferent feedback allows oscillations to occur at a wider range of drive values to the CPG than the range over which oscillations occur in the CPG without feedback and to comment on why stronger feedback leads to faster oscillations. Linking these transitions to structure in the phase plane associated with the limb segment clarifies how increased weights of afferent feedback to the CPG can restore locomotion after removal of supra-spinal drive to simulate spinal cord injury.

1. Introduction

A certain network of neurons in the mammalian spinal cord can, in isolation, generate activity consistent with a locomotor rhythm [1, 2, 3] and has thus been dubbed the locomotor central pattern generator (CPG). In an intact animal, CPG outputs control limb movements through the activation of motoneurons that drive muscle activity, with muscle afferent signals to the spinal circuits forming a feedback control loop. Although this locomotor system has been the subject of extensive past work, fundamental open questions about its structure and dynamics remain.

One characteristic feature of normal overground locomotion in most mammals is that an increase in speed is achieved through a shortening of the stance phase, during which a limb is in contact with the ground, without change in the duration of the swing phase, during which the limb moves without ground contact [4, 5]. The source of this asymmetry could lie in the CPG structure, in the set of drives to the CPG from supra-spinal sources such as the brain stem, or in the afferent feedback to the CPG, and which possibility is correct remains the subject of scientific debate [6, 7, 8]. Another open question about mammalian locomotion relates to the recovery of locomotor rhythmicity after spinal cord injury (SCI). A complete spinal transection removes supra-spinal inputs to the CPG, which, it is believed, leaves the CPG too weakly excited to maintain its rhythmic output. Locomotor training, a combination of training and pharmacology, or applied spinal cord or afferent stimulation can partly restore locomotor function in cats [3, 9, 10, 11, 12, 13]. While this recovery likely involves potentiation of afferent feedback signals, the details of the mechanism underlying this recovery remain to be elucidated.

Markin et al. recently proposed a computational model in which a locomotor CPG modeled as a form of half-center oscillator sends output through extensor and flexor pathways to a mechanical limb segment, which in turn generates feedback signals, based on muscle length/velocity and force, to the CPG [14]. The model includes a constant supra-spinal drive and generates periodic oscillations over a range of drive values, with a frequency that depends on drive strength within this range. Within the model, the CPG is symmetric, in the sense that its extensor and flexor components are identical, and in the absence of feedback, this symmetry results in similar changes in the durations of stance and swing phases with variation of drive. When afferent feedback is introduced, however, the model exhibits asymmetric changes in phase durations in response to drive alterations that matches closely with experimental results, providing evidence that CPG or drive asymmetry is not necessary for this behavior. Moreover, an increase of this feedback increases the frequency of oscillations, and simulations also yield a recovery of the locomotor rhythm with increases in feedback after a removal of supra-spinal drive to simulate SCI. In this case, the model exhibits an interesting dependence on the degrees to which different feedback signals are strengthened, although the resulting rhythm is less stable to external force perturbations than the original [14].

In this paper and a subsequent companion paper [15], our primary goal is to use dynamical systems analysis to explain the mechanisms underlying the performance of the computational model proposed by Markin et al. [14], as a step towards establishing general conditions under which the observed simulation results can be expected to hold, clarifying which model features are essential to its behaviors, and enhancing the predictive capacity of the model. As a starting point in this endeavor, we first investigate how the model produces periodic oscillations. To this end, we analyze the CPG dynamics without consideration of its effect on limb segment activity, contrasting its dynamics without afferent feedback, which can remain oscillatory given sufficient supra-spinal drive, to that observed when excitatory feedback from muscle afferents is incorporated, which broadens the range of drive values over which oscillations occur (Section 3). This analysis yields different criteria for the existence of oscillations in either case, and illuminates why the model is more robust when feedback is present. In addition, the details of this mechanism explain how the model dynamics allow faster oscillations when the feedback gain is increased. In Section 4, we continue to investigate the effect of increased feedback strength on the system, this time after the removal of supra-spinal drive, which simulates SCI. We show how strengthening the feedback can restore the conditions needed for limb oscillations and how the resulting oscillations differ from model rhythms present under baseline conditions. Analysis of this recovery reveals that sufficiently weak CPG output can render the limb unable to oscillate by failing to allow the limb to assume a positive velocity at the onset of the stance phase. In our follow-up work [15], we give a more detailed analysis of the dynamical mechanisms that yield periodic locomotor outputs in the combined CPG and limb dynamics, the ways that oscillations can be lost as parameters such as supra-spinal drive strength are varied, and the factors responsible for the asymmetric responses of the durations of the stance and swing phases of locomotion under such drive variations in the model.

2. Model description

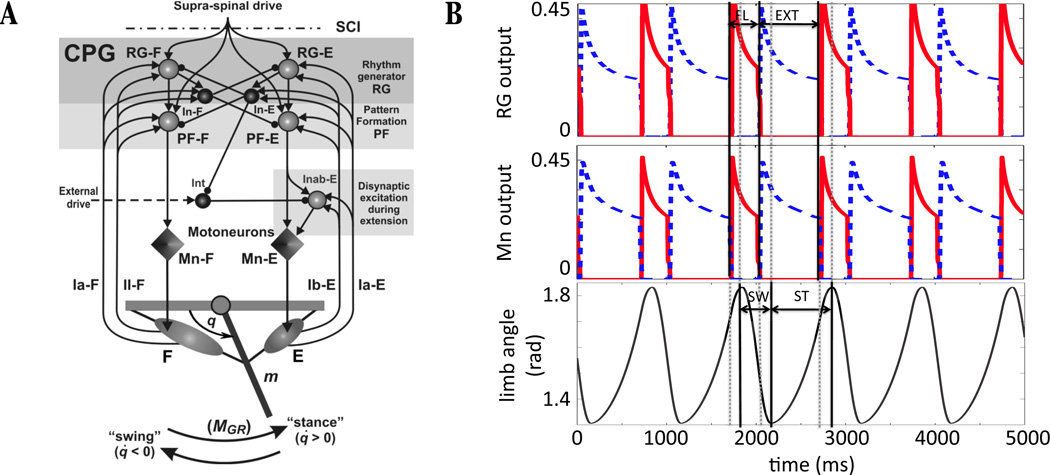
This study focuses on a simplified neuromechanical model of locomotion originally proposed by Markin et al. [14], which we now describe. A schematic diagram illustrating model components and the connections between them is shown in Figure 1A. The multi-level central pattern generator (CPG) consists of a half-center rhythm generator (RG) composed of flexor neurons (RG - F) and extensor neurons (RG - E) projecting to corresponding pattern formation neurons (PF), PF - F and PF - E, and to inhibitory interneurons, In - F and In - E, which mediate reciprocal inhibition between the flexor and extensor sides. The RGs and PFs receive a tonic drive that we refer to as supra-spinal to indicate that biologically this signal originates outside of the spinal cord. Given sufficient supra-spinal drive to yield CPG oscillations, the PF output induces alternating activity in flexor and extensor motoneurons (Mn - F and Mn - E), which correspondingly activate two antagonistic muscles, the flexor (F) and extensor (E), controlling a simple one-joint limb. An additional circuit of interneurons (Int and Inab - E in Figure 1A) provides a disynaptic pathway from PF - E to Mn - E [16, 17].

Figure 1.

Components and basic behavior of the neuro-mechanical model. (A) The two-level spinal CPG (comprised of RG, In, and PF located in the top shaded rectangle) receives tonic supra-spinal drive and generates a basic locomotor rhythm providing alternating activation of flexor and extensor motoneurons (Mn - F and Mn - E). All neurons are represented by spheres (light: excitatory, dark: inhibitory) and motoneurons by diamonds. Excitatory and inhibitory synaptic connections are indicated by arrows and small circles, respectively. The motoneurons activate antagonistic muscles that drive a single-joint limb, and feedback from muscle afferents closes the loop. (B) Sample model activity shows the output of the rhythm generator neurons (RG, top), motoneurons (Mn, middle), and limb angle (bottom). Flexor related activity is plotted with a solid red line, with active phase duration indicated by the segment labeled FL, and extensor related activity is plotted with a dashed blue line, with active phase duration indicated by the segment labeled EXT. Note that flexor and extensor phases are shifted relative to swing and stance phases (SW and ST, bottom). (A) Modified from Markin et al. [14], with permission from the New York Academy of Sciences.

Each neuron in the model is intended to represent a synchronized neural population, with the voltage drop across the membrane denoted as V (voltage) and the neuronal output represented by f(V). Based on the relation of its voltage to a threshold V_th = −50 mV, the state of a neuron is classified as either active (when V ≥ V_th) or silent (when V < V_th). The RG, PF, and Mn models incorporate some voltage-gated ionic currents. These currents in RG - F and RG - E, in combination with the reciprocal inhibition between these neurons (via the inhibitory In - F and In - E), define the rhythm generation in the CPG [18, 19]. The RG, PF, and Mn dynamics are each described by a conductance-based system of two first order ordinary differential equations

$$\begin{array}{c}C{\mathrm{V̇}}_i=-I_{\mathit{\text{NaP}}}(V_{i,}{h}_i)-I_K(V_i)-I_{\mathit{\text{Leak}}}(V_i)-I_{\mathit{\text{SynE}}}(V_i)-I_{\mathit{\text{SynI}}}(V_i)\hfill \end{array}$$

$${ḣ}_i=\frac{h_{\mathrm{\infty }}(V_i)-h_i}{{\tau }_h(V_i)}$$ (1)

where V_i refers to the voltage drop across the membrane of neuron i, C is the membrane capacitance, I_NaP is the persistent sodium current given by I_NaP (V_i, h_i) = ḡ_NaPm_NaPh_i(V_i −E_Na) with instantaneous activation m_NaP = m_NaP (V_i) and slow inactivation h_i, I_K is the potassium current given by $I_K(V_i)={ḡ}_K{m}_K^4(V_i-E_K)$ with instantaneous activation m_K = m_K(V_i), I_Leak is the leak current given by I_Leak(V_i) = ḡ_Leak(V_i − E_Leak), and I_SynE(V_i) and I_SynI(V_i) denote excitatory and inhibitory inputs to neuron i given by

$$I_{\mathit{\text{SynE}}}={ḡ}_{\mathit{\text{SynE}}}(V_i-E_{\mathit{\text{SynE}}})({\displaystyle \sum _j}{a}_{j,i}f(V_j)+c_{i}d+{\displaystyle \sum _k}{w}_{k,i}{\mathit{\text{fb}}}_k),$$ (2)

$$I_{\mathit{\text{SynI}}}={ḡ}_{\mathit{\text{SynI}}}(V_i-E_{\mathit{\text{SynI}}}){\displaystyle \sum _j}{b}_{j,i}f(V_j),$$ (3)

respectively, incorporating the output f(V) from the neurons presynaptic to neuron i, the constant supra-spinal drive d, and the sensory feedback terms fb. Each E_j denotes the reversal potential, and ḡ_j the maximal channel conductance, of current j. Details on the feedback terms will be provided at the end of this section. The terms h_∞(V_i) and τ_h(V_i) in the equation for the evolution of the persistent sodium inactivation term h_i are the voltage-dependent steady state inactivation level and inactivation time constant, respectively. Their functional forms, along with the details of other functions not elaborated here and all parameter values, are provided in the Appendix.

The interneurons (In - F, In - E, Int, and Inab - E) are each described by a single first order equation,

$$C{\mathrm{V̇}}_i=-I_{\mathit{\text{Leak}}}(V_i)-I_{\mathit{\text{SynE}}}(V_i)-I_{\mathit{\text{SynI}}}(V_i).$$ (4)

The excitatory inputs to these interneurons arrive from RG, from supra-spinal drive, and from sensory feedback. Note that In - E and In - F in particular do not receive inhibition from any source or supra-spinal drive, so the right hand sides of their voltage equations have I_SynI ≡ 0 and c_i = 0. When inputs are absent, the interneurons rest at a voltage that is below threshold. Descriptions of currents and parameter choices for these interneurons are also detailed in the Appendix.

The limb segment controlled by the CPG, which we hereafter refer to simply as the limb, is tethered at a joint and able to move in an angular direction relative to that joint. The forces acting at the limb include: (1) forces of the two antagonistic flexor and extensor muscles, (2) gravitational force, and (3) ground reaction force, whose moment (M_GR) is applied during the stance phase, when the limb moves counterclockwise, but not in the swing phase, when the limb moves clockwise. Muscle afferents provide length/velocity-dependent (type Ia from both muscles and type II - F from the flexor) and force-dependent (type Ib - E from the extensor) feedback to the CPG through additional excitation to the homonymous neurons. The limb motion is described by the second order differential equation

$$I\mathrm{q̈}=K\text{ cos}(q)-b\mathrm{q̇}+M_F(q,\mathrm{q̇},V_{\mathit{\text{Mn}}-F},t)-M_E(\pi -q,-\mathrm{q̇},V_{\mathit{\text{Mn}}-E},t)+M_{\mathit{\text{GR}}}(q),$$ (5)

where q is the generalized coordinate (the angle that the limb forms with the horizontal; see Figure 1), I is the moment of inertia of the limb with respect to the suspension point, K cos(q) is the moment of the gravitational force, b is the angular viscosity in the hinge joint, M_F and M_E are the moments of the muscle forces, and M_GR is the moment of the ground reaction force, given by

$$M_{\mathit{\text{GR}}}(q)=\{\begin{array}{cc}-M_{\mathit{\text{GRmax}}}\text{ cos}(q),\hfill & \mathrm{q̇}\ge 0;\hfill \\ 0,\hfill & \mathrm{q̇}<0;\hfill \end{array}$$

which is nonzero during the stance phase. See the Appendix for the complete description of these terms.

Figure 1B shows an example of the time course of activity of the RG, the Mns, and the corresponding limb angle. Note that a switch in which side of the CPG is active, and hence a switch between flexor and extensor activation, does not instantaneously change the direction of motion of the limb. Since the definition of stance and swing phases is based on the direction of limb motion (and correspondingly the presence or absence of ground reaction force), these phases are shifted relative to the F and E phases. Thus, we can define eSwing, eStance, fSwing, and fStance subphases, which will be important in [15], where in each subphase name, the first letter denotes the active motoneuron (‘f’ for flexor, ‘e’ for extensor) and the subsequent string indicates whether the limb is in the swing or stance phase. One cycle through these phases defines a locomotor cycle in the model. Without feedback, the limb is considered to be immobilized, so when feedback is absent, we will define the duration of the “fictive locomotor cycle” by the period of the CPG oscillations, formed by a single extensor and flexor phase (see Figure 3A).

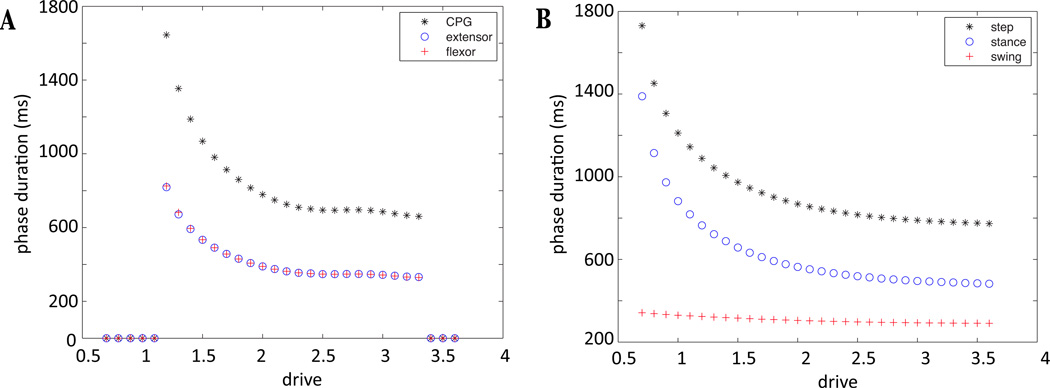
Figure 3.

Control of the locomotor speed in the neuromechanical model by a supra-spinal drive applied identically to both half-centers. (A) Extensor (blue circles) and flexor (red plus signs) phase durations sum to the CPG cycle period (black stars) and change identically as drive varies in the absence of afferent feedback (fictive locomotion state). (B) Step cycle duration (black stars) varies asymmetrically with drive when sensory feedback from the oscillating limb is incorporated into the CPG. When limb motion is included, the step cycle consists of stance (blue circles) and swing (red plus signs) phases, defined by the presence and absence of ground contact, respectively. The presence of feedback modifies the increase in locomotor speed by decreasing the duration of the stance phase, at a relatively constant swing duration. In addition, the CPG oscillates over a wider (particularly lower) range of drives, compared to the model without feedback.

The nonlinear feedback from the extensor and flexor muscle afferents provides excitatory inputs to the RG, In, PF, and Inab−E that control the timing of phase transitions at the RG/In level and the excitability of the PF neurons. Sensory feedback from the extensor muscle also accesses the additional Int/Inab - E circuit yielding a net excitation of Mn - E during extension (see Figure 1). Linear combinations of feedback terms are fed into each side of the model; Ia-F and II - F feedbacks go to the flexor side and Ia - E and Ib - E to the extensor side. In equation (1), we denote the feedback to neuron i as ∑_k w_k,ifb_k, which we will henceforth abbreviate as FB_i. For extensor neurons,

$${\mathit{\text{FB}}}_i=w_{\mathit{\text{Ia}}-E,i}\mathit{\text{Ia}}-E+w_{\mathit{\text{Ib}}-E,i}\mathit{\text{Ib}}-E$$ (6)

for i ∈ {RG-E, PF -E,In - E, Inab - E}. For flexor neurons,

$${\mathit{\text{FB}}}_i=w_{\mathit{\text{Ia}}-F,i}\mathit{\text{Ia}}-F+w_{\mathit{\text{II}}-F,i}\mathit{\text{II}}-F$$ (7)

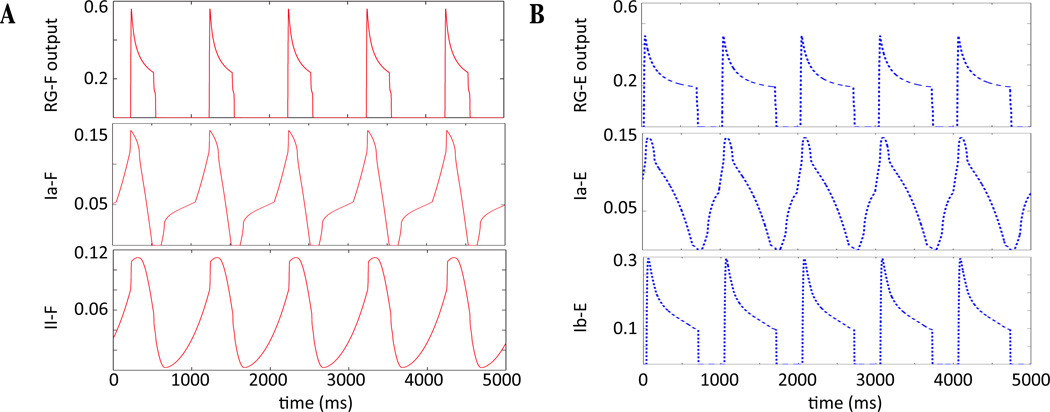
for i ∈ {RG - F, PF - F,In - F}. Figure 2 shows the time course of the Ia − E, II − F, and Ib − E feedback along with RG activity. It is important to note that the feedback to a neuron increases during its silent phase and decreases during its active phase, with the exception of force-dependent Ib - E feedback, which is only active when RG - E is. This information will be utilized in Section 3, where the dynamic mechanisms underlying oscillations in the model (e.g., Figure 1B) are described. See the Appendix for the mathematical formulations of the feedback terms Ia, Ib - E, II - F.

Figure 2.

Time courses of RG output (f(V)) and feedback activity. (A) RG - F, Ia-F, II - F output (red solid) in top, middle, and bottom panels, respectively. Feedback signals Ia-F and II - F are fed to flexor neurons, increasing while RG - F is inactive and decreasing while RG- F is active. (B) RG - E, Ia - E, Ib - E output (blue dashed) in top, middle, and bottom panels, respectively. Feedback signals Ia - E and Ib - E are fed to extensor neurons. Similarly to the flexor side, Ia - E increases while RG - E is silent and decreases while RG - E is active. Ib - E is force-dependent and is only active during the active phase of RG - E.

Figure 3 illustrates the dependence on supra-spinal drive of the durations of flexor and extensor phases and the overall locomotor cycle in the model in the absence of afferent feedback (also known as the fictive locomotion state, Figure 3A) and when afferent feedback is present (Figure 3B). In the fictive locomotion state, we can decompose each CPG oscillation into a flexor phase and an extensor phase, based solely on which set of neurons is active, and these have identical durations for each fixed drive value by construction. In the presence of afferent feedback, the limb oscillates and the increase in locomotor speed is accompanied by a decrease in stance phase duration, with a relatively constant swing duration. In addition, the CPG oscillates over a wider range of supra-spinal drive, compared to the model without feedback.

To conclude this section, in Table 1, we present a list of terms that are commonly used in this paper.

Table 1.

Key Notation

Term	Description
d	constant supra-spinal drive fed to CPG neurons
Vi	voltage drop across the membrane of neuron i
RG - k	rhythm generator neuron k; k ∈ {F,E}
In - k	inhibitory interneuron k; k ∈ {F,E}
PF - k	pattern formation neuron k; k ∈ {F,E}
Mn - k	motoneuron k; k ∈ {F,E}
q	limb angle with the horizontal
υ	limb angular velocity
Ia-F, II - F	feedback terms to the flexor side
Ia - E, Ib - E	feedback terms to the extensor side
FBi	summed feedback to neuron i
FBcrit	feedback required to excite an inactive In above threshold; independent of drive
TTC	Stance Transition Curve; location in limb phase space where flexor activates
WTC	Swing Transition Curve; location in limb phase space where extensor activates
eStance	portion of the locomotor phase where Mn - E is active and ground reaction is present
fStance	portion of the locomotor phase where Mn - F is active and ground reaction is present
eSwing	portion of the locomotor phase where Mn - E is active and ground reaction is absent
fSwing	portion of the locomotor phase where Mn - F is active and ground reaction is absent

3. CPG mechanisms differ in the model with and without feedback

Since the oscillatory behavior of the model depends on whether or not feedback is present, we begin by analyzing the activity of the CPG’s rhythm generator, which is comprised of RGs described by system (1) and Ins described by equation (4). Because the persistent sodium inactivation time constant τ_h(V) is large over the relevant voltage range (see the Appendix for details), system (1) is essentially of the form V̇ = F(V, h, I), ḣ = εG(V, h), where ε is a small parameter and I denotes time-dependent excitatory/inhibitory input from other neurons and feedback. A dynamical system in this form is called a slow-fast system, because h evolves on a much slower timescale than V due to the size of ε. Before discussing the interactions of two neurons with these dynamics, in Section 3.1 we will first consider the dynamics of a single neuron described by slow-fast equations with a fixed input I. We will see that the activity of this neuron can be completely determined from the location of intersection of its nullclines in the (V, h) phase plane. Once we understand the dynamics of a single neuron receiving a fixed input, we can analyze how our set of connected neurons coordinate their activity to generate a model oscillation when feedback is absent (Section 3.2) and when feedback is present (Section 3.3), such that the levels of input to the neurons varies in time. By illustrating the details of these mechanisms, we can explain how the model is able to oscillate at a wider drive range when feedback is present, and why strengthening this feedback supports an increase in locomotor frequency.

3.1. Intrinsic dynamics of model RGs

Consider system (1) as V̇ = F(V, h, I), ḣ = εG(V, h), where I is some fixed constant and ε is a small positive parameter. Due to the small size of ε, h is expected to evolve much more slowly than V except where |F| is small. When such a separation of timescales is present, the nullclines of the system are particularly helpful for understanding its dynamics, as we will explain below. The V -nullcline consists of the set of (V, h) that satisfy V̇ = F(V, h, I) = 0. Given the definition of F, the V -nullcline is a cubic shaped curve when drawn in the (V, h) phase plane; above this curve, F > 0, and below it, F < 0 (for an example, see Figure 4). We consider this cubic shape as composed of three (left, middle, and right) branches. The left and middle branches meet at a local maximum, which we will refer to as the left knee, and the middle and right branches connect at a local minimum, which we refer to as the right knee. The h-nullcline (the set of (V, h) that satisfy ḣ = G(V, h) = 0) is also important. When drawn in the phase plane, the h-nullcline is a non-increasing sigmoid, with G > 0 below and G < 0 above this curve.

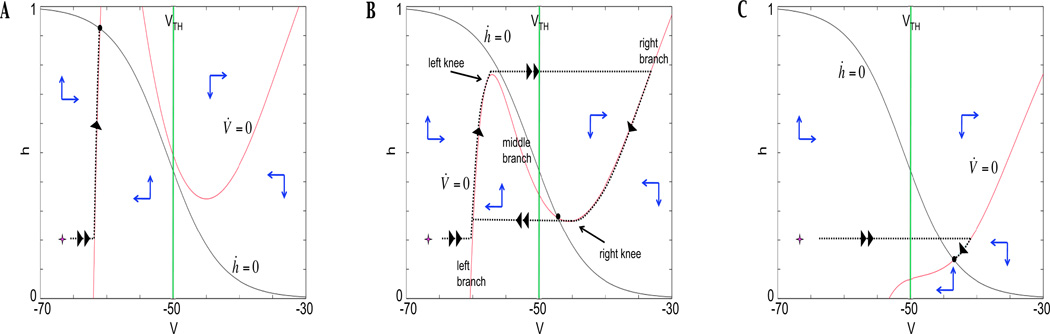
Figure 4.

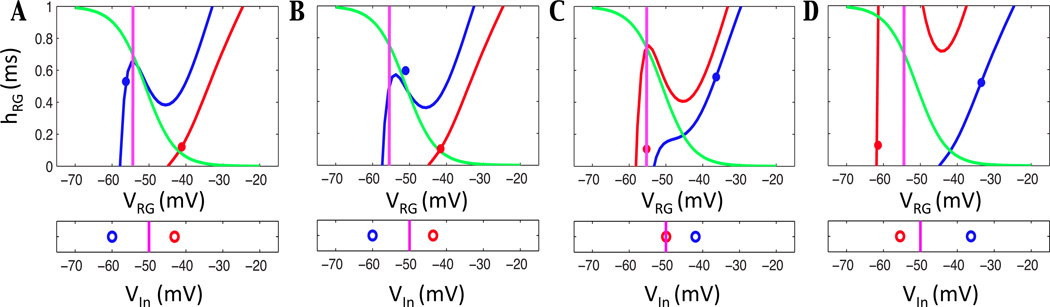
Neuron activity for three different levels of input. In each panel, the cubic shaped V -nullcline is shown in red, the sigmoid shaped h-nullcline in green. The location of their intersection determines the activity of the neuron. The trajectory is shown with a thick black dotted line from an initial condition indicated by a star. Threshold is indicated with a magenta vertical line, located at V = V_th=−50 mV. Double arrows indicate motion on the fast timescale, single arrows on the slow timescale. Blue arrows indicate the direction of the vector field, and the black dot indicates the critical point for the system in each case. (A) The neuron remains at a silent state for all time when the nullclines intersect on the left branch of the V -nullcline. (B) When the nullclines meet on the middle branch of the V -nullcline, bursting activity can occur since both knees are accessible. (C) Tonic activity results from the configuration in which nullclines intersect on the right branch of the V -nullcline.

When a neuron is described by a model with dynamics on two disparate timescales, we can simplify the analysis of its behavior by reducing the full system to two subsystems, each on its own timescale. First we consider the limit where ε goes to 0 and obtain the fast subsystem (FS): V̇ = F(V, h, I), ḣ = 0. Solutions for the fast subsystem have h fixed as a constant with flow determined by the dynamics of V. If we instead perform a change of variables and let τ = εt, and then let ε go to 0, we obtain the slow subsystem (SS): 0 = F(V, h, I), h′ = G(V, h), by using the chain rule and canceling ε in the h equation (′ denotes differentiation with respect to τ). Solutions to the slow subsystem lie on the cubic V -nullcline and flow according to the dynamics of h, with V = V (h) such that F(V (h), h, I) = 0. This evolution occurs on a much slower timescale than that of the fast subsystem due to the change of time variable. An approximate solution to the full system is formed as an appropriate concatenation of solutions of the fast and slow subsystems, where the subsystem to be solved at a particular time depends on the solution’s location in phase space at that time. Indeed, consider an initial condition starting away from the cubic nullcline. Since F(V, h, I) ≠ 0, i.e. the conditions of (SS) are not satisfied, the dynamics of the system are described by (FS). According to this subsystem, h is fixed and V evolves toward a stable critical point of (FS). As can be seen by examination of the vector field (Figure 4), each point on the left and right branches is a stable critical point of (FS), since V̇ > 0 for V below the left branch and V̇ switches sign each time a branch is crossed. In the limit as t → ∞, F(V, h, I) = 0 is satisfied and (SS) can be solved to obtain the next segment of the solution.

Overall, the activity of each neuron depends completely on the location of the intersection between the V and h -nullclines, which is a critical point of the full system. Figure 4 shows nullcline configurations for input values that cause the nullcline intersection point to lie on: the left branch of the V -nullcline in Figure 4A, the middle branch in Figure 4B, and the right branch in Figure 4C. Consider an initial condition in the lower left corner of the phase plane as shown in Figure 4A. Since F(V, h, I) ≠ 0, the trajectory approaches the nearest stable critical point of (FS), which lies on the left branch of the V -nullcline. From this critical point, the dynamics of (SS) yield a trajectory that travels up the left branch of the V -nullcline, since h′ > 0 in this region. As time increases, this trajectory approaches a point (V_s, h_s) that satisfies F(V_s, h_s) = 0, G(V_s, h_s) = 0, namely a critical point of the (V, h) system that lies below the activation threshold. This neuron will remain in this silent state for all time.

If instead the nullcline is configured as in Figure 4B, the trajectory would again follow first the (FS) then the (SS) dynamics until it travels slightly above the left knee of the V -nullcline. At that time, the (SS) conditions are not met (once we leave the cubic, F(V, h, I) ≠ 0), so V evolves to a stable state with fixed h according to (FS). This point lies on the right branch of the V -nullcline, so as t increases the trajectory crosses activation threshold and enters the active state. The trajectory evolves according to (SS) with decreasing h on the V -nullcline since it now lies to the right of the h-nullcline. An analogous transition to the silent phase occurs when the trajectory reaches the right knee of the V -nullcline. With this configuration a neuron is an intrinsic oscillator, since it spends time in both the silent and active phases.

Finally, Figure 4C shows a nullcline configured with the critical point lying on the right branch of the V -nullcline. From the starting point shown, the trajectory immediately jumps across synaptic threshold to the right branch of the V -nullcline and evolves in a direction of decreasing h. In this case, however, the trajectory encounters a critical point of the full system. This state lies above activation threshold, thus the neuron remains in an active state for all time.

This discussion details the possible activity patterns of a single neuron with a fixed input, but in system (1), the neurons receive input from sources that vary in strength over time, which means that their nullclines are constantly evolving. For instance, a neuron that is stuck in the silent regime can become active if it receives sufficient excitation (or conversely, less inhibition) to lower its V -nullcline and shift the critical point from the left to the middle branch. Analogously, a neuron with a tonic nullcline configuration could jump to the silent phase if its excitatory input decreases sufficiently, raising the nullcline so that the neuron can access the right knee [20].

When coupled neurons generate a rhythm through a combination of intrinsic dynamics and coupling-induced nullcline adjustments, we can distinguish different classes of transition mechanisms by which different neurons become active or silent. For instance, a transition might occur via an inhibited cell reaching its left knee and “escaping” from the silent phase. Once it becomes active, it may inhibit previously active cells, possibly forcing them to become silent. This transition mechanism is denoted as escape. Conversely, if an active cell reaches its right knee, then it can jump down from the active to the silent phase. Once it crosses below synaptic threshold, it “releases” the silent cell from inhibition (allowing the inhibited cell to become active). This transition mechanism is denoted as release [21, 22, 19].

In the following sections, we discuss the different mechanisms causing transitions in the CPG in the case when feedback is absent and the case when it is present.

3.2. Without feedback, CPG transitions occur through RG adaptation and escape

Our simulations show that oscillations in the CPG without feedback occur via escape controlled by RG. Details of the transition from RG - E silent to RG - E active are shown in Figure 5, and the F transition is analogous. In the top panel of each figure, the dynamics of RG - F and RG - E are tracked in phase space. In the bottom panel of each figure, the corresponding voltages of In - F and In - E are indicated. Since feedback is absent, the voltage of In is completely slaved to the activity of RG; it remains at a silent rest state of equation (4) given by the leak reversal potential when RG is silent but is excited above threshold after RG becomes active. Also, without feedback, the only time-varying input to RG comes from inhibition from In.

Figure 5.

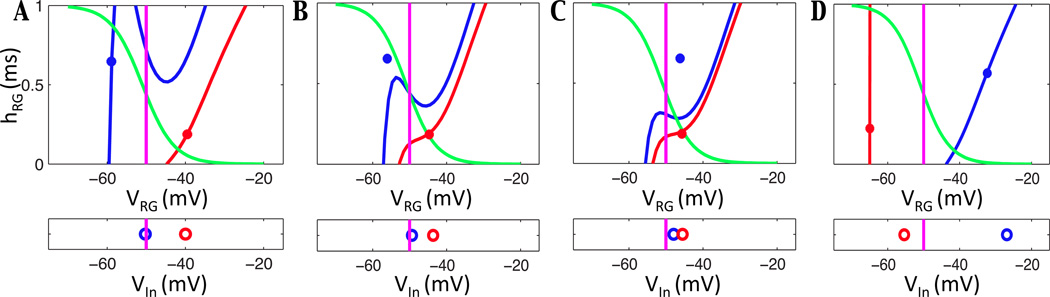
Frame by frame depiction of the escape mechanism for the model without feedback. In the top boxes RG - F and RG - E positions are plotted at various timepoints with their relevant nullclines in (V_RG, h_NaPRG) space. The corresponding voltages of In - F and In - E are tracked in the lower boxes. For all neurons and V -nullclines, red indicates flexor and blue indicates extensor, the h-nullcline is shown in green, and the voltage threshold is indicated in magenta. (A) Inhibition from In - F decreases over time, lowering RG - E’s V -nullcline until the left knee can be reached. (B) RG - E hits the knee and jumps across threshold. (C) Excitation from RG - E pushes In - E across threshold. In - E begins inhibiting RG - F which raises its V -nullcline, causing RG - F to jump below threshold. This decreases excitation to In - F, which also begins to fall below threshold. (D) RG - F and RG - E have switched dominance, as have In - F and In - E.

Starting from its position in Figure 5A, the h variable of RG - F decreases in slow time. Due to the slope of the V -nullcline, the voltage of RG - F decreases, which weakens the excitation from RG - F to In - F and correspondingly reduces the inhibition from In - F to the RG - E (see equations (2),(3) for relevant synaptic currents). This reduction in inhibition is a form of adaptation that facilitates phase transitions (e.g., [19]). During this time, RG - E travels up its inhibited V -nullcline (which lowers as output from In - F decreases) until it reaches the left knee of the relevant V -nullcline. The rest of the dynamics shown in Figure 5B–D occur on the fast timescale. In Figure 5B, RG - E escapes and jumps toward the right branch, exciting its corresponding In - E as it crosses the synaptic threshold. The newly active In - E provides partial inhibition to the opposing RG - F, causing a change in its V -nullcline. Due to this change, RG - F ends up below the right knee of the V -nullcline and jumps to the left branch of its nullcline, crossing below the synaptic threshold as it does so (Figure 5C). Without excitation from RG - F, In - F falls below threshold as well and stops inhibiting RG - E. As the fast time t → ∞, RG - F is fully inhibited from In - E (Figure 5D). This sequence represents one half-cycle, from the onset of RG - F activation to the onset of RG - E activation, after which the neurons evolve on the slow timescale again. We note that with no feedback, for all drives considered [14], the first derivative of the nullcline of the active RG neuron is always positive, so transitions by pure intrinsic release, in which an active neuron reaches a right knee and falls silent on its own, cannot occur.

The transitions by adaptation-facilitated escape seen in the absence of feedback lead to a decrease in phase durations when excitation, i.e. drive, is increased [23, 24]. Since both transitions, E to F and F to E, occur via this mechanism, we expect both the flexor and extensor durations to decrease as drive is increased as shown in Figure 3. Furthermore, this transition mechanism limits the range of drives that produce oscillations. If drive is too small, the critical point for the inhibited nullcline will lie on the left branch, and the silent neuron will be unable to complete a transition to become active. Thus, the observation that transitions occur by RG escape has allowed us to identify the bifurcation event underlying the loss of oscillations with reductions in drive in the CPG without feedback.

Given this insight, we can now address the following question: Assuming that one RG is active and the other silent, for which drives will the system oscillate? As outlined above, we must determine the equation for the inhibited nullcline, and locate the position of the critical point for the (V, h) system, to answer this question. To do this, we fix drive, and in the absence of excitatory feedback, the active RG nullcline is completely determined. We compute the steady state of this neuron, which corresponds to the minimum inhibition level that it indirectly provides to the opposing RG. If the inhibited V and h nullclines intersect on the left branch of the V -nullcline for this inhibition value obtained at this particular drive, then the neuron will be unable to escape.

Using the implicit function theorem, we find an explicit equation h = h_c(V) for the inhibited RG nullcline under the drive and inhibition pairing we described above and solve h_c(V) = h_∞(V) to find an expression for the voltage of the critical point, V_ip, where h = h_∞(V) is the equation for the h-nullcline. Separately, we calculate the voltage of the left knee, which satisfies $h_c^{\prime }(V)=0,h_c^{″}(V)$, < 0, where ′ denotes differentiation with respect to V. We will denote this as V_lk. Then, if V_ip < V_lk, the intersection point lies on the left branch of the V -nullcline, which prohibits escape. We find that the silent RG can begin to escape for inhibition and drive pairings larger than d = 1.13, which concurs with Figure 3A, where oscillations are seen for d=1.2 and larger.

For very large drives, on the other hand, the oscillations in the CPG break down in a different manner. As drive is increased, the inhibited RG nullcline can become sufficiently lowered such that almost the entire nullcline lies to the right of the synaptic threshold, V_th. Thus, the active periods of RG begin to overlap, which represents the loss of a coordinated oscillation.

We also note that for relatively large drives, PF can escape prior to the transition at the RG level, and the PF V -nullclines can move above synaptic threshold, such that PF can remain active for the entire oscillation cycle. However, this does not affect our definitions of phase durations, since these are calculated based on RG activity in this no-feedback case, nor does it affect limb dynamics, since the limb is considered as immobilized in this case.

3.3. Presence of feedback induces CPG oscillations through In escape mechanism and defines important system transition curves

The dynamics becomes more complicated when the CPG neurons receive excitatory input from sensory feedback. This feedback depends nonlinearly on the position and velocity of the limb as well as the output of the motoneurons, which makes it difficult to pinpoint whether a transition based on the intrinsic dynamics of an RG may be possible. Further, since feedback is also fed to In, their states are no longer slaved to RG activity. In fact, we observe that as feedback increases, each In can cross threshold independently of the RG that excites it, which results in oscillations featuring a different transition mechanism than in the previous case. We show details of this mechanism, from RG - E silent to RG - E active, in Figure 6, and again, the opposite transition is analogous.

Figure 6.

Frame by frame depiction of the In escape mechanism when feedback is present in the model. In the top boxes RG - F and RG - E positions are plotted at various timepoints on their relevant nullclines in (V_RG, h_NaPRG) space. The corresponding voltages of In - F and In - E are tracked in the lower boxes. For all neurons and V -nullclines, red indicates flexor and blue indicates extensor, the h-nullcline is shown in green, and the voltage threshold is indicated in magenta. (A) Feedback increases excitation to In - E, allowing it to reach threshold independently from RG - E. (B) In - E begins to inhibit RG - F, which raises the V -nullcline for RG - F (red). This change causes the voltage of In - F to decrease, yielding less inhibition to RG - E and thus lowering its V -nullcline (blue). (C) RG - E is now above the left knee of its V -nullcline, so it jumps to the right branch, crossing threshold and further exciting In - E as it does so. (D) RG - F falls below threshold after receiving full inhibition from In - E. Without excitation from RG - F, In - F falls below threshold as well.

Comparing the first frame in Figure 5 with the first frame in Figure 6, we can see that adding excitatory feedback to the system has the net effect of raising the position of the inhibited V -nullcline. This outcome may seem counterintuitive, since simply receiving more excitation should lower the silent neuron’s V -nullcline; however, the strength of the inhibition the silent neuron receives is also stronger, since increasing excitation to the active neuron allows it to inhibit the silent neuron more strongly. The effect of this stronger inhibition, despite the stronger excitation from feedback signals, is that the V -nullcline for the silent RG - E is higher in the feedback case than in the case without feedback, for the same drive value. Hence, the RG - E equations have a critical point in the silent phase, on the left branch of their V -nullcline, while the RG - F equations have a critical point in the active phase, on the right branch of their V -nullcline, as illustrated in Figure 6A. Given this situation, without any change in input, the RG will become deadlocked at steady states, unable to trade dominance, for the same drive value shown in Figure 5. Crucially, however, In - E integrates sufficient input from excitatory feedback that it can cross the synaptic threshold and begin to inhibit RG - F on its own (Figure 6A). This inhibition raises the V -nullcline of RG - F, such that its voltage drops on the fast timescale, which reduces the voltage of In - F (Figure 6C; note that the rise in In - E inhibitory output is not dependent on a change in RG - E up to this time). This change updates the RG - E nullcline, since the inhibition it receives from In - F is reduced, and eventually the nullcline lowers such that RG - E can reach the left knee and jump to the right branch. As it passes through threshold, RG - E provides additional excitation to the already active In - E (Figure 6C). During this transition, In - F shuts down completely, so RG - E converges to the right branch of the uninhibited nullcline, and RG - F settles on the left branch of the fully inhibited nullcline (Figure 6D).

Note that in this case, the active RG neuron receives more positive input (drive plus feedback) than in the case without feedback, and hence again, a departure from the active phase by the active RG neuron and associated release of the silent neuron cannot occur without some other event initiating the transition first. In some cases, the active In may reach low enough voltages that the inhibitory signal to the silent side may become significantly sub-maximal. Still, while this reduction in inhibition may facilitate switching, in the end it is the escape of the silent In that causes the full dominance switch.

Now that we have identified what event is responsible for each transfer of dominance in the CPG, we can understand the range of drives over which oscillations occur by exploring how and when that event occurs. For the silent In to become active, it must cross the activation threshold. Since its corresponding RG is silent when it first escapes, the only excitation it receives is from feedback, which increases throughout the inactive phase of a neuron as noted in Section 2. The level of excitation required for In to cross threshold can be obtained by solving for the steady state of silent In and setting this value equal to V_th. The steady state satisfies:

$$V_{\mathit{\text{In}}-\mathit{\text{silent}}}^{\mathit{\text{ss}}}=({ḡ}_{\mathit{\text{Leak}}}{E}_{\mathit{\text{Leak}}}+{ḡ}_{\mathit{\text{synE}}}{E}_{\mathit{\text{synE}}}{\mathit{\text{FB}}}_{\mathit{\text{In}}-\mathit{\text{silent}}})/({ḡ}_{\mathit{\text{Leak}}}+{ḡ}_{\mathit{\text{synE}}}{\mathit{\text{FB}}}_{\mathit{\text{In}}-\mathit{\text{silent}}}),$$

where FB_{In - silent} denotes the summed feedback to the inactive In (see equations (6),(7)), and a simple calculation determines that with our model parameter values, $V_{\mathit{\text{In}}-\mathit{\text{silent}}}^{\mathit{\text{ss}}}=V_{\mathit{\text{th}}}$ when FB_{In - silent} = 0.04. We denote this critical value as FB_crit, and we note that although the feedbacks fed to the extensor and flexor sides differ (and thus, how this value is reached differs), FB_crit is independent of side.

Feedback terms depend on limb angle (q) and velocity (υ = q̇), governed by equation (5), as well as motoneuron output. However, FB_{In - silent} = FB_crit is an equation that depends only on q and υ. Indeed, except during CPG transitions, all flexor neurons (RG - F, In - F, PF - F and Mn - F) are inactive together. Thus, when In - F is silent, Mn - F is silent, so when calculating the feedback to In - F during its silent phase, the terms in Ia-F and II - F that depend on Mn - F are zero. The situation is analogous for the extensor side. Therefore, we can use equations (6),(7) to construct curves in limb phase space that indicate where the transitions in the CPG occur. We define the sTance Transition Curve as

$$\mathit{\text{TTC}}=\{(q,\upsilon ):\upsilon \ge 0,{\mathit{\text{FB}}}_{\mathit{\text{In}}-F}={\mathit{\text{FB}}}_{\mathit{\text{crit}}}\}.$$ (8)

This curve is the collection of points in (q, v) space where the voltage of In - F reaches threshold and inhibits RG - E, initiating the switch from E to F dominance, which occurs midway through the stance phase. Similarly, the sWing Transition Curve

$$\mathit{\text{WTC}}=\{(q,\upsilon ):\upsilon \le 0,{\mathit{\text{FB}}}_{\mathit{\text{In}}-E}={\mathit{\text{FB}}}_{\mathit{\text{crit}}}\}$$ (9)

describes the set of points where the analogous switch from F to E dominance occurs in the swing phase. These two curves define vital switching manifolds for the system; see Figure 8A for their locations in limb phase space. They are precisely determined, although there is a small delay from the time when an In escapes to the time that this transition is transmitted via the corresponding Mn and manifested in the forces acting on the limb (see the Appendix for more details).

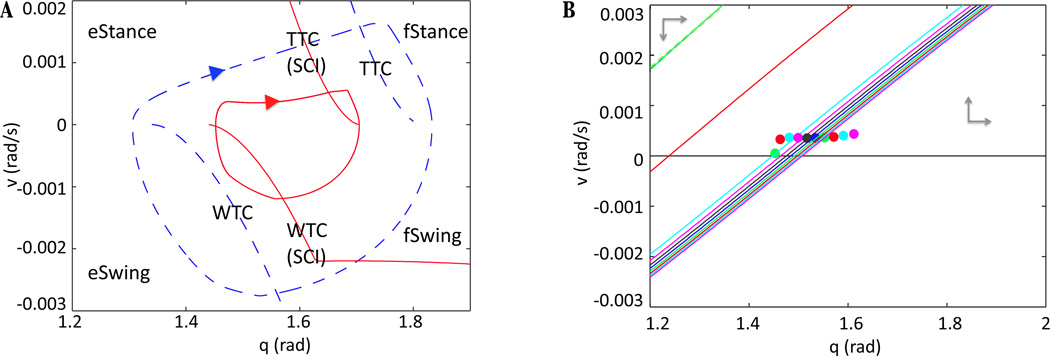
Figure 8.

Limb dynamics changes quantitatively and qualitatively after SCI. (A) Limb trajectory and transition curves under normal conditions (blue dashed) and SCI (red solid). By increasing the feedback strength, the transition curves shift, producing an oscillation of smaller amplitude as well as a qualitatively different velocity profile during eStance. (B) eStance υ-nullclines and limb position in phase space at different timepoints are indicated with corresponding colors. The earliest time points and nullclines are the farther to the left and are colored green, red, and cyan. A quick drop in the υ-nullcline near the onset of eStance, between the red time point and the cyan time point, causes the convex orbit shape seen after SCI.

Since the CPG and feedback operate in a closed loop, it is difficult to prove rigorously that phase transitions in the presence of feedback occur via In escape for all drives. For larger drives, for instance, the inhibited RG might have access to its left knee, but the inhibited In could cross threshold first (or vice versa). Without knowing the time course of the feedback, we cannot determine which mechanism occurs first. We observe numerically that the In always reaches synaptic threshold before the RG can escape. We note that, as in the case without feedback, oscillations in the CPG persist until drive is very large, and break down when the active periods of RG begin to overlap.

Since the In escape transition mechanism does not depend on any particular nullcline configuration, as was needed for RG escape in the case without feedback, feedback broadens the range of drives over which oscillations can occur, particularly for lower drives. Provided that the feedback strength to the In is sufficiently large, the system will oscillate. In our companion paper, we will return to the issue of what can cause oscillations to be lost in the presence of feedback, for example as occurs as drive is reduced, using an analysis of limb dynamics subject to Mn outputs [15].

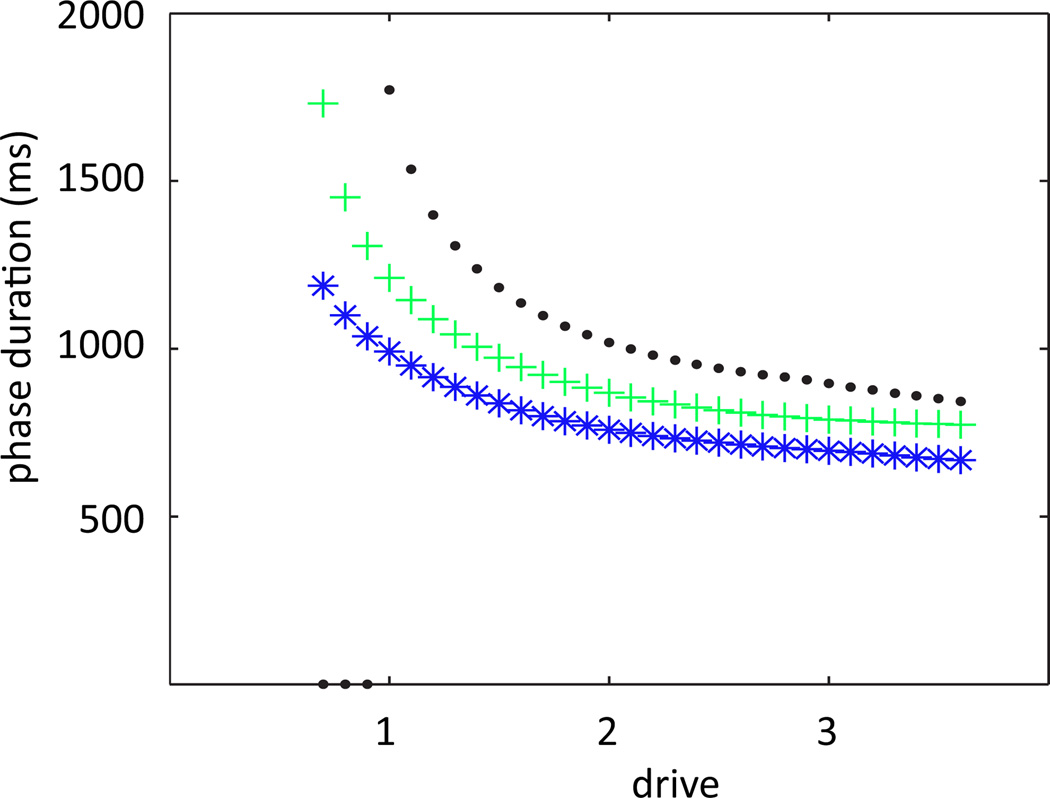
Finally, previous modeling work has proposed that stronger feedback signals should code for faster locomotor oscillations [25, 26]. The fact that an escape mechanism underlies CPG phase transitions in the model that we consider suggests that augmenting feedback signals in this model might speed up its oscillation frequency, by facilitating this escape (as opposed to models with release-based transitions, in which stronger positive inputs help sustain the dominant units and delay transitions) [23, 24, 19]. The result of such augmentation is complicated, however, by the fact that feedback signals also affect motoneuron outputs and hence limb dynamics, particularly transitions between stance and swing, which occur at different times from extensor/flexor transitions in the full model. It turns out that stronger feedback signals yield stronger motoneuron outputs, which speed up these stance/swing transitions and the associated epochs in the limb phase plane, enhancing the frequency increase expected from the CPG. The mechanisms responsible for these effects will be discussed in the next section and, in greater detail, in our subsequent paper [15]. The upshot of this analysis is that the CPG and limb responses to strengthened feedback provide complementary increases in the locomotor oscillation frequency in the model that we consider, as illustrated in Figure 7.

Figure 7.

Control of locomotor speed by supra-spinal drive for different feedback strengths. Green plus signs indicate normal strength, black dots and blue stars indicate feedback at 90 and 110 percent of normal feedback strength, respectively. Increasing feedback strength increases limb frequency, most notably at lower drive values.

Before moving on to consider spinal cord injury, we make one final note: we again observe that for relatively large drives, the extensor pattern formation (PF - E) neuron is able to intrinsically escape prior to the switch between RG - F and RG - E. Its voltage, however, remains just slightly above threshold, so although it sends signals to Mn - E, they are weak, and full motoneuron activation does not occur without the In - E escape outlined above. Furthermore, this PF - E escape plays no role in the phase asymmetry shown in Figure 3; indeed, we have verified numerically that if we reduce the parameter that controls the strength of the input to PF, we can suppress this PF - E activity yet retain full anti-phase Mn output, without qualitatively affecting the asymmetric phase response to changes in supra-spinal drive (Figure 3B).

4. Increasing feedback recovers oscillations after simulated spinal cord injury

We now elucidate the role that feedback strength plays in the model in the representation of spinal cord injury, which is achieved by setting the drive to zero. We will henceforth use the acronym SCI to refer to the model with zero drive. Without drive, under normal feedback strength, the neuromechanical model cannot generate oscillations and in particular the limb cannot exhibit a rhythm. Yet, an increase of feedback strength, representing the effects of learning or certain pharmacological manipulations, can restore oscillatory behavior. We wish to address how the feedback increase accomplishes this goal and to clarify the role of specific feedback components in this recovery. In Section 4.1, we propose an argument that reveals the mechanism responsible for oscillations under this adjustment to the system. In Section 4.2, we visualize the dynamics of the model in a completely new way, in limb phase space, and use this viewpoint to show how this feedback increase alters the qualitative form of the oscillation and the location of the transition curves defined in the previous section. This visualization will reveal a critical relationship that is necessary for oscillations to exist in the model, which we will investigate in more detail in [15].

4.1. CPG transition mechanisms under SCI

When descending input is removed and feedback is increased, how do CPG neurons coordinate their activity to generate an oscillation? Does this adjustment recover the In escape mechanism present in the full system? Or, since removing drive reduces the excitation from the an active RG to the corresponding In and hence the inhibition to the silent RG, perhaps the mechanism controlling SCI oscillations is through RG escape, which we observed when we reduced excitation in a different way, through removing the feedback. It is also possible that the oscillations are due to an entirely different, hybrid mechanism. In this subsection, we explain why, after removing the drive, increasing the feedback strength to a sufficiently large value in fact recovers oscillations controlled by the In escape mechanism.

First, suppose we set d = 0 and initialize the limb with initial conditions corresponding to a point on a normal locomotor oscillation, existing for some d > 0, in either the eStance or fSwing phase (recall that eStance refers to the part of the stance phase with extensor neurons active, with similar definitions for other phases, as introduced in Section 2). A phase transition, to fStance or eSwing respectively, requires a change in which Mn is active, which in turn must follow from a switch of active and silent neurons in the CPG. Letting d = 0 raises the RG V-nullclines, such that fixed points move to more negative V values relative to the d > 0 case, for each fixed feedback value. Since the RG could not escape from the silent phase with the original drive, this change in nullcline position implies that they certainly cannot do so with d = 0. Moreover, the nullcline change weakens the output of the active RG and hence of the active Mn. The weaker Mn output reduces the magnitude of the limb velocity and correspondingly of the feedback signals to the CPG, making it harder still for the silent RG to escape and become active. For these weaker feedback signals, the only two possibilities are that the silent In escapes and causes a phase transition or limb velocity υ → 0 before a phase transition occurs, since the weaker feedback also may prevent In escape.

We observe both of these events in simulations, depending on initial conditions. In the former case, although the CPG makes a transition due to In escape, we still cannot guarantee that an oscillation will occur, because the fStance to fSwing or eSwing to eStance phase transitions may be compromised, as we explore in the next subsection. For the remainder of this subsection, we focus on the latter case, supposing that in the absence of supra-spinal drive, no phase transition can occur. We now explain why, if feedback strengths are increased enough to restore CPG phase transitions, these transitions will still occur through In escape. To do so, we suppose that we increase proportionally the weights w_i,j of all feedback terms in the model and consider the same initial condition as previously. The stronger feedback results in lowered RG V -nullclines with less negative V values at fixed points and also increases V̇ for the Ins. At the larger voltage associated with its new nullcline, the active RG provides a stronger output to its Mn, which results in an increased limb speed and helps push the feedback amplitudes fb_i back toward their d > 0 values. If the feedback Σ_iw_i,jfb_i to a silent In becomes as strong as it was with d > 0, then the In can escape (recall that the Ins do not receive supra-spinal drive). However, in this case the total input to the silent RG would be given by this d > 0 feedback signal alone (and no drive), and hence would be smaller than the original case where it received d > 0 as well. Since the RG could not escape even with the original signal (drive plus feedback), it certainly will not be able to do so given this new, weaker signal present with drive removed. While this argument is not precise, because the limb and feedback signals will undergo altered time courses with d = 0 relative to the d > 0 case, the main idea should nonetheless be clear: even when the feedback signal to the silent In is increased enough to allow it to escape, the loss of drive results in a weaker feedback signal to the silent RG, relative to that with drive present, which maintains its suppressed status, and hence CPG phase transitions remain under In control when increased feedback weights restore locomotor oscillations in the model.

In summary, there is a positive minimal feedback strength that is required for one or more CPG phase transitions to take place in the absence of supra-spinal drive. While the strength needed depends on initial conditions, those transitions that occur will do so via In escape. In the next subsection, we consider the possibility of sustained oscillations in the absence of supra-spinal drive.

4.2. Limb phase plane dynamics under SCI

An important alternative way to visualize the activity of the neuromechanical locomotor system is to project its dynamics onto its limb phase space. We will adopt this perspective to gain insight into how recovered oscillations attained by feedback increases under SCI differ in terms of limb amplitude and velocity profiles from oscillations with supra-spinal drive present and how oscillations can be lost in general if the motoneuron output to the limb becomes too low due to insufficient drive (or any other mechanism). The latter insight is important for fully characterizing the requirements that feedback must meet to restore oscillation capabilities in the absence of supra-spinal drive.

To achieve this visualization, we write equation (5) as a first order system to obtain

$$\mathrm{q̇}=\upsilon$$

$$I\mathrm{\upsilon ̇}=K\text{ cos}(q)-b\upsilon +M_F(q,\upsilon ,V_{\mathit{\text{Mn}}-F},t)-M_E(\pi -q,-\upsilon ,V_{\mathit{\text{Mn}}-E},t)+M_{\mathit{\text{GR}}}(q).$$ (10)

We can calculate the nullclines of this system as we did in RG phase space. Although this system does not feature a separation of timescales like system (1), its nullclines are still quite useful for understanding the behavior of its solutions. The q-nullcline, where q̇ = 0, is always fixed at υ = 0. The υ-nullcline, where υ̇ = 0, has a location that depends on the strength of motoneuron output and whether the ground reaction force is on or off. The trajectories shown in Figure 8A exhibit the general shape of one step in limb phase space. Also seen in Figure 8A is the TTC (equation 8) and the WTC (equation 9), the curves that indicate the location of where the CPG transitions from E active to F active (during stance) and F active to E active (during swing), respectively. These curves are functions of q and υ only, and thus are fixed in phase space. A successful oscillation occurs when the trajectory in limb phase space completes a path through all four phases, eStance, fStance, fSwing, and eSwing. Starting on the q-axis in the eStance phase, the limb trajectory moves through phase space until it hits the TTC. At this curve, the feedback to In - E has reached the critical value to push In - E across threshold, allowing it to begin inhibiting RG - F. This results in a switch in dominance in the CPG, and hence Mn - E shuts down and Mn - F turns on. This transitiom changes the right hand side of system (10), and hence the direction of the limb trajectory. Now in fStance, the trajectory moves with decreasing velocity until it hits the q-axis, which signals the end of the stance phase (equivalently, the beginning of the swing phase), terminating the ground reaction force and updating the right hand side of system (10) once more. The trajectory continues through the fSwing phase, now with decreasing angle until it hits the WTC, signaling the opposite dominance switch in the CPG. Mn - E then activates, and the trajectory passes through eSwing to return to the q-axis once more.

By plotting the dynamics in limb phase space, we can consider the concept of In escape in terms of the limb motions needed to generate the feedback forces required for this escape to occur. Provided that the trajectory transitions through each phase, that is, hits each switching manifold in succession, the system will perform a successful oscillation. By increasing the feedback after SCI, we alter the position of the transition curves from the normal case. In the full system, the TTC is calculated by the equation FB_{In -F} = FB_crit, where specifically, FB_{In -F} = w_{Ia - F,In - F} Ia - F + w_{II - F,In - F} II - F. Increasing the strength of the feedback after SCI means changing w_{Ia - F,In - F} and w_{II - F,I n- F} to larger values, $w_{\mathit{\text{Ia}}-F,\mathit{\text{In}}-F}^{\mathit{\text{SCI}}}\text{ and }{w}_{\mathit{\text{II}}-F,\mathit{\text{In}}-F}^{\mathit{\text{SCI}}}$. Thus, the TTC satisfies a new equation, ${\mathit{\text{FB}}}_{\mathit{\text{crit}}}=w_{\mathit{\text{Ia}}-F,\mathit{\text{In}}-F}^{\mathit{\text{SCI}}}\mathit{\text{Ia}}-F+w_{\mathit{\text{II}}-F,\mathit{\text{In}}-F}^{\mathit{\text{SCI}}}\mathit{\text{II}}-F$, the right hand side of which is still just a function of (q, v), but with updated coefficients. The WTC is analogously affected. Figure 8A shows the location of these curves after SCI, which have a closer proximity to one another than in the normal case, shrinking the range of q values over which the limb oscillates. By identifying this compression of transition curves, our analysis has revealed that it is the change in the source driving the In escape mechanism in SCI that results in a smaller amplitude oscillation.

By turning next to the relationship between the trajectory and the υ-nullcline in phase space, we can identify an important mechanism through why oscillations can fail and can also explain why velocity decreases slightly during part of the eStance phase in SCI. Figure 8B shows the υ-nullcline positions at a sequence of time points during the eStance phase, along with color coordinated dots indicating the position of the trajectory when each nullcline is defined. In the eStance phase, Mn - E is active while Mn - F is not; increasing (decreasing) the Mn - E output shifts the υ-nullcline upward (downward) in phase space. To the left of a particular υ-nullcline, υ̇ is negative, and to the right of a particular υ-nullcline, υ̇ is positive. Thus, if a trajectory enters the eStance phase to the left of this nullcline, it immediately exits the phase, and the system will not produce an oscillation. To prevent this phenomenon from occurring, the output of Mn - E has to be sufficiently strong at the transition from eSwing to eStance to allow the limb trajectory to enter on the right side of the υ-nullcline and accelerate away from the q-axis. In SCI, the output of Mn - E is weaker than in normal walking, since the CPG receives no drive in the former case, as discussed in subsection 4.1. Increasing the feedback strength, however, increases excitatory input to the CPG and to Inab - E, which results in stronger Mn - E output. Hence, increasing the feedback terms shifts the υ-nullcline upwards, so that the trajectory and υ-nullcline have a relationship that allows the limb to proceed through the eStance phase. In summary, for the recovery of oscillations under SCI, feedback must be strong enough to achieve two effects: it must allow In escape to occur and it must, via effects on Mn - E output, allow the limb to achieve a positive velocity at the onset of the stance phase.

In Figure 8B at phase onset, indicated in green, Mn - E output is sufficiently strong to allow the eStance phase to progress. Shortly after the phase begins, however, feedback Ib - E shuts down (due to decreased input from Mn - E) which causes the υ-nullcline to drop significantly. The nullcline does stabilize, because of the saturating form of the Mn - E output function, as is also evident in Figure 8B. By the time this occurs, the limb trajectory lies to the left of the nullcline (e.g., light blue dot and curve), but it has been able to accelerate to sufficiently large υ values before this reversal occurs. Thus, although the limb must travel with decreasing velocity, since υ̇ < 0 in this region, it is able to cross to the right of the υ-nullcline where υ̇ > 0 and avoid hitting the q-axis, which would have prevented it from completing the rest of the phase. Once the trajectory crosses the υ-nullcline, it maintains an increasing velocity until it reaches the TTC to complete the eStance phase. This transient switch to υ̇ < 0 causes the concave shape of the trajectory in the case without supra-spinal drive, displayed in red in Figure 8A.

Markin et. al. noted that increasing the feedback weights quickly reestablished oscillations, but that the movement of the limb remained unstable until Ib - E was increased more strongly (five fold) than Ia and II - F (which were increased by 31%) [14]. Our analysis elucidates why Ib - E is the optimal feedback to increase. Recall that force-dependent Ib - E is active only when the extensor neurons are. Thus, it does not contribute to the location of the WTC, since this curve is defined by the feedback to In -E when In - E is silent. It also does not affect the location of the TTC, which is a function of Ia-F and II - F. However, since it is active while RG - E is, Ib - E provides additional excitatory input to RG - E, PF - E, and Inab - E and therefore indirectly to Mn - E. Thus, strongly increasing Ib - E retains the qualitative structure of the transition curves (Figure 8A) but sufficiently raises the eStance υ-nullcline position to allow the limb to transition from the eSwing to the eStance phase.

Such variations in the υ-nullcline position, in addition to shaping limb dynamics without supra-spinal drive, contribute to the changes in oscillation frequency with changes in feedback strength observed when drive is present, as discussed in subsection 3.3 (Figure 7). These effects are in fact fundamental to the performance of the model and will be explored further in a companion paper [15].

5. Discussion

Given a model consisting of a system of differential equations, simulations can be used to explore model behavior. Dynamical systems analysis can yield insights about which model features are responsible for which aspects of the observed model outputs, what conditions are needed for particular model behavior to occur, and what other sorts of activity might be observed from a model. In this paper, we have used dynamical systems techniques to analyze important aspects of the behavior of a simple neuromechanical model of locomotion.

In Section 3, we investigated the difference in the transition mechanisms within the CPG between the case of fictive locomotion, without afferent feedback, and normal locomotion, with feedback. In the latter case, phase transitions occur when excitatory feedback signals allow interneurons within the CPG to escape from cross-inhibition. Thus, we would predict, for example, that providing a small boost in feedback to a suppressed interneuron would be a more effective way to promote a phase change than providing a small boost to a suppressed rhythm generating neuron would be and that decreasing feedback to interneurons would compromise locomotion more drastically than would diminishing feedback to rhythm generators. Since this transition mechanism is driven by the limb component of the system that generates the feedback, we could define transition curves in the phase plane associated with this component, which will be particularly useful in subsequent analysis of model dynamics [15]. Without feedback, the interneurons cannot escape, and hence oscillations can only occur through escape of suppressed rhythm generator neurons in the CPG, which in turn requires a sufficiently large supra-spinal drive. Thus, we explained the simulation result [14] that the range of supra-spinal drives yielding fictive locomotion is more limited than those supporting normal locomotion.

In a half-center type model that generates oscillations, increases in feedback strength can increase the period, by prolonging the activity of the dominant component, or decrease the period, by promoting the onset of activity in the suppressed component. The former effect occurs with transitions through release, while the latter occurs with escape-based transitions [23, 24, 19]. Thus, our identification of escape-based transitions in the neuromechanical model in both the fictive and normal cases explains simulation results that show a speed-up in oscillations with increased feedback. In Section 4, we showed that even with SCI, if oscillations are restored through increases in feedback, then these oscillations feature transitions by escape. The consistency in transition mechanisms, and hence in frequency responses to input variations, across these difference oscillation regimes is in agreement with the general idea that top-down and feedback sensory signals to a locomotor CPG can together synergistically encode a targeted locomotor speed, although the details of this encoding process remain to be further explored [26]. Moreover, we used the In escape mechanism to explain why restored oscillations in SCI feature a smaller limb amplitude than occurs in the normal case. The analytical expressions for stance and swing transition curves that we derived show how different feedback terms contribute to limb amplitude and thus how changes in such terms would alter oscillation features.

In Section 4, we also provided an explanation of why increased feedback strength can restore locomotor oscillations after spinal cord injury, simulated by removal of supra-spinal drive, in the model. This effect was explained in terms of the relative positions of the limb trajectory and the limb velocity nullcline in the phase space for the limb dynamics, particularly near the onset of the stance phase (eStance, since the extensor output is active). To our knowledge, this locomotor recovery, although observed experimentally with locomotor training of various types [3, 9, 10, 11, 12, 13], has not been analyzed using dynamical systems methods in previous models. Our analysis predicts that restored oscillations will be particularly susceptible to perturbations near the onset of stance and that modulation of Ib - E feedback signals would be particularly effective for restoring or speeding up oscillations under SCI. For the restored oscillations, we also observe that velocity can decrease during part of the eStance phase, due to a rapid change in Mn - E output strength resulting from the cessation of the Ib - E feedback signal, but that because this output saturates, velocity subsequently increases and the eStance phase can be completed. Interestingly, this analysis generalizes to imply that there will exist a critical curve in the space of feedback strengths and drive levels, such that parameter values above this curve are required to sustain oscillations, with more feedback needed as drive decreases. For example, partial restoration of drive effects via electrical stimulation or other manipulations could reduce the amount of training-induced feedback strength enhancement required for locomotion. A dip in the limb velocity profile during eStance may signify that the system is near this critical curve and hence lies in a state where it is particularly susceptible to lose its rhythmicity via alterations in Ib - E feedback and Mn - E output. On the other hand, we did not consider the possibility of restoration of locomotor oscillations via CPG reorganization, since we are not aware of experimental evidence supporting this mechanism.

The capability of CPG circuits to generate locomotor oscillations has received extensive attention in recent review papers with various perspectives [27, 28, 29]. Many authors have worked on models of locomotor CPGs or, of particular relevance to this work, on models of combined CPG and limb dynamics. Several of these works have treated highly simplified closed loop neuromechanical systems, focusing on resonance between the CPG and the limb or CPG entrainment by the limb [25, 30, 31, 32]. Perhaps the most relevant to our approach, in which we analyze transition mechanisms within the CPG under different feedback conditions, is work by Sekerli and Butera [33]. These authors distinguish multiple possible phase transition mechanisms in their neuromechanical model, but these all involve the effects of feedback inhibition from the mechanical component to a half-center CPG, treated in as a synaptic current. In the model that we consider, all feedback signals are excitatory and the signals are more complicated, derived based on muscle stretch and velocity and motoneuron outputs [14]. Indeed, while dynamical systems methods have been used to understand CPG gait rhythm generation or closed loop neuromechanical model dynamics with perturbative feedback signals (e.g. [34, 35]), dynamical systems analysis of a closed loop neuromechanical locomotor model with excitatory, continuous or piecewise continuous afferent feedback signals (see especially [15]) still represents a frontier in this area.

While the model that we analyze is complex from a mathematical point of view, it is undoubtedly extremely simplified relative to the actual spinal/limb interactions that occur in vivo. The CPG component of our model is minimal, comprised of extensor and flexor rhythm generator neurons, interneurons, and pattern formation neurons, each represented by a single model neuron. Furthermore, the limb in the model is a simple, single-joint segment, able to move with only one degree of freedom through the actions of only two antagonistic muscles, and the interaction of the limb and ground is incorporated in a very basic way that neglects many possible effects. Future work to address these limitations will be important, as will additional modeling to incorporate the control and interaction of multiple limbs and corresponding CPG units.

In a companion paper, we develop methods and apply them to analyze additional properties of the neuromechanical model presented in this work [15]. In particular, we analyze in greater detail the dynamic mechanisms that control the generation of oscillations in the model and constrain the properties of these oscillations. Furthermore, we explain the mechanisms through which the model, despite the symmetry between its extensor and flexor CPG components, yields an asymmetric response to changes in drives, manifested in the observation that stance duration depends strongly on drive while swing duration does not. These mechanisms relate to the relationship between the limb velocity nullcline and limb trajectory in the phase plane, exploited here to understand oscillation dynamics under SCI.

Appendix

The following provides details on model functions and parameter values not specified in the main text.

CPG related terms

In equations (1),(2),(3),(4), C is the membrane capacitance, E_j denotes the reversal potential of current j, ḡ_j is the maximal conductance of the current, a_ji is the weight of the excitatory input from neuron j to neuron i, b_ji is the weight of the inhibitory input from neuron j to i, c_i is a factor scaling the drive d to neuron i, fb_k denotes the kth feedback signal, and w_k,i is the weight of that feedback to neuron i. Parameter choices associated with these currents are: C = 20 pF, E_Na = 55 mV, E_K = −80 mV, E_SynE = −10 mV, E_SynI = −80 mV for all neurons; E_Leak = −64 mV for the RG, PF, and Mn and E_Leak = −60 mV otherwise; ḡ_K = 4.5 nS, ḡ_Leak = 1.6 nS, ḡ_SynE = 10 nS, ḡ_SynI = 10 nS, ḡ_NaP = 3.5 nS for RG, ḡ_NaP = 0.5 nS for PF, ḡ_NaP = 0.3 nS for Mn. The values of the weights are provided in Table 2. We also note that Inab - E receives a second drive of strength 0.18, in addition to d.

Table 2.

Synaptic connection weights in the model.

Target neurons
	RG - F	RG - E	In - F	In - E	PF - F	PF - E	Mn - F	Mn - E	Int	Inab - E
Excitatory Connections, aji
RG - F			0.41		0.70
RG - E				0.41		0.70
PF - F							1.95
PF - E								1.30		0.35
Inab - E								0.82
Inhibitory Connections, bji
In - F			2.20			6.60
In - E	2.20				6.60				2.80
Int										0.55
Feedback Connections, wki
Ia - F	0.06		0.27		0.19
II - F	0.0348		0.1566		0.1102
Ia - E		0.06		0.44		0.10				0.16
Ib - E		0.066		0.484		0.11				0.176
Drive Connections, ci
Supra-spinal drive, d	0.08	0.08			0.40	0.40
External drive, dInt								0.18

The nonlinear function f defines the neuron output and is described as follows:

$$f(V)=\{\begin{array}{cc}1/(1+\text{exp}(-(\frac{V-V_{1/2}}{k})))\hfill & \text{if }V\ge V_{\mathit{\text{th}}};\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}$$ (11)

where V_1/2 is the half-activation voltage, k defines the slope of the output function, and V_th is the threshold for each neuron. V_1/2 = −30 mV, k = 3mV for Mn and k = 8mV for all other neurons, and V_th = −50 mV.

For each motoneuron voltage variable V, we also define a variable x with x′ = f(V) − x. Following Markin et al. [14], we use x rather than f(V) for defining transitions between eStance and fStance and between fSwing and eSwing (including for plotting transition curves in Figure 8A), for plotting motoneuron outputs (Figure 1), and for computing average Mn outputs in our subsequent paper [15]. The use of x, which slightly lags f(V), contributes to the small time differences between the dominance switches of the In used to define the TTC and WTC and the times defined for the transitions from eStance to fStance and from fSwing to eSwing, as mentioned in Section 3. A second factor in this difference is that there is a delay from In escape to the corresponding RG activation that drives Mn outputs. These time differences are all small and do not appear to affect the behavior of the model.

Voltage dependent activation and inactivation functions for the potassium rectifier and persistent sodium currents and timescale function for the persistent sodium current are:

$$m_K=1/(1+\text{exp}(-\frac{V+44.5}{5}));$$

$$m_{\mathit{\text{NaP}}}=1/(1+\text{exp}(-\frac{V+47.1}{3.1}));$$

$$h_{\mathrm{\infty }}=1/(1+\text{exp}(\frac{V+51}{4}));$$

$${\tau }_h={\tau }_{\mathit{\text{hmax}}}\text{cosh}(\frac{V+51}{8}),$$

where τ_hmax=600 ms.

Limb related terms

In the limb equation, K = 0.5mgl_s and $I={\mathit{\text{ml}}}_s^2/3$, where m = 300g denotes the mass of the segment, l_s = 300mm denotes its length, g = 0.0098 mm²/ms², b = 18000 g·mm²/ms², and M_GRmax = 585N·mm.

Muscle related terms

The muscle length is calculated as $L=\sqrt{a_1^2+a_2^2-2a_1{a}_2\text{ cos}(q)}$, and the moment arm h = (a₁a₂ sin(q))/L for the flexor muscle. The same equations are used for the extensor muscle, where q is replaced with π−q. Here, a₁ denotes the distance between the suspension point and the muscle origin and a₂ denotes the distance between the suspension point and the muscle attachment to the segment, where a₁ = 60 mm and a₂ = 7 mm.

The muscle velocities are defined as ${\upsilon }_F^m=\upsilon h_F\text{ and }{\upsilon }_E^m=-\upsilon h_E$. Here, q̇ = υ denotes the limb angular velocity and h_F, h_E denotes the moment arm of each corresponding muscle, outlined previously.

The muscle forces F_E and F_F were computed by F = f(V)F_maxF_lF_v where f is given in equation (11) and describes the output of Mn - E or Mn - F, respectively, and F_max = 72.5N and 37.7N for the flexor and extensor muscles, respectively;

$$F_l=\text{exp}({|\frac{l·\beta -1}{w}|}^{\rho })$$

describes the force dependence on muscle length, where β = 2.3, ω = 1.6, ρ = 1.62 and l is the normalized muscle length corresponding to F_l = 1, i.e. l = L/Lopt for Lopt = 68 mm; and

$$F_{\upsilon }=\{\begin{array}{cc}\frac{b_1-c_1·{\upsilon }^m}{{\upsilon }^m+b_1}\hfill & {\upsilon }^m<0\hfill \\ \frac{b_2-c_2(l)·{\upsilon }^m}{{\upsilon }^m+b_2}\hfill & {\upsilon }^m\ge 0\hfill \end{array}$$

describes the dependence of force on velocity, where c₁ = 0.17, b₁ = −0.69, b₂ = 0.18, and c₂(l) = −5.34l² + 8.41l − 4.7.

Given the above, the muscle moments are defined as M_F = F_Fh_F and M_E = −F_Eh_E.

Feedback related terms

Finally, the afferent feedback equations are derived from Prochazka [36, 37] as:

$$\mathit{\text{Ia}}=k_{\mathit{\text{IaV}}}{\upsilon }_{\mathit{\text{norm}}}^{p_{\upsilon }}(q,\upsilon )+k_{\mathit{\text{dIa}}}{d}_{\mathit{\text{norm}}}(q)+k_{{\mathit{\text{EMG}}}_{\mathit{\text{Ia}}}}f(V_{\mathit{\text{Mn}}})+C_{\mathit{\text{Ia}}};$$

$$\mathit{\text{Ib}}-E=k_{\mathit{\text{Ib}}}{F}_{\mathit{\text{norm}}}(V_{\mathit{\text{Mn}}-E});$$

$$\mathit{\text{II}}-F=k_{\mathit{\text{dII}}}{d}_{\mathit{\text{norm}}}(q)+k_{{\mathit{\text{EMG}}}_{\mathit{\text{II}}}}f(V_{\mathit{\text{Mn}}-F})+C_{\mathit{\text{II}},}$$

where υ_norm denotes the normalized muscle velocity (υ^m/L_th), d_norm is the normalized muscle lengthening: (L−L_th)/L_th if L ≥ L_th, 0 otherwise, with L_th = 59mm, and F_norm is the normalized muscle force: (F − F_th)/F_max if F ≥ F_th and 0 otherwise, with F_th = 3.38 N.

As mentioned above, the function f(V) given in equation (11) describes the output of the motoneurons, while the remaining terms in the feedback functions are constants that take the values ρ_v = 0.6, k_Iav = 6.2, k_dIa = 2, k_EMGIa = 0.06, C_Ia = 0.26, k_Ib = 1, k_dII = 1.5, k_EMGII = 0.06, and C_II = 0.