Accuracy assessment of CKC high-density surface EMG decomposition in biceps femoris muscle

Abstract

The aim of this study was to assess the accuracy of the Convolution Kernel Compensation (CKC) method in decomposing high-definition surface EMG (HDsEMG) signals from the pennate biceps femoris long-head muscle. Although the CKC method has already been thoroughly assessed in parallel-fibered muscles, there are several factors that could hinder its performance in pennate muscles. Namely, HDsEMG signals from pennate and parallel-fibered muscles differ considerably in terms of the number of detectable motor units (MUs) and the spatial distribution of the motor-unit action potentials (MUAPs). In this study, monopolar surface EMG signals were recorded from 5 normal subjects during low-force voluntary isometric contractions using a 92-channel electrode grid with 8 mm inter-electrode distances. Intramuscular EMG (iEMG) signals were recorded concurrently using monopolar needles. The HDsEMG and iEMG signals were independently decomposed into MUAP trains, and the iEMG results were verified using a rigorous a-posteriori statistical analysis. HDsEMG decomposition identified from 2 to 30 MUAP trains per contraction. 3±2 of these trains were also reliably detected by iEMG decomposition. The measured CKC decomposition accuracy of these common trains over a selected 10 second interval was 91.5±5.8 %. The other trains were not assessed. The significant factors that affected CKC decomposition accuracy were the number of HDsEMG channels that were free of technical artifact and the distinguishability of the MUAPs in the HDsEMG signal (P<0.05). These results show that the CKC method reliably identifies at least a subset of MUAP trains in HDsEMG signals from low force contractions in pennate muscles.

1. Introduction

The intramuscular EMG (iEMG) signal recorded by a needle or fine-wire electrode has been used for over 80 years (Adrian and Bronk 1929) to investigate the behavior of individual motor units (MUs). Although muscular activity can easily be recorded by a pair of electrodes on the skin surface, individual MU discharges cannot be easily distinguished in surface EMG (sEMG) signal. As result, sEMG signals have typically been analyzed as interference signals, from which the properties of individual MUs can be inferred only indirectly (Merletti and Parker 2004, Merletti et al 2008). This interpretation, however, is difficult and often prone to erroneous conclusions (Farina et al 2004, Zhou and Rymer 2004).

The recently developed technique of high-density surface EMG (HDsEMG) uses multiple electrodes on the skin surface to obtain a more detailed picture of the sEMG activity (see the following reviews: Drost et al 2006, Merletti et al 2008). Several methods have been developed to make use of the more detailed information provided by the HDsEMG signal to identify individual MU discharge trains (Rau and Disselhorst-Klug 1997, Kleine et al 2000, Hogrel 2003, Holobar and Zazula 2004, Gazzoni et al 2004, Zazula and Holobar 2005, De Luca et al 2006, Holobar and Zazula 2007, Kleine et al 2007, Kleine et al 2008). Since HDsEMG is non-invasive, these methods offer great promise for investigations of MU behavior. However, because they are quite complex it is important to thoroughly verify their accuracy.

In this paper, we assess the accuracy of the Convolution Kernel Compensation (CKC) decomposition method (Holobar and Zazula 2004, 2007) on HDsEMG signals from the biceps femoris long head muscle (BFlh). BFlh, along with biceps femoris short head, semimembranosus, and semitendinosus, constitute the “hamstring” muscles of the posterior compartment of the thigh. BFlh is the strongest and most commonly injured of the hamstring muscle group (Garrett et al 1989, Garrett 1996, Slavotinek et al 2002, Woods et al 2004, Hoskins and Pollard 2005), although multiple injury locations are also possible (De Smet and Best 2000).

BFlh is a pennate muscle, whereas the muscles studied in a previous CKC validation (Holobar et al 2010), which included biceps brachii, tibialis anterior, and abductor digiti minimi, were parallel-fibered. CKC decomposition results from BFlh differ from the results from the other muscles in several respects. Many more distinct MUs are detected in BFlh than in the other muscles, and the spatial distribution of the motor-unit action potentials (MUAPs) is quite different, resulting in more complex interference patterns on the surface of the skin. Moreover, the MUAPs in BFlh do not exhibit clear signs of action-potential propagation. Thus it is not possible, as it is in parallel-fibered muscles, to use evidence of appropriate propagation as an indication of a MUAP’s physiological consistency. For these reasons, it was of interest to perform a separate assessment of decomposition accuracy in BFlh.

We assessed the decomposition accuracy using the so-called “two-source” approach (De Luca et al 2006, Holobar et al 2009, Holobar et al 2010), which is widely accepted as reliable. This involved comparing the HDsEMG decompositions with decompositions of simultaneously recorded iEMG signals. Because the characteristics of the surface and intramuscular signals are so different, it is very unlikely that exactly the same errors will arise in both decompositions. Therefore the rate of agreement between the two decompositions provides a lower bound on the accuracy of the HDsEMG decomposition.

The analysis was limited to MUs that were seen reliably enough in the iEMG signal to be highly confident about their precise discharge times. In this way it was possible to obtain a firm estimate of the accuracy of the HDsEMG decomposition of these MUs, not just a lower bound. Limiting the analysis in this way should not have biased the results since the discriminability of MUs in the HDsEMG and iEMG signals are not directly related. The discriminability of a MU in the surface signal depends on the global architectural properties of the MU, including the total number of fibers and their spatial distribution. The discriminability of the same MU in the intramuscular signal depends on how close the intramuscular electrode happens to be to one of the fibers, and is a more-or-less random function of the precise electrode location. The intramuscular electrode essentially selects a random sample of MUs which are representative of the entire set.

Part of this material was presented previously in abstract form (Marateb et al 2010).

2. Materials and methods

Five healthy male subjects participated in this experiment (mean ± SD, age: 35 ± 5.2 years; stature: 1.79 ± 0.05 m; body mass: 80 ± 7.5 kg). Subjects did not have any history of neuromuscular disorders, pain, or regular training of the lower limb. All subjects gave informed consent to the experimental procedure. The experimental protocol was approved by the Stanford University Panel on Medical Human Subjects and conformed to the Declaration of Helsinki.

2.1 General setup

Each subject lay prone on a bed with the knee of the left leg flexed at 45° and the thigh in slight lateral rotation (following the SENIAM recommendations, Hermens et al 1999). A cuff was placed around the ankle to measure isometric knee flexion torque. The skin of the left thigh was shaved, then gently abraded using abrasive paste (Meditec–Every, Parma, Italy), and then cleaned with water in accordance with the SENIAM recommendations for skin preparation (Hermens et al 2000). Two adhesive two-dimensional grids of 64 electrodes (1-mm diameter, 8-mm inter-electrode distance (IED), 13 rows and 5 columns with the first corner electrode missing, SpesMedica, Italy) were concatenated to form a 5 column by 25 row array. This composite electrode was centered along the line between the ischial tuberosity and the lateral side of the popliteus cavity with its long axis parallel to that line (Rainoldi et al 2004). Prior to placement, the alignment of the electrode was verified by palpating the BFlh during flexion and lateral rotation of the knee against resistance at the ankle (Kendal et al 1993). The electrode was then attached to the skin using double adhesive foam and adhesive tape. The electrode holes were filled with Ag/AgCl gel (SpesMedica, Italy) except for row 13, which was unavailable because of the concatenation, and row 10 and column 3, which were used for needle insertions. Three monopolar needle electrodes (27 gauge, 37 mm) were inserted into the muscle through three of the unfilled holes.

2.2 Data acquisition

The HDsEMG signal was recorded in monopolar configuration (EMG-USB-128 channels, sampling frequency of 2048 Hz, 3dB bandwidth 10–750 Hz, 12 bit AD conversion, LISiN-OT Bioelettronica, Italy). Power line interference was reduced by using a driven right leg (DRL) circuit. The DRL-IN and the patient reference straps were connected to the left hand wrist, while the DRL-OUT electrode was connected to the right hand wrist. The monopolar iEMG signals were amplified with filter settings of 5 Hz-5 kHz (Nicolet Viking, US), sampled at 10 kHz and 12 bit resolution, and stored on a Macintosh computer, with the monopolar reference located proximal to the surface electrode and the ground electrode located on the medial knee. The iEMG and HDsEMG signal recordings were synchronized by trigger pulses generated from the iEMG recording system. The knee flexion force was measured using a load cell and custom made amplifier, and recorded concurrently with the EMG signals though an auxiliary input of the EMG-USB system with a sampling frequency of 2048 Hz. The force value was also provided as a feedback to the subject on a circular bar graph display. The iEMG signals were also high-pass filtered at 1 kHz and displayed in real time to enable the investigators to visualize the signal complexity and quality during the experiment.

2.3 Experimental protocol

The maximum voluntary contraction (MVC) force was estimated as the greatest of the force levels expressed in two maximal contractions of 5-s duration, which were separated by 2 min of rest. After an additional 5 min of rest, the subjects performed isometric constant-force knee flexion contractions, each lasting 20 s. Three isometric contraction levels were used: a very low level in which the subject maintained the limb against gravity (a.g.), and 5%, and 10% MVC. Audio feedback of the iEMG signals was provided to help the subjects maintain steady contractions (Hockensmith et al 2005, Moritz et al. 2005). Visual feedback of force was also provided for the 5% and 10% MVC contractions. One or more of the needle electrodes was moved to a new location after each set of contractions.

2.4 Data analysis

The HDsEMG signals were decomposed using the CKC technique (Holobar and Zazula 2007). Prior to the decomposition, the quality of HDsEMG signals was manually assessed and “bad” channels (either due to the bad electrode-skin contact or short circuit between two or more surface electrodes) were discarded. Only “good” channels were used for CKC decomposition. Although the CKC technique is fully automated, a quick visual inspection and editing of the decomposition results was performed by an experienced operator (20 ± 10 minutes of editing time per contraction).

The iEMG signals were decomposed by an experienced investigator using the EMGlab computer-aided decomposition tool (http://www.emglab.net, McGill et al 2005). The investigator checked and edited the results to make sure that the identified firing patterns were smooth and regular and that all the activity in the signal was accounted for. On average, 10 hours were spent on editing the three iEMG signals in each contraction.

The accuracy of the iEMG decompositions was assessed using a rigorous a-posteriori statistical analysis (McGill and Marateb 2011). This analysis used statistical decision theory in a Bayesian framework to integrate all the shape- and firing-time-related information in the signal in order to compute an objective a-posteriori measure of confidence in the accuracy of each discharge in the decomposition. Each discharge was then rated as highly confident if it was found to be accurate to within ±0.5 ms with a confidence level of > 99%, as approximate if it was found to be accurate to within ±5.0 ms with a confidence level of > 95%, and as uncertain otherwise. In cases in which the same MU was detected in more than one channel, the channel in which the MUAP had the highest signal-to-noise ratio was used. Only MUs that had no uncertain discharges were used for the CKC accuracy assessment.

The mean discharge rate (MDR) and coefficient of inter-spike interval variation (CoV) of each MUAP train were estimated using the algorithm described in (McGill 1984), which is robust against missing and erroneous discharges. Monopolar surface MUAP shapes as detected by the electrode grid were estimated by spike-triggered averaging on a 20 ms time window using the MU discharge times detected by iEMG or HDsEMG decomposition. The mean of the RMS amplitude of the surface MUAP shapes was also calculated over all HDsEMG channels. For each identified MU in the HDsEMG signal, the composite decomposability index (CDI) was computed as described in Holobar et al. (2010). This is an index of how distinguishable the MU was from all the other MUs in the HDsEMG signal. The overall quality of the HDsEMG decomposition was assessed in terms of the signal-to-interference ratio (SIR) (Holobar et al. 2010), which is an estimate of the percentage of the variance of the signal’s energy in the single-differential HDsEMG signal that was explained by the decomposition.

2.5 CKC accuracy assessment

In accordance with CKC recommendations (Holobar et al., 2010), HDsEMG MUAP trains that were incomplete (having fewer than 30% of the number of discharges expected on the basis of estimated MDR) or excessively irregular (CoV > 0.3) were rejected as potentially unreliable. The remaining HDsEMG MUAP trains were compared with the confidently decomposed iEMG MUAP trains. A pair of trains was considered to match if at least 30% of the discharges were time-locked to within ± 0.5 ms (after correcting for a possible fixed offset due to the different registration points in the two signals).

For each pair of matching MUAP trains, a 10-s analysis window was selected within the 20-s recorded signal for assessing the CKC accuracy. This window was selected so that it only contained iEMG discharges that had been rated as highly confident or approximate, and so that it did not begin or end within 100 ms of the edges of the overall recording window (in order to avoid the possibility that the corresponding HDsEMG discharge might lie outside the recording window). If no such window could be found, then this pair was not assessed.

The following parameters were calculated for the iEMG MUAP train:

• n_I, the total number of discharges that fell within the analysis window.

• n_IC, the number of those discharges that were rated as highly confident.

The accuracy of the iEMG MUAP train was then calculated as follows: n

$${\mathit{Accuracy}}_{\mathit{iEMG}}=\frac{n_{IC}}{n_I}$$ (1)

The following parameters were calculated for the HDsEMG MUAP train:

• n_SC, the number of discharges in the analysis window that matched a highly confident iEMG discharge within ± 0.5 ms. These were considered to be correct.

• n_SF, the number of discharges that did not match any iEMG discharge to within ± 5.0 ms. These were considered to be false positives.

The accuracy of the HDsEMG MUAP train was then calculated as follows:

$${\mathit{Accuracy}}_{\mathit{HDsEMG}}=\frac{n_{SC}}{n_{IC}+n_{SF}}$$ (2)

This formula assigned an accuracy of 100% if the HDsEMG train matched all the highly confident iEMG discharges to within ± 0.5 ms. The accuracy was decreased for each missed HDsEMG discharge and each false positive. HDsEMG discharges that matched approximate iEMG discharges were not counted one way or the other.

2.6 Statistical Analysis

Statistical analysis for comparing two independent samples involved parametric (t-test) and non-parametric (Mann-Whitney) tests at the 95% confidence level. Univariate regression analysis including type II sum of square was used to test for significant differences between unbalanced study groups (Langsrud 2003). The stepwise method of Multiple Linear Regression (Hosmer and Lemeshow 2000, Kutner et al 2004) was used to determine the significance of the relationship between the CKC accuracy (dependent variable) and the number of “good” channels in the HDsEMG signal, CDI, SIR, and force level (independent variables). Normality and homoscedasticity, two standard assumptions of regression diagnostics and model evaluation, were verified by Saphiro-Wilk’s test and Leven’s test, respectively. The goodness of fit of the regression was evaluated using adjusted multiple coefficient of determination (adj R²) as the most appropriate measure of R² for small samples. Data was analyzed using STATA 10, a statistical software package (StataCorp 2007).

3. Results

A total of 50 simultaneous HDsEMG and iEMG recordings were analyzed. 644 MUAP trains were identified in the HDsEMG signals, of which 1 was rejected due to an incomplete firing pattern. 1054 MUAP trains were identified in the iEMG signals, of which 60 were rejected because of incomplete firing patterns (mostly MUs that were recruited or de-recruited during the recording epoch). Thus 643 and 994 MUAP trains were analyzed from the HDsEMG and iEMG signals respectively. A total of 163 MUAP trains were found to have been identified in common (3 ± 2 per contraction). Of these, 148 had confident iEMG decompositions and were used in the accuracy assessment.

3.1 MU characteristics

The discharge characteristics of the identified MUs are shown in Table 1. The discharge characteristics of the MUs identified by HDsEMG and iEMG at the different levels of contraction were very similar. In particular, the MUs used in the accuracy assessment did not differ significantly from the entire set of HDsEMG MUs (Mann-Whitney Test; P > 0.05).

Table 1.

Firing statistics of the identified MUs

Level	MDR (pps)			CoV (%)
	HDsEMG	iEMG	Assessed	HDsEMG	iEMG	Assessed
a.g.	8.5±1.5	9.3±2.0	8.8±1.4	15±5	13±5	13±3
Nr=20	N=213	N=388	N=51
5% MVC	8.5±1.5	8.7±1.8	8.8±1.1	14±4	14±4	12±3
Nr=15	N=234	N=290	N=55
10% MVC	9.4±4.0	9.1±1.9	9.0±1.2	14±4	14±5	12±4
Nr=15	N=196	N=316	N=42

MDR: mean discharge rate; CoV: coefficient of interspike-interval variability; a.g.: against gravity; N: total number of MUs; Nr: total number of recordings.

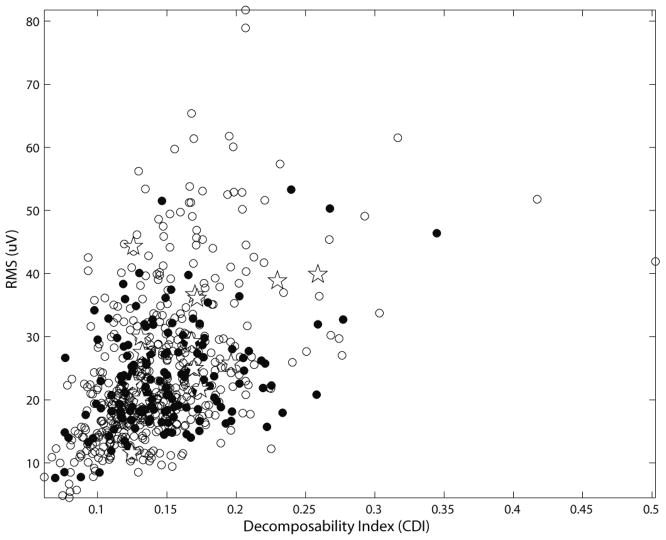
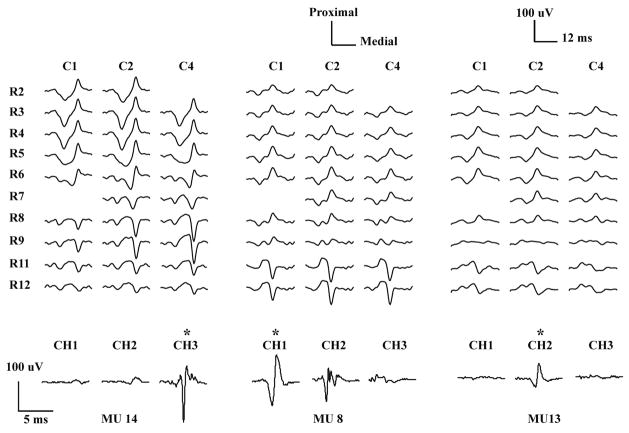
The surface RMS amplitudes and the CDIs of the identified MUs are shown in Figure 1 and Table 2. As can be seen in Figure 1, the characteristics of the MUs used for assessment (filled circles) were representative of the entire set of HDsEMG MUs (all symbols). The 15 common MUs that were rejected because of unreliable iEMG decomposition (crosses) were not noticeably biased toward lower RMS or CDI values. The surface RMS amplitudes of the MUs identified only in the iEMG signal were slightly, but not significantly, smaller than those of the MUs detected in the HDsEMG signal (independent two-sample t-test; P > 0.05). Figure 2 shows the HDsEMG and iEMG MUAPs of three of the MUs used for the accuracy assessment. The HDsEMG MUAPs can be seen to be standing waves with no visible propagation.

Figure 1.

Amplitude and decomposability of the HDsEMG MUAPs. The MUs that were reliably detected in the iEMG signal (filled circles), unreliably detected in the iEMG signal (pentagrams), and not detected in the iEMG signal (open circles) all had roughly similar distributions.

Table 2.

Amplitude and distinguishability of the HDsEMG MUAPs

Level	RMS (μV)				CDI
	HDsEMG	iEMG only	Common		Common
			Assessed	Rejected	Assessed	Rejected
a.g.	20±8	17±8	21±6	29±9	0.16±.04	0.16±.03
Nr=20	N=213	N=337	N=51	N=5	(0.09–0.28)	(0.12–0.20)
5% MVC	18±6	18±5	20±7	-	0.13±.03	-
Nr=15	N=234	N=235	N=55	N=0	(0.07–0.20)
10% MVC	23±9	21±7	25±8	28±9	0.14±.03	0.17±.05
Nr=15	N=196	N=274	N=42	N=10	(0.09–0.24)	(0.12–0.26)

CDI: composite decomposability index; a.g.: against gravity; N: total number of MUs; Nr: total number of recordings.

Figure 2.

HDsEMG and iEMG MUAP waveforms of three MUs averaged from a 10% MVC contraction. The top traces show the unfiltered monopolar HDsEMG waveforms from ten rows (R2–R11) and three columns (C1, C2, C4) of the 2-D array electrode. The bottom traces show the corresponding iEMG waveforms from three needle electrodes, high-pass filtered at 1 kHz. Two “bad” HDsEMG channels (R2C4, R7C1) were excluded from the CKC decomposition analysis. R10 and C3 were not available since they were reserved for needle insertion. For each MU, the iEMG channel used in the accuracy assessment procedure is shown with a star.

3.2 CKC Accuracy

The average number of MUs identified per contraction and the accuracy of the decompositions of the assessed MUs are listed in Table 3. On average, 95 ± 6% of the discharges of the assessed MUs were confidently seen in the iEMG signal and so were included in the analysis. The accuracy of the CKC decompositions was 91.5 ± 5.8%. No significant differences were found in the CKC accuracy between the different contraction levels (univariate regression analysis; P>0.05).

Table 3.

Decomposition Accuracy

Level	Number of identified MUs			SIR (%)	Accuracy (%)
	HDsEMG	iEMG	Assessed	HDsEMG	iEMG	CKC
a.g.	9±5	17±6	3±2	15±7	95±4	92±5
	(2–25)	(8–30)	(0–5)	(4–26)	(85–100)	(74–99)
5%	16±7	20±8	4±2	17±6	97±3	90±7
MVC	(6–30)	(9–39)	(0–6)	(7–26)	(91–100)	(70–97)
10% MVC	12±6	20±9	3±2	16±6	92±11	91±6
	(6–26)	(7–41)	(0–7)	(6–25)	(65–100)	(74–100)

SIR: signal-to-interference ratio; a.g.: against gravity.

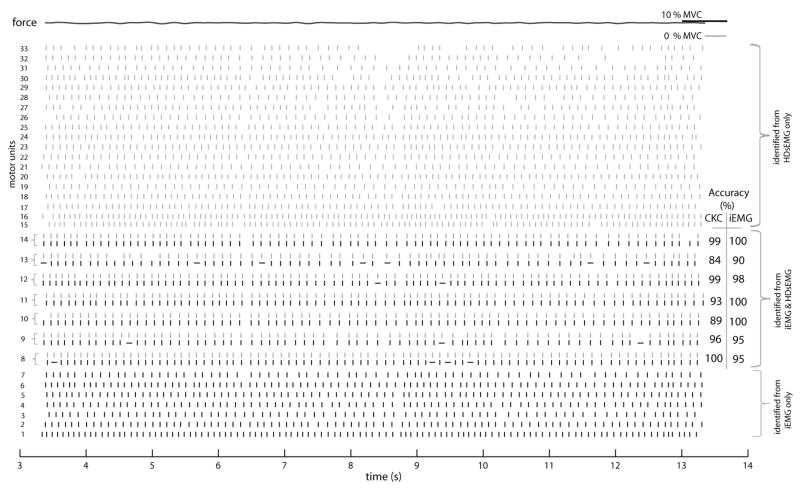
Figure 3 shows an example of the MUAP trains identified during a contraction of 10% MVC. In this case, 7 common MUs were assessed out of 14 and 26 MUs identified by iEMG and HDsEMG decomposition, respectively. Figure 4 shows the spatial distribution of three HDsEMG MUAPs with different CKC accuracies.

Figure 3.

MUAP trains identified from the HDsEMG signal (gray) and iEMG signal (black) from an isometric, constant force contraction at 10% MVC (the same contraction as in Figure 2). Each vertical line indicates a MU discharge at a given time instant. MUs 8–14 were identified in common in both the HDsEMG and iEMG signals. For these MUs, the highly confident and approximate firings in the iEMG signal are shown by vertical and horizontal lines, respectively. The force trace is shown at the top and the CKC accuracy of the common MUs is also shown.

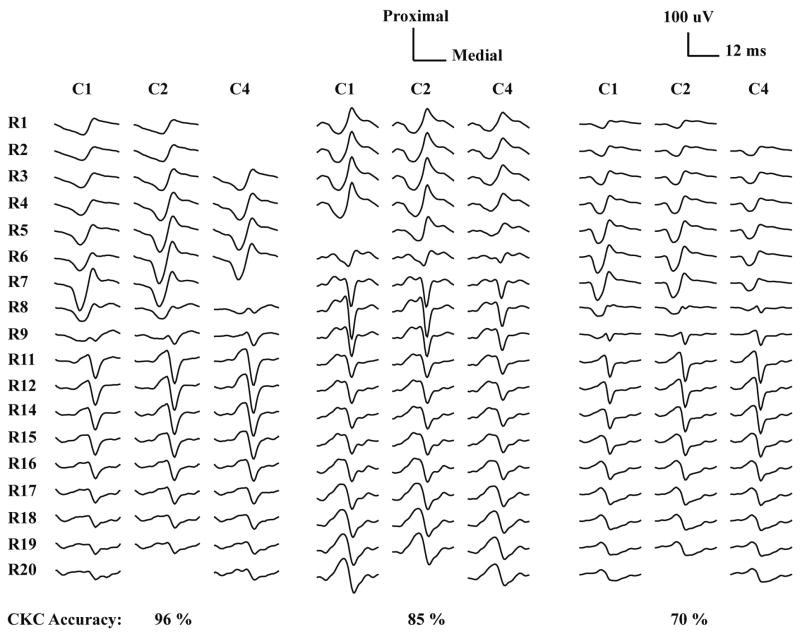
Figure 4.

Monopolar HDsEMG MUAP waveforms of three MUs from different signals that were decomposed with very high (96%), moderate (85%), and low (70%) accuracy. “Bad” channels are left blank and R10, R13 and C3 were not available since they were reserved for needle insertion.

3.3 Factors affecting the CKC Accuracy

Multiple Linear Regression models produced adequate fits (adj R²=0.97) on the transformed CKC accuracy and the Mean Square Error (MSE) value was 0.05. Preserving the regression assumption of homoscedasticity, arcsine square-root transformation was used on the CKC accuracy as proposed for the proportional data in the literature (Draper and Smith 1998, Montgomery et al 2001). Absence of multicollinearity was verified after analyzing the correlations among the different independent variables and the variance inflation factor collinearity diagnostic. The regression results showed that, in the BFlh muscle, only CDI and the number of “good” HDsEMG channels were significant (p < 0.05) in our model (Table 4).

Table 4.

Multiple linear regression model

adj R2 = 0.97, F=1158, p < 10−3
Dependent variable = transformed CKC accuracy
Predictor variable	Unstandardized Coefficients		p-value
	Beta	SE
CDI	2.80	0.350	0.000a
Force level	0.010	0.005	0.065
Number of “good” channels	0.033	0.001	0.000a
SIR	0.003	0.005	0.529

^aSignificant independent variables (p < 0.05)

4. Discussion and Conclusions

This study assessed the accuracy of the CKC algorithm in decomposing HDsEMG signals from the pennate BFlh. The assessment was performed by comparing the CKC results with decomposition results from simultaneously recorded iEMG signals. Only highly reliable iEMG results were used in order to provide an objective reference against which to assess the accuracy of the CKC results. This should not have biased the results, because the discriminability of a MUAP in the iEMG signal depends on the location of the intramuscular electrode and is not directly related to the discriminability of the same MUAP in the surface signal. The analysis was limited to a 10-s segment of the overall signal that contained only highly confident iEMG discharges. The choice of a selected segment might have led to an accuracy greater than that that would have been obtained from the entire 20s signal. The assessment was also limited to low level, constant force isometric contractions, which made it possible to verify the accuracy of the iEMG decompositions using a rigorous statistical approach (McGill and Marateb, 2011).

Only MUs for which all the iEMG discharges could be verified to be accurate to within ± 5 ms at a 95% level of confidence were included in the analysis. For these MUs, only those discharges that could be verified to be accurate to within ± 0.5 ms at a 99% level of confidence were included in the HDsEMG assessment. To receive this “highly confident” rating, the MUAP template had to match the iEMG signal to within the level of the background noise, the discharge time had to fit consistently into the MU’s firing pattern, and there had to be no other MUAP or MUAP combination for which this was the case. Some iEMG discharges could only be verified to be accurate to within ± 5 ms. It was assumed that the uncertainty of these discharges in the iEMG signal was due to noise in the iEMG signal that would not necessarily affect the detection of the discharge in the HDsEMG signal. Therefore these discharges were not included in the HDsEMG assessment.

The criterion for assessing the accuracy of the HDsEMG MUAP trains was fairly stringent. To be considered correct, an HDsEMG discharge had to agree with the iEMG discharge to within ± 0.5 ms. If the sEMG discharge only agreed within ± 5 ms it was counted as a single error (imprecise detection), and if it disagreed by more than 5 ms it was counted as two errors (a miss and a false positive).

To illustrate these points, consider MUs 8 and 11 in Figure 2. The iEMG decomposition identified 85 discharges of MU 8, 81 of them with high confidence and 4 only to within ± 5 ms. The HDsEMG decomposition identified all of the 81 highly confident discharges to within ± 0.5 ms, and was thus assessed to be 100% accurate. The iEMG decomposition identified 82 discharges of MU 11, all of them with high confidence. The HDsEMG decomposition identified all but 3 of the discharges to within ± 0.5 ms. For the other 3 it was off by amounts ranging from 10 to 20 ms. These discrepancies were counted as 6 errors, resulting in an accuracy of 93%.

Overall, the accuracy of the HDsEMG decompositions was quite good (92 ± 6%) for the 148 common MUs selected for assessment. 30% of the errors were misses, 21% were false positives, and 49% were imprecise detections. Of course the accuracy that can be achieved for a given MU in a given signal depends on the signal and noise characteristics of that particular MU and that particular signal. In our tests, the two factors that had the greatest effect on CKC accuracy were the CDI decomposability index, which is an index of how distinguishable the different MUs in the signal are compared to the overall intensity of the signal, and the number of channels that were free of technical artifact and thus provided information about the signal. It is noteworthy to stress that these results cannot easily be generalized to non-pennate muscles, as discussed in the sequel. It also remains to be seen whether comparable accuracy can be achieved in more forceful contractions.

One limitation of the two-source method is that it only allowed assessment of a subset of the MUAP trains identified by the CKC algorithm. The iEMG electrodes, because of their smaller pickup volumes, detected only 148 of the total 643 CKC MUAP trains (23%). The fact that these MUs were typical of the overall set in terms of HDsEMG amplitude and firing characteristics suggests that they may have constituted a more-or-less random sampling of the overall set. Therefore it is not unreasonable to think that many of the non-assessed trains probably also had accuracies comparable to those of the assessed trains. It should be pointed out, however, that the low SIR values and the fact that some iEMG MUs with large HDsEMG amplitudes were not detected by the CKC algorithm show that the CKC algorithm did not identify all of the MUAP trains in the HDsEMG signal.

The results of the current study differed in several respects from those reported in a previous study of HDsEMG decomposition accuracy in the biceps brachii, tibialis anterior, and abductor digiti minimi muscles (Holobar et al 2010). The number of MUs detected in the HDsEMG signal was considerably higher in BFlh than in the other muscles (2–30 compared to 1–12). Moreover, the surface MUAPs of the MUs that were detected in the iEMG signal but not in the HDsEMG signal were comparable in RMS amplitude to the ones that were detected in the HDsEMG signal. In the other muscles, the surface MUAPs of the MUs detected only in the iEMG signal were much smaller than the ones detected in the HDsEMG signal. As a result, the MUAPs detected in the HDsEMG signal in BFlh accounted for a considerably smaller part of the overall HDsEMG signal variance than in the other muscles (the mean SIR value was 16% in BFlh compared to 38% reported in (Holobar et al., 2010)). This indicates that not all the MUs that made a significant contribution to the HDsEMG signal in BFlh were identified by CKC. Finally, the surface MUAPs in BFlh were standing waves with no clear sign of propagation (e.g., Figure 3), and they had quite different longitudinal distributions than the MUAPs reported in (Holobar et al., 2010).

These differences can be explained in terms of differences in muscle architecture (Mesin et al., 2011). In the previous study, the HDsEMG recordings were all made over sections of muscle in which the muscle fibers were parallel to the skin surface, In this case, the MUAP reflects the propagating action potential volley in the muscle fibers. In BFlh, on the other hand, the muscle fibers are inclined to the skin surface, inserting obliquely onto a superficial aponeurosis (Kumakura, 1989). In this case, the main contribution to the MUAP comes from the terminal wave produced when the action potential volley reaches the aponeurosis, rather than from the propagating wave. The MUAPs have different longitudinal distributions because the MUs insert at different proximodistal locations along the aponeurosis. The pennation brings a large cross-section of the muscle into the view of the surface electrode, making it possible to detect a larger number of MUs than in parallel-fibered muscles, in which the superficial MUs are detected preferentially (Holobar et al., 2010).

BFlh is only one of many human muscles that have a pennate architecture in which the muscle fibers are not parallel to the skin surface (Aagaard et al 2001) and in which action potential propagation is not clearly seen in the sEMG signal (Masuda and Sadoyama 1987). Other pennate muscles in the leg include the other hamstring muscles (semimembranosus and semitendinosus), gastrocnemius, soleus, and the proximal part of tibialis anterior. HDsEMG techniques may provide a useful noninvasive way to study neural strategies and subject specific architecture in these muscles. For example, subject-specific information about the architecture of the hamstring muscles is important to examine the effects of stretching (Halbertsma et al 1999), to facilitate planning for surgical lengthening in children with cerebral palsy (Delp et al 1996), and to determine the precise site of strain injuries (Koulouris and Connell 2005, 2006).

In conclusion, this study provides a strong measure of confidence for users of the CKC algorithm that decompositions of HDsEMG signals from low force contractions of pennate muscles that yield MUAP trains with full, regular firing patterns and regularly distributed MUAPs can be considered trustworthy. Moreover, the results suggest that pennate muscles with superficial aponeuroses may have an advantage over parallel-fibered muscles in terms of the number of MUs that can be individually detected using HDsEMG techniques.