Fluidization, resolidification, and reorientation of the endothelial cell in response to slow tidal stretches

Abstract

Mechanical stretch plays an important role in regulating shape and orientation of the vascular endothelial cell. This morphological response to stretch is basic to angiogenesis, neovascularization, and vascular homeostasis, but mechanism remains unclear. To elucidate mechanisms, we used cell mapping rheometry to measure traction forces in primary human umbilical vein endothelial cells subjected to periodic uniaxial stretches. Onset of periodic stretch of 10% strain amplitude caused a fluidization response typified by attenuation of traction forces almost to zero. As periodic stretch continued, the prompt fluidization response was followed by a slow resolidification response typified by recovery of the traction forces, but now aligned along the axis perpendicular to the imposed stretch. Reorientation of the cell body lagged reorientation of the traction forces, however. Together, these observations demonstrate that cellular reorientation in response to periodic stretch is preceded by traction attenuation by means of cytoskeletal fluidization and subsequent traction recovery transverse to the stretch direction by means of cytoskeletal resolidification.

with every beat of the heart or inflation of the lung, the vascular endothelial cell is subjected to mechanical stretch. In response to comparable stretches in vitro, cellular microstructures rearrange locally as the cell body realigns globally (12, 17, 31, 35–37). These cellular responses are thought to underlie vital functions of the endothelium, including vascular homeostasis (5), barrier integrity (1), and vascular remodeling (22). To explain those responses, the idea of upstream mechanosensing and downstream cell signaling remains the dominant paradigm (5, 14, 17, 18, 20, 40).

The concept of mechanosensing rests upon the premise that the cell senses external mechanical cues by exerting traction forces upon neighboring cells and/or the extracellular matrix (2), which then feed back via mechanochemical transduction to alter downstream cellular functions (5, 12, 14, 17, 18, 20, 26, 36, 40, 41). Because traction forces arise in response to cellular contraction, one might predict that inhibition of cell contractility ought to diminish the cell's ability to sense and respond to mechanical stretch, and, indeed, when cell contractility is inhibited pharmacologically cell reorientation in response to stretch is slowed or abolished (37). On the other hand, it has been shown that, in response to periodic stretch, cellular traction forces become progressively attenuated (19), but the cell reorients nonetheless (12, 17, 31, 35–37). If traction forces were an important determinant of cell reorientation, then these two observations would appear to be paradoxical. To resolve this paradox, here we measured for the first time cellular traction forces in a reorienting endothelial cell.

To study reorientation of endothelial cells, experiments reported in the literature typically impose stretch waveforms that emulate those generated by the pulsating heart and typically use substrates that are quite stiff compared with the physiological range (cf., Refs. 11, 12, 17, 18, 36, 37). Here by contrast we imposed a stretch pulse waveform that corresponds more closely to the lower end of tidal lung expansion during spontaneous breathing (19). To do this, we used cell mapping rheometry, which combines uniaxial cell stretch with simultaneous assessment of cellular traction forces and cell morphology (19). Importantly, cell mapping rheometry uses a soft substrate tuned to a physiological stiffness.

We found that the cell body reoriented perpendicularly to the stretch axis but did so more rapidly than in prior studies that used sinusoidal waveforms, higher frequencies, and stiffer substrates (cf. 36, 37). Importantly, reorientation of the traction field begins with fluidization (4, 8, 19, 33) that is characterized by nearly complete ablation of tractions and is stabilized subsequently by resolidification that is characterized by recovery of tractions, especially of those traction components aligned perpendicular to the direction of stretch. Throughout these phases, cell shape was far less polarized than was the traction field, and changes of orientation of the cell body lagged those of the traction field.

MATERIALS AND METHODS

Substrate preparation.

Polyacrylamide gels were prepared according to protocols described previously (19, 38). Briefly, a 350-μl drop containing 5% acrylamide, 0.1% bis-acrylamide, and 0.5% fluorescent microbeads (0.2 or 0.5-μm diameter) was added to pretreated glass-bottom dishes (P35G-1.0–20; MatTek). The mixtures were then covered with cover slips and allowed to polymerize. After polymerization (∼1 h), the cover slips were removed to yield an ∼700-μm-thick gel layer. The free surface of the gel was then functionalized with 0.1 mg/ml collagen-1 solution. It has been shown previously that the material response of the gel is essentially elastic (Young's modulus of ∼4 kPa and Poisson's ratio of ∼0.445) and that viscous damping effects are negligible over a wide range of time scales (0.1–100 s) (28).

Cell culture.

Primary human umbilical vein endothelial cells (HUVECs; provided by Dr. Geerten van Nieuw Amerongen, Vrije University Medical Center) were cultured on plastic flasks coated with 1% gelatin. The cells were maintained in supplemented medium 199 (Lonza). Once the cells reached confluence, they were trypsinized, plated sparsely (∼10,000–20,000 cells/well) on gel substrates, and incubated overnight at 37°C and 5% CO₂.

Cell stretch.

To impose uniaxial stretch, we indented polyacrylamide gel substrates using a punch-indentation system that utilizes a pair of parallel glass plates (15 mm long, 0.2 mm thick, and set 1 mm apart). When the plates indent the gel, the gel region between the plates stretches transversely and thus imposes a pure uniaxial stretch (i.e., stretch only in one direction) to adhering cells. When the plates are lifted, the gel recoils elastically, and the cells return to an unstretched configuration (19).

Experimental protocol.

Isolated HUVECs that were at least a cell distance apart from their neighbors were selected for stretch experiments. This was done to avoid confounding effects of mechanical communication between neighboring cells (30). We did not bias our choice of cells based on their initial size, shape, or orientation. Single cells were subjected to a series of 5% (n = 6 cells) or 10% (n = 10) uniaxial trapezoidal strain pulses (≤1 s loading, 3 s hold, ≤1 s unloading) that were repeated every 49 s over ∼2 h, a series of 10% strain pulses that were repeated every 900 s (n = 6) over ∼2 h, or no strain was applied for ∼2 h (time control, n = 5). The pulse train waveform was motivated by a previous observation that, in response to a pulse waveform, cytoskeletal fluidization and resolidification become fully revealed, whereas other material responses (e.g., strain stiffening and stress relaxation) of the cell are minimized (34).

Phase-contrast images of the cell and fluorescent images of microbeads embedded in the substrate were obtained shortly before stretch onset (baseline), immediately after the first strain pulse, every ∼5 or ∼7 min thereafter, and at the end of the experiment following cell detachment with trypsin. The trypsinized image of fluorescent beads was used to establish the reference configuration.

Computation of traction forces.

We used Fourier transform traction microscopy (3) to compute cellular traction forces. Each microbead image was compared with its reference image to obtain the displacement field in the substrate plane. From the displacement field, the elastic properties of the gel, and a manual trace of the cell contour, we calculated the traction field as described previously (3). From the traction field, we calculated the contractile moment matrix (M) as a first-order moment of the traction field. By constructing an ellipse whose semiaxes are equal to the eigenvalues and directions determined by the corresponding eigenvectors of M, we could track traction field realignment, following the angle (θ) of the major axis of the ellipse relative to the axis perpendicular to stretch. By calculating components of M in the direction parallel with the stretch axis (M_‖) and in the direction perpendicular to the stretch axis (M⊥), we could track changes of the traction field along these two directions. For comparison between different cells, we normalized the semiaxes of the ellipses with the prestretch baseline value of the net contractile moment; the net contractile moment is defined as the trace of M, i.e., trM = M_‖ + M⊥ (3).

In few cases where tractions were attenuated to the level comparable with the background noise (bead displacements ≤0.2 μm), our computations yielded small but negative values of M_‖, M⊥, and the eigenvalues of M. Because these are not physically feasible, we replaced them by zero.

Quantitation of cell morphology.

To quantitate morphological changes during reorientation, we calculated the area moment of inertia matrix (J) as the second moment of the cell projected area. By constructing an ellipse whose semiaxes are equal to the eigenvalues and directions determined by the corresponding eigenvectors of J, we could track reorientation of the cell body. This reorientation was further quantified as the angle (ϕ) of the major axis of the inertia ellipse relative to the axis perpendicular to stretch. These calculations were carried out at approximately the same time points where we calculated M.

Because the axis or orientation is defined modulo π, we picked −90° to +90° as the range of both θ and ϕ, adding or subtracting180° to avoid discontinuities in the evolution of θ and ϕ. In the remainder of the text, we refer to θ and ϕ as “traction angle” and “cell body angle,” respectively.

To quantitate changes in traction field and cell body orientation during stretch, we defined the orientation variance (OV) by doubling all angles to span the range −180° to +180° and then applying the standard circular variance. This resulted in

$$OV=1-\frac{1}{N}\sqrt{{\left({\displaystyle \sum _{i=\text{l}}^N\text{cos2}{\alpha }_i}\right)}^2+{\left({\displaystyle \sum _{i=\text{l}}^N\text{sin2}{\alpha }_i}\right)}^2,}$$

where α is either θ or ϕ and N is the total number of data points. The orientation variance is a measure of variation in traction field or cell body orientation on a scale from 0 to 1; OV = 0 when all tractions or cells are oriented in the same direction and OV = 1 when the distribution is uniform.

Rho kinase inhibition.

To study how Rho signaling affects reorientation of the traction field and the cell body, we pretreated cells with 10 μM of Rho kinase inhibitor Y-27632 for 30 min. Then we imposed 10% uniaxial strain pulses that were repeated every 49 s over ∼2 h (n = 8 cells). The inhibitor was present in the culture media throughout the experiment.

RESULTS

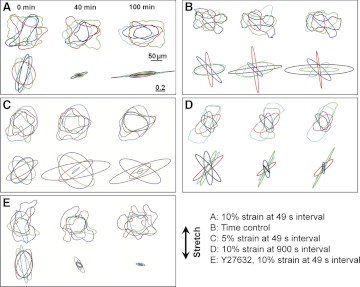
Pulses of 10% strain that were repeated every 49 s caused the cell body and the traction field to reorient (Fig. 1, A and B). Initially, each traction ellipse was large in size and random in orientation (Fig. 2A). Following onset of periodic stretch, each traction ellipse diminished in size progressively, some almost vanishing altogether (Figs. 1B and 2A). With time, however, each traction ellipse recovered, but now oriented perpendicular to the axis of stretch.

Fig. 1.

A: traction maps for a representative cell before (0 min) and during (40 and 100 min) periodic stretch pulses of 10% strain repeated every 49 s (stretch axis, double-headed arrow). B: corresponding principal contractile moments (denoted by ellipse major and minor axes) diminish almost to zero (at 40 min) but then recover with principal axes rotated. C: time course of the components of the contractile moment matrix M parallel with (M_‖) and perpendicular to (M_⊥) the stretch axis.

Fig. 2.

A: periodic stretch (10% strain pulses repeated every 49 s) causes reorientation of the cell body (top) and of the traction field (bottom). B: time controls show no systematic changes in the cell shape (top) or the traction field (bottom). C: periodic stretch of reduced amplitude (5% strain pulses repeated every 49 s) shows no systematic reorientation of the cell body (top) and of the traction field (bottom). D: periodic stretch with extended period of intermittent traction recovery (10% strain pulses repeated every 900 s) does not cause reorientation of the cell body (top) and of the traction field (bottom). E: in cells pretreated with Rho kinase inhibitor Y-27632, periodic stretch (10% strain pulses repeated every 49 s) causes reorientation of the traction field (bottom) but not of the cell body (top). From each group, superposed are shapes of five randomly oriented cells and the corresponding normalized principal dipole moments before (0 min) and during (40 and 100 min) periodic stretch. Each color corresponds to a different cell. Double-headed arrow, stretch axis. Scale bars from A apply to all other panels.

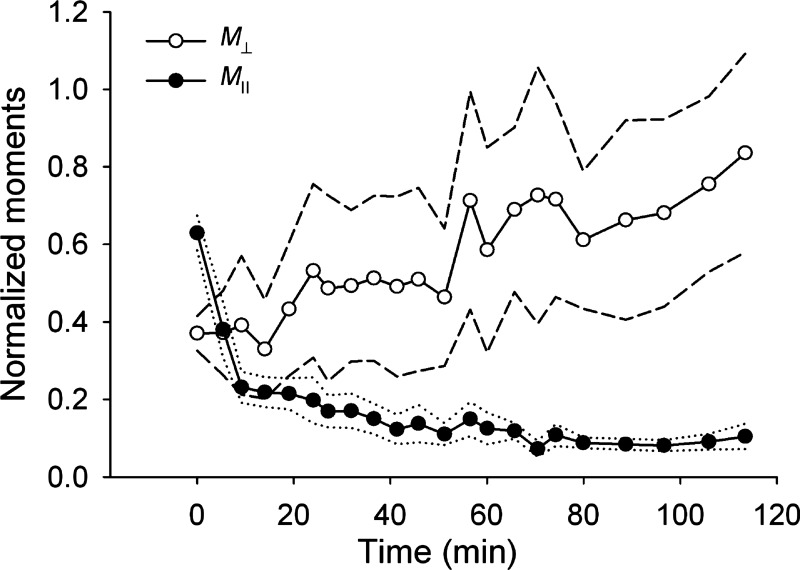
Despite the large variability in initial orientation and baseline contractility between cells, traction reorientation in every tested cell was characterized by an initial dramatic attenuation of the traction forces. Following this initial attenuation, M_‖ continued to decrease and eventually saturated at low values, whereas M_⊥ gradually recovered (Figs. 1C and 3). Using a one-way ANOVA test, we found that the differences in the mean values of M_‖ obtained at different time points (Fig. 3) were statistically significant (p < 0.001), whereas the differences between the mean values of M_⊥ were not statistically significant (p = 0.973). However, M_⊥ exhibited a significant increase with time, i.e., a linear regression slope through all data points from n = 10 cells was significantly greater than zero (p = 0.0283).

Fig. 3.

Time course of the average values of the normalized components of the contractile moment matrix parallel with (M_‖) and perpendicular to (M_⊥) the stretch axis for cells subjected to 10% strain pulses repeated every 49 s. Both M_‖ and M_⊥ were normalized with the baseline value of the net contractile moment (i.e., baseline value of M_‖ + M_⊥). Data are means (n = 10 cells); dotted lines are ± SE for M_‖ and dashed lines are ± SE for M_⊥.

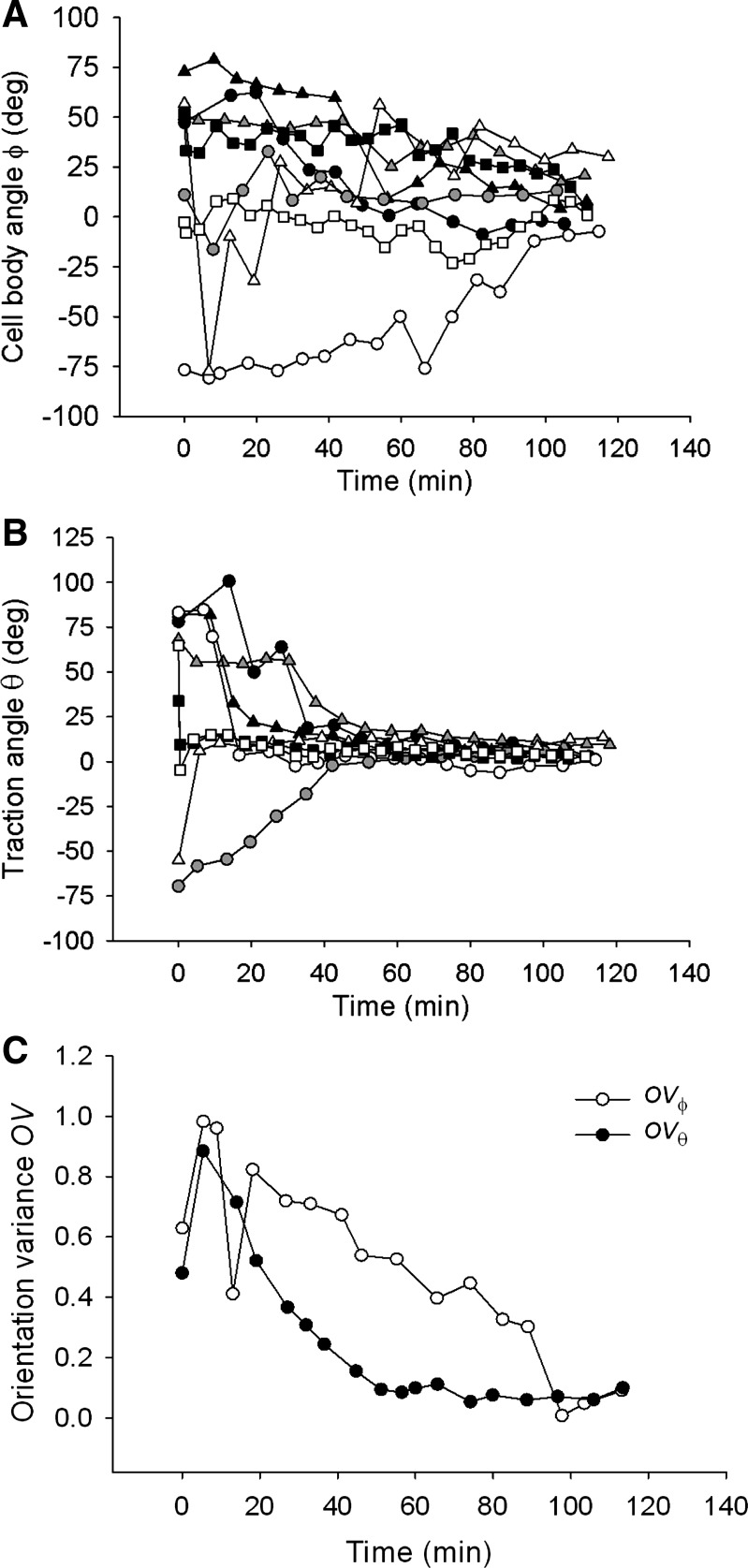
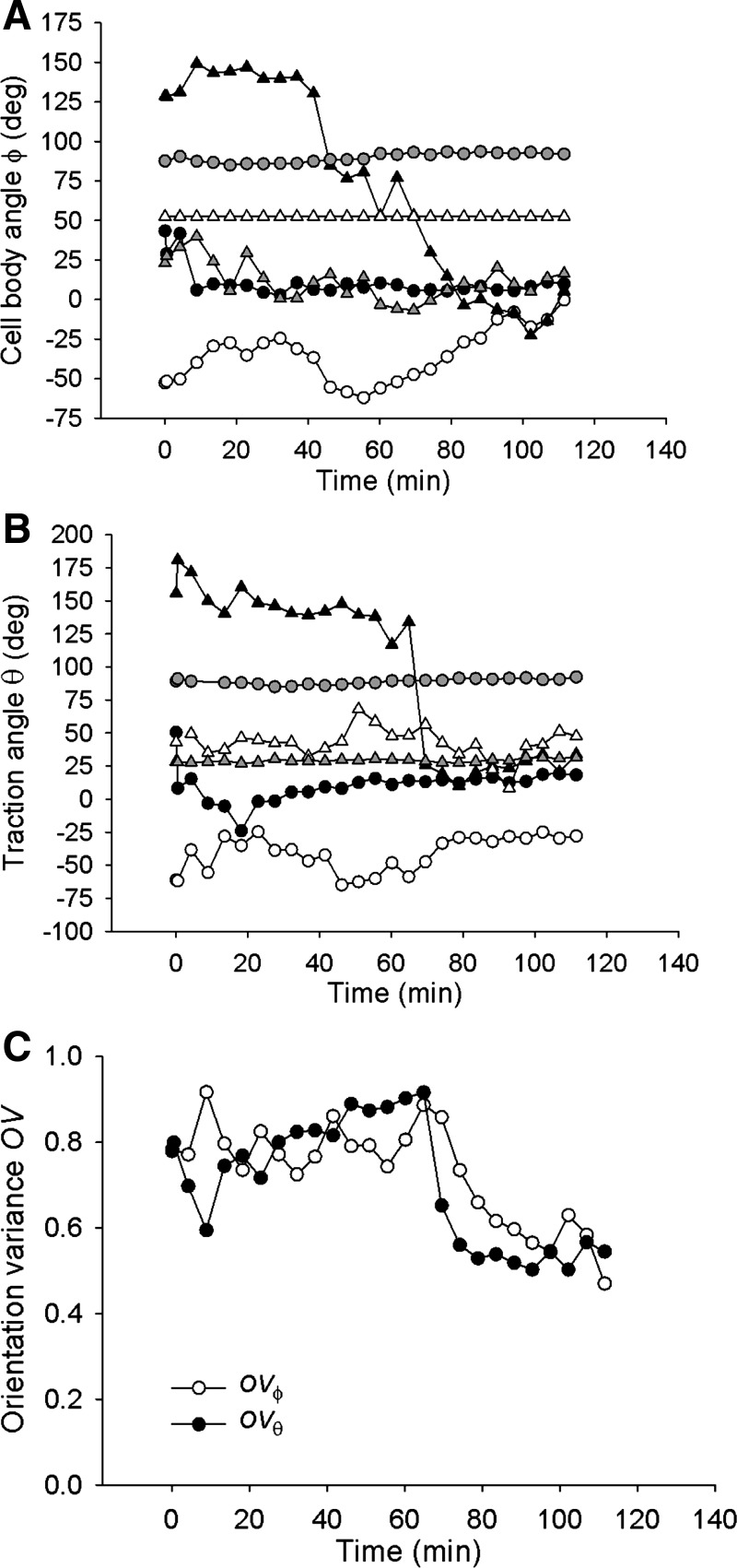
For almost all examined cells, the traction angle θ converged close to 0° within 40 min from the onset of stretch and stayed virtually unchanged thereafter (Fig. 4B). The cell body angle ϕ took much longer to converge, however, (Fig. 4A), indicating that reorientation of the cell body lagged reorientation of the traction field.

Fig. 4.

In response to 10% strain pulses that are repeated every 49 s, the cell body angle ϕ (A) and the traction angle θ (B) converge to 0° over the observed 2-h period. The rate of decrease of θ is greater than that of ϕ, as shown by the difference in the time dependence of their respective orientation variances OV_ϕ and OV_θ (C). This difference indicates that reorientation of the cell body lags reorientation of the traction field. Data shown in A and B are from 8 representative cells; each symbol corresponds to a different cell. Data shown in C are obtained from n = 10 cells.

To quantify these processes, we compared the variance of θ (OV_θ) and that of ϕ (OV_ϕ). Both decreased with increasing time (except during initial stretches), but OV_θ decreased faster than did OV_ϕ (Fig. 4C), indicating that cell body reorientation lagged traction field reorientation. At the end of the 2-h period, both OV_θ and OV_ϕ converged to near zero, indicating that both the traction field and the cell body became aligned nearly perpendicularly to the axis of stretch. In the absence of stretch, cells showed no systematic reorientation of the cell body or the traction field (Figs. 2B, 5A, and 5B). Orientation variances OV_θ and OV_ϕ showed no systematic time dependences and remained similar throughout the observed 2-h period (Fig. 5C), indicating that the traction field and the cell body stayed closely aligned. Together, these results establish that stretch-induced attenuation of traction forces does not inhibit cell realignment but rather precedes and probably facilitates that realignment. Traction field reorientation is a novel finding and, as shown below, is associated with the responses of cytoskeletal fluidization that is characterized by traction attenuation and cytoskeletal resolidification that is characterized by traction recovery (4, 8, 19).

Fig. 5.

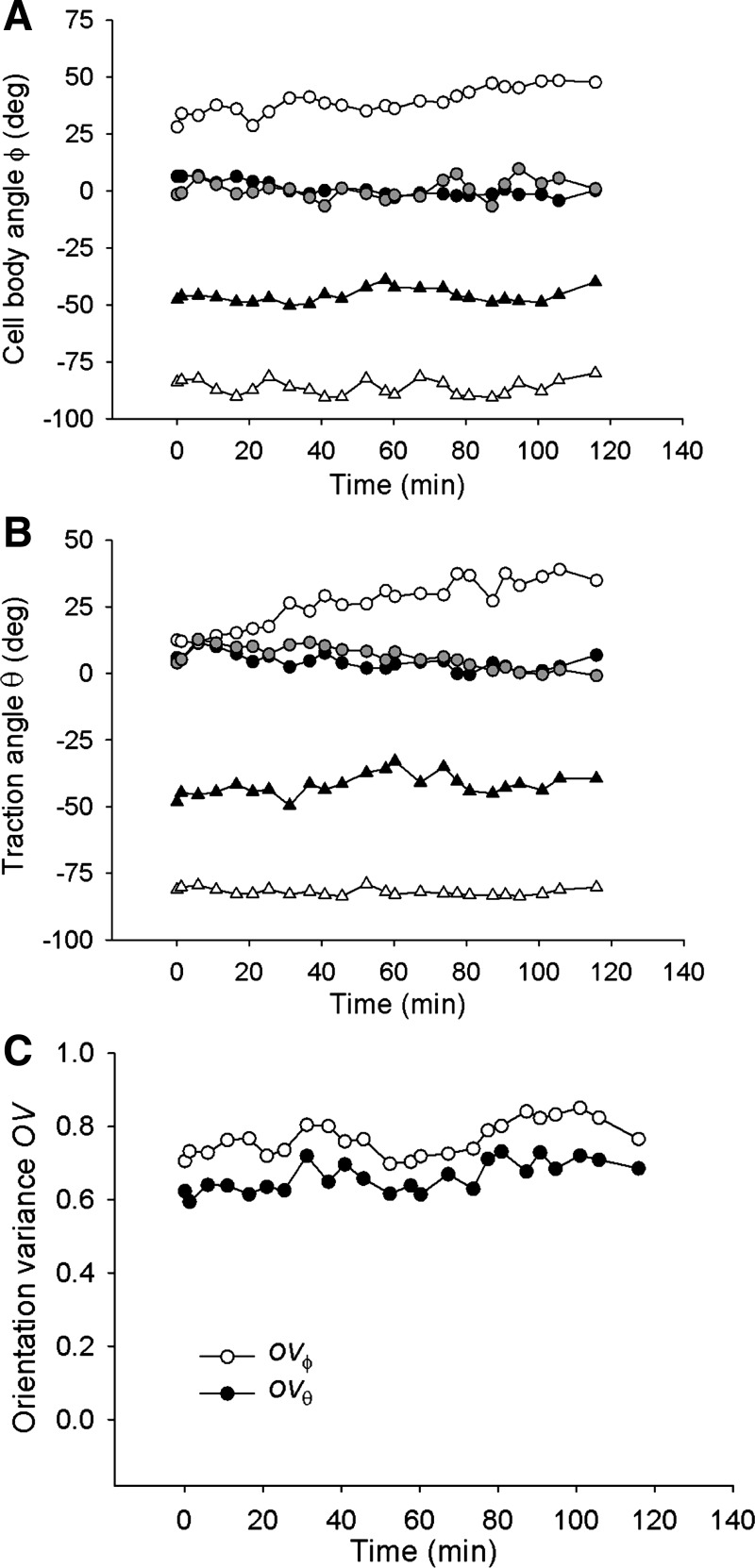
In the absence of stretch, cell body angle ϕ (A) and the traction angle θ (B) show little reorientation over the observed 2-h period. The corresponding orientation variances OV_ϕ and OV_θ exhibit no systematic time dependence and remained similar (C), indicating that the cell body and the traction field stay closely aligned during the observed 2-h period. Data are from n = 5 cells; each symbol corresponds to a different cell.

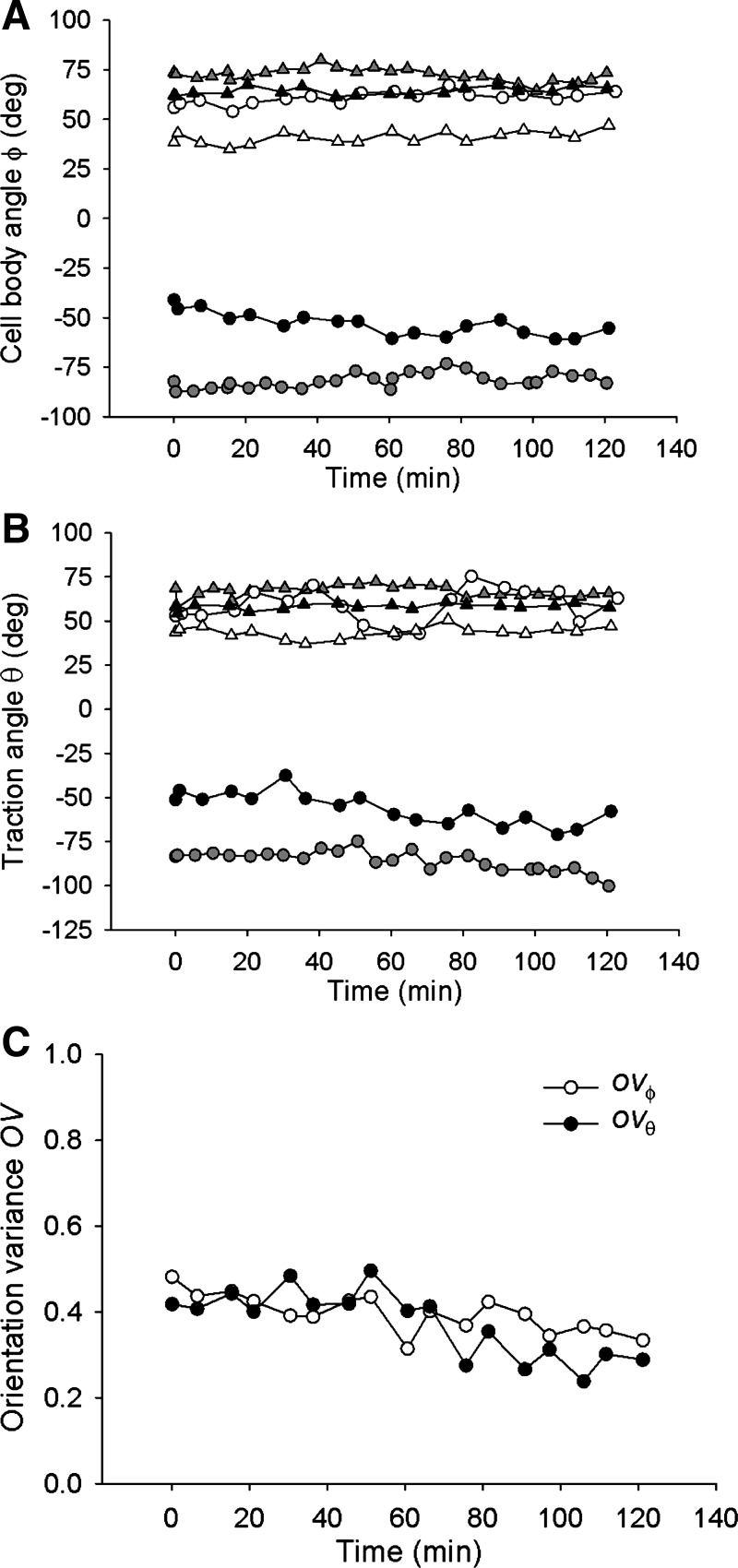
Two testable predictions follow. Reducing strain amplitude induces less attenuation of traction force, suggesting less cytoskeletal fluidization (4, 19). If so, then one would predict that, with reduced strain amplitude, it would require a greater number of stretch cycles to attenuate traction forces and then allow them to reorient. Indeed, when we lowered strain amplitude to 5% while maintaining the same strain frequency, we observed reduced traction force attenuation (by ∼20%) and reduced traction force and cell body reorientation within the 2-h stretch period (Figs. 2C and 6). Lowering strain frequency, by contrast, allows more time between stretches for traction recovery via resolidification (19). If so, then one would predict that no reorientation should occur if the frequency were low enough to allow complete traction recovery between stretches. Indeed, when we applied pulses of 10% periodic strain imposed every 900 s, we observed reorientation of neither the traction field nor the cell body within 2 h (Figs. 2D and 7). Together, these findings suggest that the characteristic time scale of cell reorientation is not that of viscoelastic relaxation processes (6) but rather is linked to that of the cytoskeletal resolidification.

Fig. 6.

In response to 5% strain pulses that are repeated every 49 s, the cell body angle ϕ (A) and the traction angle θ (B) show minimal or no reorientation over the observed 2-h period, except in one cell (black triangles) where both ϕ and θ rapidly converge to 0° ∼60 min following onset of stretch. The corresponding orientation variances OV_ϕ and OV_θ exhibit no systematic time dependence within the first 60 min and then sharply decrease (C). This decrease reflects the trend of a single cell shown by the black triangles in A and B. Data are from n = 6 cells; each symbol corresponds to a different cell.

Fig. 7.

In response to 10% strain pulses that are repeated every 900 s, the cell body angle ϕ (A) and the traction angle θ (B) show minimal reorientation over the observed 2-h period. The corresponding orientation variances OV_ϕ and OV_θ slightly decrease with increasing time and remain similar (C), indicating that the cell body and the traction field stay closely aligned during the observed 2-h period. Data are from n = 6 cells; each symbol corresponds to a different cell.

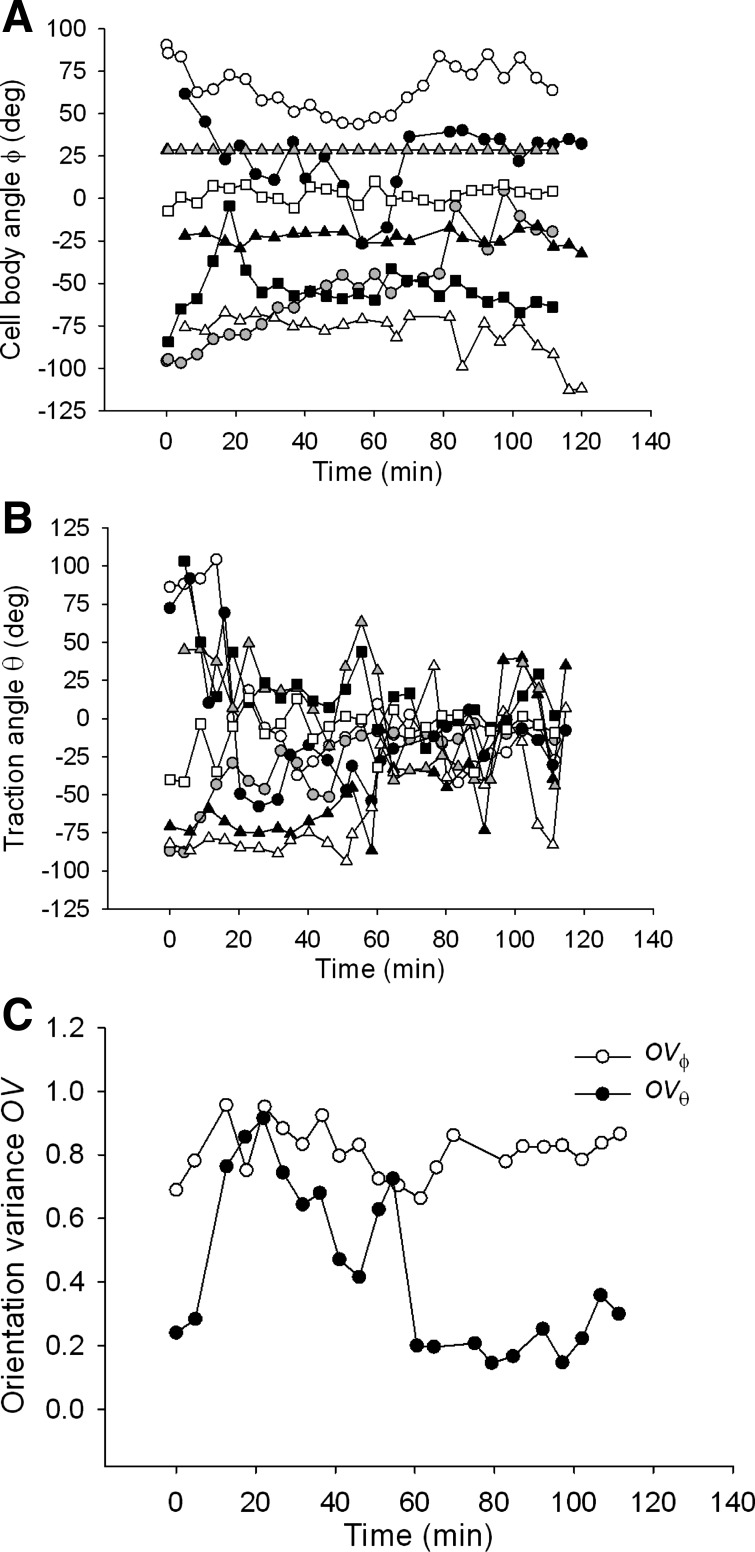
It has been shown previously that Rho signaling is required for stretch-induced reorientation of the cell body (37). In accordance with these findings, we found here that inhibition of Rho kinase signaling by Y-27632 resulted in a substantial decrease of the baseline net contractile moment relative to untreated cells [3.48 ± 1.19 vs. 39.42 ± 12.28 (SE) pJ; n = 10, p = 0.0096 t-test], abolished reorientation of the cell body, but allowed reorientation of the traction field nonetheless (Fig. 2E). However, the traction field failed to recover during the 2-h stretch period, as indicated by the diminishing size of traction ellipses (Fig. 2E). In all examined cells (n = 8), traction angle θ converged towards 0° with increasing time of stretch (Fig. 8B), whereas the cell body angle ϕ showed no systematic changes except in one cell where ϕ converged to 0° (Fig. 8A). Orientation variances OV_θ and OV_ϕ showed markedly different time dependences; OV_θ decreased while OV_ϕ did not change with increasing time of stretch (Fig. 8C), suggesting that the absence of cell body reorientation might be caused by the lack of traction recovery.

Fig. 8.

In cells pretreated with Y-27632, in response to 10% strain pulses that are repeated every 49 s, the cell body angle ϕ shows little tendency to reorient except in one cell (gray circles) (A), whereas the traction angle θ converges to 0° (B). The corresponding orientation variances OV_ϕ and OV_θ diverge over the observed 2-h period (C). This difference indicates that the cell body does not follow reorientation of the traction field. Data are from n = 8 cells; each symbol corresponds to a different cell.

Finally, the traction field was much more polarized than the cell shape (Fig. 2).

DISCUSSION

Our primary finding is that cellular reorientation in response to slow periodic stretches involved an early phase characterized by nearly complete attenuation of tractions followed by a late phase characterized by nearly complete recovery of tractions but now realigned perpendicular to the direction of stretch. Cell shape was much less polarized than the traction field, moreover, and reorientation in cell shape systematically lagged reorientation of the traction field. Together, these findings demonstrate that structural and morphological changes are only a part of a more complete physical picture of cellular reorientation.

These findings are consistent with the interpretation that cell reorientation begins with fluidization (4, 8, 19) and disassembly of the cellular contractile machinery (11, 12, 20), as described previously, especially those components aligned along the direction of stretch, and is stabilized subsequently by the resolidification and reassembly of contractile machinery perpendicular to the direction of stretch (13, 17, 20). Cytoskeletal fluidization and resolidification responses to stretch seem to be universal across cell types and species (4, 7, 8, 19, 24, 27, 33, 34). Fluidization is thought to reflect the disruption of weak molecular interactions of the cytoskeletal lattice caused by transient stretch. It is typified by prompt attenuation of cytoskeletal stiffness (33) and cellular traction forces (4, 8, 19) over the time scale of seconds. Resolidification, on the other hand, reflects the slow restoration of disrupted molecular interactions. It is typified by recovery of cytoskeletal stiffness (33) and tractions (4, 8, 19) over the time scales of minutes.

This physical picture neither ignores the role of mechanotransducive signaling pathways nor does it minimize it. Instead, it provides a framework within which to describe associated changes. Consider, for example, the Rho kinase pathway. Inhibiting Rho kinase through the drug inhibitor Y-27632 did not affect the fluidization response but inhibited resolidification (Fig. 2E). Because resolidification sets the characteristic time scale of cell reorientation, inhibiting Rho kinase also inhibited reorientation of the cell body (Fig. 8C). In this connection, it has been observed previously that, in endothelial cells with inhibited Rho kinase, actin bundles assemble in response to periodic stretch along the axis parallel with stretch (17, 20). However, those bundles are probably not contractile, for if they were we would have observed tractions oriented in the direction parallel with, not perpendicular, to stretch (Fig. 8B). Thus we conclude that those fibers are formed as a result of stretch-induced bundling of noncontractile actin filaments (20).

Also, while the drug inhibitor Y-27632 inhibits Rho kinase, it activates the small GTPase Rac1 (15). Activation of Rac1 promotes formation of lamellipodia, which during uniaxial stretch tend to form in the direction of the stretch axis (15). Because periodic stretch activates both Rac1 (21) and Rho kinase (17) in endothelial cells, their activity will have disparate effects on cell morphology; activation of Rac1 promotes cell shape polarization in the direction of stretch via lamellipodia formation (39), whereas activation of Rho kinase promotes cell shape polarity in the direction perpendicular to the stretch axis via stress fiber (SF) reorientation. These competing effects of Rac1 and Rho kinase may explain the weak correlation between the cell shape and the traction field in reorienting cells.

Transient stretch causes perturbation of the acto-myosin cross-bridge cycle (10, 16) but also causes disassembly and reassembly of the actin cytoskeleton (4). Although these concepts can explain stretch-induced reorientation of cytoskeletal SFs (13, 16), they are not sufficient to explain reorientation of the cell body. It has been shown that reorientation of the cell body also depends on focal adhesion turnover and sliding (9, 29) and on dynamics of microtubules (23). Further studies will therefore be needed to monitor concerted dynamics of the cytoskeleton, focal adhesions, and traction forces and thereby quantitate their mutual relationship in a reorienting cell.

Methodology and protocol.

Although our methodologies are generalizable, here we focused attention on a representative value of substrate stiffness (Young's modulus of ∼4 kPa), a routinely used extracellular matrix protein (collagen-1), and a commonly studied endothelial cell type, the HUVEC. In this model system, we implemented two significant advances over existing methodologies. First, we stretched cells that were cultured on soft substrates of physiological stiffness. Because matrix rigidity affects many different aspects of cell mechanobiology, it was important to show that cells reorient in a soft environment; almost all previous studies of cell reorientation used substrates whose stiffnesses were much higher than physiological values (cf., Refs. 9, 11–14, 17, 18, 20, 21, 23, 25, 26, 35–37). Second, we assessed concomitant changes in cell traction forces.

It has been shown previously that, in cells that are stretched sinusoidally at 1 Hz and a 10% strain amplitude, cytoskeletal SFs reorient along the axis perpendicular to stretch over ∼4 h (12, 13, 17, 18, 20). This reorientation, however, is hampered and eventually abolished if the stretch frequency decreases below 0.1 Hz (13). In comparison, we observed here that 10% strain pulses applied at a much lower frequency of ∼0.02 Hz resulted in reorientation of the traction field along the perpendicular axis within <1 h from the onset of stretch (Fig. 4B). Our observation is consistent with recent findings showing that SF reorientation is more responsive to the strain rate than to stretch frequency per se (32) and that the presence of relaxing intervals between subsequent stretch-unstretch maneuvers enhances SF reorientation (25).

In summary, we establish here that cellular reorientation in response to periodic uniaxial stretch is linked to the fluidization and resolidification responses of the cytoskeleton. The observation that traction field reorientation preceded cell body reorientation suggests that cellular reorientation begins with rearrangements of the cytoskeletal contractile machinery followed by global morphological changes. Together, these findings suggest that stretch-induced reorientation of the cell is centered around physical forces and the direct material responses that they induce in the cytoskeletal lattice. Thus, any comprehensive framework of cellular responses to mechanical stretch must include the contributions of physical forces and those material responses, especially that of cytoskeletal fluidization and resolidification.

GRANTS

This work was supported by National Heart, Lung, and Blood Institute Grant HL-096005 and by a Parker B. Francis fellowship grant.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

Author contributions: R.K., J.P.B., J.J.F., and D.S. conception and design of research; R.K., E.P.C., A.L.I., K.R., and G.M. performed experiments; R.K., E.P.C., A.L.I., and D.S. analyzed data; R.K., A.P.P., J.P.B., J.J.F., and D.S. interpreted results of experiments; R.K., A.P.P., M.L.S., J.P.B., J.J.F., and D.S. edited and revised manuscript; R.K., J.P.B., J.J.F., and D.S. approved final version of manuscript; E.P.C., A.L.I., and D.S. prepared figures; D.S. drafted manuscript.