Dark Light, Rod Saturation, and the Absolute and Incremental Sensitivity of Mouse Cone Vision

Abstract

Visual thresholds of mice for the detection of small, brief targets were measured with a novel behavioral methodology in the dark and in the presence of adapting lights spanning ∼8 log₁₀ units of intensity. To help dissect the contributions of rod and cone pathways, both wild-type mice and mice lacking rod (Gnat1^−/−) or cone (Gnat2^cpfl3) function were studied. Overall, the visual sensitivity of mice was found to be remarkably similar to that of the human peripheral retina. Rod absolute threshold corresponded to 12–15 isomerized pigment molecules (R*) in image fields of 800 to 3000 rods. Rod “dark light” (intrinsic retinal noise in darkness) corresponded to that estimated previously from single-cell recordings, 0.012 R* s⁻¹ rod⁻¹, indicating that spontaneous thermal isomerizations are responsible. Psychophysical rod saturation was measured for the first time in a nonhuman species and found to be very similar to that of the human rod monochromat. Cone threshold corresponded to ∼5 R* cone⁻¹ in an image field of 280 cones. Cone dark light was equivalent to ∼5000 R* s⁻¹ cone⁻¹, consistent with primate single-cell data but 100-fold higher than predicted by recent measurements of the rate of thermal isomerization of mouse cone opsins, indicating that nonopsin sources of noise determine cone threshold. The new, fully automated behavioral method is based on the ability of mice to learn to interrupt spontaneous wheel running on the presentation of a visual cue and provides an efficient and highly reliable means of examining visual function in naturally behaving normal and mutant mice.

Introduction

The study of human visual sensitivity was greatly advanced in the 20th century with the development of precision psychophysics devoted to the measurement of thresholds for small, brief stimuli delivered to prescribed retinal locations and presented to the dark-adapted eye or in the presence of an adapting background or “conditioning field.” One classical example of such work is that of Hecht et al. (1941), which unequivocally established that rods in the dark-adapted human retina could signal the capture of individual photons. Also classic are the investigations of Stiles (Stiles, 1939, 1949; Aguilar and Stiles, 1954; Stiles, 1959) with the “two-color increment threshold” method, which uses monochromatic adapting backgrounds and test stimuli of different and varied wavelengths. These investigations revealed component branches of threshold versus intensity (t.v.i.) curves governing light adaptation, and quantified many novel and important features of the threshold sensitivity and light adaptation of the visual system. Such features include the absolute and relative sensitivities of rod and cone pathways and estimation of the “dark light” of the signaling pathways of each photoreceptor class. Dark light refers to intrinsic visual system noise present in complete darkness that acts as a determinant of threshold sensitivity (Barlow, 1956, 1972). It is widely held that the neural mechanisms underlying the sensitivity and adaptive properties of the visual system revealed in human increment threshold investigations reside in the retina, though definitive evidence for this claim has not yet been provided. An adequate animal model in which to investigate these classic features of the visual system would provide a means for determining their neural mechanisms.

The mouse is now the species most widely used for the experimental investigation of nervous system function and the molecular mechanisms of its diseases. Reasons for this choice include the genomic proximity of mice to humans, the great array of molecular tools for making targeted gene manipulations in mice, the vast knowledge base of molecular, cellular and behavioral experimentation using mice, the large number of mouse lines that already exist with targeted manipulations in genes of relevance to visual function and disease, the relatively short generation time, and the economics of mouse husbandry. Though extensively used in the investigation of basic retinal function and genetic eye disease, the value of the mouse for eye research would be enhanced considerably were it possible to measure visual sensitivity quantitatively and noninvasively in the manner of Stiles (1939). Here, we attempt to achieve this goal.

Materials and Methods

Mouse husbandry and strain sources

All experimental procedures were performed in accord with protocols approved by the Institutional Animal Care and Use Committee at Northeastern University. Breeding pairs of wild-type (WT) C57BL/6 mice were purchased from Charles River Laboratories. Pups were born and raised under cyclic lighting (12 h light/dark cycle with 1.5 photopic cd m⁻² light). The mice were at least 60 d old when they were first individually moved to an experimental cage in which they would remain for months. The cyclic lighting was then set for 18 h dark, 6 h light (1 cd m⁻²), and experiments were conducted during the nominally dark phase of the cycle. The 18 h dark period gave the mice time to complete a sufficient number (60–80) of trials in experiments that required the dark-adapted state. During experiments requiring light adaptation, the background light effectively extended the light cycle up to ∼14 h, until the mice had completed 40–60 trials.

Seven male and five female C57BL/6 mice were used in experiments that measured their absolute sensitivity, the increment threshold response, or spectral sensitivity. Three Gnat1^−/− mice, 3 to 4 months of age, were kindly provided by Dr. Janis Lem (Tufts University, Boston, MA). Six Gnat2^cpfl3 mice, three pigmented and three albinos (ALS/LtJ), 2 to 4 months of age, were generously provided by Dr. Bo Chang (The Jackson Laboratory, Bar Harbor, ME).

Physical geometry of the apparatus and calibration of the stimuli at the retina

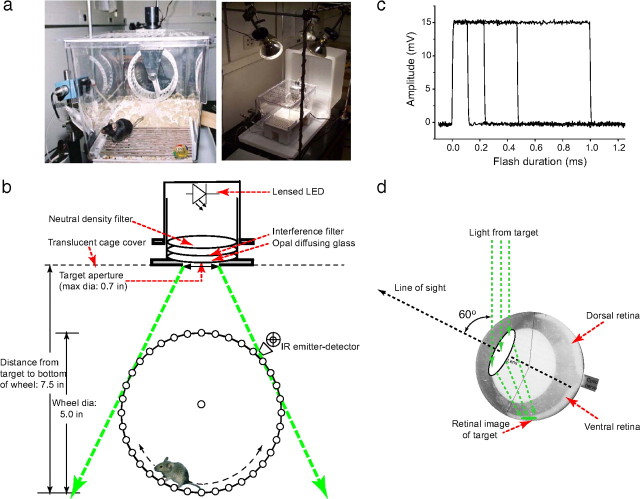
Here we provide details about the running wheel apparatus and the method and calculations used to estimate the retinal image size of targets used in the study and the retinal flux and photon capture by rods. Figure 1a provides photographs with two views of the experimental cage, showing several critical components of the apparatus. The left image shows the water spout with a mouse standing on a grounding grid about to take a lick, the running wheel, and the housing for the stimulus light source above the wheel. The right image shows the experimental cage from a greater viewing distance, with flood lamps and the translucent plastic cover (set back), which covers the cage during experimentation.

Figure 1.

Schematic of the “running mouse” apparatus and details of light calibrations. a, Photographs of the mouse cage. Left, A mouse is seen near the water spout extending from the wall on the lower left. The black cylindrical assembly mounted above the running wheel contained an LED that provided the variable-intensity light flash (see Materials and Methods). Right, During all experiments, the mouse cage was placed inside an inverted translucent box raised slightly above the table to permit the free flow of fresh air; the box also served as a light diffuser for experiments in which the mouse was light adapted. b, Scale drawing of the running wheel and LED light source, identifying important components and distances. IR, Infrared. c, Sample calibration traces obtained with PIN photodiode located at the bottom of the wheel at the level of the mouse's eye; each trace represents one of the timed flashes delivered to the mouse's eye on different trials. d, Magnified image of a mouse eye by Remtulla and Hallett (1985), as reproduced in (Lyubarsky et al., 2004), oriented with respect to the light field as it would be for a mouse on the lowermost position of the wheel.

Geometry of the apparatus.

Figure 1b presents a scaled diagram of the apparatus, identifying its principal components, including in particular the running wheel and light source. The light source consists of an interchangeable, lensed light-emitting diode (LED) source mounted at a fixed position in a light-proof, baffled black Lexan cylinder, which also contained a narrow band (∼10 nm) interference filter; one to three calibrated, absorptive neutral density filters; and a circumscribed opal diffusing glass window through which light exits (details of the LED sources are provided in supplemental Table S2, available at www.jneurosci.org as supplemental material). Visual inspection and calibrations showed the diffusing window to act as a Lambertian source for the viewing angles at which the mouse would see it, which range from approximately perpendicular to the source (mouse at the lowermost point of wheel) to ∼30° from perpendicular (highest point on wheel that the mouse reaches). The exposed surface of the diffusing glass has a diameter of 1.8 cm and is situated directly above the apex of the running wheel. The diameter of the target could be reduced (as in the spatial summation experiments) by opaque baffles with calibrated circular apertures placed in front of the diffusing glass.

Geometry of visual targets in the running wheel apparatus.

We will consider the calibration of the largest diameter visual target in detail; calibration of the targets of smaller diameter was done in a similar manner. At the low point of the running wheel, the distance from the diffusing glass surface to the mouse's head is 19.0 cm. Thus, the largest target used subtended a visual angle of tan⁻¹(1.8/19.0) = 5.3°.

Geometry of the mouse eye and retinal area subtended by the target.

The adult C57BL/6 mouse retina can be accurately described as lying on a hemisphere of radius 1.69 mm (Fig. 1d) (cf. Lyubarsky et al., 2004). Thus, the retinal image of a disc target subtending 5.3° visual angle has a diameter of (5.3/180) × π × 1.69 mm = 0.156 mm. The retinal surface area occupied by the 5.3° target is thus π × (0.156/2)² mm² = 0.0191 mm², and so a visual target of area 1 deg² projects to a retinal image area of ∼870 μm². As the average density of rods in the C57BL/6 mouse retina is 4.37 × 10⁵ mm⁻² (Jeon et al., 1998), the 5.3° diameter circular target subtends 8350 rods. Because the density of cones in the mouse retina is 1:30 relative to that of rods (Carter-Dawson and LaVail, 1979), the 5.3° diameter target also subtends ∼280 cones.

Calibration of background luminance.

In increment threshold experiments, the adapting background was constituted by an inverted translucent plastic container illuminated from above and the sides by flood lamps or by fiber optic cables that transferred light from a xenon arc lamp (Fig. 1a). The container diffused the light and created an effective “ganzfeld” environment. Both monochromatic and broadband (“white”) illumination were used, the latter to generate more intense backgrounds. The calibration of the backgrounds was performed both radiometrically and photometrically for monochromatic illumination and photometrically for broadband illumination. Photometric calibrations of the luminance (scotopic candela per square meter) were made with a Model S370 optometer (UDT Instruments). Radiometric measurements were made with a planar PIN silicon photodiode (Model 1223A; UDT Instruments) to determine the incident light flux at the position of the mouse's head during running. (An “artificial mouse” was created that held the PIN photodiode in place on the running wheel.) Radiant flux incident at the pupil plane was converted to luminance as described by Lyubarsky et al. (2004, their Eqs. 1, 2). However, the combination of the casing of the photodiode, effects of angle of incidence, and some decline in the radiance of the sidewalls of the container relative to the radiance of the ceiling above the light emitting diode target caused the flux measured by the photodiode to be reduced to 40% of the flux expected to be received by an idealized planar diode in a perfect ganzfeld [in terms of Eq. 2 of Lyubarsky et al. (2004) with θ_crit = 50°]. With proper adjustment for θ_crit, the radiometric and photometric calibrations were in good agreement.

Flux density measurements at the cornea for the target.

All test targets were monochromatic and calibrated radiometrically. Specifically, taking into consideration the duration of the test flashes (Fig. 1c) and any attenuation by calibrated neutral density filters (Fig. 1b), we estimated the flux density at the mouse cornea produced by the extended source of the opal glass surface for any specific stimulus. Here we report the angular size and the flash strength of the targets used, with the latter specified in units of photons per square millimeter at the cornea. Where we compare the thresholds of mice and men, we present threshold intensities in “quanta at the cornea adjusted for pupil capture area.” In this case we multiply the flux density measured at the position of the mouse's cornea by the effective dark-adapted pupil area (Fig. 1d). We adopt as the pupil area of the dark-adapted C57BL/6 mouse along the line of sight the value 4.0 mm², obtained in the study by Grozdanic et al. (2003); this value is also close to that (3.7 mm²) reported by Do et al. (2009). We estimated the line of sight of the mouse, defined as the axis on which the pupil projection is maximal, to be ∼60° from the vertical (Fig. 1d). The effective pupil area for light capture from the overhead target is thus 4.0 mm² × cos(60°) = 4.0 × 0.5 = 2.0 mm². Additional details about the dependence of the pupil area on luminance are provided in supplemental Figures S2 and S3 (available at www.jneurosci.org as supplemental material).

Retinal flux density.

The retinal flux density of a target of wavelength λ was estimated as the flux density at the cornea, multiplied by the effective pupil area and transmissivity of the preretinal media, divided by the retinal image area:

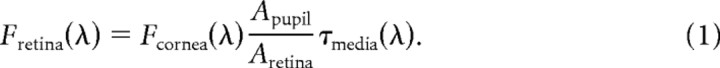The retinal energy density of a specific flash was determined as the flux density multiplied by the measured flash duration (Fig. 1c). As described above, the effective pupil area (A_pupil) for the overhead targets is 2.0 mm², and the 5.3° target projects to a circular retinal region of area 0.0191 mm² or 19,100 μm² (A_retina). We expressed the retinal flux density in photons per square micrometer. We made no corrections for transmission through the ocular media, i.e., assumed τ_media(λ) = 1, as to our knowledge this has not been measured in the mouse, and we wished to be conservatively high in estimating the number of photoisomerizations produced by threshold stimuli. A lower bound for τ_media(λ) can be obtained from the study of (Alpern et al., 1987) on the rat eye; for λ = 500 nm they measured τ_media(λ) = 0.66.

Photoisomerizations per rod or cone.

For understanding the behavioral data in neural terms, it is important to estimate the number of photoisomerizations per photoreceptor at threshold. The number of photoisomerizations/rod (or per cone) produced by a specific stimulus was calculated as the corresponding retinal flux density multiplied by the end-on collecting area.

The end-on collecting area a_c,end-on is the effective cross-sectional area of the total pigment content of a photoreceptor for axially propagating light. The contributions of various factors to a_c,end-on for a rod can be written as follows:

In Equation 2, σ_rods is the rod density in the retina, f_guided ≤1 is the fraction of light that impinges on the inner segment layer that is guided into the outer segment, D(λ) is the axial optical density of rhodopsin in the outer segment, and γ is the quantum efficiency with which a photon absorbed by a rhodopsin molecule induces an isomerization. The rod density σ_rods is determined by the packing at the inner segment layer, where waveguiding begins. For the mouse, σ_rods was determined by Jeon et al. (1998) to be 437,000 mm⁻²; this density is essentially identical to that of cat (450,000 mm⁻²) (Sterling et al., 1988), whereas the maximal human rod density is only 177,000 mm⁻² (Curcio et al., 1990). The fraction f_guided is unknown for the mouse retina, but hexagonal packing sets an upper limit of ∼0.85. The axial density D(λ) is the product of the specific density per unit length (taken to be 0.019 optical density units μm⁻¹ for λ = λ_max = 498 nm) and the pathlength L (taken to be 24 μm; (Carter-Dawson and LaVail, 1979)); thus, D(λ) = 0.456, and the fraction of light entering the outer segment that is absorbed is [1−10^−D(λ)] = 0.65. The quantum efficiency γ was assumed to be 0.67. Inserting these values of the several factors into Equation 2 yields the estimate a_c,end-on (500 nm) = 0.85 μm² for mouse rods. A similar analysis was made by Lyubarsky et al. (2004), who obtained a_c,end-on = 0.87 μm² for rods and a_c,end-on ∼ 1 μm² for cones. The slightly higher value for cones than for rods owes to the “funneling” effect of their larger diameter inner segments, which more than compensates for their smaller outer segments.

Rigorous upper and lower bounds for a_c,end-on for rods are available. A lower bound comes from estimates of the collecting area of mouse rod outer segments recorded with suction pipettes and stimulated from the side: many different laboratories, using classic analyses and variance/mean analysis have concluded the collecting area a_c,sideways for a mouse rod outer segment under such conditions to be ∼0.4 to 0.5 μm² (Calvert et al., 2001; Nikonov et al., 2005; Dunn et al., 2006; Krispel et al., 2006). The value of a_c,end-on may be as much as twofold higher than a_c,sideways because of the dichroism arising from the orientation of the rhodopsin chromophore in the plane of the discs. An upper bound for a_c,end-on is obtained from the reciprocal of the rod packing density: (1/σ_rods) = (1/0.437 μm⁻²) = 2.3 μm². This latter value would apply if every 500 nm photon reaching the inner segment mosaic isomerized a rhodopsin molecule. The value a_c,end-on = 0.85 μm² is clearly reasonable.

From Equations 1 and 2 it follows that a flash of wavelength λ = λ_max = 498 nm, duration ΔT, and flux density F_cornea(λ) (in photons mm⁻² at the cornea) produces an average number of photoisomerizations rod⁻¹ in the target of retinal image area A_retina given by the following:

The average total number of isomerizations produced by such a flash is then given by the following:

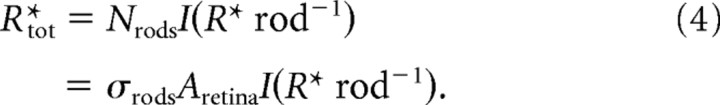Equations 1–4 were used with the underlying parameter values specified above when flash strengths are specific in units of R* rod⁻¹ or R* cone⁻¹, the only difference between the two being specified by the small differences in a_c,end-on.

An alternative approach was used to calibrate the broadband (“white”) backgrounds in terms of photoisomerizations rod⁻¹ s⁻¹. Specifically, the luminance (scotopic cd m⁻²) of the steady background was measured and multiplied by the effective pupil area in square millimeters to obtain the retinal illuminance in scotopic trolands, which in turn was converted to photoisomerizations per rod per second by multiplying by a conversion factor, 181, determined by Lyubarsky et al. (2004) from experiments in which rhodopsin was bleached in the intact mouse eye.

Additional considerations arising from the running wheel.

Considerations of the position of the mouse on the wheel at the time of the flash give rise to a number of potential concerns about the calibrations. Because running orients the mouse's body axis tangent to the wheel's circumference (as depicted in Fig. 1b), the optical axis of the eye relative to the overhead LED is well defined (Fig. 1d). Our standard calibrations are for a mouse in the lowermost position on the wheel; in this position (or any other it occupies while running), the axle of the running wheel does not occlude any portion of the target. However, the bars or “runners” of the wheel block a measurable portion of the light emitted by the target from reaching the mouse's eye. Specifically, the diameter of each running bar is 4.8 mm, and the spacing between adjacent bars is 5.5 mm, so that the bars on average block 4.8/(4.8 + 5.5) = 47% of the light, and we adjusted the light flux at the cornea for this factor. Three additional considerations are as follows. First, the mouse's running sometimes takes it to a position as high as 30° up from its lowermost position on the wheel; this will put the mouse 10% closer to the target. Second, the variable position of the mouse on the wheel when the flash is triggered alters the location on the retina of the target image: thus, the target will be variously located over an ∼30° arc of the ventral retina (see Fig. 1b,d). Third, the position of the mouse on the wheel when the flash is delivered will slightly alter the effective pupil area. Although we do not dismiss these latter factors, we think them negligible and contributing mainly to nonsystematic error. Another issue regarding the running wheel is the possibility that mice were responding to light reflected from nearby objects such as the wheel rungs rather than to light arriving directly from the overhead source. To address this issue, the entire wheel assembly was treated with a matte black paint except for a narrow strip on the wheel rungs that enabled infrared light to be reflected for measurement of the wheel rotations (Fig. 1b). Absolute threshold intensities measured for mice running on the painted wheel are very similar to thresholds obtained on unpainted wheels, indicating that the mice are responding predominantly to light coming directly from the overhead LED.

Summary of calibrations.

We summarize the calibrations with an example of the calculation of the total number of photoisomerizations at absolute threshold for the 5.3° diameter target. The threshold expressed in average number of 500 nm photons at the pupil for a group of five extensively tested mice is 67 (see Table 1). This number is adjusted for the projected or effective pupil area (Fig. 1d); assuming no ocular media transmission losses, and given that the target subtends 19,100 μm² at the retina, the photon flux density at the retina is 68/19100 = 0.0036 photons μm⁻². Given an end-on collecting area of a mouse rod of 0.85 μm², the probability that any rod in the target area underwent a photoisomerization is 0.0036 × 0.85 = 0.0031. Since the target area contained 8350 rods, the average total number of rhodopsin photoisomerizations at absolute threshold is 0.0031 × 8350 = 26.

Table 1.

Absolute thresholds of C57BL/6 mice

	Animal no.						Avg.
	1	2	3	4	5	6
Observed threshold (avg. # of photons “at the pupil”)a	69	76	60	63	71	64	67
95% confidence interval	±10	±13	±10	±8	±16	±18	±6
False positive rate (# of trials)b	1.0% (500)			0.67% (500)	1.6% (750)		1.2% (1750)
Estimated threshold (Θ) of counter model (Eq. 5)	29	29	28	30	30	31	30
Conversion efficiency (QE) of counter model (Eq. 5)	0.22	0.12	0.17	0.19	0.14	0.22	0.18
Predicted false positive rate of counter model	1.3%	3.3%	4.4%	1.8%	2.0%	3.0%	2.6%

The test target was a 5.3° visual angle circular target with duration <1 ms imaged on the ventral retina. FOS data were collected with a series of 500 nm flashes whose energy was varied (Fig. 3) and which were fitting with a logistic function to extract the threshold (Fig. 2).

^aEach mouse produced at least 9 (range 9 to 15) experiments, corresponding to between three and six complete FOS sets; the pooled data are shown in Fig. 3. The distribution of the pooled data was normal (Kolmogorov–Smirnov distribution, 0.113; p = 0.064), and differences among animals were marginal (ANOVA, F_(df1,df2) = 2.29; p = 0.071).

^bTo determine the false positive rate, trials were presented that were either blank or contained a flash of an intensity about twice the average absolute threshold. The Sakitt (1971) counting model with thermal noise (Eq. 5) was fitted by least-squares minimization to the composite FOS data of individual mice to extract the model parameters Θ and Q_E (Fig. 3).

Behavioral methodology

The method took advantage of a natural behavior of a caged mouse: it will run, on average, 9 km per night, at an average speed of 0.9 revolutions s⁻¹ (data from 12 mice, 14 nights; SD, 2 km). A running mouse was trained by operant conditioning to associate a light flash delivered from an overhead LED with the brief (12 s) availability of water at a spout that could detect the mouse's licking.

The training of the mice was performed in two stages. In stage 1, an association between the presentation of an overhead light flash and the availability of water was established. In stage 2, the mice were trained to work for water. During stage 1, an animal was placed in the experimental cage and given unrestricted access to food and water. On the second day, the availability of water was conditional, that is, it depended on the detection of the light flash. By wheel running the mouse triggered on every 20th wheel turn a bright flash that was always followed by a time interval during which water was available: first for 600 s, then gradually for shorter times down to 12 s. Mice learned to associate the light flash with water availability within 10 h after the first bright flash presentation. During stage 2, the association between the flash presentation and water availability was strengthened by decreasing the flash intensity and by increasing the random number of wheel turns at which the flash would be triggered. As the flash intensity decreases, the number of errors made by the animal inevitably increases. To insure that it gets enough water (a mouse drinks 5–6 ml per day), bright light flashes are randomly interspersed. By letting the mouse work for water, its motivation to respond to the light stimulus is made integral to its natural daily routine. We have found that the association between the flash and water availability lasts a lifetime.

A computer program and electronic interface controlled all aspects of the experiments, including the timing of the flash presentation, flash intensity, water availability, background light intensity, and trial sequencing. The program randomized the number of revolutions (between 200 and 500) that the mouse had to run before a flash was presented. The trial ended immediately after the 12 s period of the water-availability interval: counters and timers were reset by computer, and a new trial began, regardless whether the mouse was on or off the wheel.

Analysis of frequency of seeing data

Frequency of seeing (FOS) data were collected from individual mice during nightly sessions under dark- and light-adapted conditions with the method of constant stimuli. Before an experiment began, mice dark adapted for at least one hour. During light-adapted experiments, the background light was turned on and fixed at one intensity level for the duration of the experiment. Each flash intensity level was presented 15 times, on for a minimum of 40 and maximum of 60 trials. The trials were organized in 12 blocks; each block contained five trials of fixed flash intensity. The blocks were presented in random order. The intensity range was occasionally extended to five or six flash strengths spanning a range of ∼1.3 log units. The grand average of the correct responses per intensity level was calculated along with the SD; the error terms reported in the text and plotted in figures are 2 SEM, an approximate 90% confidence interval. The threshold was defined at the intensity that gave rise to 50% detection by the mouse. This intensity was found by least-squares fitting of a logistic function of the form y = [1 + exp(−(x − x₅₀)/b))]⁻¹ to the FOS data, where y is the fraction of correct responses, x is flash intensity, x₅₀ is the intensity giving rise to 50% detection, taken to be the threshold, and 1/b is the slope of the curve x = x₅₀.

We also fitted the threshold model of Sakitt (1971) to the absolute threshold data. This model treats the observer as an event-counting detector that reports seeing a flash if a criterion number of events (ϴ) is registered in a critical integrating time (t_int); it generalizes the model of Hecht et al. (1941) by including dark photon-like events. We modified the model slightly to accommodate an apparent lack of attention of the animals on a small fraction of the trials. The modified model predicts the probability that a mouse will respond as though it saw a flash delivering an average of N̄ photons to the cornea (through an effective pupil of area A_pupil) to be given by the following:

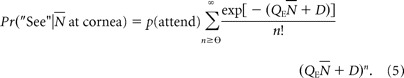Here, p(attend) is the probability that the mouse is attending to the target at the time of the flash, D is the number of dark events (i.e., rhodopsin thermal isomerizations) that occur in the retinal image area of the target in a time window of duration t_int containing the flash, Θ is the threshold criterion of the event counter, and Q_E is an overall efficiency factor. From Equations 1–4 the following can be seen:

which from the parameter values above for λ = 500 nm has the value Q_E = 0.24. The combined uncertainty in the several factors contributing to Q_E is probably ∼50%, and Q_E = 0.24 represents a conservative overestimate. An important feature of the counting detector model embodied in Equation 5 is that it automatically predicts the false alarm rate, which is given by evaluating Equation 5 with N̄ = 0.

Equation 5 was fitted to the extensive FOS data sets of six mice obtained in measuring the absolute threshold for 500 nm targets of 5.3° diameter with least-squares minimization using the DIRECT search algorithm in Matlab (MathWorks) (Finkel, 2003). The error term for each intensity N̄ (including N̄ = 0) was weighted by the fraction of trials performed at that intensity, relative to the total number of trials at all intensities. In the fitting process Q_E and Θ were treated as free parameters, and N̄ was calculated as N̄ = F_cornea A_pupil, where A_pupil is the effective pupil area (2 mm²), and the value of D was held fixed. The value of D was obtained by computing the expected number of thermal isomerizations in the population of rods in the target area during an integration time t_int = 0.2 s, taking I_dark (R* rod⁻¹), the rate of spontaneous isomerizations in a mouse rod, to be that value, 0.012 s⁻¹, measured by Burns et al. (2002). Thus, we obtained the value D = σ_rodsA_retinaI_dark(R* rod⁻¹)t_int = 0.437 (rods μm⁻²) × 19100 (μm²) × 0.012 (R* rod⁻¹ s⁻¹) × 0.2 s = 20 R*.

Results

Absolute sensitivity of mice is very similar to that of the human peripheral retina

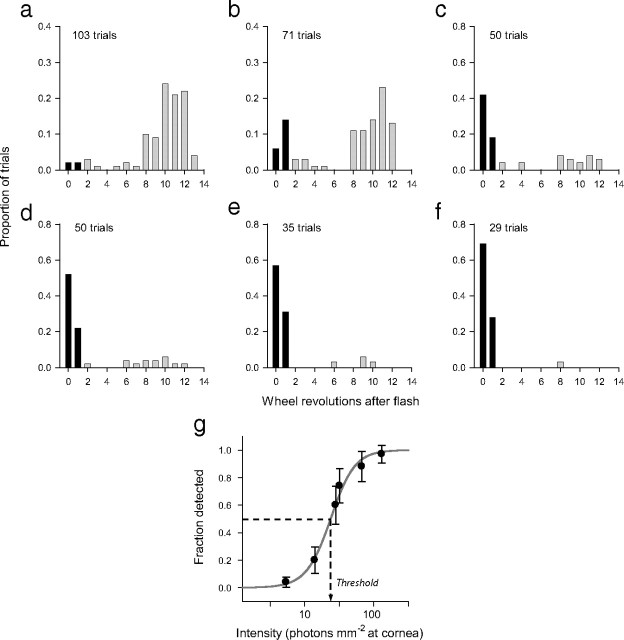
A threshold trial required the mouse to run a randomly selected number (between 200 and 500) of wheel cycles before a stimulus was flashed. The stimulus was deemed correctly detected if the mouse stopped running in less than two wheel revolutions after the flash presentation. In a sample set of experiments performed over the course of six days, when the light flash was very dim, the mouse rarely detected it and continued to run throughout the 12 s water-availability period (Fig. 2a). As the flash was made more intense, the mouse detected it more frequently (Fig. 2b–f). A plot of the fraction of trials in which the mouse produced a correct response as a function of the flash intensity gave a “frequency of seeing curve” from which a detection threshold was readily and precisely determined as the curve's midpoint on the intensity axis (Fig. 2g).

Figure 2.

Measurement of visual thresholds of a freely running mouse. a–f, Histograms show the distribution of trials across the number of wheel revolutions completed in the 12 s after-flash period: black bars represent the trials on which the mouse interrupted the running in less than two wheel turns after the flash, whereas gray bars indicated trials for which the mouse remained on the wheel for two or more turns. The flashes delivered, on average, 5.4, 14, 28, 32, 67, and 130 photons mm⁻², respectively, at the mouse's cornea. g, The flashes on trials in which the mouse exited the wheel in less than two revolutions after the flash were deemed “correctly detected”; the fraction of such trials is plotted as a function of flash intensity to generate an FOS function. The sigmoidal curve fitted to the data represents the logistic function y = [1 + exp(−(x − x₀)/b)]⁻¹, where y is the fraction of correct responses, x is flash intensity, x₀ = 24 photons mm⁻² is the intensity giving rise to 50% detection, taken to be the threshold, and 1/b is the slope of the curve x = x₀.

To determine the dark-adapted mouse's absolute visual sensitivity, we initially measured thresholds for 500 nm targets of 5.3° visual angle (Table 1). The absolute threshold measured at the cornea was 67 ± 6 photons (mean ± 95% confidence interval), remarkably similar to the threshold of humans for targets presented in the near retinal periphery (Table 2). Because the retinal image of the 5.3° target subtends 8350 rods, the probability that any of the rods in the retinal image of the target captured more than one photon at threshold is negligible (<0.003). Thus, it can be concluded that in mice, as in humans (Hecht et al., 1941), the isomerization of a single rhodopsin molecule in a rod can be signaled through the retina to higher neural centers that underlie its choice behavior.

Table 2.

Comparison of mouse and human absolute thresholds

References	Retinal eccentricity (degree)	Stimulus duration (ms)	Stimulus wavelength (nm)	Retinal image area (mm2)	Rods subtended by target	Photons at the corneaa
Mouse
This study		<1b	500	2.2 × 10−3	960	31 ± 7 (5)
This study		<1b	500	1.9 × 10−2	8350	67 ± 6 (6)
Human
Hallett et al. (1962)	20	2.6	520	2.5 × 10−4	55	90
Sharpe et al. (1993)	12	10	520	1.8 × 10−3	465	55
Hecht et al. (1942)	20	1	510	1.8 × 10−3	480	90
Hallett et al. (1962)	20	2.6	520	6.5 × 10−2	10,000	100

^aThe number of photons at the cornea at threshold was calculated as the product of the reported photon flux density at the cornea (in photons deg⁻² s⁻¹) multiplied by the retinal image area and flash duration.

^bFor the mouse experiments, the stimulus flashes were generated by time-gated LED pulses, which ranged in duration from 10 μs to 1 ms to control the total flash energy. The photon flux density measured at the cornea was multiplied by the flash duration and the effective dark-adapted pupil area, 2 mm² (see Materials and Methods). For the human experiments, target areas in degrees squared were converted to millimeters squared using relations provided in Wyszecki and Stiles (1982). Areas were multiplied by rod densities at the appropriate retinal eccentricity, as given in Oesterberg (1935).

Application of a counting model of absolute threshold to frequency of seeing data

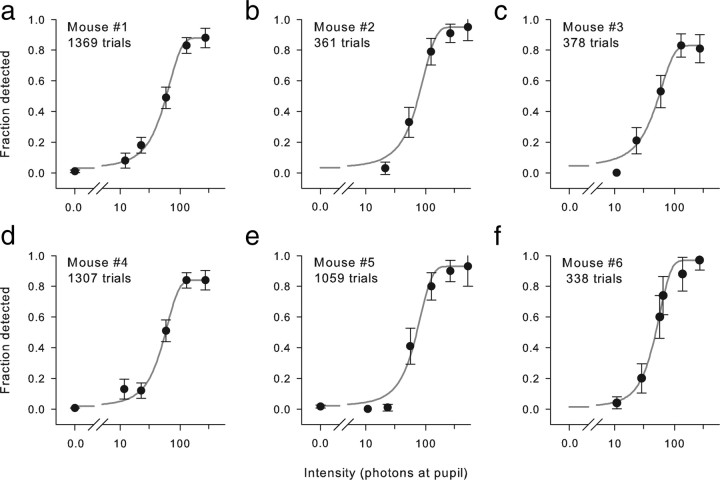
Since the classic work of Hecht et al. (1941) human absolute threshold FOS data have been analyzed with models that characterize the detection process as that of an event counter with a fixed threshold, with and without intrinsic noise (for review, see Field et al., 2005). Given the similarity of the dark-adapted thresholds of mouse and man measured at the cornea (Table 2), it seemed worthwhile to apply the event-counter model of Sakitt (1971) (Eq. 5) to the mouse FOS data (Fig. 3). The model gives a good account of the FOS data with a counter threshold of ∼30. The average value of Q_E estimated with the model is 0.18, two-thirds of the upper limit, 0.24, expected on the basis of independent measurements (Eq. 6). This modest difference can probably be accommodated by uncertainty in the factors underlying Q_E. A difficulty in the application of the Sakitt (1971) model is that it is agnostic about the spatial pooling of single-photon responses, which, as we now show, is an important determinant of the threshold.

Figure 3.

a–f, Frequency of seeing curves of six different mice fitted with the Sakitt event-counter model of absolute threshold (see Materials and Methods) (Eq. 5). Each panel presents the FOS data of one mouse, including (for mice 1, 4, and 5) blank trials (flash intensity, 0) to estimate the false positive rate. The event-counter model of Equation 5, which explicitly includes rhodopsin thermal isomerization noise, was fitted by least squares to each set of data to extract the model's parameters (counter threshold, Θ; transmission efficiency factor, Q_E). Table 1 presents the values of the parameters of best fit for the six mice. Error bars indicate ±2 SEM.

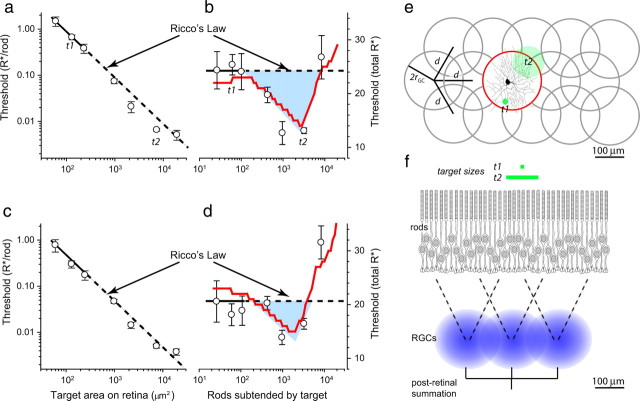
Spatial supersummation at absolute threshold takes advantage of dark noise

Absolute visual thresholds for mice obeyed perfect spatial summation (Ricco's law) for adequately small targets: the thresholds for such targets were found to be inversely proportional to the target area (Fig. 4a,c). Surprisingly, however, for retinal images whose areas are 1000 to 10,000 μm², thresholds were lower than the extrapolation of the perfect summation obeyed for the smallest targets (Fig. 4b,d). In other words, mice exhibited substantially greater sensitivity for targets subtending 400 to 4000 rods than predicted by the linear spatial pooling of the single-photon responses of the rods in the retinal image of the targets. To examine the idea that this “supersummation” manifests an important characteristic of the retina, we developed a neural model of the phenomenon (Fig. 4e,f; supplemental material, available at www.jneurosci.org). The model is based on the anatomical dimensions of mouse retinal ganglion cells (RGCs) and three well-established functional features of the mammalian retina: first, that single rhodopsin isomerizations in rods generate signals that can propagate reliably through the retina to higher visual centers (Hecht et al., 1941; Barlow et al., 1971; Mastronarde, 1983) (Tables 1, 2); second, that thermal (“dark”) isomerizations of rhodopsin occur and are indistinguishable in their properties from photoisomerizations (Barlow et al., 1971; Baylor et al., 1979, 1984; Mastronarde, 1983); and third, that ganglion cells tessellate the retina with receptive fields well described by overlapping Gaussian sensitivity profiles (Fig. 4e). As a consequence of these features, the signaling of targets at absolute threshold by the responsible population of retinal ganglion cells is necessarily triggered by a combination of thermal- and light-triggered isomerizations. The model can provide a good account of the supersummation results (Fig. 4b,d, solid red curves) with parameters derived from the literature on mouse ganglion cell dendritic field size (Sun et al., 2002) and mouse rod dark noise (Burns et al., 2002) (for the average results of all mice tested, see supplemental material, available at www.jneurosci.org). The model suggests that spatial summation for the smallest targets is obeyed because a stimulus falls mostly within a single receptive field (Fig. 4e, target t1), and thus excites one ganglion cell to a much greater extent than its neighbors. Supersummation occurs for larger targets (Fig. 4e, target t2), which provide a similar level of excitation for two or more neighboring ganglion cells: the combined thermal and stimulus-generated isomerizations increase sensitivity and in effect boost the combined signal of the ganglion cells above the threshold of the downstream detector.

Figure 4.

Spatial summation at absolute threshold in dark-adapted, WT mice. a, c, The absolute threshold intensity, expressed in photoisomerizations/rod (R*/rod) as a function of the retinal image area subtended by the target for two different C57BL/6 mice. The test flash wavelength was 500 nm with a duration of ≤1 ms. Threshold (mean ± 2 SEM) for each target was determined as the midpoint of a frequency of seeing curve (Fig. 2) and averaged over at least two replications for each target size. Lines of slope −1 were fitted by least squares to the thresholds for the three smallest targets; the dashed lines represent the extrapolation of these lines to the larger target sizes. These lines represent Ricco's law: perfect spatial summation. b and d replot the data of a and c, respectively, in terms of the total number of R* (R*/rod times the number of rods subtended by target). The dashed line represents perfect spatial summation: several points for each mouse for targets subtending 400 to 4000 rods lie highly reliably below this line. The region of “supersummation” is indicated by the blue field. The curves (red lines) through the data points were derived by application of a model in which the signals from rods undergoing thermal isomerizations and target-induced photoisomerizations are combined by a retinal ganglion cell to exceed a threshold for signaling to higher visual centers. Similar results were obtained from two additional mice. e and f describe aspects of the model. e, Mosaic of a population of RGCs with receptive field radius 2r_GC ∼ 100 μm distributed on a hexagonal lattice with center-to-center distance d. An image of a mouse RGC dendritic field from the study of Sun et al. (2002) is shown approximately at scale circumscribed in the central cell in the lattice (red circle). Two circular targets (t1, t2) of sizes used in the experiments (see labels on a, b) are presented as green circles: t1 is much smaller than the RGC dendritic field, whereas t2 is of a size that will cause it to often stimulate more than one RGC. f, A flow diagram of the model: the RGC receptive fields (blue circles) are modeled as Gaussians with SD r_GC truncated at the dendritic field radius 2r_GC. Details of the model are provided in the supplemental material (available at www.jneurosci.org).

An alternative explanation of the supersummation results is that the hypothesized stimulus-associated correlations could arise in AII amacrine cells. The feasibility of an explanation in terms of AII amacrine cells depends on the size of the receptive field of these cells in the mouse retina. Anatomical studies in cat retina (which has a rod density of 450,000 mm⁻², very close to that of mouse, 437,000 mm⁻²) have shown that each AII amacrine cell receives input from ∼300 rods via rod bipolar cells (Sterling et al., 1988), but results from wild-type and connexin36^−/− mice indicate that gap-junctional coupling may increase the AII amacrine receptive field by as much as a factor of four (Dunn et al., 2006). An AII amacrine receptive field subtending 1200 rods approaches the retinal region (2000 rods) for which the supersummation effect becomes maximal, so an explanation of the phenomenon in terms of AII amacrines cannot be ruled out. Recordings examining spatial summation at threshold in mouse retinal cells will be needed to discriminate between the competing hypotheses.

Absolute threshold for the ultraviolet sensitive cones of Gnat1^−/− mice

Mouse retinal photoreceptors express three distinct opsins: in rods, rhodopsin (λ_max = 498 nm; gene, Rho), and in cones two distinct opsins, one maximally sensitive in the ultraviolet wavelengths (λ_max = 360 nm; gene Opn1sw) and one maximally sensitive in the middle wavelengths (λ_max = 508 nm; gene Opn1mw) (Sun et al., 1997; Yokoyama et al., 1998). The three mouse opsins are homologous to human rhodopsin, S-cone-opsin, and the M/L-cone visual opsins, respectively. As an initial effort to determine whether spectral sensitivities corresponding to the mouse rod and cone opsins could be isolated with our behavioral method, we measured dark-adapted thresholds of WT mice, and mice with no rod function (Gnat1^−/−) (Calvert et al., 2000) for flashes of two wavelengths, 365 nm and ∼500 nm, expected to discriminate between mouse rhodopsin and S-opsin (Fig. 5). For WT mice, sensitivity was approximately threefold higher for 500 nm than for 365 nm flashes, as expected if rods govern threshold, whereas for Gnat1^−/− mice sensitivity was higher at 365 nm, consistent with the expectation that S-opsin-dominant ventral cones govern threshold in this line (Fig. 5a). The dark-adapted threshold of mouse cones measured in nightblind Gnat1^−/− mice was ∼3.5 log₁₀ units higher than the dark-adapted threshold of the WT mouse (Fig. 5b), consistent with classic human results in the retinal periphery (Stiles, 1939, 1946, 1949; Sharpe et al., 1989, 1992).

Figure 5.

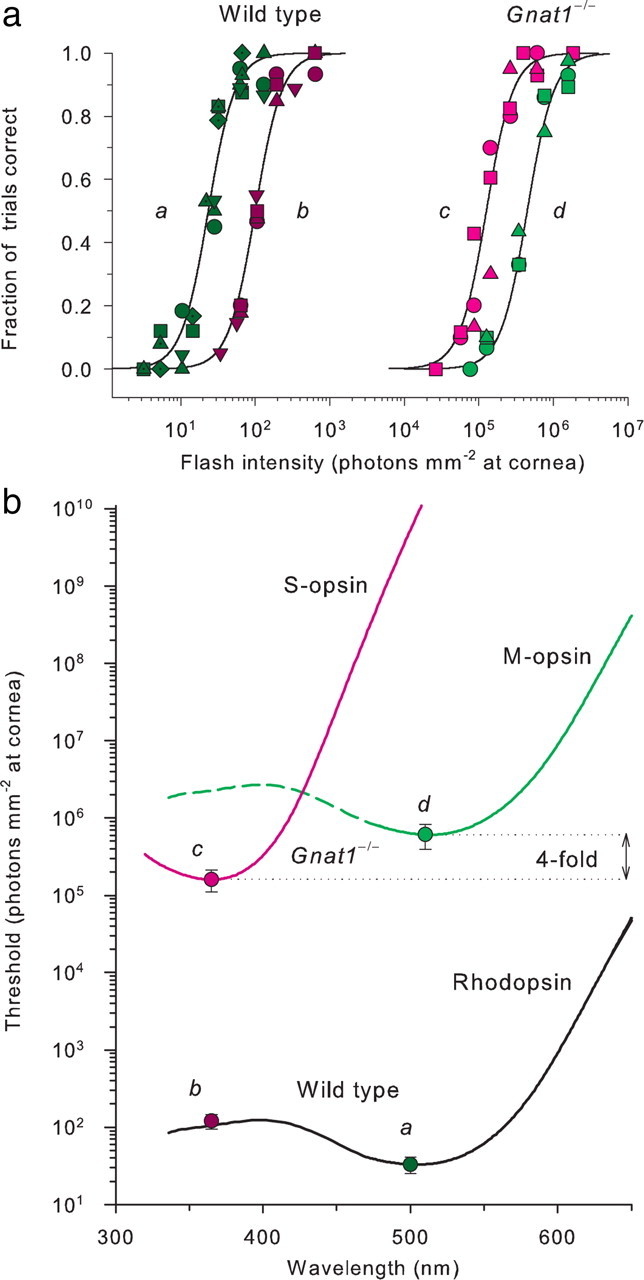
Absolute visual thresholds of dark-adapted WT and nightblind (Gnat1^−/−) mice for midwave and ultraviolet targets. a, FOS data, on the left, obtained from WT mice (n = 6) with 500 nm (dark green symbols) and 365 nm (dark violet symbols) test flashes, and on the right, obtained from Gnat1^−/−) mice (n = 3) with 365 nm (magenta) and 510 nm (light green symbols) test flashes. Target size was 5.3°; its duration was ≤1 ms. Two to four FOS data sets were averaged for each mouse. The smooth curves are logistic functions, fitted to the composite data by eye; to extract thresholds, each FOS data set was fitted separately. b, Absolute threshold intensities (mean ± 2 SEM) of dark-adapted WT and Gnat1^−/− mice for midwave and ultraviolet stimuli extracted from the experiments illustrated in a and plotted as function of wavelength; the italic labels (a, b, c, d) near the threshold data correspond to the four experimental conditions correspondingly labeled in a. The smooth curves are pigment template spectra for mouse S-opsin (magenta), M-opsin (green), and rhodopsin (black) in situ taken from Lyubarsky et al. (1999), who used them to fit the spectral sensitivity of the mouse a-wave and cone b-wave of the electroretinogram; they were derived from the pigment template formulation of Lamb (1995).

Ventral cones of mice express predominantly S-opsin, but most also coexpress M-opsin at a lower level in a dorsoventral gradient (Applebury et al., 2000; Nikonov et al., 2006). The 5.3° diameter target used in the experiments of Figure 5 had a retinal image area of 19,100 μm² and subtended ∼280 cones, with end-on collecting areas of 1 μm² (see Materials and Methods). Thus, assuming an effective pupil area of 2 mm² for the dark-adapted mouse on the wheel with respect to the target direction, the average threshold of Gnat1^−/− mice for the 365 nm target of 1.6 × 10⁵ photons mm⁻² at the cornea corresponds to the isomerization of 17 S-opsin molecules per cone. The template spectrum of S-opsin (Fig. 5b, magenta curve) shows that “pure S-cone” sensitivity is expected to be reduced ∼100,000-fold at 500 nm [see Nikonov et al. (2006) (their Fig. 3C) for an experimentally measured spectrum of a pure S-opsin mouse cone; see also Ng et al. (2010)]. Because measured threshold sensitivity at 510 nm is reduced only fourfold from that at 365 nm, the 510 nm threshold signals must arise from isomerizations of M-opsin. However, because M-opsin is only present in the ventral retina in S-dominant cones, the threshold for the 510 nm flash must arise from isomerization of M-opsin coexpressed in the S-dominant cones. This result thus establishes for the first time that the coexpressed M-opsin, shown previously to drive phototransduction in ventral cones (Nikonov et al., 2006), provides useful vision for the mouse. Assuming that Gnat2, the G-protein of cone phototransduction, is equally well activated by M-opsin as by S-opsin, the fourfold elevation of the threshold at 510 nm above that at 365 nm indicates a 1:4 M-opsin level to S-opsin expression ratio in the cones in the retinal image of the target. This ratio of coexpression is within the range measured in recordings from single mouse cones (Nikonov et al., 2006).

Stiles's two-color increment threshold method

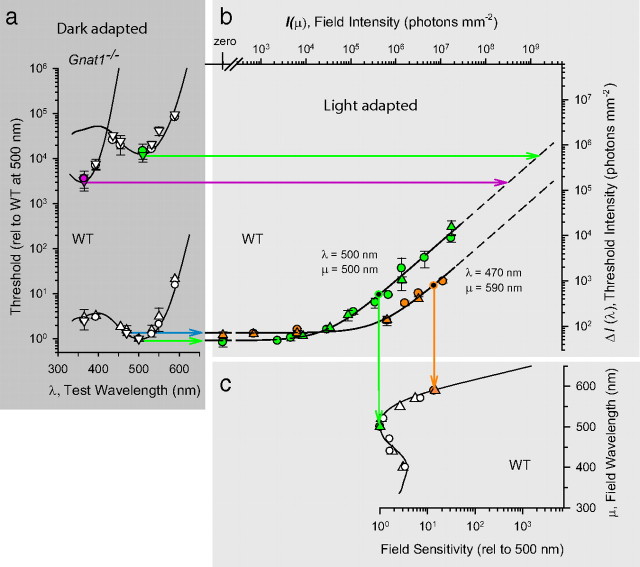
Implementation of the full two-color increment threshold paradigm of Stiles (1939) enabled measurement of the spectral sensitivity of rod vision for both test targets and backgrounds, and of the test sensitivity of S-opsin- and M-opsin-driven responses of cones of WT mice (Figs. 6, 7). Increment threshold experiments using monochromatic test flashes and backgrounds obey Stiles's classic displacement laws: changing the test flash wavelength (λ) from 500 to 470 nm shifts the double-logarithmic t.v.i. curves upward on the ordinate axis, whereas changing the background wavelength (μ) from 500 to 590 nm shifts the curve rightward along the abscissa axis (Fig. 6) (Stiles, 1939) (for review, see Pugh and Kirk, 1986). Other changes of test and background wavelengths produced similar translational shifts (data not shown). The shape invariance of the t.v.i. curves over changes of λ and μ allows criterion-independent test and field spectral sensitivities to be determined for scotopic vision; these spectral sensitivities are well predicted by template spectra for mouse rhodopsin in situ (Fig. 6a,c).

Figure 6.

Spectral sensitivities of WT and Gnat1^−/− mice for detection of test flashes in darkness and for adaptation by backgrounds. a, Thresholds for flashes of various wavelengths presented to fully dark-adapted mice; the data of WT and Gnat1^−/− mice are presented on a common ordinate. b, Two-color increment t.v.i. experiments for two WT mice in the manner of Stiles (1939); the curves in this panel plot Equation 7 with n = 0.9. The black circles identify 10-fold elevation of threshold above the dark-adapted threshold; the reciprocal of the associated background intensity defines the “field sensitivity,” that is, the sensitivity of the component curve to field (background) light of that particular wavelength. c, Field spectral sensitivity function for two WT mice derived from t.v.i. curves such as (and including the data) illustrated in b. The field sensitivities at 500 and 590 nm derived from the experiments in b are identified by arrows. Error bars indicate ±2 SEM.

Figure 7.

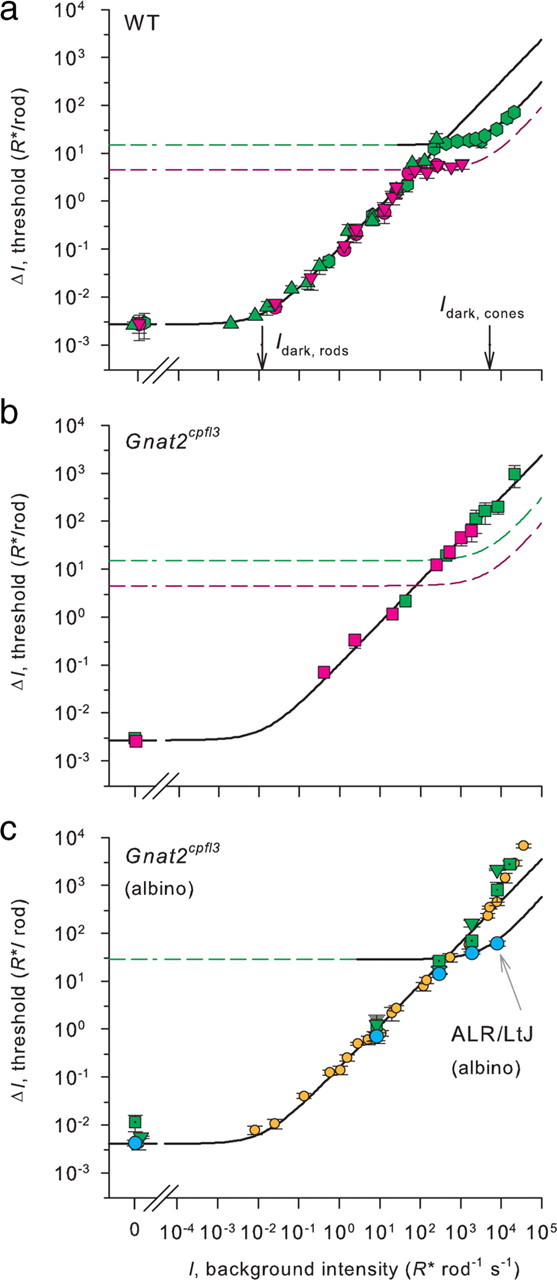
Cone branches of mouse increment threshold curves and rod saturation. a, Threshold versus increment experiments with WT mice using broadband (“white”) backgrounds and two different wavelength test flashes, 500 nm (green symbols) and 365 nm (magenta) symbols. The smooth curve fitted to the lower (rod) branch of the t.v.i. data is a generalized Weber function (Eq. 7) with I_dark = 0.012 R* rod⁻¹ s⁻¹, ΔI_dark = 0.0027 R* rod⁻¹, and n = 0.87. The curve fitted to the upper (cone) branch (λ = 500 nm, green symbols) has the parameters I_dark = 5200 R* rod⁻¹ s⁻¹, ΔI_dark = 15 R* rod⁻¹, and n = 1.0 (the parameters can be converted to cone isomerization units by multiplying by 1.0/0.85, the ratio of the cone to the rod collecting areas) (see supplemental material, available at www.jneurosci.org). b, A t.v.i. experiment with cone-defective Gnat2^cpfl3 mice with 500 nm (green) and 365 nm (magenta) test flashes. The smooth curve through the data is replotted from a with no alteration in horizontal or vertical position. c, Threshold versus increment experiments with albino Gnat2^cpfl3 mice (green symbols) and an albino ALR/LtJ control (light blue symbols). The smooth curve through the rod branch of the t.v.i. data is replotted from a with no alteration in horizontal position, but has been shifted vertically by a factor of 1.5 (i.e., 0.18 log₁₀ units). The smooth curve through the cone branch of the t.v.i. data is replotted from that fitted to the cone branch for 500 nm in a; it was shifted vertically up by a factor of 1.9 (0.28 log₁₀ units), but not shifted laterally. The yellow circles replot the data of a human rod monochromat (Sharpe and Nordby, 1990). Error bars indicate ±2 SEM.

The t.v.i. data are well described by the generalized Weber–Fechner function:

where ΔI(λ, μ) is the measured threshold for light of wavelength λ in the presence of a background of wavelength μ and intensity I(μ), ΔI_dark(λ) is the threshold in darkness, and I_dark and n are parameters characterizing the lateral position and slope, respectively, of the t.v.i. curve plotted in double-log coordinates. For all of the mice investigated here, n was ∼0.9 (range, 0.87 to 0.89). In human scotopic adaptation experiments, values of n range from 0.95 (Aguilar and Stiles, 1954) to 0.78 (Sharpe et al., 1992), but depend on the wavelength of the background except in the rod monochromat (Sharpe and Nordby, 1990; Sharpe et al., 1992). The absence of such dependence in mice suggests that cones have little influence in the intensity range used on the network adaptation that underlies most of the rod t.v.i. function. An important feature of the data is that I_dark expressed in intrinsic units of rhodopsin isomerizations (R*) corresponds to 0.012 R* rod⁻¹ s⁻¹ (Fig. 7a, arrow on abscissa), the exact rate of thermal isomerizations measured in mouse rods in the absence of light (Burns et al., 2002).

Cone signaling is more sensitive than that of rods in light far dimmer than that which causes rod saturation

The dark-adapted thresholds of the functionally rodless Gnat1^−/− mice predict that cones in the WT mouse should overtake signaling from rods when background light elevates threshold ∼3.5 to 4.0 log₁₀ units (Fig. 6b, colored arrows intersecting the t.v.i. curves). To test this prediction, we extended the investigation to higher background intensities with broadband “white” illumination (Fig. 7). To combine results obtained with different test wavelengths, we converted the background and test flash intensities measured at the cornea to retinal fluxes by adjusting for steady-state pupil area, and then converted the retinal fluxes to R* rod⁻¹ s⁻¹ (see Materials and Methods). For WT mice, branches of the t.v.i. curve with the threshold level approximately as predicted from the Gnat1^−/− data were clearly observed with both 365 and 500 nm test flashes (Fig. 7a); additional confirmation of the cone origin of the branches comes from the higher sensitivity to 365 nm than to 500 nm light.

Three features of cone signaling revealed by the data are noteworthy. First, the threshold for 365 nm light corresponds to only five photoisomerizations per cone in the image field comprising 280 cones (see Materials and Methods). In comparison, human t.v.i. experiments with a 6°, 200 ms, 520 nm test flash presented 12° off the fovea (Sharpe et al., 1992), cone absolute threshold is ∼4 isomerizations per cone in an image field containing ∼5000 cones (Curcio et al., 1990). This comparison suggests that signaling by mouse S-cones is as sensitive as that of human peripheral L- and M-cones, though a detailed comparison with varied target sizes in the two species is needed (the 10-fold smaller size of the mouse eye means that a target of any specific visual angle subtends a 10-fold greater retinal length in the human eye). Second, signaling by mouse cones becomes clearly more sensitive than that of rods in the presence of a background that produces ∼100 R* rod⁻¹ s⁻¹, revealing that the mouse retina begins to switch from rod to cone function when rod signaling is not yet saturated. Third, absolute threshold of mouse cone vision is determined by a dark light equivalent to ∼5000 isomerizations cone⁻¹ s⁻¹, 10⁵-fold higher than the dark light of rods, but very close to the dark light (equivalent to 4000 to 6000 isomerizations cone⁻¹ s⁻¹) measured in primate cones (Schnapf et al., 1990; Schneeweis and Schnapf, 1999). A threshold of 5 isomerizations cone⁻¹ in the presence of a dark light equivalent to 5000 isomerizations cone⁻¹ s⁻¹ may seem implausible. However, the peak of the dim-flash response of mouse cones is ∼60 ms (Nikonov et al., 2006), and the integration time for synaptic cone signaling is likely no greater, so the dark light corresponds to ∼300 events per cone per unit integrating time. The summed total number of S-opsin isomerizations at threshold is 1400 (equal to 5 cone⁻¹ × 280 cones), and thus spatial summation in a brief time window allows cone signaling to achieve high sensitivity in the teeth of high intrinsic noise, most likely by fast spatial averaging that reduces the noise.

Psychophysical rod saturation in the mouse

An important problem in understanding the duplex retina of any species is characterization of the adaptation conditions under which rods cease to signal, and cones alone are responsible for vision. Recordings from mouse rods show that they are capable of responding in the presence of backgrounds whose intensity exceeds by >10-fold that (∼100 R* rod⁻¹ s⁻¹) (Fig. 7a) at which cones become more sensitive than rods in vivo (Burns et al., 2002). To explore rod vision in the presence of such intensities, we performed experiments with Gnat2^cpfl3 mice, which lack the cone-specific G-protein α-subunit, and as a consequence do not have functional cones (Chang et al., 2006). The t.v.i. curve for Gnat2^cpfl3 mice for lower background intensities was indistinguishable from that of the rod branch of WT mice, indicating normal rod function, but continued along the Weber line above the WT cone t.v.i. branch for more than two log₁₀ units (Fig. 7b). The threshold deviated slightly upward from the Weber line on the most intense background, hinting at the appearance of psychophysical rod saturation (Aguilar and Stiles, 1954). As light limitations of the apparatus precluded using more intense backgrounds, we explored the matter further with albino Gnat2^cpfl3 mice, using an albino strain (ALR/LtJ) as a control (Fig. 7c). Rhodopsin in the albino mouse eye is more strongly activated by a background of a given luminance than it is in the pigmented eye: thus, for example, the rhodopsin bleaching versus intensity curve for BALB/c (albino) mice is more sensitive by a factor of 3.4 than that of C57BL/6 (pigmented) mice with fully dilated pupils; this shift can be fully accounted for by taking the effective pupil areas of the two strains into consideration (Lyubarsky et al., 2004). The t.v.i. data of two albino Gnat2^cpfl3 mice show unequivocal upward deviation from the Weber line (Fig. 7c). This upward deviation corresponds closely to that measured in the human rod monochromat (Hess et al., 1989; Sharpe and Nordby, 1990; Sharpe et al., 1992) and is the first demonstration in a nonhuman species of the classic result of Aguilar and Stiles (1954), which defined psychophysical rod saturation. The results show that mouse rods in vivo can provide detectable signals in the presence of steady lights that produce as much as ∼30,000 R* rod⁻¹ s⁻¹, but also that the rod signals under such conditions are desensitized well above the Weber line and are much less sensitive than those arising from cones.

Discussion

Mice have highly sensitive and behaviorally useful cone vision

Within the neuroscience community, a common misapprehension about mice is that they have poor vision and, in particular, that as “nocturnal animals” they have negligible cone vision. The experiments presented here strongly refute this idea. Thresholds in the mouse under night vision conditions are indeed closely comparable to those of the exquisitely sensitive human retinal periphery (Tables 1, 2; Figs. 2, 3). However, the sensitivity of the mouse's cone vision is also closely comparable to that of the human periphery. Moreover, our results clearly show that both rod and cone vision can be used naturally by the mouse for the sensitive detection of targets in a task with survival relevance.

Dark light of rods

An inescapable feature of vertebrate night vision is the presence of “dark light” arising from the thermal isomerization of rhodopsin (Baylor et al., 1979, 1984; Burns et al., 2002). It has long been hypothesized that such dark light determines the absolute threshold sensitivity of the dark-adapted eye (Barlow, 1956). The dark light of rod-based vision (I_dark in Eq. 7, as determined in Fig. 7) corresponds precisely to the rate of thermal isomerization of rhodopsin, 0.012 R* rod⁻¹ s⁻¹, measured in mouse rods (Burns et al., 2002), arguing that thermal activation of rhodopsin is the principal source of visual system dark noise relevant to the detection threshold of dark-adapted mice. Additional support for this conclusion comes from the application of the Sakitt (1971) (cf. Eq. 5) event-counter model of threshold detection, which explicitly incorporates dark noise arising from rhodopsin thermal isomerization (Fig. 3, Table 1). Previous work comparing absolute threshold of toads and of humans (Aho et al., 1988) with the rates of thermal isomerization of toad rhodopsin (Baylor et al., 1980) and of macaque rhodopsin (Baylor et al., 1984), respectively, also concluded that thermal isomerization of rhodopsin is the dominant source of visual system noise limiting absolute, dark-adapted sensitivity.

Absolute thresholds of dark-adapted retinal ganglion cells have been estimated from physiological recordings of several species, including toad, cat, and mouse (Barlow et al., 1971; Copenhagen et al., 1990; Dunn et al., 2006). Direct comparison of physiologically determined ganglion cell thresholds with thresholds measured behaviorally is complicated by a number of factors, including, for example, the analysis of false positives and the selection of the threshold criterion. The most pertinent physiological results for comparison with our behavioral data were obtained in recordings by Dunn et al. (2006) from mouse α RGCs, which have the largest somata among mouse RGCs and respond in a sustained manner to steps of light (Pang et al., 2003). Dunn et al. (2006, their Fig. 9) report the average αRGC threshold to be ∼0.008 R* rod⁻¹, or 33 total R* for an αRGC with receptive field assumed to subtend 4096 rods. In comparison, the average behavioral threshold for the optimum sized target is 31 photons at the pupil (Fig. 4, Table 2); assuming no losses in the ocular media, this value corresponds to 0.006 R*/rod or 12 total R* in a field of 2000 rods. The behavioral threshold would be lower still if photons are lost in transit through the ocular media, or could the mouse be induced to operate with a higher false alarm rate (Sakitt, 1971). Thus, the behaving mouse exhibits a threshold that is approximately threefold lower in total R* than that of individual αRGC as reported by Dunn et al. (2006). This suggests that either the αRGCs do not govern the behavioral threshold, or that their threshold as determined by Dunn et al. (2006) is elevated by recorded noise that plays no role in the behavioral decisions of the mouse in the experiments reported here. An additional indication that such noise is present in the physiological measurements comes from the conclusion of Dunn et al. (2006) that some source of noise elevates the αRGC absolute threshold to ∼2.5-fold above that determined by thermal isomerizations of rhodopsin, whereas, as discussed above, our behavioral data are consistent with the latter being the principal source of relevant noise.

Dark light of cones

The apparent dark light (I_dark ∼ 5200 R* cone⁻¹ s⁻¹) in the cone signaling pathway (Fig. 7a) also corresponds well with that measured in single mammalian cones (Schnapf et al., 1990; Schneeweis and Schnapf, 1999). It remains controversial whether the dominant source of dark light in mammalian cone vision arises from thermal isomerizations of cone photopigments. Two recent investigations in which mouse M-opsin (Sakurai et al., 2007) and human cone L-opsin (Fu et al., 2008) were transgenically expressed in mouse rods have led to the conclusion that thermal M/L cone opsin isomerization occurs at a rate ∼1000-fold higher than that of rhodopsin, which predicts a dark noise in a mouse or human cone exclusively expressing this class of opsin corresponding to ∼10 isomerizations s⁻¹. Remarkably, this latter rate is 500-fold lower than the dark light of mouse cones estimated here (Fig. 7a). Two possible explanations for the discrepancy are that cone opsins are less likely to undergo thermal isomerizations in rod membranes than in their native membranes, or that the dark noise in cones arises downstream of the opsin, for example in the spontaneous activation of phosphodiesterase (Rieke and Baylor, 2000). Our results are more consistent with the latter hypothesis, as the cones responsible for threshold detection in our experiments are in the ventral retina and express primarily mouse S-opsin (Applebury et al., 2000; Nikonov et al., 2006), which has an even lower thermal isomerization rate than L/M-opsins (Rieke and Baylor, 2000). The dark noise in the cone signaling pathway could of course also arise downstream of the photoreceptors.

Cone vision and rod saturation

The universal and perhaps most fundamental characteristic of cone-based vision in vertebrates is that cones allow the organism to see under daytime illumination, when rod responses saturate (Aguilar and Stiles, 1954; Sharpe et al., 1992). The most intense backgrounds used here correspond to daylight luminances, produced ∼10⁵ R* rod⁻¹ s⁻¹, and clearly caused psychophysical saturation, i.e., upward deviation from Weber behavior (Fig. 7). As WT mice readily performed the detection task under such conditions, they clearly saw well in such bright illumination with signals arising exclusively from cones. On the other hand, when detecting ultraviolet stimuli, the duplex retina of the WT mouse switches from rod- to cone-based vision in the presence of illumination that produces only ∼100 R* rod⁻¹ s⁻¹ (Fig. 7a), corresponding to a modest ganzfeld (e.g., sky) luminance of only ∼1 scotopic cd m⁻² (Rodieck, 1998). Thus, cones in the mouse actually take over vision at lower luminances than they do in humans, and provide very sensitive vision to mice.

Comparison with results obtained in other mouse behavioral paradigms

Various aspects of mouse vision have been investigated with behavioral methods, including threshold sensitivity (Hayes and Balkema, 1993a,b; Herreros de Tejada et al., 1997; Nathan et al., 2006), spectral sensitivity and discrimination (Jacobs et al., 1999, 2004), temporal acuity (Nathan et al., 2006; Umino et al., 2008), and spatial acuity (Gianfranceschi et al., 1999; Prusky et al., 2002, 2004; Umino et al., 2008). Thresholds measured with the method used here appear to be ∼20-fold lower than those reported previously. Expressed in terms of the luminance of the visual targets, absolute thresholds of pigmented WT mice measured with the frequently used six-arm water maze technique (Hayes and Balkema, 1993a,b) are approximately threefold higher than that (10^−5.5 scotopic cd m⁻²) obtained with an operant conditioning method in which the target subtended 8° of visual angle and was flickered with a two-thirds duty cycle for 5 s (Herreros de Tejada et al., 1997). Applying the conversions used in this paper, the threshold stimulus in the latter case produced 0.0023 R* rod⁻¹ s⁻¹ in a field of 30,560 rods, so that a total of 230 R* were generated at absolute threshold during the 5 s presentation of the stimulus: this total is 15- to 20-fold greater than the absolute thresholds we measured (Table 1). The method applied here also yields much steeper frequency of seeing curves (Figs. 2, 3) than those reported previously (Herreros de Tejada et al., 1997); i.e., the mouse's behavior goes from nondetection to perfect detection over a 100-fold smaller range of intensities. Increment thresholds of mice adapted to several specific background levels have been measured with a three-alternative forced choice method (Jacobs et al., 1999, 2004). Although these latter experiments provided unequivocal spectral evidence for mouse cone vision, absolute thresholds were not measured, nor were t.v.i. curves obtained.

Very recently, the investigation of mouse spatial and temporal vision was expanded by the introduction and refinement of a computer controlled grating stimulus that elicits reflexive optokinetic head movements without previous training (Prusky et al., 2002, 2004), and this method has been applied to WT mice and to the rod- (Gnat1^−/−) and cone-defective (Gnat2^cpfl3) strains investigated here (Umino et al., 2008). Though the very large field of view (up to 360°) used in the optokinetic experiments precludes any direct comparison with the threshold sensitivity measured here for small, flashed targets, the results are reasonably comparable with respect to the steady backgrounds that cause the transition from rod to cone signaling. Specifically, cone signaling governs the optokinetic response in the presence of backgrounds of luminance exceeding ∼0.1 (photopic) cd m⁻², which by our calculations produces 270 R* rod⁻¹ s⁻¹; in the experiments presented here, cone signaling becomes more sensitive than that of rods in the presence of a background producing ∼100 R* rod⁻¹ s⁻¹ (Fig. 7a).

Different behavioral methods can be expected to have different strengths and weaknesses. One strength of that used here is that the mice are highly motivated yet apparently unstressed in performing the running task, allowing effective control of both stimulus and reward. The low false alarm rate of 1 to 2% (Table 1) reveals the mouse to be sensitive to the reward contingency: because it has to run a randomly selected 200–500 wheel cycles to trigger a flash that will signal access to water, false alarms are costly in terms of substantial lost effort. Another strength is that the properties of the retinal stimulus, including its size, location, duration, and wavelength, can be controlled precisely, allowing among other things direct comparison with classical human experiments (Tables 1, 2; Fig. 7c). When the comparisons bear out, as they do here, the door is open for discovering and characterizing the common neural circuitry that can be presumed to underlie the collective results.