A phylogenetic analysis of normal modes evolution in enzymes and its relationship to enzyme function

Abstract

Since the dynamic nature of protein structures is essential for enzymatic function, it is expected that the functional evolution can be inferred from the changes in the protein dynamics. However, dynamics can also diverge neutrally with sequence substitution between enzymes without changes of function. In this study, a phylogenetic approach is implemented to explore the relationship between enzyme dynamics and function through evolutionary history. Protein dynamics are described by normal mode analysis based on a simplified harmonic potential force field applied to the reduced C_α representation of the protein structure while enzymatic function is described by Enzyme Commission (EC) numbers. Similarity of the binding pocket dynamics at each branch of the protein family’s phylogeny was analyzed in two ways: 1) explicitly by quantifying the normal mode overlap calculated for the reconstructed ancestral proteins at each end and 2) implicitly using a diffusion model to obtain the reconstructed lineage-specific changes in the normal modes. Both explicit and implicit ancestral reconstruction identified generally faster rates of change in dynamics compared with the expected change from neutral evolution at the branches of potential functional divergences for the alpha-amylase, D-isomer specific 2-hydroxyacid dehydrogenase, and copper-containing amine oxidase protein families. Normal modes analysis added additional information over just comparing the RMSD of static structures. However, the branch-specific changes were not statistically significant compared to background function-independent neutral rates of change of dynamic properties and blind application of the analysis would not enable prediction of changes in enzyme specificity.

Introduction

Enzyme function critically relies on the flexibility and dynamics of the protein structure.^{1; 2} Since the catalytic functions of enzymes control all biochemical pathways essential for life, evolutionary conservation of the dynamics relevant to the enzymatic function is expected when function is conserved. Previous studies have investigated the relationship of protein flexibility and dynamics with protein families, architecture, and folds^3–6 as well as the relationship of enzymatic functional divergence within protein families.^{7; 8} However the relationship between protein dynamics and functional divergence in a phylogenetic context has not yet been examined. This relationship can be rationalized by the direct connection between the protein flexibility and its structure, which is dictated by the amino acid sequence, which, in turn, is subject to substitutions at the genetic level. In this study, we for the first time explore the connection between the phylogeny and evolution of enzyme dynamics with relation to its catalytic function.

Many previous attempts to predict functional shifts in enzymes relied purely on evolutionary signals from sequence (changes in amino acid substitution rates), without explicitly considering either enzyme structure or dynamics. For example, Sonnhammer and coworkers attempted prediction of functional change as defined by the Enzyme Commission (EC) numbers within the same Pfam family through analysis of the conservation shifting sites and rate shifting sites in the amino acid sequence.^{7; 8} EC numbers from the ENZYME database were used as a means of categorizing enzymes by their specific catalytic functions and the database Pfam 25.0 provided a source of protein families, or protein domains, that are evolutionarily related.^{9; 10}

Divergence in dynamics, just like in structure, is a potential representation of evolutionary distance. Various studies comparing the relationship between structural root mean square deviation (RMSD), sequence identity and similarity, and evolutionary divergence have observed protein structure to be three to ten times more evolutionarily conserved than the sequence.^{11; 12} Dynamics builds upon structure and constraint at the structural level to play a role in functionally-dictated evolutionary constraint. Echave and coworkers have shown that amino acid substitutions within a fold family conserve the vibrational dynamics and flexibility of the proteins just as much as the static structure⁴ and that homologous proteins diverge slowly in the slow vibrational dynamics and backbone flexibility as defined by normal modes (NM) and B-factor profile similarity.^4–6 Furthermore, proteins of the same structural architecture and fold tend to have high similarities when comparing their fluctuation profiles.³

These previous studies of protein dynamics were all based on the normal mode analysis (NMA). NMA reduces complex protein motions to harmonic vibrational modes around its energetic minimum.¹³ While normal modes analysis accounts mostly for the larger global motions of macromolecules rather than specific local motions, it has been shown that the lowest few frequency normal modes are capable of describing over half of the collective, functionally important motions of a protein, which include the enzyme binding pocket.^13–15 Secondly, the NMA also provides a straightforward and simple means for systematic comparison of the motions, through the normal modes, which would be significantly more complicated with more advanced molecular dynamics (MD) simulation methods. To date, the studies of the evolution of protein dynamics using normal modes have not taken into account the phylogenetic context.^{3–6; 14–22} (see also ref. ²³ for a recent review). Our study builds upon sequence substitution rate-based work^{24; 25} to further examine the relationship between enzyme dynamics and catalytic function within the underlying phylogenetic framework. While many computational methodologies in molecular evolution examine model parameters in the absence of explicit reconstruction of the ancestral states,^{26; 27} the complexity of structural analysis necessitates the use of such reconstruction or other approximations. Ancestral sequence reconstruction at nodes of phylogenetic trees is a valuable tool to statistically predict the sequences of the ancestral states, or internal nodes, of a tree.²⁸ Analysis of dynamics requires the structures of all contemporary and ancestral domains of interest. Given the sequence and experimentally determined structures of contemporary homologs of a protein, homology modeling can be utilized to construct structures for all ancestral sequences across a tree.^29–31 Changes in dynamics and flexibility can then be assessed by comparing the normal modes among the structures at each end of a branch of a phylogenetic tree.

An alternative technique to explicit sequence reconstruction is implicit ancestral reconstruction with diffusion models of continuous characters (like normal modes) to statistically predict the rates of change on each branch of the phylogenetic tree without depending on a particular ancestral state sequence.^{32; 33} A diffusion model can predict the reconstructed lineage-specific change in dynamics (RLSCD) with only the original phylogeny and the dynamics of the leaves of the tree. However, it is unclear that a diffusion model is an appropriate characterization of normal mode evolution. This study uses a diffusion model to crosscheck with the results from explicit ancestral sequence reconstruction. Instead, the diffusion calculations involve implicit ancestral reconstruction and can be performed using the diffusion model. Though this technique is based on different assumptions, one can expect similar results to the use of explicit ancestral sequence reconstruction if underlying signal is robust to the differences in assumptions (and their violations) between the two approaches.

With the available computational tools for ancestral reconstruction, homology modeling and NMA, as well as protein databases, detailed in the methods, it is possible to examine and compare the dynamics of the ancestral states of a protein family with known functional divergence. Such comparison offers previously unexplored insights into the relationship between enzyme flexibility, dynamics, function, and evolution (both neutral and with selection). The aim is to examine the along-branch differences in normal modes for branches where function may have changed in comparison to where they appear not to have changed. Since it can be expected that the enzymatic function is most directly connected to the enzyme dynamics at or near the catalytic active site,³⁴ we focus specifically on the comparison between dynamic motions in spatial proximity to the active site.

While investigations have been published examining protein dynamics conservation and characterizing functional divergence in homologous or structurally related enzymes,^{3–6; 14–23} there has yet to be a study that examines these findings phylogenetically to account for neutral evolution.

Results

Protein normal modes play a role of enzyme function

Prior to developing a scoring scheme to describe functional divergences in phylogenetic trees of enzymes based on dynamics, it is necessary to confirm that normal mode analysis (NMA) recapitulates the types of signal previously observed for changes of protein sequence and function.¹⁶ In Figure 1, the NM dynamics overlap, as described in Methods, was calculated for the binding pocket residues between all pairs of catalytic domains from the alpha-amylase protein family. The individual proteins in the family were categorized by those with different and the same EC numbers (see Methods), which serves as an indication of divergence and conservation of catalytic function, respectively. For the subset that did not include a phylogenetic approach (two leftmost plots in Figure 1), it is clear that the pairs of enzymes with the same EC number (and more similar sequences) had a higher overlap of their collective motions than those with different EC numbers. This has been statistically confirmed by a Wilcoxon rank-sum test resulting in a P-value of less than 4.2e-4. These results might suggest that enzyme dynamics are indicative of the enzyme function, since enzymes that catalyze the same reaction conserve these motions more than enzymes that catalyze different reactions. However, the enzymes with different functions are more evolutionarily diverged and, as has been shown, the dynamics deviate with sequence divergence.^{5; 6; 20} A phylogenetic characterization may enable us to correct for the inherent divergence in the enzyme dynamics due to natural increase in the sequence variation with evolutionary time and therefore to isolate the point of functional divergence in the phylogeny.

Figure 1.

Distributions of the dynamics overlap of the binding pocket residues of enzymes in the alpha- amylase protein family with Pfam identity PF00128. The two distributions to the left of the figure described the distributions of the protein family without consideration of its phylogeny. The leftmost distribution contains the overlap scores of pairwise proteins that have the same EC number. The second distribution from the left shows the distribution of only pairs of enzymes with the different EC number within the protein family.

A further control was available to us. Thornton and coworkers have generated crystal structures of ancestral proteins that along branches of a phylogenetic tree show conserved and changed binding functions. ^35–38 While the structures are of complexes rather than unbound, comparisons of the normal modes and RMSD of the static structures can be evaluated along a branch estimated as 0.10 substitutions per site without a change of binding partner and along a branch with length 0.14 substitutions per site with a change of binding partner. The first branch shows a static RMSD of 0.51 Å and a normal modes overlap of 0.72. The longer branch with the change of binding partner showed a static RMSD of 0.87–0.93 Å depending upon the binding partner in complex and a normal modes overlap of 0.56–0.58. While the analysis does not exactly replicate the gene family analysis that will be performed, it does provide validation that the approach will detect signal when available, as a positive control.

To explore the relationship of dynamics, sequence evolution, and function phylogenetically, a tree is constructed based on the assumption that sequence divergence is reflective of shared ancestry. As described in Methods, ancestral reconstruction was implemented on the internal nodes and the ends of each branch of the phylogenetic tree. These points then were then used for pairwise comparison along each branch dictated by the tree. An overlap score normalized for their evolutionary distance as defined by their branch lengths was calculated on each ancestral reconstructed node pair (rightmost plot in Figure 1). Due to the score’s dependence on the evolutionary distance between pairs, the distribution is skewed suggesting higher conservation of dynamics when only examining the phylogeny. Correcting the score for evolutionary distance by normalizing the overlap converted to a distance with the branch lengths leads to a higher similarity score in terms of their collective motions, because of the expected change in motion with increased evolutionary distance caused by neutral substitutions that naturally occur over time are included in the scoring scheme.

Pipeline for selecting protein family candidates

In order to properly evaluate the correlation between enzyme dynamics, function, and evolution, data sets of homologous proteins where the function has changed at short evolutionary distance are needed. Therefore, the selected protein family candidates were chosen after filtering the Pfam database¹⁰ for families of catalytic domains that showed 1) divergences in catalytic function as defined by their EC numbers and 2) high sequence identity (see Methods). While one would expect many more families to be potential candidates for this study, only five remain after filtering through the Pfam database. This low number of candidate families is attributed to a number of different factors. First, only 1812 protein families were identified with sequences that have been categorized by the ENZYME database⁹, with all but 543 families excluded due to their lack of at least two proteins classified for at least two different EC numbers. Second, in order to ensure that the chosen protein families are directly involved in the function of the enzyme as assigned by the ENZYME database, only families that are classified as catalytic domains were included in the pipeline, leaving less than a hundred candidates. Third, an additional filter that proteins of different catalytic functions must possess at least 50% sequence identity was applied.

As a result of this filtering, only five candidates remained in the pipeline. Of the five potential candidates, Pfam families PF00128, PF00389, and PF01179 were chosen for two reasons. First, the chosen families had to contain multiple sequences of each EC number to minimize false positives and for evaluation of the evolutionary trends. Second, the families had to produce homology modeled structures of the explicit ancestral sequences that had high local model qualities, global model qualities, and stereochemical qualities as defined by Anolea,³⁹ Gromos,^{40; 41} QMEAN6,^42–45 DFire,⁴⁶ and Procheck^{47; 48} to ensure accuracy of the normal mode comparisons.³¹ These tests assessed the favorability of the energy environment for each amino acid,^39–41 the potential terms for local (torsional potential and solvation potential) and global (secondary structure and solvent accessibility) regions of the protein,^42–45 the non-bonded atomic interactions as defined by pseudo energy models,⁴⁶ and the geometry of the residues compared with high-resolution structures.^{47; 48} All of these issues were factored into the selection of three families that were determined to be appropriate for further analysis (Table 1).

Table 1.

Selected Protein Families and Substrates

Pfam Identity	Famil y Name	EC Numbers	IUBMB Substrates
PF00128	Alpha-amylase	3.2.1.10	sucrose, isomaltose
		3.2.1.70	isomaltoheptaose
		3.2.1.93	trehalose 6-phosphate
PF00389	D-isomer specific	1.1.1.26	glycolate
	2-hydroxyacid	1.1.1.215	5-dehydro-D-gluconate, L-idonate, D-gluconic acid
	dehydrogenase	1.1.1.95	2-hydroxyglutarate, 3-phospho-D-glycerate
PF01179	Copper-containing	1.4.3.21	various primary amines (not including histamine)
	amine oxidase	1.4.3.22	histamine

Analysis of the alpha-amylase family

The first protein family that was examined is the catalytic domain of alpha-amylase, which is a monomeric enzyme that performs hydrolysis of alpha linkages in large α-linked polysaccharides (Figure 2A). Such enzymes exhibit an elongated shape, and usually consist of three distinct domains.⁴⁹ Common to the alpha-amylase family, the catalytic domain consists of a (beta/alpha)8-barrel with the extended active site cleft at the C-terminal end of the (beta/alpha)8-barrel.^{50; 51} A subset of the protein family contains the EC numbers 3.2.1.10, 3.2.1.70, and 3.2.1.93, which only differ in the specificity of the substrates for the hydrolysis reaction that alpha-amylase enzymes catalyze (Figure 2A–C, Table 1). Only the residues that are within 6.5 Å from these specific ligands were considered in the NMA. This distance threshold was chosen from a previous study showing that the density is highest at that distance from radial distributions of residue packing in protein crystal structures.⁵² When constructing a phylogenetic tree of this subset with the maximum-likelihood method, the clustering of sequences corresponds well with the groups of different EC numbers (Figure 4A). This clustering of enzymes that share the same catalytic reaction suggests that a divergence in function likely occurred at the marked branches of the tree. From the phylogeny, we hypothesize that the ancestral branch connecting the three branches likely shares the same function as EC number 3.2.1.93 since this is the most parsimonious solution, while the node connecting the clades with functions 3.2.1.10 and 3.2.1.70 could be any of the three functions with equally parsimony. From this scenario, branches with labels I, II, and III are candidates for functional change. Enzymes that are categorized with EC number 3.2.1.10 perform hydrolysis on alpha linkages of sucrose and isomaltose, while EC numbers 3.2.1.93 and 3.2.1.70 have the same function but substrate specificity for trehalose 6-phosphate and isomaltoheptaose respectively.

Figure 2.

Chemical structures of the substrates of each enzyme in the chosen protein families grouped by EC number. For the alpha-amylase family, the EC numbers evaluated are (A) 3.2.1.10, (B) 3.2.1.70, and (C) 3.2.1.93. For the D-isomer specific 2-hydroxyacid dehydrogenase family, the EC numbers are (D) 1.1.1.26, (E) 1.1.1.215, and (F) 1.1.1.95. For the copper-containing amine oxidase, the EC numbers are (G) 1.4.3.21 and (H) 1.4.3.22. Graphics of the structures are from their respective KEGG ENZYME Database Entry.^{84; 85}

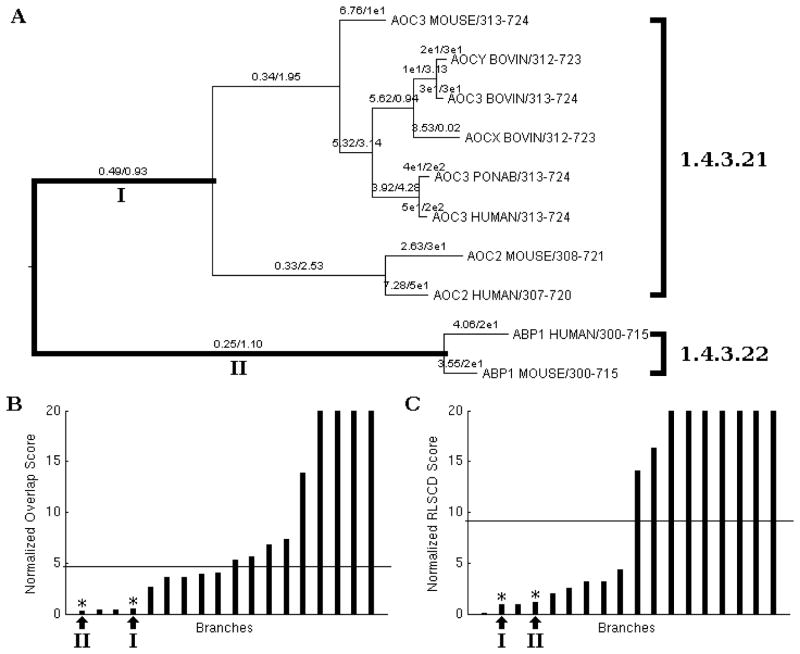
Figure 4.

Results for the alpha-amylase family. (A) The phylogenetic tree of the protein family with the three branches likely to exhibit functional divergences bolded and labeled. The first value on each branch is the normalized overlap score followed by the normalized RLSCD score. The EC numbers are labeled to the right of the tree. (B) Graphical display of the scores based on the vector field overlap of explicit ancestral sequence reconstruction with the branches of interest marked and median drawn. The branches of interest correspond to those labeled on (A). (C) Graphical display of the scores based on the diffusion branch rates with implicit ancestral reconstruction with the branches of interest marked and median drawn.

To test for the signatures of functional divergence in the protein dynamics, NMA was analyzed on the branches of the phylogenetic tree using both explicit and implicit ancestral reconstruction of the internal nodes. With explicit ancestral reconstruction, each ancestral node of the phylogeny had its sequence explicitly determined and its structure modeled for comparison with the other nodes. Since NM could be calculated on any protein with a defined structure, a vector field overlap was implemented on every branch to compare the ancestral nodes at the ends of the branches. (Figure 3A). Since the vector field overlap scores are constrained from 0 to 1, a constrained exponential decay is applied to the data (see Methods). From the fit to the exponential decay, it is possible to determine the theoretical branch length based on the distribution of the dynamics against the original branch lengths. This theoretical branch length represents the expected branch length under neutral evolution. Dividing the theoretical branch length by the actual branch lengths derived from the sequence phylogeny gives a rate ratio describing the amount of dynamics change observed on each branch. Hence, a low score describes a faster rate of divergence in dynamics compared to what is expected from neutral evolution, while a high score describes slower change in dynamics. The threshold to describe neutral changes in evolution is the median of the dataset, therefore scores indicate high and low rates of NM changes per branch depending on whether they are below or above the median, respectively. These results are shown on Figure 4A and 4B.

Figure 3.

Comparison of results from explicit and implicit ancestral reconstruction. (A, D, G) The raw values with fit of vector field overlap with explicit ancestral sequences are plotted against evolutionary distance. (B, E, F) The raw values for the reconstructed lineage-specific changes in dynamics (RLSCD) are based on implicit ancestral reconstruction and are plotted against evolutionary distance. (C, F, I) The scores derived from the methods based on explicit and implicit ancestral reconstruction are plotted against one another for comparison. The specific protein families of which each figure describes are the alpha-amylase family (A–C) with correlation coefficients −0.26, −0.09, and 0.75, D-isomer specific 2- hydroxyacid dehydrogenase family (D–F) with correlation coefficients −0.20, 0.18, and 0.55, and copper-containing amine oxidase family (G–I) with correlation coefficients −0.59, −0.18, and 0.84.

In the case of implicit ancestral reconstruction, however, the sequences of the internal nodes are not determined. Instead, a diffusion model is applied to the phylogenetic tree with only the branch lengths and the NM dynamics of the leaves defined (by the NM overlaps). In this way, reconstructed lineage-specific changes in dynamics (RLSCD) can be calculated without explicitly determining the sequence of the ancestral nodes (Figure 3B). In order to determine a score to compare the rate of the change in dynamics with respect to neutral evolution, the RLSCD are divided by the original branch lengths. As before using the explicit sequence reconstruction, scores below the median describe a faster rate of change in dynamics compared with neutral evolution, and scores above the median describe a slower rate of dynamics change. These results are shown on Figure 4A and 4C.

Since both explicit and implicit ancestral reconstruction of the internal nodes are based on different assumptions, a comparison of the two methods is necessary to unify the results. The calculated scores for all branches from both techniques are plotted to identify whether or not the two methods exhibit a correlation (Figure 3C). For the alpha-amylase family, the results from both methods have a correlation coefficient of 0.75 (Figure 4). All the branches of potential functional divergence exhibited a faster rate of dynamics change compared with the rate expected from neutral evolution, which is represented by the median of the dataset (Figure 4A). On the other hand, the order of the scores from the three marked branches is different between the two techniques. In the case of explicit ancestral reconstruction, the dynamics change on branch III leading to EC number 3.2.1.10 gave the lowest score, close to 0, compared with the scores of 0.37 and 0.48 for branches I and II respectively. This might suggest an ancestral function of 3.2.1.70 at the node joining branches II and III, with substrate specificity for isomaltohepaose. By contrast, analyzing the NM with implicit ancestral reconstruction describes branch II possessing a low score of 0.56, branch I possessing a score of 1.29, and branch III possessing a score of 2.81. This result would imply a change of function along branch II, but would not differentiate between the other two competing hypotheses.

These results demonstrate that including dynamics into the analysis of phylogenetics allows for a novel perspective on the data. Traditionally, using only evolutionary distance as the criteria would suggest that the nodes of branches I and II are very different while only the nodes of branch III are similar. However, the phylogenetic analysis showed a different pattern.

Analysis of the D-isomer specific 2-hydroxyacid dehydrogenase family

The second protein family selected for the application of this analysis was that of D-isomer specific 2-hydroxyacid dehydrogenase (Figure 2B).^{53; 54} These enzymes oxidize specific substrates through NAD+ and NADP+ cofactors acting as electron acceptors. Two domains are typically found for NAD(P)- dependent dehydrogenases: the substrate-binding domain (SBD) and the nucleotide-binding domain (NBD).⁵⁵ The subset for this family included members with EC numbers 1.1.1.26, 1.1.1.95, and 1.1.1.215 (Figure 3D-F, Table 1). The residues used in NMA were again determined using a threshold of 6.5 Å from the specific substrates. Examining the phylogeny of these selected members reveals a clustering of enzymes with specific EC numbers, which describe different substrate specificity (Figure 6A). This suggests that functional divergence may exist at the marked branches that connect these clusters in the phylogenetic tree. From this phylogeny, we hypothesize that the ancestral node that connects the three branches is most parsimoniously 1.1.1.95, while all three functions are equally parsimonious at the node connecting branches II and III. Enzymes categorized with EC number 1.1.1.26 are responsible for the oxidation of glycolate in an oxidation-reduction reaction. EC number 1.1.1.215 share the same function except has substrate specificity for 5-dehydro-D-gluconate, L-idonate, and D-gluconic acid, while EC number 1.1.1.95 have substrate specificity for 2-hydroxyglutarate and 3-phospho-D-glycerate.

Figure 6.

Results for the copper-containing amine oxidase family. (A) The phylogenetic tree of the protein family with the two branches likely to exhibit functional divergences bolded and labeled. The first value on each branch is the normalized overlap score followed by the normalized RLSCD score. The EC numbers are labeled to the right of the tree. (B) Graphical display of the scores based on the vector field overlap of explicit ancestral sequence reconstruction with the branches of interest marked and median drawn. The branches of interest correspond to those labeled on (A). (C) Graphical display of the scores based on the diffusion branch rates with implicit ancestral reconstruction with the branches of interest marked and median drawn.

Results of the same analyses as described above for the alpha-amylase family, based on explicit and implicit ancestral reconstruction, are shown in Figure 3D-F and Figure 5. When comparing the two methods in Figure 3F, the correlation coefficient between the rates produced from the two analyses is 0.55. In both cases, branch I contains the lowest scores of 0.28 and 1.70 for using explicit and implicit ancestral reconstruction respectively compared with the other two branches of potential functional divergence. Branch I connects to leaves that have been categorized with EC number 1.1.1.95, which have substrate specificity for 2-hydroxyglutarate and 4-phospho-D-glucerate. Low scores suggest that changes in NM enzyme vibrational dynamics and flexibility are occurring at a faster rate than is expected if only neutral evolution was a factor. For the other results, branch II gave scores of 1.38 and 2.61 for explicit and implicit ancestral reconstruction respectively, and branch III gave scores of 0.57 and 2.92 for explicit and implicit ancestral reconstruction respectively. Branch III is associated with enzymes of EC number 1.1.1.215, which have substrate specificity for 5-dehydro-D-gluconate, L-idonate, and D-gluconic acid. Branch II is associated with the cluster of leaves with EC number 1.1.1.26, which have substrate specificity for glycolate. Higher scores describe a rate of dynamics change that is occurring slower than the lower scores. Therefore, it might be expected from both approaches that the ancestral internal node that connects branches II and III will not have the same function as EC number 1.1.1.95 with substrate specificity for 2-hydroxyglutarate and 3-phospho-D-glycerate.

Figure 5.

Results for the D-isomer specific 2-hydroxyacid dehydrogenase family. (A) The phylogenetic tree of the protein family with the three branches likely to exhibit functional divergences bolded and labeled. The first value on each branch is the normalized overlap followed by the normalized RLSCD score. The EC numbers are labeled to the right of the tree. (B) Graphical display of the scores based on the vector field overlap of explicit ancestral sequence reconstruction with the branches of interest marked and median drawn. The branches of interest correspond to those labeled on (A). (C) Graphical display of the scores based on the diffusion branch rates with implicit ancestral reconstruction with the branches of interest marked and median drawn.

Analysis of the copper-containing amine oxidase family

The catalytic function of copper-containing amine oxidase family is the oxidative deamination of primary amines to the corresponding aldehydes, with the concomitant reduction of oxygen to hydrogen peroxide (Figure 2C).⁵⁶ The homodimer enzyme domain, located near the C-terminal of each subunit, contains the active site and provides the dimer interface.⁵⁶ The EC numbers that are assigned to the members of the copper-containing amine oxidase family are 1.4.3.21 and 1.4.3.22 (Figure 3G–H, Table 1). As before, the residues examined in the normal modes scoring scheme were those within 6.5 Å of the specific substrates. The phylogeny of this protein family subset revealed a clustering of enzymes consistent with the substrate types (Figure 7A). From this phylogeny, the ancestral function of the enzyme family could be either function. Enzymes categorized with EC number 1.4.3.21 are responsible for the oxidation deamination of various primary amines including 3-diaminopropane, N-methylputrescine, aminoacetone, cadaverine, dopamine, methylamine, phenethylamine, and tyramine. EC number 1.4.3.22 is associated with enzymes with substrate specificity for only the primary amine histamine.

Figure 7.

Structural RMSD scores for three protein families. The scores based on structural RMSD are displayed with the branches of interest marked and median drawn for the (A) alpha-amylase family, (B) D-isomer specific 2-hydroxyacid dehydrogenase family, and (C) copper-containing amine oxidase family.

The results of NMA, based on explicit and implicit ancestral reconstruction, are shown in Figure 3G–I. The correlation coefficient of the two datasets (Figure 3I) is 0.84. However, despite the high correlation coefficient, the two methods resulted in slightly different inferences on the rate of change of the marked branches. Explicit ancestral reconstruction gave branch II the lowest score while implicit ancestral reconstruction gave branch I the lowest score. Branch I is associated with EC number 1.4.3.21, whose substrates are primary amines such as 3-diaminopropane, N-methylputrescine, aminoacetone, cadaverine, dopamine, methylamine, phenethylamine, and tyramine. Branch II, on the other hand, is associated with EC number 1.4.3.22, which is specific for histamine. But even though there is a discrepancy in which branch has a faster rate of change on the collective motions of the enzyme binding pocket, the dynamics of both branches are still faster than neutral evolution as defined by the median.

Static Structural Analysis

Our study proposes the use of dynamics to examine lineage-specific functional differences, though the necessity of factoring dynamics into the analysis is undetermined. Thus, as a control, structural analysis was implemented, since differences in the “static” protein structure are inherently included in the dynamics. We hoped to determine whether or not the extra step of calculating enzyme flexibility leads to different results from analysis of only structure and sequence. Therefore, the same methods as described before for the comparison of NM dynamics were implemented for structural RMSD of the binding pocket to measure likeness of the tertiary structure. This is to reflect an idealized notion of the thermodynamic minimum of each enzyme. As before, the values are normalized so that scores lower than the median are considered to have fast rate of structural change whereas scores higher than the median indicates a slow rate of structural change between enzymes along the same branch (Figure 7).

The results of the structural RMSD are comparable, but are not in exact correspondence, with the dynamics analysis. In the case of the alpha-amylase family, the structural RMSD analysis gave scores that indicate that the rate of structural change is faster than neutral evolution, which is defined by the median (Figure 7A). These results mirror those that were obtained using the NMA methods with branch III showing the least overlap. In the case of the D-isomer specific 2-hydroxyacid dehydrogenase family, the analysis of the structural RMSD indicated that branches I and II are changing structurally at a rate slower than neutral evolution (Figure 7B). In comparison, NMA indicates that all three branches of interest are changing at a rate faster than neutral evolution. In the case of the copper-amine oxidase family, the structural analysis concluded that both branches are changing at a rate faster than neutral evolution, with branch I evolving faster than branch II (Figure 7C). The variation in results for all three families indicates that structure alone is not perfectly correlated with protein dynamics. Nevertheless, the dependence of the dynamics on structure can be clearly seen by a rough comparison of the distribution of scores.

Discussion

It has been suggested that changes in dynamics as measured by normal modes can detect ligand binding to a protein and that these may vary depending on the ligand.^{16; 22} Here we attempt to exploit this observation and disentangle it from the expected neutral change in dynamics with sequence divergence using a phylogenetic analysis. The above data are to our best knowledge the first attempt to relate the evolution of the dynamics and biological function of enzyme families in a phylogenetic context. As the above results demonstrate, this approach can potentially add a new dimension to the analysis of the diversification of protein function through evolution alone or to structure alone as it enables accounting for changes not linked to those involved in function. However, there are also some important limitations of this approach, which need to be discussed, as the phylogenetic analysis detected little signal for functional divergence.

First, our approach is based on the understanding that the chosen sequences of each enzyme protein family are descended from a common ancestor. This implies that all contemporary proteins can be rooted back to ancestral proteins that eventually branched into the diverse protein selection observed today in each gene family. As a consequence, the first step after choosing a suitable protein family is the sequence alignment of the constituent proteins. Alignment error is known to occur due to the heuristic nature of multiple sequence alignment^{57; 58} and errors in alignment have been shown to cause downstream errors in phylogenetic inference⁵⁹ and the detection of positive selection.⁶⁰ While MAFFT has been shown to perform well in evolutionary studies,^61–63 potential alignment errors may affect the results of the analysis.

Second, our method relies partially on the accuracy of the ancestral sequence reconstruction method. Since the ancestral proteins associated with the divergence in function no longer exist, the statistical method of inferring ancestral proteins from modern proteins should be carefully considered when determining the confidence of the inferences being made. Errors in reconstructed sequences are known to increase with individual branch length and with tree length, but decrease with the number of included sequences for a given tree length.⁶⁴ In a study comparing the ancestral reconstructed proteins using evolution simulations, it was pointed out that the maximum-likelihood method had a tendency of overestimating the thermodynamic stability of the proteins,⁶⁵ so the errors might have a directional effect on inference. With low sequence divergence, these errors are likely to be small, but may exist.

Third, homology modeling was used to reconstruct the structures of the ancestral proteins with sequences explicitly determined, which were the basis of the dynamics calculations. Homology modeling is a powerful technique that takes advantage of the assumption that homologous proteins have similar structures and that the protein structures of homologs are more conserved than their sequences. However, homology modeling becomes increasingly inaccurate with increasing sequence divergence, since the sequence still affects the final tertiary structure of the protein being analyzed. As a result, major shifts in the structural properties between homologous proteins may be underestimated if the structures diverge significantly from one another in evolutionary history. In our case, the divergence in the sequences was constrained to having pairwise sequence identities of above 50%. The reliability of the homology modeling for this level of structural divergence is reasonable since a sequence identity of over 30% is often enough to predict the X-ray structure of a protein.⁶⁶

Finally, the protein dynamics were represented as vibrational, harmonic normal modes. This is clearly an approximation, since the functional dynamics of enzymes is known to be inherently anharmonic.¹ In particular, the low frequency collective motions of proteins are likely to significantly deviate from simple harmonic oscillations. It is possible that more rigorous representation of the protein dynamics might reveal more distinct trends and potentially better insights into the role of dynamics in evolution. However, in the interest of simplicity and computational tractability, the harmonic NMA is a first, useful approximation for evaluation of the enzyme dynamics and its relation to the functional evolution.^{6; 14} Furthermore, in the light of the above discussed limitations of the methodology related to the ancestral sequence reconstruction, homology modeling etc., any more advanced treatment of the protein dynamics is not expected to significantly increase the reliability of our results.

Despite the above mentioned limitations, the methodology used in this study represents the state of the art available today. The fact that we were able to observe clear indication of dynamical similarity only suggests that with the improvement of the methodology such studies may become even more useful and specific in tracking the protein functional evolution.

Unfortunately, there is often also a significant uncertainty associated with the substrate specificities of particular enzymes. First, biochemical experiments were done for very few enzymes in gene families and when multiple enzymes were tested, they were not always tested with the same substrates. For example, some enzymes may have broad specificity and act upon different substrates, but only a small subset of these substrates was actually tested to annotate function. Alternatively, sometimes it is known that different substrates are selectively disadvantageous for specific enzymes to act upon,⁶⁷ and there is selective pressure for changes in specificity. Functional annotation of enzymes does not indicate all of the positive substrates on which an enzyme acts and rarely indicates negative substrates on which it does not act. If an enzyme does not act on a substrate, it does not need to be because there is a selective pressure against acting on the particular substrate. This incomplete information on enzyme function also affects the analysis undertaken. Beyond that, enzyme annotations are frequently wrong. Gene annotation is frequently performed after gene or genome sequencing solely by a BLAST search. As the field of phylogenomics has developed, it has become increasingly clear that many gene annotations are incorrect.^{68; 69}

With these caveats explicitly stated, it may be that errors in the pipeline caused a loss of signal. However, there is another explanation rooted in the underlying nature of the relationship between sequence divergence and protein dynamics. As shown by the work of Echave,^{4–6; 20} as proteins diverge in sequence, the dynamics also diverge and this sequence divergence effect is a strong predictor of dynamics divergence. As the proteins with functional change tend to be more distant than the proteins with the same function, a stronger signal is actually seen in the pairwise comparisons between proteins of divergent function rather than the phylogenetic analysis. This is because the pairwise signal conflates neutral sequence driven changes in dynamics with functional change driven changes in dynamics. Therefore, our study attempts to separate the change in motions that results from neutral sequence changes and those that are actually associated with a functional divergence. This is only possible after analyzing the phylogeny to identify the potential location of divergence between internal nodes. The lack of strong remaining signal on average may indicate that more sophisticated methods are needed, that better underlying experimental validation of protein specificities is needed, or that selection does not in general act strongly on the slowest vibrational dynamics to account for changes in enzyme specificity.

The breadth of specificity as well as differences in size between substrates, transition states, and/or products are expected to necessitate changes in ranges of motion of the active site and binding pocket. In the case of the alpha-amylase family, all the substrates are different polysaccharides of different lengths connected by alpha-linkages that are cleaved by the alpha-amylase enzymes. While sucrose, isomaltose, and trehalose 6-phosphate possess only one alpha-linkage, the isomaltoheptaose possesses six due to the repetition of its starch structure. Consequently, a larger substrate will likely require a greater flexibility in dynamic movements of the binding pocket in order to accommodate for the longer polysaccharide chain and in generating binding to the product, substrate, and transition state. In the case of the D-isomer specific 2-hydroxyacid dehydrogenase family, the structures were fairly similar with the glycolate containing the shortest chain out of all the substrates being oxidized in the oxidation-reduction reaction catalyzed by this family of enzymes. However, unlike isomaltoheptaose of the alpha-amylase family, the chemical structure of glycolate is not expected to change the dynamics of the binding pocket as drastically, since the size is not as substantially different. All the substrates have a carbonyl group that acts as an electron donor in the reaction. In the case for the copper-containing amine oxidase, all the substrates of the enzymes described in this study were primary amines. The difference is that EC number 1.4.3.22 specifically describes the deamination of only histamine while EC number 1.4.3.21 describes eight different primary amines that vary in structure and size. Therefore, one would expect the substrate, transition states, and products to play a large role in the collective motions of the active site and binding pocket. However, the signal for any such change was not strong enough to make functional predictions in the absence of an a priori hypothesis, and even in such cases, strong statistical support was not obtained, only suggestive evidence.

Conclusion

In this study, for the first time, the evolution of enzyme dynamics was analyzed in a phylogenetic context in order to test whether information about enzyme functional divergence can be obtained. Comparison of the enzyme dynamics, in terms of the normal modes, is a step beyond traditional approaches relying solely on the amino acid sequences and even protein structures. The use of a phylogenetic context is important since it provides a measure of the evolutionary distance and identifies points in evolutionary history where individual events occurred with greater precision than combinations of pairwise analysis. As expected, an inherent decrease in the normal mode similarity with the evolutionary distance was detected. However, after accounting for this natural drift, distinctions in the similarity of the dynamical motions could be evaluated. In combination with the phylogenetic analysis it was possible to isolate branches of the phylogenetic trees where the divergence in function likely occurred in some cases, lending weight to one ancestral function over the other. Despite the limitations discussed above, the analysis of protein dynamics may provide additional important insights into the protein evolution, complementary to the sequence and structure. With the rapidly increasing amount of information about the protein structural and functional universe through proteomics and metabolomics, improvement upon the method presented here are expected to be of increasing importance for understanding the evolution of protein biological function. New available data will also allow for further refinement and more rigorous testing and validation of such methodologies.

Materials and Methods

Dataset of Protein Families

The test dataset was generated by a systematic filtration process of the proteins families defined by the Pfam 25.0 database.¹⁰ Each entry of the Pfam database was searched for the existence of a divergence in catalytic function as defined by multiple Enzyme Commission (EC) numbers from the ENZYME database of the domains listed in the multiple sequence alignments that were generated by Pfam using hidden Markov models.⁹ Pfam entries that do not contain protein domains identified in the ENZYME database with an EC number were ignored in the dataset. The remaining Pfam families in the dataset were selected 1) if they were identified by Pfam annotations as catalytic domains and 2) if they had high sequence conservation between protein domains of different enzymatic function. Conservation between domains was defined as having pairwise sequence identities of over 50%. The final three protein families, PF00128, PF00389, and PF01179, were selected through manual examination of the preliminary phylogenetic trees for clear patterns in functional divergence and for notable sizes of each functional clad. Domain entries within the final dataset that were not listed in the ENZYME database with an EC number were discarded from the study due to ambiguous function.

To validate the method, ancestral precursors of glucocorticoid receptor (GR) enzymes were used, which were experimentally resurrected and their x-ray crystal structures solved by Thornton and coworkers.^35–38 The structures analyzed included the ancestral corticoid receptor (AncCR) bound to desoxycorticosterone,³⁵ ancestral glucocorticoid receptor 1 (AncGR1) bound to desoxycorticosterone,³⁷ ancestral glucocorticoid receptor 2 (AncGR2) bound to dexamethasone,³⁶ and AncGR2 bound to mometanone furoate.³⁸ Ortlund et al reported that both AncCR and AncGR1 have a substrate preference for cortisol while AncGR2 loses this function after specific residue changes.³⁵ In the previously published phylogeny, the branch length between AncCR and AncGR1 is 0.10 and the branch length between AncGR1 and AncGR2 is 0.14.³⁵ A normal modes and RMSD analysis as described below was conducted to explore the extent dynamics and structure can indicate functional differences on ancestral enzymes.

Protein Family Phylogenetics

Protein domains with defined EC numbers of each protein family were aligned by their amino acid sequences with the multiple sequence alignment software MAFFT, using the substitution matrix BLOSUM 62, a gap open penalty of 1.53, and a gap extension penalty of 0.123.⁷⁰ The ProtTest software was run on the aligned sequences to select for the best-fit amino acid replacement model for protein evolution.⁷¹ The selected models given by ProtTest with the AIC model selection criterion were LG+G (the Le-Gascuel Model⁷² with gamma distributed rates across amino acid sites), LG+I+G (LG plus gamma plus an additional category of evolutionarily invariant sites), and LG+F+I+G (LG plus gamma plus invariants plus additional parameters for unequal amino acid equilibrium frequencies from the dataset) for protein families PF00128, PF00389, and PF01179 respectively. These models were used to build a maximum- likelihood tree with bootstrap values and branch lengths using the PhyML software.⁶¹ To identify the root of the maximum-likelihood tree, two different methodologies were implemented. First, an out-group was added to the tree that was known to be a part of the protein family, but exhibited a catalytic function different from the main portion of the tree. Second, a species tree was constructed using the Taxonomy common tree tool of the NCBI taxonomy database and reconciled against the generated protein trees using NOTUNG 2.6.^{73; 74} These two methods were brought together for each tree to confirm the location of the root. Also, due to different requirements of different software suites, the Readseq tool was used to interchange different file formats between the programs.⁷⁵

Explicit Ancestral State Sequences and Structures

The sequences of the ancestral states of each protein family were generated using a maximum-likelihood approach of reconstruction incorporated into the joint reconstruction methods of the FastML software.^{76; 77} Protein structures for the sequences generated by FastML were modeled using the homology modeling technique implemented by the web-based environment, SWISS-MODEL.^29–31 An apoenzyme template without the ligand bound to the protein was chosen for the homology modeling based on the high sequence identity of the template with the other sequences in the family. The ancestral reconstruction probabilities are given on Supplementary Figure 2. The templates for homology modeling by SWISS-MODEL of the ancestral states of each protein family were chosen from the structures of highest resolution from RCSB Protein Data Bank.⁷⁸ Structural models were assessed in the SWISS-MODEL environment by examining various local, global, and stereochemistry model quality estimations as defined by Anolea,³⁹ Gromos,^{40; 41} QMEAN6,^42–45 DFire,⁴⁶ and Procheck.^{47; 48} Upon completion and assessment of the homology modeling of all the internal and external nodes of the maximum-likelihood trees generated for each selected protein family, a structural alignment (using MUSTANG⁷⁹) was employed as quality control to ensure that the selected residues for analysis are comparable. ⁷⁹

Implicit Calculation of Diffusion Branch Rates

Implicit calculation of branch rates does not require explicit determination of the ancestral sequences. Instead, a diffusion model is applied to the phylogeny based on maximum-likelihood methods described above with the NM vector fields as traits on the leaves of the tree. Diffusion branch rates can then be calculated with the software suite BEAST, which allows continuous traits to be given to the tree.^{32; 33; 80} A starting tree and NM traits on the leaves of the tree are supplied to the BEAST software for the random walk based on a continuous diffusion model. The topology and the raw branch lengths of the starting tree are fixed for the calculations since the amino acid sequences are given to the software suite. For the random walk, a million runs are implemented and only the diffusion branch rates resulting from the best lnP (logarithm of the likelihood ratio) are considered for further analysis.

Normal Mode Calculations

Calculations of the vibrational motions of the protein via normal modes utilized the open source Molecular Modelling Toolkit (MMTK) Python and C libraries.^{81; 82} The proteins were modeled as an elastic network model (ENM) consisting of only the backbone Cα with a simplified energy force field approximated from the potential minimum of the Amber94 force field.⁸³ The force field models the entire protein in terms of its harmonic potentials between any two Cα beads that represent the position of the residue as

$$U({\mathit{R}}_1,\dots ,{\mathit{R}}_N)={\sum }_{\mathit{all}\mathit{pairs}\alpha ,\beta }{U}_{\alpha \beta }({\mathit{R}}_{\alpha }-{\mathit{R}}_{\beta })$$ (1)

with the harmonic pair potential defined as

$$U_{\alpha \beta }(\mathit{r})=\frac{1}{2}k({\mathit{R}}_{\alpha \beta }^{(0)}){(\mid \mathit{r}\mid -\left|{\mathit{R}}_{\alpha \beta }^{(0)}\right|)}^2$$ (2)

and the harmonic pair force constant defined as

$$k(r)=\{\begin{array}{r}\hfill 8.6\ast {10}^5{\mathit{kJmol}}^{-1}{nm}^{-3}\ast r-2.39\ast {10}^5{\mathit{kJmol}}^{-1}{nm}^{-2},r<0.4nm\\ \hfill 128{\mathit{kJnm}}^{4}mo{l}^{-1}\ast r^{-6},r\ge 0.4nm.\end{array}$$ (3)

In these equations, r is the distance vector between the two residues and R_α and R_β is the distance vector between the two residues at their stable equilibrium configuration, which is defined as the local minimum of the potential well. ⁸³ Taking the eigenvalues and eigenvectors of the Hessian matrix, which is a matrix comprising of the second partial derivatives of the potential energy function (1) with respect to the Cα coordinates, gives the mode frequencies squared and vector field matrices describing the normal modes motions respectively. Since functional dynamics are dominated by slow, collective motions, the NMA was only applied on the normal modes associated with the five lowest vibrational frequencies. Illustrations of the representative low frequency normal modes for a member of each of the three studied protein families are shown in Figure 8.

Figure 8.

Example structure and normal mode vector fields for three protein families. The eigenvectors of one normal mode frequency out of the lowest five is depicted for a representative enzyme structure in the (A) alpha-amylase family, (B) D-isomer specific 2-hydroxyacid dehydrogenase family, and (C) copper-containing amine oxidase family. Vector arrows start from the Cα of the backbone and are scaled up for visual purposes.

Normal Mode Alignment

Quantifying normal mode similarity (vide infra) requires that comparison is made between the normal modes corresponding to the same collective motions in the different proteins. The normal mode calculation typically yields the modes ordered by their vibrational frequency. However, as shown in Supplementary Figure 1, the same frequency ordering does not necessarily correspond to the most similar motion. For this reason, the normal modes were aligned so that only the comparison is made between the motions of the highest similarity. The alignment was determined by looping through the lowest five frequency mode indices of one protein and identifying the mode that contains the highest dynamics overlap of another protein. This process was repeated for every protein pair in the dataset.

Normal Mode Comparison

Tracing a given protein family tree, vector field overlaps were calculated between normal modes of internal nodes that share a phylogenetic branch. Mirroring the calculations by Maguid et al.,⁶ the overlap of the modes are defined by the equation

$$S_{ab}=\frac{{\sum }_{\mathit{all}\mathit{residues}}{q}_a{q}_b}{\sqrt{{\sum }_{\mathit{all}\mathit{residues}}{(q_a)}^2\ast {\sum }_{\mathit{all}\mathit{residues}}{(q_b)}^2}}$$ (4)

where proteins a and b are structurally aligned with normal modes and respectively.⁶ The overlap, ranges from 0 to 1 where a value of 1 corresponds to a complete overlap between the motions as defined by the two vector fields. For this study, only the residues that are determined to be part of the binding pocket, or within 6.5 Å of the enzyme substrate, are considered in the vector fields for overlap calculations. The 6.5 Å threshold is determined by the distance of highest density during residue packing as determined by its radial distribution.⁵² However, because NMA is run on ancestral nodes independently from the other nodes, the normal modes describing the collective motions of the residues of one node did not always align with the others due to deletions and insertions in the sequences. This is an important detail to note because Eqn. 4 compares the normal mode vectors residue by residue. Therefore, a sequence alignment is necessary to determine which amino acids of protein a are comparable with the residues of protein b. Residues that have been deleted in the sequences of either enzyme a or b are ignored during the normal mode overlap calculations.

Normal Mode Scoring Scheme

For the method with explicit ancestral sequences of the internal nodes, the data was fit to the exponential decay equation

$$S_{ab}(BL)=c\ast e^{k\ast BL},$$ (5)

which can be rewritten as

$$BL=\frac{ln(S_{ab}(BL)/a)}{k}$$ (6)

where S_ab is the NM vector field overlap between nodes of a branch, c is a constant fixed to 1, k is a decay rate determined by a fit, and BL is the theoretical branch length. This allows for a calculation of the theoretical branch length, BL, which is divided by the actual branch length. For the method with implicit ancestral reconstruction, the diffusion branch rates are divided by the actual branch lengths. In both cases (explicit and implicit ancestral reconstruction), the resulting value describes the relationship between the evolutionary distance based on dynamics and the evolutionary distance based on sequence alone. The median of each dataset is considered to be the amount of change expected when only neutral evolution is a factor, so values lower than the median corresponds to a high rate of NM dynamics change whereas values above the median corresponds to a low rate of NM dynamics change at the branch of interest.

Supplementary Material

01

Supplementary Figure 1. Example heat plot of the alignment of normal modes.

Supplementary Figure 2. Probabilities of ancestral sequence reconstruction with FastML.

Highlights.

• Used analysis of normal modes evolution in a phylogenetic framework to separate neutral divergence in dynamics from changes in motion due to changes of function or specificity

• Candidate lineages where signal for function shifts was weakly observed in the protein families for alpha-amylase, D-isomer specific 2-hydroxyacid dehydrogenase family, and copper-containing amine oxidase.

• Taken together these results show the importance of using combined evolutionary and physical approaches to understand enzyme biochemistry and its evolution and the potential danger in not considering neutral evolutionary processes in the analysis of sequence-structure-function relationships.

Abbreviations

NM

normal modes

NMA

normal modes analysis

EC

Enzyme Commission

RMSD

root mean square deviation

MD

molecular dynamics

MMTK

Molecular Modeling Toolkit

ENM

elastic network model

RLSCD

reconstructed lineage-specific changes in dynamics