Biomechanical Effects of Simulated Resorption Cavities in Cancellous Bone Across a Wide Range of Bone Volume Fraction

Abstract

Resorption cavities formed during bone remodeling may act as “stress risers” and impair cancellous bone strength, but biomechanical analyses of the effects of stress risers have been limited. To provide further insight, we assessed the theoretical biomechanical effects of virtually-added resorption cavities in cancellous bone specimens spanning a wide range of bone volume fraction (BV/TV=0.05–0.36) and across different anatomic sites (hip and spine) and species (human and canine). Micro-CT scans of 40 cubes of cancellous bone were converted into non-linear finite element models (voxel element size ~ 20 µm) for strength assessment. In each model, uniform trench-like resorption cavities with nominal dimensions 500 µm (length) × 200 µm (width) × 40 µm (depth), were virtually added either at random locations throughout the specimen, or, preferentially at locations of high tissue-level strain. We found that cancellous bone strength (p<0.0001) and its relation with bone volume fraction (p<0.001) were both altered by the virtual addition of the resorption cavities. When the resorption cavities were added at random locations throughout the specimen, the reduction in strength did not depend on bone volume fraction or anatomic site or species. When the resorption cavities were instead added preferentially at locations of high tissue-level strain, the effect was accentuated and was greatest in low-BV/TV bone. We conclude that, in theory, uniform-sized resorption cavities can reduce cancellous bone strength over the full range of BV/TV and across species, and the effect is larger if the cavities occur at highly strained locations in low-BV/TV bone.

Introduction

Vertebral fracture risk reduction after antiresorptive treatment for osteoporosis is typically not commensurate with changes in bone mineral density (BMD) ^(1,2). It has been proposed that fracture risk is decreased in part because antiresorptive therapy reduces the number of resorption cavities on unsupported vertical trabeculae in low-density cancellous bone, thereby reducing susceptibility to buckling of individual trabeculae and increasing overall strength of the cancellous bone ^(3–5). The engineering term “stress riser” has been used to describe how high stresses might be generated locally around resorption cavities ^(4,6) and recent ex vivo mechanical loading experiments on elderly human cadaveric cancellous bone have confirmed that mechanically-induced tissue damage occurs primarily near resorption cavities ⁽⁷⁾. Results from micro-CT-based finite element simulations support the idea that resorption cavities alter the apparent strength of elderly human cancellous bone ⁽⁸⁾, but it remains unclear if such stress-riser effects are manifested in the thicker, well supported, and plate-like trabeculae more typical of the animal bone used in preclinical studies of antiresorptive treatments ^(9–12). Without a clearer understanding of this issue, it is difficult to interpret biomechanical results from pre-clinical models. Correct interpretation of pre-clinical data is particularly important concerning bone quality since direct biomechanical testing of treated bone is really only feasible using animal bone due to the difficulty of obtaining sufficient amounts of bone material from clinical studies. Therefore, in an attempt to provide a mechanistic link between pre-clinical and clinical studies on bone quality as it pertains to stress-riser effects, we report here a theoretical investigation of the biomechanical effects of resorption cavities in cancellous bone spanning a wide range of BV/TV and of species and anatomic sites.

Materials and Methods

Study design

We used micro-CT-based nonlinear finite element analysis to assess the strength behavior of excised cubes of canine vertebral cancellous bone (n=10) and elderly human vertebral (n=16) and proximal femoral (n=14) cancellous bone, which together spanned a wide range of microarchitecture and bone volume fraction (BV/TV). Three different finite element models of each specimen were created: 1) the original specimen, 2) a random remodeling simulation in which cavities added to the finite element model at random locations on the bone surface, and 3) a high strain simulation in which cavities were added to the finite element model preferentially in regions of cancellous bone experiencing the greatest tissue strain. In this study design, the models with added cavities simulate a condition of increased remodeling while the models without added cavities represent a reduced bone remodeling condition (although some naturally formed cavities likely exist, the cavities added to the other two models were not present). Each model was virtually compressed to failure to estimate the strength of the specimen for each of the three scenarios. The effect of the introduction of the resorption cavities on strength and the strength-volume fraction relationship was assessed.

Specimen preparation and imaging

Specimens were harvested from human cadavers and the non-treated placebo arm of a previously reported canine study ⁽¹³⁾. For the human specimens, cylindrical cores (8 mm diameter) from the vertebral body (n=16 spines, L4 or L5, 9 female/7 male, age range: 54–90 years, mean ± SD: 72.9 ± 11.7 years) and femoral neck (n=14 hips, 8 female/6 male, age range: 58–85 years, mean ± SD: 70.4 ± 10.1 years) were excised, each from separate donors with no documented history of metabolic bone disease (e.g. metastatic cancer, hyper- or hypothyroidism). Analysis of the vertebral specimens has been previously reported ⁽⁸⁾. For both sites, each bone specimen was imaged with micro-CT (mCT 40, Scanco Medical AG) at 22-micron voxel size. The resulting three-dimensional image was thresholded using an automated adaptive threshold algorithm (Scanco Medical AG) to separate bone tissue from the surrounding material, and then a cube, 5 mm on each side, was digitally removed from the center of the cylinder (BV/TV in vertebral body: 11.2 ± 3.7%, in femoral neck: 22.5 ± 5.9%).

Canine vertebrae were harvested from female beagle dogs (n=10 spines, T-10, age: 2–3 years). Each canine vertebra was imaged with micro-CT (µCT 80, Scanco Medical AG) at 18-micron voxel size and then thresholded. A cube (4 mm per side, BV/TV: 22.6 ± 2.5%, mean ± SDs) was digitally removed from the vertebral body, avoiding the basivertebral foramen and the cortex. For all specimens, the cubes were aligned along the principal trabecular orientation. The following trabecular microarchitecture measurements were made in three-dimensional images using micro-CT software (CTAn, SkyScan): trabecular thickness (Tb.Th), trabecular number (Tb.N), trabecular separation (Tb.Sp), and structure model index (SMI) ⁽¹⁴⁾.

Resorption cavity models

For each bone cube, we made three different finite element models, resulting in a total of 120 models (Figure 1). The first model was not altered. The other two models of each specimen had resorption cavities added virtually using custom software ⁽⁸⁾: for the random remodeling simulation, the resorption cavities were added in a randomly distributed fashion on the trabecular surfaces; for the high-strain remodeling simulation, the resorption cavities were added preferentially to regions of greatest magnitude principal strain, as computed from an initial linear elastic finite element analysis for each specimen.

Figure 1.

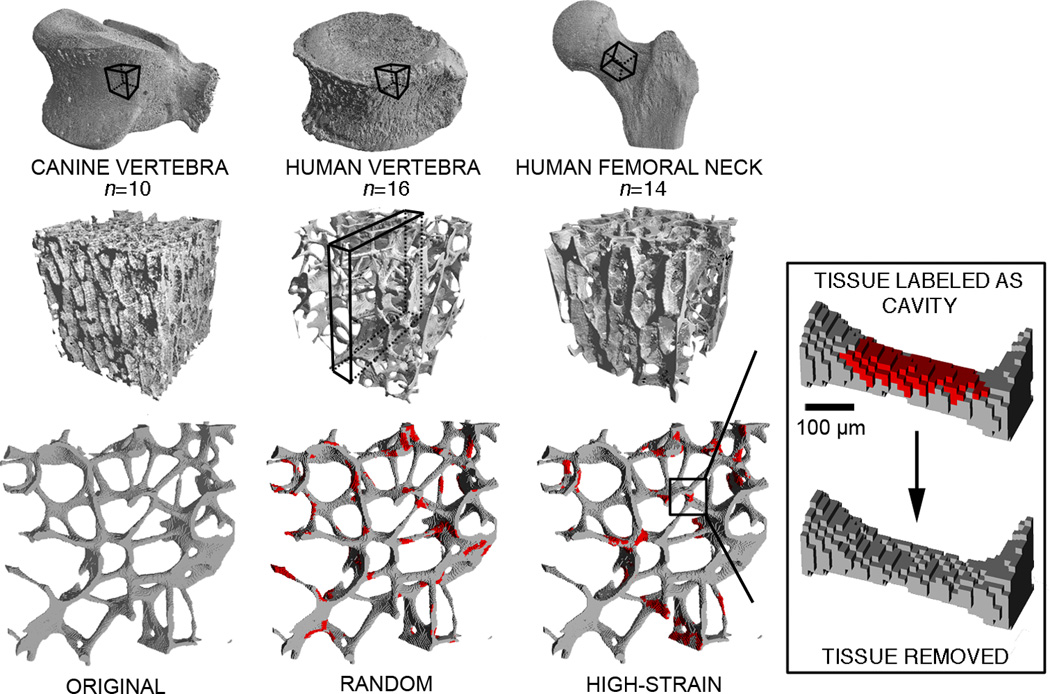
Micro-CT images of cubes of cancellous bone from canine vertebrae, human vertebrae, and human femoral necks were each converted into three finite element models containing simulated resorption cavities: 1) original model (no cavities added); 2) cavities distributed randomly; and 3) cavities targeted to regions of most highly-strained tissue.

The size and shape of the uniform resorption cavities that were virtually added to each specimen did not vary across specimens and were based on mean values of measurements reported for human bone. The resorption cavities were trench-like with a surface size of 500 microns long by 200 microns wide ^(15,16) and a depth of 44 microns ⁽¹⁷⁾ — approximately two finite elements at the resolution of these images (Figure 1). Cavities were added until a total of 6% of the original volume of bone tissue was removed from each bone cube ⁽¹⁸⁾. Cavities were allowed to overlap one another, but not completely disconnect any trabeculae. The morphology of these virtually-added resorption cavities was approximately the same within and across all bone specimens, that is to say, heterogeneity in resorption cavity morphology within or across specimens was not simulated.

Evaluation of bone strength

The 0.2% offset yield strength was estimated by virtually compressing each cube to failure in the direction of the principal trabecular orientation using nonlinear finite element analysis. In these analyses, both material and geometric nonlinearities were included as these two aspects of the finite element model are necessary to predict strength of both low BV/TV and high BV/TV cancellous bone ^(5,19). The bone tissue was modeled using a validated finite plasticity model that included tension-compression asymmetry ^(19,20). Each element in the models was assigned an effective tissue modulus reported previously for the respective anatomic site: 10 GPa for the human vertebral bone ⁽²¹⁾, and 18.5 GPa for the canine bone ⁽²²⁾ and the human femoral bone ^(19,21). A Poisson’s ratio of 0.3 and tissue-level tensile and compressive yield strains of 0.33% and 0.81% ⁽¹⁹⁾, respectively, were assigned to all canine and human models. Each finite element model contained between 0.6 and 4.3 million elements, depending on the bone volume fraction of each specimen, and was solved using a custom highly scalable, implicit finite element code ⁽²³⁾ on a supercomputer (Datastar, San Diego, CA or Ranger, Austin, TX). Using 16–56 processors in parallel per analysis, the total processor time required for all analyses was approximately 550 hours.

Role of large deformations

Since it has been proposed that resorption cavities might specifically promote large deformations and buckling ^(3–5), we performed additional analyses on a subset of specimens examining the role of large deformations. The analyses described above used finite element modeling approaches that accounted for both material non-linearities (i.e. yielding) and geometric non-linearities such as large deformations and buckling. To determine the degree to which the effects of cavities depended on large deformations and buckling, we also performed finite element analyses using models that did not include geometrically non-linear large-deformation effects (but material non-linearity was still included). Since large deformations of individual trabeculae have a greater role in the strength of low-BV/TV bone ⁽¹⁹⁾, we hypothesized that virtually suppressing large deformations would diminish any strength effects of resorption cavities in low-BV/TV bone. We performed these additional finite element analyses in a subset of five specimens, spanning a wide range of bone volume fraction (vertebral body: n=3, BV/TV=0.05, 0.07, and 0.08; femoral neck: n=2, BV/TV=0.28 and 0.36), and compared the results to those obtained when the geometric non-linearities were included in the analysis.

Outcomes and statistics

To test our main hypothesis, we determined the effect of virtually adding resorption cavities on the finite element-derived values of cancellous bone strength and the relationship between cancellous bone strength and bone volume fraction. Specifically, we tested for a correlation between the percent reduction in strength (vs. the unaltered models) caused by the virtual addition of cavities, and how this reduction depended on bone volume fraction, microarchitecture, and anatomic site. Then, we evaluated the effect of virtually adding resorption cavities on the relationship between yield strength and volume fraction using repeated measures analysis of covariance in which bone volume fraction was the covariate (SPSS Statistics v18, SPSS Inc.). We also examined the ratio of the change in strength caused by cavities to the change in strength expected from the associated reduction in bone volume fraction (⨂S/⨂S_BV/TV, Figure 2). All tests were performed for both the random and high-strain cavity-placement schemes. Statistical significance is reported for p<0.05.

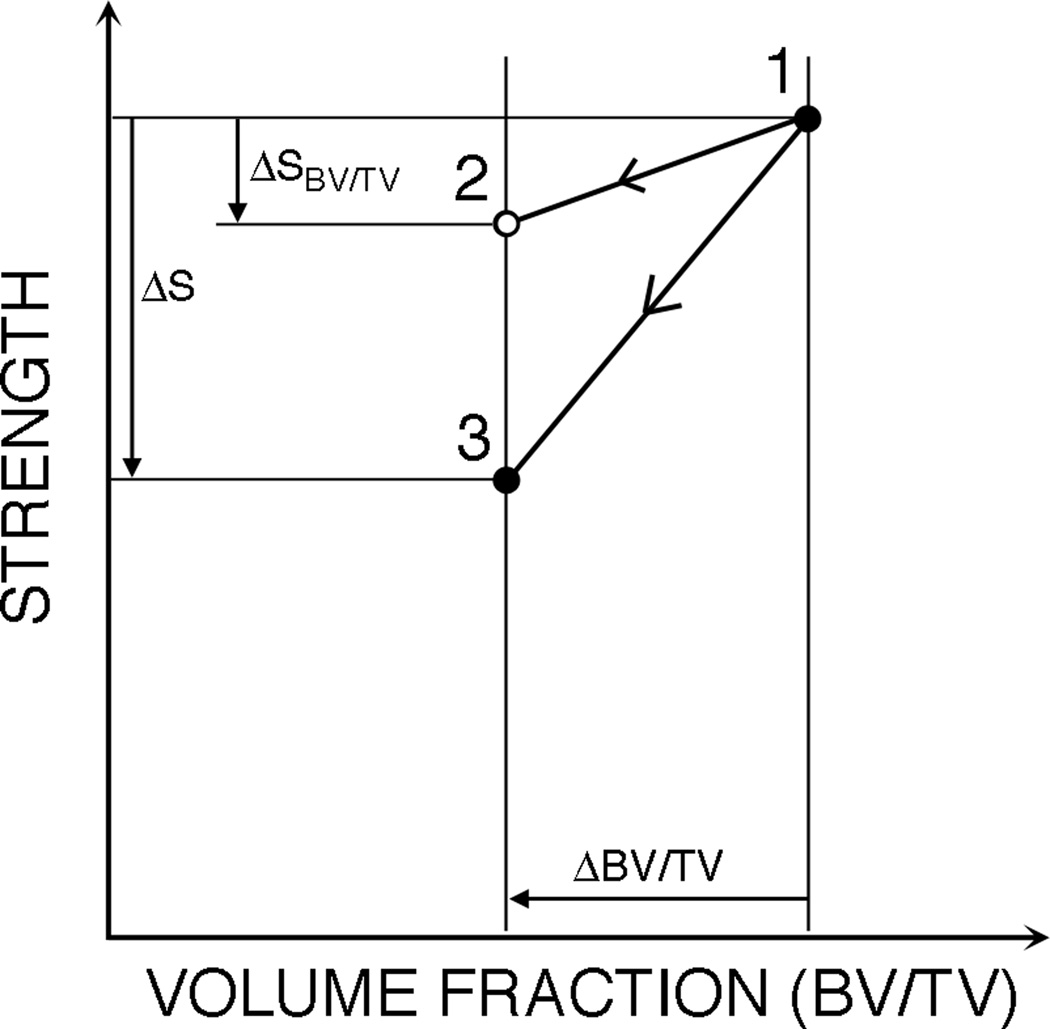
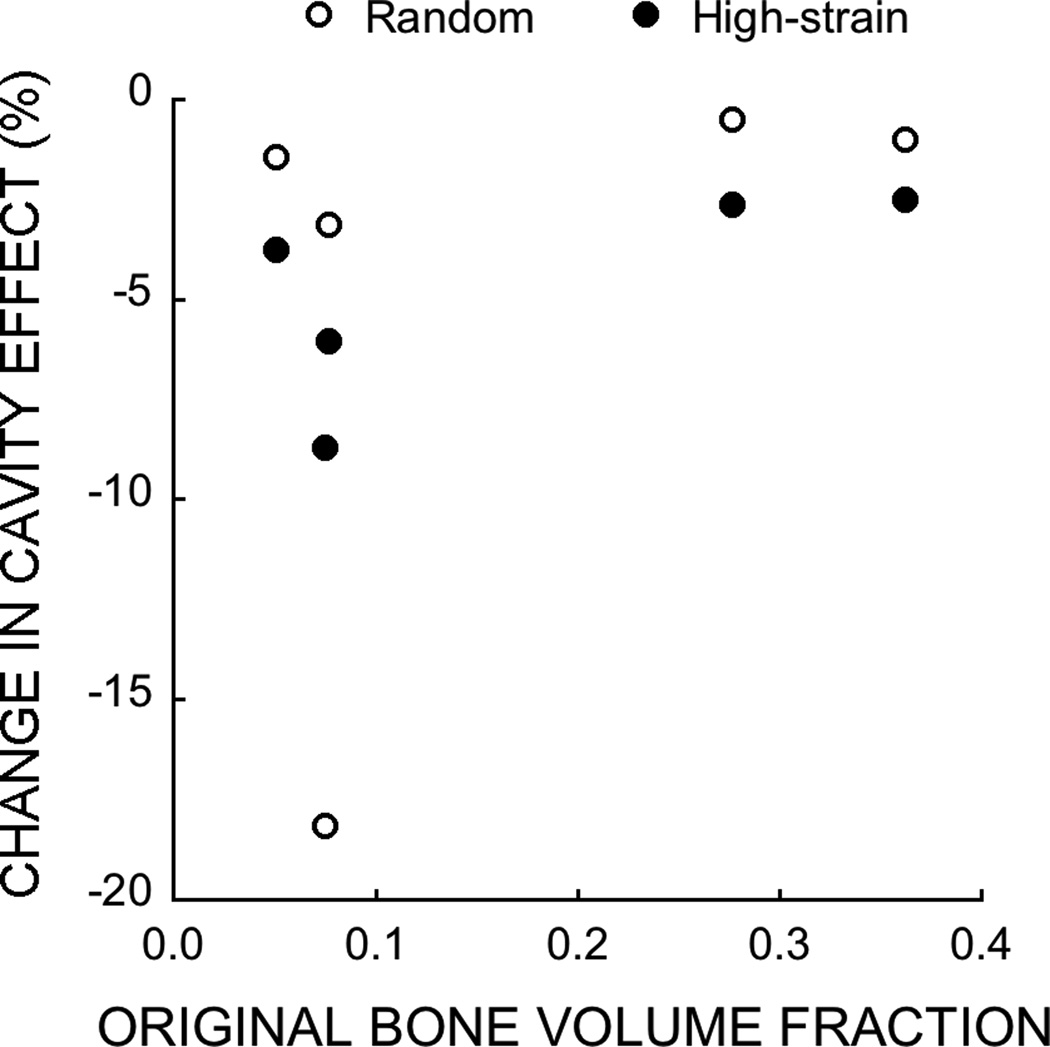
Figure 2.

A normalized reduction in strength (⨂S/⨂S_BV/TV) was defined to quantify the effect of resorption cavities on strength beyond the effect of reduced volume fraction. First, the strength-volume fraction relationship (line 1–2) for each original model (point 1) was used to predict strength after a 6% reduction in volume fraction (point 2). Then the actual strength reduction computed for each simulation (point 1 minus point 3) was normalized by this predicted strength reduction (point 1 minus point 2). A normalized strength reduction value of one indicates that the reduction is entirely due to the reduction in volume fraction, while a value greater than one indicates that there is some additional effect of the resorption cavities.

Results

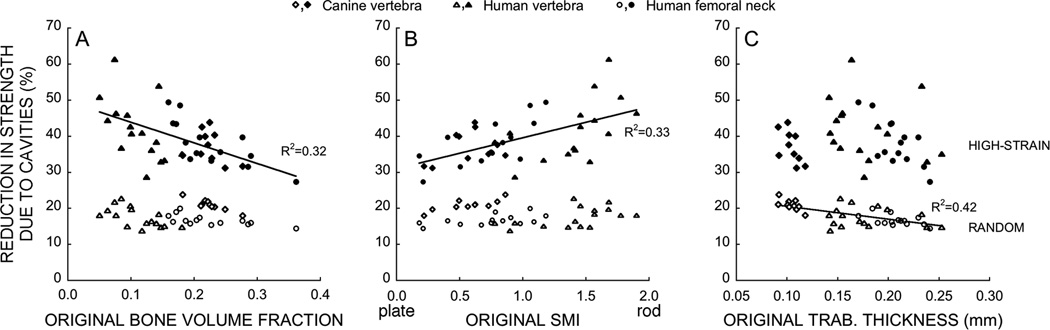
The virtual addition of resorption cavities reduced the computed yield strength of the cancellous bone at all three anatomic sites (p<0.0001), although the magnitude of this effect depended on the spatial distribution of the remodeling cavities, the bone volume fraction, and trabecular microarchitecture (Figure 3). In the random remodeling simulations, the reduction in strength associated with adding resorption cavities was not associated with BV/TV (18.0 ± 2.7%; p=0.43 vs. BV/TV) and did not differ among anatomic sites; the small variation that did exist was associated with the variation in mean trabecular thickness (p<0.0001). The biomechanical effect of resorption cavities was larger in the high-strain simulations than in the random remodeling simulations (p < 0.0001). Additionally, the effect of resorption cavities in the high-strain simulations was greater in lower-BV/TV specimens (p<0.0001) and more rod-like (SMI p<0.0001) specimens. Thus, the difference in computed strength between specimens having resorption cavities placed in random locations compared to the same specimens having cavities placed in regions of high strain was greater in lower-BV/TV bone.

Figure 3.

(A) The percent reduction in yield strength associated with adding resorption cavities to cancellous bone, compared to the case without cavities, depended on bone volume fraction (p<0.0001, n=40) and (B) SMI (p<0.0001) when cavities were targeted to regions of highly-strained tissue (filled symbols) but not when they were distributed randomly (unfilled symbols, p>0.43). (C) When resorption cavities were distributed randomly, the percent reduction in yield strength associated with adding such cavities depended on mean trabecular thickness (Tb.Th, p<0.0001).

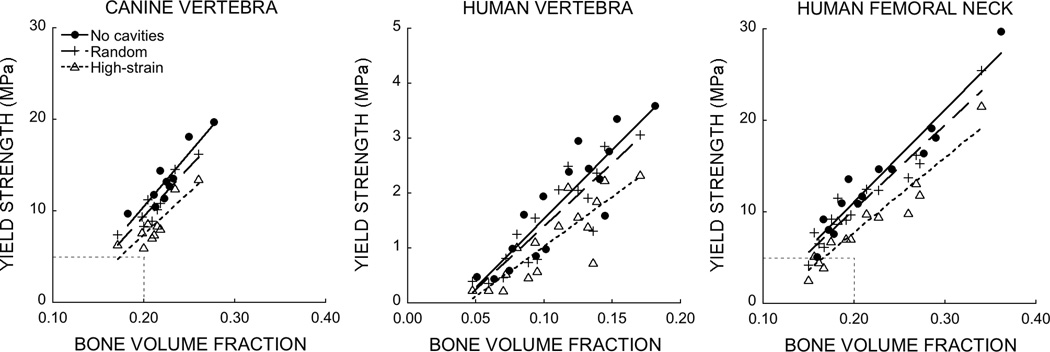
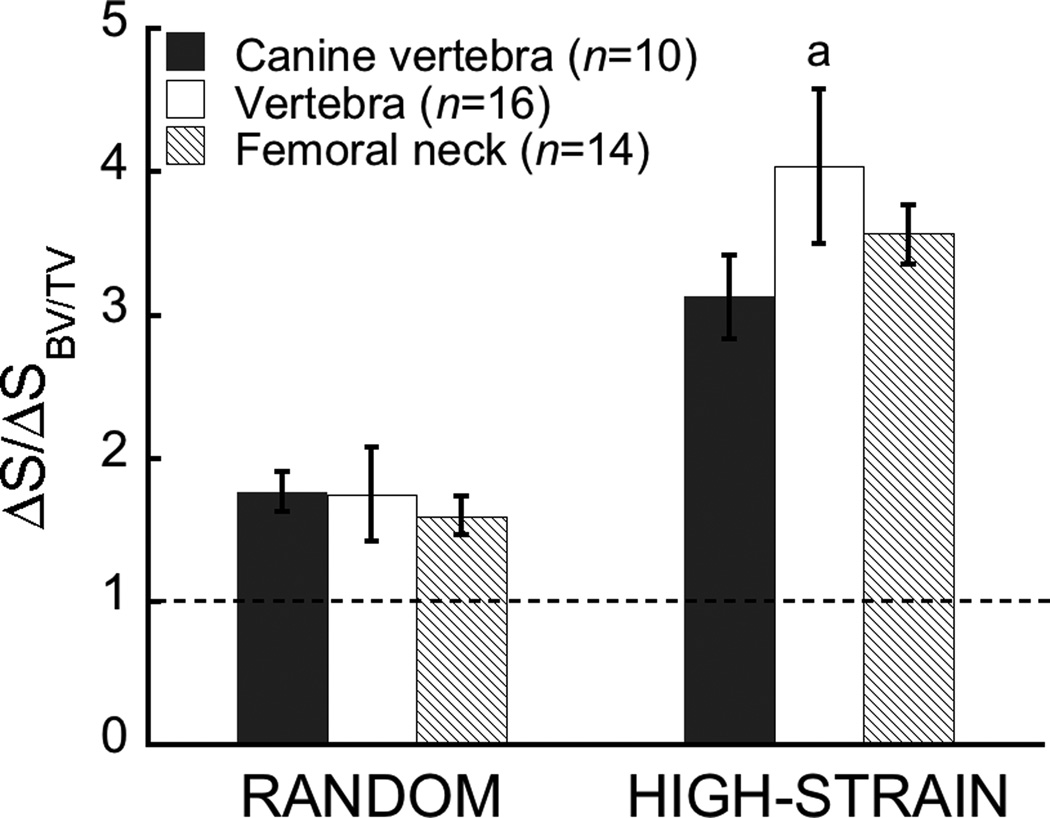
The virtual addition of resorption cavities also decreased the slope of the strength-volume fraction relationship — indicating reduced bone quality — in all cases (p<0.001), and this decrease was larger in the high-strain simulations and in low-BV/TV bone (Figure 4, Table 1). In the random remodeling simulation, the reduction in the slope of the strength-volume fraction relationship associated with virtual addition of the resorption cavities was constant (8%) regardless of anatomic site. Additionally, the normalized strength reduction, ⨂S/⨂S_BV/TV was near 1.7, indicating that the change in computed strength was about 70% larger than expected for the change in bone volume fraction (p=0.52, Figure 5; this effect did not depend on anatomic site). In contrast, in the high-strain simulations, the slope of the strength-bone volume fraction relationship decreased by about 20% in the high-density canine vertebral and human femoral neck bone, respectively, compared to about 28% in the low-density human vertebral bone (Table 1). The normalized strength reduction indicated the change in computed strength was 3–4 times larger than expected for the change in bone volume fraction, and that the effect varied among anatomic sites (p=0.01, Figure 5). These results indicate that adding resorption cavities to the model caused reductions in cancellous bone strength greater than those caused by the associated decrease in bone volume. Further, the size of this biomechanical effect depended on the location of the simulated resorption cavities (random vs. high-strain placement) and on anatomic site.

Figure 4.

Strength-volume fraction relationships were altered by the addition of random and high-strain resorption cavities in cancellous bone from canine vertebrae, human vertebrae, and human femoral necks. All comparisons p<0.001. Dashed boxes in the left and right plots show the boundary of the center plot. Differences in the slope of the strength-volume fraction relationship across these groups result from differences in trabecular microarchitecture; cancellous bone from the human femoral neck and canine vertebral body have a much more plate-like structure giving it a mechanical advantage over the more rod-like structure prevalent in human vertebral body cancellous bone ^(33,34).

Table 1.

Relationship between predicted strength and bone volume fraction for the three cavity-placement schemes per specimen.

	Canine vertebra (n=10)		Human vertebra (n=16)		Human femoral neck (n=14)
	Sy = m (BV/TV) + b		Sy = m (BV/TV) + b		Sy = m (BV/TV) + b
Cavity placement	m	b	m	b	m	b
None	117.1a (36.5)	−13.0 (8.3)	25.1a (6.8)	−0.97 (0.79)	100.9a (15.9)	−9.1 (3.7)
Random	107.8a (30.6)	−12.2 (6.5)	23.0a (6.1)	−0.89 (0.67)	92.6a (15.1)	−8.2 (3.3)
High-strain	92.8a (34.9)	−11.2 (7.5)	18.1a (5.9)	−0.77 (0.65)	81.7a (15.4)	−8.6 (3.4)

Data shows parameter estimate means (± 95% confidence interval) from linear regression. Strength has units of MPa (10⁶ N/m²). Multiple comparisons performed using the Bonferroni adjustment. n denotes the number of bone specimens per group; each specimen was analyzed assuming three different types of cavity placement.

^ap<0.01 vs. both other cavity-placement schemes.

Figure 5.

The reduction in strength after normalizing for the effect of the 6% decrease in volume fraction (⨂S/⨂S_BV/TV, see Figure 2) depended on anatomic site when resorption cavities were targeted to highly-strained tissue (^a p<0.05 vs. canine vertebra) but not when they were distributed randomly. A value of one indicates the change in strength is due entirely to the change in volume fraction. Data given as mean ± 95% CI.

When we removed the ability of the individual trabeculae to undergo geometric nonlinearities (large deformations and buckling) in our finite element analyses, the change in strength associated with resorption cavities was reduced by up to 18% in the low-BV/TV specimens, although the magnitude of this biomechanical effect did not appear to follow a clear pattern (Figure 6). In contrast, in the high-BV/TV specimens, suppressing geometric nonlinearities did not appreciably alter the reduction in strength associated with adding resorption cavities (<2.6% change in computed strength). These results suggest that the increased susceptibility of individual trabeculae to fail via “large deformation” effects is a small contributor to the mechanism by which resorption cavities weaken low-BV/TV bone.

Figure 6.

Percent change in effect of simulated resorption cavities on bone strength due to suppressing large deformations in the analyses of a subset of human cancellous bone from the vertebra and femoral neck.

Discussion

Despite the intuitive appeal of the stress-riser theory as applied to resorption cavities, the direct mechanical consequences of resorption cavities as stress risers in vivo have never been directly demonstrated in human bone — thus the need for pre-clinical and simulation studies. Our previous simulation study on this topic analyzed the human vertebral specimens used in this analysis ⁽⁸⁾; our current analysis generalizes the result to include cancellous bone from the human proximal femur and the canine vertebra. Using this large sample of diverse specimens, our results suggest that randomly placed resorption cavities reduce cancellous bone strength by 15–20% more than would be expected based on the associated decrease in bone volume fraction and that such an effect is present in both canine and human cancellous bone across the range in BV/TV observed in clinical and preclinical studies. This biomechanical effect is greater when cavities are placed in regions of high tissue-level strain and is more pronounced in low-BV/TV bone. A major caveat of this study is that our simulations did not account for the variability in resorption cavity breadth and depth within specimens. Regardless, our simulations shed unique insight into how resorption cavities might alter cancellous bone strength because they reveal that, in theory, uniform-shaped resorption cavities can alter strength in all types of cancellous bone, and the biomechanical effect can be substantial in very porous bone if resorption cavities are preferentially located in regions of high tissue-level strain.

Biomechanical analysis of the stress-riser effect is an inherently difficult problem. Even if one has actual treated vs. non-treated bone tissue available for direct biomechanical testing, it is difficult to quantify the effect of altered remodeling on bone strength, in part because treatments alter BV/TV as well and it can be difficult to distinguish the biomechanical effects of resorption cavities from those associated with changes in BV/TV (and perhaps also microarchitecture). One statistically powerful way is to do this is to quantify changes in the relation between strength and BV/TV ⁽²⁴⁾. Since most animal studies to date have not directly addressed the issue of stress risers in this manner, there are only few experimental data available for such purposes. Supporting the existence of a stress-riser effect, bisphoshonate treatment in glucocorticoid-induced osteoporosis in minipigs significantly increased cancellous bone strength by about 30% without increasing bone volume fraction ⁽⁹⁾. Denosumab treatment in ovariectomized monkeys showed a trend toward increased cancellous bone strength independent of changes in bone mineral (see the offset in regressions lines in Figure 4A of Ominsky ⁽¹⁰⁾). However, earlier biomechanical studies in minipigs and dogs treated with antiresorptive agents ^(11,12,22) did not detect any such effects. Thus, while definitive evidence of any stress-riser effect even in animal bone remains somewhat of an enigma, there is an emerging picture that some effect may occur, regardless of BV/TV or architecture. Further animal experiments are required to confirm our findings and until such confirmation is obtained, the stress-riser issue remains open.

The current simulations provide insight into the mechanisms by which any stress-riser effect might be greater in low-BV/TV cancellous bone. One possible reason is the difference in failure mechanisms between low- and high-density cancellous bone. Because of the importance of geometrically non-linear large deformations and buckling, low-BV/TV cancellous bone is more likely to fail due to excessive bending and deformation of individual trabeculae ⁽¹⁹⁾ than is high-BV/TV bone ⁽¹⁹⁾. It has been asserted that resorption cavities have a biomechanical effect primarily on “unsupported” trabeculae which have lost horizontal support and are more likely to fail under buckling ^(3–5). Our finding that the biomechanical effects of resorption cavities can be more pronounced in low-BV/TV cancellous bone supports this assertion. However, we found that suppressing large deformations of trabeculae in our finite element models only reduced the biomechanical effect of resorption cavities by a small amount – removing 18% or less of the biomechanical effect of cavities in low-BV/TV bone, and much less in high-BV/TV bone. Hence, our finite element models suggest that while cavities may have a greater biomechanical effect in low-BV/TV cancellous bone that undergoes large deformation bending and buckling, the large deformation bending and buckling processes themselves may not be necessary for resorption cavities to have an appreciable biomechanical effect. The current study did not permit resorption cavities to completely perforate an individual trabecula so it does not provide insight into the degree to which loss of horizontal trabeculae may influence the biomechanical effects of resorption cavities ⁽⁵⁾.

Our results have potentially important implications for future studies designed to further assess the biomechanical effects of resorption cavities. In our previous micro-CT-based finite element analysis of vertebral cancellous bone specimens excised from dogs treated with high doses of risedronate ⁽²²⁾, we found that treatment did not alter the relationship between the computed strength and BV/TV. This finding is consistent with experimental results showing no effect on the relationship between compressive strength and areal BMD in canine vertebrae after treatment with the same bisphosphonate ⁽²⁵⁾. But these findings are in direct contrast to the results from the current study, which showed stress-riser effects for all cancellous bone regardless of BV/TV. One possible explanation for this discrepancy is related to the spatial resolution of the micro-CT imaging. In our prior study, although we used the same type of micro-CT-based finite element analysis as in this current study, we did not virtually add resorption cavities and instead relied on the actual morphology of the bone as observed from the 18-micron micro-CT scans and compared the strength-BV/TV relation in separate groups of dogs (treated vs. non-treated). One inference to take from these collective findings is that much smaller voxels sizes than 18 microns may be required if one is to directly image resorption cavities for the purposes of biomechanical analysis. Recent work using very high resolution (0.7-microns in-plane) 3D serial milling images of rat vertebrae found that resorption cavities could not be visually identified when the images were coarsened to a voxel size greater than 1.4 × 1.4 × 5.0-microns ⁽²⁶⁾, in part because eroded surfaces (crenated surfaces) were not evident in the coarser resolutions. However, although 0.7 micron resolution may be necessary to visually recognize and classify a resorption cavity by way of eroded surface, the major biomechanical effects may be captured at coarser resolutions, particularly if the biomechanically important resorption cavities are relatively deep. Given this uncertainty into how resolution issues may have influenced our findings, future biomechanical studies addressing stress risers might well consider such resolution issues.

Another possible explanation for the discrepancy between the current results and our prior results on canine bone is our assumption that the morphology and prevalence of real resorption cavities are the same in canine and human bone. The size and shape of cavities in all our simulations in the current study were based on mean values of morphological measurements reported for postmenopausal women ^(15–18). While such measurements have not been reported for canine bone, histomorphometric analysis of canine cancellous bone suggests that the depth of cavities is generally similar to that in humans ^(27,28). However, measurements in cortical bone — which are more straightforward to make than measurements in cancellous bone ⁽¹⁶⁾ — indicated that the Haversian diameter is smaller in canine than human bone ⁽²⁹⁾. If the cellular mechanisms associated with remodeling are largely the same on cortical and trabecular surfaces ⁽¹⁶⁾, then these measurements suggest that the depth of resorption cavities in cancellous bone may also be smaller in canine than human bone. If that is true, then the biomechanical effects of such different cavities may also differ since micro-CT-based finite element simulations have shown that cancellous strength was reduced less by shallower cavities ^(30,31). Further, if there are fewer cavities in canine bone than in bone from postmenopausal women, this too could reduce the biomechanical impact of any stress-riser effect. It is possible therefore that the stress-riser effect does not exist in canine bone because cavities are smaller or fewer than assumed in our current simulation study.

One limitation of this study is that we did not consider heterogeneity in the resorption cavity geometry within and among specimens. In particular, we simulated resorption cavities that had a uniform depth similar to the reported mean depth ⁽¹⁷⁾, and did not account for geometry or depth variations within or across resorption cavities. It is not clear how the variations in cavity geometry within a single specimen would alter our study conclusions. Variability of resorption cavity depth within a specimen might increase the biomechanical effect of cavities because some of the deeper cavities might lie in regions of high strain. But such variability instead might decrease the biomechanical effect because deep cavities could be fewer in number and less likely to be in a region of high strain. Simply increasing the depth of the resorption cavities in our models to values similar to the maximum depth reported for a population of BMUs — rather than the mean depth — would likely accentuate the effects we observed but would not likely alter our general conclusions regarding how stress-riser effects depend on cavity placement, BV/TV, or species. Clearly, additional insight would be forthcoming from addressing the theoretical effects of heterogeneity in cavity shape and size.

Another limitation is that we use computational models to assess strength, rather than direct biomechanical testing. While our finite element technique has been well validated for assessment of strength in human cancellous bone ^(19,32), it has not been validated to assess biomechanical effects of changes in remodeling. Again, animal experiments are required to resolve the true biomechanical effects of stress risers, although interpretation of any such results would be enhanced by micro-CT imaging and finite element analysis of the same specimens performed at appropriately high resolution. A final limitation is that the current study addresses only the behavior of isolated cancellous bone specimens, and it remains to be determined how stress risers might influence whole-bone mechanics. Because the stress-riser effect in the current study can be related to BV/TV, it is possible that load transfer between cancellous and cortical bone and the effect on the whole bone may differ in the spine vs. the hip based on local BV/TV and the relative importance of the cortex at these two anatomic sites. This too remains a topic of further research.

Despite these limitations, one major strength of the finite element-based cavity simulation technique is that it enables precise control over the size and placement of the virtually added resorption cavities and thus provides a sound basis for theoretical analysis of this overall effect. We used a repeated-measures study design to isolate the importance of location of resorption cavities, i.e., whether randomly placed or targeted to regions of high tissue-level strain, and our statistical tests were well powered to detect even subtle changes in bone strength and the strength-volume fraction relationships. Regarding external validity, the bone samples included in this study spanned a wide range of bone volume fractions, tissue morphologies, and donor ages indicating that any trends observed from this set should extend to a larger population.

In summary, we found that the biomechanical effects of simulated stress risers were present in cancellous bone of different sites, species, and BV/TV. These effects were greater if resorption cavities were virtually added in regions of high tissue-level strain in low-BV/TV bone. However, because our analysis assumed only a uniform morhphology of any simulated stress risers, and because the literature shows no definitive evidence using purely experimental animal models, whether or not stress risers play an important role in the fracture efficacy of antiresorptive treatments remains somewhat of an enigma, and further research is recommended to address this interesting issue.