Improved throughput traction microscopy reveals pivotal role for matrix stiffness in fibroblast contractility and TGF-β responsiveness

Abstract

Lung fibroblast functions such as matrix remodeling and activation of latent transforming growth factor-β1 (TGF-β1) are associated with expression of the myofibroblast phenotype and are directly linked to fibroblast capacity to generate force and deform the extracellular matrix. However, the study of fibroblast force-generating capacities through methods such as traction force microscopy is hindered by low throughput and time-consuming procedures. In this study, we improved at the detail level methods for higher-throughput traction measurements on polyacrylamide hydrogels using gel-surface-bound fluorescent beads to permit autofocusing and automated displacement mapping, and transduction of fibroblasts with a fluorescent label to streamline cell boundary identification. Together these advances substantially improve the throughput of traction microscopy and allow us to efficiently compute the forces exerted by lung fibroblasts on substrates spanning the stiffness range present in normal and fibrotic lung tissue. Our results reveal that lung fibroblasts dramatically alter the forces they transmit to the extracellular matrix as its stiffness changes, with very low forces generated on matrices as compliant as normal lung tissue. Moreover, exogenous TGF-β1 selectively accentuates tractions on stiff matrices, mimicking fibrotic lung, but not on physiological stiffness matrices, despite equivalent changes in Smad2/3 activation. Taken together, these results demonstrate a pivotal role for matrix mechanical properties in regulating baseline and TGF-β1-stimulated contraction of lung fibroblasts and suggest that stiff fibrotic lung tissue may promote myofibroblast activation through contractility-driven events, whereas normal lung tissue compliance may protect against such feedback amplification of fibroblast activation.

pulmonary fibrosis is associated with aberrant tissue repair and persistent activation of myofibroblasts (29, 37, 60, 72). Myofibroblasts are mechanically active cells (23) that interact with the extracellular environment by secreting matrix proteins and exerting forces necessary for matrix rearrangement (28, 60). Myofibroblast contractility also contributes to activation of transforming growth factor (TGF)-β1 (68), a profibrotic cytokine whose liberation from a matrix-bound latent complex perpetuates fibroblast activation and matrix deposition (18, 39). Thus delineating cellular, molecular, and mechanical mechanisms regulating fibroblast force generation and matrix deformation is central to understanding the function of these pivotal fibrosis-promoting cells.

Although fibroblast contractile status can be inferred from the formation of stress fibers and phosphorylation of regulatory myosin light chain (21, 32, 36, 50, 61, 65), a number of methods are now available to directly measure the contractility of individual fibroblasts. These methods include techniques to measure cell-mediated deflections of micropillar substrates (57, 70) or deformations of micropatterned surface markers on hydrogel cell culture substrates (51, 62). Measurement of the cell-mediated displacement of beads embedded within polyacrylamide gels is one of the most common and simplest to implement approaches for assessing fibroblast contractile function based on minimal technical requirements for gel casting and the availability of software solutions such as Fourier Transform Traction Cytometry (FTTC) (7) to extract cellular tractions from measured displacement fields. In FTTC, cells are grown on soft polyacrylamide (PA) matrices, and cell-mediated substrate deformations are measured by comparing the positions of fluorescent beads embedded in the PA gel and that of the same beads in an unstressed substrate after cell removal (7, 14, 58). However, the existing methodology requires several user-dependent steps, such as manual focusing of the imaging system on the topmost beads and manual outlining of cell boundaries, which limit the throughput of the technique. Here, we aim to improve the experimental procedure and make FTTC suitable for higher-throughput applications.

We use our improved method to test whether increasing matrix stiffness changes the force-generating capacity of lung fibroblasts. Our results, obtained over a pathophysiological range of substrate stiffness (39), reveal a strong effect of extracellular matrix stiffness on fibroblast tractions. We further show that TGF-β1 treatment augments fibroblast force-generating capacity on stiff substrates approximating fibrotic lesions in the lung but not on substrates approximating normal lung stiffness, despite similar effects of TGF-β1 on Smad2/3 activation. Thus we observe that soft matrix conditions suppress fibroblast contractility and selectively uncouple a profibrotic signal from fibroblast contractile function, suggesting that normal lung matrix compliance may protect against an important functional effect of TGF-β1.

MATERIALS AND METHODS

Cell culture.

IMR-90 fetal lung fibroblasts (ATCC) were cultured in Kaighn's modification of Ham's F-12 medium (F-12K) supplemented with 10% FBS, 100 U/ml penicillin, and 100 μg/ml streptomycin (all from Mediatech) in a humidified incubator with the atmosphere containing 5% CO₂ at 37°C. The cells were seeded at 10 cells/mm² in six-well plates containing polyacrylamide hydrogel matrices of one of six discrete elastic (Young's) moduli: 0.3, 1, 6, 13, 17, and 20 kPa. All gels were functionalized with 10 μg/ml of collagen I. In some experiments, the cells were treated with 5 ng/ml of TGF-β₁ (purchased from R&D Systems and reconstituted according to manufacturer's recommendations) immediately after seeding. The cells were used at passages 3–8.

Polyacrylamide gel preparation and surface conjugation of microspheres.

Glass-bottom six-well plates (In Vitro Scientific) were treated with a 0.4% aqueous solution of 3-methacryloxypropyltrimethoxysilane (Acros Organics) at pH 3.5 for 1 h, rinsed three times in distilled water, and air dried. Six prepolymerization solutions of variable ratios of acrylamide:bisacrylamide (Bio-Rad) were prepared as described previously (43) [% acrylamide:% bisacrylamide (Young's modulus, kPa); 3:0.05 (0.3), 3:0.11 (1), 7.5:0.05 (6), 7.5:0.12 (13), 7.5:0.19 (17), 7.5:0.34 (20)]. Twenty-five microliters of each prepolymerization mixture was delivered into selected wells and sandwiched with SurfaSil (Thermo Scientific) treated, hydrophobic glass coverslips (18 mm in diameter) for 10 min. The thickness of resulting gel was ∼100 μm. After polymerization, the gel surface was derivatized with heterobifunctional cross-linker Sulfo-SANPAH (G-Biosciences), as described previously (43), and fluorescent (505/515, Ex/Em nm), 0.2 μm in diameter, sulfate-modified latex microspheres (FluoSpheres, Invitrogen) were conjugated to the gel surface by delivering a sonicated aqueous suspension of the beads (diluted at 1:200) on top of the gels for 30 min. The gels were rinsed three times in distilled water to remove all remaining nonattached beads, UV sterilized, and functionalized by incubation for 2 h with 10 μg/ml of sterile collagen I (PureCol) in PBS. In some experiments, in addition to conjugating microspheres to the gel surface, fluorescent (580/605 Ex/Em nm), 0.2 μm in diameter, carboxylate-modified latex microspheres (Invitrogen) were embedded within gels by addition to polymerization solution before casting.

High-throughput traction microscopy.

We employed a Pathway HT fluorescence imaging system (Atto Bioscience) to acquire images of gel surface-conjugated fluorescent beads two times for each selected cell, one image acquired before and one after removal of the cell by treatment with Trypsin/EDTA (10× − 0.5%/0.2%, Sigma). At the time of original image acquisition, we obtained a paired fluorescent image of the cell membrane, visualized by transducing cells with CellLight Plasma Membrane-RFP (Invitrogen) as described below. Vollath F4, a robust, correlation-based autofocusing algorithm (66) was used to automate the focusing of the imaging system on the surface of the gel, and an automatic stage-positioning system was used to record the positions of several cells selected across each plate, allowing multiple cells to be studied in each experiment. All images were taken using a ×20 magnification objective. For each cell, a displacement field on the surface of the gel was computed from the pairs of images of the beads, before and after cell removal, by utilizing two-dimensional cross-correlation algorithm, implemented in Matlab (MathWorks) as described previously (58). On the basis of previous work (58) and our system setup (magnification, camera pixel size, bead density, and cross-correlation window size), we estimate that our method is sensitive to displacements of less than 0.25× pixel size. Because the pixel size for our camera is 6.4 μm and our microscope magnification is ×20, the pixel size in our images is 6.4/20 = 0.32 μm, and we estimate that our experiments are sensitive to displacements as small as 0.25 × 6.4/20 = 0.08 μm. Constrained FTTC (7) was used to compute traction fields based on the measured displacement fields and Young's moduli of the gel substrates. To compare traction fields, both within and across stiffness conditions, we computed root-mean-square traction (RMST) for each cell as the square root of the average squared magnitude of tractions for each traction field. In time-course experiments, all displacement fields in time were computed relative to one image of the beads that was taken following removal of the cell by trypsinization.

Transduction and measurement of projected cell area.

We utilized CellLight Plasma Membrane-RFP to visualize the cell membrane. Five microliters of the reagent (1:200 dilution) were added directly to the cells cultured on flexible hydrogel substrate and incubated overnight. Fluorescent images of the cells were taken by using an appropriate combination of excitation/emission (555/584 nm) filters. The outline of a cell was extracted by utilizing simple “contrast stretching” implemented in Matlab's Image Processing Toolbox. By selecting an appropriate region in the histogram representing the distribution of intensities in the image of each fluorescent cell, contrast stretching ensured that pixel values below a specified value are displayed as black, and pixel values above a specified value are displayed as white. Black pixels are then selected as those belonging to the area within the cell outline. The coordinates of the points outlining the cell were loaded into Matlab code implementing constrained FTTC. Projected cell area was calculated by multiplying the total number of pixels within the cell outline by the size of the pixel in μm².

Immunofluorescence staining.

IMR-90 fibroblasts cultured in six-well plates on polyacrylamide substrates for 24 h were immunostained after fixation with 4% formalin, permeabilization with 0.5% Triton X-100 (EMD Chemicals), and blocking with 5% goat serum. The cells were incubated for 2 h with a rabbit monoclonal antibody against phospho-Smad2 (Ser465/467)/Smad3 (Ser423/425) (Cell Signaling Technology), diluted at 1:200. After being washed, cells were incubated for 1 h with AlexaFluor 546 conjugated goat anti-rabbit IgG (H+L) antibody (Invitrogen), diluted at 1:1,000 in PBS. The cells were washed, and F-actin and nuclei were stained with AlexaFluor 488-phalloidin and Hoechst 33342 (both from Invitrogen), respectively.

Analysis of phospho-Smad fluorescence intensity.

Quantification of nuclear phospho-Smad2/3 fluorescence staining was carried out by using a series of Matlab-based image-processing functions. Briefly, nuclei and projected cell areas were extracted from the fluorescent images by applying a global image threshold using Otsu's method (47). Those areas were further used to extract and integrate nuclear and cytoplasmic phospho-Smad2/3 fluorescence. Finally, for each image, integrated intensity of nuclear phospho-Smad2/3 fluorescence per unit area was nondimensionalized as a ratio of the integrated intensity of cytoplasmic phospho-Smad2/3 fluorescence per unit area.

Statistical analysis.

Linear regression analysis was done in Excel (Microsoft). One-way ANOVA followed by Tukey's test or two-tailed t-test were done in Stata statistical software (StataCorp LP).

RESULTS

Increasing the throughput of traction microscopy.

Traction microscopy involves two relatively time-consuming procedures that are amenable to improvement, focusing the imaging system on the topmost surface of the gel to measure cell-mediated gel displacements and outlining the perimeter of each cell to constrain tractions within the cell boundary. We have addressed both of these limitations and integrated the improved methodology with an automated microscopic imaging approach to vastly improve the throughput capabilities of traction microscopy, as detailed below. On the basis of the broad biological variability in tractions generated by individual cells, this improved methodology will accelerate efforts to compare force generation across different cell populations and to identify novel regulators of cellular force generation.

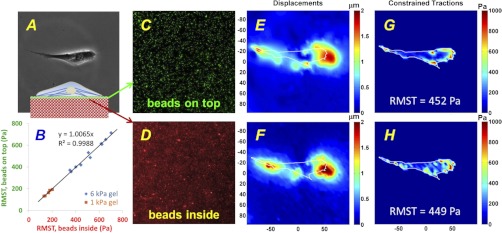
Typically in traction microscopy, fluorescent beads are embedded throughout the PA substrate during polymerization (7, 14, 58), requiring the user to focus the microscope on the topmost focal plane containing beads to accurately measure displacements at the gel surface. To overcome this limitation, we developed an approach to conjugate fluorescent microspheres, 0.2 μm in diameter, to the gel surface, as described in materials and methods. This change in experimental methodology allowed us to use the autofocusing capabilities of fluorescence microscopy-based imaging systems and automate a key step in the experimental procedure for traction measurements. To compare the new approach of using surface-bound beads to the standard gel-embedded bead approach, we seeded IMR-90 lung fibroblasts on gels with elastic moduli of 1 and 6 kPa that were prepared with fluorescent beads with different excitation/emission wavelengths inside and on top of the gels (Figs. 1A, inset). We then computed RMST values separately using the two groups of fluorescent beads, inside and on top of the gel, for each cell (Fig. 1B). Fluorescent images of the beads bound to the gel surface (Fig. 1C) were captured using the autofocusing function of the imaging system (Atto Bioscience Pathway HT), before and after cell removal by trypsinization. Corresponding images of the topmost beads embedded within the gel (Fig. 1D) were taken using the same focal plane setting. The surface-bound beads remained attached to the gel after trypsinization, confirming that the beads were not internalized by the cells. The displacement fields (Fig. 1, E and F) were computed from the images of the beads before and after trypsinization, and accompanying traction fields (Fig. 1, G and H) were computed by constrained FTTC (7). Our measurements revealed excellent agreement between tractions calculated using the two sets of images, with an overall correlation coefficient (R²) of 0.99 from 15 cells with RMST ranging from ∼100 to 700 Pa on 1 and 6 kPa matrices (Fig. 1B). On the basis of our observation that fibroblasts grown on PA gels with and without surface beads are morphologically indistinguishable, and our finding of similar fibroblast tractions using surface-coupled or only gel-embedded beads (not shown), we conclude that the surface-bound fluorospheres do not impact fibroblast appearance and contractile function.

Fig. 1.

Experimental validation of improved methods for traction measurements. A: top-down phase-contrast image of an IMR-90 fibroblast seeded at low density on a polyacrylamide gel coated with collagen I. Fluorescent beads were both embedded inside and conjugated on top of the gel, as illustrated in the transverse inset. Elastic modulus of the gel was 6 kPa. B: 2D scatter plot of root mean square tractions (RMSTs) calculated for multiple cells using images of the beads inside the gel (abscissa) vs. beads on top of the gel (ordinate). Tractions were computed for cells seeded on substrates with elastic moduli of 1 and 6 kPa. 95% confidence interval for the slope of linear regression with zero intercept was (0.9864, 1.0266). C and D: fluorescent images of the same field of view in A showing 200-nm beads linked on top of the gel (green, C) and beads inside the gel (red, D) taken using the same focal plane setting. All images were obtained at ×20 magnification. E and F: displacement fields computed from the fluorescent images of the beads taken before and after cell detachment by trypsin-EDTA treatment. Colors denote absolute magnitudes of displacements, in μm (see color bars). Labels at the axes, in μm, indicate the length scale. Displacement field was computed either from the fluorescent images of the beads on top of the gel (C) or from the images of the beads embedded in the gel (D), all taken at the same focal plane. G and H: traction fields computed from the displacement fields in C and D. Colors denote the magnitudes of traction vectors in Pa (see color bars). RMSTs were computed for both traction fields and shown on the maps as RMST values. E–H: outline of the cell shown in A was superposed on the maps of displacement and traction fields.

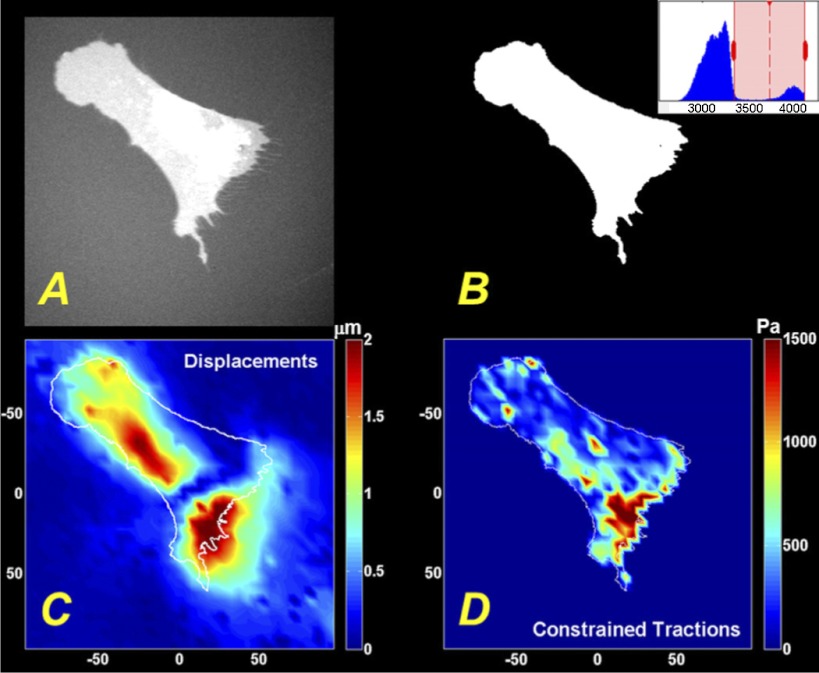
The cell boundaries in Fig. 1, E–H were manually traced based on phase contrast images, a time-consuming procedure necessary to impose the appropriate boundary condition and constrain tractions to the area underneath the cell (7). To automate this step, we treated lung fibroblasts with CellLight Plasma Membrane-RFP (Invitrogen), a fluorescent protein construct that localizes to the plasma membrane, immediately after seeding them on soft hydrogel substrates. Following incubation for 24 h, a time typical for traction microscopy, high-contrast images of cells expressing the plasma membrane-associated fluorescent protein (approximate transduction efficiency of >80%) could be obtained (Fig. 2A) in conjunction with the images of yellow-green fluorescent beads conjugated to the gel surface. The prominent contrast in the images greatly simplified outlining of the boundary of the cell using a fast, computationally inexpensive threshold algorithm, implemented in Matlab as described in materials and methods (Fig. 2B). Threshold pixel values were determined empirically for each image to account for cell-to-cell variability in fluorescence intensity, but this was the only user-defined step in the procedure and was accomplished in a small fraction of the time that would be needed to manually outline the cell boundary. Of note, in some images small RFP-positive narrow extensions were observed emanating from the perimeter of cells (Fig. 3). These appear in some cases to be related to the “membrane remnants” previously observed to be left behind by retracting or migrating fibroblasts (9, 38, 52); they remained on the cell surface when cells were trypsinized and were not visible in phase-contrast images both in our hands and in previously published work (52). More importantly, these membrane extensions were not associated with detectable bead displacements, even when they appeared to remain linked to the cell. Thus, although we could visualize these features around some transduced cells, we did not develop additional image-analysis procedures to capture these features in cell outlines. After computing the displacement field (Fig. 2C) for the beads on the gel surface, the outline of the cell boundary could be used in constrained FTTC to calculate the corresponding traction field (Fig. 2D).

Fig. 2.

Automation of cell boundary detection for traction mapping. A: IMR-90 fibroblasts were transduced with CellLight Plasma Membrane-RFP immediately after seeding on polyacrylamide (PA) substrate (elastic modulus of the gel was 13 kPa), and fluorescent image was taken after 24 h. B: cell boundary was detected by using a simple threshold algorithm. Inset: Matlab generated histogram showing the distribution of intensities in the image, with the red rectangle denoting the pixel intensities above the user-defined threshold. C: displacement field computed from the fluorescent images of the beads conjugated on top of the gel. Color-coded absolute magnitudes of displacements are shown on the color bar, in μm. D: traction field computed from displacement field in C. Color-coded magnitudes of traction vectors are shown on the color bars, in Pa. C and D: labels at the axes indicate the length scale, in μm. Outline of the cell in B was superposed on the maps of displacement and traction fields.

Fig. 3.

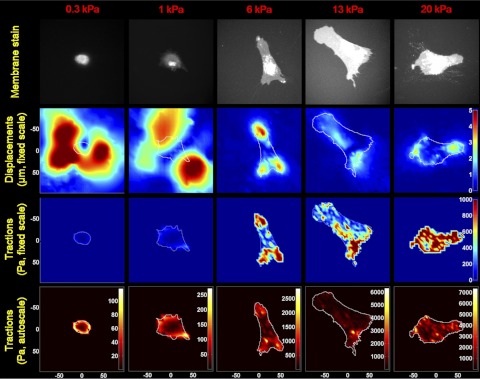
Cell-mediated displacements and tractions vary across matrix stiffness conditions. Fibroblasts were seeded on PA gels with discrete elastic moduli of 0.3, 1, 6, 13, and 20 kPa. Each column in the figure corresponds to a discrete substrate stiffness indicated at the top of the column. Row 1 shows fluorescent images of the cells transduced with CellLight Plasma Membrane-RFP; row 2 shows displacement fields from surface-conjugated fluorescent beads; row 3 shows the corresponding traction fields displayed using a fixed traction scale across all matrix stiffness conditions; row 4 shows the same traction fields using an autoscaled traction scale to better visualize the pattern of tractions within each image. In the second row, color-coded magnitudes of displacements are fixed to a single length scale, in μm, shown on the color bar in the right-most column. In the third row, color-coded magnitudes of traction vectors, in Pa, are shown on the color bar in the right-most column. In the fourth row, color-coded magnitudes of tractions, in Pa, are indicated on the color bars next to each map in the row. Labels at the axes indicate the length scale, in μm.

Fibroblast tractions vary dramatically across a pathophysiological range of substrate stiffness.

The autofocus capability engendered by using surface-bound beads prompted us to combine this approach with an imaging system featuring a programmable microscope stage, allowing us to study multiple cells efficiently from individual experiments. On the basis of the recent observation that the stiffness of the extracellular matrix of the lung changes during fibrotic tissue remodeling (39), we seeded IMR-90 fibroblasts at a subconfluent density on PA gels with elastic moduli ranging from 0.3 to 20 kPa (Fig. 3, row 1), encompassing the median observed in normal (∼1.4 kPa) and fibrotic (∼7.5 kPa) mouse lung tissue (39). We then measured the cell-generated displacements of surface-bound beads using images obtained before and after cell trypsinization. Strikingly, our experiments revealed that matrix displacements are largest on the softest matrices and diminish in magnitude dramatically in the range of normal and fibrotic lung (1 to 13 kPa) (Fig. 3, row 2, and Fig. 4A). The distribution of displacements in the substrate greatly exceeded the cell perimeter at low stiffness. These displacements of the beads outside the cell area are the result of force transmission through a continuum (the gel substrate). Simply put, a point force in the plane of the gel surface produces a displacement field with local maxima at the location where the force acts, with the magnitude of displacement declining in space with a rate inversely proportional to the substrate stiffness. Hence, the more compliant the matrix, the further the displacements are transmitted, in general agreement with our findings. We also noted prominent transitions in cell morphology across stiffness conditions, consistent with prior findings (25, 56). Notably, our finding that fibroblast-induced matrix displacements vary across substrate stiffness conditions contrasts with a previous observation that epithelial cells induce constant displacements across stiffness conditions by developing tractions in proportion to changing substrate rigidity (53).

Fig. 4.

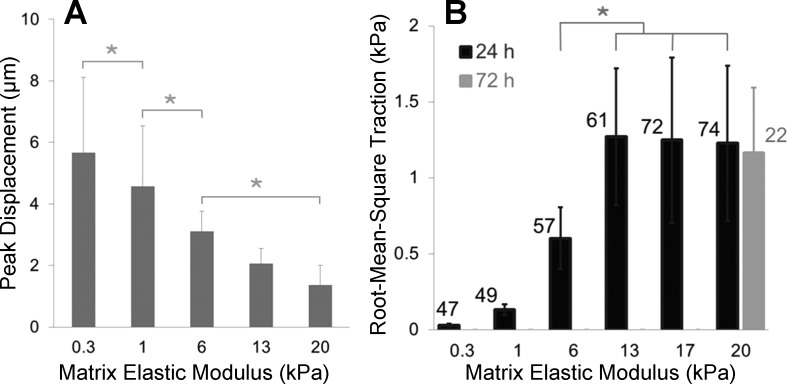
Peak displacements and RMSTs exhibit opposite trends across matrix stiffness conditions. A: bar plot showing peak displacements found in displacement fields from all cells whose tractions are reported in B. Lung fibroblasts were seeded at low density on PA substrates of discrete stiffnesses for 24 h. Data are means ± SD (n ≥ 47). Asterisk indicates statistically significant differences in peak displacements (P < 0.05, 1-way ANOVA followed by Tukey's test). B: RMSTs measured by high-throughput traction microscopy. Data are means ± SD (n ≥ 47 cells, as indicated on the chart next to each bar). Asterisk indicates statistically significant differences between RMSTs on substrate stiffness of 6 vs. 13, 17, or 20 kPa (P < 0.0001, 1-way ANOVA followed by Tukey's test). The gray bar on the right demonstrates that tractions measured on 20-kPa substrates at 72 h after seeding were statistically indistinguishable from those measured at 24 h after seeding.

On the basis of the measured displacements, we then calculated RMST from each displacement field (Fig. 3, row 3) and observed that RMST increased dramatically with matrix stiffness and reached a plateau on the substrates above 13 kPa (Fig. 4B). Interestingly, the localized pattern of tractions also varied across matrix stiffness, as visualized using the autoscaled heatmaps in Fig. 3, row 4, with the typical punctate concentration of force transmission on stiff substrates (associated with focal adhesions) giving way to a more uniform ring of force transmission on the softest substrates. Without these autoscaled heatmaps, it would be easy to assume that cells on very soft substrates do not exert any tractions (see row 3), but clearly the autoscaled heatmaps and the accompanying displacement maps in row 2 demonstrate that cell-generated physical forces are transmitted to the matrix under these conditions. Nevertheless, when we compiled data from many cells on each matrix stiffness condition, we observed that tractions were indeed increasing significantly across matrix stiffness, with a plateau on matrices of 13 to 20 kPa. Interestingly, the matrix stiffness range associated with increasing tractions encompasses the range of matrix stiffness observed in normal and fibrotic lung tissue (39). The plateau in tractions on stiff matrices prompted us to ask whether this reflected insufficient time (24 h) to maximally organize cell-matrix adhesions and the contractile apparatus of the cell (4, 16). However, when we measured tractions in fibroblasts grown on 20-kPa PA gels for an extended duration (72 h), we found that tractions were indistinguishable from those measured 24 h after seeding (Fig. 4B). On the basis of the sensitivity of our displacement mapping system (∼0.08 μm, see materials and methods) and the still sizable displacements on 13- to 20-kPa substrates (Fig. 3, row 2), we conclude that this plateau in computed tractions represents a biological response and not a limitation in our measurement system.

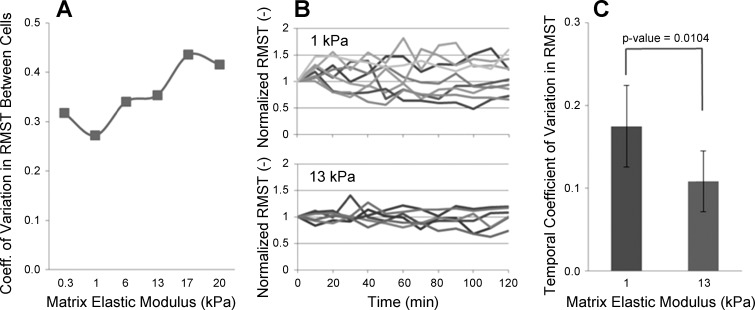
We noted in measurements of RMST that the variance in tractions increased with increasing stiffness (Fig. 4B), and this remained true, although less dramatic, when computing the coefficients of variation (CVs, standard deviation/mean) in RMST across all stiffness conditions (Fig. 5A). To address whether this increased variance reflected increased temporal fluctuations in tractions exerted by individual cells, we tracked bead displacements over time on two different stiffness substrates, with RMST calculated every 10 min for 2 h. We then normalized the tractions of each cell to its value at time zero (Fig. 5B) to better visualize how cell tractions changed over time. The resulting plots demonstrate that temporal variations in tractions are actually higher on soft matrices than on stiff matrices, and this observation was confirmed by computing the temporal CV for each cell and comparing the distribution of CVs between soft (1 kPa) and stiff (13 kPa) gels (Fig. 5C). These results demonstrate that, as matrix stiffness increases, temporal fluctuations in the traction exerted by individual cells decrease. We conclude from this finding that the larger variation in tractions observed on stiff substrates (Figs. 4B and 5A) reflects the emergence of increasing phenotypic heterogeneity (cell-to-cell variation) in cell force-generating capacity on stiff matrices that is absent on softer matrices.

Fig. 5.

Increased cell-to-cell variation in force-generating capacity emerges with increasing matrix stiffness. A: coefficients of variation (SD/mean, CVs) in RMST calculated at discrete substrate stiffnesses using the data in Fig. 4B. B: RMST time courses measured on substrates with elastic moduli of 1 and 13 kPa (9 and 6 cells, respectively), with RMST for each cell normalized to its value at arbitrary time zero. C: temporal CV was calculated for each cell shown in B based on the SD and mean of tractions measured over the time course. The mean and SD of the CVs across cells for the 2 stiffness conditions were then calculated and shown here. Asterisk indicates statistically significant difference in mean CVs at 0.05 level of significance (P = 0.0104, 2-tailed t-test assuming unequal variances), demonstrating lower temporal fluctuations in tractions on the stiffer substrate.

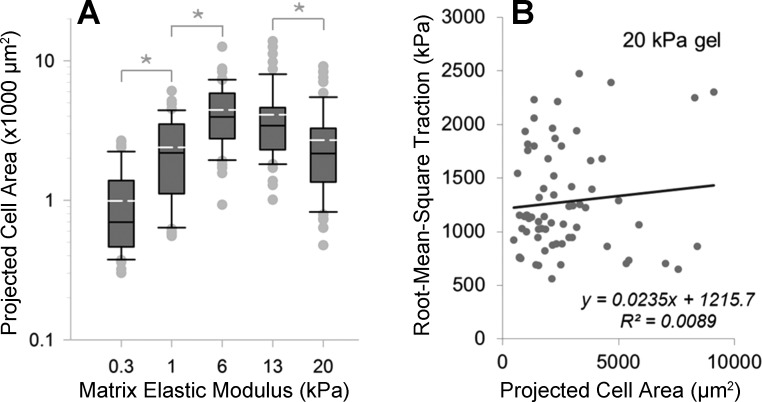
Previous work has suggested a link between cell spread area and tractions (40, 46). As we had already observed changes in cell spreading with stiffness (Fig. 3, row 1), we compared RMST to cell area in our experiments. The median 2D projected area of cells peaked at 6 kPa (Fig. 6A) in IMR-90 cells, with considerable variation in cell area within each stiffness condition. Regression analysis of the relationship between projected cell area and RMST on 20-kPa gels demonstrated no significant correlation between these features (Fig. 6B), a result that is in agreement with an earlier report on fibroblasts by Chen et al. (10) and contrary to previous findings in smooth muscle and endothelial cells (8, 46, 59). The absence of any correlation between RMST and 2D spread area extended to the other matrix stiffness conditions we studied (data not shown).

Fig. 6.

Cell spreading varies across stiffness conditions but does not correlate with cell-to-cell variation in tractions. A: distributions of projected cell areas for cells whose traction fields were measured across the range of substrate stiffnesses. Dashed lines within the boxes represent the means of area distributions. Boxes represent the 25th and 75th percentiles; whiskers indicate 10th and 90th percentiles. Asterisk indicates statistically significant difference between projected cell areas (P < 0.05, 1-way ANOVA followed by Tukey's test). B: linear regression model fitted to scattered data of projected cell area vs. RMST on substrates with elastic modulus of 20 kPa. 95% confidence interval for the slope of linear regression line was (−0.6031, 1.3635).

TGF-β1 treatment selectively promotes cell tractions on stiff substrates.

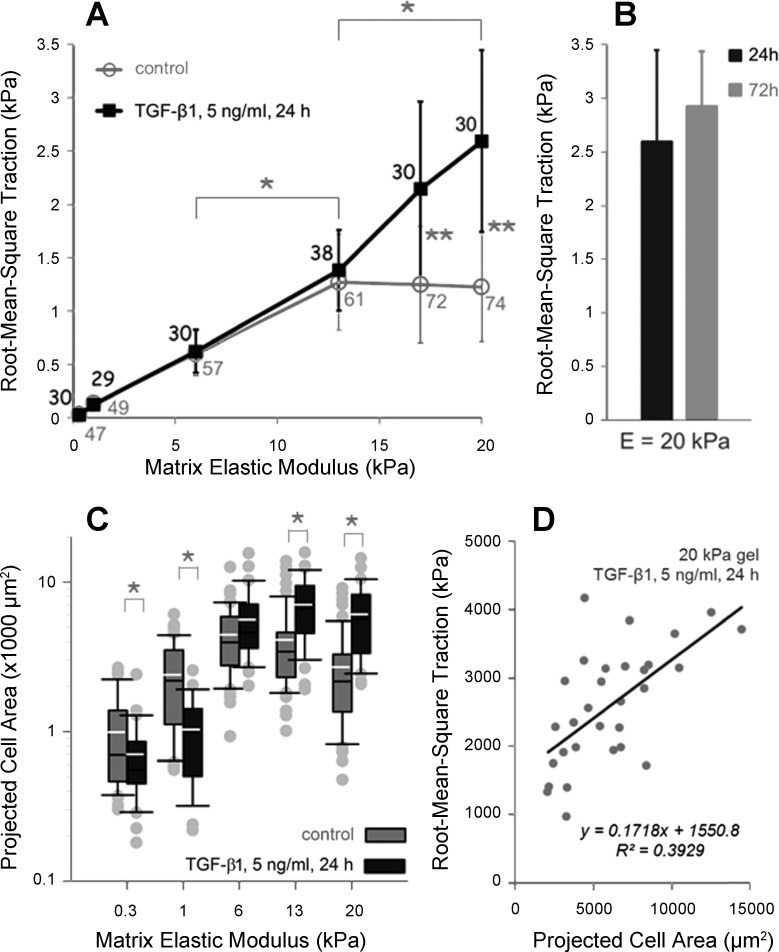
In wound healing and fibrosis, fibroblasts often express markers of a contractile phenotype including the smooth muscle marker α-smooth muscle actin (α-SMA) (33), leading them to be termed myofibroblasts. TGF-β1 promotes α-SMA expression and is thought to be the central regulator of fibroblast conversion to myofibroblast (71). When we treated IMR-90 lung fibroblasts for 24 h with 5 ng/ml of active TGF-β1, we noted a selective effect on the observed traction fields (Fig. 7A). On stiffer substrates with elastic moduli above 13 kPa TGF-β1 significantly increased RMST in proportion with increase in matrix stiffness. However, on matrices with elastic modulus of 13 kPa and less TGF-β1 did not exert any distinguishable effect on fibroblast tractions (Fig. 7A). Similar to the case in untreated fibroblasts, prolonged (72 h) exposure to TGF-β1 did not significantly alter RMSTs observed with shorter exposure (24 h, Fig. 7B).

Fig. 7.

TGF-β1 selectively promotes fibroblast tractions on stiff matrices. A: IMR-90 fibroblasts were seeded on PA substrates of discrete stiffness and treated with 5 ng/ml of activated TGF-β1 for 24 h. RMSTs computed for treated cells across 6 stiffness conditions are shown (dark line). Data are means ± SD (n ≥ 29 cells, as indicated on the plot next to each data point). As a comparison, data from untreated controls are replotted from Fig. 4A (gray line). Asterisks indicate statistically significant differences between RMSTs both within (*P < 0.01, 1-way ANOVA followed by Tukey's test) and across (**P < 0.0001, 2-tailed t-test) treatment conditions. B: Bar plot of RMSTs measured on PA gel substrates with Young's modulus of 20 kPa, 24 (dark) and 72 (gray) h after treatment with 5 ng/ml of TGF-β1 (P = 0.0723 vs. 24 h, 2-tailed t-test). C: distributions of projected cell areas of fibroblasts treated with TGF-β1 (gray boxes) across the range of substrate stiffnesses. As a comparison, distributions of projected cell areas of untreated controls are replotted from Fig. 6A (dark boxes). Asterisk indicates statistically significant difference between projected cell areas in TGF-β1-treated cells vs. controls (*P < 0.05, 2-tailed t-test). D: linear regression model fitted to scattered data of projected cell area vs. RMST from the fibroblasts treated with TGF-β1 and cultured on the substrates with elastic modulus of 20 kPa. 95% confidence interval for the slope of linear regression line was (1.1862, 3.3870).

Based on a previous observation that TGF-β1 treatment promotes cell spreading (16), we measured the 2D projected area of cells exposed to active TGF-β1 for 24 h. Compared with untreated controls, TGF-β1 treatment increased 2D projected area of cells grown on stiff substrates but decreased 2D area of cells grown on soft substrates, demonstrating another matrix stiffness-specific effect (Fig. 7C) of TGF-β1 stimulation. In contrast to our prior observation in untreated fibroblasts (Fig. 6B), TGF-β1-treated fibroblasts exhibited a modest positive correlation between 2D projected area and RMST on 20-kPa gels (Fig. 7D).

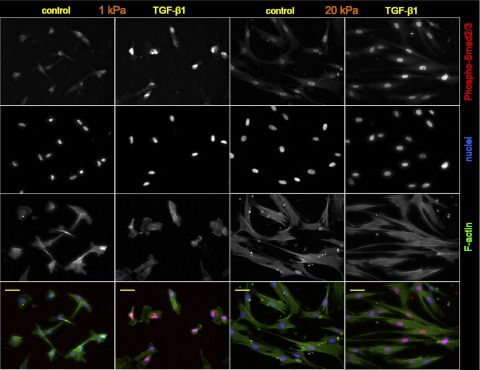
Because TGF-β1 effects are known to be mediated by rapid phosphorylation and nuclear translocation of Smad2 and Smad3 (19, 42), we further tested whether soft matrix conditions suppress transduction of TGF-β1-induced Smad signaling. As our immunofluorescent staining illustrates, treatment with TGF-β1 (5 ng/ml) induced prominent phospho-Smad2/3 nuclear localization on both soft and stiff matrices (Fig. 8, Table 1). Thus fibroblasts resident on both soft and stiff matrices are capable of transducing TGF-β1 stimulation into Smad activation, suggesting that downstream signal processing and/or alternative pathways must be responsible for the stiffness-specific effects of TGF-β.

Fig. 8.

Phosphorylation of SMAD2/3 on soft and stiff matrices. Confocal immunofluorescence images of serum-starved IMR-90 fibroblasts grown on PA substrates with elastic moduli of 1 kPa (columns 1 and 2) or 20 kPa (columns 3 and 4), untreated (columns 1 and 3, control) or treated (columns 2 and 4) with human TGF-β1 (5 ng/ml, 45 min). The cells were stained for phospho-Smad2/3 (red), F-actin (phalloidin, green), and nuclei (Hoechst 33342 counterstain, blue). Scale bars = 50 μm. Results from multiple images are summarized in Table 1.

Table 1.

Normalized phospho-Smad2/3 nuclear staining intensity

Elastic Modulus	Treatment	Fluorescence Index
1 kPa*	control	1.610 ± 0.196 [171]
	TGF-β1, 5 ng/ml, 45 min	2.157 ± 0.236 [160]
20 kPa*	control	1.643 ± 0.076 [128]
	TGF-β1, 5 ng/ml, 45 min	2.027 ± 0.293 [161]

Data are given as means ± SD (a.u.) calculated from 15 images for each combination of stiffness and treatment conditions. Values in brackets are numbers of cells included in analysis.

^*Indicates statistically significant difference between means (controls versus treated cells) at 0.05 level of significance (P value <0.001, two-tailed t-test).

DISCUSSION

Traction microscopy is a valuable tool for studying force-generating and contractile cell behaviors. To improve the throughput of this technique, we first revised the typical experimental setup (14) by replacing fluorescent beads embedded into PA gel with sulfate modified fluorospheres attached to the gel surface. This modification, in conjunction with automated microscope stage positioning and an autofocusing-capable imaging system, enabled tracking of multiple cells in multi-well formats in a single experiment, greatly expanding the potential throughput for measuring cell tractions. Because constrained FTTC estimates traction fields by solving a mixed boundary value problem, where tractions outside the boundary are nonexistent (7), the method requires defined coordinates of the cell boundary. Outlining the cell boundary is typically performed manually by tracing from phase-contrast images (7, 14). To streamline that process, we transduced the cells with a fluorescent construct, which provided an effective method for introducing a membrane-targeted label within living fibroblasts. Transduction efficiency, estimated to be >80%, and high-contrast fluorescent images made it possible to employ a simple image-processing technique to efficiently extract the boundaries of cells.

We combined these improved methodologies to measure tractions exerted by IMR-90 lung fibroblasts across a range of substrate stiffness conditions encompassing the mechanical properties measured in normal and fibrotic lung tissue (39). Our traction measurements confirmed previous findings that tractions gradually rise when substrate stiffness is increased (8, 48, 67) and demonstrated the profound influence that substrate stiffness, within the range observed in normal and fibrotic lung (39), exerts on fibroblast contractile function. Interestingly, fibroblast tractions reached a plateau on substrates approximating the stiffness of fibrotic lesions (Fig. 4B), indicating that otherwise unstimulated fibroblasts have a limited capacity for force generation that is reached within pathophysiological matrix stiffness conditions. On the other hand, the relatively small tractions on soft matrices were sufficient to produce prominent substrate deformations (Figs. 3 and 4A), demonstrating the ability of lung fibroblasts to participate in matrix rearrangements even within the compliant mechanical conditions present in normal lung parenchyma.

In addition to increasing tractions, we observed increasing cell-to-cell variations in traction with increasing matrix stiffness (Fig. 5). Wrobel et al. (69) previously showed that dermal fibroblast tractions vary not only with matrix stiffness, but also in time. Hence, we investigated whether increasing cell-to-cell variability could be accounted for by increasing temporal variations in tractions with increasing stiffness. Instead we observed the opposite trend, with greater fluctuations in tractions on compliant matrices and smaller fluctuations on stiffer matrices (Fig. 5). These trends suggest that the fibroblast actomyosin machinery, or its linkage to the extracellular matrix, is less stable on compliant matrices, resulting in greater variation in force transmission to the matrix; also these trends are consistent with prior observations that cytoskeletal architecture and cell-matrix adhesions become increasingly organized with increasing stiffness (15). We interpret these findings to indicate that the increasing cell-to-cell variability in tractions that emerges with increasing matrix stiffness must therefore represent phenotypic heterogeneity in capacity to generate forces among individual fibroblasts, governed by variations in the expression and organization of contractile machinery and the activity of pathways regulating contractile machinery function. Our results suggest that these cell-to-cell variations are largely masked on more compliant matrices by the fact that tractions there are limited more by formation and reinforcement of cell-matrix adhesions, which function more uniformly across individual cells. It will be interesting to study in greater depth whether traction generation represents a stable and persistent phenotype in individual cells and what molecular constituents [e.g., α-SMA (30, 31)] and pathways are most responsible for variations in tractions.

Prior studies have indicated a correlation between projected cell area and average traction (8, 46, 59) in smooth muscle and endothelial cells. However, in our study of human lung fibroblasts under baseline culture conditions, we did not observe any correlation between projected cell area and RMST (Fig. 6B), in agreement with a prior report in corneal fibroblasts (10). However, we did observe a correlation between projected cell area and RMST in lung fibroblasts after TGF-β treatment (Fig. 7D). Together, these findings suggest that the correlation of cell spreading with traction is a cell-type-specific phenomenon, and, although this correlation is absent at baseline in fibroblasts, it can be induced with TGF-β. Whether the changes in cell-projected area under such stimulation are functionally linked to, and not just correlated with, the organization of contractile machinery discussed above remains to be determined, although prior work has indicated an intriguing relationship between cell-matrix adhesion size, contractile protein organization, and resulting tractions (26).

Although multiple soluble factors may contribute to contractile activation of lung fibroblasts, we focused on the effects of TGF-β1, a dominant profibrotic mediator implicated in the expression of the myofibroblast phenotype, on fibroblast contractility. Previous experiments, conducted mostly in 3D collagen gels, have shown that TGF-β1 enhances contractility in fibroblasts (3, 5, 20, 22, 27, 34, 35, 44) and other cells (1, 41). In our experiments, even though TGF-β1 triggered phosphorylation and nuclear translocation of Smad2/3 that was indistinguishable on soft and stiff substrates, we found that TGF-β1 selectively increased cell-generated tractions only on stiff matrices. The substantial rise in tractions on stiff gels occurred within 24 h of TGF-β1 treatment and was not further augmented by prolonged stimulation for 72 h (Fig. 7B). Intriguingly, our results suggest that alterations in matrix stiffness may selectively couple and uncouple TGF-β1 signaling from integrated cellular functions such as matrix contraction.

Although somewhat speculative, one potentially interesting implication of these findings relates to cell traction-mediated activation of latent TGF-β1. Prior work has shown that cell-generated mechanical forces play a critical role in triggering bioavailability of active TGF-β1 from its extracellular matrix-bound latent complex (2, 6, 54, 68), and a recent study of latent TGF-β crystal structure by Shi et al. (54) identified the preferred orientation of force that is needed to unfasten the “straitjacket” that encircles each TGF-β monomer. Buscemi et al. (6) recently estimated that ≈40 pN force is needed to release TGF-β from the latency associated peptide, and this force is in the range of reported values that individual integrin molecules are able to support (45). Although it is difficult to translate our whole cell traction measurements to force per molecule, we observed that tractions reach 2,000 Pa (or 2,000 pN/μm²) in isolated areas on matrices of 6 kPa (Fig. 3, bottom row), with higher and more frequent high-traction values observed on stiffer matrices (4,000 to 6,000 Pa peak tractions). On the basis of one estimate by Patla et al. (49) that the number of cell-substrate-interacting structures is ≈170 per μm², if we assume equal force bearing in parallel across 170 linkages, local tractions of 2,000 Pa would translate to 12 pN/molecule, with 24 and 36 pN/molecule forces associated with 4,000 and 6,000 Pa tractions. These higher values are similar to the estimate of force needed for TGF-β activation (40 pN). Consistent with these estimates, Wipff et al. (68) observed a modest matrix stiffness-dependent increase in fibroblast activation of TGF-β1 of ≈1.3-fold between 5- and 20-kPa substrates. Because the latent complex is in mechanical series with extracellular matrix, they suggested that substrate rigidity must be high enough to resist the cell-generated tension and allow for liberation of TGF-β1. Upon thrombin stimulation, to induce fibroblast contraction, they observed increased TGF-β1 activation on 20-kPa matrices by ≈1.75-fold but strikingly found no effect on TGF-β activation on 6 kPa. Our results demonstrate that matrix stiffness dramatically modulates fibroblast tractions and determines whether an exogenous stimulus, in our case TGF-β1, augments cellular force transmission to the matrix. We show that fibroblasts residing on a stiff matrix exert significantly higher tractions at baseline than cells residing on a more compliant matrix, and their RMST is augmented by exogenous TGF-β1 stimulation by ≈2.1-fold on 20-kPa gels. Hence, uniting our observations with the known tension-dependent activation of TGF-β1 and its broad functional fibrogenic effects supports the concept that TGF-β1 and fibroblast contractile function could engage in an adverse feedback cycle of increased fibroblast activation on stiff matrices, promoting and sustaining a profibrotic environment in the lung. In contrast, the low endogenous force-generating capacity of fibroblasts on soft matrices and the failure of exogenous TGF-β1 stimulation to augment tractions in such a context could provide a powerful homeostatic mechanism to suppress such an unstable feedback cycle, providing the lung, by virtue of its normally compliant matrix, with an endogenous brake on TGF-β1-mediated fibrogenic processes. Hence the underlying matrix stiffness in the lung may be a critical determinant of whether TGF-β1 stimulation results in a transient or self-sustaining fibrotic response.

How TGF-β1 stimulation is decoupled from force generation on soft matrices despite Smad2/3 activation remains to be determined. As discussed above, alterations in actin cytoskeleton and integrin-based adhesions with variations in extracellular matrix stiffness are widely reported and presumably play important roles in limiting contractile force generation on soft substrates (45). Consistent with a necessary role for matrix adhesions in enhancing force generation, we observed that cells grown on soft substrates responded to TGF-β1 treatment by reducing their 2D spread area, suggesting that instability of focal adhesion complexes on compliant gels (4, 24, 32, 60) may prevent fibroblasts from exerting increased tractions. In contrast, on stiff matrices, we observed that TGF-β1 enhanced cell spreading in parallel with increases in tractions.

Whereas mechanical regulation of adhesion complexes offers one perspective for understanding stiffness-dependent TGF-β1 effects, several Smad-independent or downstream signaling mechanisms may also be differentially regulated in response to matrix stiffness and play important roles in the stiffness-dependent TGF-β1 effects observed here. For instance, recent studies in aortic valve interstitial cells (11) identified β-catenin as a key stiffness-dependent cofactor for TGF-β1-induced myofibroblast differentiation. Similarly, myocardin-related transcription factors are actin polymerization-dependent regulators of TGF-β1-induced myofibroblast differentiation and α-SMA protein expression (13, 55) that may respond to variations in matrix stiffness. A recent study also identified the transcription factors YAP and TAZ as sensors of matrix stiffness (17), and in separate work TAZ has been shown to control Smad nuclear shuttling and the duration of TGF-β signaling (63, 64). Clearly, Smads can bind to a high number of Smad-interacting proteins (12), many of them transcription factors, but their role in Smad-controlled target gene transcription has not been extensively studied in the context of matrix stiffness and fibrosis. Investigating matrix stiffness-modulated cross-talk between TGF-β1 signaling and multiple interacting pathways will likely be necessary to reveal a fuller picture of how matrix stiffness modulates fibroblast function and TGF-β1 responsiveness.

Taken together, our study validates improved methodology for higher-throughput traction measurements and illustrates the utility of such methods for investigating contractile responses of single cells. In combination with already developed methods for casting PA gel substrates in multiwell formats (43), our traction methodology has the potential to be applied in small-scale screening of drugs and reagents that may affect cytoskeletal tension and its transmission to extracellular matrix. Our findings demonstrate that matrix stiffness is a pivotal regulator of fibroblast contractility and the contractile response to TGF-β1 stimulation. When combined with prior evidence for force-dependent TGF-β1 activation, our results suggest that a mechanobiological traction-feedback loop may promote the fibrogenesis observed in stiff fibrotic lesions, whereas normal lung compliance may protect against such an adverse feedback response. Understanding the mechanisms involved in maintaining fibroblast quiescence and low tractions on soft matrices and further elucidation of the pathways linking mechanoresponses on stiff substrates to fibrogenic fibroblast activation may result in new avenues for intervening in pulmonary fibrosis. The improved methodology developed here for higher-throughput study of fibroblast tractions provides an important step forward and should accelerate such efforts.

GRANTS

Support for this study was provided by National Institutes of Health Grants RO1HL092961 and T32HL007118.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

Author contributions: A.M., J.D.M., and D.J.T. conception and design of research; A.M., J.-A.P., and F.L. performed experiments; A.M., J.-A.P., F.L., and D.J.T. analyzed data; A.M. and D.J.T. interpreted results of experiments; A.M. prepared figures; A.M. drafted manuscript; A.M., J.D.M., J.-A.P., F.L., and D.J.T. approved final version of manuscript; J.D.M., J.-A.P., F.L., and D.J.T. edited and revised manuscript.