Predictive Modeling and Integrative Physiology: The Physiome Projects

Abstract

The fundamental paradigm in physiological research is integration. Biological researchers are now ready to define for a species a mathematical construct, the Physiome, the all-encompassing quantitative model of an organism. The goal of the human Physiome project is improved health care, through deep understanding of the organism, all the way down to the genes, reconciling contradictions and clarifying cause and effect. The strategies for accomplishing this long term aim include the systematic gathering of old and new knowledge into shared databases, and integrating the information into self consistent, reproducible, mathematical models. Multiscale models, for practicality, cover only a few levels at a time. Beginning at the middle level, the cell, where the knowledge base is largest and most secure, and the elements well defined as functional biophysical/biochemical modules, the plan is to work up to the organism level and down to the gene level, in the end providing clear linkages between phenotype and the genome.

INTRODUCTION

Since the time of Hippocrates a goal of medicine has been to understand the causes of illnesses and to learn methods for guiding therapy. Hippocrates was an astute, observant physician, but his emphasis on science was based on anatomy and on looking at the balance of the four humors (earth, air, fire, water) in the patient. Galen’s anatomic and medical teachings went further, but therapy was mostly by empiricism and doctrine. The thinking on medical treatment through understanding physiology of the body’s systems began really with Harvey [1], whose analysis and logic revealed the workings of the circulatory system. From the recent decades of molecular biology, the genome and the proteome, we now dream that medical therapy can be developed scientifically by creating an understanding of physiology from genome to phenotype, and serving in the delivery of personalized medicine: the treatment of the individual through that person’s genomics, physiology and pathophysiology. This is the Physiome Project.

Here we examine the questions of whether the dream can be made realistic and how the development of the Physiome Project would contribute. First, a definition: The Physiome of an organism is the integrative, quantitative description of the functional state of that organism from the regulation of genomic transcription and cellular biochemistry and biophysics to the behavior of the organism as a whole. In its ultimate but rather distant form it should provide the basis for predicting the remodeling of structures and functions in response to injury, drugs and time. It should link genotype and environmental influences to the phenotype in health and disease, and indeed serve as the basis for personalized medicine. Now, what has to be accomplished to make this scenario realistic?

CONSTRUCTING THE PHYSIOME

The underlying concept on which the physiome rests is that biology can be considered as explicable in terms of physics and chemistry, that is, as mechanical and biochemical processes. The belief in “vitalism,” the idea that there exists a life-force unique to living organisms that cannot be explained by physics and chemistry, is relegated to history. Explanations therefore will be expressible in mathematical descriptions of the physics and chemistry. As knowledge advances and as quantitative explanations are developed, contradictions and inconsistencies will be found and then, through experimentation or observation and analysis, resolved.

A prime vehicle for the development lies in considering hypotheses in quantitative terms, as mathematically definable, precise statements representing the physics and chemistry: mathematical models. The approach inspired by “Strong Inference” [2] is to strengthen the power of an experimental test by figuring out an alternative hypothesis, one as strong as the initial hypothesis, and then designing and executing the experiment that will distinguish between the two. (Using the pair of computer models representing the two hypotheses to define the experiment and to understand the error space and sensitivities is highly efficient.) The results of the experiment must relegate at least one hypothesis, maybe both, to the dust-heap. As T.H. Huxley put it, “The great tragedy of Science: the slaying of a beautiful hypothesis by an ugly fact.” The repetition of hypothesis development and its refutation by disproof defines the progress of science. In this sense the Physiome strategies will satisfy the pure scientist even before aiding the clinician. And the “strong inference protocol” is not only good in the lab, but in the classroom as well [3].

Biology is multiscale. Start analyzing at any level, and one finds that another level impacts the situation. The electrophysiology of an isolated excitable cell can be expressed accurately in terms of the time- and voltage-dependence of a finite set of ion channels and ion pumps and exchangers. But put that cell into its normal habitat, and one has to consider capacitance coupling and even gap junctional connections with neighboring cells of the same or different types. The propagation of excitation within the myocardium depends on lots of details, for example, cell fiber direction and the degree of cell-to-cell coupling, and then, complicating it further, how the degree of cell stretch as shortening occurs and force is developed changes the conductance of calcium channels and influences the form of the action potential. At a yet higher level, the compliance and reflected pressure waves in the aorta affect the myofilament shortening and the stretch. Other organs are at least as complex. The sheer magnitude of the multiscale system, from gene, protein, biochemical system, cell, organ, to organism, is a challenge to experimenter, to analysts and the would be multiscale modelers. The Physiome Project is a very long-term effort.

PREREQUISITES FOR THE PHYSIOME PROJECT

What is needed to reach the goal? The scope of the effort is inevitably international, so in addition to accomplishing experimental and analytical research, communication amongst investigators should be free, flexible and unconstrained. Many issues are involved. I classify the issues as scientific, sociological, and political: scientific because the biologists and mathematicians are the ones needed to do it even if some of it is just hard work, filling in the chinks in the edifice of knowledge, sociological since it must involve not only social interactions amongst scientist but be understandable and supportable by others, and political, since the expense is considerable and the rewards are for the whole of society. My list of particulars is in Table 1.

Table 1.

Efforts Required for the Physiome Projects

Scientific: New experimental studies, hypothesis driven, to elicit specific information on which to base the understanding of biological systems. Databases for protein dynamics, biochemical and physiological systems, cell biology, and organism level information. Models integrating the information on proteins, cells and systems and databases of running, documented, validated models. Ontologies: explicit naming systems for anatomy, physiological data, chemical and physical terms

Sociological: Free exchange of scientific information. Open source: information on models, algorithms, hypotheses, tools, data. Standards: ontologies, databases for structures, experimental observations, models in archival and reproducible operational form, Sharing: Total honesty, revealing everything, and transparency.

Political: Support for integrated development and translation into applications Establish and support databases. (structure, material and chemical properties, and experimental data on physiological functions, and the models to capture the essence of the data. Support for multi-institutional collaborations including industry Emphasis on reproducibility in science in general and modeling in particular.

For the science the databasing of biological information is essential to making progress. The integrators of the information are detailed, thermodynamically, chemically, and mechanically correct, mathematical models. They individually may be describing anything from the behavior of individual proteins to that of cellular biochemical systems, cell and tissue mechanical systems. Models must include the information transfer systems for immune system cells, hormones and neural impulses throughout an organism. Ultimately they must describe the overall functions of the body during daily activity, and explain the mechanisms and time course of recovery from injury. Understanding the robustness of the body’s responses to perturbations and refining the predictability of responses to interventions will play a role in personalized medicine.

The practicalities require organized capturing of a huge range of information not previously attempted: detailed anatomic and physiological data over a lifetime; the mechanical, chemical, and physical attributes of cells, tissues and organs; assessing and curating the data; making the data accessible; constructing the models to consistent standards; providing detailed descriptions and operating manuals for each model, assuring that the models are reproducible by others. While acquiring experimental data and related information sets is a part of the normal expectation for a research project, the further effort to archive and disseminate the results is only now being recognized as critical to the advancement of the science and the application to bettering health care.

WHY THE PHYSIOME?

Individual organs like the heart and lungs comprising the circulatory systems are inevitably complex and multiscalar, composed of elements of diverse scale: molecules, cells, tissues and organs, arranged spatially in a hierarchical fashion [4]. To model such systems requires linking together different types of structures and functions at the various levels. It is possible to model at the organ and system levels in ways similar to the molecular and cellular levels, using descriptive ordinary and partial differential equations. There are huge incentives to bring these levels together, from the organism down to the regulation of transcription: the reward is the understanding of nature and the power to intervene on behalf of the health of individuals and of the society. Intrinsic to the effort is the search for scientific understanding, for determining cause and effect relationships in complex networks, identifying the cascades of linkages between genome, environmental influences, and the healthy or diseased phenotype.

These purposes are embodied in the definition of the Physiome: it is the quantitative description of the functioning of the living organism, expressed in reproducible mathematical terms and provided in open source as models of biological systems forming a basis for the operational management of experimental research and of patient therapy and disease prevention. The Physiome Project has been underway for a long time, the most definitive beginning being the concepts of Claude Bernard [5], who wrote of the regulation of the “milieu interieure,” the internal state in a healthy humoral balance, “homeostasis,” as being the central objective of integrated regulation in human physiology [6].

Physiological science has been peppered with mathematical models and quantitative analyses since the time of Harvey [1], but deliberate attempts at large scale analysis came only after many biophysical and biochemical models had already come into use. Key models in electrophysiology of the nerve [7] and cardiac cells [8] demonstrated how complex signals could be parsed and identified in terms of ion-selective channel conductances. Guyton et al. [9] demonstrated the overall behavior of the cardiovascular system in regulating blood volume and blood pressure; this model, though incorporating merely descriptive functional relationships instead of well-researched biophysical/ biochemical operators in quite a number of places, worked well in approximating the real system over both short and long times, minutes or weeks. This was not recognized by the scientific community for the milestone that it was, simply because it used these “incorrect” empirical relationships. If one thinks of these artificial, descriptive relationships simply as holding places and markers identifying gaps requiring definitive explanation, pointing the finger at necessary further experimentation, then the Guyton model, though incomplete like all models, can be seen as a legitimate stepping stone in the river of science.

There are innumerable examples of thinking on the systems level. Stephenson [10–12] and Zierler and colleagues [13–15] used engineering strategies in examining mass transport in the circulation, ideas similar to those of Danckwerts [16] and of Shinnar and Naor [17] on chemical reactors. Chinard [18], Goresky [19] and Crone [20] pioneered the idea of obtaining multiple data sets simultaneously in order to ascertain mechanisms of solute transport through an organ, stimulating my thinking on integrated approaches [21, 22]. Putting these kinds of ideas together in the broader context of biology and bioinformatics, on the occasion of lecturing at a drug design conference in 1990 I had the temerity to suggest a strategy for identifying the side effects of drugs by prediction from their binding characteristics. The idea was to formulate a broad quantitative approach to biochemical systems, in order to predict sites of drug interactions with proteins. I called it the Physionome Project [23, 24]. This name was cumbersome. In discussions with Ewald Weibel, who became the president of the International Union of Physiological Sciences (IUPS), we shortened it to Physiome, loosely translated as “life as a whole.” The IUPS backed the general idea and assisted by asking me to form a new Bioengineering Commission in 1993. The formal kickoff was a satellite meeting to the 1997 IUPS Congress at St. Petersburg, Russia, “On designing the Physiome Project.” The second formal Physiome meeting was in Seattle in 1999, this time with full, written reports [25]. With modern computation and the immense numbers of discoveries in genomics and cell biology and physiology, what was only a dream in the early ‘90s is now formally identified effort worldwide as the Physiome Projects [26–28]. The plural form is used in accord with the reality that there are many projects independently initiated and funded that contribute to what is really still mainly a grass roots program. Noble’s beautiful monograph, “The Music of Life” [29], puts it in the context of modern biology, persuasively arguing that regulation of genome and proteome require accounting for the influences of environment and behavior, integrating over the whole of the organism and its development over time.

By this time there were a good many projects in integrative systems biology and physiology, but identification of the Physiome and its mission using quantitative modeling as a key element in the program followed slowly. The first of the projects including the name Physiome was ours at the University of Washington (www.physiome.org); the National Institutes of Health (NIH) supported this first through the National Center for Research Resources (NCRR) and then through the National Institute for Biomedical Imaging and Bioengineering (NIBIB). It was soon followed by the IUPS Physiome Project, sited at Auckland University (www.physiome.org.nz) and supported primarily by the Wellcome Trust. These sites also present archives of a few hundred models. Ours are written in JSim’s Mathematical Modeling Language (MML). MML is easily read by humans since it is just the equations (Ordinary Differential Equations ODEs, Partial Differential Equations PDEs and Differential Algebraic Equations DAEs). JSim's models, captured in project files with all the parameters, graphs, optimizers and numerical solvers, can also be run over the internet at www.physiome.org. The IUPS site’s markup form, CellML, stores ODEs and DAEs in a physiologically oriented Extensive Markup Language (XML) variant; these structured files are downloadable into various computational languages, including JSim and Oxford’s Physiological Computing Environment (PCEnv) for solving and display. The European Bio informatics Institute (EBI http://www.ebi.ac.uk/biomodels-main/static-pages.do?page=home) and JWSOnline (http://jjj.biochem.sun.ac.za/index.html) present many downloadable biochemical system models archived in Systems Biology Markup Language (SBML).

In 1998 NIH’s National Institute of General Medical Sciences (NIH/NIGMS) led the nation’s funding agencies in inviting applications for programs in integrative, quantitative biology. There has been a gradual but strong development of Physiome-type efforts since. The initial NIGMS-funded grant programs in integrative systems paralleled some modeling efforts supported by National Center for Research Resources (NCRR), though this agency’s focus was more on the technology than the science. With the shifts in allocation of funds within NIH in 2002, most of the modeling-oriented NCRR programs were moved into a new institute, National Institute for Biomedical Imaging and Bioengineering (NIBIB). By 2003, the NIBIB was taking a leadership role in establishing the Interagency Modeling and Analysis Group (IMAG, www.nibib.nih.gov/research/multiscalemodeling/imag), centered on developing multiscale modeling. Starting with collaboration initially amongst nine NIH institutes and three National Science Foundation (NSF) directorates, IMAG later included National Aeronautic and Space Administration (NASA), Department of Energy (DOE), Department of Defense (DOD), Veterans Affairs and the Department of Agriculture as well as eight additional NIH Institutes under the spirited leadership of NIBIB’s Grace Peng. IMAG serves as a coordinating body for investigators working in the field, and their website serves as a vehicle for collaborations and for the development of standards for models and for the modular construction of models.

The European Economic Commission (EEC), the first funding agency to demonstrate formal recognition of the Physiome’s potential, started Steps Toward the European Physiome (STEP) in 2003. This evolved to become the Virtual Physiological Human project (VPH hosted at http://www.vph-noe.eu/). The VPH set of projects is now being supported by the EEC to the tune of about US$100M/year, with seven major project topics and a Network of Excellence program as a coordinating body providing tools and facilitating joint efforts. The projects are linked to applications by translation to manufacturable devices or to procedural or therapeutic applications to medical care. A wide variety of industrial partners contribute to the effort and share the work. All of these have goals related to quantitative biology, though not all will end up with integrated models of biological systems.

Both IMAG and VPH are supporting the development of usable standards for the reporting, archiving and dissemination of models. This is critical for model reproducibility and sharing. Most models reported in the literature have not been fully enough described to be reproducible. There were notable exceptions: the standard set by Hodgkin and Huxley [30] was exemplary: all of the figures can be reproduced from the equations and parameters provided in the paper; the work won a Nobel Prize. The field of electrophysiology leads all others in making models available in reproducible form [31– 34]. This has not only advanced the field, but positioned it so that predictive modeling is playing an important role in new drug reviews by the Federal Drug Administration and in assessing and understanding drug effects on channel conductances, for example in cardiac arrhythmias [35].

Three particular developments are essential for advancing the quality and quantity of accomplishment in Physiome modeling. These are: (1) databases of structural and functional information to use as the basis for modeling, (2) standards for reproducible modeling, and (3) technologies for the automated combining of models or component modules, for aggregating models at the same level and for composing multiscale models of large systems.

Databases

There are excellent databases of genomic information stored as base sequences and as gene locations and sequences. These are curated and improved as more information is gathered. Proteomic information now goes beyond sequencing and into protein structures and even properties to some extent; the databases at SwissProt (http://ca.expasy.org/sprot/) and Protein Data Bank (http://www.rcsb.org/pdb/home/home.do), are exemplary. Some relatively specialized databases were developed over many years, particularly deeply for enzymes; they provided affinities and reaction rates for large varieties of enzymatic reactions. These are of great importance for biochemical modeling. The KEGG database (http://www.genome.jp/kegg/), though huge, does not lend itself very well to detailed kinetic modeling since for each enzyme one needs a lot of information not generally available on KEGG: individual on- and off- rate constants, equilibrium binding coefficients, the temperature, pH and ionic composition of the solutions where the data were obtained. The UW Physiome site also makes available over 72,000 KEGG biochemical system models, providing links to the biochemical reaction diagrams, and offering the SBML form or the JSim MML form for computation. Only a fraction of these are fully parameterized by KEGG, and often more information is needed. For phosphorylation reactions one needs also the redox state, and the concentrations of ATP and its buffers. Daniel Beard and colleagues in Biotechnology/Bioengineering at the Medical College of Wisconsin are developing a detailed database on individual enzymes, starting with those of intermediary metabolism (http://june.phys.mcw.edu/BioWiki/index.php/BISEN). These archives store information covering a range of conditions so that the equations for the complex enzymatic reactions can be developed for particular states. This is a tremendous time saver for those building multilevel models, and lends itself well to developing modules as components of complex models.

Forbes Dewey [36] gave detailed consideration to the database characteristics suited to databasing the information and models. Neither relational nor object-oriented databases are entirely suitable; the composite object-relational database is probably best. Problems remain in long term stability of the systems and in backward compatibility as they advance, a difficult issue. Given that there are databases, another approach is to use the models as entry ports to the databases, for networked connections from a model could go to many databases. This was one of the intentions of Randall Thomas. An application of this sort has been worked out amongst Thomas (in Paris), Peter Harris (in Melbourne) and Peter Hunter (in Auckland) with respect to the Virtual Kidney [37].

Standards

Developing standards is relatively straightforward for simple biochemical and biophysical models, as suggested by Table 2:

Table 2.

Checklist for Model Standards

CHECKLIST FOR MODEL AGAINST DESIRED STANDARDS: CHECK X FOR THOSE MET
Check YES (either manual or auto if standard met)	X = YES
model author = checked by author; checked within model code by math?	model author	checked in code?	Problem? Limit? Other?
Group 1: Identification and Description
1. Model Name, Key words (generic and specific)	X
2, Brief one or two line description	X
3. Detailed description, diagrams, equations	X
4. Reference to Publication describing the model	X
5. Pointer to the publication or pdf	X
6. Related Models, antecedents, comparables, and successors	X
Group 2. Model Structure and Content
1. Domain definition (cells, mito, tissues, organ system, organism)	soln		compart
2. Main variables (chemicals, pressures, etc.), with units	X
3. Parameters, with units, and with source references	X
4. Descriptions and references for subsidiary models	N/A
5. Source Code: Clear, deeply commented, explained, referenced.	X
6. Inputs and outputs defined. All nodes and edges defined.	X
7. Define linkage type (Chemical, electrical, mechanical,etc.)	X		chem
8. Ontology base for notation
9. Numerical solvers used, and conditions set	X
Group 3. Verification: math of model and solution methods are sound
1. Unitary Balance: (units on all variables and parameters)	X
2. Mass balance: (list constituents whose conservation is checked)	X
3. Charge balance: (ion currents, membrane potential)	N/A
4. Osmotic balance: (volume, total activities, fluxes)	N/A
5. Thermodynamic Balance (Haldane constraints on reactions)	N/A
6. All equations correct, units balance, with all terms defined	X
7. Numerical solutions checked against analytical solutions	N/A
8. Running code supplied in a common format	X
9. Solutions show little dependence on time or space step size	X
10. Methods for verification defined. Reference model solution?	X
Group 4. Validation: model is physiologically realistic
1. Initial and boundary conditions in accord with physiology	N/A
2. Data provided, and fitted by model	X
3. Model is predictive, shown to fit other data not used as basis	X
4. Parameters justified (sources provided) and evaluated	X
Group 5: Availability of Source Code and Forum for critiques
1. Website source from which to download model code and data	X
2. Website or email or address to accept queries	X
3. Website for public commentary and responses	X
4. References to subsequent publications or alternative models

Table 2 is an example of Standards being considered by the IMAG group of US agencies, and discussion can be found at the website for model sharing efforts (www.imagwiki.org/mediawiki/index.php?title=Working_Group_10). But for more complex models, particularly for finite element and finite volume models combining three dimensional structure and function, developing standards is more complicated since the separation between the model definition and the computational method is not so clear. The emphasis on standards is to enhance the dissemination of working models that can be thoroughly understood, taught, and reproduced. Models often need also detailed instructions on how to use them. One of our models for convection-diffusion-permeation-reaction and metabolism within an organ [38] can use, in multicapillary form, over 100,000 ODEs or equivalents and has an 80-page manual.

Modular Modeling

Large, multiscale models are naturally in a continuing state of development as research progresses. It is essential therefore to preserve the component modules separately from the comprehensive model in a form that can be easily reused in constructing the revised big model.

A model of the electrophysiology of a single cell can be composed of a set of channels, ionic pumps and exchangers. Each channel can be defined as a functional module, independent of the others. Each biophysical/ biochemical module can be coded for computation in a fashion that allows for the automated combining of independent modules into composite multicomponent models. For an electrophysiological channel module, or a passive ion exchanger, the external variables are the ionic concentrations inside and outside the cell, including H⁺, and the transmembrane potential. These define the driving force for the currents. For active transport, an ion pump for example, one needs also the intracellular ATP level to provide energy. The concentrations and the voltage also set the conditions or state of the channel protein, but its response to changing conditions is determined by the nature of the protein, its time constants and its probabilities to be in open or closed state. Ion flux through the channel induces changes in the concentrations inside and outside; concentration changes do not affect the parameters of the channel kinetics, but a change in transmembrane voltage does. So each module can be constructed as having separable “connectors” to its surroundings, and stably functional internal machinery, whose coding need have no connection with the code for the changing concentrations.

It is possible to build a multicomponent single scale cell electrophysiological model from the elemental modules in automated fashion by pulling the modules from a preconstructed library and parsing them to ascertain the common variables. The integrated cell model provides the external and intracellular conditions to the module. The module, e.g. a channel, through its internal code supplies its response, the time- and voltage-dependent channel conductance. The driving forces determine the current flux through the particular module and through the other modules and therefore govern the rates of change of driving forces. Building a multicomponent biochemical reaction system is done in an analogous fashion: the enzyme affinities and rate constants are in the module’s internal code, and the substrates, ions, pH and temperature make up the driving conditions for the flux. Beard’s Biochemical Simulation Environment (BISEN http://bbc.mcw.edu/bisen) will provide the detailed description of a module for each enzyme.

A cell model performs as the integrator of the activities of its biophysical and biochemical modules and the resultant fluxes. Different cell types can be composed of the same modules, but with differing proportions. For example, a cardiac sinus node cell has fewer fast sodium channels and more calcium channels than a cardiomyocyte from the left ventricle.

When one considers the cell as a component of the heart, and introduces receptor activation or drug delivery as another layer of control over cell behavior, these affect the responses of certain modules. The cell model is then a component of a multiscale model, and its behavior is changed by these agonists or drugs. The fundamental point is that the responses are at the level of protein functions within the cell or cell membrane. We can generalize: the robustness of an organism always involves changes in the operating characteristics at the cellular level and involves changes in the dynamics of the proteins.

Changes in the general activity level of a cell can be counted on to be followed by changes in the rates of transcriptions of cellular proteins. All proteins break down with time, natural proteolysis or enzymatic degradation. (Enzymes are degraded more rapidly when they are not bound to a substrate molecule, so diminish their concentrations when not much in use.) Exercise training builds muscle, increasing the concentrations of myofilament proteins, inferring that their transcription rates are increased. Thus organism level behavior regulates gene utilization, not the other way around. We would consider the modules for regulation of transcription to be driven by signals derived ultimately from the needs of the organism but delivered to the genetic machinery by messengers inside the cell.

From the point of view of building the Physiome or the VPH as a mathematical construct, the natural place to start is at the cell or perhaps tissue levels [28, 39]. These are the levels needed to put organ and high level systems (humoral and endocrine) on a solid biochemical/ biophysical basis. The cell level is, in the adult, certainly and probably all through development, the regulator of gene expression and transcription. This is the middle level, the level at which our knowledge of biology is on its firmest setting. Consequently the Physiome should be built “from the middle out”; ultimately this “middle” will link genotype to phenotype and phenotype, environment, and activity to gene expression. The pathways of understanding from gene to phenotype, i.e. from control of transcription through to system behavior run up and down the multiple levels through the cell.

An Example of a Strategy in Modeling Analysis of Experimental Data

In the whole organ approach to cellular metabolism, recognizing that the processes of capillary permeation, cellular entry, and intracellular reaction kinetics are complex and vary from organ to organ, we try to apply a set of principles unifying the approaches to elucidating the kinetics of these processes [4, 38, 40]. The general approach to endogenous metabolism has been to carry out tracer transient studies during each of a variety of steady states at different concentrations, and for xenobiotics, to study the disposition of tracer under a variety of circumstances such as different steady-state bulk concentrations, using samples from inflow, outflow, and the tissue itself.

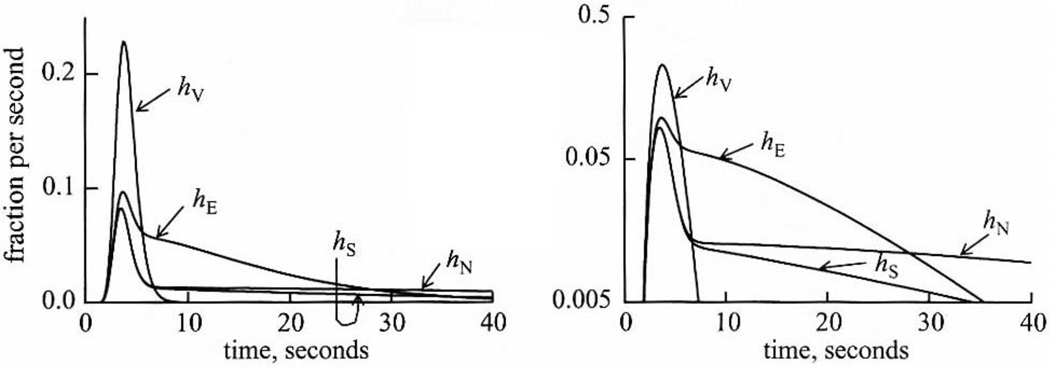
To study processes in vivo, the relatively non-invasive multiple-indicator dilution technique, introduced by Chinard et al. [18] has been the approach of choice for high resolution studies of intraorgan transport and metabolism in vivo. Mostly it has been applied to isolated organ studies [41] or animal studies [19] and is well worked out. It is based on the use of multiple simultaneous controls, each being represented by the transient response to a molecule similar to the targeted solute S. For studying capillary permeability, the tracer substance under study, S, and a reference tracer, V, which does not escape from the capillary plasma, are injected together intra-arterially, and the pair of outflow dilution concentration-time curves are recorded by rapid sampling. From a model-based comparison of the outflow patterns for the two substances, the capillary permeability-surface area product PS of solute S can be deduced [20, 42]. If S enters tissue cells, a second reference needs to be added to the injection mixture, a substance that enters the interstitial space but does not enter the tissue cells, solute E, for extracellular. The reference substances are chosen so that their kinetics match those of solute S as closely as possible. One, however is restricted to being carried within the vascular space (solute V). Another is restricted to the extracellular space (solute E). A third reference solute N is transported across cell membranes like S but is not metabolized, unlike S; it serves as to define the transporter characteristics. Idealized time courses, model solutions following bolus injection of the four tracers into the inflow to an organ are shown in Fig. (1), an idealized situation using a 4-region model of capillary blood, endothelial cells, interestitial fluid, and parenchymal cells [43]. The modeling uses the same intravascular transport of all four solutes, described by the vascular impulse repsonse course h_v(t). The same interendothelial PS is used for solutes E, N and S. The same cell membrane transporter parameters are used for N and S. Through these controls the intracellular reaction rate for S is clearly identified, distinct from all of the other processes leading to that reaction.

Fig. (1).

The Ideal Multiple Indicator Dilution (MID) experiment, an example of multiscale modeling: (left panel: linear scale; right panel: semilog scale) A set of 4 indicators are injected as a bolus into the inflow. The impulse response function, h(t), is subscripted: S is the solute of interest metabolized intracellularly, N is its non-consumed analog that is also transported; E is the extracellular reference and V the intravascular one. E compared to V gives capillary permeability. N compared to E gives cell permeability, S compared to N gives intracellular metabolic reaction rate. The levels of modeling cover intracellular reaction sequences in two cell types (endothelial cell and the tissue’s parenchymal cells) and two extracellular spaces, the plasma and the interstitial fluid space. The processes include convective transport along a spatially distributed capillary-tissue exchange unit, axial diffusion, radial permeation via passive and transporter-mediated processes. (Curves computed from a 4-region, 4-solute model [43]).

Some of the model parameters are anatomic: diffusion distance, capillary lengths, extracellular and intracellular volumes. To reduce the numbers of free parameters to be estimated it is both well-principled and expeditious to use a priori information on the anatomic volumes of the spaces when these are accurately known for the same experimental conditions, for example, using the anatomic information [44–46] when analyzing cardiac indicator dilution data. The practical result of using the four MID data sets simultaneously, along with the a priori anatomic data, is to constrain the free parameters and narrow their confidence limits. In such studies one has about 60 points per dilution curve (but not 60 independent items of information), plus the anatomic constraints, so that the degrees of freedom are small. This basic strategy was used by Schwartz et al. [47] in studies on adenosine uptake in the heart. Using GENTEX, a multi-unit, multi-solute expansion of [43], which accounts for all of the exchanges and the reactions and gives an exact mass balance at the same time, along with a constrained parameter set, to fit the experimental data, appears to give reliable and reproducible estimates of parameters.

SUMMARY

The Physiome Projects, examples of the utility of mathematical models in defining working hypotheses about the nature and kinetics of biological systems, are natural developments in quantitative and integrative physiology. From the past decades of reductionist research one constructs well understood modules, then uses them as components of multiscale models. As models become more comprehensive and encompass more of the multiple scales from proteome to organism, they become more meaningful, but more like the organism itself, and more difficult to understand. Multiscale models are commonly found to exhibit emergent behavior, i.e behavior not attributable to any single component, so, like patients, are often difficult to diagnose. Proceeding from the present status, having solid information at cellular and tissue levels but less at the levels of proteomics and gene regulatory networks, and likewise at the whole body level, a strategy of working from the middle, the cell and organ level, out to the less well integrated levels of proteome and gene, and to the higher systems level of the organism, seems models are commonly found to exhibit emergent behavior, i.e behavior not attributable to any single component, so like patients are often difficult to diagnose. Proceeding from the present status, having solid information at cellular and tissue levels but less at the levels of proteomics and gene regulatory networks, and likewise at the whole body level, a strategy of working from the middle, the cell and organ level, out to the less well integrated levels of proteome and gene, and to the higher systems level of the organism, seems most sensible.