Abstract
Unlike common engineering materials, living matter can autonomously respond to environmental changes. Living structures can grow stronger, weaker, larger, or smaller within months, weeks, or days as a result of a continuous microstructural turnover and renewal. Hard tissues can adapt by increasing their density and grow strong. Soft tissues can adapt by increasing their volume and grow large. For more than three decades, the mechanics community has actively contributed to understand the phenomena of growth and remodeling from a mechanistic point of view. However, to date, there is no single, unified characterization of growth, which is equally accepted by all scientists in the field. Here we shed light on the continuum modeling of growth and remodeling of living matter, and give a comprehensive overview of historical developments and trends. We provide a state-of-the-art review of current research highlights, and discuss challenges and potential future directions. Using the example of volumetric growth, we illustrate how we can establish and utilize growth theories to characterize the functional adaptation of soft living matter. We anticipate this review to be the starting point for critical discussions and future research in growth and remodeling, with a potential impact on life science and medicine.
Keywords: living matter, density growth, volumetric growth, area growth, functional adaptation, remodeling
1. A brief history of growth and remodeling
In the century of quantitative biology, the mechanics community seems to keep ignoring the tremendous impact it could have on fusing live science and medicine by providing a unified, holistic, multiscale approach to characterize the fascinating features of living matter. On the small scale, biophysicists, who have long believed they could solve this challenging problem alone, are now coming to realize that their building block approach is inherently limited: Nature is more than the sum of its parts. On the large scale, clinical researchers keep incrementally refining existing treatment strategies, with only few truly innovative advances. Their classical observational approach is undoubtably successful when comparing different treatment outcomes; yet, it fails to provide a mechanistic and predictive understanding of the underlying key phenomena. So what is the role that mechanics as a discipline could play in quantitative biology?
1.1. Where it all began: Density growth of hard tissues
The fathers of modern biomechanics have impressively demonstrated that both biomechanics and mechanobiology play an important role when trying to understand biological form and function [105, 112]. On the one hand, biology can have a significant impact on mechanics: Mechanical stiffness changes with biological microstructure. For almost half a century, we have known that these changes are not just linear, and that nature is more than the sum of its parts. Bone stiffness, for example, not only increases linearly with bone density, but exponentially, with exponents typically varying from two to three depending on the number and thickness of the individual trabaeculae [19]. These types of non-linearities are indeed very familiar to the mechanics community [33]. We deal with geometric and constitutive non-linearities on a daily basis, and we know that superposition only holds in very few limited cases.
On the other hand, mechanics can have a tremendous impact on biology: Biological microstructure changes with mechanical loading. Unlike engineering materials, living biological materials are not just constant throughout an individual's life time; they can adapt to environmental changes. Bone density, for example, changes in response to environmental forces, a phenomenon that has become known as the functional adaptation of bone [23]. For more than a century, researchers in different disciplines have been fascinated by this functional adaptation. Figures 4 and 5 are only two out of many famous examples that illustrate how tissue microstructure is capable to align with the directions of maximum principal stress in the femur and in the tibia [112]. Non-constant densities are unconventional in classical mechanics, and we still struggle with characterizing them using our standard tools. Changes in mass, absolutely common in biology, require a characterization as a multi-phase material within the framework of mixture theories [11, 31, 50] or as a single-phase material within the framework of open system thermodynamics [28, 62, 63].
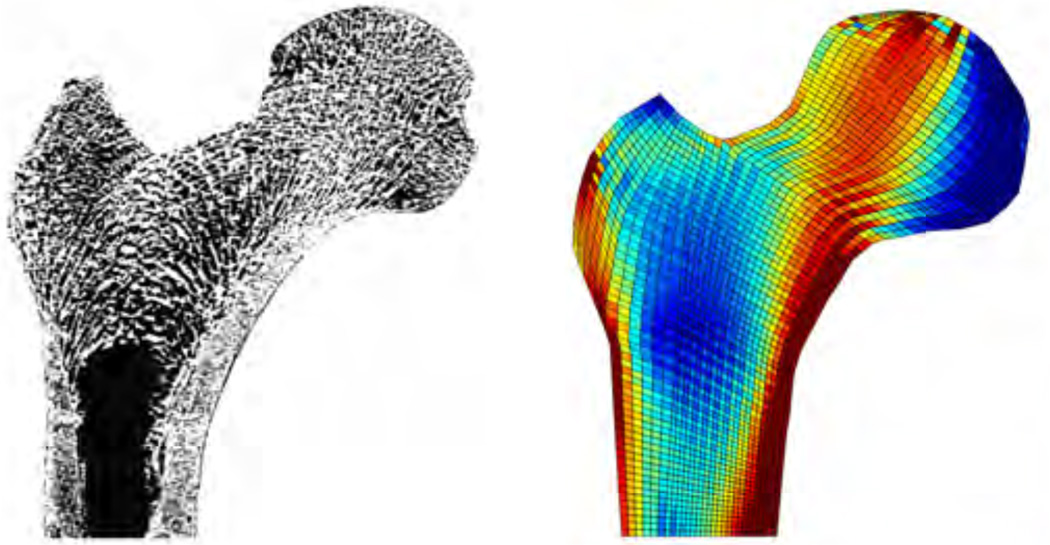
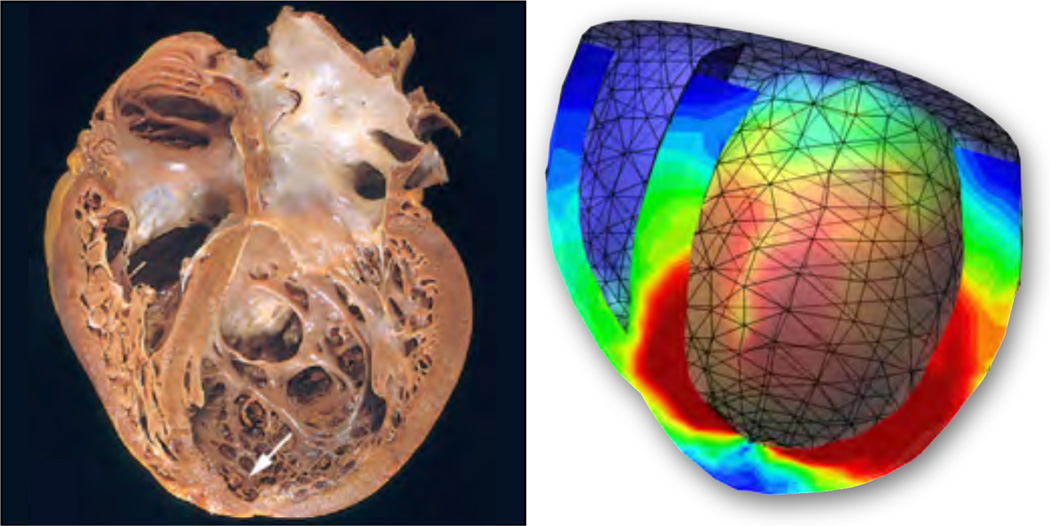
Figure 4.
Density growth of the proximal femur for an energy-driven mass source, ρ̇0 = R0 with , according to equations (17) and (39). Photograph of a thin section, left, demonstrates microstructural arrangement of trabeculae in the femur head aligned with the axis of maximum principal stress [112]. Computational simulation of density growth, right, predicts higher bone densities in regions of large mechanical stress and lower bone densities in unloaded regions [64, 65].
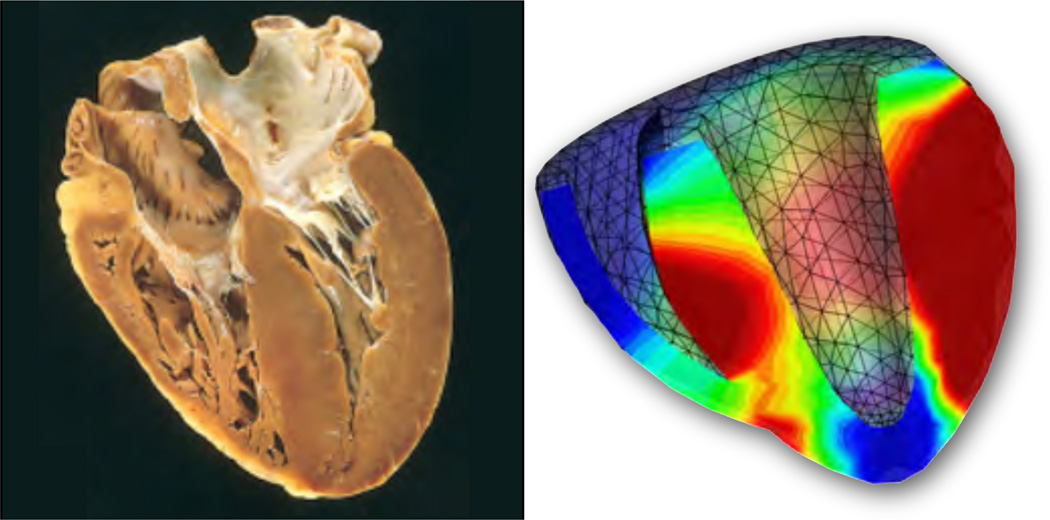
Figure 5.
Density growth of the proximal tibia for an energy-driven mass source, ρ̇0 = R0 with , according to equations (17) and (39). Photograph of a thin section, left, displays microstructural arrangement of trabeculae in the tibia head aligned with the axis of maximum principal stress [112]. Computational simulation of density growth, right, predicts a higher bone density in regions of large mechanical stress and lower bone density in unloaded regions [91, 110].
Hard tissues such as bone are admittedly a great model system to begin with, mainly for three reasons: First, since they do not undergo large deformations in vivo, a linear kinematics characterization is usually sufficiently accurate. Second, although they are multiphase materials consisting of solid and fluid constituents, for most technical applications, a single phase characterization in terms of the solid constituent alone represents their behavior sufficiently well [64]. Third, since they are relatively easy to preserve, and their ex vivo response closely matches their in vivo behavior, they are relatively easy to test. This special issue provides a state-of-the-art overview on bone regeneration [52] and illustrates how we, as engineers, can adopt the design paradigms of nature when creating optimal, strong, and lightweight structures [111].
Overall, studying the functional adaptation of hard tissues has tremendously enhanced our understanding of bone density profiles in health and disease. We now know why astronauts lose bone in space [65]. We know why stiff implants used in hip replacement and repair induce a local loss of bone density through stress shielding [8]. We know why dental implants loosen over time in response to bone remodeling. We know that osteoporosis is associated with a local bone loss, which can be correlated to gait profiles [91]. And we know why high-performance athletes in asymmetric sports, such as tennis players or baseball pitchers, have a significantly stronger dominant arm, in which they might develop chronic pain [104].
1.2. Why it became complicated: Volume growth of soft tissues
But why did we stop here? Translating what we know from hard tissues to soft is non-trivial for multiple reasons: First, soft tissues typically undergo large deformations and their accurate characterization requires a finite kinematic approach [95]. Second, their multi-phase character often plays a critical role, and their reduction to single-phase materials could sometimes be overly simplified [85]. Third, they are difficult to preserve, and their ex vivo response might vary significantly from their in vivo behavior [57]. This difference might be attributed to residual stress [4, 5, 78, 103] or to a pronounced active response [29, 53, 86].
Despite these challenges, a second generation of researchers in biomechanics has laid out a successful strategy how to characterize the living nature of soft biological tissues through iterative loops of establishing a theory, formulating testable hypotheses, designing experiments, probing the theory, calibrating the model parameters, and validating the model [49, 102]. Key to these developments was the re-interpretation of growth in terms of an incompatible configuration [47, 99] and its mathematical characterization through the multiplicative decomposition of the deformation gradient into an elastic and a growth part [38, 78, 95]. This kinematic approach was soon recognized to enable the modeling of growth in various soft biological tissues [32, 75]. Figure 6 illustrates one of the first attempts to utilize this concept and model isotropic volumetric growth of the arterial wall in response to balloon angioplasty and restenosis [43, 68]. Within the past decade, several groups in mathematics and theoretical and applied mechanics have focused on formalizing the concept of volumetric growth, both within the frameworks of mixture theories [11, 31] and open system thermodynamics [20, 74, 77], and, only recently, within a combined framework of second order mass transport [22]. These attempts and recent trends are summarized in several illustrative overview articles [8, 24, 109].
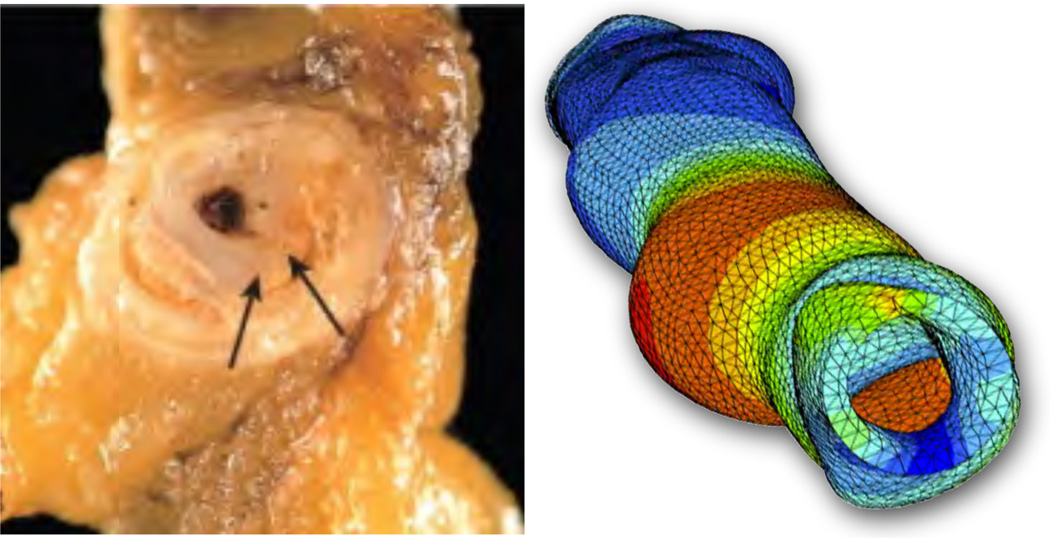
Figure 6.
Volume growth of an artery for stress-driven isotropic growth, Fg = ϑg I with ϑ̇g = kϑ , according to equations (62) and (66.1). Photograph of restenosis following balloon angioplasty, left, demonstrating residual atherosclerotic plaque and a new proliferative lesion caused by intimal thickening [70]. Computational simulation of isotropic volume growth, right, predicts wall thickening and re-narrowing of the lumen in response to stent-induced changes in the mechanical environment [43, 68].
In addition to the mechanics community, the applied mathematics community has contributed tremendously to our understanding of growing soft biological tissues. Insightful theoretical contributions address the mathematical instabilities associated with growth [13], and the analytical solutions for growing plates [26], membranes [36, 76], and shells [37]. More applied contributions typically focus either on plant growth [27, 108] or on clinically relevant growth [6]. This special issue contains one application of the former class, growing pollen tube [59], and three of the latter class, growing tumors [9], growing skin [21], and growing cells in general [11].
Now that all these growth theories are more or less established, it is surprising that they attract so little attention. Why is it that the potential of growth theories is still underappreciated? Using growth theories to predict biological phenomena requires intense cross-talk between the different disciplines. We need to specify the individual growth laws for particular types of cells, plants, or tissues, isotropic, transversely isotropic, orthotropic, or generally anisotropic [48]. We need to identify the driving forces for growth, stress, strain, or energy, and ideally tie them to the underlying mechanotransduction cascades that mediate the growth process [54, 113]. And, most importantly, we need to identify relevant phenomena of growth in health and disease that warrant thorough investigation.
Typical health-relevant examples of volumetric growth are growing tumors [6, 7, 93] and growing mucous membranes [72, 84]. Figures 7 and 8 illustrates a health-relevant example of transversely isotropic growth characteristic for growing thin biological membranes such as skin [17, 115]. In contrast to tumor growth, here, growth is initiated on purpose to create extra tissue for defect correction in plastic and reconstructive surgery [18, 101, 116]. This special issue also addresses another health-relevant example of biological growth in vision, with typical examples of glaucoma and myopia [40].
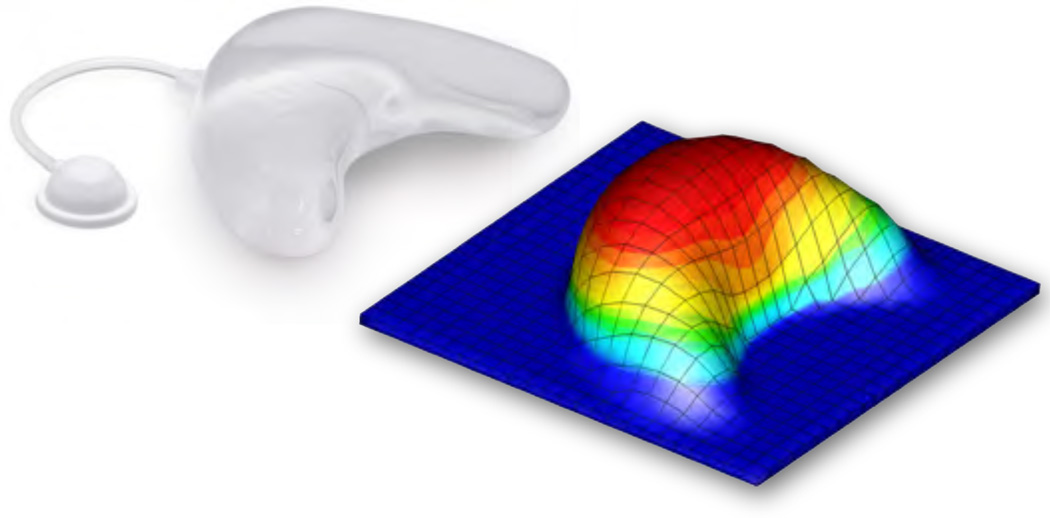
Figure 7.
Area growth of skin for stretch-driven transversely isotropic growth, with , according to equations (69) and (73.2). Photograph of a tissue expander to induce controlled in situ skin growth for defect correction in reconstructive surgery, left, reprinted with permission, Mentor Worldwide LLC [17]. Computational simulation of transversely isotropic area growth, right, predicts area growth in response to controlled mechanical overstretch during tissue expansion [18].
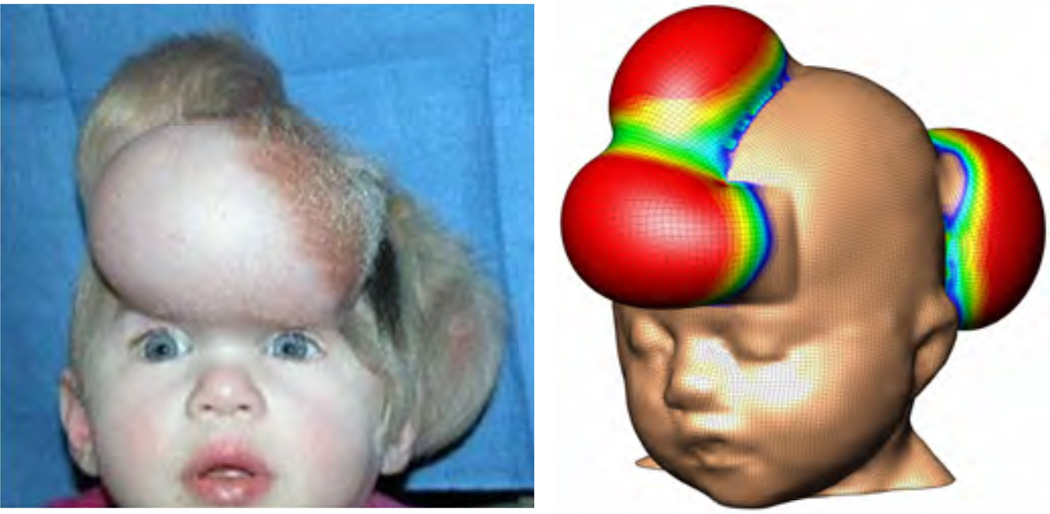
Figure 8.
Area growth of skin for stretch-driven transversely isotropic growth, with , according to equations (69) and (73.2). Photograph of tissue expansion in pediatric forehead reconstruction, left, shows forehead, anterior and posterior scalp expansion to trigger skin growth in situ [17, 39]. Computational simulation of transversely isotropic area growth, right, predicts area growth in response to controlled mechanical overstretch during tissue expansion [115, 116].
The cardiovascular system undoubtably remains the prototype model system for soft tissue growth. Growth related phenomena in arteries have attracted both theoretical [2, 3, 96] and computational [4, 43] researchers equally, with characteristic problems as illustrated in Figure 6. Two contributions of this special issue give insight into growing arterial tissue in general [107] and abdominal aortic aneurysms in particular [114]. A specific challenge is associated with the anisotropic nature of growth in cardiovascular tissue. Resent studies have characterized anisotropic growth in response to myocardial infarction in vivo [106]. Not only can the microstructural directions of anisotropy reorient themselves [67, 77, 78, 83], as discussed in one contribution of this special issue [92], but the tissue may also grow anisotropically in response to different loading scenarios [34, 55]. Cardiac muscle, for example, can grow isotropically [61], undergo eccentric growth in response to volume overload [35], or concentric growth in response to pressure overload [94], as illustrated in Figures 9 and 10. This special issue contains a collection of manuscripts related to the heart, to provide a state-of-the-art overview on cardiac growth in health and disease [10, 12, 55, 56]. Last, we discuss a possible reorientation of the underlying microstructure through the evolution of structural tensors [44, 78] as illustrated in Figure 11.
Figure 9.
Fiber growth of the heart for strain-driven transversely isotropic growth, Fg = I + [ϑg − 1] n ⊗ n with , according to equations (76) and (80.2). Photograph of a heart in dilated cardiomyopathy, left, illustrates an increase in cavity size at a constant wall thickness, typically associated with volume-overload induced eccentric growth [70]. Computational simulation of transversely isotropic fiber growth, right, predicts an enlargement of the left ventricular cavity in response to mechanical overstretch [34, 35].
Figure 10.
Cross-fiber growth of the heart for stress-driven wall thickening, Fg = I + [ϑg − 1] n ⊗ n with , according to equations (76) and (66.1). Photograph of a heart in hypertrophic cardiomyopathy, left, illustrates an increase in wall thickness at a constant cardiac size, typically associated with pressure-overload induced concentric growth [70]. Computational simulation of transversely isotropic cross-fiber growth, right, predicts a significant wall thickening of the left ventricular wall in response to hypertension [34, 94].
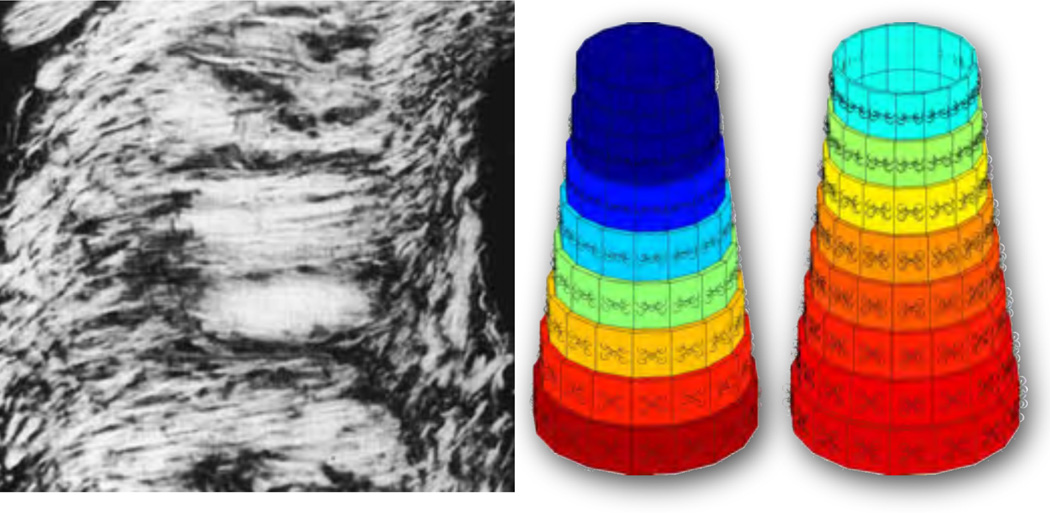
Figure 11.
Evolution of structural tensor in layered artery for stress- and strain-driven evolution of microstructural direction, ṅ = [I − n ⊗ n] · Me · n / t* and ṅ = [I − n ⊗ n] · Ce · n / t* according to equations (87.1) and (87.2). Polarized light micrograph of tangentially sectioned brain artery, left, showing variation of collagen fiber orientation from circumferential inner to helical outer layer [30]. Computational simulation of stress- and strain-driven fiber distribution, left and right, predicts a smooth variation of collagen fiber orientation from circumferential inner to helical outer layer [68].
2. Kinematics of growth
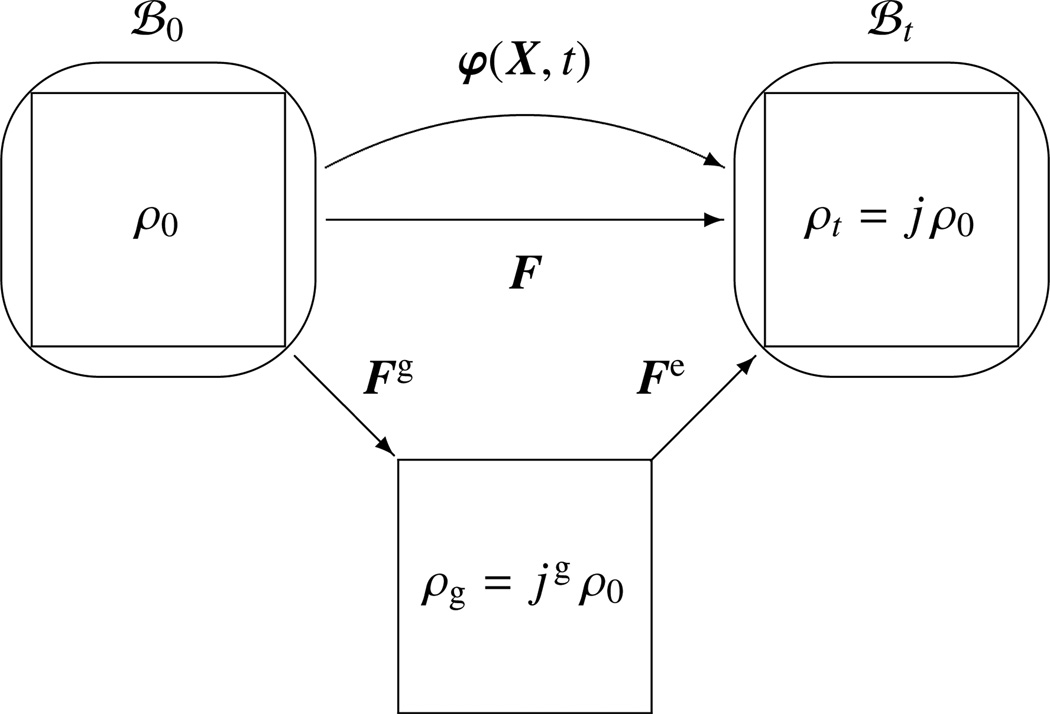
Let us consider a body B embedded in the three-dimensional space. We distinguish between a chosen material or reference configuration 𝔅0 and the spatial or current configuration 𝔅t of the body B. The spatial motion of referential position vectors of particles, X ∈ 𝔅0, to their spatial position in 𝔅t at time t is denoted by
| (1) |
and is assumed to be sufficiently smooth; see Figure 1 for a graphical illustration of the spatial motion problem. As this work proceeds, we will make use of the related gradient operations ∇X{o} = dX{o}|t and {ȯ} = dt{o}|X, with the latter referring to the material time derivative. When applying theses operations to equation (1), we obtain the well-established spatial motion deformation gradient and the spatial velocity,
| (2) |
along with the spatial velocity gradient,
| (3) |
where J = det(F) > 0 so that F−1 exists. In complete analogy, we can consider the material motion problem
| (4) |
and introduce the corresponding gradient operations ∇x{o} = dx{o}|t and see Figure 1 for a graphical illustration of the kinematics of the material motion problem. When applying these operations to equation (4), we obtain the material motion deformation gradient and the material velocity,
| (5) |
along with the material velocity gradient,
| (6) |
where j = det(f) > 0 so that f−1 exists. Since Φ is the inverse map of φ, we can relate both formulations through f = F−1 and V = − f · v.
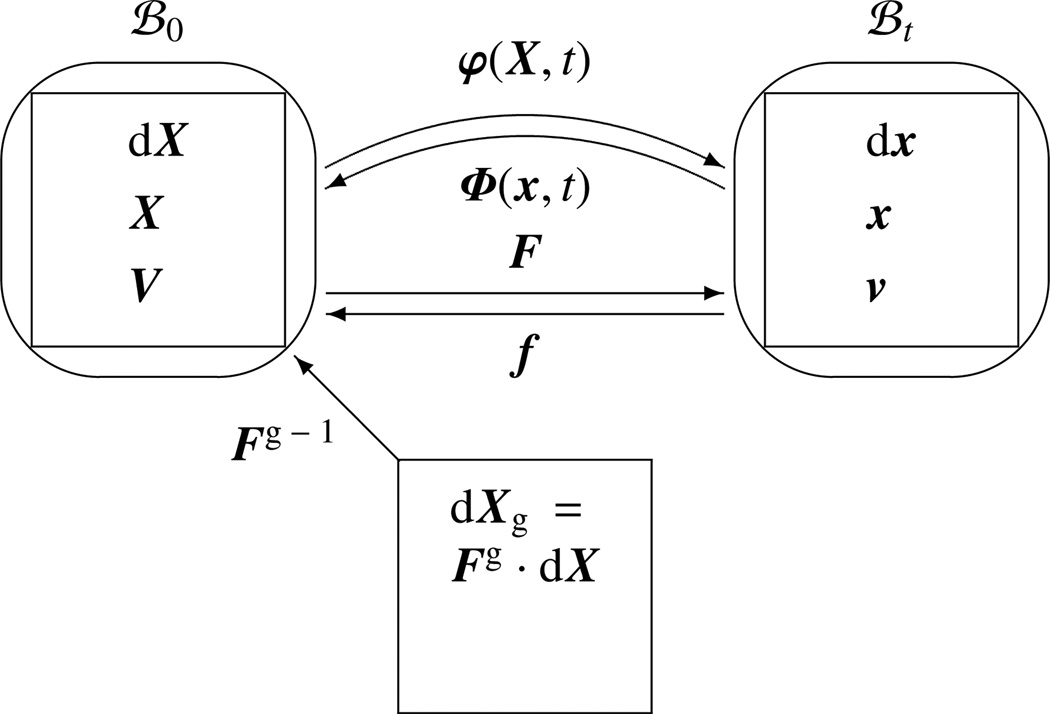
Figure 1.
Graphical illustration of the direct motion problem φ(X, t) mapping referential particles X at time t onto their spatial position x = φ(X, t) and of the inverse motion problem Φ(x, t) mapping spatial particles x at time t onto their referential position X = Φ(x, t). The local material transformation Fg − 1 maps infinitesimal line elements dXg at time t onto referential line elements dX = Fg − 1 · dX.
2.1. Compatibility
We focus the subsequent brief discussion on compatibility-related properties of configurations. Here, we focus on the spatial motion problem, but identical relations hold for the material motion problem as Φ(x, t) is the inverse map of φ(X, t). Since the deformation gradient represents the derivative of a vector potential, the related Piola identity is valid. In other words, the divergence of the cofactor of the deformation gradient vanishes identically,
| (7) |
where cof(F) = dF J = J F−t and ∇X · {o} denotes the divergence operation. A general field representation of a second-order tensor includes further contributions in addition to the gradient form present in the definition of F in equation (2). To derive this general form, we consider the Helmholtz representation of a vector field,
| (8) |
where denotes the curl operation and hc is a constant vector [25]. A second-order tensor can be represented as H(X) = hi(X) ⊗ ei, wherein ei is a Cartesian base system, so that the application of equation (8) results in
| (9) |
with Hc = const. When comparing the general field representation of a second-order tensor in equation (9) with the definition of F in equation (2), we conclude that the so-called incompatible part is not activated and that, in consequence, equation (7) holds. We can further specify the vector field a(X) and the tensor field B(X) in equation (9) by means of the representations in equations (8) and (9). This results in the representation
| (10) |
including the scalar, vector, and tensor potentials a(X), b(X) and C(X). In order to make these potentials independent of each other, b(X) and C(X) must fulfill additional constraints. To give an example, when choosing the representation C(X) = ci(X)⊗ei the vector fields incorporated are constrained to be divergence-free, i.e., ∇X · ci = 0; for further background information and representations in view of related null Lagrangians see [90, 98]. Applying the curl operation twice, such as in equation (10), is commonly denoted as the incompatibility operator frequently used in the context of continuum dislocation theories [60, 73, 80].
2.2. Volume growth
The local evolution of material inhomogeneities, e.g., growth related to changes in volume and mechanical properties, can be interpreted as local material transformations or local deformation measures. Since the deformation gradient is a second-order tensor, we can replace F with F · Fg−1, where Fg represents the local referential transformation; see Figure 1. This modeling framework was first proposed in the context of general material inhomogeneities and finite elasto-plasticity [71, 88] and, later on, applied in the context of growth [95]. The approach is commonly denoted as the multiplicative decomposition of the deformation gradient
| (11) |
into an energy-storing, reversible elastic part Fe and an irreversible growth part Fg, with the related Jacobians
| (12) |
see Figure 2. Unlike F in equation (2), neither Fe nor Fg can be derived from a vector field. Accordingly, unlike F, neither Fe nor Fg do fulfill the Piola identity in equation (7). When applying the Helmholtz representation in equation (9) to Fe and Fg, in general, the incompatible parts do not vanish. In other words, Fe and Fg can not be defined as gradients of a vector potential. This implies that the interpretation of Fe and Fg as representing an additional global configuration is misleading. In view of the spatial motion problem, we can additively decompose the spatial velocity gradient
| (13) |
into an elastic and growth related part according to equation (11) with
| (14) |
Figure 2.
Graphical illustration of the multiplicative decomposition of the deformation gradient F = ∇Xφ = Fe · Fg into a reversible elastic part Fe and an irreversible growth part Fg. The local mass density ρt = j ρ0 and ρg = j ρ0 are transformations of the referential density ρ0 in terms of the Jacobians j = det(F−1) and jg = det(Fg−1).
It proves convenient to also introduce their material counterparts Le = Fe−1 · le · Fe and Lg = Fe−1 · lg · Fe as
| (15) |
where the growth velocity tensor Lg will play a key role in the formulation of constitutive equations in section 4. We could also perform a similar transformation of l in terms of F instead of Fe, but this would be less relevant in the sequel.
2.3. Surface growth
It is not always straightforward to distinguish between bulk and surface growth [100]. Let us consider a bar with equidistant markers and choose a cross-section Г at one of its ends. Now, let the bar grow in longitudinal direction such that its end-to-end distance increases while its referential mass density and its cross-sectional area remain constant. If the distances between the markers remain constant and all markers move away from Г, we classify the process as surface growth and conclude that the new material is supplied at the surface Г. If the distances between the markers increase equally, we classify the process as bulk growth and conclude that the new material is supplied continuously within the bulk of the bar itself. Although the underlying mechanisms are fundamentally different, the final grown geometries could be entirely identical in both cases.
From a continuum mechanics point of view, Г represents an internal surface with respect to which material moves in the case of surface growth. As such growth processes change the chosen reference configuration of the body, the velocities of material particles relative to the surface Г can be best characterized in terms of the material motion problem (4). This motivates the additive decomposition of the material velocity V of a particle of the surface
| (16) |
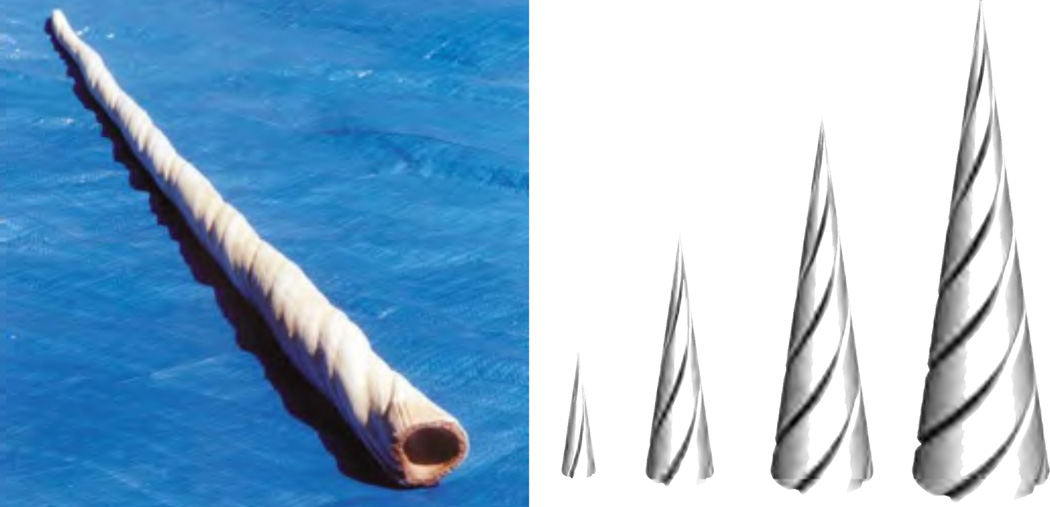
into the velocity VГ of the surface itself, and the velocity Vg of material grown at the surface Г. Typical examples of surface growth include growing tusks, as shown in Figure 3, horns, seashells, teeth [100], and plant tips [27, 58] as discussed in [59] of this special issue.
Figure 3.
Surface growth of a narwhal tusk with an upward pointing material velocity, V = VГ + Vg, according to equation (16). Photograph of a narwhal tusk, left, demonstrates the characteristic helical growth pattern. Computational simulation of surface growth, right, with an outward pointing velocity VГ of the growth surface Г, here characterized through the bottom ring, and a helically upward pointing velocity Vg of material grown at the surface Г.
Remark 1 (Multiplicative decomposition). Kinematic approaches to finite inelasticity are frequently based on the multiplicative decomposition of the deformation gradient into an elastic and an inelastic part as suggested in equation (11). This approach was proposed in the context of finite crystal plasticity [71], where the multiplicative decomposition has a clear geometric interpretation and the so-called intermediate configuration is assumed to be stress-free. However, the decomposition (11) is not unique, since the rotational part can be chosen arbitrarily [16, 87]. In view of finite growth, we apply the following polar decompositions
of the elastic part Fe into an elastic left stretch tensor ve and an elastic rotation Re, and of the growth part Fg into a growth rotation Rg and a growth right stretch tensor Ug. We can then combine the special orthogonal tensors Re and Rg to a single rotation tensor Reg, such that
Based on the right polar decomposition of Fg, the growth velocity tensor Lg takes the representation
with Ωg = Ṙg · Rg t = −Ωg t. If we restrict the growth tensor Fg to be symmetric and a priori assume Fg = Ug, the spin Ωg vanishes identically. If we additionally constrain the principal directions of Ug to remain constant in time, e.g., referring to a prescribed orientation of the underlying microstructure, the growth velocity tensor Lg turns out to be symmetric as well, i.e., Lg = Lg t.
3. Balance equations of growth
The balance equations of a growing body must account for possible changes in mass. This implies that the local referential mass density ρ0 can change in response to a possible mass source R0 and a possible mass flux R. This implies that the balance equations of growing open systems may deviate from their standard representations for bodies with a constant mass. As this work proceeds, we briefly revisit some essential balance equations in the context of open system thermodynamics. Thereby, we restrict ourselves to the balance equations of the spatial motion problem for one single constituent, similar to [111] of this special issue, and neglect the additional interaction terms that would be present in general mixture theories. These are discussed in detail, e.g., in [11, 114] of this special issue.
3.1. Balance of mass
The local form of the balance of mass for open systems balances the rate of change of the referential density ρ̇0 with a possible in- or outflux of matter R and a possible mass source R0,
| (17) |
From a microscopic point of view, the mass flux can be associated with cell migration and the mass source can be related to cell proliferation, hyperplasia, hypertrophy, mitosis, necrosis, and apoptosis.
3.2. Balance of linear momentum
In the context of open system thermodynamics, we can distinguish between the volume- and mass-specific formats of all higher-order balance equations [62]. The volume specific form of the local spatial motion balance of linear momentum
| (18) |
relates the rate of momentum ρ̇0 v + ρ0 v̇, the momentum flux P, and the momentum source ρ0 b. Subtraction of the velocity-weighted version of equation (17) results in the reduced mass specific local formulation of the linear momentum balance,
| (19) |
which we will utilize in the sequel. By neglecting the mass flux, R = 0, assuming a quasi-static setting, v̇ = 0, and considering a separation of time scales as the speed of growth is significantly smaller than v, such that v = 0, we end up with the reduced representation
| (20) |
where P represents the standard Piola stresses.
3.3. Balance of entropy
To ensure that the overall dissipation remains non-negative, we discuss the local balance of entropy in form of the Clausius Duhem inequality. We assume that the temperature θ remains constant, which is a reasonable assumption for living biological tissues. The local form of the deformation-related part of the dissipation inequality for open systems reads
| (21) |
where ψ0 = ρ0 ψ is the volume specific free energy density, and S and S0 denote an extra external entropy flux and source to account for the living nature of biological systems [62, 77].
Remark 2 (Residual stresses). Biological tissues often possess so-called residual stresses, which we will denote as Pres. By following the outline and argumentation in [46, Ogden, pp. 65–108], we make use of the relation
| (22) |
Application of the divergence theorem to the integral form of equation (22) results in
| (23) |
with N denoting the outward referential unit vector. The residual stresses Pres must fulfill the local form of the balance of linear momentum (20). By assuming the momentum source ρ0 b to vanish, we conclude that the local equilibrium equation ∇X · Pres = 0 holds. Moreover, the surface integral in equation (23) must be identical to zero as external surface forces are excluded for the unloaded body considered. Accordingly, all integrals in (23) are zero and ∫𝔅0 Pres dV = 0 implies either that Pres = 0 or that Pres is distributed inhomogeneously within 𝔅0. Note that the growth related part Fg allows to conveniently include residual stresses at vanishing local strains, i.e., F = I; see section 4.3 below. For further background information on the incorporation of residual stresses as additional arguments in the constitutive equations, we refer the reader to [45] and references cited therein. Typical experiments to demonstrate residual stresses in growing tissue are the classical opening angle experiment, e.g., in arteries [29], and peeling of living bilayers, which grow at different rates, e.g., in rhubarb [108].
4. Constitutive equations of growth
To close the systems of equations, we must introduce constitutive relations for the source terms R0, S 0, b as well as for the flux terms R, S, P, and, if present, for the evolution of internal variables. Here, we will neither provide a specific representation for b, such as volume forces resulting from gravity, nor for the external entropy flux S and entropy source S0, which we simply assume to take values such that inequality (21) is satisfied. In order to evaluate the dissipation inequality (21), we first specify the free energy
| (24) |
where we have admitted the explicit dependency on X to simplify the notation. The additional variable AP constitutes a so-called structural tensor to account for a possible anisotropic elastic behavior. A typical assumption for this tensor is a symmetric rank one form, AP = aP ⊗ aP, where the vector aP characterizes a specific direction of anisotropy. Here, we focus on only one structural tensor and refer to [78] for a growth model including anisotropic elasticity with multiple structural tensors. Using equations (17) and (24), and assuming θ̇ = 0, we can re-write the dissipation inequality in the following form.
| (25) |
In the following subsections, we will use this dissipation inequality to specify functional dependencies of the mass source, the mass flux, the momentum flux, and the evolution of growth.
4.1. Mass source
In general, the mass source R0 is a scalar-valued tensor function of the state variables, their material time derivatives, and additional arguments to be specified. When neglecting the introduction of additional arguments, such as additional structural tensors, rates, and gradients of the state variables, the mass source function may take the following representation
| (26) |
4.2. Mass flux
In analogy to the mass source, the mass flux R is a vector-valued tensor function of the state variables, their rates, their gradients, and additional arguments to be specified. We assume R to be independent of the rates of the state variables, but formally introduce another tensorial variable AR and include only one additional gradient contribution, namely the gradient of the referential mass density. As a result, the mass flux function may take the following representation
| (27) |
4.3. Momentum flux
To introduce the momentum flux in a thermodynamically motivated way, we explore the first term of the dissipation inequality (25). We adopt a hyperelastic format to define the momentum flux, and introduce the Piola stress P as energetically conjugate to the rate of the deformation gradient Ḟ, i.e.,
| (28) |
This implies that the first term of the dissipation inequality (25) vanishes identically for all Ḟ.
4.4. Evolution of growth
To characterize the evolution of growth, we explore the second term of the dissipation inequality (25). In analogy to considerations common in finite strain plasticity,
| (29) |
we introduce the Mandel stresses Me = Fe t · Pe as thermodynamically conjugate to the growth velocity tensor Lg. These thermodynamic considerations motivate to introduce the evolution of the growth tensor Ḟg in form of Lg to be a function of the Mandel stresses Me and additional variables such as a structural-tensor-type quantity Ag, i.e.,
| (30) |
Since Lg is assumed to depend on Me, the particular type of evolution equation (30) is, by analogy, similar to models in finite plasticity, here denoted as stress-driven growth. Alternatively, we could consider an ad hoc introduction of Lg, i.e., not motivated by direct thermodynamical considerations, for example in a strain-driven format,
| (31) |
4.5. Evolution of structural tensor
In analogy to the evolution of Fg, the evolution of the structural tensor AP can be introduced in a stress-driven form,
| (32) |
where −ρ0 ∂Apψ takes the interpretation as stress-type tensor conjugate to AP, or in a strain-driven form,
| (33) |
Alternatively, since AP = aP ⊗ aP, we could introduce evolution equations for the microstructural vector ȧP itself, instead of its structural tensor ȦP. This would then allow us to separately address the evolution of its length ∥aP∥ and the evolution of its orientation of aP. In particular, when tying these evolution equations to observable variables, evolution equations for the microstructural vector ȧP might be more illustrative. The tensor functions in equations (32) and (33) are assumed not to include further structural tensors such as AR and Ag which, in general, could also be included. Moreover, AR and Ag may also evolve with time, and follow evolution equations of similar forms as introduced in (32) and (33). Evolving structural tensors are typically used to characterize remodeling effects when the living structure undergoes changes is anisotropic material properties such as microstructural reorientations, see [44, 67, 78], or [92] of this special issue.
Remark 3 (Thermodynamically conjugate pairs). Using the dissipation inequality (25), we have identified the Piola stress P and the rate of the deformation gradient Ḟ as thermodynamically conjugate pairs in Section 4.3. In addition, we have identified the elastic Mandel stress Me and the growth velocity tensor Lg as thermodynamically conjugate pairs in Section 4.4. Alternatively, we could have introduced the growth part of the Piola stress, Pg = −ρ0 ∂ψ / ∂Fg, and the rate of the growth tensor Ḟg as conjugate pairs. In analogy to equation (30), this format would then motivate the introduction of the following evolution of growth,
as a function of the growth related Piola-type stresses, Pg, and all other variables, i.e., Ag, ρ0 and θ.
5. Examples
In the previous section, we have introduced generalized functional forms of the constitutive equations, which characterize growth. Now, we will specify and discuss some particular examples. As such, this section is by far not intended to be complete; it is rather meant to provide guidelines and common practise when modeling particular types of growth. For simplicity, we restrict ourselves to transversely isotropic materials with one pronounced structural direction a, such that the structural tensors of the baseline elastic response AP, of the density distribution AR, and of volume growth Ag coincide.
| (34) |
Here, we will neither focus on the introduction of several or higher-order structural tensors, nor on the introduction of dispersion parameters or so-called orientation distribution functions; for further background information see [78, 79, 83, 42] and references cited therein.
5.1. Mass source
The mass source R0 in equation (26) may take different specific forms. One possibility is to make use of the transformation of the local mass densities in terms of the determinants of individual contributions of the deformation gradient. For the special case that the mass density remains constant upon growth, ρg = const, we can express the referential mass density ρ0 as a function of the growth tensor Fg. This implies that
| (35) |
where ρg is the mass density related to the local transformation Fg, Jg = det(Fg), and jg = 1/Jg, see Figure 2. Recall that Jg > 1 implies a growth-related volume increase and jg > 1 implies a volume reduction, i.e., positive and negative growth. Assuming a constant transformed mass density, ρg = const, and thus
| (36) |
we can extract the following evolution equation for the referential mass density ρ0,
| (37) |
with Ḟg · Fg − 1 = − Fg · Ḟg − 1 and the trace operation tr{o} = {o} : I where I denotes the second-order identity tensor. For most biological tissues, it is a reasonable assumption that the mass flux R is constant in space, i.e., ∇X · R = 0. In this special case, equation (17) implies that the rate of the referential mass density ρ̇0 is identical to the mass source R0, with
| (38) |
which allows us to explicitly calculate changes in mass in terms of the growth tensor Fg. This approach is relatively common to characterize the mass increase in growing soft tissues such as arteries [43] or skin [17]. Hard tissues, however, are typically characterized through an energy-driven evolution of the mass density, and the mass source R0 is specified in terms of the referential mass density ρ0 and the free energy ψ,
| (39) |
Herein, denote the reference value of the density and of the free energy, m is an additional parameter to ensure algorithmic stability, and kρ has the unit of time divided by length squared to govern the speed of the adaption process, see [41] and [111] of this special issue. Typical examples of this type of density growth have been used extensively in the literature to characterize density profiles in the proxima femur [64, 65, 112], see Figure 4. Additional applications include density profiles in the humerus of high performance athletes [104], and density profiles in the proxima tibia in the context of osteoarthritis [91, 110, 112], see Figure 5.
5.2. Mass flux
We can essentially distinguish two types of mass flux in open system thermodynamics; a gradient-based flow of matter which is typically associated with volume growth, and a surface-based flow of matter which is typically associated with surface growth. Gradient-based formulations are motivated in analogy to Fick’s law of diffusion, or Fourier’s law of heat conduction,
| (40) |
such that the symmetric conductivity tensor D maps the gradient of the referential mass density ∇Xρ0 onto the mass flux R [64]. A typical example might be cell migration towards low density regions, e.g., in wound healing, with the goal to equilibrate density concentrations [66]. Surface-based formulations can be motivated by the creation of new material at growing surfaces, which we have introduced as Г in Section 2.3. If we denote their unit normal vector by nГ, we can interpret surface growth as a flux of matter away from the surface Г,
| (41) |
such that the symmetric conductivity tensor D maps the normal nГ onto the mass flux R [100]. Typical examples of surfaces from which mass grows are nail beds, roots of hairs, or growth plates of long bones. In both cases, for the special case of transverse isotropy, the conductivity tensor takes the following explicit representation,
| (42) |
with the isotropic and anisotropic mass conduction coefficients δiso and δani.
5.3. Momentum flux
The momentum flux is specified by a hyper-elastic form so that the Piola stresses are obtained from the derivative of the free energy function with respect to the deformation gradient. We assume the free energy to be an isotropic function, invariant under superposed rigid body motions. This implies that
| (43) |
with Ce = Fe t · Fe and  = Fg · A · Fg t = â ⊗ â, such that ψ̆ = ψ̂ is restricted to be a function of an irreducible set of invariants. Here,  and â can be interpreted as the push forward of the structural tensor A and of the vector a, characterizing the microstructural orientation in the incompatible growth configuration. A possible set of strain invariants is the following
| (44) |
Alternatively, we can represent the identical set of irreducible invariants in terms of spatial or material arguments, see [81, 82] for a detailed discussion. Based on these considerations together with equation (28), the representation of the Piola stresses results in
| (45) |
5.3.1. Isotropic elasticity
For the special case of an isotropic elastic response, the free energy function can be reduced to the following functional format in terms of the first three isotropic invariants only
| (46) |
Since the choice of the elastic baseline characterization strongly depends on the particular type of tissue, we do not further specify the free energy function at this stage, but refer the reader to [89, 97] for further background information on non-linear isotropic elasticity.
5.3.2. Transversely isotropic elasticity
For the special case of a transversely isotropic elastic response for which both the growth tensor and the structural tensor are constant in time, i.e., Fg = I and  = A, the free energy function can be reduced to account for five invariants only
| (47) |
For the general case of a transversely isotropic elastic response, the free energy could account for all ten invariants
| (48) |
A typical example for an anisotropy-related strain-type deformation measure is the difference . This strain measure vanishes identically for Ce = I, whereas with does generally not vanish in case of evolving structural tensors. The reader is referred to [15, 46, 49, 97] for different aspects on the constitutive modeling of finite deformation anisotropic elasticity and particular examples of transversely isotropic free energy functions.
5.4. Evolution of growth
Three conceptually different approaches have been suggested to constitutively characterize the evolution of growth according to equations (30) or (31): the general tensor function concept, the homestatic equilibrium concept, and the microstructural concept. While the former two approaches can, in principle, define a simultaneous growth and reorientation of the microstructural directions, the third approach allows us to address growth and reorientation individually. Since we believe this is the most versatile way of characterizing growing tissues with a pre-defined microstructure, we will introduce the first two concepts briefly and address the third one in more detail. For all three cases, the growth tensor Fg is commonly assumed to be equal to the identity tensor initially, i.e. Fg|t=0 = I, such that Fe|t=0 = F.
General tensorial evolution of growth
The general tensor function concept has traditionally been advocated by the continuum physics community [51]. Using the concept of representation theorems [15], a generic tensorial evolution equation for the growth tensor Fg is introduced. In accordance with the discussion in remark 2, the growth tensor is restricted to by symmteric, i.e., Fg = Ug, and, moreover, assume isotropic hyper-elasticity so that Me = Me t. Accordingly, the evolution of growth can formally be introduced either in a stress-based form,
| (49) |
or in a strain-based form,
| (50) |
Here, for example, we have selected the elastic Mandel stresses Me and the elastic right Cauchy Green tensor Ce as representative stress and strain measures to drive the growth process. The material parameters characterize load-independent growth for both the stress- and strain-based case. While characterize isotropic growth, characterize anisotropic growth as these parameters weight contributions including the structural tensor Â.
Homeostatic equilibrium evolution of growth
The homeostatic equilibrium concept is typically advocated by the biomechanics community, since concepts of homeostatic stresses or strains take an intuitive interpretation in biochemistry. A generic evolution law based on a homeostatic stress state could take the following format,
| (51) |
where Me denotes a fourth-order mobility tensor and is a tensorial so-called target stress. Alternatively, we could formulate the evolution law based on a homeostatic strain state,
| (52) |
where Ce denotes a fourth-order mobility tensor and is a tensorial target deformation. For the special case of volumetric target states, we can choose scalar-valued quantities such as pressure or dilation as homeostatic target stress or target strain . If we assume an isotropic mobility, such that the mobility tensors are proportional to the fourth-order identity tensor with proportionality factors Me and Ce, equations (51) and (52) are of purely volumetric nature, i.e., or , see [96] for details. For the example of tumor growth, a fully tensorial stress-driven format, , based on the elastic Eshelby tensor Σe = ψ0 I − Me is discussed in [9] of this special issue. For the example of glaucoma, i.e., growth and remodeling in the eye, a scalar stretch-driven format of collagen fibril growth towards a homeostatic equilibrium state is illustrated in [40] of this special issue.
Microstructural evolution of growth
The microstructural concept, which we will follow here, has been advocated by the material science community and by the theoretical and computational mechanics community, since it closely follows concepts introduced for crystal plasticity [16, 71, 87]. As outlined in remark 1, this concept motivates the definition of the growth tensor by microstructural considerations. In analogy to equation (42), we formally incorporate the underlying microstructure through the structural tensor A = a ⊗ a in terms of the microstructural direction a,
| (53) |
where ϑiso and ϑani characterize the amount of isotropic and anisotropic growth, such that ϑiso|t=0 = 1 and ϑani|t=0 = 1 in the initial ungrown state. Accordingly, we have Jg = [ϑiso]2[ϑiso + ϑani − 1], and Fg|ϑiso=1,ϑani=1 = I. The definition (53) implies that the growth tensor is a priori symmetric, Fg = Ug. As the rotational part of Fg is neglected, Fg transforms the direction vector a co-linearly to itself and scales a with the total amount of growth in this direction,
| (54) |
With n constant in time, the material time derivative of growth can be expressed as follows,
| (55) |
Using the Sherman-Morrison-Woodbury formula, we obtain the following explicit representation of the inverse of the growth tensor,
| (56) |
for ϑiso ≠ 0 and ϑiso + ϑani ≠ 1. Accordingly, we can derive the following explicit formulation for the growth velocity tensor
| (57) |
The explicit evaluation of the growth part of the dissipation inequality (29)
| (58) |
suggests to introduce the first term in brackets as the driving force for isotropic growth, ϑiso, and the second term in brackets as the driving force for anisotropic growth, ϑani. Here, in analogy with the definitions in equation (44), we have introduced the first and fourth invariants of the Mandel stress, , which take the interpretation of the pressure and fiber stress. We could adopt a conceptually similar format
| (59) |
to motivate the evolution of the growth multipliers for the case of microstructurally motivated strain-driven growth. Again, in analogy with equation (44), we have introduced the first and fourth invariants of the elastic right Cauchy Green deformation tensor, , which are associated with the volume change and fiber stretch. In the context of a vanishing mass flux contribution according to equation (38), the mass source reduces to the following expression
| (60) |
We will now elaborate three special cases of this general formulation for volume growth: isotropic growth, area growth, and fiber growth. We will specify the underlying kinematics, discuss possible driving forces for growth, and illustrate specific types of tissue for which the individual formulations can be used.
5.4.1. Volume growth
For the special case of isotropic growth, we characterize the growing tissue through a single isotropic growth multiplier ϑg, while the amount of anisotropic growth vanishes identically,
| (61) |
This implies that equation (53) reduces to the following format,
| (62) |
so that Jg = [ϑg]3 and Fg|ϑg=1 = I. Along with the following explicit expressions for the inverse growth tensor according to equation (56),
| (63) |
the definition of the growth velocity tensor reduces to the following expression according to equation (15),
| (64) |
The term of the dissipation inequality according to equation (58), and its strain based counterpart (59),
| (65) |
motivates the following stress- and strain-based evolution equations for growth
| (66) |
where kϑ denotes a saturation-type target stress or strain function. The mass source, in the context of a vanishing mass flux and ρg ≐ const according to equation (38), takes the following simplified representation
| (67) |
Isotropic growth models are typically used to characterize growing tissue on a phenomenological level [43, 96], as also demonstrated in [12] of this special issue. Some typical examples addressed in the literature include growth of tumors [6], growing arteries [68], see Figure 6 growing hearts of athletes [35], growing hearts in general [61], or the specific analysis of surface wrinkling in skin, as discussed in [21] of this special issue.
5.4.2. Area growth
For the special case of transversely isotropic in-plane growth, for example present in growing biological membranes, the growth model becomes transversely isotropic. We can again characterize such growth phenomena through a single growth multiplier ϑg, which we can interpret as the in plane area growth, such that
| (68) |
The generic growth tensor introduced in equation (53) then reduces to the following expression,
| (69) |
so that Jg = ϑg and Fg|ϑg = 1 = I, which we can invert in closed form using equation (56)
| (70) |
This allows us to define the growth velocity tensor according to equation (15),
| (71) |
and to evaluate equations (58) or (59)
| (72) |
to characterize possible stress- and strain-based evolution equations for growth
| (73) |
in terms of a saturation-type target stress or strain function kϑ For the special case of a vanishing mass flux and ρg ≐ const according to equation (38), the mass source can be expressed as follows
| (74) |
Area growth of this form is characteristic for growing biological membranes. Issues of interest intensely discussed in the literature are instabilities in growing plates [26], membranes [36, 76], and shells [37]. Particular biomechanical applications include growing mucous membranes [72] and growing skin [17, 101, 116], see Figures 7 and 8.
5.4.3. Fiber growth
For the special case of directional fiber growth, the growth model becomes transversely isotropic. We can again characterize growth in terms of a single growth multiplier ϑg, which we can interpret as the growth-induced fiber stretch,
| (75) |
Accordingly, the generic growth tensor of equation (53) reduces to the following expression
| (76) |
such that Jg = ϑg and Fg|ϑg=1 = I. The explicit representation of its inverse according to equation (56) results in
| (77) |
and allows us to introduce the growth velocity tensor according to equation (15),
| (78) |
The driving force for growth according to equations (58) or (59),
| (79) |
may be combined with a saturation-type target stress or strain function kϑ, which motivates the following stress- and strain-based evolution equations for growth,
| (80) |
In the context of a vanishing mass flux and ρg ≐ const according to equation (38), the mass source takes the representation
| (81) |
Fiber growth is characteristic for biological tissues, which grow along specific microstructural directions, as illustrated for one [95] and three [108] specific directions of anisotropy. Some typical examples include growing skeletal and cardiac muscle [34, 94], as discussed in [55, 56] of this special issue. Figures 9 and 10 illustrate the associated cases of strain-driven cardiac dilation and stress-driven cardiac wall thickening [34, 35].
5.5. Evolution of structural tensor
While we have previously placed emphasis on the evolution of the growth tensor Fg in the form of equation (53) with n remaining constant in time, we now address the evolution of the anisotropy direction itself. This reorientation model can easily be combined with the evolution of ϑani. To specify the evolution of n in time, let us denote its initial orientation by n0 = n |t=0 and define its current orientation in terms of an orthogonal tensor Rn,
| (82) |
This allows us to express the rate of n as
| (83) |
where Ωn is the related spin tensor and ωn is its axial vector. By further specifying the axial vector ωn, we can introduce an evolution equation for the micros tructural orientation n. We may, for instance, construct ωn in terms of a vector product, so that n aligns with a specific direction. Typical examples are either principal stress or principal strain directions. With the spectral decompositions
| (84) |
we can express the reorientation of n either in a stress- or strain-driven form,
| (85) |
where t* represents a scaling parameter similar to the relaxation time in models for viscous bahavior. The vectors m and c represent particular directions associated with either Me or Ce, e.g., a direction associated with the maximum principal value or . Since the form of reorientation model in equation (85) defines ωn perpendicular to the anisotropy direction n itself, so-called drilling rotations are a priori excluded [14]. By combining equations (83) and (85) and using the ε δ-rule we obtain the following representations of the evolution equations for the microstructural direction,
| (86) |
From equation (86), we conclude that the constraint ṅ · n = 0 is satisfied so that n remains a unit vector. Alternatively, we may also replace m or c in equation (86) with a stress- or strain-based mapping of the preferred direction n itself, which results in
| (87) |
It is interesting to note that saturation-type evolution of the re-orientation of n is directly implied in equations (86) and (87): the rate of n goes to zero for n aligning with m or c, or, respectively with Me · n or Ce · n. This indicates that both types of evolution equations, either (86) or (87), may result in one and the same stress- or strain-based reorientation direction as an alignment of n with Me · n or Ce · n implies that n evolves towards a principal stress or strain direction. The evolution of the direction vector n also contributes to the dissipation inequality. For conceptual simplicity, consider the case where ϑiso and ϑani do not evolve in time. The rate of the growth tensor then reduces to
| (88) |
so that the growth velocity tensor takes the representation,
| (89) |
Note that Lg becomes unsymmetric due to the reorientation of n even though Fg remains symmetric and the rotational part of Fg is not activated, i.e., Rg = I see remark 1. Accordingly, the unsymmetric part of Me, as generally present in case of anisotropic elasticity, contributes to the growth-related dissipation part Me : Lg.
Evolving structural tensors have been applied successfully to explain characteristic tissue microstructures, for example in native arteries [68], see Figure 11, and in the healthy heart, as discussed in [92] of this special issue. A reorientation of these native microstructures can be a severe problem in specific forms of disease, as illustrated for the case of glaucoma in the excellent overview [40] of this special issue. Reproducing the correct native microstructural orientation is one of the biggest challenges in tissue engineering. Artificial tissue constructs grown in a dish are typically pre-conditioned to align their microstructural directions with either stress or strain to reproduce the native microstructure. Typical examples are tissue engineering of functional vascular grafts [1], tendons or ligaments [31], with the particular example of a strain-driven reorientation along the maximum principal direction c according to equation (86.2) illustrated in [67]. For the algorithmic treatment of fiber reorientation the interested reader is referred to [44, 78].
Remark 4 (Thermodynamically conjugate pairs). Here, we have evaluated the dissipation inequality (29) in terms of the elastic Mandel stress Me and the growth velocity tensor Lg as thermodynamically conjugate pairs, introducing equation (58). Alternatively, we could introduce the Piola stress Pg = −ρ0∂Fgψ and the rate of the growth tensor Ḟg as thermodynamically conjugate pairs as introduced in equation (29), see also remark 3. In view of the specific form of Fg introduced in equation (53) and by assuming n to remain constant in time, we obtain
where we have introduced the first and fourth invariant of the Piola stress, . In contrast to equation (58), the above equation clearly reflects the isotropic-anisotropic decoupling, with acting as driving force for isotropic growth ϑiso and acting as driving force for anisotropic growth ϑani. This is not the case for the evaluation in terms of Me and Lg, see equation (58), where the driving forces for ϑiso depends on ϑiso, ϑani, and the force driving ϑani is a function of ϑiso, ϑani, .
Remark 5 (Incompressibility and growth). Although it may appear rather trivial, there is a controversy of growth in combination with incompressibility [96]. The first possibility is to first perform the volumetric-isochoric decomposition of the total deformation gradient, F = J1/3 F̄, where F̄ = j1/3 F, and then perform the multiplicative decomposition of the purely isochoric part, F̄ = F̄e · F̄g, i.e.,
Although computationally attractive, this approach is limited to the special case where growth remains purely isochoric, i.e., Jg = 1, a case we have not discussed in the examples of this section. The second possibility is to first perform the multiplicative decomposition of the total deformation gradient, F = Fe · Fg, and then perform the volumetric-isochoric decomposition on the elastic part only, Fe = Je 1/3 F̄e, i.e.,
Although most intuitive when growth is associated with volumetric changes, i.e., Jg ≠ 1, this approach may severely impact the algorithmic realization. It may require to reconsider existing computational algorithms, since elastic incompressibility can no longer be ensured on the element level by using existing element formulations that constrain the overall deformation to be incompressible, J = 1, or quasi-incompressible, J ≈ 1.
6. Discussion
Research in the 1970s and 1980s, mainly lead by mechanical and bioengineering, has been driven by the quest for experimental evidence of growth and adaptation in hard tissues. Research in the 1990s, mainly lead by continuum mechanics and computational modeling, has allowed us to predict heterogeneous density profiles in agreement with these experimental findings. Research in the past decade has focused mainly on soft tissue growth. The community has grown exponentially from biologists, biophysicists, computer scientists, mathematicians, and engineers, to radiologists and clinicians in various disciplines. Right now, we are at the verge of appreciating that, in order to fully understand growth of biological tissues, we require a holistic and not just a reductionist view, we need mechanistic and not just phenomenological models, and we need to perform predictive and not just reproductive science.
Predictive modeling of biological growth is a challenging problem, but as mechanics community, we are optimally trained to face it: Modern continuum mechanics is multiscale, we are inherently passing information across the scales, most of our current models are not just phenomenological but microscopically motivated. Modern continuum mechanics is multifield, we are inherently passing information across the fields, most of our current field theories are based on coupled mechanical, thermal, electrical, and magnetic fields. The additional incorporation of biology and chemistry should, in principle, not introduce unre-solvable difficulties. If we manage to understand mechanotrans-duction pathways in growth and remodeling, if we manage to integrate biomechanics and mechanobiology seamlessly into our models, and if we manage to manipulate these pathways systematically through a profound mechanistic understanding, our impact on life science and medicine could be tremendous. Continuum mechanics and computational mechanics have suffered from a severe identity crises within the past two decades. Growth and remodeling present an incredible opportunity to reposition our community at the forefront of science.
Acknowledgements
This work was supported by the National Science Foundation CAREER award CMMI-0952021 and by the National Institutes of Health Grant U54 GM072970.
References
- 1.Abilez O, Benharash P, Mehrotra M, Miyamoto E, Gale A, Picquet J, Xu C, Zarins C. A novel culture system shows that stem cells can be grown in 3D and under physiological pulsatile conditions for tissue engineering of vascular grafts. J Surg Res. 2006;132:170–178. doi: 10.1016/j.jss.2006.02.017. [DOI] [PubMed] [Google Scholar]
- 2.Alford PW, Taber LA. Computational study of growth and remodelling in the aortic arch. Comp Meth Biomech Biomed Eng. 2008;11:525–538. doi: 10.1080/10255840801930710. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Alford PW, Humphrey JD, Taber LA. Growth and remodeling in a thickwalled artery model: effects of spatial variations in wall constituents. Biomech Mod Mechanobio. 2008;7:245–262. doi: 10.1007/s10237-007-0101-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Alastrue V, Martinez MA, Doblare M. Modelling adaptative volumetric finite growth in patient-specific residually stressed arteries. J Biomech. 2009;41:1773–1781. doi: 10.1016/j.jbiomech.2008.02.036. [DOI] [PubMed] [Google Scholar]
- 5.Alastrue V, Martínez MA, Doblare M, Menzel A. Anisotropic microsphere-based finite elasticity applied to blood vessel modelling. J Mech Phys Solids. 2009;57:178–203. [Google Scholar]
- 6.Ambrosi D, Mollica F. On the mechanics of a growing tumor. Int J Eng Sci. 2002;40:1297–1316. [Google Scholar]
- 7.Ambrosi D, Preziosi L, Vitale G. The insight of mixtures theory for growth and remodeling. ZAMP. 2010;61:177–191. [Google Scholar]
- 8.Ambrosi D, Ateshian GA, Arruda EM, Cowin SC, Dumais J, Goriely A, Holzapfel GA, Humphrey JD, Kemkemer R, Kuhl E, Olberding JE, Taber LA, Garikipati K. Perspectives on biological growth and remodeling. J Mech Phys Solids. 2011;59:863–883. doi: 10.1016/j.jmps.2010.12.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Ambrosi D, Preziosi L, Vitale G. The interplay between stress and growth in solid tumors. Mech Res Comm. 2012;42:87–91. [Google Scholar]
- 10.Arts T, Reesink K, Kroon W, Delhaas T. Simulation of adaptation of blood vessel geometry to flow and pressure: implications for arteriovenous impedance. Mech Res Comm. 2012;42:15–21. 2012. [Google Scholar]
- 11.Ateshian GA, Borrison B, Holmes JW, Hung CT. Mechanics of cell growth. Mech Res Comm. 2012;42:118–125. doi: 10.1016/j.mechrescom.2012.01.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Bellomo FJ, Armero F, Nallim LG, Oller S. A constitutive model for tissue adaptation: necrosis and stress driven growth. Mech Res Comm. 2012;42:51–59. [Google Scholar]
- 13.Ben Amar M, Goriely A. Growth and instability in elastic tissues. J Mech Phys Solids. 2005;53:2284–2319. [Google Scholar]
- 14.Betsch P, Menzel A, Stein S. On the parametrization of finite rotations in computational mechanics. A classification of concepts with application to smooth shells. Comp Meth Appl Mech Eng. 1998;155:273–305. [Google Scholar]
- 15.Boehler JP, editor. Number 292 in CISM Courses and Lectures. Springer; 1987. Applications of Tensor Functions in Solid Mechanics. [Google Scholar]
- 16.Boyce MC, Weber GG, Parks DM. On the kinematics of finite strain plasticity. J Mech Phys Solids. 1989;37:647–665. [Google Scholar]
- 17.Buganza Tepole A, Ploch CJ, Wong J, Gosain AK, Kuhl E. Growin skin: A computational model for skin expansion in reconstructive surgery. J Mech Phys Solids. 2011;59:2177–2190. doi: 10.1016/j.jmps.2011.05.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Buganza Tepole A, Gosain AK, Kuhl E. Stretching skin: The physiological limit and beyond. Int J Nonlin Mech. doi: 10.1016/j.ijnonlinmec.2011.07.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Carter DR, Hayes WC. The behavior of bone as a twophase porous structure. J Bone Jt Surgery. 1977;59:785794. [PubMed] [Google Scholar]
- 20.Chen YC, Hoger A. Constitutive functions of elastic materials in finite growth and deformation. J Elast. 2000;59:175–193. [Google Scholar]
- 21.Ciarletta P, BenAmar M. Papillary networks in the dermal-epidermal junction of skin: a biomechanical model. Mech Res Comm. 2012;42:68–76. [Google Scholar]
- 22.Ciarletta P, Ambrosi D, Maugin GA. Mass transport in morphogenetic processes: a second gradient theory for volumetric growth and material remodeling. J Mech Phys Solids. 2012;60:525–537. [Google Scholar]
- 23.Cowin SC, Hegedus DH. Bone remodeling. 1. Theory of adaptive elasticity. J Elast. 1977;6:313–326. [Google Scholar]
- 24.Cowin SC. Tissue growth and remodeling. Ann Rev Biomed Eng. 2004;6:77–107. doi: 10.1146/annurev.bioeng.6.040803.140250. [DOI] [PubMed] [Google Scholar]
- 25.Dassiso G, Lindel IV. On the Helmholtz decomposition for polyadics. Quart Appl Math. 2001;59:787–796. [Google Scholar]
- 26.Dervaux J, Ciarletta P, Ben Amar M. Morphogenesis of thin hyperelastic plates: A constitutive theory of biological growth in the Föppl-von Karman limit. J Mech Phys Solids. 2009;57:458–471. [Google Scholar]
- 27.Dumais J, Shaw SL, Steele CR, Long SR, Ray PM. An anisotropicviscoplastic model of plant cell morphogenesis by tip growth. Int J Dev Bio. 2006;50:209–222. doi: 10.1387/ijdb.052066jd. [DOI] [PubMed] [Google Scholar]
- 28.Epstein M, Maugin GA. Thermomechanics of volumetric growth in uniform bodies. Int J Plast. 2000;16:951–978. [Google Scholar]
- 29.Famaey N, Vander Sloten J, Kuhl E. A three-constituent damage model for arterial clamping in computer-assisted surgery. Biomech Model Mechanobio. 2012 doi: 10.1007/s10237-012-0386-7. [DOI] [PubMed] [Google Scholar]
- 30.Finlay HM, McCullough L, Canham PB. Three-dimensional collagen organization of human brain arteries at different transmural pressures. J Vas Res. 1995:301–312. doi: 10.1159/000159104. [DOI] [PubMed] [Google Scholar]
- 31.Garikipati K, Arruda EM, Grosh K, Narayanan H, Calve S. A continuum treatment of growth in biological tissue: The coupling of mass transport and mechanics. J Mech Phys Solids. 2004:1595–1625. [Google Scholar]
- 32.Garikipati K. The kinematics of biological growth. Appl Mech Rev. 2009;62:030801.1–030801.7. [Google Scholar]
- 33.Gibson LJ, Ashby MF. 1997 The mechanics of three–dimensional cellular materials. Proc R Soc London A. 1997;382:43–59. [Google Scholar]
- 34.Göktepe S, Abilez OJ, Parker KK, Kuhl E. A multiscale model for eccentric and concentric cardiac growth through sarcomerogenesis. J Theor Bio. 2010;265:433–442. doi: 10.1016/j.jtbi.2010.04.023. [DOI] [PubMed] [Google Scholar]
- 35.Göktepe S, Abilez OJ, Kuhl E. A generic approach towards finite growth with examples of athlete’s heart, cardiac dilation, and cardiac wall thickening. J Mech Phys Solids. 2010;58:1661–1680. [Google Scholar]
- 36.Goriely A, Tabor M. Biomechanical models of hyphal growth in actinomycetes. J Theor Bio. 2003;222:211218. doi: 10.1016/s0022-5193(03)00029-8. [DOI] [PubMed] [Google Scholar]
- 37.Goriely A, BenAmar M. Differential growth and instability in elastic shells. Phys Rev Letters. 2005;94:198103. doi: 10.1103/PhysRevLett.94.198103. [DOI] [PubMed] [Google Scholar]
- 38.Goriely A, BenAmar M. On the definition and modeling of incremental, cumulative, and continuous growth laws in morphoelasticity. Biomech Mod Mechanobio. 2007;6:289296. doi: 10.1007/s10237-006-0065-7. [DOI] [PubMed] [Google Scholar]
- 39.Gosain AK, Cortes W. Pediatric tissue expansion for forehead reconstruction: A 13-year review and an algorithm for its use. Am Soc Plast Surg. Baltimore. 2007 Abstract 13288. [Google Scholar]
- 40.Grytz R, Girkin CA, Libertiaux V, Downs JC. Perspectives on biomechanical growth and remodeling mechanisms in glaucoma. Mech Res Comm. 2012;42:92–106. doi: 10.1016/j.mechrescom.2012.01.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Harrigan TP, Hamilton JJ. An analytical and numerical study of the stability of bone remodelling theories: dependence on microstructural stimulus. J. Biomechanics. 1992;25:477–488. doi: 10.1016/0021-9290(92)90088-i. Corrigendum, 1993;26:365–366. [DOI] [PubMed] [Google Scholar]
- 42.Harrysson M, Ristinmaa M, Wallin M, Menzel A. Framework for deformation induced anisotropy in glassy polymers. Acta Mech. 2010;211:195–213. [Google Scholar]
- 43.Himpel G, Kuhl E, Menzel A, Steinmann P. Computational modeling of isotropic multiplicative growth. Comp Mod Eng Sci. 2005;8:119–134. [Google Scholar]
- 44.Himpel G, Menzel A, Kuhl E, Steinmann P. Time-dependent fiber reorientation of transversely isotropic continua - Finite element formulation and consistent linearization. Int J Num Meth Eng. 2008;73:1413–1433. [Google Scholar]
- 45.Hoger A. The elasticity tensor of a transversely isotropic hyperelastic material with residual stress. J Elast. 1996;42:115–132. [Google Scholar]
- 46.Holzapfel GA, Ogden RW, editors. Number 441 in CISM Courses and Lectures. Springer; 2003. Biomechanics of Soft Tissue in Cardiovascular Systems. [Google Scholar]
- 47.Hsu HF. The influence of mechanical loads on the form of a growing elastic body. J Biomech. 1968;1:303–311. doi: 10.1016/0021-9290(68)90024-9. [DOI] [PubMed] [Google Scholar]
- 48.Humphrey JD. Stress, strain, and mechanotransduction in cells. J Biomech Eng. 2001;123:638–641. doi: 10.1115/1.1406131. [DOI] [PubMed] [Google Scholar]
- 49.Humphrey JD. Cardiovascular tissue mechanics: Cells, tissues, and organs. Springer; 2002. [Google Scholar]
- 50.Humphrey JD, Rajagopal KR. A constrained mixture model for growth and remodeling of soft tissues. Math Mod Meth Appl Sci. 2002;12:407–430. [Google Scholar]
- 51.Imatani S, Maugin GA. A constitutive model for material growth and its application to three-dimensional finite element analysis. Mech Res Comm. 2002;29:477–483. [Google Scholar]
- 52.Isaksson H. Recent advances in mechanobiological modeling of bone regeneration. Mech Res Comm. 2012;42:22–31. [Google Scholar]
- 53.Itoh A, Krishnamurthy G, Swanson J, Ennis D, Bothe W, Kuhl E, Karlsson M, Davis L, Miller DC, Ingels NB. Active stiffening of mitral valve leaflets in the beating heart. Am J Physiol Heart Circ Physiol. 2009;296:1766–1773. doi: 10.1152/ajpheart.00120.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Jaalouk DE, Lammerding J. Mechanotransduction gone awry. Nature Rev Mol Cell Bio. 2009;10:63–73. doi: 10.1038/nrm2597. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Kerckhoffs R, Omens J, McCulloch AD. A single strain-based growth law predicts concentric and eccentric cardiac growth during pressure and volume overload. Mech Res Comm. 2012;42:40–50. doi: 10.1016/j.mechrescom.2011.11.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Klepach D, Lee LC, Wenk JF, Ratcliffe MB, Zohdi TI, Navia JL, Kassab GS, Kuhl E, Guccione JM. Growth and remodeling of the left ventricle: A case study of myocardial infarction and surgical ventricular restoration. Mech Res Comm. 2012;42:134–141. doi: 10.1016/j.mechrescom.2012.03.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Krishnamurthy G, Ennis DB, Itoh A, Bothe W, Swanson-Birchill JC, Karlsson M, Kuhl E, Miller DC, Ingels NB. Material properties of the ovine mitral valve anterior leaflet in vivo from inverse finite element analysis. Am J Physiol Heart Circ Physiol. 2008;295:H1141–H1149. doi: 10.1152/ajpheart.00284.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Kroeger J, Daher FB, Grant M, Geitmann A. Microfilament orientation contrains vesicle flow and spatial distribution in growing pollen tubes. Biophys J. 2009;97:1822–1831. doi: 10.1016/j.bpj.2009.07.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Kroeger J, Geitmann A. Pollen tube growth: getting a grip on cell biology through modeling. Mech Res Comm. 2012;42:32–39. [Google Scholar]
- 60.Kröner E. Physics of Defects. North-Holland: 1981. Continuum theory of defects; pp. 215–315. [Google Scholar]
- 61.Kroon W, Delhaas T, Arts T, Bovendeerd P. Computational modeling of volumetric soft tissue growth: Application to the cardiac left ventricle. Biomech Mod Mechanobio. 2009;8:310–309. doi: 10.1007/s10237-008-0136-z. [DOI] [PubMed] [Google Scholar]
- 62.Kuhl E, Steinmann P. Mass- and volume specific views on thermodynamics for open systems. Proc Royal Soc. 2003;459:2547–2568. [Google Scholar]
- 63.Kuhl E, Steinmann P. On spatial and material settings of thermohyperelastodynamics for open systems. Acta Mech. 2003;160:179–217. [Google Scholar]
- 64.Kuhl E, Menzel A, Steinmann P. Computational modeling of growth - A critical review, a classification of concepts and two new consistent approaches. Comp Mech. 2003;32:71–88. [Google Scholar]
- 65.Kuhl E, P Steinmann P. Theory and numerics of geometrically nonlinear open systems. Int J Num Meth Eng. 2003;58:1593–1615. [Google Scholar]
- 66.Kuhl E, Steinmann P. Computational modeling of healing - An application of the material force method. Biomech Mod Mechanobio. 2004;2:187–203. doi: 10.1007/s10237-003-0034-3. [DOI] [PubMed] [Google Scholar]
- 67.Kuhl E, Garikipati K, Arruda EM, Grosh K. Remodeling of biological tissue - Mechanically induced reorientation of a transversely isotropic chain network. J Mech Phys Solids. 2005;53:1552–1573. [Google Scholar]
- 68.Kuhl E, Maas R, Himpel G, Menzel A. Computational modeling of arterial wall growth: Attempts towards patient-specific simulations based on computer tomography. Biomech Mod Mechanobio. 2007;6:321–331. doi: 10.1007/s10237-006-0062-x. [DOI] [PubMed] [Google Scholar]
- 69.Kuhl E, Holzapfel GA. A continuum model for remodeling in living structures. J Mat Sci. 2007;42:8811–8823. [Google Scholar]
- 70.Kumar V, Abbas AK, Fausto N. Robbins and Cotran Pathologic Basis of Disease. Elsevier Saunders; 2005. [Google Scholar]
- 71.Lee EH. Elastic-plastic deformation at finite strains. J Appl Mech. 1969;36:1–6. [Google Scholar]
- 72.Li B, Cao YP, Feng XQ, Gao H. Surface wrinkling of mucosa induced by volumetric growth: Theory, simulation and experiment. J Mech Phys Solids. 2011;59:758–774. [Google Scholar]
- 73.Lodge AS. Body Tensor Fields in Continuum Mechanics – With Application to Polymer Rheology. Academic Press; 1974. [Google Scholar]
- 74.Lubarda A, Hoger A. On the mechanics of solids with a growing mass. Int J Solids & Structures. 2002;39:4627–4664. [Google Scholar]
- 75.Lubarda VA. Constitutive theories based on the multiplicative decomposition of deformation gradient: Thermoelasticity, elastoplasticity and biomechanics. Appl Mech Rev. 2004;57:95108. [Google Scholar]
- 76.McMahon J, Goriely A, Tabor M. Spontaneous cavitation in growing elastic membranes. Math Mech Solids. 2010;15:57–77. [Google Scholar]
- 77.Menzel A. Modelling of anisotropic growth in biological tissues - A new approach and computational aspects. Biomech Mod Mechanobiol. 2005;3:147–171. doi: 10.1007/s10237-004-0047-6. [DOI] [PubMed] [Google Scholar]
- 78.Menzel A. A fibre reorientation model for orthotropic multiplicative growth. Biomech Mod Mechanobiol. 2007;6:303–320. doi: 10.1007/s10237-006-0061-y. [DOI] [PubMed] [Google Scholar]
- 79.Menzel A, Harrysson M, Ristinmaa M. Towards an orientation-distribution-based multi-scale approach for remodelling biological tissues. Comput. Meth. Biomech. Biomed. Eng. 2008;11:505–524. doi: 10.1080/10255840701771776. [DOI] [PubMed] [Google Scholar]
- 80.Menzel A, Steinmann P. On the continuum formulation of higher gradient plasticity for single and polycrystals. J. Mech. Phys. Solids. 2000;48:1777–1796. Erratum, 2001;49:1179–1180. [Google Scholar]
- 81.Menzel A, Steinmann P. A view on anisotropic finite hyper-elasticity. Euro. J. Mech. A/Solids. 2003;22:71–87. [Google Scholar]
- 82.Menzel A, Steinmann P. On the spatial formulation of anisotropic multiplicative elasto-plasticity. Comput. Methods Appl. Mech. Engrg. 2003;192:3431–3470. [Google Scholar]
- 83.Menzel A, Waffenschmidt T. A micro-sphere-based remodelling formulation for anisotropic biological tissues. Phil Trans R Soc A. 2009;367:3499–3523. doi: 10.1098/rsta.2009.0103. [DOI] [PubMed] [Google Scholar]
- 84.Moulton DE, Goriely A. Circumferential buckling instability of a growing cylindrical tube. J Mech Phys Solids. 2011;59:525–537. [Google Scholar]
- 85.Mow VC, Holmes MH, Lai WM. Fluid transport and mechanical properties of articular cartilage - A review. J Biomech. 1984;17:377–394. doi: 10.1016/0021-9290(84)90031-9. [DOI] [PubMed] [Google Scholar]
- 86.Murtada SI, Kroon M, Holzapfel GA. A calcium-driven mechanochemical model for prediction of force generation in smooth muscle. Biomech Mod Mechanobiol. 2010;9:749762. doi: 10.1007/s10237-010-0211-0. [DOI] [PubMed] [Google Scholar]
- 87.Naghdi P. A critical review of the state of finite plasticity. J App Math Phys. 1990;41:315–394. [Google Scholar]
- 88.Noll W. Materially uniform simple bodies with inhomogeneities. Arch Rational Mech Anal. 1967;27:1–32. Erata. Noll W, Toupin RA, Wang CC. Arch Rational Mech Anal. 1968;31:401. [Google Scholar]
- 89.Ogden RW. Non–Linear Elastic Deformations. Dover; 1997. [Google Scholar]
- 90.Olver PJ. Application of Lie Groups to Differential Equations, volume 107 of Graduate Texts in Mathematics. 2nd edition. Springer; 1993. [Google Scholar]
- 91.Pang H, Shiwalkar AP, Madormo CM, Taylor RE, Andriacchi TP, Kuhl E. Computational modeling of bone density profiles in response to gait: A subject-specific approach. Biomech Mod Mechanobiol. 2012;11:379–390. doi: 10.1007/s10237-011-0318-y. [DOI] [PubMed] [Google Scholar]
- 92.Pluijmert M, Kroon W, Delhaas T, Bovendeerd P. Adaptive reorientation of cardiac myofibers: the long-term effect on initial and boundary conditions. Mech Res Comm. 2012;42:60–67. [Google Scholar]
- 93.Preziosi L, Tosin AR. Multiphase modelling of tumour growth and extracellular matrix interaction: Mathematical tools and applications. J Math Bio. 2009;58:625–656. doi: 10.1007/s00285-008-0218-7. [DOI] [PubMed] [Google Scholar]
- 94.Rausch MK, Dam A, Göktepe S, Abilez OJ, Kuhl E. Computational modeling of growth: Systemic and pulmonary hypertension in the heart. Biomech Mod Mechanobiol. 2011;10:799–811. doi: 10.1007/s10237-010-0275-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.Rodriguez EK, Hoger A, McCulloch AD. Stress-dependent finite growth in soft elastic tissues. J Biomech. 1994;27:455–467. doi: 10.1016/0021-9290(94)90021-3. [DOI] [PubMed] [Google Scholar]
- 96.Schmid H, Pauli L, Paulus A, Kuhl E, Itskov M. How to utilise the kinematic constraint of incompressibility for modelling adaptation of soft tissues. Comp Meth Biomech Biomed Eng. 2012;15:547–561. doi: 10.1080/10255842.2010.548325. [DOI] [PubMed] [Google Scholar]
- 97.Schröder J, Neff P, editors. Number 516 in CISM Courses and Lectures. Springer; 2010. Poly-, Quasi- and Rank-One Convexity in Applied Mechanics. [Google Scholar]
- 98.Šilhavý M. Texts and Monographs in Physics. Springer; 1997. The Mechanics and Thermomechanics of Continuous Media. [Google Scholar]
- 99.Skalak R. Growth as a finite displacement field. IUTAM Symposium on Finite Elasticity. Martinus Nijhoff. 1981:347–355. [Google Scholar]
- 100.Skalar R, Farrow DA, Hoger A. Kinematics of surface growth. J Math Bio. 1997;35:869–907. doi: 10.1007/s002850050081. [DOI] [PubMed] [Google Scholar]
- 101.Socci L, Rennati G, Gervaso F, Vena P. An axisymmetric computational model of skin expansion and growth. Biomech Mod Mechanobiol. 2007;6:177–188. doi: 10.1007/s10237-006-0047-9. [DOI] [PubMed] [Google Scholar]
- 102.Taber LA. Biomechanics of growth, remodeling and morphogenesis. Appl Mech Rev. 1995;48:487–545. [Google Scholar]
- 103.Taber LA, Humphrey JD. Stress-modulated growth, residual stress, and vascular heterogeneity. J Biomech Eng. 2001;123:528–535. doi: 10.1115/1.1412451. [DOI] [PubMed] [Google Scholar]
- 104.Taylor RE, Zheng C, Jackson PR, Doll JC, Chen JC, Holzbaur KRS, Besier T, Kuhl E. The phenomenon of twisted growth: Humeral torsion in dominant arms of high performance tennis players. Comp Meth Biomech Biomed Eng. 2009;12:83–93. doi: 10.1080/10255840903077212. [DOI] [PubMed] [Google Scholar]
- 105.Thompson AW. On Growth and Form. Cambridge University Press; 1917. [Google Scholar]
- 106.Tsamis A, Cheng A, Nguyen TC, Langer F, Miller DC, Kuhl E. Kinematics of cardiac growth - In vivo characterization of growth tensors and strains. J Mech Behavior Biomed Mat. 2012;8:165–177. doi: 10.1016/j.jmbbm.2011.12.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 107.Valentin A, Holzapfel GA. Constrained mixture models as tools for testing competing hypotheses in arterial biomechanics: a survey. Mech Res Comm. 2012;42:126–133. doi: 10.1016/j.mechrescom.2012.02.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 108.Vandiver R, Goriely A. Differential growth and residual stress in cylindrical elastic structures. Phil Trans Royal Soc A. 2009;367:3607–3630. doi: 10.1098/rsta.2009.0114. [DOI] [PubMed] [Google Scholar]
- 109.Verdier C, Etienne J, Duperray A, Preziosi L. Review: Rheological properties of biological materials. Comptes Rendus Phys. 2009;10:790–811. [Google Scholar]
- 110.Waffenschmidt T, Menzel A, Kuhl E. Anisotropic density growth of bone. A computational micro-sphere approach. submitted for publication. 2012 [Google Scholar]
- 111.Waffenschmidt T, Menzel A. Application of an anisotropic growth and remodeling formulation to computational topology optimization. Mech Res Comm. 2012;42:77–86. [Google Scholar]
- 112.Wolff J. Über die innere Architectur der Knochen und ihre Bedeutung für die Frage vom Knochenwachstum. Virchows Archiv für Pathologische Anatomie und Physiologie und für Klinische Medizin. 1870;50:389–453. [Google Scholar]
- 113.Wong VW, Akaishi S, Longaker MT, Gurtner GC. Pushing back: Wound mechanotransduction in repair and regeneration. J Invest Dermatol. 2011 doi: 10.1038/jid.2011.212. [DOI] [PubMed] [Google Scholar]
- 114.Zeinali-Davarani S, Baek S. Medical image-based simulation of abdominal aortic aneurysm growth. Mech Res Comm. 2012;42:107–117. [Google Scholar]
- 115.Zöllner AM, Buganza Tepole A, Gosain AK, Kuhl E. Growing skin - Tissue expansion in pediatric forehead reconstruction. Biomech Mod Mechanobio. 2012;11:855–867. doi: 10.1007/s10237-011-0357-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 116.Zöllner AM, Buganza Tepole A, Kuhl E. On the biomechanics and mechanobiology of growing skin. J Theor Bio. 2012;297:166–175. doi: 10.1016/j.jtbi.2011.12.022. [DOI] [PMC free article] [PubMed] [Google Scholar]