Magnetic resonance assessment of parenchymal elasticity in normal and edematous, ventilator-injured lung

Abstract

Magnetic resonance elastography (MRE) is a MR imaging method capable of spatially resolving the intrinsic mechanical properties of normal lung parenchyma. We tested the hypothesis that the mechanical properties of edematous lung exhibit local properties similar to those of a fluid-filled lung at transpulmonary pressures (P_tp) up to 25 cm H₂O. Pulmonary edema was induced in anesthetized female adult Sprague-Dawley rats by mechanical ventilation to a pressure of 40 cm H₂O for ∼30 min. Prior to imaging the wet weight of each ex vivo lung set was measured. MRE, high-resolution T₁-weighted spin echo and T₂* gradient echo data were acquired at each P_tp for both normal and injured ex vivo lungs. At P_tps of 6 cm H₂O and greater, the shear stiffness of normal lungs was greater than injured lungs (P ≤ 0.0003). For P_tps up to 12 cm H₂O, shear stiffness was equal to 1.00, 1.07, 1.16, and 1.26 kPa for the injured and 1.31, 1.89, 2.41, and 2.93 kPa for normal lungs at 3, 6, 9, and 12 cm H₂O, respectively. For injured lungs MRE magnitude signal and shear stiffness within regions of differing degrees of alveolar flooding were calculated as a function of P_tp. Differences in shear stiffness were statistically significant between groups (P < 0.001) with regions of lower magnitude signal being stiffer than those of higher signal. These data demonstrate that when the alveolar space filling material is fluid, MRE-derived parenchymal shear stiffness of the lung decreases, and the lung becomes inherently softer compared with normal lung.

recent advances in magnetic resonance (MR) imaging have demonstrated that the mechanical properties of various biological tissues can be noninvasively quantified and spatially resolved (20, 21, 24, 31, 33, 34). The technique, first described in 1995 (18) involves visualization of a propagating shear wave field induced by some form of mechanical vibration using phase contrast-based MR imaging techniques. Resolution of the local shear wavelength at each voxel allows estimation of the shear stiffness by inversion of the wave equation that describes shear wave propagation within an elastic or viscoelastic medium. Visualization of propagating shear wave fields followed by mathematical inversion to spatially resolve shear stiffness is collectively known as MR elastography (MRE) (18). Recently, it has been demonstrated that conventional (i.e., proton) MRE can be applied to the lung and that it is possible to both quantify and spatially resolve the elastic properties of this organ under ex vivo (16), in situ (15), and in vivo (14) imaging conditions. The relevance of MRE to lung physiology is its potential to noninvasively probe the intrinsic mechanical properties of the lung that result from the balance of forces due to prestress of the tissue network and surface tension produced by the gas-liquid interface within each alveolus (26, 27).

Historically, the mechanical properties of the lung have been quantified in terms of lung compliance, which is given as the volume change per unit of pressure change (ΔV/ΔP) of the pressure-volume curve in liters per centimeter of water (22) and is known to be altered under a variety of conditions. For instance, in the case of surfactant depletion, surface tension increases, decreasing lung compliance (i.e., the lung becomes harder) (1). In contrast, filling of alveolar spaces with saline, in effect, eliminating interfacial forces, increases overall lung compliance (i.e., the lung becomes softer) (30). Inflammatory processes associated with acute lung injury also lead to disruption of the alveolar-capillary barrier and often involve surfactant deactivation by plasma proteins. In acute lung injury, the mechanical properties of the air-space filling material are highly variable because of its heterogeneous composition, which can consist of fluid, gel, and foam. Under these conditions, lung compliance decreases (2, 4), and the lung as a whole appears stiffer. However, the determinants of whole lung compliance in injury states are complex and largely reflect a reduction in the number of recruitable alveoli rather than a change in their individual mechanical properties themselves. This insight may be attributed to Gattinoni, who, after examining chest CT scans, likened injured lungs to small “baby lungs” (6, 7). The behavior of edematous lungs is also complex, as large pressures are required to brake or displace liquid bridges in small airways and/or move air-liquid interfaces toward the alveolar gas exchange surface (32). As long as the alveolar exudate is liquid, lung regions that are occluded by liquid plugs may be recruited through the intermittent application of high airway pressures. However, once the alveolar liquid turns into a gel or becomes organized, i.e., has been infiltrated with matrix-secreting cells, the airspace-filling material can no longer be displaced at physiological pressures and the alveolus can no longer be recruited.

When a terminal lung unit becomes flooded, its mechanical properties will mimic those of a fluid-filled lung as long as the space-filling material is a liquid and the energy required to change the shape of the air-fluid interface is small. Stamenovic and Yager (25) illustrated this concept in air- and fluid-filled lungs by demonstrating that under isovolumetric conditions, the elastic properties of fluid-filled lungs were less (i.e., softer) than air-filled lungs while at constant P_tp, air-filled lungs were more elastic (i.e., stiffer), pointing to the contribution of surface tension as a moderator of lung elasticity. In the absence of surface tension forces, the lung will more readily undergo isovolumic deformation due to the decreased prestress within the parenchyma. In contrast, the impedance of fluid within the injured lung is expected to be high, requiring relatively large pressures to displace air-fluid interfaces into the lung periphery. Therefore, under injurious conditions characterized by the presence of a liquid exudate, there is a disassociation between the intrinsic mechanical properties of lung parenchyma and P_tp, indicating that conventional pressure–volume-based methods for assessing function cannot be applied to accurately quantify lung mechanical properties. Therefore, we hypothesize that edematous regions of the lung are inherently less elastic (i.e., softer) than fully aerated or normal lung, independent of P_tp. The objective of this study was to test this hypothesis by demonstrating that MRE is capable of quantifying and spatially resolving lung injury, and in doing so, providing evidence that lung mechanical properties provide new insights into the extent and nature of lung disease processes.

The noninvasive nature of MRE and the ability to spatially resolve an important biomarker (i.e., shear stiffness) of function within the lung means that MRE can be applied to assess the central hypothesis proposed in this work that when the space-filling material is fluid, the lung will be soft. This new lung biomarker also has the potential to answer as yet unresolved questions in lung disease, including, but not limited to the following: 1) Are the mechanics of the unaffected portions of injured lungs normal or not? 2) Are partially flooded aerated regions stiffer than normally aerated regions? and 3) Does a foam plug proximal to a fully flooded region influence the mechanics of those regions (i.e., does it make the flooded region stiffer compared with a completely saline-filled lung?). Therefore, we propose that MRE-based estimates of parenchyma shear stiffness are sufficiently sensitive to detect changes in the mechanical properties of the lung, resulting from the disruption of the alveolar gas-liquid interface. To test this hypothesis, MRE was performed in both injured (i.e., edematous) and fully normal adult rat lungs as a function of transpulmonary pressure (P_tp). MRE-derived estimates of global shear stiffness were compared between groups, while regional estimates were compared between regions of various degrees of alveolar flooding within a single injured lung.

MATERIALS AND METHODS

Animal Preparation

Injured and normal lung shear stiffness for 3 cm ≤ P_tp < 12 cm H₂O.

Two groups of six female adult Sprague-Dawley (Harlan Laboratories, Indianapolis, IN) rats served as a source for injured and normal lungs, respectively. The animals of the injury group were anesthetized with pentobarbital sodium (30 mg/kg ip) followed by intubation with a tracheal cannula. The cannula was then connected to a small animal ventilator (Flexivent, Montreal, Quebec CA), and the animal was ventilated at a respiratory rate of 80 cycles/min, a maximum inspiration/expiration ratio of 50% and a maximum tidal volume of 55 ml/kg, resulting in a peak airway pressure of between 30 and 40 cm H₂O for ∼30 min or until foam was observed at the tip of the cannula. Immediately following ventilation, the animal was killed and the lungs, heart, thymus, and trachea were removed en block. All organs were kept intact to avoid leakage of blood products from the lungs. A wet weight for the lung set was then obtained (Ohaus SP6001, Parsippany, NJ). Normal lungs were harvested from animals after receipt of a fatal dose of pentobarbital sodium (100 mg/kg). For these lungs, the atria and ventricles of the heart were removed so as to obtain a wet weight of only the lungs, trachea, and thymus. Immediately prior to imaging, normal lungs were degassed to a pressure of −760 mmHg for ∼2 min using an in-house vacuum pump and bell jar system (17). After removal of the vacuum, the lungs were allowed to return to atmospheric pressure and were then inflated to a pressure of 20 cm H₂O. While a total of six normal lungs were used in this study, two data sets from a previously published report were included (17). Thus, the total number of animals killed in this study was 10 (6 injured and 4 normal).

Injured lung shear stiffness for 0 cm ≤ P_tp < 25 cm H₂O.

To investigate the effect of lung shear stiffness in injured lungs over a large range of P_tp values, lung injury was created in an additional three female adult Sprague-Dawley rats using the methods described above. Animal preparation protocols for all lungs were approved by the Institutional Animal Care and Use Committee of Mayo Clinic Rochester.

Experimental Apparatus

All experiments were performed on a 1.5-T whole body MRI system (GE Healthcare, Waukesha, WI). For the comparison of normal and injured lungs, lungs were inflated to a pressure of 3 cm H₂O and were then placed on a custom-built pneumatic MRE shear driver and stage that inserted into a 6-cm diameter transmit-receive RF birdcage coil as described previously (17), after which ¹H MR imaging was performed. Throughout each experiment, real-time P_tp measurements were acquired as previously described (17). For injured lungs, imaging was repeated at pressures of 3, 6, 9, and 12 cm H₂O in sequential order. In contrast, after imaging at 3 cm H₂O, normal lungs were inflated to a pressure of 20 cm H₂O for 1 min followed by deflation to 6 cm H₂O, after which imaging was repeated. This process was repeated for additional inflation pressures of 9 and 12 cm H₂O and performed to ensure that data were obtained along the deflation phase of the pressure-volume curve. The second set of injured lungs were removed en bloc from the host and placed on the stage of the shear driver. Imaging was then performed at P_tp values of 0 cm, 3 cm, 10 cm, 15 cm, 20 cm, and 25 cm H₂O. For normal lungs, the expiratory phase of the pressure-volume curve was used to ensure consistency with previously reported normal lung MRE data (17). In contrast, injured lungs did not undergo the same pressure cycles but were instead imaged on the inspiratory phase of the pressure-volume curve. Although both lung sets were not imaged with the same pressure-volume history, imaging of injured lungs in this manner was necessary to preserve fluid plugs and foam bridges that would be disrupted if the lungs were cycles to a maximum inflation pressure of either 20 or 25 cm H₂O.

MR Imaging

At each P_tp, both conventional MR imaging and MRE data were acquired. Imaging parameters for MRE included pulse sequence = spin echo, field of view (FOV) = 6 cm, slice = 5 mm, k_x = 128, k_y = 64, TE/TR = 13/318 ms, shear wave motion encoding = 220 Hz, phase offsets = 4. Between 8 and 10 two-dimensional axial MRE slices were acquired with motion sensitization along the physical z-axis or through plane. Conventional MR imaging sequences were also acquired at each inflation pressure. The first was a T₁-weighted two-dimensional spin echo sequence (TE/TR = 10/600 ms, k_x = 192, k_y = 160, FOV = 8 cm, slice = 4 mm, interslice spacing 4 mm), which was processed using an in-house software application to calculate the volume of the lung in cubic centimeters (cc). The second was a T₂*-weighted multiecho gradient echo sequence (no. echoes = 3, TE_1,2,3 = 1.6, 2.6, 3.6 ms, TR = 12.5 ms, α = 10°_, k_x = 128, k_y = 128, FOV = 15 cm, slice = 5 mm). Before acquisition of the T₂*-weighted data, a 3-cc tube of gadolinium (Magnevist, Berlex Laboratories, Wayne, NJ) doped normal saline (0.9% sodium chloride; Baxter Healthcare, Deerfield, IL) at a concentration of 1:5,500, consistent with that reported by Theilmann et al. (29) was placed below the stage supporting the lung specimen. The signal from the saline-doped tube was used as a normalization factor and assumed to represent a density of 1,000 kg/m³ or 1.0 g/cm³. T₂*-weighted images were processed using an in-house software program that calculated the T₂* of each pixel by solving the pair of simultaneous equations of the form S_i = S₀e ^{−TE_i/T₂*}, where S_i was the signal for echo number i, S₀ the signal at TE = 0 (i.e., proton density), and TE_i is the echo time for echo number i, with i being equal to the first and third echoes in the series. The application then solved for S₀ using the first echo data. The signal from the saline tube was used to normalize S₀, as reported by Theilmann et al. (29). This ratio was then assumed to be equal to the density of the lung in units of grams per centimeter cubed (g/cm³). Linear interpolation was performed to reconstruct T₂*-derived density maps obtained for the injured lungs to a 6-cm field of view.

Global and Regional Shear Stiffness Estimation

To quantitate the shear stiffness of both injured and normal lungs, principal frequency analysis (PFA) (17) was applied to those two-dimensional MRE slices that included lung only (i.e., did not include heart and/or thymus) and in which shear wave propagation was evident. Because PFA analysis estimates the principal spatial frequency of the shear wave field within the image and, therefore, provides only a single estimate of shear stiffness within a single slice, those slices that included lung only were analyzed. Despite the global nature of this method, PFA analysis has been shown to accurately calculate the shear stiffness of low signal-to-noise (SNR) data, such as normal lung (17). When the density of the tissue is not equal to 1.0 g/cm³, the value reported by PFA is equal to the wave shear wave speed squared and must be corrected for by the density of the tissue to obtain the shear stiffness in units of kilopascals. To perform this conversion, PFA values were multiplied by the physical density of the entire lung, which was given by the ratio of the wet weight (obtained postresection and described above) to the total lung volume where the total lung volume in cc was obtained from contouring of the spin-echo anatomical images acquired at each inflation pressure. Injured lungs were also processed with the local frequency estimation (LFE) method (13) so as to spatially resolve shear stiffness throughout the lung. LFE elastograms were multiplied by the T₂*-derived density maps to account for regional density variations. For both LFE and PFA analysis, directional filtering of the phase-difference shear wave fields using a Butterworth band pass filter with cut-off frequencies of 0.5 and 40 waves per field of view was performed prior to estimation of the shear stiffness.

It is important to appreciate that both PFA and LFE algorithms quantify shear modulus by calculating the local wave speed of the propagating shear wave. The product of the wave speed squared and density is equal to the shear modulus. If the material is linearly elastic, the shear stiffness is a purely real number and exactly quantified by both methods. For viscoelastic tissues, the wave speed includes the effects of attenuation and the shear modulus is a complex quantity. Under these conditions, the value calculated by both algorithms represents and effective shear modulus and is described as the shear stiffness of the material. By acquiring data at multiple frequencies, both approaches can provide estimates of the real and imaginary components of the complex shear modulus, providing insight into the exact nature of the tissue. In this work, a single shear wave frequency was used to determine the effective stiffness of both injured and normal lungs. Calculation of shear stiffness does not presume that the lung is either linearly elastic or includes a viscous component consistent with other biological tissues.

Identification of Regional Lung Flooding

After calculation of LFE-derived shear stiffness maps for all six edematous lungs, a single observer (DLL) surveyed the magnitude of MRE images and identified two regions within each lung set using an in-house image display program. The first region consisted of heterogeneous and low signal intensity, while the second region consisted of higher signal and uniform intensity distribution. The low-signal, highly heterogeneous regions were considered to be areas where partial flooding was present, while the areas of uniform signal intensity were considered fully flooded. These sections were visually correlated with optical images of the lungs obtained during imaging. Changes in both the LFE T₂*-derived density corrected shear stiffness and signal intensity of the magnitude image were recorded for both regions within each lung as a function of inflation pressure.

Statistical Analysis

Several statistical tests were applied to the MRE-derived estimates of shear stiffness. A hierarchical linear model was used to test whether shear modulus was differentially affected by pressure change in injured vs. normal lungs. Pressure was treated as a factor with four levels. The compound symmetry covariance pattern was used to describe the association of shear modulus readings within an individual animal lung (i.e., repeated-measures analysis). To determine whether differences between the two estimates of density (physical vs. T₂*-derived) exist, a paired t-test was applied to the density estimate for each of the injured lungs as a function of inflation pressure. To determine whether differences between observer-identified partially and fully flooded regions exist, the same hierarchical model was applied to both the average value of LFE-derived shear stiffness and magnitude within each region as a function of inflation pressure. To test for differences in shear stiffness of injured lungs over the pressure range of 0 to 25 cm H₂O, a mixed model was used to account for the repeated measurements within each lung. Post hoc comparisons across pressures were tested for statistical significance using the Tukey-Kramer correction for multiple comparisons. Post hoc differences with P value < 0.05 after correction were interpreted as statistically significant.

RESULTS

Lung Density

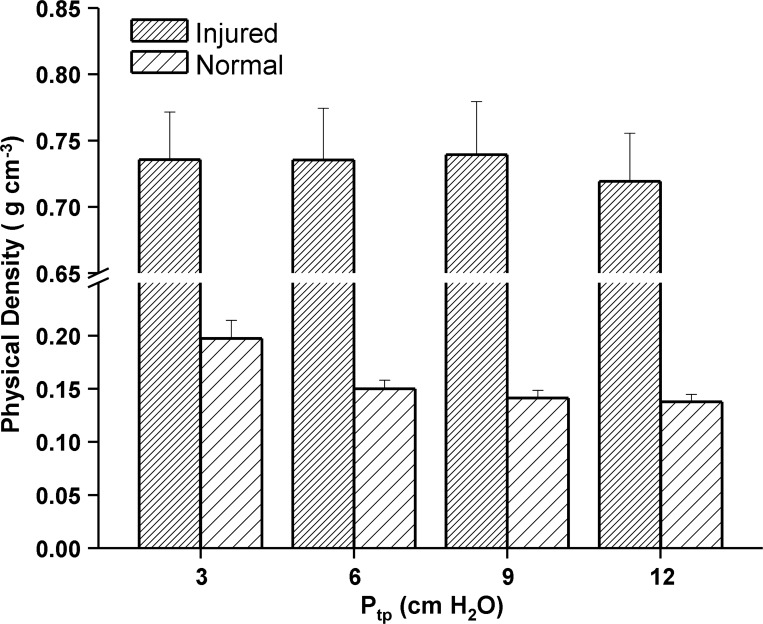
The physical density of normal, fully aerated lungs ranged from 0.123 g/cm³ to 0.269 g/cm³ while injured, edematous lung physical density ranged from 0.231 g/cm³ to 0.883 g/cm³ over the range of inflation pressures used in this study. Figure 1 is a plot of the physical density for both injured and normal lungs imaged at P_tp values ranging from 3 to 12 cm H₂O (i.e., data set one). Error bars represent one standard error (SE). The larger standard error of the injured lungs reflects the heterogeneity of the ventilator-induced injury. The noninjured lungs were of lower physical density and exhibited a negative dependence with increasing P_tp, which was not observed in the injured density estimates. The T₂*-derived physical density for injured lungs ranged from 0.234 g/cm³ to 0.955 g/cm³ over the full range of P_tp values used in this study (0 to 25 cm H₂O). To determine whether differences between the physical and T₂* estimates of density were statistically significant, a paired Student's t-test was applied to both density estimates at each inflation pressure. The difference in the mean density across all pressures was 9.74 × 10⁻³ g/cm³, which was not statistically significant (t = −0.274, P = 0.784, degrees of freedom = 90).

Fig. 1.

Histogram of whole lung physical density (wet weight/volume) for normal and injured lungs as a function of transpulmonary pressure (P_tp). Each histogram represents the group average, while the error bar is equal to one SD. Injured lungs exhibited little change in physical density, while normal lungs were of lower density and decreased with increasing inflation pressure as expected.

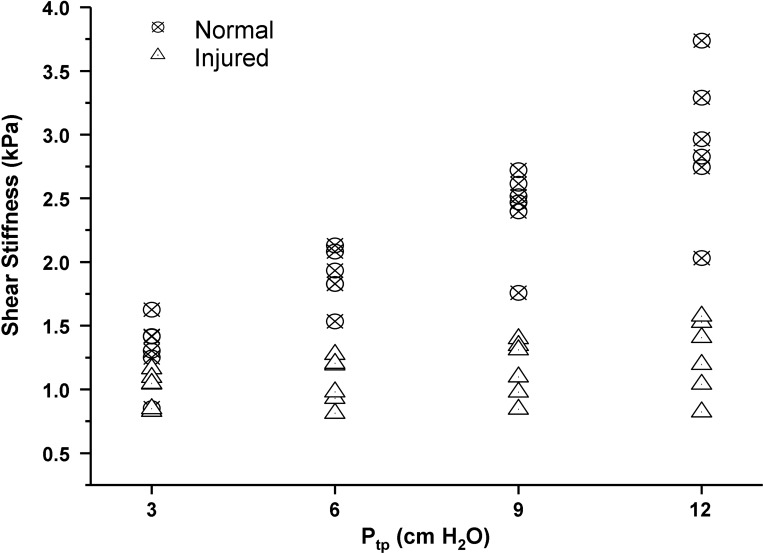
Injured and normal shear stiffness for 3 cm < P_tp < 12 cm H₂O.

PFA-derived estimates of shear stiffness for injured and normal lungs as a function of P_tp are plotted in Figure 2. Each shear stiffness estimate was obtained by averaging PFA values for each slice across all processed slices within a single data set. For each data set, between three and five slices were used to obtain the global, average shear stiffness value. Normal lungs exhibited an increase in shear stiffness with P_tp as expected (10), while injured lungs exhibited almost no increase in stiffness with inflation pressure. Injured lungs were also softer (i.e., lower shear stiffness) than normal lungs, suggesting that the filling of alveolar air spaces with fluid decreased surface tension and hence elastic recoil of the lung as a whole.

Fig. 2.

Principal frequency analysis (PFA)-based shear stiffness estimates for injured and normal lungs. Each data point represents the average shear stiffness per lung set, which was calculated from the individual estimate of shear stiffness per slice. At 3 cm H₂O P_tp, the difference in means between groups were not statistically significant (P = 0.099), while for pressures of 6 cm and higher, the average difference in shear stiffness was statistically significant (P ≤ 0.003).

Table 1 presents post hoc tests for differences in shear stiffness between normal and injured lungs at each P_tp. At 3 cm H₂O P_tp, the difference in average shear stiffness between groups was not statistically significant (P = 0.099). However, at P_tp values of 6 cm H₂O and higher, the average shear stiffness of normal lungs was significantly greater than injured lungs (P ≤ 0.0003). It is important to appreciate that, neither anatomical nor MRE images were capable of resolving atelectatic (collapsed) and fluid-filled regions of injured lungs. As a result, it is highly probable that injured lungs included in this study were composed of varying degrees of both types of injury.

Table 1.

Shear stiffness for normal and injured lungs as a function of transpulmonary pressure

	Lung Group
	Injured		Normal
Ptp, cm H2O	Mean	SE	Mean	SE	Unadjusted P Value
3	1.003	0.125	1.312	0.125	0.099
6	1.066	0.125	1.890	0.125	0.0003
9	1.162	0.125	2.413	0.125	<0.0001
12	1.261	0.125	2.933	0.125	<0.0001

P_tp, transpulmonary pressure.

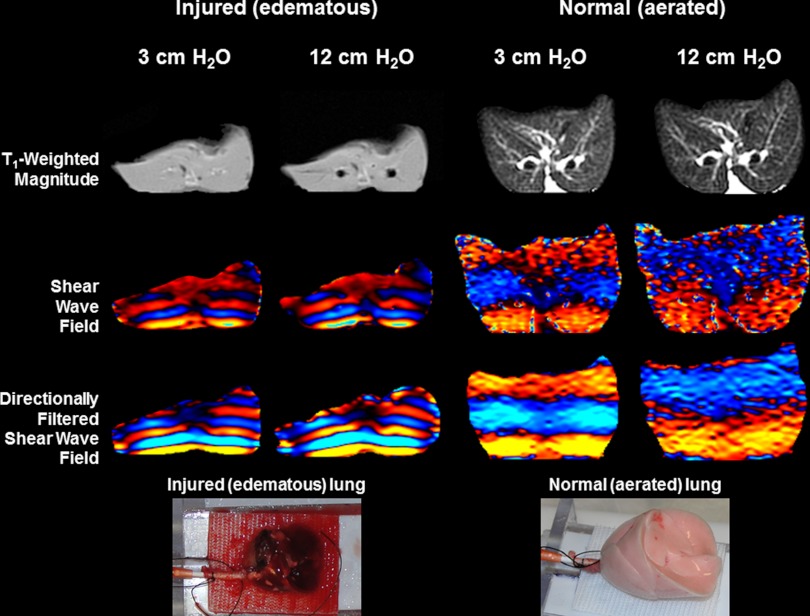
Normal and injured data at inflation pressures of 3 cm and 12 cm H₂O are shown in Fig. 3. The bottom row of the figure includes optical photographs of both lungs. T₁-weighted spin echo axial magnitude images demonstrate the degree of flooding within the injured lung, while the normal lung shows an absence of alveolar flooding. While the injured lung does not show a large increase in size, the opening of major airways within the lung is observable at 12 cm H₂O P_tp. Rows three and four show the phase difference directionally filtered shear wave displacement fields within each slice at the two inflation pressures of 3 cm and 12 cm H₂O, respectively, for both lung sets. The much shorter wavelengths for the edematous lungs indicate that edematous lungs are softer than aerated lungs (some but not all of the wavelength difference is due to the density variations). In addition, there is little change in shear wavelength for the edematous lungs at the two inflation pressures compared with the aerated lungs. These observations are reflected in the PFA estimates of shear stiffness of each slice identified in the figure, which were 0.927 kPa and 0.865 kPa for the injured and 1.40 kPa and 3.04 kPa for the normal lungs at P_tp values of 3 cm and 12 cm H₂O, respectively.

Fig. 3.

Comparison of injured and normal lung data at inflation pressures of 3 cm and 12 cm H₂O. The top row shows the T₁-weighted spin echo data used to calculate lung volume. The second row includes a single-phase offset of the MRE phase-difference images, which encode the propagating shear wave within the lung, while the third row shows the directionally filtered shear-wave field. The bottom row includes optical photographs of the two lung sets (left = injured, right = normal) from which the MRE data were obtained. Shear wavelength (transition from blue to red in phase-difference data) is proportional to the square root of stiffness, indicating that injured lungs are less stiff (softer) than normal. Normal lungs also exhibit an increase in wavelength with inflation pressure.

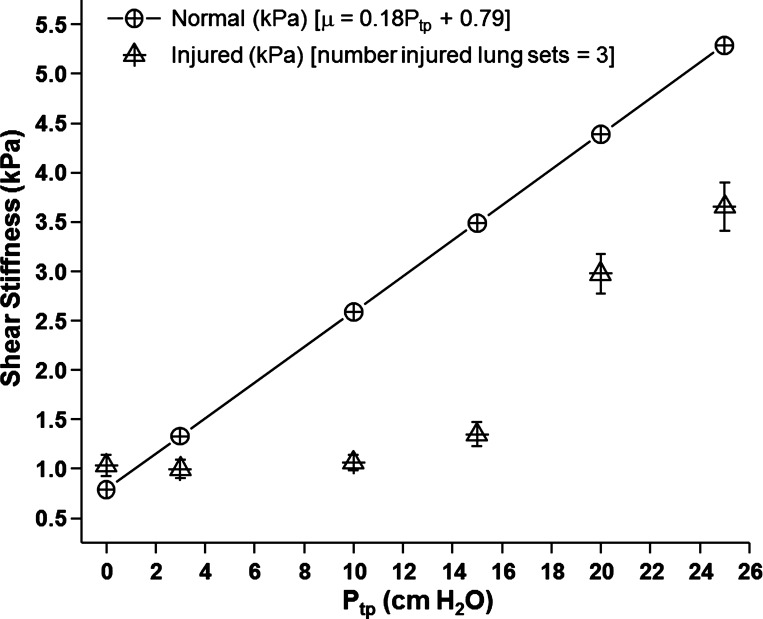
Injured shear stiffness for 0 cm < P_tp < 25 cm H₂O.

Figure 4 is a plot of density-corrected PFA-derived shear stiffness as a function of P_tp for the three injured lung sets. Four slices per lung set were processed at each pressure, providing 12 estimates of shear stiffness per pressure point (total number estimates per pressure = 12 = 4 slices × 3 lung sets). Shear stiffness at each P_tp was averaged across all slices and data sets. Error bars are equal to the SE of the pooled data at each pressure. In addition, the linear least squares fit of the shear stiffness as a function of P_tp for normal lung data from Fig. 3 is also plotted for comparison. The equation for the MRE-derived shear stiffness of the normal fitted data is μ_MRE (kPa) = 0.79 + 0.18 P_tp (cm H₂O). The R value of the linear fit was 0.870. At pressures of 15 cm H₂O or less, injured lung demonstrated no relative change in shear stiffness, consistent with the data presented in Fig. 3. At pressures of 20 cm and greater, shear stiffness increased with increasing pressure. However, at all pressures beyond 3 cm H₂O, the shear stiffness of the injured lung was less than that of the normal or fully aerated lung. Table 3 lists the results of the test of statistical significance of shear stiffness as a function of P_tp. Differences in shear stiffness for P_tps of 0, 3, 10, and 15 cm H₂O were not statistically significant. In contrast, shear stiffness at pressures of 20 and 25 cm H₂O were significantly stiffer than at pressures of 15 cm H₂O and below. Differences in shear stiffness between P_tps of 20 and 25 cm H₂O were not significant.

Fig. 4.

PFA estimates of global shear stiffness for injured lungs as a function of transpulmonary pressures (P_tp) ranging from 0 cm H₂O to 25 cm H₂O. For each injured lung, four slices were processed, resulting in 12 shear stiffness values per pressure (12 = 4 slices × 3 animals). At pressures of 15 cm H₂O and less, there is no significant increase in shear stiffness. At pressures greater than 15 cm H₂O, lung stiffness increases with increasing pressure. However, these global estimates are less than those of normal lungs, as seen in the straight line derived from a linear least squares fit of the normal lung data presented in Fig. 2 (total number of lung sets = 6).

Table 3.

Statistical analysis of shear stiffness vs. of transpulmonary pressure in injured lung

Ptp-1, cm H2O	Ptp-2, cm H2O	Difference	SE	DF	t Value	Adjusted P
0	3	−0.184	0.272	63.1	−0.67	0.984
0	10	0.0509	0.272	63.1	0.19	1.00
0	15	−0.0965	0.272	63.1	−0.35	0.999
0	20	−1.18	0.272	63.1	−4.33	0.0008
0	25	−1.86	0.272	63.1	−6.82	<.0001
3	10	0.235	0.266	63	0.88	0.950
3	15	0.08712	0.266	63	0.33	1.00
3	20	−0.996	0.266	63	−3.74	0.0051
3	25	−1.67	0.266	63	−6.29	<.0001
10	15	−0.147	0.266	63	−0.55	0.994
10	20	−1.23	0.266	63	−4.62	0.0003
10	25	−1.91	0.266	63	−7.17	<.0001
15	20	−1.08	0.266	63	−4.07	0.0018
15	25	−1.76	0.266	63	−6.62	<.0001
20	25	−0.681	0.266	63	−2.55	0.126

P_tp-1, transpulmonary pressure one; P_tp-2, transpulmonary pressure two. Difference equals PFA-derived average shear stiffness at P_tp-1 minus P_tp-2.

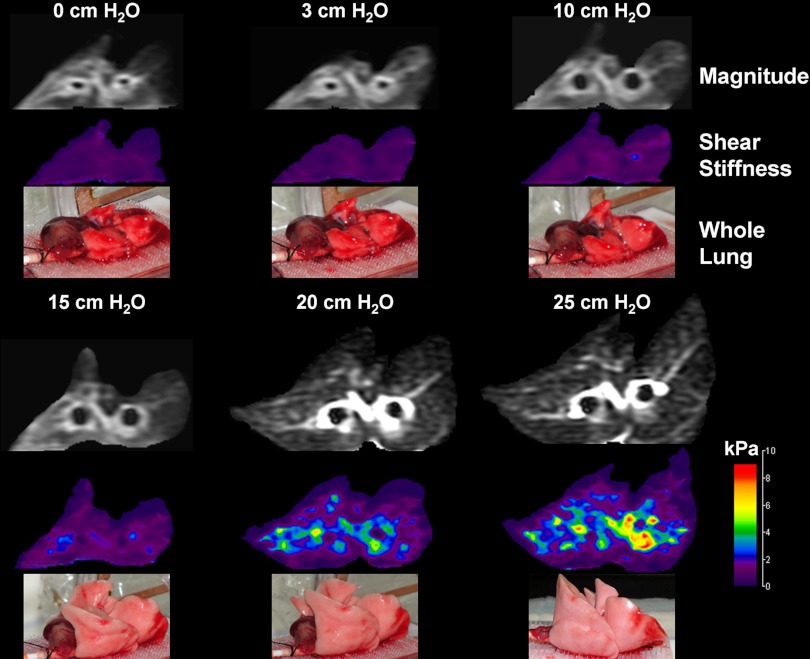
Figure 5 shows a single transaxial slice through one of the injured lungs at all pressures. For each pressure, the magnitude, LFE elastogram, and optical photograph are presented. The magnitude and elastogram images correspond to a slice approximately midway between the apex and inferior margin of the whole lung. For elastograms, little detail is distinguishable for pressures ≤ 15 cm H₂O due to the choice of window and level, which was necessary to avoid clipping of higher stiffness values at higher pressures. At pressures of 20 cm H₂O and greater, regional heterogeneity is observed, with regions about both bronchii being stiffer than parenchyma distant to these airways. The average (T₂*-derived density corrected) shear stiffness for each slice was equal to 0.789, 0.860, 1.15, 1.58, 2.73, and 3.83 kPa for pressures of 0, 3, 10, 15, 20, and 25 cm H₂O, respectively. The optical photographs also show little change in volume for these data for pressures less than 10 cm, while at pressures above this, lung volume increases, indicating expansion of acinii. Residual edema can also be seen at the inferior margin of the lung, consistent with this being the furthest from the pressure source.

Fig. 5.

Magnitude (top), local frequency estimation (LFE) elastogram (middle) and optical (bottom) images of injured lungs for pressures of 0, 3, 10, 15, 20, and 25 cm H₂O. At pressures of 15 cm H₂O and less, little change in shear stiffness is observed. Beyond 15 cm H₂O, lung volume increases with a corresponding increase in global shear stiffness. At 25 cm H₂O, regional increases in shear stiffness are observed around and radiating from the two bronchii within the imaging slice, indicating that prestress within the relatively rigid airway wall is being communicated to the surrounding parenchyma.

Assessment of Regional Flooding

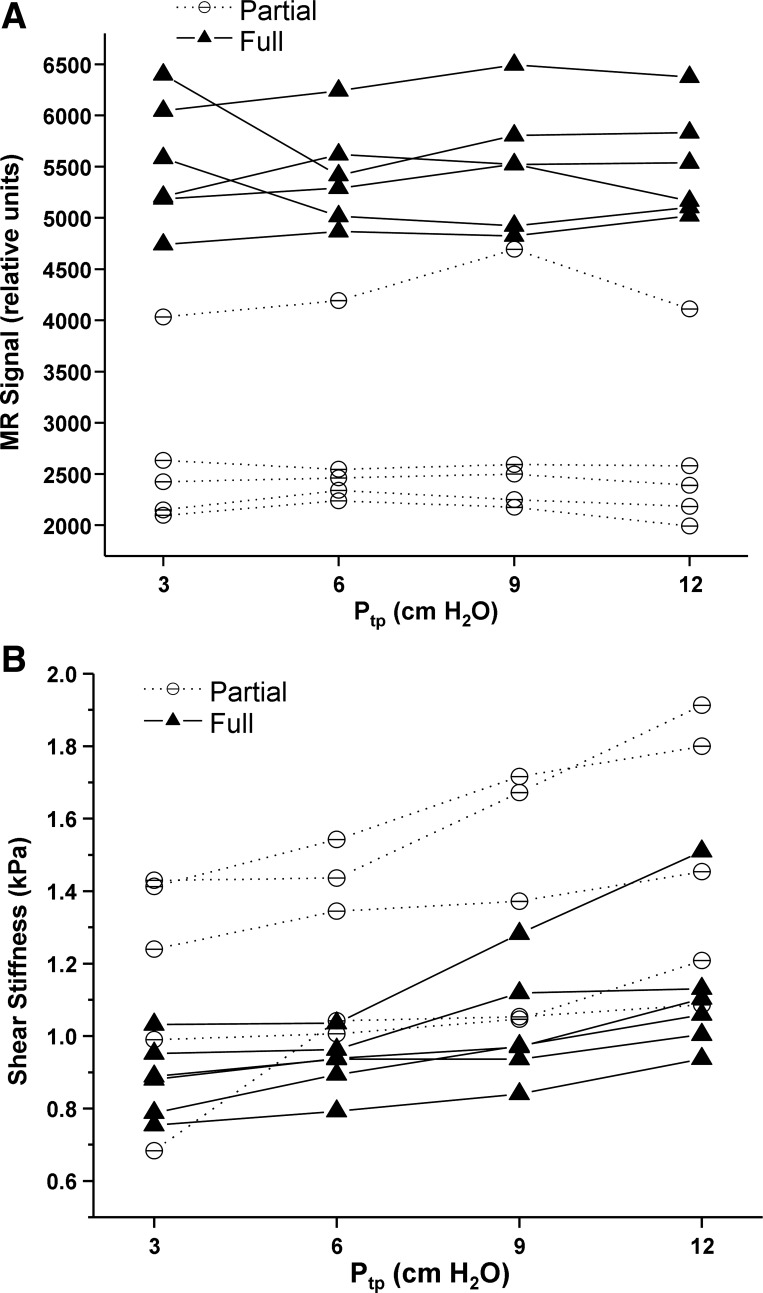
Figure 6A is a plot of the MRE magnitude signal intensity as a function of inflation pressure for the observer-identified fully and partially flooded regions. The MRE magnitude image signal intensity of fully flooded regions was statistically significantly higher than partially flooded regions (P < 0.0001), as shown in Table 2. Neither group exhibited change in signal intensity as a function of inflation pressure, as determined by linear region analysis of MRE magnitude signal vs. P_tp (F value = 0.37, P = 0.55). This is expected because, as shown by Wilson et al. (32), the pressure required to destroy liquid bridges and, thereby, recruit collapsed or flooded regions, is significantly greater than the maximum P_tp of 12 cm H₂O used in this study. Fig. 4B is a plot of LFE-derived shear stiffness as a function of inflation pressure for the two flooded regions. Fully flooded regions as identified by their relative homogeneity and increased MRE magnitude signal intensity were of lower shear stiffness (softer) than partially flooded regions across all pressures with the difference being statistically significant (P < 0.0001). Table 4 shows the results of within-group differences in least square means of shear stiffness between two P_tps. For partially flooded regions, the difference in shear stiffness increased with increasing P_tp difference, but only one pressure difference (3 cm H₂O vs. 12 cm H₂O) was statistically significant (P = 0.0221). For fully flooded regions, shear stiffness increased with increasing P_tp, but the differences were less than partially flooded regions with none being statistically significant.

Fig. 6.

Regional analysis of MRE magnitude and LFE-derived elastograms for injured lungs. A: T₁-signal intensity of partially flooded (circle) and fully flooded (triangle) regions identified by an expert reader (D. L. Levin). B: average shear stiffness as a function of inflation pressure for fully flooded (triangle) and partially flooded (circle) regions identified in A.

Table 2.

Difference in MRE magnitude signal for partially flooded and fully flooded regions as identified by a single blinded expert reader

Ptp, cm H2O	Difference	SE	DF	t Value	P Value
3	2685.20	229.06	12	11.72	<0.001
6	2650.40	229.06	12	11.57	<0.001
9	2614.40	229.06	12	11.41	<0.001
12	2787.80	229.06	12	12.17	<0.001

MRE, magnetic resonance elastography; P_tp, transpulmonary pressure; DF, degrees of freedom. Difference equals change in MRE magnitude signal between regions of interest.

Table 4.

Differences of least square shear stiffness means within expert reader identified partially flooded and fully flooded lung regions

Region	Ptp-1, cm H2O	Ptp-2, cm H2O	Difference	SE	DF	t Value	P Value
P	3	6	−0.123	0.142	31	−0.87	0.391
P	3	9	−0.221	0.142	31	−1.56	0.129
P	3	12	−0.341	0.142	31	−2.41	0.0221
F	3	6	−0.0439	0.129	31	−0.34	0.737
F	3	9	−0.137	0.129	31	−1.06	0.296
F	3	12	−0.242	0.129	31	−1.87	0.0711
P	6	9	−0.0976	0.142	31	−0.69	0.496
P	6	12	−0.218	0.142	31	−1.54	0.134
F	6	9	−0.0936	0.129	31	−0.72	0.474
F	6	12	−0.198	0.129	31	−1.53	0.136
P	9	12	−0.120	0.142	31	−0.85	0.402
F	9	12	−0.104	0.129	31	−0.81	0.427

Regions: P denotes observer-identified partially flooded region, while F denotes observer-identified fully flooded region, Difference equals LFE-derived average shear stiffness of region at P_tp-1 minus P_tp-2.

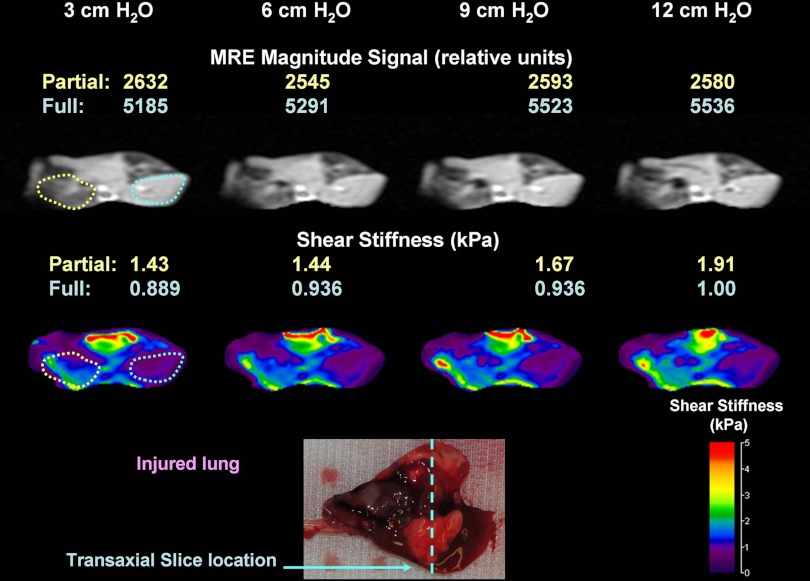
MRE magnitude image and elastograms of an injured lung set are shown in Fig. 7. The top row includes the MRE magnitude image for all four P_tp values, while the LFE-derived T₂* density corrected elastograms are shown directly below. The two regions representing the partially flooded (yellow dash) and fully (blue dash) lung selected by a single expert reader are identified on both images at 3 cm H₂O. The average magnitude and shear stiffness within each region are identified as a function of P_tp in the figure. As noted in Fig. 7, the shear stiffness of the partially flooded region increased by 34% (1.43 kPa to 1.91 kPa), while the fully flooded region increased by only 12% (0.889 kPa to 1.00 kPa). At all inflation pressures, the shear stiffness of the partially flooded region was greater (i.e., stiffer) than the fully flooded region. In contrast, there was little observable change in the magnitude signal for both regions, with the partially flooded region decreasing by 2% (2,632 to 2,580 relative units) and the fully flooded region increasing by 6% (5,185 to 5,536 relative units). These data suggest that MRE-derived shear stiffness maps provide additional information on the underlying mechanical properties of tissue that are not reflected in magnitude-only data. An optical photograph of the lung prior to imaging with the location of the transaxial MRE slice is also shown in the figure.

Fig. 7.

LFE of injured lung with regions of partial and full flooding at inflation pressures of 3, 6, 9, and 12 cm H₂O P_tp. MRE magnitude images of a transaxial slice through the mid-portion of the lung are shown at each inflation pressure. At 3 cm H₂O, the partially flooded (dashed yellow line) and fully flooded (dashed blue line) regions identified by the expert reader (D. L. Levin) are shown. LFE-derived elastograms at each inflation pressure are also shown below the magnitude data.

DISCUSSION

The main findings of the study are that 1) regional flooding following injury decreases lung elasticity as quantified by MRE-based shear stiffness compared with normal lung at a given P_tp, 2) unlike conventional pressure-volume approaches that provide an estimate of global lung function, MRE provides information on the topographical distribution of injury, and 3) in the presence of alveolar flooding, there is a disassociation between airway pressure and prestress of lung parenchyma. These results provide evidence to support the hypothesis that MRE is capable of spatially resolving injurious change in parenchymal elasticity. In addition, the ability to differentiate between normal and injured lung as a function of inflation pressure provides validation of the sensitivity of this method and suggests that this approach could be applied to a spectrum of lung diseases.

The data presented in this work highlight the fundamental limitations of using pressure–volume-derived parameters such as compliance as descriptors of lung tissue mechanical properties. Although these parameters can provide information on the state of the lung as a whole, they include the contributions from both airway and conduction zone structures without the ability to discriminate between them. In addition, they do not provide any information on local (i.e., regional) tissue mechanical properties. Pressure-volume-based measurements are also limited in their ability to characterize the nature of the alveolar space-filling material. Yet such information is vital for understanding pathogenesis and devising an appropriate management plan. In contrast, MRE provides a method to spatially resolve shear modulus or the ability of local tissue to undergo isovolumetric deformation. The presence of space-filling materials directly affects local prestress of the parenchyma, which is reflected in changes in local shear stiffness, as demonstrated in this work. In particular, the data indicate that, provided certain conditions are met, fluid-filled alveoli exhibit similar mechanical characteristics to those of a fluid-filled lung. These data thus highlight the fact that MRE provides new insights into the fundamental mechanical properties of the lung that conventional methods have thus far not afforded.

To understand why the shear stiffness of normal and injured lungs differs, it is worthwhile to consider the mechanical forces that contribute to parenchymal prestress and, hence, stiffness. It is known that surface tension forces resulting from the alveolar gas-liquid interface contribute significantly to the mechanical properties of the lung and that their perturbation is known to dramatically alter parenchymal mechanical properties. For example, when respiratory gases are replaced by saline, thereby eliminating the air-fluid interface, lung compliance increases compared with the fully normal lung, reflecting the intrinsic properties of lung parenchyma as opposed to the intrinsic properties of the lung and the prestress generated by surface tension forces (12). Even in the presence of this interface, lung compliance can be affected by the alteration of pulmonary surfactant due to surfactant overproduction (9) or its absence, such as is the case of preterm infant lungs (23). The presence of pulmonary edema induced alveolar flooding and the associated loss of the gas-liquid interface would be expected to result in an increase in lung compliance similar to the situation encountered within the completely flooded lung. Paradoxically, pulmonary edema results in a decrease in lung compliance (8, 19), despite the fact that the lung is characterized by an increase in interstitial fluid and flooding of alveolar spaces. The reason for this apparent discrepancy is that the decrease in compliance is due primarily to the presence of foam. Wilson et al. (32) demonstrated that at low airway pressures, compliance decreased significantly compared with normal lungs due to the increased impendence of airways clogged with injured foam products. However, above a threshold, the pressure was sufficient to force fluid and foam beyond the terminal airways and into the alveolar sacs, restoring the gas-liquid interface and producing an increase in compliance within those portions of the lung.

It may appear contradictory that MRE estimates of lung shear stiffness in injured lungs are lower than those of normal lungs. The decrease in compliance of injured lungs suggests that overall stiffness would increase compared with normal lungs and is supported by changes in lung volumes measured in this study. For injured lungs, volume increases were between 0.2% and 5.2% between P_tps of 3 to 12 cm H₂O, while normal lungs increase in volume ranged from 32% to 70%, confirming that compliance decreases in pulmonary edema. In contrast, shear stiffness data demonstrated the reverse with injured lungs being statistically softer than normal lungs. This apparent discrepancy can be understood by reference again to Wilson et al. (32), who demonstrated that at low P_tp values, lung volumes remained relatively unchanged due to the high impedance of fluid- and foam-filled airways with a correspondingly low compliance. Pressure differences across foam plugs are not communicated to the alveolar spaces, which are mostly fluid filled and void of surface tension forces. Because MRE assesses the intrinsic properties of the parenchyma, this measure is not related to the inability to move foam through narrow air spaces unlike compliance. The net result of this is a low shear stiffness of injured lungs. Until airways can be cleared of fluids and foam, the lung will remain soft (low shear stiffness). This is also supported by regional MRE data, which showed that regions of lower MR signal intensity were stiffer than regions with high signal. For regions of lower signal intensity (less fluid), the probability of patent airways is higher than regions with higher signal, suggesting that tracheal pressure or P_tp is communicated into these spaces with the corresponding increase in stiffness. Increase in shear stiffness with increasing P_tp provides additional evidence to support this concept.

The data provided in Figs. 4 and 5, collected over P_tps ranging from 0 cm to 25 cm H₂O provide additional evidence demonstrating that at relatively low pressures (P_tp < 15 cm H₂O), the shear stiffness of the lung remains unchanged and is equal to the unstressed or instrinsic properties of the parenchyma itself (i.e., there is no statistical difference between shear stiffness at 0 cm H₂O and pressures of <15 cm H₂O). At 15 cm H₂O, an inflection point occurs, indicating that airway pressure is sufficient to force fluid and foam into respiratory zones of the lung. This is also evident in the magnitude images in Fig. 5, which show not only an increase in lung volume but also a loss of signal for P_tp > 15 cm H₂O, indicating a decrease in tissue density- and susceptibility-induced signal loss due to the presence of air-tissue interfaces within the lung. These figures also demonstrate that average shear stiffness is less than what would be expected for normal lung at that same pressure. The increase in surface tension as a result of the injury-induced loss of surfactant serves to restrict volumetric expansion of the respiratory zone structures, creating less prestress on lung parenchyma compared with normal lung at the same airway pressure. In addition, residual fluid within respiratory zone structures acts to attenuate strain introduced by surface tension forces across the fluid-parenchymal interface, further reducing the prestress of the parenchyma. As MRE-based estimates quantify the intrinsic mechanical properties of the tissue, the reduced prestress of the parenchyma is evident in a lower average shear stiffness compared with normal lung. Because of hysteresis of the pressure-volume curve of normal lung, measurement of shear stiffness during the expiratory phase creates a potential bias toward higher shear stiffness estimates, an effect that will be most dominant at low pressures. At higher pressures, differences between inflation and deflation decrease, reducing this bias. Finally, regional elastic information, as shown in Fig. 5, highlight the fact that while the global shear stiffness of the lung is less than normal, regions of high prestress exist, most notably around patent airways. This is most evident at 25 cm H₂O in which the shear stiffness around the left bronchii is ∼10 kPa, twice the average value of normal lung at this pressure (5.3 kPa).

While global estimates of shear stiffness derived from PFA analysis confirm that MRE-derived estimates of shear stiffness are sufficiently sensitive to detect changes in the intrinsic mechanical properties of the lung by, for example, the loss of surface tension forces, the potential diagnostic power of MRE lies in the ability to spatially differentiate the mechanical properties of regions that appear isointense or show little alteration with inflation pressure on conventional imaging (i.e., CT and MR). Preliminary analysis of regional changes of both magnitude and shear stiffness suggest that signal intensity alone is insufficient to determine the ability of lung regions to undergo expansion with increasing inflation pressure. In lung disease management, this may be important, particularly in lungs with parenchymal diseases, which are known to contain fewer than the expected number of alveoli, which accounts for their apparent increase in stiffness and reduced total lung capacity. In addition, conventional imaging methods, most notably CT, while sensitive in detecting clinically overt parenchymal disease, lack specificity in terms of differentiating between the loss of functional alveolar units due to alveolar flooding, gas absorption atelectasis, gelation of the inflammatory alveolar exudate, or fibroproliferation associated with varying degrees of tissue remodeling and scar formation. Although in some cases, patterns of CT grayscale suggest specific diagnoses (3), it is generally not possible to attribute regions with increased X-ray density to edema, atelectasis, or fibroproliferation (5, 11, 28). Because of this, the efficacy of tissue sampling for histological analysis via open lung biopsy remains hotly debated. Because of these limitations and notwithstanding the fact that major knowledge gaps about the pathogenesis of specific syndromes associated with lung restriction exist, an assessment of pulmonary microstructure is generally required before a specific management plan can be crafted. Thus, MRE-derived estimates of regional shear stiffness may provide new insight into the underlying causes of lung consolidation, as well as the ability to differentiate between differing etiologies.

Regional data presented in this work, most notably LFE-derived elastograms as seen in Figs. 5 and 7, are to be interpreted as being highly encouraging but also preliminary. In Fig. 7, a region of increased shear stiffness can be seen not only in the yellow outlined region but also superior to and between both yellow and blue regions. Although the signal intensity of this region is similar to that of the flooded region, the shear stiffness is visibly greater. Of note also is that this region appears to be the stiffest portion of the lung but decreases with increasing P_tp. The presence of an airway in the magnitude image at 12 cm H₂O compared with the 3 cm H₂O indicates that there is a communicating pathway between this region and the trachea and suggests that this region is not completely flooded. It is also important to appreciate that this region is subject to interfacial interference effects of the propagating shear wave, which directional filtering may not completely remove, biasing the filtered data toward a larger wavelength and hence stiffness. These considerations, thus, highlight the preliminary nature of these results and point to the need for further investigations.

Observer-identified fully flooded regions were not statistically significant across P_tp. As discussed above, the cause of which is that transpulmonary pressure is insufficient to force fluid and/or foam trapped within airways into the respiratory zone of the lung. As a result, pressure increases were not communicated into the alveolar spaces, as reflected by the lack of change in shear stiffness. In contrast, a statistically significant change in shear stiffness was observed for partially flooded regions between P_tp values of 3 cm H₂O and 12 cm H₂O, indicating that airway pressure changes were communicated into alveolar spaces. Because of the lack of statistical significance, it remains unknown as to whether this effect was observed at P_tp values of less than 12 cm H₂O. The lack of statistical significance is due, in part, to the low statistical power of this study as a result of the small sample size (n = 6) and the large standard error, which is of the order of the within-group differences between differing P_tp values (see Table 4). Increasing the statistical power will require additional injured lung sets and improved identification and stratification of injured regions, such as correlation with CT micrographs of the same lung and high resolution T₂*-derived density mapping. This remains an ongoing research effort within our program. While the magnitude signal of the MRE data was used to visually demarcate regions differing degrees of flooding, the data did not distinguish between the contents of the space-filling material. MRE, therefore, holds the potential to differentiate between differing types of material (liquid, gel, and foam) based on shear stiffness in combination with conventional imaging methods, which can distinguish differing degrees of aeration due to air-tissue susceptibility-induced signal loss.

It should also be recognized that, because of the preliminary nature of this study, there are several limitations, the most notable being the inability to resolve between regions of alveolar flooding vs. atelectasis. In flooded regions, the shear stiffness would be expected to reflect the inherent stiffness of lung parenchyma and be less than that of an aerated lung, echoing the data presented in this study and consistent with a completely saline-filled lung. In contrast, atelectatic lung can be theorized as being stiffer due to the cohesive forces between folded portions of lung parenchyma. Because of the inability of MRE magnitude and conventional imaging methods used in this study to resolve these two regions, this question remains unresolved. A second limitation is that this study does not resolve the exact relationship between the role of fluid/foam plugs and the mechanical properties of flooded alveoli distal to the plug. It is theorized that, because of the large pressure drop across the plug that completely flooded alveoli would easily undergo isovolumetric distortion with a corresponding low bulk and shear moduli. Previous theoretical studies suggest that this is true (32), especially at such low P_tp values used in this study. However, validation of this would require comparison of shear stiffness between normal, completely saline-filled, and injured lungs, which is beyond the scope of this work.

In this ex vivo study, uniform shear wave fronts propagated throughout the lung as a result of the direct mechanical contact between the shear driver plate and the lung (see Figs. 3 and 5). Under in vivo conditions, direct mechanical contact between the driver and lung is impossible. However, previous studies in both animals (15) and humans (14) have demonstrated that a relatively simple pneumatic drum driver placed on the anterior chest wall is capable of generating propagating shear waves within the lungs noninvasively. Although the wave patterns are complex, they can be mathematically processed to generate elastogram images of the lung and have been shown to correlate with respiratory induced changes in lung stiffness (15). These studies also demonstrated that the greatest contributor to loss of SNR of the shear wave displacement fields are the relatively large echo times necessary to encode shear waves at frequencies of less than 100 Hz.

In summary, this study has demonstrated that alteration of the intrinsic mechanical equilibrium that exists in the lung following ventilator-induced injury and subsequent pulmonary edema can be quantified by MRE. This study provides ongoing validation of the central role of surface tension as a contributor to the mechanical properties of the lung, and suggests that MRE may have additional diagnostic potential as a noninvasive method for differentiating among various types of alveolar space-filling materials.

GRANTS

This study was supported by National Institute of Biomedical Imaging and Bioengineering Grants EB07593 and EB00198.

DISCLOSURES

Kiaran McGee, Richard Ehman, Yogesh Mariappan, Armando Manduca, and Mayo Clinic have intellectual property relating to the subject.

AUTHOR CONTRIBUTIONS

Author contributions: K.P.M., R.D.H., and A.M. conception and design of research; K.P.M. and Y.K.M. performed experiments; K.P.M., Y.K.M., R.E.C., Z.B., and D.L.L. analyzed data; K.P.M., R.D.H., R.E.C., A.M., and R.L.E. interpreted results of experiments; K.P.M. prepared figures; K.P.M. drafted manuscript; K.P.M., R.D.H., R.E.C., D.L.L., and R.L.E. edited and revised manuscript; K.P.M. and D.L.L. approved final version of manuscript.