Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2012 Aug 22;2:595. doi: 10.1038/srep00595

Two-dimensional universal conductance fluctuations and the electron-phonon interaction of surface states in Bi2Te2Se microflakes

Zhaoguo Li 1, Taishi Chen 1, Haiyang Pan 1, Fengqi Song 1,a, Baigeng Wang 1,b, Junhao Han 1, Yuyuan Qin 1, Xuefeng Wang 2, Rong Zhang 2, Jianguo Wan 1, Dingyu Xing 1, Guanghou Wang 1
PMCID: PMC3424525  PMID: 22916331

Abstract

The universal conductance fluctuations (UCFs), one of the most important manifestations of mesoscopic electronic interference, have not yet been demonstrated for the two-dimensional surface state of topological insulators (TIs). Even if one delicately suppresses the bulk conductance by improving the quality of TI crystals, the fluctuation of the bulk conductance still keeps competitive and difficult to be separated from the desired UCFs of surface carriers. Here we report on the experimental evidence of the UCFs of the two-dimensional surface state in the bulk insulating Bi2Te2Se microflakes. The solely-B⊥-dependent UCF is achieved and its temperature dependence is investigated. The surface transport is further revealed by weak antilocalizations. Such survived UCFs of the surface states result from the limited dephasing length of the bulk carriers in ternary crystals. The electron-phonon interaction is addressed as a secondary source of the surface state dephasing based on the temperature-dependent scaling behavior.

In the new class of quantum condensed matter, namely three-dimensional (3D) topological insulators (TIs), the anomalous topological transition casts with a gapless and low-dissipation state on the solid surface1,2. The Dirac fermions within the surface states (SSs) are protected by the time-reversal symmetry3. Their spin helicity forbids backscattering of the Dirac carriers4. Robust coherence has been demonstrated in spite of the strong spin-orbit couplings in current 3D TI samples5,6,7,8,9. Such unique transport sheds light on the emergence of new mesoscopic physics10. The Aharonov-Bohm11,12, Atshuler-Aronov-Spivak5,13 and Aharonov-Casher effect14 as well as two-dimensional (2D) weak antilocalizations (WAL)6,7,8,9 of the SSs have been demonstrated in TIs of Bi2Se315,16,17,18, Bi2Te315,19,20, Bi2Te2Se21,22,23 and Ag2Te24, etc. These transport investigations provide the solid evidence on the conducting SSs and pave the way to the TI-based microdevices25.

The universal conductance fluctuation (UCF)26,27,28 is of intense interest in the TIs due to the expectation of the enhanced SS contributions as well as new fractional quantized amplitudes29. A main problem with TIs is the contribution from the bulk carriers3,4,10, which is dominant over the SS transport even in the insulating TI samples due to their great numbers of electron states20,22. The UCF is featured by a reproducible aperiodic structure in the magnetoconductance (MC) curves of small weakly-disordered specimens. Such MC fluctuations are sensitive to the variations of disorder configurations and thus a “fingerprint” of the mesoscopic samples is visualized. One of the unique characteristics of the UCF is the nearly universal zero-temperature amplitudes in the order of e2/h. For each individual transport channel, it keeps independent of the sample size and degree of disorders within the dephasing length 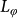Inline graphic 26,28. In the UCF of TIs, both surface and bulk states are expected to have the comparable UCF amplitudes. Therefore, such unique UCF properties may result in a dominant SS's contribution when careful optimizations of the samples' transport environments are made26. This leads to great interests in the UCF measurements of TIs. The conductance fluctuations (CFs) from over 6 to 0.01 e2/h have been reported in Bi2Se330,31,32. The CFs were even observed in well-refined macroscopic crystals30. One often determines the 2D character of the transport by field-tilting measurement due to the fact that the parallel field has no contribution to the phase7. However, such efforts on searching for the 2D UCFs remain challenging. In this report, we give the experimental evidence of the UCF effect in the bulk insulating Bi2Te2Se microflakes. The 2D nature of the UCF is revealed by the field-tilting MC measurements.

Results

Sample preparation and characterization

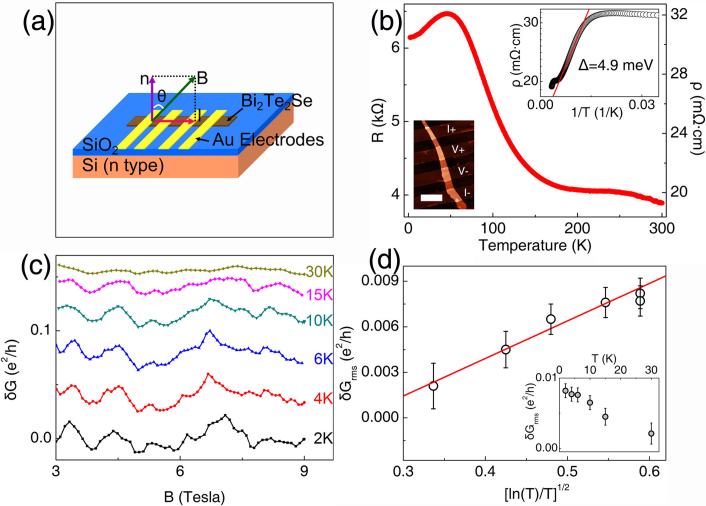
The Bi2Te2Se TI microflakes are prepared on a silica-capped silicon wafer by a mechanical exfoliation method. The four-probe electrodes were then applied onto the microflakes by a standard lift-off procedure. Fig. 1(a) shows the typical configuration during the transport measurement. The height (H), width (W) and length (L) of the present sample are 62 nm, 1.2 μm and 1.5 μm respectively, where L is defined as the distance between the voltage probes in the four-probe configurations. Fig 1(b) shows the temperature dependence of its resistance, indicating the bulk insulating of the sample. The energy gap Δ is 4.9 meV determined by adopting the Arrhenius equation22. The MC curves of the microflakes are measured from −9 to 9T while rotating the samples and varying the temperatures.

Figure 1. The UCF and its temperature dependence.

Figure 1

Open in a new tab

(a) the schematic diagram of the measurement configuration. (b) Temperature dependence of the resistance and resistivity of a Bi2Te2Se microflake. The left inset shows its AFM image with the scale bar of 4 μm. The right inset shows the Arrhenius fitting of ρ(T) with the result of a 4.9 meV band gap. (c) Conductance fluctuations plotted against B at various temperatures (θ = 0). The aperiodic δG-B patterns appear repeatedly. For clarity, adjacent curves are displaced vertically. (d) δGrms and its temperature dependence. The inset shows the data in a linear scale. The solid curve is fit by the traditional UCF theory.

Identifying the UCF features in the MC measurement

The UCF patterns can be identified while the magnetic field (B) is perpendicular to the sample (θ = 0°) as shown in Fig. 1(c). The conductance displays the aperiodic features and strongly temperature-dependent fluctuations. These features originate from the UCF effect as supported by the following characteristics. Firstly, the “noisy” (or aperiodic) CF patterns can be observed repeatedly. It shows the similar features in the different MC curves measured at the different temperatures because some specific “fingerprints” of the samples can be seen. Secondly, The root mean square of the CFs 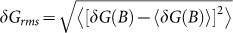Inline graphic, where <…> expresses the ensemble average, also decays from nearly 0.008 to 0.002 e2/h when the temperature increases from 2 to 30 K, implying its quantum mechanical nature. It is well known that the UCF amplitudes undergoes the average reduction when the sample dimensions are longer than 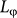Inline graphic 26,28. Quantitatively, following the calculations in Ref.28,33, the 2D UCF theory predicts δGrms~0.86(e2/h)/(2N)1/2 at T = 0 K which agrees to the experimental value in orders, where 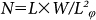Inline graphic represents the number of independent phase-coherent regions on the TI's surface. Finally, the temperature-dependent δGrms is investigated. According to the UCF theory for 2D system26,28, we have δGrms∝(lnT/T)1/2, which also agrees to our experimental data, as shown in Fig 1(d). All the above experimental observations unambiguously support the UCFs in Bi2Te2Se TI microflakes and suggest the 2D nature of the carriers.

Experimental evidence of the 2D origin of the UCF

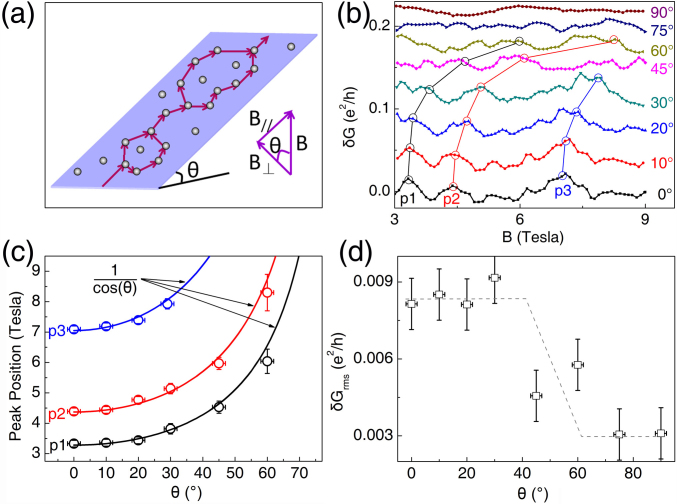
We investigate the 2D origin of the UCF by the magnetic field-tilting MC measurements. As schematically shown in Fig 2(a), the phase shifts along some enclosed paths determine the UCF patterns upon the application of an external field26,28,33. In an ideal 2D electronic system, such phase shifts solely depend on the normal components (B⊥ = Bcosθ) of the magnetic field. The UCF patterns accordingly evolve as a function of B⊥. Therefore, the solely-B⊥-dependent UCF patterns can manifest the UCF of a 2D electron system, essentially the novel SS for a TI sample34. It is indeed observed as shown in Fig. 2(b), where the angular-dependent UCFs are clearly seen. We can find three small peaks (p1, p2 and p3) in the δG-B curves shift towards the high-B direction and their widths are monotonically broaden with increasing θ, as guided by the circle-marked lines. The locations of three peaks are plotted against θ in Fig. 2(c). The solid curves are the least square fittings, which ideally display the characteristic of 1/cosθ dependence. The 2D nature of the UCF pattern is further confirmed by the angle-dependent δGrms, as shown in Fig. 2(d). Generally, δGrms is expected to be unchanged while varying θ due to the isotropic 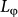Inline graphic in a 3D system. We can find δGrms maintains comparable while θ is below 40°. However, when θ exceeds 45°, δGrms drops abruptly, which can be explained by the contribution of a 2D conducting states. In a TI system, the UCF contributions from the electrons of the bulk states gradually predominate while θ is increasing17,20. The present anisotropic δGrms rules out the 3D origin. We confirmed the θ-variable MC measurements in other samples, proving the generality of the above evidence. Both the solely-B⊥-dependent UCF patterns and anistropic UCF amplitudes further conclusively demonstrate the 2D UCF of the SSs in TI Bi2Te2Se.

Figure 2. The 2D UCFs demonstrated by the field-tilting measurement.

Figure 2

Open in a new tab

(a) The schematic diagram showing the 2D UCF solely depends on the perpendicular component of the magnetic field (B⊥). (b) The B-tilting δG-B data of a Bi2Te2Se microflake measured at 2 K. The black, red and blue circle-marked lines respectively show the similar features, namely p1, p2 and p3, in all the δG-B curves. For clarity, adjacent curves are displaced vertically. (c) The positions of the UCF features plotted against θ. The black, red and blue data are from those of p1, p2 and p3 in (b), respectively. The solid curves are the 1/cosθ fitting. (d) θ dependent δGrms. The dashed curve is for eye guiding. The UCF measured at θ = 90° is interpreted as the contribution from the bulk carriers in TIs.

The WAL features dominated by surface carriers

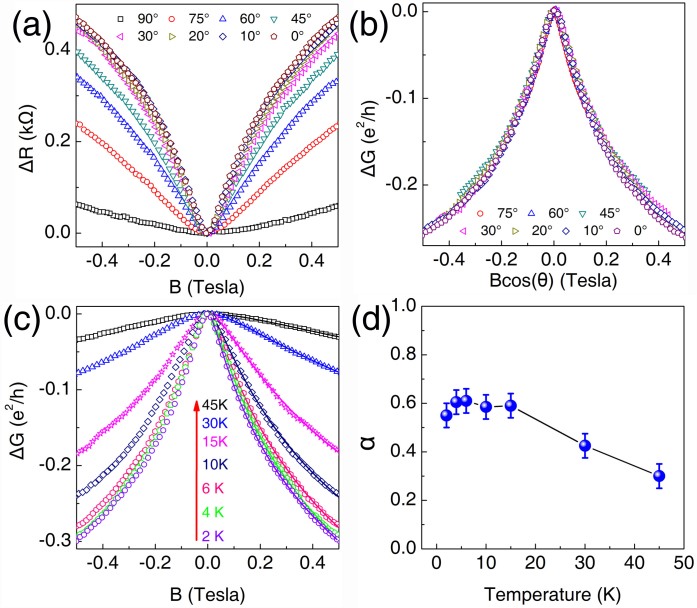
The SS transport in our samples is further examined by the solely-B⊥-dependent WAL effect. Fig. 3(a) shows the angular-dependent magnetoresistance (MR) at 2 K. It can be seen that the WAL-characteristic MR dips gradually disappear with increasing θ. At θ = 90°, where B is along the current direction, the MR dip completely disappears and the MR curve shows a parabolic B dependence. Such semiclassical B2 dependence comes from the Lorentz deflection of the bulk carriers. According to the previous analysis7,8, we plot ΔG against B⊥, where all the MC curves at various angles coincide with each other [Fig. 3(b)], strongly confirming the transport of the 2D SSs7. The temperature dependence of the WAL features at θ = 0° has also been measured as shown in Fig. 3(c). According to the 2D localization theory, in the limit of strong spin-orbit interaction and low mobility, the Hikami-Larkin-Nagaoka equation is reduced to6,7,35:

graphic file with name srep00595-m1.jpg

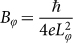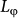where α = 1/2 stands for the transport through only one TI surface channel36, ψ(x) is the digamma function, and Inline graphic is a Inline graphic-related characteristic field. By applying Eq. (1) to the experimental curves, the fitting parameters of α and 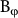Inline graphic are obtained. Fig. 3(d) shows the fitting results of α, whose value around 0.5 can be seen. This indicates that only a single surface channel participates in the transport of our TI samples.

Figure 3. The 2D WAL effect of the SSs in TIs.

Figure 3

Open in a new tab

(a) ΔR = R(B) - R(0) as a function of B measured at various θ at 2 K. (b) ΔG(B⊥) curves after subtracting the bulk contribution. The data were measured at T = 2 K. (c) ΔG(B) as a function of B at various temperatures (θ = 0). The solid curves are the least-square fittings according to the 2D WAL theory. (d) α as a function of temperature obtained from the fitting. Its value near 0.5 rules out the issue of electron interference between two surfaces.

Discussions

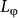Inline graphic characterizes the mesoscopic electron interference and its temperature-dependence may reveal the phase relaxation mechanism of the SSs. The temperature-dependent scaling of 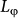Inline graphic, extracted from either WAL or UCF data, both present a similar trend as shown in Fig 4. In the previous framework of WAL and UCF26,27,28,37, the electron-electron (e-e) scattering and electron-phonon (e-ph) scattering are considered as two main sources of the electrons' phase relaxation. The e-e interaction theory predicted a power law of 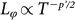Inline graphic, where p' = 1 for the 2D system27,37, as employed in the previous studies of graphene38 and TIs8,32. The dashed line in Fig. 4 is the T−1/2 power-law curve following the 2D e-e interaction, which clearly shows the failure of the fitting. Even if we optimize the parameter p' it still does not work. This indicates that our data can not be explained by the e-e interaction dominated dephasing mechanism.

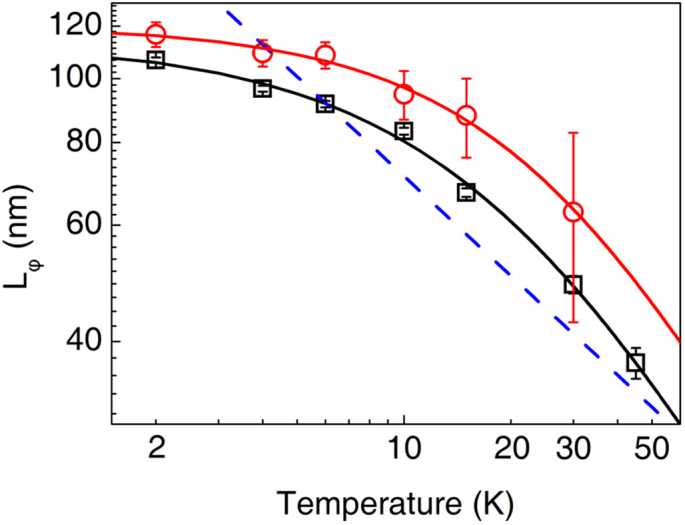
Figure 4. Temperature dependence of Inline graphic obtained from the WAL (square) and UCF data (circle).

Figure 4

Open in a new tab

The big error of 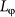Inline graphic at 30 K from UCF is due to nearly disappearance of the UCF. The solid curve shows the fitting of the experimental data according to the scaling formula (2) with p' = 1 and p = 2. The dashed line is the e-e interaction fitting.

Here we propose an e-ph interaction dependent scaling behavior for the dephasing length 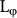Inline graphic of the SS electrons in the TIs. It is well-known that the e-e scattering used to be dominant in the 2D system, while the e-ph scattering predominates in the 3D system37. However, as compared to graphene, an ideal 2D electronic system, a huge phonon “sea” attaches to the SS electrons in a TI. The e-ph interaction is supposed to emerge in the present study39, which contributes an additional term in the formula as shown in the following37:

graphic file with name srep00595-m2.jpg

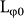where Inline graphic represents the zero-temperature dephasing length, A'eeTp' and A'epTp represents the contribution from the e-e and e-ph interaction respectively. We have known p' = 1 according to the above analysis. In the current samples of the Bi2Te2Se microflakes, the electron-transverse phonon (e-t.ph) interactions should be dominant over the electron-longitidunal phonon (e-l.ph) interactions because of the larger sound velocity of longitidunal phonons than that of transverse phonon in the material40,41. According to e-ph interaction theory41,42, the e-ph scattering length L−2e-ph∝Tp. The e-t.ph scattering leads to the value of p = 2 while the e-l.ph interaction yields p = 341. Therefore, p is close to 2 in our samples. As shown in Fig. 4, the Eq. (2) with p' = 1 and p = 2 results in a perfect fitting with the parameter 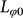Inline graphic = 114 nm. Such a fitting formula is applicable for all of our samples. This highlights the e-t.ph interaction in the electron relaxation of the present TI samples.

The above study of the transport environment well explains the present observations of the solely-B⊥-dependent 2D UCF. In TIs, the UCF patterns are composed of contributions from the SS and bulk carriers, both of which undergo the average reduction of their amplitudes while the sample size exceeds 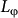Inline graphic. A poor-man approach to obtain the SS-dominated UCF is to suppress the amplitudes of the UCF from bulk carriers, as has been implemented in this work. One may know δGrms is dominantly contributed by the bulk electrons while measuring the MC curve at some high angles near θ = 90°. Such UCF amplitudes from the bulk electrons should be isotropic for a 3D interference system. In our samples, δGrms (θ = 90°) equals 0.003 e2/h, which is much lower than the amplitudes of SS UCF. This confirms the suppression of the bulk UCF firstly. Secondly, 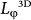Inline graphic~12 nm can be estimated with a comparable error by applying the 3D UCF theory28. All of our samples exhibit the similar bulk dephasing lengths. Due to the fact that 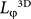Inline graphic < H, L, W, we believe the 3D interference transport of the bulk electrons in our samples. Accordingly, the 2D UCF discussed above reasonably originates from the SSs. Thirdly, we see the transport quality of the samples. Generally, the TI samples have been delicately prepared to keep the perfection of the crystals in order to maintain the topological anomaly and the well-defined SS transport3, which leads to some high values of bulk mobilities, especially for the binary TIs. This accordingly expects a satisfactory 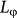Inline graphic and a UCF amplitude for the bulk electrons competitive to those of the SS electrons. However in the ternary TIs, high defect ratios and low mobilities have been demonstrated23 due to plenty of antisite defects between Te and Se and related vacancies. A much lower 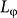Inline graphic, i.e. about 10 nm, for the bulk carriers is then reasonable, while a relatively good value, i.e.about 120 nm, is obtained for the SS since the SS carriers may immune to some scatterings due to their helical transport3,4. Therefore, we finally argue that the “deteriorated” electronic environment in the ternary TIs suppresses the bulk UCF and helps the survival of the 2D UCFs in the present study.

In summary, we have successfully demonstrated the UCF of the 2D SSs by measuring the solely-B⊥-dependent UCF patterns in TI Bi2Te2Se microflakes. It is observed in the TI samples with a short 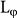Inline graphic of the bulk carriers, which suppress the UCF's amplitudes from the bulk carriers and helps the survival of the UCF of the 2D SS. The e-ph scattering is suggested as the other dephasing source for the SS of TI samples. The present work may pave the TI-based spintronic devices and quantum information materials and their room-temperature applications.

Methods

Crystal growth and characterization

The well-refined Bi2Te2Se crystals were grown by melting the high purity powders (99.999%) of Bi, Te, Se with a molar ratio of 2:2:1 at 850°C in evacuated quartz tubes for 3 days. It was followed by cooling slowly to 550°C for 8 days and then an annealing for 5 days before rapidly cooling to room temperature. The ordering of the chalcogen layers in the Bi2Te2Se precursor crystals was confirmed by the x-ray powder-diffraction22. The Bi2Te2Se microflakes were then exfoliated and transferred onto the wafers5. The four-probe electrodes were then applied onto the microflakes by a standard lift-off procedure.

Transport measurements and data analysis

The transport measurements were carried out in a Quantum Design Physical Property Measurement System-9T system and a homemade MR measurement system. The MR curves of the microflakes were measured from -9 up to 9T while rotating the samples from 0 to 90°and changing the temperatures from 2 to 300 K. The UCF features are always mixed with the WAL dips. We first fit the MC curves according to the traditional WAL description. After subtracting the smooth background, we obtained the resultant aperiodic structures as the UCF features as discussed in the main text. The dephasing length can be extracted from both WAL and UCF effect. In the WAL description, the dephasing length 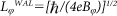Inline graphic was obtained by fitting the characteristic field. In the UCF theory, the correlation function F(ΔB) = <δG(B)δG(B+ΔB)> must be calculated with the result of a critical field Bc satisfy F(Bc) = F(0)/2. Using 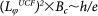Inline graphic, we then reach the dephasing length from UCF data. The UCF features decayed faster than the WAL dips with the increase of the temperature and nearly vanished at 30 K. Therefore, the 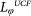Inline graphic data presents of larger error and 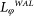Inline graphic will be more discussed.

Author Contributions

F. S., Z. L. and B. W. conceived the work and wrote the paper. Z. L. and T. C. prepared the samples. Z. L. T. C., Y. Q., H. P., J. H. and F. S. performed the experiments. Z. L., F. S. and B. W. analyzed the data, X. W., D. X. and J. W. assisted with interpretation of the data. X. W., D. X. , R. Z. and G. W. had valuable discussions and edited the manuscript. All authors commented on the manuscript.

Acknowledgments

We thank the National Key Projects for Basic Research of China (Grant numbers: 2010CB923400, 2011CB922103), the National Natural Science Foundation of China (Grant numbers: 11023002, 11134005, 60825402, 61176088, 11075076), the PAPD project and the Fundamental Research Funds for the Central Universities for financially supporting the work. Helpful assistance from Nanofabrication and Characterization Center at Physics College of Nanjing University, Yanfang Wei and Prof. Zhiqing Li at Tianjin University, Prof. J. J. Lin at Taiwan Chiao Tung University, Dr. Li Pi and Prof. Yuheng Zhang at High Magnetic Field Laboratory CAS are acknowledged.

References

  1. Moore J. E. The birth of topological insulators. Nature 464, 194–198 (2010). [DOI] [PubMed] [Google Scholar]
  2. Fu L. & Kane C. L. Topological insulators with inversion symmetry. Physical Review B 76, 045302 (2007). [Google Scholar]
  3. Hasan M. Z. & Kane C. L. Colloquium: Topological Insulators. Reviews of Modern Physics. 82, 3045 (2010). [Google Scholar]
  4. Qi X.-L. & Zhang S.-C. Topological insulators and superconductors. Reviews of Modern Physics 83, 1057 (2011). [Google Scholar]
  5. Li Z. et al. Experimental evidence on the Altshuler-Aronov-Spivak interference of the topological surface states in the exfoliated Bi2Te3 anoflakes. Applied Physics Letters 100, 083107 (2012). [Google Scholar]
  6. Chen J. et al. Gate-Voltage Control of Chemical Potential and Weak Antilocalization in Bi2Se3. Physical Review Letters. 105, 176602 (2010). [DOI] [PubMed] [Google Scholar]
  7. He H.-T. et al. Impurity Effect on Weak Antilocalization in the Topological Insulator Bi2Te3. Physical Review Letters 106, 166805 (2011). [DOI] [PubMed] [Google Scholar]
  8. Cha J. J. et al. Weak Antilocalization in Bi2(SexTe1–x)3 Nanoribbons and Nanoplates. Nano Letters 12, 1107–1111 (2012). [DOI] [PubMed] [Google Scholar]
  9. Liu M. et al. Crossover between Weak Antilocalization and Weak Localization in a Magnetically Doped Topological Insulator. Physical Review Letters 108, 036805 (2012). [DOI] [PubMed] [Google Scholar]
  10. Li Y.-Q., Wu K.-H., Shi J.-R. & Xie X.-C. Electron transport properties of three-dimensional topological insulators. Front. Phys. 7, 165–174 (2012). [Google Scholar]
  11. Peng H. et al. Aharonov-Bohm interference in topological insulator nanoribbons. Nat Mater 9, 225–229 (2010). [DOI] [PubMed] [Google Scholar]
  12. Xiu F. et al. Manipulating surface states in topological insulator nanoribbons. Nat Nano 6, 216–221 (2011). [DOI] [PubMed] [Google Scholar]
  13. Sulaev A. et al. Aharonov-Bohm interference and colossal magnetoresistance in anisotropic topological insulator β-Ag2Te. arXiv, 1204.3816 (2012). [Google Scholar]
  14. Qu F. et al. Aharonov-Casher Effect in Bi2Se3 Square-Ring Interferometers. Physical Review Letters 107, 016802 (2011). [DOI] [PubMed] [Google Scholar]
  15. Zhang H. et al. Topological insulators in Bi2Se3 Bi2Te3 and Sb2Te3 with a single Dirac cone on the surface. Nat Phys 5, 438–442 (2009). [Google Scholar]
  16. Xia Y. et al. Observation of a large-gap topological-insulator class with a single Dirac cone on the surface. Nat Phys 5, 398–402 (2009). [Google Scholar]
  17. Analytis J. G. et al. Two-dimensional surface state in the quantum limit of a topological insulator. Nat Phys 6, 960 (2010). [Google Scholar]
  18. Kim D. et al. Surface conduction of topological Dirac electrons in bulk insulating Bi2Se3. Nat Phys 8, 460–464 (2012). [Google Scholar]
  19. Chen Y. L. et al. Experimental Realization of a Three-Dimensional Topological Insulator Bi2Te3. Science 325, 178–181 (2009). [DOI] [PubMed] [Google Scholar]
  20. Qu D.-X., Hor Y. S., Xiong J., Cava R. J. & Ong N. P. Quantum Oscillations and Hall Anomaly of Surface States in the Topological Insulator Bi2Te3. Science 329, 821–824 (2010). [DOI] [PubMed] [Google Scholar]
  21. Arakane T. et al. Tunable Dirac cone in the topological insulator Bi2-xSbxTe3-ySey. Nature Communications 3, 636 (2012). [DOI] [PubMed] [Google Scholar]
  22. Ren Z., Taskin A. A., Sasaki S., Segawa K. & Ando Y. Large bulk resistivity and surface quantum oscillations in the topological insulator Bi2Te2Se. Physical Review B 82, 241306 (2010). [Google Scholar]
  23. Xiong J. et al. Quantum oscillations in a topological insulator Bi2Te2Se with large bulk resistivity. Physica E: Low-dimensional Systems and Nanostructures 44, 917–920 (2012). [Google Scholar]
  24. Zhang W. et al. Topological Aspect and Quantum Magnetoresistance of β-Ag2Te. Physical Review Letters 106, 156808 (2011). [DOI] [PubMed] [Google Scholar]
  25. Pesin D. & MacDonald A. H. Spintronics and pseudospintronics in graphene and topological insulators. Nat Mater 11, 409–416 (2012). [DOI] [PubMed] [Google Scholar]
  26. Akkermans E. & Montambaux G. Mesoscopic Physics of Electrons and Photons (Cambridge University Press, 2007). [Google Scholar]
  27. Altshuler B. L. & Aronov A. G. Electron-electron interaction in disordered systems (North-Holland, 1985). [Google Scholar]
  28. Lee P. A., Stone A. D. & Fukuyama H. Universal conductance fluctuations in metals: Effects of finite temperature, interactions, and magnetic field. Physical Review B 35, 1039 (1987). [DOI] [PubMed] [Google Scholar]
  29. Zhang L., Zhuang J., Xing Y. & Wang J. Disorder induced quantized conductance with fractional value and universal conductance fluctuation in three-dimensional topological insulators. arXiv, 1110.3883 (2011). [Google Scholar]
  30. Checkelsky J. G. et al. Quantum Interference in Macroscopic Crystals of Nonmetallic Bi2Se3. Physical Review Letters. 103, 246601 (2009). [DOI] [PubMed] [Google Scholar]
  31. Checkelsky J. G., Hor Y. S., Cava R. J. & Ong N. P. Bulk Band Gap and Surface State Conduction Observed in Voltage-Tuned Crystals of the Topological Insulator Bi2Se3. Physical Review Letters 106, 196801 (2011). [DOI] [PubMed] [Google Scholar]
  32. Matsuo S. et al. Weak antilocalization and conductance fluctuation in a submicrometer-sized wire of epitaxial Bi2Se3. Physical Review B 85, 075440 (2012). [Google Scholar]
  33. Yang P.-Y., Wang L. Y., Hsu Y.-W. & Lin J.-J. Universal conductance fluctuations in indium tin oxide nanowires. Physical Review B 85, 085423 (2012). [Google Scholar]
  34. Kaplan S. B. & Hartstein A. Universal conductance fluctuations in narrow Si accumulation layers. Physical Review Letters 56, 2403 (1986). [DOI] [PubMed] [Google Scholar]
  35. Hikami S., Larkin A. I. & Nagaoka Y. Spin-orbit interaction and mangetoresistance in the two dimensional random system. Prog. Theor. Phys. 63, 707–710 (1980). [Google Scholar]
  36. Steinberg H., Laloë J. B., Fatemi V., Moodera J. S. & Jarillo-Herrero P. Electrically tunable surface-to-bulk coherent coupling in topological insulator thin films. Physical Review B 84, 233101 (2011). [Google Scholar]
  37. Lin J. J. & Bird J. P. Recent experimental studies of electron dephasing in metal and semiconductor mesoscopic structures. J. Phys.: Condens. Matter. 14, R501–R596 (2002). [Google Scholar]
  38. Tikhonenko F. V., Kozikov A. A., Savchenko A. K. & Gorbachev R. V. Transition between Electron Localization and Antilocalization in Graphene. Physical Review Letters 103, 226801 (2009). [DOI] [PubMed] [Google Scholar]
  39. Zhu X. et al. Electron-Phonon Coupling on the Surface of the Topological Insulator Bi2Se3 Determined from Surface-Phonon Dispersion Measurements. Physical Review Letters 108, 185501 (2012). [DOI] [PubMed] [Google Scholar]
  40. Giraud S., eacute bastien. & Egger R. Electron-phonon scattering in topological insulators. Physical Review B 83, 245322 (2011). [Google Scholar]
  41. Sergeev A. et al. Electron-phonon interaction in disordered conductors. Physica B 263–264, 190–192 (1999). [Google Scholar]
  42. Reizer M. Y. & Sergeev A. V. Electron-phonon interaction in impure metals and superconductors. Sov. Phys. JETP 63, 616–624 (1986). [Google Scholar]

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES