A brief historical perspective: Hodgkin and Huxley

Working together in 1939, and again from 1946 to 1952, Alan Hodgkin and Andrew Huxley formed one of the most productive and influential collaborations in the history of physiology. Their work, both in the Physiological Laboratory in Cambridge and at the Laboratory of the Marine Biological Association in Plymouth, provided fundamental insights into nerve cell excitability. Their legacy is not only our understanding of how voltage-gated ion channels give rise to propagating action potentials, but also the very framework for studying and analysing ion channel kinetics. Their work won them a share of the 1963 Nobel Prize in Physiology or Medicine (Fig. 1) as well as laying the foundations for other Nobel Prize-winning work including that of Erwin Neher and Bert Sakmann ‘for their discoveries concerning the function of single ion channels in cells’ and Roderick MacKinnon ‘for structural and mechanistic studies of ion channels’.

Figure 1. The cover of the 1963 Nobel Prize Programme.

Huxley, left, looks on as Hodgkin adjusts a brand-new Tektronix 502A oscilloscope. Together with John Carew Eccles (27 January 1903–2 May 1997), Andrew Fielding Huxley (22 November 1917) and Alan Lloyd Hodgkin (5 February 1914–20 December 1998) won the 1963 Nobel Prize in Physiology or Medicine ‘for their discoveries concerning the ionic mechanisms involved in excitation and inhibition in the peripheral and central portions of the nerve cell membrane’ Programme provided by Deborah Hodgkin.

Squid, mercury and Poland (1939)

Huxley, a bright student fresh from his final undergraduate year in Physiology at Cambridge, had accepted Hodgkin's invitation to join him in Plymouth to work on nerve conduction (Fig. 2). Eventually in August 1939, after weeks of waiting, the trawlers operating beyond Plymouth Sound began to bring in catches of squid. Hodgkin had spent the previous summer at Woods Hole (USA), with K. S. Cole, learning to dissect squid giant axons. His enjoyment of that collaboration and the skills he acquired proved pivotal. Huxley started by trying to measure the viscosity of axoplasm by observing the passage of mercury droplets through it, but the experiments were not a great success (Huxley, 2004). The droplets sat obstinately at the top of cut axons, descending only if the axoplasm was damaged. The failure of those experiments, however, triggered something much more exciting.

Figure 2. J. Z. Young, squid and the Marine Biological Association (MBA).

A, John Zachary Young (1907–1997). His discovery of the squid giant axon in the 1930s was pivotal since it provided an electrically excitable membrane of sufficient area for Hodgkin and Huxley's experiments. B, Loligo forbesi, the long-finned squid (∼60 cm long). The giant axon allows the rapid conduction of action potentials driving the escape response. Squid image taken by David Nicholson, courtesy of the MBA, Plymouth. C, it was here at the MBA on Citadel Hill in Plymouth that Hodgkin and Huxley made their recordings from squid giant axons. 1937 photo taken from Southward AJ & Roberts EK (1987). J Mar Biol Ass UK, 67, 465–506, with permission from the MBA.

Both Hodgkin and Huxley have stated that, following the failed attempts with the mercury droplets, it was the other who made the suggestion that a fine capillary electrode might be inserted inside the nerve fibre (Fig. 3A) to record the potential difference across the membrane.

Figure 3. Intracellular recording of the squid giant axon action potential.

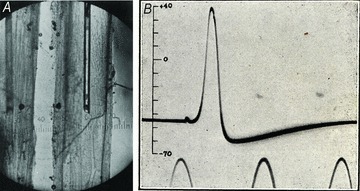
A, photomicrograph of an electrode inside a squid giant axon (diameter ∼500 μm). Two views of the same axon are visible from an ingenious system of mirrors devised by Huxley. This allowed simultaneous viewing of the electrode from both front and side and was essential to avoid the electrode damaging the nerve membrane as it was threaded down the axon. Image taken from Hodgkin & Huxley (1945). B, the first intracellular recording of an action potential. The sine wave time marker has a frequency of 500 Hz. Reproduced from Hodgkin & Huxley (1939) by permission from Macmillan Publishers Ltd: Nature©1939.

The idea was an immediate success and provided the first recording of an intracellular action potential. In particular, it revealed a large action potential overshooting the apparent zero potential. But, only a few weeks after their first measurements, Hitler invaded Poland and the subsequent declaration of war meant that further research stopped. Hodgkin and Huxley hastily published their remarkable result (Fig. 3B) in Nature on 21 October (Hodgkin & Huxley, 1939).

Their brief collaboration thus ended, not to be resumed in earnest for ∼7 years since both took on important war work. Hodgkin first went to Farnborough where he helped design oxygen masks for pilots, followed by 5 years working on radar for use in aircraft. Huxley worked on improving gunnery including the use of predictors in targeting. Both benefited greatly from experiences beyond their academic specialties, in particular Hodgkin's involvement with feedback control systems and Huxley's manipulation of mathematical equations.

The voltage-clamp (1947–1949)

It is unclear who first proposed the idea of voltage control across the axonal membrane. K. S. Cole and G. Marmont working at Woods Hole were using the technique in 1947 but Hodgkin and Huxley had independently discussed the idea before the end of the war. Certainly a whole range of war work, both radar and guidance systems, involved feedback control (servo) systems. What is beyond doubt is that Hodgkin and Huxley stamped their ownership on voltage-clamping with the remarkable family of currents produced in July and August of 1949 (Fig. 4). Their dual electrode approach, which avoided the problem of electrode polarization, and series-resistance compensation proved to be a considerable advance over the technique being used by Cole and Marmont. The voltage-clamp allowed them to record, directly, the ionic currents flowing across the axonal membrane of the giant axon without any resultant change in membrane potential. The voltage-clamp also removed the problems of capacitance and created an isopotential membrane. Thus, they were able to investigate the voltage sensitivity and kinetics of the underlying ion channels, helped in some experiments by Bernard Katz (Hodgkin et al. 1952).

Figure 4. A family of currents acquired using large depolarizations under voltage-clamp control.

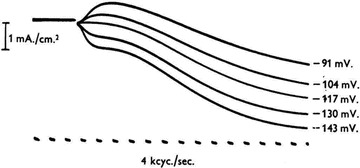
There are a few unusual features of this original recording. Both the traces and voltages have the opposite sign to the current convention, inward currents are shown plotted upwards and depolarizations are given relative to the holding potential as that of the outside with respect to the inside. The –91 mV step represents a depolarization of the inside of the nerve fibre to ∼+15 mV. Modified from Hodgkin et al. (1952).

Modelling: m³h, n⁴ (1949–1952)

The culmination of Hodgkin and Huxley's partnership was the publication of their mathematical model of the action potential in 1952 (Hodgkin & Huxley, 1952a,b,c,d,e). Not only was this the first quantitative description of electrical excitability in nerve cells, but it also incorporated physical correlates that elegantly predicted recent results concerning the gating structures of ion channels (Fig. 5). It remains one of the best examples of how phenomenological description with mathematical modelling can reveal mechanisms long before they can be directly observed.

Figure 5. ‘The modern history of ion channels began in 1952 when Hodgkin and Huxley published their seminal papers on the theory of the action potential in the squid giant axon …’.

Roderick MacKinnon Nobel Prize Lecture, 2003. Image taken from Jiang et al. (2003). Reprinted by permission from Macmillan Publishers Ltd: Nature©2003.

The initial analysis of the data they collected in the summer of 1949 came as a disappointment to them as the unusual delayed-onset kinetics were unexpected. According to Hodgkin it was Huxley who eventually proposed the n⁴, m³ and h models that provided an excellent fit to the families of currents they had recorded.

Thus, in modelling the K⁺ channel they assumed that a certain number of charged particles had to move, under the influence of the membrane potential, to allow K⁺ to pass. They denoted the open probability of each charged particle as n. They found that n⁴ introduced the appropriate delay to the onset kinetics to produce a good experimental fit to their voltage-clamp data. Similarly, for the Na⁺ current the activation was fitted well by three charged particles (m³) for activation, and one for inactivation (h). Using their voltage-clamp data they then derived equations for determining n, m and h at a range of potentials.

The Hodgkin–Huxley equation

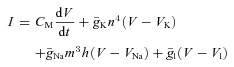Hodgkin and Huxley thus emerged with a model which incorporated four currents (capacitance, K⁺, Na⁺ and leak). These, when iteratively summed to give a total current, I, predict the action potential time course with remarkable accuracy. The three voltage- and time-dependent, but otherwise uncoupled ‘variables’ (n, m and h), which define the proportion of the K⁺ and Na⁺ channels available as a proportion of the maximum available conductance (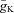 and 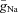) at any given time within the trajectory of an action potential, underlie the model's elegance.

Hodgkin and Huxley solved their mathematical model for both stationary and propagating action potentials using what might best be described as a ‘brute force’ method. The iterative solution for the propagating action potential, whose results are shown in Fig. 6A, took a few weeks and many thousands of rotations of the mechanical calculator crank (Fig. 6B). For each small step in time, new values of n, m and h had to be calculated.

Figure 6. Modelling the action potential.

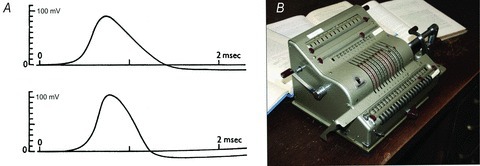
A, calculated (upper) and measured (lower) action potentials in squid giant axons. Using their qualitative descriptions of n, m and h based upon the infinity proportions and rate constants, Hodgkin and Huxley iteratively calculated the current carried by Na⁺ and K⁺ flowing across the membrane. By assuming that these currents flowed for a short period of time, they derived a new voltage. Since every iteration produced a new voltage, a new set of n, m and h variables had to be calculated for the next time step. To produce such a trace required many hundreds of iterations. Figure taken from Hodgkin & Huxley (1952e). B, the Brunsviga 20 (produced in Braunschweig by Brunsviga Maschinenwerke, Grimme, Natalis & Co.), one of the most popular mechanical calculators. It was produced up to the early 1970s and marketed with the slogan ‘Brains of Steel’. This particular one was photographed in what was Alan Hodgkin's space in the basement of the Physiological Laboratory in Cambridge and, whilst its original owner is unknown, it has belonged to Richard Adrian, then Trevor Lamb and now Hugh Robinson. Photograph taken by Christof Schwiening.

In 1992 Alan Hodgkin wrote ‘We had settled all the equations and constants by March 1951 and hoped to get these solved on the Cambridge University computer. However, before anything could be done we learnt that the computer [EDSAC 1] would be off the air for 6 months or so while it underwent a major modification. Andrew Huxley got us out of that difficulty by solving the differential equations numerically using a hand-operated Brunsviga. The propagated action potential took about three weeks to complete and must have been an enormous labour for Andrew …’ (Hodgkin, 1992).

In the 1950s Alan Hodgkin's interest in the squid giant axons continued with work on calcium and the sodium pump. Andrew Huxley, however, had moved his attention to the mechanisms of activation of skeletal muscle contraction. Whilst they did not collaborate again, they both continued to make substantial individual contributions to physiology.

Step change in electrophysiology

The effect of Hodgkin and Huxley's work was tremendous, leading to an explosion of interest in electrophysiology. The voltage-clamp technique began to be used on a range of large cells. However, it was Neher and Sakmann's development of the patch-clamp in the 1970s that allowed the first recordings of single ion channels from even the smallest of cells. Such recordings of these small currents were impossible using the valve-based amplifiers of 1949, and equally they would not have been possible in the 1970s without Hodgkin and Huxley's pioneering work. However, the impact of their work extended well beyond experimental electrophysiology. The Hodgkin–Huxley model contained within it probabilistic representations of the activation and inactivation of ionic conductances. In 1955 Hodgkin and Keynes published data that predicted that K⁺ channels would be occupied by multiple ions simultaneously (Hodgkin & Keynes, 1955). The molecular structural description of K⁺ channels, confirming this prediction, won Rod MacKinnon the 2003 Nobel prize in Chemistry (see Fig. 5). Indeed, the ideas and equations behind their model are now the standard building blocks of neuronal modelling software for both teaching and research.

The landmark papers of 1952 heralded the start of the modern era of biological research in general. Simple qualitative descriptions of how things might work were being replaced by quantitative modelling that could predict, in a robust fashion, the behaviour of non-linear feedback systems.

In setting the bar so high, Hodgkin and Huxley have left neuroscience with a daunting task. Their action potential was modelled for one cell with two ion channel types and uniform distributions and morphology. We now know that there are ∼40 subunit genes coding for K⁺ channels alone, producing a vast array of channels with differing characteristics. Attempting to model the behaviour of specific sets of these channels, clustered into heterogeneous regions with an equally diverse array of Ca²⁺, Na⁺, Cl⁻ and other non-specific conductance channels and voltage-sensitive transporters in complex and morphologically dynamic neurones, modulated by second messenger systems and interacting with myriad other cells is no simple matter. We are going to need some really clear thinking and a seriously big calculator.