Gibbs distribution analysis of temporal correlations structure in retina ganglion cells

Abstract

We present a method to estimate Gibbs distributions with spatio-temporal constraints on spike trains statistics. We apply this method to spike trains recorded from ganglion cells of the salamander retina, in response to natural movies. Our analysis, restricted to a few neurons, performs more accurately than pairwise synchronization models (Ising) or the 1-time step Markov models (Marre et al. (2009)) to describe the statistics of spatio-temporal spike patterns and emphasizes the role of higher order spatio-temporal interactions.

1 Introduction

Modern advances in neurophysiology techniques, such as two-photons imaging of calcium signals or micro-electrode arrays electro-physiology, have made it possible to observe simultaneously the activity of assemblies of neurons, Stevenson and Kording (2011). Such experimental recordings provide a great opportunity to unravel the underlying interactions of neural assemblies. The analysis of multi-cells spike-patterns constitutes an alternative to descriptive statistics (e.g cross-correlograms or joint peri-stimulus time histograms) which become hard to interpret for large groups of cells, Brown et al. (2004); Kass et al. (2005). Earlier multi-cells approaches, e.g., Abeles and Gerstein (1988), focus on synchronization patterns. Using algorithms detecting the most frequent instantaneous patterns in a data set, and calculating their expected probability, these approaches aim at testing whether those patterns were produced by chance, Grün et al. (2002). This methodology relies however on a largely controversial assumption, namely Poisson-statistics, Pouzat and Chaffiol (2009); Schneidman et al. (2006).

A second type of approach has become popular in neuroscience after works of Schneidman et al. (2006); Shlens et al. (2006). They used a maximum entropy approach model spike trains statistics as the Gibbs distribution of the Ising model. The parameters of this distribution are determined from the mean firing rate of each neuron and their pairwise synchronizations. These works have shown that for a small group of cells (10-40 retinal ganglion cells) the Ising model describes most (~ 80 – 90%) of the statistics of the instantaneous patterns, and performs much better than a non-homogeneous Poisson model.

However, several papers have pointed out the importance of temporal patterns of activity at the network level, Abeles et al. (1993); Lindsey et al. (1997); Villa et al. (1999); Segev et al. (2004a). Recently, Tang et al. (2008); Ohiorhenuan et al. (2010), have shown the insufficiency of the Ising model to predict the temporal statistics of the neural multi-cells activity. Therefore, some authors, Marre et al. (2009); Amari (2010); Roudi and Hertz (2010), have attempted to define time-dependent Gibbs distributions on the basis of a Markovian approach (1-step time pairwise correlations). The application of such extended model in Marre et al. (2009) increased the accuracy of the statistical characterization of data with the estimated distributions.

In this paper we propose an extension of the maximal entropy approach to general spatio-temporal correlations, based on the transfer-matrix method in statistical physics, Georgii (1988) (section 2). We describe a numerical method to perform the estimation of the Gibbs distribution parameters from empirical data (section 3). We apply this method to the analysis of spike trains recorded from ganglion cells using multi-electrodes devices in the salamander retina (section 4). We analyse retinal spike trains taking into account spatial patterns of two and three neurons with triplets and quadruplets terms, and temporal terms up to 4 time steps. Our analysis emphasizes the role of higher order spatio-temporal interactions. Section 5 contains the discussion and conclusions.

2 Theoretical framework

2.1 Spike trains and Raster Plots

Let N be the number of neurons and denote i = 1,…,N the neuron index. Assume that we have discretised time in steps of size Δ. Without loss of generality (change of time units) we may set Δ = 1. This provides a time discretisation labelled with an integer index n. We define a binary variable ω_i (n) ∈ {0, 1}, which is ’1’ if neuron i has emitted a spike in the n-th time interval and is zero otherwise. We use the notation ω to differentiate our binary variables ∈ {0, 1} to the notation σ or S traditionally used for “spins” variables ∈ {−1, 1}. The spiking pattern of the neural network at time n is the vector $\omega (n)={({\omega }_i(n))}_{i=1}^N$. We denote ${[\omega ]}_m^n$ the ordered sequence or spike block ω(m) … ω(n), m ≤ n. In practice, from recordings and after applying spike sorting algorithms, one obtains a sequence of spiking patterns called a raster plot. In our notations a raster plot is thus a spike block ${[\omega ]}_0^T$ where T is the total length of the spike time sequences, measured Δ in time-units.

2.2 Observables and monomials

We call observable a function ϕ which associates to a raster a real number. Although the method developed here holds for general functions, we focus on observables called monomials. These are functions of the form ϕ(ω) = ω_i1 (n₁) ω_i2 (n₂) … ω_im (n_m) which is equal to 1 if and only if neuron i₁ fires at time n₁, …, neuron i_m fires at time i_m in the raster ω. Thus monomials attribute the value ’1’ to characteristic spike events. We use the convention that n₁ ≤ n₂ ≤ ⋯ ≤ n_m. Then, the range of a monomial is n_m − n₁ + 1.

A typical monomial is ϕ(ω) = ω_i(0) which is equal to ’1’ if neuron i spikes at time 0 in the raster ω and is ’0’ otherwise. This a function of a single event, of range 1. Likewise ϕ(ω) = ω_i(0) ω_j(0) is ’1’ if and only if neuron i and j fire synchronously at time 0 in the raster ω. This is a function of pairwise event, of range 1 too. As a last example, ϕ(ω) = ω₁(0) ω₂(1) ω₃(2) ω₄(5) is a function of a quadruplet of spikes, of range 6.

2.3 Hidden probability

Collective neuron dynamics, submitted to noise, produce spike trains with randomness, although some statistical regularity can be observed. The spike trains statistics are assumed to be characterized by an hidden probability μ^h giving the probability of spatio-temporal spike patterns. A current goal in experimental analysis of spike trains is to approximate μ^h from data. A model is a probability distribution μ which approaches μ^h. We give a precise meaning of approaching a probability by another one below. Typically, μ must predict the probability of spike blocks occurrence with a good accuracy.

Given a model μ we note μ [ϕ] the average of an observable ϕ with respect to μ. For example the average value of ϕ(ω) = ω_i(n) is given by μ [ω_i(n)] = Σ_ωi(n) ω_i(n) μ [ω_i(n)] where the sum holds on all possible values of ω_i(n) (0 or 1). Thus, finally μ [ϕ] = μ [ω_i(n) = 1] is nothing but the probability of firing of neuron i at time n, predicted by the model μ. Likewise, the average value of ω_i1 (n) ω_i2 (n) is the predicted probability that neuron i₁ and i₂ fire at the same time n: this is a measure of pairwise synchronization. More generally, for the monomial ϕ = ω_i1 (n₁)ω_i2 (n₂) … ω_im(n_m), μ [ϕ] is the predicted probability of occurrence of the event “neuron i₁ fires at time n₁, …, neuron i_m fires at time i_m”.

We assume here, as in most papers dealing with spike train statistics, that hidden statistics are stationary so that the average value of functions is time-translation invariant. As a consequence we consider time-translation invariant models (e.g., μ [ω_i(n) = 1] is independent on n).

2.4 Time-average

Given an experimental raster ω of duration T, and an observable ϕ we note ${\pi }_{\omega }^{(T)}[\varphi ]$ the time-average of ϕ. For example, when ϕ(ω) = ω_i(n), ${\pi }_{\omega }^{(T)}[\varphi ]=\frac{1}{T}{\sum }_{n=0}^{T-1}{\omega }_i(n)$ provides an estimation of the firing rate of neuron i (it is independent of time from the stationarity assumption). If ϕ is a monomial ω_i1 (n₁) … ω_im(n_m), 1 ≤ n₁ ≤ n₂ ≤ n_m < T then ${\pi }_{\omega }^{(T)}[\varphi ]=\frac{1}{T-n_m}{\sum }_{n=0}^{T-n_m}{\omega }_{i_1}(n_1+n)\dots {\omega }_{i_m}(n_m+n)$, and so on. We use the cumbersome notation ${\pi }_{\omega }^{(T)}[\varphi ]$ to remind that such time averages are random variables. They fluctuate from one raster to another and the amplitude of those fluctuations depend on T. We assume ergodicity which is a common hypothesis in this field. Then, for any observable ϕ, ${\pi }_{\omega }^{(T)}[\varphi ]\to {\mu }^h[\varphi ]$ as T → + ∞, where the limit is independent of the raster ω.

2.5 Gibbs distribution

Fix a set of observables ${\{{\varphi }_l\}}_{l=1}^L$ whose time average ${\pi }_{\omega }^{(T)}[{\varphi }_l]$ has been measured and is equal to C_l. To match those empirical statistics, the model μ has to satisfy:

$$\mu [{\varphi }_l]={\pi }_{\omega }^{(T)}[{\varphi }_l]=C_l,l=1,\dots ,L.$$ (1)

This is a minimal, but insufficient requirement, since one can construct infinitely many probability distributions satisfying the constraints (1).

However, with the additional requirement that the model has to “Maximize the statistical entropy under the constraints (1)”, a unique model is selected. This is the maximal entropy principle, Jaynes (1957) that amounts to solving, i.e. find the maximum of: a variational principle:

$$P(\psi )=\underset{\nu \in m^{(\mathit{inv})}}{\sup }(h[\nu ]+\nu [\psi ]).$$ (2)

The term ψ defined by:

$$\psi =\sum _{l=1}^L{\lambda }_l{\varphi }_l,$$ (3)

is called a potential. The λ_l are free parameters (Lagrange multipliers). ψ is thus a linear combination of the observables defining the constraints (1). The supremum in (2) is taken over m^(inv), the set of time-translation invariant (stationary) probabilities on the set of rasters for N neurons. h is the entropy rate, see Ruelle (1969, 1978); Keller (1998); Chazottes and Keller (2009) for the general definition.

A probability μ which realizes the supremum (2), i.e.,

$$P(\psi )=h[\mu ]+\mu [\psi ],$$ (4)

is called a Gibbs distribution. This name has its roots in statistical physics and we discuss this connection in the next paragraph. The term P(ψ), called the topological pressure in this context is the formal analog of a thermodynamic potential (free energy density). It is a generating function for the cumulants of ψ. In particular;

$$\frac{\partial P(\psi )}{\partial {\lambda }_l}=\mu [{\varphi }_l].$$ (5)

Let us summarize what we have just obtained. To a set of experimental constraints, associated with a set of observables ${\{{\varphi }_l\}}_{l=1}^L$, one associates a probability distribution μ, called a Gibbs distribution, parametrized by the potential (3), a linear combination of ϕ_l’s. Now, comparing equations (1) and (5), one sees that the free parameters λ_l can be adjusted so that the Gibbs distribution μ matches the constraints (1). We will explain how this computation can be done in section 3. It turns out that P(ψ) is a convex function. Therefore, there is a unique set of λ_l so that μ matches the constraints (1). Hence the maximal entropy principle provides a unique statistical model matching the experimental constraints (1).

Note that μ depends on ψ, thus (i) on the choice of observables; (ii) on the parameters λ_l. However, we drop this dependence in the notation to ease legibility.

2.6 A remark. Links with previous approaches

The maximal entropy principle is commonly used in statistical physics and has been applied by several authors for spike trains analysis, Schneidman et al. (2006); Tkačik et al. (2009, 2010); Schaub and Schultz (2010); Ganmor et al. (2011a,b). Here we would like to insist on the main difference between our approach and the one of these authors.

In those references, constraints correspond to simultaneous spike events (monomials of the form ω_i1 (n) … ω_im (n)) corresponding to spatial patterns. On the opposite, our observables ϕ_l correspond to spatio-temporal events so that ψ depends on the raster plot over a (finite) time horizon R, i.e. $\psi (\omega )\equiv \psi ({[\omega ]}_0^{R-1})$. We speak of “range-R potentials”. Thus, our method imposes constraints on general spatio-temporal events instead of focusing on spatial constraints.

The difference is not anecdotic. Imposing spatio-temporal constraints amounts to considering a statistical model in which the probability of a spiking pattern depends on the past history: the system has a memory and its actual state depends on its past via a set of causal spatio temporal relations. Typically, this is described by a Markovian process, (although non Markovian dynamics also occur in neural networks models, Kravchuk and Vidybida (2010); Cessac (2011a,b)). The Markovian case has been considered by several authors in the field of spike statistics analysis, but with one time step memory only, and under assumptions such as detailed balance, Marre et al. (2009) or conditional independence between neurons, see eq. (1) in Roudi and Hertz (2011).

The method introduced here does not use these assumptions and allows us to consider, on a theoretical ground, general spatio-temporal constraints. It is based on a mathematical object called, in statistical physics, “transfer matrix” Georgii (1988) and in ergodic theory “Ruelle-Perron-Frobenius operator”, Bowen (1975); Ruelle (1978); Meyer (1980). Although this method extends to non-Markovian dynamics, Cessac (2011a,b), in the present paper, we restrict to finite memory. In this restricted case, this method has its roots in matrix representation of Markov chains and Perron-Frobenius theorem, Gantmacher (1998); Seneta (2006). So this method is well known but, to our knowledge, it is the first time that it is applied to the analysis of spike trains.

Since we focus on Markovian dynamics here, Gibbs distribution could also be introduced in this setting, see Cessac and Palacios (2011) for a didactic presentation in the realm of spike train analysis. However, the advantage of the presentation adopted here is its compactness compatible with the limited allowed space of the paper.

3 Estimation of Gibbs Distributions

Let us now show how P(ψ) and μ, the main objects of our approach, can be computed.

3.1 The transition matrix

The range R of the potential ψ is the maximum of the ranges of monomials defining ψ. If R = 1 the potential depends only on simultaneous events and corresponds to considering a memory-less process as a model. On the opposite, if R > 1 the potential accounts for spatio-temporal events and corresponds to taking into account memory and time-causality in the model.

We assume here that R > 1 and come back to the case R = 1 below. The starting point is to consider that a block ${[\omega ]}_n^{n+R-1}$ is a transition from a block ${[\omega ]}_n^{n+R-2}$, of range R − 1, to a block ${[\omega ]}_{n+1}^{n+R}$ of range R − 1 too. Therefore, the two blocks overlap (the sequence ${[\omega ]}_{n+1}^{n+R-1}$ is common to both blocks). It is useful to choose a symbolic representation of spike blocks of range R − 1. Indeed, there are M = 2^N(R−1) such possible spike blocks, requiring, to be represented, N(R−1) symbols (’0”s and ’1”s). Instead, we associate to each block ${[\omega ]}_n^{n+R-1}$ an integer:

$$w_n=\sum _{r=0}^{R-1}\sum _{i=0}^{N-1}{2}^{i+\mathit{Nr}}{\omega }_i(n+r).$$ (6)

We write $w_n~{[\omega ]}_n^{n+R-1}$. Now, for integer m, n such that m ≤ n, n − m ≥ R, a spike sequence ${[\omega ]}_m^n=\omega (m)\omega (m+1)\dots \omega (m+R-1)\dots \omega (n)$ can be encoded as a sequence of integers w_m, w_m+1 … w_n−R+1. Clearly, this representation introduces a redundancy since successive blocks w_n, w_n+1 have a strong overlap. But what we gain is a convenient matrix representation of the spike trains process. Note that each symbol w_n belongs to {0,…,2^N(R−1)}. However, when encoding spike trains by a sequence of such symbols, we cannot have any possible succession of symbols w_n, w_n+1. Indeed, the corresponding blocks must overlap (they must have the sequence ${[\omega ]}_{n+1}^{n+R-1}$ in common). We say that the succession w_n, w_n+1 is legal if the corresponding blocks overlap.

For two integers w′, w ∈ {0, …, 2^N(R−1)}, we define the transition matrix L(ψ) with entries:

$$L_{w^{\prime },w}(\psi )=\{\begin{array}{ll}{e}^{{\psi }_{w^{\prime }w}}& \mathrm{if}{w}^{\prime },w\mathrm{is\; legal}\\ 0,& \mathrm{otherwise}.& \end{array},$$ (7)

where ψ_{w′ w} stands for $\psi ({[\omega ]}_0^{R-1})$. Indeed, for a legal transition w′, w, fixing w′, w is equivalent to fixing the block ${[\omega ]}_0^{R-1}$ as well.

Remark

L(ψ) is a huge matrix (with 2^N(R−1) ×2^N(R−1) symbols). However,

1. This is a sparse matrix. Indeed, on a each row, there are at most 2^N non-zero entries.

2. If, instead of considering all possible symbols, one restricts to symbols (blocks) effectively appearing in an experimental raster, the dimension is considerably reduced.

3.2 The Perron-Frobenius theorem

Since, L(ψ) is a positive matrix it obeys the Perron-Frobenius theorem, Gantmacher (1998); Seneta (2006). Instead of stating it in its full generality, we give it under the assumption that the L(ψ) is primitive, i.e. ∃n > 0, s.t. ∀w, w′ $L_{w\prime ,w}^n(\psi )>0$. This assumption holds for Integrate and Fire models with noise and is likely to hold for more general neural networks models where noise renders dynamics ergodic and mixing. Then, the Perron-Frobenius theorem states that L(ψ) has a unique real positive maximal eigenvalue s(ψ) associated with a right eigenvector ∣b〉 and a left eigenvector 〈b∣ such that L(ψ)∣b〉 = s(ψ)∣b〉, and 〈b∣L(ψ) = s(ψ)〈b∣. Those vectors can be chosen such that the scalar product 〈b ∣ b〉 = 1. The remaining part of the spectrum is located in a disk in the complex plane, of radius strictly lower than s(ψ).

It can be shown, Bowen (1975); Ruelle (1978); Keller (1998), that the topological pressure P(ψ) is:

$$P(\psi )=\log s(\psi ).$$ (8)

Moreover, the Gibbs distribution μ is:

$$\mu =\left|b\rangle \langle b\right|,$$ (9)

i.e. the probability of a spike block ~ w of range R − 1 is

$$\mu (w)=\left|b_w\rangle \langle b_w\right|,$$

where ∣b_w〉 is the w-th component of ∣b〉. So we have a simple way to compute the topological pressure and the Gibbs distribution by building the transition matrix of the model. Note that we don’t have to compute a partition function.

3.3 The case R = 1

Our method can be applied to this case as well, although other methods for range 1 potentials have been applied in the literature and are more efficient Schneidman et al. (2006); Tkačik et al. (2009). In our setting, a range-1 potential ψ depends on w′ only and the matrix L(ψ) has constant non zero coefficients e^ψ_w′ on each raw. Then, it is straightforward to check that this matrix has N − 1 eigenvalues equal to 0, while the largest one is $Z={\sum }_{w^{\prime }}{e}^{{\psi }_w^{\prime }}$, the partition function of a lattice model with potential ψ. So P(ψ) = logZ. Likewise the left eigenvector is 〈b∣ = (1, …, 1), while the right eigenvector has entries ∣b_w〉 = e^ψ_w. Thus, the corresponding probability is ${\mu }_w=\frac{1}{Z}{e}^{{\psi }_w}$, the Gibbs distribution on a lattice, with potential ψ.

3.4 Comparing several Gibbs statistical models

The choice of a potential (3), i.e. the choice of a set of observables, fixes a statistical model. Since, there are many choices of potentials one needs to propose a criterion to compare them.

The Kullback-Leibler (KL) divergence d_KL(μ, ν) provides some notion of asymmetric “distance” between two probabilities, μ and ν. The computation of d_KL(μ, ν) is numerically delicate but, in the present context, the following holds. For ν a time-translation invariant probability and μ a Gibbs measure with a potential ψ, one has, Keller (1998); Chazottes and Keller (2009):

$$d_{\mathit{KL}}(\nu ,\mu )=P(\psi )-\nu [\psi ]-h(\nu ).$$

This allows to estimate the divergence of our model to the hidden probability μ^h, providing the exact spike train statistics. The smaller the quantity d_KL(μ^ex, μ) = P(ψ) − μ^ex [ψ] − h(μ^ex), the better is the model. Obviously, since μ^h is unknown this criterion looks useless. However,

1. As stated in the section “Time average”, μ^ex [ψ] is well approximated by ${\pi }_{\omega }^{(T)}[\psi ]={\sum }_{l=1}^L{\lambda }_l{\pi }_{\omega }^{(T)}[{\varphi }_l]$, where, by definition ${\pi }_{\omega }^{(T)}[{\varphi }_l]=C_l$. Therefore, ${\mu }^{\mathit{ex}}[\psi ]\sim {\sum }_{l=1}^L{\lambda }_l{C}_l$, where ~ means that the right-hand side approaches the left-hand side as T → ∞. More precisely, the distance between the two quantities converges to 0 as $\frac{K_l}{\sqrt{T}}$, where $K_l=\frac{{\partial }^{2}P(\psi )}{\partial {\lambda }_l^2}$, Bowen (1975); Ruelle (1978); Georgii (1988).

2. The entropy h(μ^ex) is unknown and its estimation by numerical algorithms becomes more and more cumbersome and unreliable as the number of neuron increases, Grassberger (1989); Schürmann and Grassberger (1996); Gao et al. (2008). However, when comparing two statistical models μ₁, μ₂ with potentials ψ₁, ψ₂, for the analyse the same data, h(μ^ex) is a constant since it only depends on data. Thus, comparing these two models amounts to comparing $P[{\psi }_1]-{\pi }_{\omega }^{(T)}[{\psi }_1]$ and $P[{\psi }_2]-{\pi }_{\omega }^{(T)}[{\psi }_2]$. Introducing

   $$\stackrel{\sim }{h}[\psi ]=P[\psi ]-{\pi }_{\omega }^{(T)}[\psi ]=P[\psi ]-\sum _{l=1}^L{\lambda }_l{C}_l,$$ (10)

   (where the λ_l depend on the potential via (5)), the comparison of two statistical models ψ₁, ψ₂, i.e. determining if model ψ₂ is significantly “better” that model ψ₁, reduces to the condition:

   $$\stackrel{\sim }{h}[{\psi }_2]\ll \stackrel{\sim }{h}[{\psi }_1].$$ (11)

The advantage of (10) (sometimes called “cross-entropy”) compared to the KL divergence is that we have removed the entropy, which is subject to huge fluctuations when determined numerically from a finite raster with many neurons. Thus, (10) is less sensitive to statistical bias. What we loose, is an absolute criterion for model comparison. We can just say that a model is a better than another one but we cannot say how close we are from the hidden probability. For this latter purpose, we estimate the entropy explicitly using the method proposed by Strong et al. (1998). An example is given below, for a small number of neurons.

3.5 Numerical implementation

Let us now briefly discuss how to numerically estimate the Gibbs distribution. For details see Vasquez et al. (2010). The code is available at http://enas.gforge.inria.fr/. The algorithmic procedure proposed decomposes in three steps.

• Choosing a statistical model, i.e. choosing a guess potential $\psi ={\sum }_{l=1}^L{\lambda }_l{\varphi }_l$ or equivalently, a set of observables.

• Computing the time averages C_l. To compute the time-average we use a data structure of tree type, with depth R and degree 2^N, see e.g., Grassberger (1989) for a formal introduction. The nodes count the number of occurrences of blocks encountered in the raster. Thus, we do not store explicitly blocks of occurrence zero. Moreover, when comparing the distributions for distinct ranges R we can count in one pass, and in a unique data structure, block of different ranges.

• Performing the parametric estimation. The parametric estimation aims at finding the λ_l minimizing (10), by calculating the topological pressure. Note that, from (10), finding a point where h̃ is extremal is equivalent to solving (5). Additionally, P(ψ) is convex, thus h̃ is convex too as a linear combination of convex functions. Thus, there is a unique minimum corresponding to the solution of (5).

  We start with a random guess for the λ_l, and then iterate the following steps:

  1. Build the matrix L(ψ) from the values of λ_l and equation (7).

  2. Compute the eigenvectors 〈b∣,∣b〉 of L(ψ) and the highest eigenvalue s(ψ) using a standard power-method series.

  3. From this eigenvalue, compute the topological pressure. This gives h̃.

  4. From the left and right eigenvectors, we have the Gibbs distribution μ corresponding to this set of parameters λ_l. One then computes the average value of ϕ_l under μ, μ [ϕ_l] Now, from (5) the derivative of P(ψ) with respect to λ_l is exactly μ [ϕ_l]. This provides an exact expression for the gradient of P(ψ).

  5. To update the λ_l toward the minimum of h̃, we have tried several methods. The most efficient are based on gradient algorithms where the gradient of P(ψ) is exactly known from the previous step. The most efficient method seems to be the Fletcher-Reeves conjugate gradient algorithm from the GSL http://www.gnu.org/software/gsl, while other methods such as the Polak-Ribiere conjugate gradient algorithm, and the Broyden-Fletcher-Goldfarb-Shannon quasi-Newton method appeared to be less efficient. We have also used the GSL implementation of the simplex algorithm of Nelder and Mead which does not require the explicit computation of a gradient. This alternative is usually less efficient than the previous methods. All these methods are available in our library http://enas.gforge.inria.fr/.

  6. Repeat the previous steps until h̃ attains its minimum.

4 Analysis of Biological data

4.1 Methods

Retinae from the larval tiger salamander (Ambystoma tigrinum) were isolated from the eye, placed over a multi-electrode array and perfused with oxygenated Ringer’s medium at room temperature (22 °C). Extracellular voltages were recorded by a micro-electrode array and streamed to disk for offline analysis. Spike sorting was performed as described earlier in (Segev et al. (2004b)) to extract 40 cells. The stimulus was a natural movie clip showing a woodland scene. The 20-30 s movie segment was repeated many times. All visual stimuli were displayed on an NEC FP1370 monitor and projected onto the retina using standard optics. The mean light level was 5 lux, corresponding to photopic vision. The total recording time was around 3200s with sampling frequency of 10000Hz.

4.2 Analysis of spike train-statistics

We have used the recorded spike trains of retinal ganglion cells to fit models with different sets of constraints.

The Linear model has a potential ψ (ω) = Σ_i=1^N λ_i ω_i(0) (thus constraints are only imposed on firing rates). The corresponding Gibbs probability is a Bernoulli distribution where spikes are independent. For a fixed range R, we call All-R a potential containing all possible and non redundant monomials of range R. For example, a monomial containing products of the form ${\omega }_i^k(n)$, k > 1 is redundant since ${\omega }_i^k(n)={\omega }_i(n)$. The next equation shows for clarity the potentials Linear, All-1, All-2 for a pair of neurons. Note that for a pair of neurons All-1 coincides with the usual Ising statistical model but for a triplet of neurons it contains an extra triplet synchronization term.

$$\begin{array}{lll}\mathrm{linear}:\psi (\omega )& =& {\lambda }_1{\omega }_1(0)+{\lambda }_2{\omega }_2(0).\\ \mathrm{All}­1:\psi (\omega )& =& {\lambda }_1{\omega }_1(0)+{\lambda }_2{\omega }_2(0)+{\lambda }_3{\omega }_1(0){\omega }_2(0).\\ \mathrm{All}­2:\psi (\omega )& =& {\lambda }_1{\omega }_1(0)+{\lambda }_2{\omega }_2(0)+{\lambda }_3{\omega }_1(0){\omega }_2(0)\\ & & +{\lambda }_4{\omega }_1(0){\omega }_1(1)+{\lambda }_5{\omega }_2(0){\omega }_2(1)\\ & & +{\lambda }_6{\omega }_1(0){\omega }_2(1)+{\lambda }_7{\omega }_1(1){\omega }_2(0)\\ & & +{\lambda }_8{\omega }_1(1){\omega }_2(0){\omega }_2(1)+{\lambda }_9{\omega }_1(0){\omega }_1(1){\omega }_2(0)\\ & & +{\lambda }_{10}{\omega }_1(0){\omega }_2(0){\omega }_1(1){\omega }_2(1).\end{array}$$ (12)

For the model estimation we bin the spike trains using bin sizes of 10 ms (we obtain similar results with larger bin sizes). We estimate the model parameters and the Kullback-Leibler divergence between the model distribution and the empirical distribution. To have an error bar on the latter, we divide the raster in 15 equal subsets, and we randomly pick 13 subsets, on which we estimate the d_KL. This process is repeated many times (more than 100) and we estimate the error bar from the distribution of the d_KL values obtained.

We first focus on the statistics of spiking patterns using models with range from 1 up to 3. The KL divergence between the empirical Distribution and the model is depicted in figure 1, for 3 examples of pairs. Figure 1 (left plot) shows the effect of including all interaction terms within the chosen number of time bins. Increasing in the hierachy of models, from Linear to All-3 shows significant improvements. Naturally, the number of possible interaction terms explodes combinatorially with the range of the models. Therefore, we estimate the impact of adding higher order interaction terms in a range 3 model. Figure 1 (right plot) shows that, although the largest improvement happens when adding the pairwise terms, adding triplets interactions also allows a significant decrease of d_KL. Beyond third order, we did not see any improvement.

Figure 1.

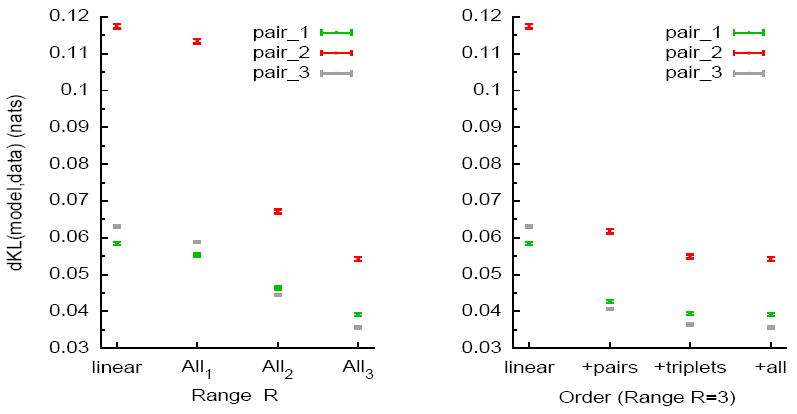
The KL divergence between empirical distribution computed from observed data and the distribution of the estimated model (different models are shown for several pairs, and error bars are included). “nats” means “natural units” (the KL divergence is divided by log 2). (Left) This figure depicts d_KL for the Linear model and All-R from R = 1 to R = 3. Note that for a cell pair, All-1 model corresponds to the pairwise Ising model. (Right) The d_KL divergence for models of range R = 3 are examined versus the role of pairs, then triplets and finally the full set of terms that constitute the All-3 model. The KL divergence of the linear model is included for comparison.

One could think that the improvement shown when adding monomials to the model is due to overfitting. To discard this hypothesis, we divide the raster in 5 subsets, fit the model with 4 of them, and compute the cross-entropy between the model and the fifth subset. We then change the tested subset and repeat the calculation to obtain error bars. Figure 2 shows that there is no difference in the mean value of the cross-entropy between the training and testing sets, and the error bar is still smaller than the difference between the models. So the improvement we see when adding terms is significant. Note that using the cross-entropy h̃, instead of Kullback-Leibler divergence d_KL, eliminates the effects of using biased entropy estimators, as pointed out in section 3.4.

Figure 2.

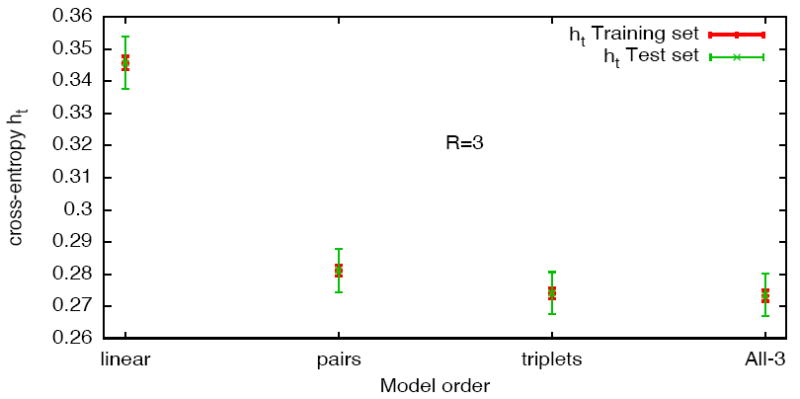
5-fold cross-validation for over-fitting of the cross-entropy (written h_t on the figure). For a single pair, the y-axis shows the cross-entropy estimated on the same models than in the previous figure, for both training and testing sets.

The results depicted above for the three pairs can be generalized to any pair randomly selected among the cells available. We estimate the improvement gained from the model of range 1, similar to Schneidman et al. (2006), or range 2, Marre et al. (2009), to the model of range 3, quantified by the difference of d_KL between the data and the range 1 or 2 model, and between the data and the range 3 model. We randomly pick 100 pairs of cells and estimate these d_KL differences. Fig. 3 shows the histogram of differences, d_KL, between d_KL for an All-1 model and an All-3 model (left), as well as for an All-1 model and an All-2 model (right). Note that it is equivalent to consider δh̃ or δd_KL since the term h(μ^ex) cancels when taking the difference. The average value of δd_KL for an All-1 model and an All-3 model (Fig. 3 left) is 0.012 with a standard deviation 0.01 while the average value of δd_KL for an All-1 model and an All-2 model (Fig. 3 right) is 0.0056 with a standard deviation 0.004. In the former case, the difference δd_KL can be more than 0.04. So our range 3 model improves the statistical description of the data compared to previously used ones, confirming the result observed on individual pairs. The amount of improvement is highly heterogeneous depending on the pair chosen.

Figure 3.

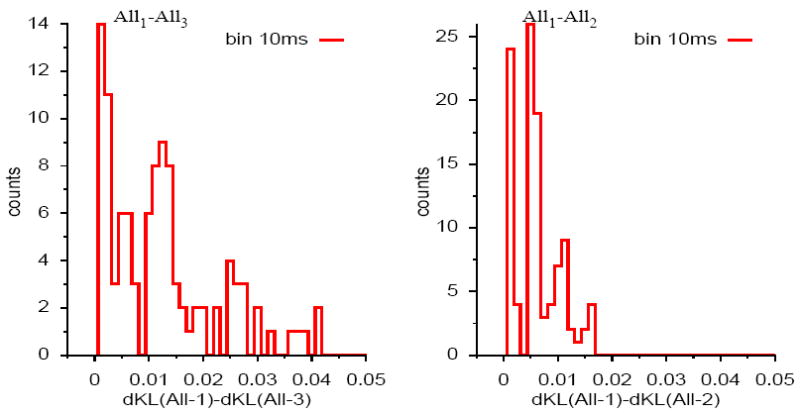
Histogram of differences, δd_KL, between d_KL, for an All-1 model and an All-3 model (left), as well as for an All-1 model and an All-2 model. The histogram has been computed for 100 pairs.

Can these models predict statistics on which they were not fitted? To answer that question, we estimate the rate of spiking pattern of two neurons and 1 to 4 time bins. Figure 4 shows the empirically-observed pattern rate against the pattern rate predicted by each model All-1, All-2 and All-3. Each point corresponds to a spike block. It appears that the model All-3 provides a much better description of the statistics than All-1 and All-2. The result also holds for triplets of neurons (data not shown) and still holds for a bin size of 20ms. In addition, to explore the effects of including higher order spatio-temporal interactions given a range, we show in Figure 5 the same type of plot, for a set of N=4 neurons with models of range R=3 with pairs and triplets. So triplet terms do enhance statistical description of spatio-temporal patterns.

Figure 4.

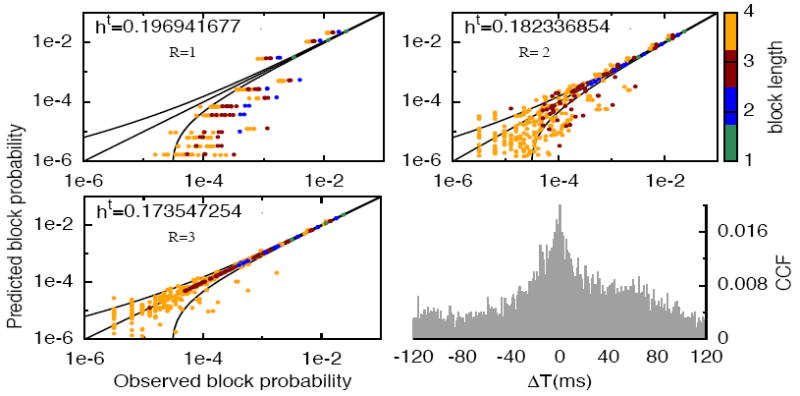
The estimated block probability versus the observed block probability for all possible blocks from range 1 to 4 (coded by colors), one pair of neurons (pair 3) using All-R models R = 1,2,3 with data binned at 10 ms. We include the equality line y = x and the confidence bounds (black lines) for each model, corresponding to $\mu (w)={\pi }_{\omega }^{(T)}[w]\pm 3{\sigma }_w$, σ_w being the standard deviation for each estimated probability given the total sample length T ~ 3 · 10⁵. The cross-correlation function (CCF) of this pair is also depicted (bottom right).

Figure 5.

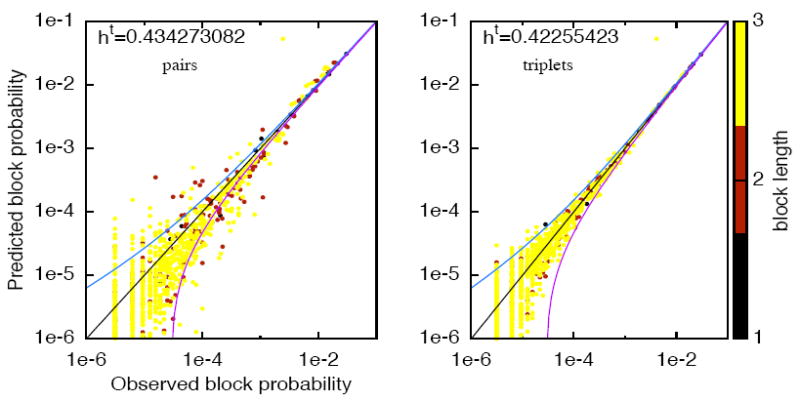
The estimated block probability versus the observed block probability for all blocks from range 1 to 4 (coded by colors), for N = 4 neurons with a model of range R = 3 for pairs and triplets. Data is binned at 10 ms.

We also assess the performance of the models in predicting the total number of spikes during a given window of time. Figure 6 shows this performance for several models, fitted with two different bin sizes. The number of spikes, measured or predicted, is counted over 80 and 120 ms windows. The All-2 model already predicts well the statistics, and the All-3 model improves marginally the performance. These two models are visually almost indistinguishable when a small number of bins is used (i.e, bin size of 20ms corresponding to bottom row uses 4 and 6 bins, while the bin size of 10ms depicted on the upper row uses 8 and 12 bins).

Figure 6.

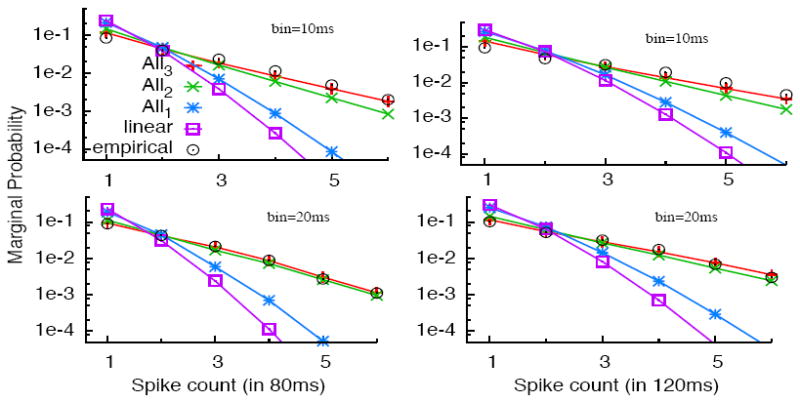
Distribution of the number of spikes fired by a pair of cells in 80ms (left column) and 120ms (right column), compared with predictions by several models: Linear (independent), All-1, All-2, All-3 and bin sizes 10ms (upper row) and 20ms (bottom row).

We examine the coefficients of the parametric estimation by plotting the distribution of the monomial coefficients values after estimation of a All-3 model over 50 different pairs for single spikes, pairs, and triplets. They are depicted in figure 7. Note that none of them is centred at zero, in particular triplet terms are not negligible, suggesting that higher order spatio-temporal interactions do matter. The same conclusion holds for groups of three neurons (data not shown). Additionally, we remark that taking larger bin sizes (20, 50ms) reduces the relative value of coefficients but distribution is still not centred.

Figure 7.

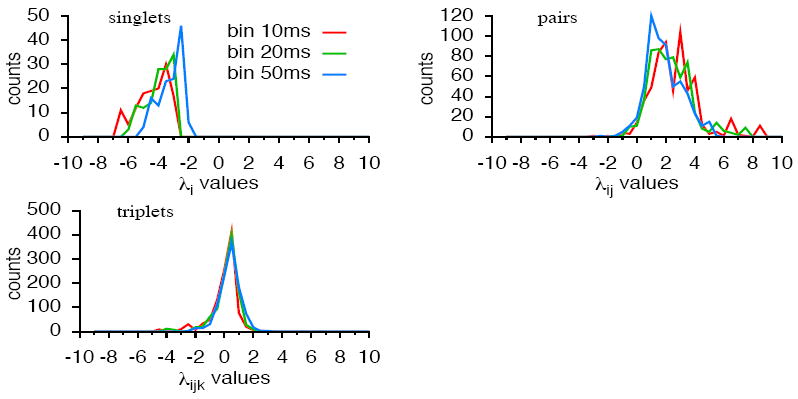
Distribution of the monomial coefficients values has been computed after estimation of a All-3 model over 50 different pairs, for several choices of bin size. The histogram has been constructed separately for single spikes, pairs and triplets. Note that in our framework we consider only non redundant monomials so there is a single coefficient for each monomial. For instance, for the monomial ω_i(0) ω_j(0) there is only one coefficient i j without a symmetrical ji present

5 Discussion and Conclusion

In this paper, we have developed a Gibbs distribution analysis for general spatio-temporal spike patterns. Our method allows one to handle Markovian models with memory up to the limits imposed by the finite size of the data. Our analysis on retina data suggests that higher order interaction terms, as well as interaction between non consecutive time bins, are necessary to model the statistics of the spatio-temporal spiking patterns, at least for small populations of neurons.

An important issue is to determine whether these higher order terms are still essential when looking at much larger groups of neurons: either the complexity of the models will grow with the number of neurons, or adding neurons will have a similar effect as uncovering hidden variables, and might then weaken these interactions. The extension to large networks of our method is, thus, an important future step to progress in our understanding of the spatio-temporal statistics of spike trains. However, the identification of the relevant neural subsets in a large number of neurons remains an open problem. Moreover, to explore models with larger ranges, one needs to control the confidence level due to finite size effects given the available amount of data, which can be addressed through Neyman-Pearson results for Markov chains of finite order Nagaev (2002). Additionally, the spectrum of the Perron-Frobenius matrix provides information about the correlation decay time, which can be used to determine the optimal range of the model. Both issues are to be developed in a forthcoming paper.

Highlights.

• >A method to estimate general maximum-entropy models (beyond Ising).
• >A method to compare statistical models by minimizing Kullback-Leibler divergence.
• >Application to analyse multi-electrode arrays spike-trains for small groups of neurons.
• >For spatio-temporal patterns of two/three neurons, higher orders terms, and Markovian interactions of finite memory improve the description of the statistics.