Abstract
There is much experimental evidence for the existence of biomechanical constraints which simplify the problem of control of multi-segment movements. In addition, it has been hypothesized that movements are controlled using a small set of basic temporal components or activation patterns, shared by several different muscles and reflecting global kinematic and kinetic goals. Here we review recent studies on human locomotion showing that muscle activity is accounted for by a combination of few basic patterns, each one timed at a different phase of the gait cycle. Similar patterns are involved in walking and running at different speeds, walking forwards or backwards, and walking under different loading conditions. The corresponding weights of distribution to different muscles may change as a function of the condition, allowing highly flexible control. Biomechanical correlates of each activation pattern have been described, leading to the hypothesis that the co-ordination of limb and body segments arises from the coupling of neural oscillators between each other and with limb mechanical oscillators. Muscle activations need only intervene during limited time epochs to force intrinsic oscillations of the system when energy is lost.

Francesco Lacquaniti (right), Myrka Zago (centre) and Yuri Ivanenko (left) work in the Laboratory of Neuromotor Physiology of IRCCS Santa Lucia Foundation in Rome. They use Galileian custom-made equipment to investigate the role of gravity in arm and leg movements. Francesco Lacquaniti is the Laboratory Head, as well as Professor of Physiology at the University of Rome Tor Vergata. He obtained his MD and Neurology specialization from the University of Turin, and did a post-doc with John Soechting and Carlo Terzuolo at the University of Minnesota, Minneapolis. Myrka Zago obtained her degree and PhD in Biomedical Engineering from La Sapienza University in Rome under the supervision of Guglielmo D’Inzeo. Yuri Ivanenko obtained his degree and PhD in biophysics at the Moscow Physics and Technology Institute under the supervision of Victor Gurfinkel, and did a post-doc with Alain Berthoz at Collège de France in Paris. Both M.Z. and Y.I. are Research Directors at IRCCS Santa Lucia.
Introduction
Biologists seek to understand complex organismal processes in terms of the molecular components. In a similar vein, systems motor physiologists aim at understanding the organization and production of movements in terms of the elementary components, that is, the basic control units with which the central nervous system (CNS) constructs a movement.
A typical limb movement involves angular motion at several articular degrees of freedom, and the activation of many more different muscles. For instance, there are more than 50 muscles in each lower limb and at least half of them participate actively in the control of leg motion in the sagittal plane during walking (Winter, 1991). In line of principle, the CNS might control the activity of each individual muscle and the motion (as well as the stiffness) at each articular degree of freedom independently of the control of all other muscles and degrees of freedom. If so, motor control would be extremely fractionated, meaning that the elementary motor components match individual degrees of freedom. The organization of neural pathways in primates does permit the selective activation of single muscles, motor units or neurons, and there is evidence that the CNS learns to control individuated degrees of freedom with training (Fetz, 2007; Kutch et al. 2008). In practice, however, it would be very difficult to implement a strategy of individual control outside of a limited number of specific cases. Consider that even the human fingers, the limb segments with the highest selectivity of control, normally do not move independently of each other because of mechanical and neural constraints (Schieber & Santello, 2004; van Duinen & Gandevia, 2011), so that it takes a great deal of training in pianists to minimize the movement spillover of the striking finger to the adjacent fingers (Furuya et al. 2011).
There are several reasons why fractionated motor control is often impractical to implement. First, because of physics, a torque exerted at one joint tends to determine angular motion not only at the corresponding joint, but also at the other dynamically coupled joints of the limb. A muscle torque would result in substantial unwanted motion, unless mechanical coupling was taken into account by the motor commands. Moreover, several muscles are bi- or multi-articular, that is, they cross more than one joint and act on several degrees of freedom simultaneously. In addition to biomechanical coupling, there is also neural coupling inherent in motor commands: most descending and sensory pathways to α-motoneurons are highly divergent and convergent. For instance, many corticospinal axons branch over several spinal segments providing terminal arbors in the motoneuron pools of multiple muscles of the monkey (Shinoda et al. 1981). Also, the projection patterns of spinal interneuronal systems are highly divergent, as are the central projections of muscle spindle afferents (Jankowska, 1992). Moreover, even low-order sensory signals, such as those from muscle spindle afferents or dorsal spino-cerebellar neurons, may reflect whole limb dynamics, rather than local, uniarticular information (Bosco & Poppele, 2001).
On the other hand, the smooth execution of multi-segment movements in healthy subjects indicates that such complications are somehow addressed by the CNS (Soechting & Lacquaniti, 1981; Lacquaniti et al. 1999; Scott, 2004). One hypothesis is that basic patterns of muscle activation represent elementary components or building blocks for the generation of limb movements. According to this hypothesis, the CNS emits a time series of command signals – the basic activation patterns (Fig. 1). Each command is based on both feedforward and feedback signals, and is output at a specific phase of the motor task. A single command recruits several pools of α-motoneurons quasi-synchronously, and activates several different muscles of the limb. In this manner, each patterned command influences multiple motor outputs, owing to the fan-out of connections from the neurons encoding the corresponding signal. In other words, there are only a few basic patterns which are shared by multiple muscles involved in a given motor task, resulting in a considerable reduction of the number of degrees of freedom of neural control. Thus, the activity profile of each muscle, measured as electromyographic (EMG) activity, results from the weighted combination of all basic patterns (Fig. 1). The weight is related to the recruitment strength of the α-motoneuron pools from a given command signal, and may change as a function of the condition allowing highly flexible control (Ivanenko et al. 2006). A related hypothesis is that of modular control (Grillner, 1985; Bizzi et al. 2008; Clark et al. 2010): a given module involves a basic activation pattern (temporal structure) and the weights of distribution (spatial structure) to different muscles.
Figure 1. Schematic of patterned control.
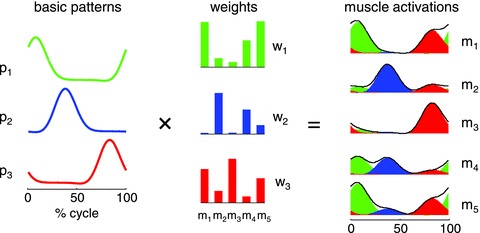
Simulated example of muscle activity profiles as weighted sum of three basic temporal patterns. A given pattern and its associated weights of distribution to all muscles represent a control module. The outputs of the first (green), second (blue) and third (red) modules are summed together to generate overall muscle activation (black envelope) according to the equation: mi(t) = ∑jpj(t)wij, where m is muscle activation, p is pattern and w is weight.
A further qualifying aspect of the hypothesis is that a similar strategy of reduction of the number of degrees of freedom holds true across different behavioural conditions, such as a wide range of different speeds, amplitudes or directions of a given movement, loading or unloading of the limb and body, or even different motor tasks involving the same set of muscles. The neural controllers issue basic activation patterns which, based on both a forward model of limb biomechanics and feedback signals from the periphery, take into account the dynamic state of the whole limb, such as the interaction torques in multi-jointed limbs. The coupling of activation patterns and limb biomechanics then results in balanced net joint torques and smooth movements.
Here we review evidence for patterned control of human locomotion, but converging evidence for similar control schemes has been gained for a variety of other motor behaviours, ranging from swimming, kicking and jumping (Bizzi et al. 2008) to nociceptive wiping responses (Giszter et al. 2010), whole body postural responses (Ting & MacKay, 2007), arm reaching (d’Avella et al. 2006), hand manipulation (Soechting & Flanders, 2008), and in several other animal species in addition to humans (Gillner, 1985; Bizzi et al. 2008; Drew et al. 2008; Tresch & Jarc, 2009; Giszter et al. 2010; Dominici et al. 2011). Alternative versions of the hypothesis of patterned control mainly differ in the emphasis placed on the relative invariance of the temporal versus spatial parameters of the muscle commands (Kargo & Giszter, 2008; Tresch & Jarc, 2009; Clark et al. 2010; Gizzi et al. 2011; Safavynia & Ting, 2012). Two extreme versions are that: (i) the waveform and timing of each pattern are invariant across different test conditions, while the weights are unconstrained and can change as a function of the specific task, or conversely, (ii) the weights are invariant across different test conditions, while the temporal waveforms are unconstrained and can change as a function of the specific task. However, as it will become apparent from this review, these extreme versions are too rigid to be physiologically plausible for human locomotion: both the timing and the weight of the patterns may vary with the specific context.
Activation patterns in human locomotion
Several studies consistently showed that the EMG activity of trunk and leg muscles during human adult locomotion is adequately reconstructed as a linear combination of four to five basic patterns, each one timed at a different phase of the gait cycle (Fig. 2A; Patla, 1985; Davis & Vaughan, 1993; Olree & Vaughan, 1995; Ivanenko et al. 2004, 2005, 2008; Cappellini et al. 2006; Clark et al. 2010; McGowan et al. 2010; Gizzi et al. 2011). The average shape of each pattern, once it is time-normalized to stride duration, is little affected by changes in walking speed (Ivanenko et al. 2004), direction (walking backwards versus walking forwards, see Fig. 3; Ivanenko et al. 2008a), loading or unloading of the limb and body (Ivanenko et al. 2004; McGowan et al. 2010; see Fig. 4), or changes in locomotion mode (running versus walking; Cappellini et al. 2006; Ivanenko et al. 2008a). The similarity of the average waveforms irrespective of walking or running speed suggests that each command is shaped relative to the overall duration of the gait cycle, so that the resulting muscle activations have a short duration at high speeds and a longer duration at low speeds. The main peak of each activation pattern lasts about 15–20% of the cycle, and they are spaced between each other by roughly the same amount.
Figure 2. Basic patterns and effect of walking speed.
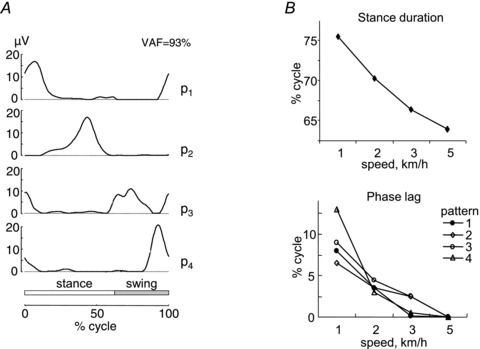
A, basic patterns obtained by non-negative matrix factorization of averaged (across steps) rectified EMG profiles of 16 unilateral leg muscles (see list in Fig. 3A) in 10 walking subjects. Patterns are plotted versus normalized gait cycle. VAF cumulative variance accounted for by all patterns. B, upper plot: changes in the relative duration of the stance phase with speed. Lower plot: phase lag required to provide the best fit between each pattern and the pattern determined from the 5 km h−1 data. B is modified from Ivanenko et al. 2004.
Figure 3. Forward versus backward locomotion.
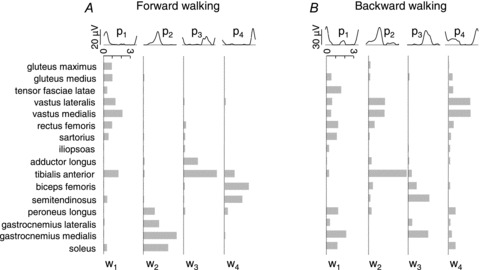
Patterns and weights in forward (A) and backward (B) walk at 5 km h−1 on treadmill. Notice that the patterns are similar between forward and backward locomotion, but the weights are drastically different.
Figure 4. Effect of loading and unloading.
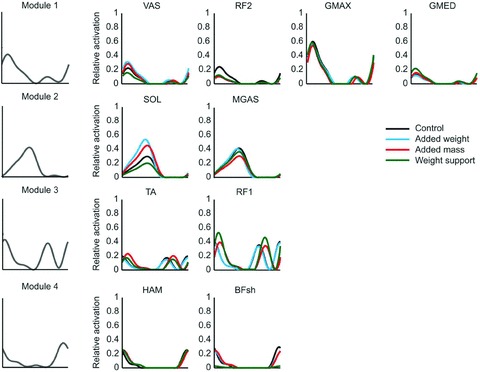
In each row, a basic pattern is plotted versus normalized gait cycle (as in Figs 2 and 3), and scaled in amplitude for the indicated muscles and loading conditions (see legend). For each condition, all muscles within a module received the same activation timing and waveform, but the magnitude was allowed to vary. Both timing and magnitude were allowed to vary between conditions. GMAX, gluteus maximus; GMED, gluteus medius; VAS, 3-components vastus (medialis, lateralis, intermedius); RF, rectus femoris; HAM, hamstrings; BFsh, short head of biceps femoris; MGAS, medial gastrocnemius; SOL, soleus; TA, tibialis anterior. Modified from McGowan et al. (2010) with permission from Elsevier.
In contrast with the shape, the timing and the weight of the patterns may change considerably as a function of walking direction (Fig. 3), speed changes and body weight unloading or loading (Fig. 4; Ivanenko et al. 2004; McGowan et al. 2010). Thus, in Fig. 4 one notices that the weight of pattern no. 2 (labeled Module 2 in the Figure) changes differentially between soleus and medial gastrocnemius muscle as a function of different loading conditions, although these two muscles are traditionally considered as strict synergists. The possibility of a functional uncoupling of muscles (such as the medial and lateral gastrocnemius) belonging to the same anatomical group has also been described in walking around curves (Courtine et al. 2006) and cycling (Wakeling & Horn, 2009). Irrespective of speed or loading, each pattern is shared by several different muscles which may act on different joints of the limb (Figs 3 and 4; Ivanenko et al. 2004; Cappellini et al. 2006; McGowan et al. 2010). Conversely, some muscles load on more than one pattern, while others load heavily on a single pattern.
Neural controllers of each leg can generate rhythmic muscle activity relatively autonomous of the contralateral leg, as shown by split-belt walking (Choi & Bastian, 2007). Normally, however, there is strong bilateral coordination, and several proximal muscles (e.g. the glutei) also affect the contralateral limb via their action on the pelvic girdle (Winter, 1991). Accordingly, when the basic patterns are extracted from bilateral EMG recordings (instead of unilateral recordings as those of Figs 2–4), two patterns (nos 3 and 4) are almost carbon-copies of the other two (nos 1 and 2), phase-shifted by half a cycle (Olree & Vaughan, 1995; Dominici et al. 2011).
Biomechanical correlates of the activation patterns
The results reviewed above are consistent with the hypothesis that the CNS controls a variety of different locomotor tasks by distributing a few basic temporal patterns of activation to several different muscles acting on different joints of the limb. Several studies showed systematic correlations between the timing of the activation patterns and the occurrence of specific biomechanical events of the gait cycle (Ivanenko et al. 2003, 2004; Cappellini et al. 2006; Dominici et al. 2011). Thus, the maximum of each pattern shifts slightly toward successively earlier phases of the gait cycle as walking or running speed increases, and this time-shift parallels the corresponding reduction of relative duration of the stance phase (Fig. 2B; Ivanenko et al. 2004; Cappellini et al. 2006). These time-shifts may depend on proprioceptive feedback about the onset of stance and the transition between stance and swing. Also, both the time-normalized waveform of the patterns and that of output kinetics (e.g. joint torques and powers) are roughly independent of walking speed (Winter, 1991).
Correlational analyses (Davis & Vaughan, 1993; Ivanenko et al. 2006) and biomechanical simulations based on the experimentally derived activation patterns (Neptune et al. 2009; Fig. 5) show that pattern no. 1 (involving primarily hip and knee extensors) contributes to weight acceptance at heel contact in early stance, pattern no. 2 (ankle plantar flexors) contributes to body support and forward propulsion in late stance, pattern no. 3 (ankle dorsiflexors and hip flexors) contributes to foot lift-off in early- to mid-swing and pattern no. 4 (hamstrings) decelerates the leg in late swing in preparation for heel contact and then stabilizes the pelvis after contact. Depending on the context, there may be an additional pattern associated with ilio-psoas and erector spinae muscles, accelerating the leg forward and stabilizing the trunk in late stance and early swing (Ivanenko et al. 2004, 2005; Cappellini et al. 2006). This approach has recently been extended to three-dimensional coordination of walking (unpublished obs, Jessica L. Allen and Richard R. Neptune). The same basic patterns, which are involved in the control in the sagittal plane of forward progression, are also involved in the control of motion in non-sagittal planes. An additional pattern (loading on adductor magnus), however, contributes to the control of medio-lateral accelerations of the centre of body mass (COM).
Figure 5. Contributions of basic patterns to walking biomechanics.
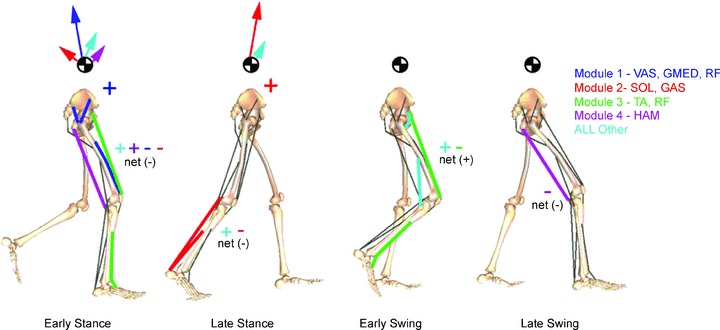
Contribution of different patterns (modules) to the walking sub-tasks of body support, forward propulsion and leg swing. Early stance (15% of gait cycle), late stance (45%), early swing (70%) and late swing (85%) are shown. Arrows departing from the COM denote the resultant module contributions to the horizontal and vertical ground reaction forces that accelerate the COM providing body support and forward propulsion. Net energy flow by each module to the trunk or leg is denoted by a + or – for energy increases or decreases, respectively. Muscle abbreviations are as in Fig. 4. Modified from Neptune et al. (2009) with permission from Elsevier.
The overall behaviour of the body and limbs during walking is determined by the net forces and torques, as resulting from the interplay of neural and mechanical factors. Because the activation patterns are pulsatile, muscle activations intervene only briefly at specific phases of the gait cycle to re-excite the intrinsic oscillations of the system when energy is lost. At optimum speed (about 5 km h−1), walking saves energy by exchanging forward kinetic energy and gravitational potential energy of the COM during the inverted-pendulum oscillation of stance (Fig. 6A; Cavagna & Margaria, 1966), and by oscillating the limb ballistically as an upright compound-pendulum during swing (Mochon & McMahon, 1980). Thus, in the absence of external perturbations, muscle activity is only required to oppose gravity, maintain postural configurations in the face of interaction torques, and reintegrate energy losses during each cycle. Mechanical (and metabolic) energy is mainly expended to redirect COM velocity during step-to-step transitions (Fig. 6A; Kuo et al. 2005), and to force leg oscillation for swing (Marsh et al. 2004). As in pushing a swing which oscillates back and forth, muscle activations are timed at the apex of limb and body oscillations to replace dissipated energy. In running, instead, kinetic and gravitational potential energy is stored as elastic strain energy in muscles, tendons and ligaments at foot strike, and then is partially recovered during propulsion (Alexander, 1991). Interestingly, the time-varying rostro-caudal migration of bilateral motoneuron activity in the human lumbo-sacral spinal cord mirrors the changes in COM energy during both walking and running (Cappellini et al. 2010).
Figure 6. Mechanical oscillations during walking.
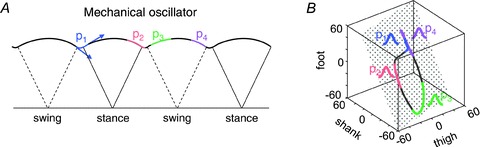
A, schematic trajectory of COM during a few consecutive steps. Arrows denote COM velocity before and after heel contact. Notice that p1 and p4 timing coincides with the redirection of COM velocity. B, planar co-variance of thigh elevation angle versus shank and foot angles identifies counter-clockwise loops, with heel contact and toe-off at the top and bottom. Each coloured trace in both A and B denotes the trajectory segment over which the indicated pattern is active.
The trajectories of the COM and feet are highly regular and repeatable in human gait (Winter, 1991). They are determined by the combined rotation and translation of the lower limb segments. The pelvis, thigh, shank and foot oscillate back and forth relative to the vertical with a similar waveform, time-shifted across different segments (Borghese et al. 1996; Bianchi et al. 1998), and in so doing they carry the trunk and feet along. When the segment elevation angles are plotted one versus the others, they describe regular loops constrained close to a plane common to both the stance and swing phase (Borghese et al. 1996; Lacquaniti et al. 1999; Ivanenko et al. 2008b). Figure 6B shows the planar covariance in walking, with the corresponding muscle activation patterns inserted at the time of occurrence along the gait loop. The specific orientation of the planar covariance reflects the phase relationships between the segment elevation angles, and therefore the timing of the inter-segmental coordination (Bianchi et al. 1998). The phase-coupling between the elevation angles shifts systematically with increasing speed, just as the phase-coupling of the activation patterns, once again demonstrating the tight linkage between kinematic events and the activation patterns.
Development of locomotor patterns
An important question is whether the activation patterns of locomotion are inborn, or whether they emerge during development as learnt task solutions (Giszter et al. 2010). According to the first viewpoint, a set of primitives is available at birth because they are built into the motor system by evolution. According to the second viewpoint, instead, the motor system is organized to learn optimal feedback controllers, and to construct the motor patterns based on specific task requirements discovered with experience (Todorov, 2004).
In fact, these two views can be reconciled (Giszter et al. 2010), as demonstrated by a recent study on different developmental stages of the basic activation patterns of locomotion (Dominici et al. 2011). When supported and placed with the feet in contact with a firm surface, human newborns display a stepping response which generally disappears at ∼2 months after birth (unless stepping is trained, Yang et al. 1998), and reappears several months later when it evolves into intentional walking. Analysis of EMG activity during newborn stepping reveals two basic patterns that are roughly similar to pattern no. 2 and pattern no. 4 of the adult, but more prolonged in duration (Dominici et al. 2011). As in adults, pattern no. 2 helps to provide body support during stance, while pattern no. 4 helps to drive the limb during swing. In newborns, however, there is no specific activation pattern at either touch-down or lift-off. In toddlers (∼1-year-old) at their first unsupported steps, one finds the same two patterns (no. 2 and no. 4) of the newborn, plus two new patterns timed at touch-down and lift-off which are similar to pattern no. 1 and pattern no. 3 of the adult, and contribute shear forces necessary to decelerate and accelerate the body, respectively. In pre-schoolers (2–4 years), all four patterns show transitional shapes: with increasing age, the peak becomes narrower and shifts in time relative to the step cycle, becoming closer and closer to the adult waveform.
Dominici et al. (2011) also compared the development of locomotor patterns in humans with that in other vertebrates. In newborn rats, they found two patterns essentially identical to those of human newborns, while in adult rats, cats, macaques and guinea fowl they found four patterns, closely resembling those of human children. These results suggest that locomotion of several animal species is built starting from common elements, perhaps related to ancestral neural networks (Grillner, 2011). However, with development, the motor patterns may become tuned to the specific biomechanical requirements of a given animal species. Thus, brief, pulsatile activations timed at the apex of limb oscillations may be specific to human adult locomotion, perhaps in relation to our unique erect bipedal locomotion on extended legs and a heel-contact well ahead of the body.
Central pattern generators
The muscle activation patterns and their weights reflect global motoneuron output, and motoneuron activation during locomotion is the end-product of several neural processes (Fig. 7). A crucial role is played by central pattern generators (CPGs), i.e. spinal neuronal networks that control the basic rhythms and patterns of motoneuron activation during locomotion and other rhythmic behaviours (e.g. Grillner, 2006; Kiehn, 2011). Hart & Giszter (2010) showed that pulsatile patterns of muscle activation, similar to those described in human locomotion, are associated with the wiping responses of spinalized frogs, and appear to be encoded by intermediate-zone interneurons. They proposed that the pulsed activation patterns emerge from a multi-layered organization of the spinal neural networks. A similar proposal has emerged for mammalian locomotor CPGs (McCrea & Rybak, 2008). They would include a rhythm-generating layer and a pattern-generating layer which coordinate flexor–extensor and left–right side activity (Fig. 7A). The circuit of two mutually inhibiting neurons depicted in Fig. 7A represents the classic half-centre oscillator (Grillner, 2006). The neurons in the rhythm-generating layer are two or more synapses upstream from motoneurons and project to pattern-generating neurons; the latter project monosynaptically to motoneurons.
Figure 7. Schematics of neural substrates.
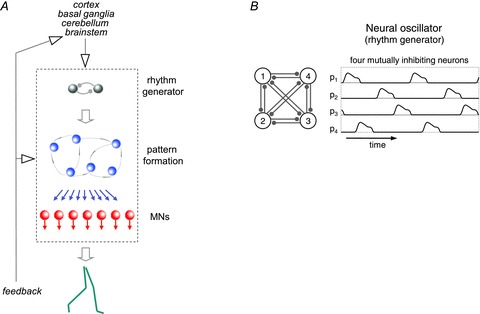
A, multi-layered organization of rhythm and patterns generators in the spinal cord under descending and sensory influence. B, Matsuoka neural oscillators. See text for explanation.
In addition to multi-layered circuits, there are other schemes of neuronal organization that may explain pattern formation. For instance, in Matsuoka oscillators (Matsuoka, 1985) neurons receive the same magnitude of excitatory stimuli from outside the network, and inhibitory stimuli from inside the network. Increasing the number of neurons augments the number of bursts of activity or basic activation patterns (Matsuoka, 1985). Thus, four mutually inhibiting neurons (presumably half-centres of stance–swing and left–right activity) are able to reproduce the four basic activation patterns reported for human locomotion (Fig. 7B).
We remarked above that two out of four patterns are already present in stepping newborn babies, at a stage when major inputs from the brain onto the spinal CPGs are still immature (Martin, 2005). Indeed, automatic stepping has been reported also in premature infants and anencephalic newborns (Peiper, 1961). Cortico-spinal drive on leg muscles matures relatively slowly during human development (Petersen et al. 2010). Adults who have suffered a spinal cord injury (Ivanenko et al. 2003) or a stroke disrupting the descending drive from supraspinal pathways (Clark et al. 2010; Gizzi et al. 2011) display the full set or a subset of unaltered basic activation patterns, although the weights of distribution of the patterns and the corresponding profiles of EMG activities are often drastically altered. Altogether, these observations in children and adults support the idea that spinal CPGs independent of supraspinal influences can generate at least some of the basic commands underlying human locomotion (Dominici et al. 2011; Grillner 2011).
Sensory feedback
CPGs and motoneurons receive extensive feedback from various sensory receptors for the control of balance, direction and speed of locomotion (Pearson, 2000; Grillner, 2006). Thus, the timing and magnitude of EMG activity are tuned via proprioceptive feedback, as shown by the tight relationship between these parameters and critical kinematic and kinetic events (Figs 2–6). In particular, the time-shift of the patterns with increasing walking speed parallels the corresponding decrease of duration of the stance phase relative to the swing phase (Fig. 2B). In reduced cat preparations, the transition from stance to swing is known to be heavily influenced by sensory inputs, such as those signalling hip extension (Grillner & Rossignol, 1978) or unloading of extensor muscles (Duysens & Pearson, 1980). Also in human infants, stance is prolonged and swing delayed when the hip is artificially flexed or the load on the limb is increased; conversely, stance is shortened and swing anticipated when the hip is extended or the load is decreased (Pang & Yang, 2000). In human adults, these effects are much weaker, being presumably overridden by voluntary intervention (Stephens & Yang, 1999). However, also in adults, feedback is exquisitely sensitive to changes in peripheral conditions and alterations in mechanical requirements (Pearson, 2000), as is the functional state of the spinal circuitry where sensory afferents project (Hultborn, 2001). This state variability should not be viewed simply as biological noise, but rather as a neural basis for flexibility of motor execution as a function of the needs prevailing at any given time, while the general constraint of a reduction in the number of degrees of freedom would be enforced via the patterned control of muscle activations. Feedback would also take care of error-detection and correction in the motor output.
Supraspinal control
Supraspinal control of locomotion has been extensively investigated in the cat (see Armstrong, 1988; Orlovsky et al. 1999). Several brainstem, cerebellar and cerebral structures influence the spinal locomotor networks by means of both tonic descending drive and rhythmic bursts of activity which are phase-locked to the step cycle. It has recently been suggested that motor cortical neurons which are active sequentially during the step cycle may regulate the activity of small groups of synergistic muscles (Drew et al. 2008). Cortico-spinal regulation is especially critical during visually guided gait adjustments, such as those required to step over an obstacle. During gait adjustments, motor cortical neurons might modify the magnitude and phase of the EMG activity of all muscles contained within a given synergy (Drew et al. 2008). This would be tantamount to modifying the activation patterns we considered in this review.
Much less is known about the supraspinal control of human locomotion. Although the human spinal cord is capable of autonomously generating the basic activation patterns sustained by sensory feedback, descending supra-spinal signals are probably critical to drive and modulate the overall locomotor output in healthy adults (Nielsen, 2003). Indirect evidence of the role of supraspinal control is provided by the very limited recovery of gait in patients with complete spinal cord injury (Dobkin et al. 1995). Direct evidence in healthy humans is provided by trans-cranial magnetic stimulation (TMS) over the motor cortex during walking: TMS transiently inhibiting cortico-motoneuronal cells produces a reduction of EMG activity in lower limb muscles (Petersen et al. 2001).
Integration between supraspinal and spinal mechanisms is revealed by the study of the coordination of locomotor activity with voluntary movements such as kicking a ball, stepping over an obstacle or reaching down to grasp an object on the floor while walking (Ivanenko et al. 2005). The basic activation patterns underlying locomotion are always present, but there is an additional activation pattern timed to the voluntary task. This suggests that when the timing is basically the same for the components of a combined task, the result will have the same activation timing. A discrepancy between the activation timing in the component tasks results in additional activation components. Thus, voluntary activation patterns are generated separately from the locomotor patterns, but a coupling of corticospinal with propriospinal circuits might result in partial synchronization of activation patterns (Ivanenko et al. 2006).
Conclusions
We argued that the co-ordination of limb and body segments in locomotion arises from the coupling of neural oscillators between each other and with limb mechanical oscillators. Muscle activations intervene at discrete times to re-excite the intrinsic oscillations of the system when energy is lost. The idea of a minimal active tuning of the passive inertial and visco-elastic coupling among limb segments is consistent with the hypothesis that walking has evolved according to minimum energy criteria (Alexander, 1991; Lacquaniti et al. 1999). The modular, patterned activation of muscles simplifies the control problem by reducing the effective number of degrees of freedom, but this does not imply a rigid, stereotypical behaviour. In fact, there exists considerable flexibility in engaging different muscles, as shown by the considerable trial-to-trial variability of the EMG profiles (Winter, 1991). The distribution of the activation patterns and the selection of muscle synergies probably occur downstream relative to the timing in a network that is dynamically configured by sensory feedback and central control. There may be no need to explicitly compute a desired kinematic trajectory or the required muscle forces. Indeed developmental studies suggest that the CNS learns very gradually how to map between input and output, until the mature CNS becomes able to map desired locomotion into the required muscle forces (Dominici et al. 2011).
Acknowledgments
Our work was supported by the Italian Ministry of Health, Italian Ministry of University and Research (PRIN grant), Italian Space Agency (DCMC and CRUSOE grants) and European Union FP7-ICT program AMARSi grant no. 248311).
Glossary
Abbreviations
- CNS
central nervous system
- COM
centre of body mass
- CPG
central pattern generator
- EMG
electromyographic activity
- TMS
trans-cranial magnetic stimulation
References
- Alexander RM. Energy-saving mechanisms in walking and running. J Exp Biol. 1991;160:55–69. doi: 10.1242/jeb.160.1.55. [DOI] [PubMed] [Google Scholar]
- Armstrong DM. The supraspinal control of mammalian locomotion. J Physiol. 1988;405:1–37. doi: 10.1113/jphysiol.1988.sp017319. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bianchi L, Angelini D, Orani GP, Lacquaniti F. Kinematic coordination in human gait: relation to mechanical energy cost. J Neurophysiol. 1998;79:2155–2170. doi: 10.1152/jn.1998.79.4.2155. [DOI] [PubMed] [Google Scholar]
- Bizzi E, Cheung VC, d’Avella A, Saltiel P, Tresch M. Combining modules for movement. Brain Res Rev. 2008;57:125–133. doi: 10.1016/j.brainresrev.2007.08.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Borghese NA, Bianchi L, Lacquaniti F. Kinematic determinants of human locomotion. J Physiol. 1996;494:863–879. doi: 10.1113/jphysiol.1996.sp021539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bosco G, Poppele RE. Proprioception from a spinocerebellar perspective. Physiol Rev. 2001;81:539–568. doi: 10.1152/physrev.2001.81.2.539. [DOI] [PubMed] [Google Scholar]
- Cappellini G, Ivanenko YP, Dominici N, Poppele RE, Lacquaniti F. Migration of motor pool activity in the spinal cord reflects body mechanics in human locomotion. J Neurophysiol. 2010;104:3064–3073. doi: 10.1152/jn.00318.2010. [DOI] [PubMed] [Google Scholar]
- Cappellini G, Ivanenko YP, Poppele RE, Lacquaniti F. Motor patterns in human walking and running. J Neurophysiol. 2006;95:3426–3437. doi: 10.1152/jn.00081.2006. [DOI] [PubMed] [Google Scholar]
- Cavagna GA, Margaria R. Mechanics of walking. J Appl Physiol. 1966;21:271–278. doi: 10.1152/jappl.1966.21.1.271. [DOI] [PubMed] [Google Scholar]
- Choi JT, Bastian AJ. Adaptation reveals independent control networks for human walking. Nat Neurosci. 2007;10:1055–1062. doi: 10.1038/nn1930. [DOI] [PubMed] [Google Scholar]
- Clark DJ, Ting LH, Zajac FE, Neptune RR, Kautz SA. Merging of healthy motor modules predicts reduced locomotor performance and muscle coordination complexity post-stroke. J Neurophysiol. 2010;103:844–857. doi: 10.1152/jn.00825.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Courtine G, Papaxanthis C, Schieppati M. Coordinated modulation of locomotor muscle synergies constructs straight-ahead and curvilinear walking in humans. Exp Brain Res. 2006;170:320–335. doi: 10.1007/s00221-005-0215-7. [DOI] [PubMed] [Google Scholar]
- d’Avella A, Portone A, Fernandez L, Lacquaniti F. Control of fast-reaching movements by muscle synergy combinations. J Neurosci. 2006;26:7791–7810. doi: 10.1523/JNEUROSCI.0830-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davis BL, Vaughan CL. Phasic behavior of EMG signals during gait: use of multivariate statistics. J Electromyogr Kinesiol. 1993;3:51–60. doi: 10.1016/1050-6411(93)90023-P. [DOI] [PubMed] [Google Scholar]
- Dobkin BH, Harkema S, Requejo P, Edgerton VR. Modulation of locomotor-like EMG activity in subjects with complete and incomplete spinal cord injury. J Neurol Rehabil. 1995;9:183–190. [PubMed] [Google Scholar]
- Dominici N, Ivanenko YP, Cappellini G, d’Avella A, Mondì V, Cicchese M, Fabiano A, Silei T, Di Paolo A, Giannini C, Poppele RE, Lacquaniti F. Locomotor primitives in newborn babies and their development. Science. 2011;334:997–999. doi: 10.1126/science.1210617. [DOI] [PubMed] [Google Scholar]
- Drew T, Kalaska J, Krouchev N. Muscle synergies during locomotion in the cat: a model for motor cortex control. J Physiol. 2008;586:1239–1245. doi: 10.1113/jphysiol.2007.146605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duysens J, Pearson KG. Inhibition of flexor burst generation by loading ankle extensor muscles in walking cats. Brain Res. 1980;187:321–332. doi: 10.1016/0006-8993(80)90206-1. [DOI] [PubMed] [Google Scholar]
- Fetz EE. Volitional control of neural activity: implications for brain–computer interfaces. J Physiol. 2007;579:571–579. doi: 10.1113/jphysiol.2006.127142. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Furuya S, Flanders M, Soechting JF. Hand kinematics of piano playing. J Neurophysiol. 2011;106:2849–2864. doi: 10.1152/jn.00378.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Giszter SF, Hart CB, Silfies SP. Spinal cord modularity: evolution, development, and optimization and the possible relevance to low back pain in man. Exp Brain Res. 2010;200:283–306. doi: 10.1007/s00221-009-2016-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gizzi L, Nielsen JF, Felici F, Ivanenko YP, Farina D. Impulses of activation but not motor modules are preserved in the locomotion of subacute stroke patients. J Neurophysiol. 2011;106:202–210. doi: 10.1152/jn.00727.2010. [DOI] [PubMed] [Google Scholar]
- Grillner S. Neurobiological bases of rhythmic motor acts in vertebrates. Science. 1985;228:143–149. doi: 10.1126/science.3975635. [DOI] [PubMed] [Google Scholar]
- Grillner S. Biological pattern generation: the cellular and computational logic of networks in motion. Neuron. 2006;52:751–766. doi: 10.1016/j.neuron.2006.11.008. [DOI] [PubMed] [Google Scholar]
- Grillner S. Human locomotor circuits conform. Science. 2011;334:912–913. doi: 10.1126/science.1214778. [DOI] [PubMed] [Google Scholar]
- Grillner S, Rossignol S. On the initiation of the swing phase of locomotion in chronic spinal cats. Brain Res. 1978;146:269–277. doi: 10.1016/0006-8993(78)90973-3. [DOI] [PubMed] [Google Scholar]
- Hart CB, Giszter SF. A neural basis for motor primitives in the spinal cord. J Neurosci. 2010;30:1322–1336. doi: 10.1523/JNEUROSCI.5894-08.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hultborn H. State-dependent modulation of sensory feedback. J Physiol. 2001;533:5–13. doi: 10.1111/j.1469-7793.2001.0005b.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ivanenko YP, Cappellini G, Dominici N, Poppele RE, Lacquaniti F. Coordination of locomotion with voluntary movements in humans. J Neurosci. 2005;25:7238–7253. doi: 10.1523/JNEUROSCI.1327-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ivanenko YP, Cappellini G, Poppele RE, Lacquaniti F. Spatiotemporal organization of alpha-motoneuron activity in the human spinal cord during different gaits and gait transitions. Eur J Neurosci. 2008a;27:3351–3368. doi: 10.1111/j.1460-9568.2008.06289.x. [DOI] [PubMed] [Google Scholar]
- Ivanenko YP, d’Avella A, Poppele RE, Lacquaniti F. On the origin of planar covariation of elevation angles during human locomotion. J Neurophysiol. 2008b;99:1890–1898. doi: 10.1152/jn.01308.2007. [DOI] [PubMed] [Google Scholar]
- Ivanenko Y, Grasso R, Zago M, Molinari M, Scivoletto G, Castellano V, Macellari V, Lacquaniti F. Temporal components of the motor patterns expressed by the human spinal cord reflect foot kinematics. J Neurophysiol. 2003;90:3555–3565. doi: 10.1152/jn.00223.2003. [DOI] [PubMed] [Google Scholar]
- Ivanenko YP, Poppele RE, Lacquaniti F. Five basic muscle activation patterns account for muscle activity during human locomotion. J Physiol. 2004;556:267–282. doi: 10.1113/jphysiol.2003.057174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ivanenko YP, Poppele RE, Lacquaniti F. Motor control programs and walking. Neuroscientist. 2006;12:339–348. doi: 10.1177/1073858406287987. [DOI] [PubMed] [Google Scholar]
- Jankowska E. Interneuronal relay in spinal pathways from proprioceptors. Prog Neurobiol. 1992;38:335–378. doi: 10.1016/0301-0082(92)90024-9. [DOI] [PubMed] [Google Scholar]
- Kargo WJ, Giszter SF. Individual premotor drive pulses, not time-varying synergies, are the units of adjustment for limb trajectories constructed in spinal cord. J Neurosci. 2008;28:2409–2425. doi: 10.1523/JNEUROSCI.3229-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kiehn O. Development and functional organization of spinal locomotor circuits. Curr Opin Neurobiol. 2011;21:100–109. doi: 10.1016/j.conb.2010.09.004. [DOI] [PubMed] [Google Scholar]
- Kuo AD, Donelan JM, Ruina A. Energetic consequences of walking like an inverted pendulum: step-to-step transitions. Exerc Sport Sci Rev. 2005;33:88–97. doi: 10.1097/00003677-200504000-00006. [DOI] [PubMed] [Google Scholar]
- Kutch JJ, Kuo AD, Bloch AM, Rymer WZ. Endpoint force fluctuations reveal flexible rather than synergistic patterns of muscle cooperation. J Neurophysiol. 2008;100:2455–2471. doi: 10.1152/jn.90274.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lacquaniti F, Grasso R, Zago M. Motor patterns in walking. News Physiol Sci. 1999;14:168–174. doi: 10.1152/physiologyonline.1999.14.4.168. [DOI] [PubMed] [Google Scholar]
- McCrea DA, Rybak IA. Organization of mammalian locomotor rhythm and pattern generation. Brain Res Rev. 2008;57:134–146. doi: 10.1016/j.brainresrev.2007.08.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McGowan CP, Neptune RR, Clark DJ, Kautz SA. Modular control of human walking: Adaptations to altered mechanical demands. J Biomech. 2010;43:412–419. doi: 10.1016/j.jbiomech.2009.10.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marsh RL, Ellerby DJ, Carr JA, Henry HT, Buchanan CI. Partitioning the energetics of walking and running: swinging the limbs is expensive. Science. 2004;303:80–83. doi: 10.1126/science.1090704. [DOI] [PubMed] [Google Scholar]
- Martin JH. The corticospinal system: from development to motor control. Neuroscientist. 2005;11:161–173. doi: 10.1177/1073858404270843. [DOI] [PubMed] [Google Scholar]
- Matsuoka K. Sustained oscillations generated by mutually inhibiting neurons with adaptation. Biol Cybern. 1985;52:367–376. doi: 10.1007/BF00449593. [DOI] [PubMed] [Google Scholar]
- Mochon S, McMahon TA. Ballistic walking. J Biomech. 1980;13:49–57. doi: 10.1016/0021-9290(80)90007-x. [DOI] [PubMed] [Google Scholar]
- Neptune RR, Clark DJ, Kautz SA. Modular control of human walking: a simulation study. J Biomech. 2009;42:1282–1287. doi: 10.1016/j.jbiomech.2009.03.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nielsen JB. How we walk: central control of muscle activity during human walking. Neuroscientist. 2003;9:195–204. doi: 10.1177/1073858403009003012. [DOI] [PubMed] [Google Scholar]
- Olree KS, Vaughan CL. Fundamental patterns of bilateral muscle activity in human locomotion. Biol Cybern. 1995;73:409–414. doi: 10.1007/BF00201475. [DOI] [PubMed] [Google Scholar]
- Orlovsky GN, Deliagina TG, Grillner S. Neuronal Control of Locomotion. Oxford: Oxford University Press; 1999. [Google Scholar]
- Pang MY, Yang JF. The initiation of the swing phase in human infant stepping: importance of hip position and leg loading. J Physiol. 2000;528:389–404. doi: 10.1111/j.1469-7793.2000.00389.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patla AE. Some characteristics of EMG patterns during locomotion: implications for the locomotor control process. J Mot Behav. 1985;17:443–461. doi: 10.1080/00222895.1985.10735360. [DOI] [PubMed] [Google Scholar]
- Pearson KG. Neural adaptation in the generation of rhythmic behavior. Annu Rev Physiol. 2000;62:723–753. doi: 10.1146/annurev.physiol.62.1.723. [DOI] [PubMed] [Google Scholar]
- Peiper A. Cerebral Function in Infancy and Childhood. New York: Consultants Bureau; 1961. [Google Scholar]
- Petersen NT, Butler JE, Marchand-Pauvert V, Fisher R, Pyndt HS, Hansen NL, Nielsen JB. Suppression of EMG activity by transcranial magnetic stimulation in human subjects during walking. J Physiol. 2001;537:651–656. doi: 10.1111/j.1469-7793.2001.00651.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petersen TH, Kliim-Due M, Farmer SF, Nielsen JB. Childhood development of common drive to a human leg muscle during ankle dorsiflexion and gait. J Physiol. 2010;588:4387–4400. doi: 10.1113/jphysiol.2010.195735. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Safavynia SA, Ting LH. Task-level feedback can explain temporal recruitment of spatially-fixed muscle synergies throughout postural perturbations. J Neurophysiol. 2012;107:159–177. doi: 10.1152/jn.00653.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schieber MH, Santello M. Hand function: peripheral and central constraints on performance. J Appl Physiol. 2004;96:2293–2300. doi: 10.1152/japplphysiol.01063.2003. [DOI] [PubMed] [Google Scholar]
- Scott SH. Optimal feedback control and the neural basis of volitional motor control. Nat Rev Neurosci. 2004;5:532–546. doi: 10.1038/nrn1427. [DOI] [PubMed] [Google Scholar]
- Shinoda Y, Yokota J, Futami T. Divergent projection of individual corticospinal axons to motoneurons of multiple muscles in the monkey. Neurosci Lett. 1981;23:7–12. doi: 10.1016/0304-3940(81)90182-8. [DOI] [PubMed] [Google Scholar]
- Soechting JF, Flanders M. Sensorimotor control of contact force. Curr Opin Neurobiol. 2008;18:565–572. doi: 10.1016/j.conb.2008.11.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Soechting JF, Lacquaniti F. Invariant characteristics of a pointing movement in man. J Neurosci. 1981;1:710–720. doi: 10.1523/JNEUROSCI.01-07-00710.1981. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stephens MJ, Yang JF. Loading during the stance phase of walking in humans increases the extensor EMG amplitude but does not change the duration of the step cycle. Exp Brain Res. 1999;124:363–370. doi: 10.1007/s002210050633. [DOI] [PubMed] [Google Scholar]
- Ting LH, McKay JL. Neuromechanics of muscle synergies for posture and movement. Curr Opin Neurobiol. 2007;17:622–628. doi: 10.1016/j.conb.2008.01.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Todorov E. Optimality principles in sensorimotor control. Nat Neurosci. 2004;7:907–915. doi: 10.1038/nn1309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tresch MC, Jarc A. The case for and against muscle synergies. Curr Opin Neurobiol. 2009;19:601–607. doi: 10.1016/j.conb.2009.09.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Duinen H, Gandevia SC. Constraints for control of the human hand. J Physiol. 2011;589:5583–5593. doi: 10.1113/jphysiol.2011.217810. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wakeling JM, Horn T. Neuromechanics of muscle synergies during cycling. J Neurophysiol. 2009;101:843–854. doi: 10.1152/jn.90679.2008. [DOI] [PubMed] [Google Scholar]
- Winter DA. The Biomechanics and Motor Control of Human Gait: Normal, Elderly and Pathological. Waterloo, Ontario: University of Waterloo Press; 1991. [Google Scholar]
- Yang JF, Stephens MJ, Vishram R. Infant stepping: a method to study the sensory control of human walking. J Physiol. 1998;507:927–937. doi: 10.1111/j.1469-7793.1998.927bs.x. [DOI] [PMC free article] [PubMed] [Google Scholar]


