Abstract
According to current estimates of genomic deleterious mutation rates (which are often of the order 0.1–1) the mutation load (defined as a reduction in the average fitness of a population due to the presence of deleterious alleles) may be important in many populations. In this paper, I use multilocus simulations to explore the effect of spatial heterogeneity in the strength of selection against deleterious alleles on the mutation load (for example, it has been suggested that stressful environments may increase the strength of selection). These simulations show contrasted results: in some situations, spatial heterogeneity may greatly reduce the mutation load, due to the fact that migrants coming from demes under stronger selection carry relatively few deleterious alleles, and benefit from a strong advantage within demes under weaker selection (where individuals carry many more deleterious alleles); in other situations, however, deleterious alleles accumulate within demes under stronger selection, due to migration pressure from demes under weaker selection, leading to fitness erosion within those demes. This second situation is more frequent when the productivity of the different demes is proportional to their mean fitness. The effect of spatial heterogeneity is greatly reduced, however, when the response to environmental differences is inconsistent across loci.
Keywords: deleterious mutation, environmental heterogeneity, island model, linkage disequilibrium, multilocus model, mutation load
Introduction
Recurrent deleterious mutations are likely to have important consequences on a variety of evolutionary processes, including the evolution of genetic recombination and reproductive systems (Lande and Schemske, 1985; Kondrashov, 1988; Barton, 1995; Charlesworth, 2006; Keightley and Otto, 2006; Otto, 2009), the evolution of life cycles (Otto and Goldstein, 1992; Otto and Marks, 1996), mate choice (Rowe and Houle, 1996) and dispersal( Guillaume and Perrin, 2006; Ravigne et al., 2006; Roze and Rousset, 2009). Deleterious alleles may also increase the extinction risk of small, endangered populations (Lynch et al., 1995a, 1995b) by decreasing the mean fitness of populations (an effect which was first described as a ‘load' by Muller 1950). In a classical paper, Haldane 1937 showed that in a panmictic diploid population, the load generated by a recurrent deleterious allele at mutation selection equilibrium is independent of the selective effect of the allele (s) and is approximately equal to 2u (where u is rate at which the allele is generated by mutation), provided that the dominance coefficient of the allele (h) is not too small (it becomes u in the case of a fully recessive allele). Assuming independent fitness effects of mutations at different loci (no epistasis) and sufficiently strong selection relative to mutation and drift, the load generated by mutations occurring over a whole genome is approximately L≈1−exp(2U), where 2U is the deleterious mutation rate per diploid genome (Crow, 1970). When the strength of selection against mutations is of order 1/Ne (where Ne is the effective population size), however, deleterious alleles may drift to high frequencies, in which case the load (usually called ‘drift load' in this regime) becomes dependent on s, and is maximized for an intermediate value of s (Kimura et al., 1963).
Plugging current estimates of genomic deleterious mutation rates, which are often of the order 0.1–1 (Baer et al., 2007), into the deterministic formula above leads to substantial values of the mutation load (for example, L≈0.63 if U=0.5 while L≈0.84 if U=1). Whether such high values of the load are compatible with the survival of populations depends on the interplay between selection and demography. Haldane (1937) defined fitness as the absolute number of offspring left by an individual at the next generation (after a full life cycle), a definition which is still commonly used, particularly (but not only) in the kin selection literature (Rousset, 2004). However, in simple models of density-regulated populations with constant population size, mean fitness W̄ is necessarily 1 using the definition above, in which case the load (defined as a reduction in mean fitness) is always zero. Under such scenarios (for example, in the Wright–Fisher model where individuals produce a very large number of juveniles, but the number of surviving adults is fixed to a constant value) many authors use a different definition of fitness, standing for the reproductive output (that is, number of juveniles produced) before competition among juveniles. In that case fitness is not defined over the whole life cycle (it does not take competition into account), and W̄ may be different from 1 even if population size remains constant from one generation to the next; however, as long as s ≫1/Ne the calculation of the mutation load remains the same as in an unregulated population (L≈1–exp(2U) at mutation selection balance). For example, a load of 0.6 would mean that the average number of juveniles produced per individual is only 40% the number of juveniles that a mutation-free individual would produce (either because of survival or fecundity effects of mutations). Under this scenario, selection and competition are somehow decoupled. Alternatively, selection may occur during the competition stage, in which case differences in fitness may stem for differences in competitive ability: here L>0 would not imply that mutation-free individuals produce more juveniles, but rather that these individuals are better competitors for resources. This is the ‘soft selection' scenario described by Wallace 1975, where ‘the suboptimal fitness of certain genotypes depends upon the actual presence of individuals possessing the optimal genotype' under this scenario, selection has no impact on demography. By contrast, under ‘hard selection' differences in fitness stand for differences in survival or fecundity that do not depend on the genotypes of other individuals (for example, selection against a lethal mutation). The terms soft and hard selection were not originally defined in the context of a mathematical model, which has sometimes led to some disagreement about their exact definition; however, they have been useful in introducing the idea that a fraction of selected mutations may not have any consequence on demography (Agrawal, 2010), although how large this fraction is remains largely unknown (but see Laffafian et al., 2010).
Different mechanisms may reduce the mutation load: for example, Kimura and Maruyama (1966) showed that synergistic epistasis among deleterious alleles reduces the load in recombining populations. Mating systems generating an excess of homozygotes (such as self-fertilization) also tend to decrease the load generated by deleterious alleles at mutation selection equilibrium (Crow, 1970), although such mating systems may also reduce Ne (Caballero and Hill, 1992) and thus increase the proportion of mutations generating drift load. Moderate amounts of drift (or local drift in the case of a subdivided population) may reduce the load generated by partially recessive deleterious alleles (as long as selection remains stronger than drift) but this effect is usually very slight (Kimura et al., 1963; Whitlock, 2002; Roze and Rousset, 2004); in most cases, the overall effect of population subdivision (with local competition) is to increase the load due to local drift (Whitlock, 2002; Roze and Rousset, 2004.
The subdivided population models cited above assumed a homogeneous habitat. How does environmental heterogeneity affect the mutation load? Spatial heterogeneity may generate local adaptation, in which case gene flow constantly brings maladapted alleles into local populations, a form of load described as ‘migration load' (Lenormand, 2002). Local adaptation involves antagonistic environmental effects of alleles (where a given allele is either beneficial or deleterious depending on the environment); however, genotype × environment interactions may not necessarily be antagonistic: for example, a given allele may be deleterious in all environments, but more in some environments than in others. In particular, results from mutation accumulation studies and measurements of inbreeding depression have suggested that selection against deleterious alleles may be stronger in harsher environments (Kondrashov and Houle, 1994; Lynch et al., 1999; Agrawal, 2010; Fox and Reed, 2010 and references therein), although the interpretation of these results is still debated (Martin and Lenormand, 2006; Agrawal, 2010). However, evolutionary consequences of variations of the deleterious effect of mutations across environments have been little investigated (but see Kawecki 1994). In this paper, I explore this question using individual-based multilocus simulations of selection in a subdivided population with two habitats. The results show that very different qualitative outcomes are possible depending on parameter values and on assumptions on the migration process. In a first regime, deleterious alleles are maintained at a mutation selection equilibrium in all demes, in which case selection and migration generate multilocus genetic associations that can greatly reduce the mutation load (assuming that the direction of the difference in selection across habitats is the same for most mutations). In a second regime, however, mutations accumulate within demes under harsh conditions due to migration pressure from demes under mild conditions, which may eventually lead to a decline in fitness in the whole metapopulation.
Materials and methods
Simulation programs
The simulation programs (written in C++, and available on request) represent a diploid population subdivided into n demes, each containing N individuals. I assume that there are two types of environments: a parameter α measures the proportion of demes where the environment is of type 1, while in the n(1−α) other demes environment is of type 2 (the environment stays constant over time within each deme). The modeled life cycle is the following: generations are discrete and non-overlapping, each adult individual produces a very large number of juveniles. These juveniles migrate with probability m; migration follows the island model of dispersal (each migrant reaches any other deme with the same probability). Finally, N individuals are sampled randomly within each deme, to form the next adult generation. Two different programs were used, corresponding to different scenarios concerning the distribution of mutational effects across loci: in the first program, all mutations have the same selection and dominance coefficient sx and hx in environment x (where x=1 or 2), whereas in the second program, selection coefficients in environments 1 and 2 are sampled for each locus in a bivariate probability distribution. The first program has faster execution speed and was used to explore a variety of parameter values, whereas the second program can be used to explore the effects of variances and covariances of mutational effects across loci and environments.
The first program (all mutations have the same selection coefficient in each environment) is similar to multilocus programs described in previous papers (Roze and Rousset, 2005, 2009; Roze, 2009.) Each individual carries two copies of one chromosome. Every generation, the number of new mutations on each chromosome is sampled from a Poisson distribution with parameter U. The number of sites at which mutations can occur is effectively infinite (each chromosome is represented by a table of real values corresponding to the positions of mutations present on the chromosome). The fitness of each individual is calculated as:
where x is the environment to which the individual is exposed, and nHe, nHo the number of heterozygous and homozygous mutations in the genome of the individual. Two different scenarios regarding the migration process and the scale of competition will be considered. In the first scenario, the number of juveniles is supposed to be regulated to a constant value (the same for all demes) just before migration (this number is supposed to be still very large); in that case, each deme contributes equally to the migrant pool, independently of mean fitness within the deme (‘soft selection' Christiansen, 1975). In the second scenario no such regulation occurs, so that different demes contain different numbers of juveniles at the time of migration; in this case, the productivity of a deme in terms of migrants is proportional to mean fitness within the deme. Note that in this second scenario an extra parameter must be included, measuring the fitness of mutant-free individuals in environment 2 relative to their fitness in environment 1; this parameter will be denoted η. More precisely, backward migration rates (proportion of immigrant individuals, just after migration and before population regulation) are given by:
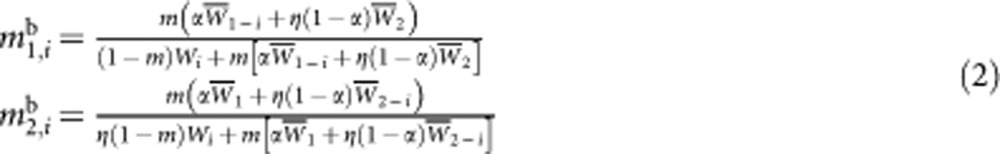 |
where mx,ib is the backward migration rate within deme i in environment x, Wi the mean fitness in deme i, W̄x the mean fitness of demes present in environment x and W̄x-i the mean fitness of demes in environment x, with deme i removed. To generate the next generation, the parents of each new individual are sampled from its deme of origin, the probability of sampling a given parent being proportional to its fitness. Both chromosomes of the offspring are then generated by recombining the parental genomes: the number of cross-overs per meiosis is sampled from a Poisson distribution with parameter R (genome map length), the position of each cross-over along the chromosome is random (no interference). At the start of the program, each individual is free of mutation; the program then runs for 105 generations, and mean fitness is measured in each deme every 100 generations.
In the second program, the strength of selection varies among loci. This program assumes that selection is multiplicative both within and across loci: the fitness of an individual in environment x is given by
 |
where the product is over all loci, si,x is the strength of selection against the mutant allele at locus i in environment x, and Xi1, Xi2 are indicator variables that equal 1 if the individual carries the mutant allele at locus i on its first and second haplotype, respectively. For each locus i, log10(si,1) and log10(si,2) are sampled in a bivariate normal distribution with means ν1, ν2, standard deviations σ1, σ2 and correlation coefficient ρ (the distributions of si,1 and si,2 are thus lognormal). For the parameter values considered in the paper, many mutations may have very small effects and thus, genomes may contain a very large number of mutations if the number of mutable sites is very large; for this reason the second program assumes a fixed, finite number of loci nL (nL=105 throughout the paper). The genome is divided into K chromosomes, and the program is parallelized (using the MPI library) to run on K processors (K=10 was used for all results shown in the paper), the jth processor dealing with all copies of chromosome j present in the population. This parallelization can considerably increase execution speed when the mutation rate per chromosome and chromosome map length (in Morgans) are sufficiently small (both values were fixed to 0.1), so that the majority of chromosomes are transmitted to offspring without mutation or cross-over. Only the soft selection scenario (each deme contributes equally to the migrant pool) was investigated using this second program.
Mean fitness and mutation load
Under soft selection, changes in allele frequencies are not affected by any difference in absolute fitness of mutant-free individuals in habitat 1 versus habitat 2 (it is only the fitness of individuals relative to the fitness of mutant-free individuals in the same environment that matters). Such a difference may have an effect on the mutation load, however, depending on how the load is defined. In a single population with a constant environment, the load is classically defined as L=1−W̄/Wmax, where Wmax is the fitness of mutant-free individuals. With habitat heterogeneity, Wmax may differ between environments (for example, mutant-free individuals may have lower fitness in harsher environments). If the load is defined relative to the maximum possible fitness across all environments (that is, the fitness of mutant-free individuals in the best environment), then any difference in absolute fitness of mutant-free genotypes across environments would affect the value of the load. Alternatively, the load may be computed by comparing the fitness of individuals to the maximum possible fitness in the same environment. In that case, the load is simply 1−W̄ when fitness W is defined relative to mutant-free individuals in the same environment (as in equations 1 and 3). The next section provides results on W̄, and thus on the mutation load under this second definition. When each deme contributes to the migrant pool in proportion to its mean fitness, however, changes in allele frequencies (and the mutation load) are affected by any difference in fitness of mutant-free individuals in habitat 1 versus habitat 2 (parameter η defined above).
Results
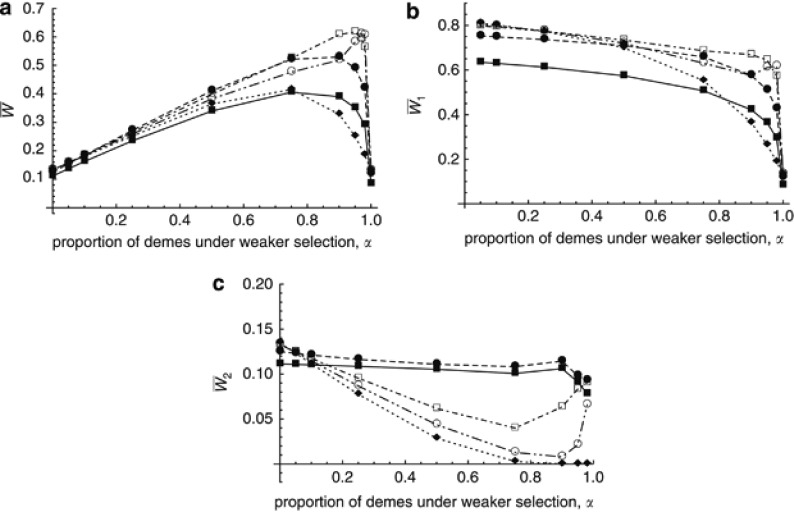
Figure 1 shows results from the first simulation program under soft selection, where selection against deleterious alleles is weaker in environment 1 than in environment 2 (s1=0.001, s2=0.01). The mutation rate is set to U=1, so that mean fitness in a panmictic population would be W̄≈ exp(−2U)≈0.135. From equation 36 in Roze and Rousset 2004, mean fitness in an island model with a homogeneous environment and additive mutations (h=0.5) is approximately exp[−2U(1+1/4Nm], which for N=500 gives W̄≈0.082, 0.122, 0.133, 0.134 and 0.135 for m=0.002, 0.01, 0.05, 0.1 and 0.5, respectively. Figure 1 confirms these results when α=0 (s=0.01 everywhere) and α=1 (s=0.001 everywhere). Note that the approximation from Roze and Rousset, 2004 cited above assumes m>s, which explains why the value of W̄ observed for m=0.002 and α=0 (W̄≈0.11) is higher than the predicted value of 0.082; by contrast, the value observed for m=0.002 and α=1 (W̄≈0.084) fits better with the prediction. As shown in Figure 1a, environmental heterogeneity (0<α<1) always increases mean fitness, the greatest increase being observed for values of α close to 1 (that is, when selection is stronger only in a small proportion of demes) and intermediate values of the migration rate; among the different parameter combinations shown in Figure 1, the highest mean fitness (W̄≈0.62) is obtained for α=0.95 and m=0.05.
Figure 1.
Mean fitness in the whole metapopulation (a) and in demes under weaker (b) and stronger selection (c), as a function of α (the proportion of demes under weaker selection), for different values of the migration rate m: 0.002 (filled squares, solid line), 0.01 (filled circle, dashed line), 0.05 (empty squares, dashed-dotted line), 0.1 (empty circles, dashed-double-dotted line), 0.5 (diamonds, dotted line). Other parameters are: number of demes n=100, deme size N=500, mutation rate per chromosome U=1, selection coefficients s1=0.001, s2=0.01, h1=h2=0.5, map length R=10. Simulations were performed for α=0, 0.05, 0.1, 0.25, 0.5, 0.75, 0.9, 0.95, 0.98 and 1. Selection is soft.
Analysis of the simulation results show that W̄ is always very accurately predicted by:
where μ1 and μ2 are the mean numbers of mutations per individual in demes of type 1 and 2 (results not shown). If migration is sufficiently strong, it erases any difference in mean number of mutations in the different demes, giving 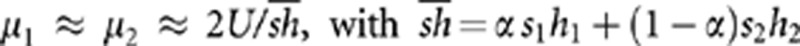 . Indeed, plugging this expression for μ1 and μ2 into equation 4 gives predictions that match very well the simulation results for m=0.5 in Figure 1a. (I am grateful to Aneil Agrawal for pointing this out.) When m is lower, however, the different strength of selection in habitats 1 and 2 generates differences in allele frequencies between the two types of demes (μ1≠μ2), that in turn generate positive linkage disequilibria (Slatkin, 1975), increasing the efficiency of selection against deleterious alleles. This effect of linkage disequilibria may be understood as follows. An individual migrating from a deme where selection is stronger tends to carry relatively few mutations; such a migrant thus benefits from a strong advantage in a deme where selection is weaker (and where individuals tend to carry many mutations). This advantage persists over a few generations, during which the immigrant genotype is gradually diluted into local genetic backgrounds by recombination. This effect increases the mean fitness of demes where selection is weaker (as illustrated in Figure 1b). By contrast, the mean fitness of demes under stronger selection is reduced by the input of heavily loaded genotypes arriving from demes under weak selection. As shown in Figure 1c, the latter effect is minor as long as the migration rate is not too large (m=0.002, 0.01) because these genotypes are quickly eliminated by selection. Stronger migration rates generate significant reductions in mean fitness in demes under stronger selection, in particular when the proportion of demes under weaker selection (α) is large (Figure 1c, m=0.05, 0.1, 0.5). However, even in those cases the overall effect is an increase in fitness at the metapopulation level (that is, the decrease in fitness within demes under stronger selection is compensated by the increase in fitness within demes under weaker selection).
. Indeed, plugging this expression for μ1 and μ2 into equation 4 gives predictions that match very well the simulation results for m=0.5 in Figure 1a. (I am grateful to Aneil Agrawal for pointing this out.) When m is lower, however, the different strength of selection in habitats 1 and 2 generates differences in allele frequencies between the two types of demes (μ1≠μ2), that in turn generate positive linkage disequilibria (Slatkin, 1975), increasing the efficiency of selection against deleterious alleles. This effect of linkage disequilibria may be understood as follows. An individual migrating from a deme where selection is stronger tends to carry relatively few mutations; such a migrant thus benefits from a strong advantage in a deme where selection is weaker (and where individuals tend to carry many mutations). This advantage persists over a few generations, during which the immigrant genotype is gradually diluted into local genetic backgrounds by recombination. This effect increases the mean fitness of demes where selection is weaker (as illustrated in Figure 1b). By contrast, the mean fitness of demes under stronger selection is reduced by the input of heavily loaded genotypes arriving from demes under weak selection. As shown in Figure 1c, the latter effect is minor as long as the migration rate is not too large (m=0.002, 0.01) because these genotypes are quickly eliminated by selection. Stronger migration rates generate significant reductions in mean fitness in demes under stronger selection, in particular when the proportion of demes under weaker selection (α) is large (Figure 1c, m=0.05, 0.1, 0.5). However, even in those cases the overall effect is an increase in fitness at the metapopulation level (that is, the decrease in fitness within demes under stronger selection is compensated by the increase in fitness within demes under weaker selection).
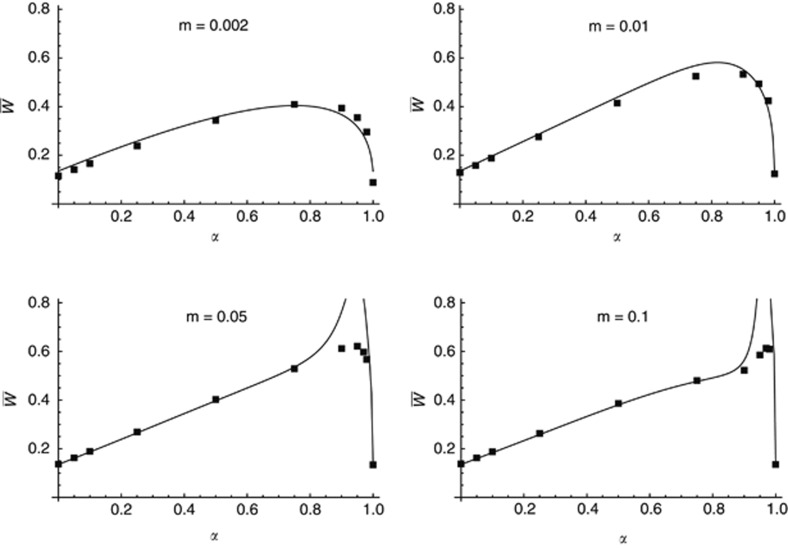
Analyses shown in the Supplementary Material demonstrate that the effect of genetic associations does not only involve linkage disequilibria between pairs of loci, but also higher-order disequilibria: for the numerical example given in the Supplementary Material, accurate predictions would require obtaining expressions for associations between up to seven loci, which would be very difficult using standard multilocus methods (Kirkpatrick et al., 2002; Roze and Rousset, 2008). However, some analytical predictions can be obtained using an infinitesimal model, and assuming gaussian distributions of the number of mutations per individual in each type of deme just after reproduction. Appendix A shows that simple recursions (equation A10) can be obtained for the mean number of mutations per individual in each type of deme, assuming weak migration and selection, infinite deme size and free recombination between all loci. These recursions can be solved numerically to obtain an expression for mean fitness at equilibrium. Figure 2 shows that predictions from this gaussian approximation fit well with the simulation results, except when α is high and the migration rate is high. Simulation results shown in Figure 2 are the same as those in Figure 1 and were obtained with a map length of 10 Morgans however, simulations assuming free recombination lead to almost undistinguishable results (not shown).
Figure 2.
Comparison of simulation results with analytical predictions obtained from an infinitesimal model, assuming gaussian distributions of the number of mutations per individual in each type of deme. Simulation results are the same as in Figure 1; analytical predictions are obtained from equations A10 and A11, solving numerically equation A10 using Mathematica.
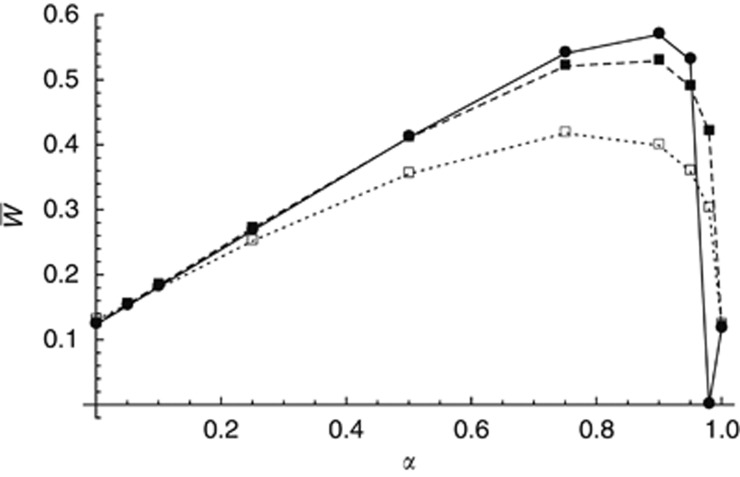
How do differences in dominance affect mean fitness? Because deleterious alleles remain at low frequency, they should almost always be in the heterozygous state, and selection should act through the product sh: thus, differences in s and differences in h should have similar effects; this was confirmed by simulations (results not shown). Figure 3 shows the effect of varying the strength of selection against mutations: for the same s1/s2 ratio (0.1 in Figure 3), decreasing the strength of selection generally increases mean fitness, in particular when the proportion of demes under stronger selection is small. This is likely due to the fact that when selection is weaker, a larger number of loci segregate for deleterious alleles, and the overall effect of genetic associations among loci become stronger. However, when selection is weak (s1=0.0005, s2=0.005) and the frequency of demes under stronger selection is small (α=0.98), mean fitness slowly decreases towards zero. The same effect is observed with the same parameter values as in Figure 1 (s1=0.001, s2=0.01) and lower deme size (N=200, see Supplementary Figure S1), still for α=0.98; reducing the recombination rate (by decreasing map length R) amplifies this effect (results not shown). As shown in Supplementary Figure S2, this is due to the fact that for these parameter values, mutation selection balance cannot be maintained within demes under stronger selection (due to the constant input of heavily loaded genomes from demes under weaker selection), and deleterious alleles accumulate in these demes. Because this accumulation is relatively slow, immigrants arriving from demes under stronger selection are still advantaged within demes under weaker selection, leading to the gradual fixation of deleterious alleles (and fitness erosion) in the whole metapopulation—note that the population cannot go extinct in the simulations, as the fecundity of individuals is effectively infinite.
Figure 3.
Effect of varying the strength of selection on the population mean fitness. Mean fitness is shown as a function of α (the proportion of demes with type 1 environment), for s1=0.0005, s2=0.005 (filled circles, solid line), s1=0.001, s2=0.01 (filled squares, dashed line) and s1=0.005, s2=0.05 (empty squares, dotted line). Other parameters are as in Figure 1, with m=0.01; selection is soft.
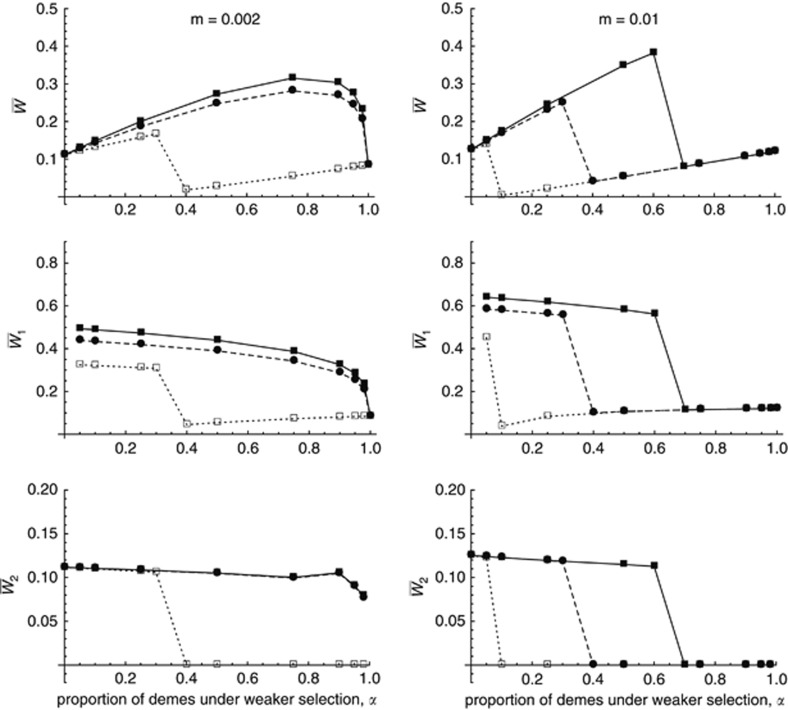
The previous results concerned the soft selection scenario (all demes contribute equally to the migrant pool). This scenario may seem unrealistic, however, particularly in situations where mean fitness becomes very low in some of the demes. Figure 4 shows simulation results for the case where no population regulation occurs before migration, so that demes contribute to the migrant pool in proportion to their mean fitness. As explained in the previous section, this case requires introducing an extra parameter η, representing the fitness of mutant-free individuals in demes of type 2, relative to their fitness in demes of type 1. As shown in Figure 4, results are similar to the soft selection case when the migration rate m is small (m=0.002) and η is high; however, as the migration rate increases and/or the productivity of demes under stronger selection (η) decreases, a transition to a different regime occurs, in which deleterious alleles accumulate within demes under stronger selection due to migration pressure (see Figure 4, bottom). In this regime, mean fitness within demes under weaker selection is little affected by immigrants from demes under stronger selection (as these demes produce very few migrants) and remains close to mean fitness in a structured population without environmental heterogeneity. For higher migration rates (m=0.05, 0.1 and 0.5), this regime was observed for all values of α between 0 and 1 and all values of η (results not shown).
Figure 4.
Mean fitness in the whole metapopulation (top rows) and in demes under weaker (middle rows) and stronger selection (bottom rows), as a function of α (the proportion of demes under weaker selection), without population regulation before migration. Left column: m=0.002; right column: m=0.01. The different curves correspond to different values of η (the fitness of mutant-free individuals in demes under harsh selection versus the fitness of the same individuals in demes under weaker selection): filled squares, solid lines: η=1; filled circles, dashed lines: η=0.5; empty squares, dotted lines: η=0.1. Other parameters are as in Figure 1.
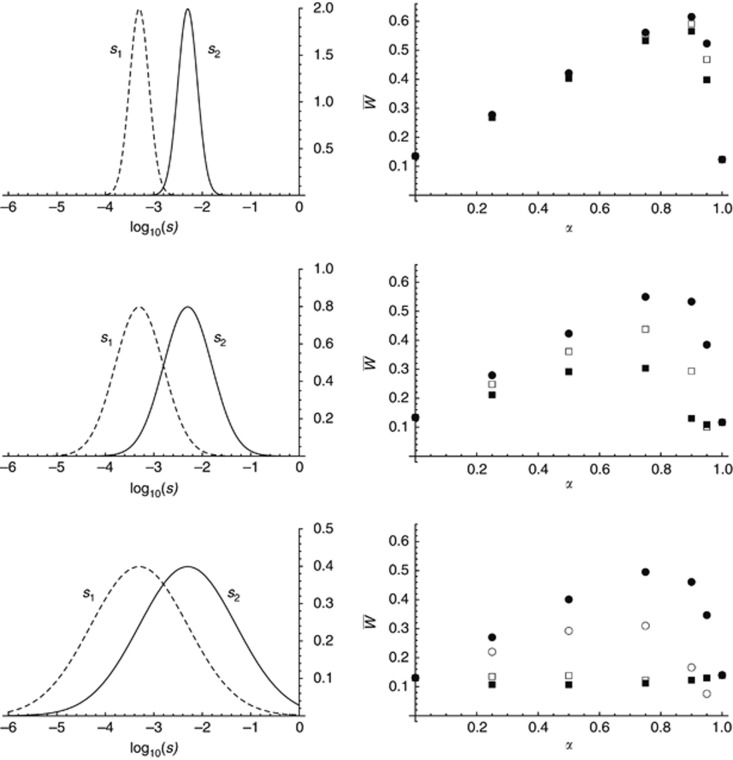
Finally, Figure 5 shows the effect of introducing variation in the deleterious effect of mutations in both types of demes, using the second simulation program (note that this program assumes soft selection). As shown in Figure 5, when the overlap between the distributions of s1 and s2 is small (top of Figure 5) results are similar to the results from the first program with fixed s1 and s2, and the correlation between s1 and s2 has little effect. When the overlap between the two distributions increases (which is done by in Figure 5 by increasing the variances of the distributions), mean fitness decreases as the correlation between s1 and s2 decreases. When the overlap is important (bottom figures), the correlation needs to be high for environmental heterogeneity to increase mean fitness. Indeed, when the overlap is important and the correlation is low, a substantial proportion of the mutations have stronger effect in environment 1 than in environment 2; migration generates negative linkage disequilibria between these mutations and mutations that are more strongly selected in environment 2, reducing the efficiency of selection. Supplementary Figure S3 shows additional simulation results using a model with only two values of s, but where a proportion p of loci are under stronger selection in environment 1, whereas the other 1−p are under stronger selection in environment 2. As shown in Supplementary Figure S3, the increase in fitness due to environmental heterogeneity is substantial only when p is close to 1 (or, by symmetry, close to zero), that is, when the difference in selection across environments goes in the same direction for most loci.
Figure 5.
Results from the second program (distributions of mutational effects). Left figures show the marginal distributions of s1 and s2 (which now measure effects of mutations in the heterozygous state); right figures show mean fitness as a function of α, for different values of the correlation coefficient ρ between s1 and s2: ρ=0 (filled squares), 0.5 (empty squares), 0.8 (empty circles, bottom figure only) and 1 (filled circles). The mean mutational effects are fixed to 0.0005 in environment 1 and 0.005 in environment 2. Other parameters are n=100, N=500, m=0.05, K (number of chromosomes) =10, R/K, U/K (chromosome map length and mutation rate per chromosome) =0.1, nL (number of loci) =105. SD of the distributions of log10(s1), log10(s2): 0.2 (top), 0.5 (middle), 1 (bottom).
Discussion
The simulation results presented in this article show that differences between habitats of the average strength of selection against deleterious alleles can have important effects on the equilibrium mean fitness of populations. In general, mean fitness within demes under relatively weaker selection is increased by the input of better purged genomes produced by demes under stronger selection; by contrast, mean fitness within demes under stronger selection may be reduced by the immigration of heavily loaded genomes from demes under weaker selection. Two different regimes are observed, depending on whether deleterious alleles are maintained at a stable equilibrium within demes under stronger selection, or accumulate over time due to constant migration pressure from demes under weaker selection. Under the first regime, environmental heterogeneity may greatly increase the mean fitness of the whole metapopulation, particularly when the proportion of demes under stronger selection is small. This effect involve positive genetic associations among selected loci, generated by differences in selection across habitats and by migration (see Supplementary Material). These positive associations increase the efficiency of selection against deleterious alleles, particularly within demes under weaker selection—this effect can also be understood from King's (King, 1966) principle (later adjusted by Kondrashov and Crow, 1988) that the genetic load decreases as the number of deleterious alleles eliminated per selective death increases. By contrast, fitness within demes under stronger selection is little affected by environmental heterogeneity, unless migration is strong and the proportion of demes under weaker selection is important: indeed, immigrants carrying many deleterious alleles have very low fitness in demes under harsh selection, and are thus quickly eliminated by selection. Under the second regime, however, selection cannot prevent the fixation of deleterious alleles (introduced by recurrent immigration) within demes under stronger selection, leading to a monotonous fitness decline within those demes. This situation was observed only in a few cases under soft selection (Figure 3 and S1 for high α), but occurs much more frequently in the (probably more realistic) case where deme productivity is proportional to mean fitness (Figure 4): indeed, this assumption may generate strongly asymmetric migration rates between demes under weaker selection (that produce many juveniles) and demes under stronger selection (that produce fewer juveniles). In general, the fitness decline occurring within demes under stronger selection has little impact on mean fitness within demes under weaker selection (except in the soft selection scenario, where deleterious alleles may accumulate in the whole metapopulation). Finally, it is important to note that the impact of environmental heterogeneity on the mutation load is greatly reduced when the effect of environmental differences on the strength of selection is inconsistent across the genome, as illustrated by Figure 5 and S3. The conditions required to observe a strong reduction in mutation load due to environmental heterogeneity may thus seem restrictive (but see below).
An important assumption of the present model is that environments remain constant over time. Introducing temporal variations in the distribution of mutational effects would be an important extension of this work. Although similar effects may appear (positive genetic associations generated by temporal changes in selection), the combined effect of spatial and temporal heterogeneity on the mutation load is not a priori obvious. Another possible extension could be to introduce some loci involved in local adaptation: by reducing the effective migration rate, these loci would affect the dynamics of deleterious alleles and the mutation load. Conversely, conditions for the maintenance of local adaptation may be affected by the type of process described here (which increase the effective migration rate from demes under stronger selection).
Is habitat heterogeneity likely to have important effects on the mutation load in natural populations? As outlined above, the answer strongly depends on the covariance between loci of the difference in strength of selection across habitats. Although it has been suggested repeatedly that stressful conditions may increase selection, conclusive evidence that this is indeed the case is still lacking. From a survey of mutation accumulation experiments, Martin and Lenormand (2006) concluded that stress may increase the variance of the distribution of mutational effects, rather than the average strength of selection against deleterious alleles. Agrawal and Whitlock (2010) showed that overall experimental studies do not show clear evidence that density-independent forms of stress (temperature, food quality, toxicity of the medium) increase selection; however, among the eight available studies that used increased density as a form of stress, seven found stronger selection at high density. This suggests that high density may enhance the effect of differences in competitive ability between genotypes. Interestingly, one could easily imagine that an increase in density would increase selection on all loci involved in competitive ability, and therefore the change in selection due to increased density may be highly correlated across loci. In that case, variations in density across space may have strong effects on the mutation load. This could be explored further using experimental measures of the strength of selection such as the ones described in Agrawal and Whitlock (2010), and more realistic theoretical models incorporating demographic effects.
Data Archiving
Data have been deposited at Dryad; doi:10.5061/dryad.9g1ns087.
APPENDIX A: GAUSSIAN APPROXIMATION
Analytical predictions can be obtained from an infinitesimal model (very large number of loci, very low frequency of each deleterious allele within each deme), by assuming gaussian distributions of the number of mutations per individual in both types of demes. The different events of the life cycle are assumed to take place in the following order: migration, selection, reproduction (meiosis with free recombination and random mating within demes), mutation; deme size is infinite (no drift). The distribution of the number of mutations per individual is assumed to be gaussian just after reproduction, with means and variances (μ1,v1) in environment 1 and (μ2,v2) in environment 2. In the following, I denote ϕ1 and ϕ2 for these two distributions. In the infinitesimal limit, deleterious alleles are always in the heterozygous state, and the fitness of an individual carrying x mutations is (1−s1h1)x≈exp(−s1h1x) in environment 1, and (1–s2h2)x≈exp(–s2h2x) in environment 2. In the following, I use the notations θ1 and θ2 for s1h1, s2h2.
The average number of mutations per individual in demes of type 1, after migration and selection, is given by:
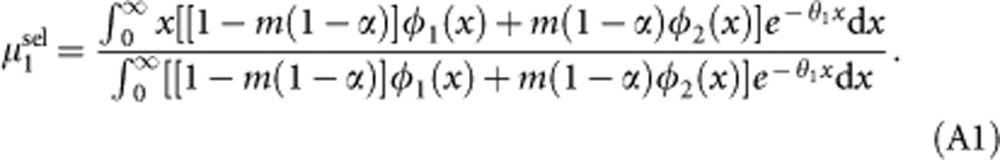 |
Assuming that the number of mutations per individual is sufficiently large so that we can integrate from −∞ to ∞ rather than from 0 to ∞, this yields:
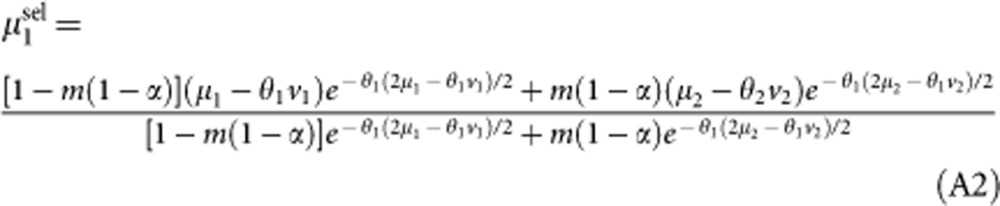 |
The average number of mutations per individual in demes of type 2 after selection (μ2sel) is given by the same expression, replacing 1−α by α and exchanging 1 and 2 subscripts. These averages are not affected by reproduction, but are increased by mutation (the mutation rate is 2U per diploid individual), so that at the next generation:
The variance in number of mutations per individual in demes of type 1 after selection is given by:
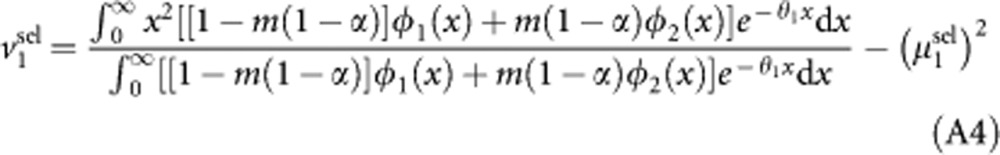 |
while after reproduction, the variance becomes:
 |
(Bulmer, 1985, Kondrashov, 1995). This result stems from the fact that in the infinitesimal limit, and under free recombination, the probability that an offspring carries x mutations given that its parents carry x1 and x2 mutations is:
 |
In the following, I assume that migration is weak and derive results to the first order in m only. I also assume that θ1, θ2 are small (of order ɛ) and that μ1, μ2, v1 and v2 are large (of order 1/ɛ). Under these assumptions, equations 4 and 5 give to leading order:
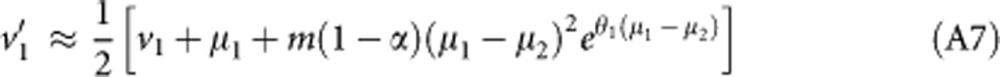 |
Neglecting the effect of mutation on v1' and solving at equilibrium gives:
Similarly,
Plugging these expressions into equations 2 and 3 and using the same assumptions (weak migration and selection) yields:
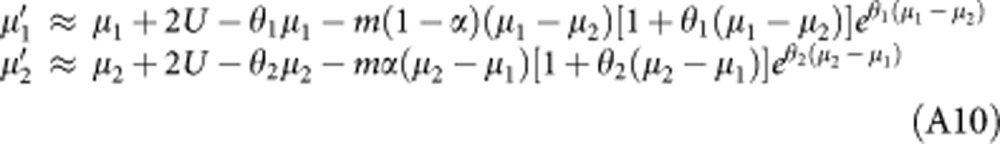 |
which can be solved numerically to obtain μ1 and μ2 at equilibrium. The mean fitness in demes of type 1 is given by exp[−θ1(2μ1−θ1v1)/2]≈exp(−θ1μ1), whereas the mean fitness in demes of type 2 is ≈exp(−θ2μ2), giving:
Simulation results show that equation A11 always predicts very accurately W̄ when μ1 and μ2 are measured directly from the simulation. Strictly, μ1 and μ2 in equation A11 should be measured just after migration (before selection), while solving equation A10 gives values just before migration; however, taking into account the effect of migration has very little effect on the analytical predictions for the different parameter values tried.
The author declares no conflict of interest.
Footnotes
Supplementary Information accompanies the paper on Heredity website (http://www.nature.com/hdy)
Supplementary Material
References
- Agrawal AF. Ecological determinants of mutation load and inbreeding depression in subdivided populations. Am Nat. 2010;176:111–122. doi: 10.1086/653672. [DOI] [PubMed] [Google Scholar]
- Agrawal AF, Whitlock MC. Environmental duress and epistasis: how does stress affect the strength of selection on new mutations. Trends Ecol Evol. 2010;25:450–458. doi: 10.1016/j.tree.2010.05.003. [DOI] [PubMed] [Google Scholar]
- Baer CF, Miyamoto MM, Denver DR. Mutation rate variation in multicellular eukaryotes: causes and consequences. Nat Rev Genet. 2007;8:619–631. doi: 10.1038/nrg2158. [DOI] [PubMed] [Google Scholar]
- Barton NH. A general model for the evolution of recombination. Genet Res. 1995;65:123–144. doi: 10.1017/s0016672300033140. [DOI] [PubMed] [Google Scholar]
- Bulmer MG.1985The Mathematical Theory of Quantitative Genetics2nd editionOxford University Press: Oxford [Google Scholar]
- Caballero A, Hill WG. Effective size of nonrandom mating populations. Genetics. 1992;130:909–916. doi: 10.1093/genetics/130.4.909. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Charlesworth D. Evolution of plant breeding systems. Curr Biol. 2006;16:R726–R735. doi: 10.1016/j.cub.2006.07.068. [DOI] [PubMed] [Google Scholar]
- Christiansen FB. Hard and soft selection in a subdivided population. Am. Nat. 1975;109:11–16. [Google Scholar]
- Crow JF.1970Genetic loads and the cost of natural selectionin Kojima K edMathematical Topics in Population Genetics Springer-Verlag:Berlin; 128–177. [Google Scholar]
- Fox CW, Reed DH. Inbreeding depression increases with environmental stress: an experimental study and meta-analysis. Evolution. 2010;65:246–258. doi: 10.1111/j.1558-5646.2010.01108.x. [DOI] [PubMed] [Google Scholar]
- Guillaume F, Perrin N. Joint evolution of dispersal and inbreeding load. Genetics. 2006;173:497–509. doi: 10.1534/genetics.105.046847. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haldane JBS. The effect of variation on fitness. Am Nat. 1937;71:337–349. [Google Scholar]
- Kawecki TJ. Accumulation of deleterious mutations and the evolutionary cost of being a generalist. Am Nat. 1994;144:833–838. [Google Scholar]
- Keightley PD, Otto SP. Interference among deleterious mutations favours sex and recombination in finite populations. Nature. 2006;443:89–92. doi: 10.1038/nature05049. [DOI] [PubMed] [Google Scholar]
- Kimura M, Maruyama T. The mutational load with epistatic gene interactions in fitness. Genetics. 1966;54:1337–1351. doi: 10.1093/genetics/54.6.1337. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kimura M, Maruyama T, Crow JF. The mutation load in small populations. Genetics. 1963;48:1303–1312. doi: 10.1093/genetics/48.10.1303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- King JL. The gene interaction component of the genetic load. Genetics. 1966;53:403–413. doi: 10.1093/genetics/53.3.403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kirkpatrick M, Johnson T, Barton NH. General models of multilocus evolution. Genetics. 2002;161:1727–1750. doi: 10.1093/genetics/161.4.1727. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kondrashov AS. Deleterious mutations and the evolution of sexual reproduction. Nature. 1988;336:435–440. doi: 10.1038/336435a0. [DOI] [PubMed] [Google Scholar]
- Kondrashov AS. Dynamics of unconditionally deleterious mutations: Gaussian approximation and soft selection. Genet Res. 1995;65:113–121. doi: 10.1017/s0016672300033139. [DOI] [PubMed] [Google Scholar]
- Kondrashov AS, Crow JF. King's formula for the mutation load with epistasis. Genetics. 1988;120:853–856. doi: 10.1093/genetics/120.3.853. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kondrashov AS, Houle D. Genotype-environment interactions and the estimation of the genomic mutation rate in Drosophila melanogaster. Proc Roy Soc B. 1994;258:221–227. doi: 10.1098/rspb.1994.0166. [DOI] [PubMed] [Google Scholar]
- Laffafian A, King JD, Agrawal AF. Variation in the strength and softness of selection on deleterious mutations. Evolution. 2010;64:3232–3241. doi: 10.1111/j.1558-5646.2010.01062.x. [DOI] [PubMed] [Google Scholar]
- Lande R, Schemske DW. The evolution of self-fertilization and inbreeding depression in plants. I. Genetic models. Evolution. 1985;39:24–40. doi: 10.1111/j.1558-5646.1985.tb04077.x. [DOI] [PubMed] [Google Scholar]
- Lenormand T. Gene flow and the limits to natural selection. Trends Ecol Evol. 2002;17:183–189. [Google Scholar]
- Lynch M, Blanchard J, Houle D, Kibota T, Schultz S, Vassilieva L, et al. Perspective: spontaneous deleterious mutation. Evolution. 1999;53:645–663. doi: 10.1111/j.1558-5646.1999.tb05361.x. [DOI] [PubMed] [Google Scholar]
- Lynch M, Conery J, Burger R. Mutation accumulation and the extinction of small populations. Am Nat. 1995a;146:489–518. [Google Scholar]
- Lynch M, Conery J, Burger R. Mutational meltdowns in sexual populations. Evolution. 1995b;49:1067–1080. doi: 10.1111/j.1558-5646.1995.tb04434.x. [DOI] [PubMed] [Google Scholar]
- Martin G, Lenormand T. The fitness effect of mutations across environments: a survey in light of fitness landscape models. Evolution. 2006;60:2413–2427. [PubMed] [Google Scholar]
- Muller HJ. Our load of mutations. Am J Hum Genet. 1950;2:111–176. [PMC free article] [PubMed] [Google Scholar]
- Otto SP. The evolutionary enigma of sex. Am Nat. 2009;174:S1–S14. doi: 10.1086/599084. [DOI] [PubMed] [Google Scholar]
- Otto SP, Goldstein DB. Recombination and the evolution of diploidy. Genetics. 1992;131:745–751. doi: 10.1093/genetics/131.3.745. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Otto SP, Marks JC. Mating systems and the evolutionary transition between haploidy and diploidy. Biol J Linn Soc. 1996;57:197–218. [Google Scholar]
- Ravigné V, Olivieri I, González Martínez SC, Rousset F. Selective interactions between short-distance pollen and seed dispersal in self-compatible species. Evolution. 2006;60:2257–2271. [PubMed] [Google Scholar]
- Rousset F. Genetic Structure and Selection in Subdivided Populations. Princeton University Press:Princeton; 2004. [Google Scholar]
- Rowe L, Houle D. The lek paradox and the capture of genetic variance by condition dependent traits. Proc Roy Soc B. 1996;263:1415–1421. [Google Scholar]
- Roze D. Diploidy, population structure and the evolution of recombination. Am Nat. 2009;174:S79–S94. doi: 10.1086/599083. [DOI] [PubMed] [Google Scholar]
- Roze D, Rousset F. Joint effects of self-fertilization and population structure on mutation load, inbreeding depression and heterosis. Genetics. 2004;167:1001–1015. doi: 10.1534/genetics.103.025148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roze D, Rousset F. Inbreeding depression and the evolution of dispersal rates: a multilocus model. Am Nat. 2005;166:708–721. doi: 10.1086/497543. [DOI] [PubMed] [Google Scholar]
- Roze D, Rousset F. Multilocus models in the infinite island model of population structure. Theor Popul Biol. 2008;73:529–542. doi: 10.1016/j.tpb.2008.03.002. [DOI] [PubMed] [Google Scholar]
- Roze D, Rousset F. Strong effects of heterosis on the evolution of dispersal rates. J Evol Biol. 2009;22:1221–1233. doi: 10.1111/j.1420-9101.2009.01735.x. [DOI] [PubMed] [Google Scholar]
- Slatkin M. Gene flow and selection in a two-locus system. Genetics. 1975;75:733–756. doi: 10.1093/genetics/75.4.733. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wallace B. Hard and soft selection revisited. Evolution. 1975;29:465–473. doi: 10.1111/j.1558-5646.1975.tb00836.x. [DOI] [PubMed] [Google Scholar]
- Whitlock MC. Selection, load and inbreeding depression in a large metapopulation. Genetics. 2002;160:1191–1202. doi: 10.1093/genetics/160.3.1191. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.