Confounding Due to Changing Background Risk in Adaptively Randomized Trials

Background

Adaptive and other flexible trial designs have received increasing attention from researchers [1], pharmaceutical companies [2], and regulatory bodies [3,4]. An adaptive trial uses accumulating data to make design modifications at interim stages [5]. Although such designs promise more efficiency and more ethical justification while maintaining validity [6,7], they introduce complications. For example, in a trial that uses adaptive randomization, the clinician administering the treatment may presume that a perceptible change in the allocation ratio is due to weighting the randomization probability toward the better treatment, which may thus influence his or her outcome assessment. This particular possibility may be addressed by concealment of treatment assignments from these clinicians [2,3].

In many settings the source population varies during the trial [8]. For instance, with adaptive rules for inclusion and exclusion criteria, the source population during the beginning of enrollment may be quite different from the source population at the end of enrollment [9]. This evolution may affect parameter estimates and both Type-I and Type-II error rates. Suggested adjustments include using estimates of parameter changes with time [8], possibly based on a linear model [9]. These techniques introduce auxiliary assumptions, and bias may ensue when those assumptions are violated. Time trends have long been recognized as a potential source of bias in adaptive trials, and methods have been proposed to deal with them [10-14]. To paraphrase Clayton [11], secular trends may serve to reinforce earlier (possibly wrong) decisions, although the essence of this concern (i.e., that you might be wrong) is not unique to adaptive trials [13].

We here revisit bias due to time trends in the case of adaptive allocation, with the goal of providing further insight and tools using basic bias-sensitivity formulas. Specifically, we describe in detail how time trends in disease risk may bias the unadjusted (crude) effect measure in an adaptively randomized trial, and how to deal with this possibility. We restrict our discussion to clinical trials that use adaptive randomization to compare two therapies for a disease. We will use X to represent the treatment indicator, where X is + for the new treatment and – for the control. For simplicity we will also assume that the trial outcome is a binary disease outcome, although all our points extend to other outcome variables as well.

To motivate the discussion, consider the first example of time trend bias given by Altman and Royston [12]. They describe a multicenter, placebo-controlled trial of azathioprine for patients with primary biliary cirrhosis. Adverse patient outcomes were strongly associated with elevated serum bilirubin levels. Over the course of the 7-year trial, entering patients were progressively healthier, as evidenced by falling serum bilirubin levels across enrolled subjects by time (see their Figure 1). Below we consider the consequences of changing the treatment allocation ratio in the middle of such a trial, where (as here) earlier patients have a different prognosis than later patients.

Causal Model

We employ a standard potential-outcome model for treatment effects (e.g., see reference 15 for more details). Each patient is assumed to have two outcome indicators which are coded + if the outcome under study (e.g., death within a year) occurs and – if not: Y_X=+ for the patient’s outcome when given the new treatment (X = +) and Y_X=− for the patient’s outcome when given the control treatment (X = –). A patient may have one of four possible patterns of response to treatments:

$$\text{Response type}1:{\mathrm{Y}}_{\mathrm{X}=+}=+,{\mathrm{Y}}_{\mathrm{X}=-}=+;$$

$$\text{Response type}2:{\mathrm{Y}}_{\mathrm{X}=+}=+,{\mathrm{Y}}_{\mathrm{X}=-}=-;$$

$$\text{Response type}3:{\mathrm{Y}}_{\mathrm{X}=+}=-,{\mathrm{Y}}_{\mathrm{X}=-}=+;$$

$$\text{Response type}4:{\mathrm{Y}}_{\mathrm{X}=+}=-,{\mathrm{Y}}_{\mathrm{X}=-}=-.$$

We can thus classify a group of patients into four possible response types. (See Table 1, where we define disease status given exposure, give a verbal description of the response types, and give the formal probability statements for outcome conditioning on exposure.) Let π_i be the proportion of patients in the group of each response type. Then the proportion experiencing the outcome (average risk) if given the new treatment (X = +) is π₁ + π₂, and the proportion experiencing the outcome if given the control treatment (X = –) is π₁ + π₃. The causal risk ratio measuring the effect of the new treatment relative to the control is thus (π₁ + π₂) / (π₁ + π₃). Similarly, the causal risk difference for this effect is (π₁ + π₂) – (π₁ + π₃) = π₂ – π₃, which is the difference between the proportion harmed and the proportion helped by the new treatment (the net loss from adopting the new treatment instead of the control; gain is negative).

Table 1.

Response types in a deterministic potential-outcome model.

	Disease status with treatment:		Description	Probability of Y = + (or proportion of Y = +) among each type
	X = +	X = −
Type 1	Y = +	Y = +	Doomed	P(Y = +) = 1
Type 2	Y = +	Y = −	Exposure causal	P(Y = + | X = +) = 1 P(Y = + | X = −) = 0
Type 3	Y = −	Y = +	Exposure preventive	P(Y = + | X = +) = 0 P(Y = + | X = −) = 1
Type 4	Y = −	Y = −	Immune	P(Y = +) = 0

X = exposure or treatment variable; Y = disease variable.

P(Y = + | X = +) = probability of disease (Y = +) conditional on getting treatment (X = +)

P(Y = + | X = −) = probability of disease (Y = +) conditional on getting control (X = −)

Because a patient cannot simultaneously receive (X = +) and not receive (X = −) the new treatment, only one of Y_X=+ and Y_X=− can be observed. Hence if the new treatment is received (X = +) then Y_X=+ is observed and Y_X=− (the outcome in the hypothetical case that the patient had instead received the control treatment) is a missing variable; if the control treatment is received (X = –) then Y_X=− is observed and Y_X=+ is a missing variable. In lieu of having the missing variables available to us, we divide the patient group in two, with some members assigned to the new treatment and others to the control. Denote the proportion of response type i in the X = + group by p_i and in the X = – group by q_i. The observed risk ratio and risk difference are then (p₁ + p₂) / (q₁ + q₃) and (p₁ + p₂) – (q₁ + q₃), respectively. The observed association measures are equal to the causal effect measures given above if both p₁ + p₂ = q₁ + q₂ and p₁ + p₃ = q₁ + q₃. Confounding is said to occur when these equalities do not hold, for in that case at least one of the measures will incorporate differences between the group outcomes that are not due to the treatment. We note that this definition of confounding includes differences that are purely due to random variation in allocation, as is the norm in much of epidemiology.

Factors that may affect the outcome and differ between groups may cause confounding. Such factors range from those easily enumerated and controlled (such as age and gender) to those unknown and thus uncontrollable (such as unknown genetic differences). Randomizing the patient group to the two arms of a trial does not prevent confounding, but does make the extent of confounding by baseline covariates random. This random confounding is accounted for by statistical methods even when some confounders remain unidentified. Confidence intervals and p-values are constructed assuming randomization has taken place within levels of adjustment factors (such as age and sex). Hence these statistics are justifiable for measuring uncertainty in a randomized study with no source of bias, i.e., a trial with no nonrandom source of outcome differences other than treatment. (Examples of bias sources include nonadherence, misdiagnosis, misreporting, and loss to follow-up.) As we will describe below, adaptive randomization opens another avenue for bias when background risk changes over time, and must thus be used with attention to possible time trends in risk.

Example

Suppose that treatment never causes the outcome event under study, i.e., there are no type 2s in the population (commonly called a “monotonicity of effect” assumption). Table 2 describes a population (at time period 1) in which 1/5 would get the outcome regardless of treatment (response-type 1), 3/5 would have the outcome prevented by treatment (type 3), and the remaining fifth would not have the outcome regardless of treatment (type 4). If we apply the treatment to this population, the incidence proportion (proportion getting the outcome, or average risk) would be 1/5 = 0.2, whereas if we apply the control to everyone in this population, the incidence proportion would be 1/5 + 3/5 = 0.8. The effect of treatment versus control is thus to decrease risk by a factor of 0.2/0.8 = 0.25 or a quarter of what it would have been without treatment, which here corresponds to a risk difference of 0.2 – 0.8 = −0.6, i.e., an absolute risk reduction of 0.8 – 0.2 = 0.6.

Table 2.

Distributions of causal types, risks, and risk ratios for an example adaptive trial with two time periods.

	Arm (X)	Causal Type Proportions				Enrollment By Causal Type
		1	2	3	4	N	1	3	4	Risk	RR
Period 1	+	0.200	0	0.600	0.200	30	6	18	6	0.200	0.250
	−	0.200	0	0.600	0.200	30	6	18	6	0.800
Period 2	+	0.050	0	0.150	0.800	40	2	6	32	0.050	0.250
	−	0.050	0	0.150	0.800	20	1	3	16	0.200
Combined	+	0.114	0	0.343	0.543	70	8	24	38	0.114	0.204
	−	0.140	0	0.420	0.440	50	7	21	22	0.560

+ denotes treatment arm; − denotes control arm.

RR = ratio of risks in the two arms.

Of course the causal structure just described will be unknown to the investigators. Suppose they decide to study the treatment’s effect in the population using two sequential samples and the following adaptive scheme: First, the subpopulation in period 1 is randomized to treatment or control with 1:1 odds (probability of ½ for treatment). Next, if the outcomes observed in the first period favor treatment, the subpopulation in period 2 is then randomized to treatment with 2:1 odds (probability of 2/3 for treatment).

Sequential randomization ensures that, within each period, the treatment and control arms have the same expected causal type distributions. Between the two periods, however, there is a shift in the population’s background risk of the disease of interest, perhaps due to a change in the prevalence of an unknown risk factor. In Table 2, we see that the subpopulation studied during the first period has a higher background incidence of disease than the subpopulation in the second period, with the risks of disease in the control groups being 0.8 and 0.2, respectively. Nonetheless, despite the different background incidences of disease, the risk ratio in each period remains 0.25. (The risk ratio is the same because we held constant the ratio of type 3s to type 1s over the time periods while varying the proportion that are type 4s.) Because there are no type 2s, the risk of disease in the control group is just the proportion that are type 1s and 3s in the group, which is one minus the proportion that are type 4s.

If the results of the study were analyzed under the assumption of constant baseline risk of disease, the 2×2 table would be derived from the “Combined” rows in Table 2. The unadjusted (associational) risk ratio is 0.204, which is confounded because the distribution of causal types is not the same between the treatment and control arms. More precisely, the totals of type 1s and 3s in the two arms are not equal; i.e., 0.114 + 0.343 = 0.447 ≠ 0.140 + 0.420 = 0.560. Although the distribution of causal types is equal between the control and treatment arms within each time period, the change in allocation ratio (which characterizes adaptively randomized designs) led to different distributions in the arms when they were combined. Thus the shift in distribution of causal types over time, combined with the use of adaptive randomization, resulted in confounding of the unadjusted associations.

Stratifying by time period yields an association unconfounded by time period. If the allocation ratio were the same across the time periods, the unadjusted associations would also not be confounded. As an example, if the first time period had 20 and 10 subjects in the treatment and control arms, respectively, the unadjusted RR for the combined group would still be 0.25 since both periods would have 2:1 allocation. The 2×2 table for the combined periods would have 6 of 60 treatment patients with disease and 12 of 30 control patients with disease.

Confounding also occurs under the null hypothesis, i.e., when there is no effect of treatment X = + on the outcome relative to X = −, so there are no type 2s or type 3s. In that case, risk is determined only by the proportion of type 1s. As an example, suppose in Table 2 we change all the type 3s to type 1s, so that the proportion of type 1s is 0.8 in the first period and 0.2 in the second period. The risk ratios in each group are now 1. The ratio of treatment type 1s to control type 1s in the combined analysis, however, is 0.457/0.560 (i.e., ((30 × 0.8 + 40 × 0.2) / (30 + 40)) / ((30 × 0.8 + 20 × 0.2) / (30 + 20))) = 0.82, which is pure confounding by time period. Because being in group 2 (versus group 1) is associated with an increased risk of receiving treatment and a decreased risk of disease, the risk ratio is biased downward.

Directed acyclic graphical analysis

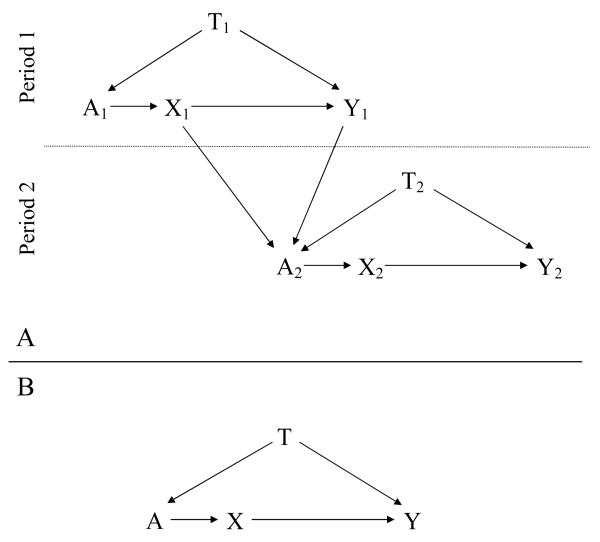
A causal diagram in the form of a directed acyclic graph (DAG) enables visualization of bias sources in the example (see reference 16 for a primer on these diagrams, and reference 17 for a more detailed introduction). Figure 1A is a DAG for the adaptive study whose data are shown in Table 2. The variables in the graph, which are all binary, are: X, the exposure (treatment or control); Y, the outcome (disease or no disease); A, the treatment-assignment mechanism (here, the investigators), that assigns exposure using a randomization scheme (which may be imbalanced); and T, the period indicator (which also represents possibly unknown changes in background risk factors across time), where all subjects in the first period have T = 1, and all those in the second period have T = 2. Note that unless necessary for clarity, variable subscripts have been suppressed below for simplicity.

Figure 1.

A: Directed acyclic graph for the study described in the text, with enrollment of subjects in period 1 preceding enrollment of subjects in period 2. B: Directed acyclic graph of the same study, where the data are now combined across enrollment periods. X – exposure; Y – disease; T –period indicator; A – subject exposure allocation mechanism. Subscripts indicate period sequence, so that, e.g., X₁ occurs before X₂.

We show our causal assumptions by drawing arrows from X to Y (exposure assignment affects disease probability), A to X (the investigator assigns exposure), T to A (the investigator’s decisions regarding exposure assignment in this adaptively randomized design change with the study period), and T to Y (there is a change in background risk of disease between the two time periods due to uncontrolled risk factors). We also draw arrows from X₁ and Y₁ to A, since the results of the first period’s exposure and outcome experience also influence A’s choice for the randomization probabilities used for period 2; this is what defines the study as using response-adaptive, adaptive randomization.

Within each period, an association in our data between X and Y can come from either or both of two sources: The direct (causal) path X → Y, and the path X ← A ← T → Y. Note that the latter is called a “backdoor path” from X to Y because it begins with an arrow into X; here, X is not influencing Y, but rather T, a classic confounder, is influencing both X and Y. This dual effect of T would ordinarily bias the unadjusted association between X and Y away from the effect under study. Because T can only take on the value 1 in the first period and can only take on the value 2 in the second period, stratifying on time means we have T constant in the upper and lower halves of the graph (i.e., for each period, there is only one stratum of T within which to analyze the data). Therefore, the backdoor path from X to Y is said to be closed (or blocked) when we stratify on T, and any nonrandom association between X and Y in the data can be attributed to X’s effect on Y. If there were no arrow from X to Y (i.e., if X had no effect on Y), then we would expect to see no association in the data within strata of T.

Figure 1B depicts an analysis of the combined periods. Note that because of a time trend, P(Y | T = 1, X = −) P(Y | T = 2, X = −), where X = − denotes getting the control as opposed to test treatment. In addition to the direct path X → Y representing the effect of interest, now the backdoor path X ← A ← T → Y is also open. We therefore expect that the observed association will be a mixture of the X effect on Y and confounding from the backdoor path. If X had no effect on Y, which we would indicate on the graph by removing the arrow from X to Y, then any nonrandom association would come from the backdoor path. Stratifying on T removes the confounding by closing the open backdoor path, which is the situation in Figure 1A.

Adaptive randomization implies a T → A → X path. Therefore, for confounding to occur, we need only a time trend in a risk factor for disease: this creates arrow T → Y and completes the backdoor path. If the allocation ratio (randomization odds) did not change, then the arrow from T to A would be removed, and there would no longer be an open backdoor path to produce confounding.

Bias

We now proceed to derive formulas for bias due to changes in risk over time. These formulas provide the exact magnitude of bias under different scenarios, and thus can be used for trial planning and for sensitivity analysis of trial reports that do not give period-specific data. Let α_T,X be the proportion of subjects in period T (1 or 2) assigned to exposure X (+ for new treatment, – for control) who are causal type 1s. Similarly, with β_T,X, γ_T,X, and δ_T,X, for causal types 2, 3, and 4, respectively. Also let N_T,X be the total number of subjects in period T assigned to exposure X, and N_X = N_1,X + N_2,X.

The causal risk ratio for disease given treatment versus control in period 1 is

$$\frac{\frac{{\alpha }_{1,+}+{\beta }_{1,+}}{{\alpha }_{1,+}+{\beta }_{1,+}+{\gamma }_{1,+}+{\delta }_{1,+}}}{\frac{{\alpha }_{1,-}+{\gamma }_{1,-}}{{\alpha }_{1,-}+{\beta }_{1,-}+{\gamma }_{1,-}+{\delta }_{1,-}}}=\frac{{\alpha }_{1,+}+{\beta }_{1,+}}{{\alpha }_{1,-}+{\gamma }_{1,-}}$$

because α_1,X + β_1,X + δ_1,X = 1. If we add the assumption that treatment never causes disease, i.e., that there are no type 2s (βs) in the population, we can write the risk ratio as α_1,+/ (α_1,− + γ_1,−).

For simplicity, assume that the true risk ratio is constant across periods. In the absence of causal effects (type 2s), this implies that the ratio of γs to s in any particular period and exposure group is fixed, and we can define r = α_T,X/γ_T,X for any pair T, X. r/(1 + r) is the ratio of risk of disease in the treatment (i.e., exposed) group to risk of disease in the control (i.e., unexposed) group, which is the causal risk ratio (RR_Causal) under our assumptions. We can therefore write the unadjusted risk ratio as

$$\frac{{\gamma }_{1,+}}{{\gamma }_{1,-}}\frac{r}{(1+r)}=\frac{{\gamma }_{1,+}}{{\gamma }_{1,-}}{\mathit{RR}}_{\mathit{Causal}}$$ 1

The ratio γ_1,+/γ_1,− is thus the bias factor. If the control group is an appropriate surrogate for what the treated group would have experienced under the control regimen, then γ_1,+ = γ_1,− and the observed risk ratio equals the causal risk ratio (i.e., it is unconfounded).

The above bias applies to any single period. When we combine two periods, the risk ratio becomes

$$\frac{\frac{N_{1,+}+{\alpha }_{1,+}+N_{2,+}{\alpha }_{2,+}}{N_{+}}}{\frac{N_{1,-}({\alpha }_{1,-}+{\gamma }_{1,-})+N_{2,-}({\alpha }_{2,-}+{\gamma }_{2,-})}{N_{-}}}$$

which reflects the time-varying weighting of subjects due to the changing allocation ratio. We add two more variables to simplify terms. First, we define g = α_2,−/α_1,−. If the true risk ratio is constant, it follows that α_2,− = gγ_1,− to preserve the ratio of s to γs in each period. We also define h = α_2,+/α_1,+. Then

$$\frac{\frac{N_{1,+}r{\gamma }_{1,+}+N_{2,+}\mathit{hr}{\gamma }_{1,+}}{N_{+}}}{\frac{N_{1,-}(r{\gamma }_{1,-}+{\gamma }_{1,-})+N_{2,-}\mathsf{g}(r{\gamma }_{1,-}+{\gamma }_{1,-})}{N_{-}}}=\frac{\frac{r{\gamma }_{1,+}(N_{1,+}+h{N}_{2,+})}{N_{+}}}{\frac{(1+r){\gamma }_{1,-}(N_{1,-}+\mathsf{g}{N}_{2,-})}{N_{-}}}=\frac{{\gamma }_{1,+}(N_{1,+}+h{N}_{2,+})}{{\gamma }_{1,-}(N_{1,-}+\mathsf{g}{N}_{2,-})}\frac{N_{-}}{N_{+}}{\mathit{RR}}_{\mathit{Causal}}$$ 2

The bias factor is thus derived from both the partial exchangeability assumption (i.e., the departure from γ_1,+/α_1,− = 1) and a weighted average of the period-exposure enrollment. The components are not completely separable: Within-period exchangeability implies that g = h, which happens, for instance, when patient distribution in each period is perfectly randomized. (Note that the γs quantify an intraperiod comparison, whereas g and h quantify interperiod comparisons for the two different arms of the trial.) If the risk ratio is constant and g = h, then γ_1,+ = γ_1,− implies γ_2,+ = γ_2,−. When g = h = 1, the distribution of causal types 1 and 3 is the same in all arms across all periods, and the bias factor reduces to Equation 1. If g = h = 1 and the true risk ratio is constant, there is no confounding because γ_1,+ = γ_1,− (equal causal type 1 and 3 distributions between the periods removes the association between period and disease).

Define vN₋ = N_1,− and wN₊ = N_1,+; v, w reflect subject assignments whereas g, h indicate causal-type distributions. Then, from the middle of Equation (2),

$$\frac{(N_{1,+}+h{N}_{2,+})}{(N_{1,-}+\mathsf{g}{N}_{2,-})}\frac{N_{-}}{N_{+}}=\frac{w{N}_{+}+h(1-w)N_{+}}{v{N}_{-}+\mathsf{g}(1-v)N_{-}}\frac{N_{-}}{N_{+}}=\frac{w(1-h)+h}{v(1-\mathsf{g})+\mathsf{g}}$$ 3

Therefore, if v = w (which occurs when the allocation ratio is fixed) then there is no contribution from the allocation scheme to the confounding. In the example in Table 2, γ_1,+ = γ_1,− = 0.6 and g = h = 0.25, so that the arms are exchangeable within the periods; however, because v = 3/5 ≠ w = 3/7 the unadjusted risk ratio across all subjects (i.e., combined) is confounded.

Bias factor for multiple periods, constant risk ratio

We now generalize the bias factors given above. Let i be the period number, and I the total number of periods. Define α_i,− = g_iα_1,− and α_i,+ = h_iα_1,+, with g₁ = h₁ = 1, and v_iN₋ = N_i,− and w_iN₊ = N_i,+. Equation 2 is now

$$\frac{{\gamma }_{1,+}\sum _{i=1}^I{h}_i{N}_{i,+}}{{\gamma }_{1,-}\sum _{i=1}^I{\mathsf{g}}_i{N}_{i,-}}\frac{N_{-}}{N_{+}}{\mathit{RR}}_{\mathit{Causal}}$$

And in place of Equation 3, we have

$$\frac{\sum _{i=1}^I{w}_i{h}_i}{\sum _{i=1}^I{v}_i{\mathsf{g}}_i}$$

This formula shows that the bias arises from the change in allocation ratios over time, where w and v are the allocation weights (with ${\sum }_{i=1}^I{w}_i={\sum }_{i=1}^I{v}_i=1$ ) and g and h measure the causal type departures from the first (“standard”) period.

Bias for constant risk difference

The risk difference is defined as α_1,+ + β_1,+ – (α_1,− + γ_1,−). If the treatment and control groups are exchangeable, then α_1,+ = α_1,−. And if we again assume that there are no type 2s (βs) in the population, then the risk difference is –γ_1,− which is also –γ_1,+ under exchangeability. A constant causal risk difference across periods thus implies that γ is constant across the periods, provided that exchangeability is maintained within each period when each period is divided into exposure arms.

In an adaptive randomization trial with a constant causal risk difference, the unadjusted (and thus potentially biased) risk difference is

$${\mathit{RD}}_{\mathit{Causal}}+\sum _{i=1}^I{w}_i{h}_i{\alpha }_{1,+}-\sum _{i=1}^I{v}_i{\mathsf{g}}_i{\alpha }_{1,-}$$

Assuming within-period exchangeability, α_1,− = α_1,+ and g_i = h_i for all i, and this formula simplifies to

$${\mathit{RD}}_{\mathit{Causal}}+\sum _{i=1}^I{\mathsf{g}}_i{\alpha }_{1,-}(w_i-v_i)$$

As an example derived from Table 2, change the proportion of type 3s in the second period to 0.6, and the proportion of type 4s to 0.35. The population now has 60% type 3s and 27.5% type 4s. The treatment lowers the risk of disease from 0.8 to 0.2 in the first period, and from 0.65 to 0.05 in the second period, so that the risk reduction (negative of the risk difference) for each period is 0.60. The unadjusted risk difference is −0.6 + 1 × 0.2 × (0.429 – 0.6) + 0.25 × 0.2 × (0.571 – 0.4) = −0.63.

Even if the risk difference varies, the simple average of the two period risk differences is equal to the causal population risk difference; in Table 2, (−0.6 + −0.15)/2 = −0.375. For any period i, RD_i = (RR_Causal – 1) × R_i, where R_i is the baseline risk in period i. For two periods, the average of the risk differences is thus (RR_Causal – 1) × (R₁ + R₂)/2.

Discussion

Time trends may result from a variety of sources, including changes in covariate distributions, background rates, and selection factors [13]. In a randomized trial with fixed allocation, we would not expect a trend in risk to result in confounding. In adaptively randomized trials in which the allocation ratio changes over time, however, associations (or paths) are created between time-varying risk factors and the treatment, and thus checks or adjustments for risk trends should be part of the analysis protocol of such trials. At its simplest, this check requires assessment of whether the treatment-specific risks vary across periods. If such variation may be present, one way to account for it is to stratify by allocation ratio in all analyses; in the adaptively randomized designs we described, this amounts to stratification by allocation time. If allocation time is not used as the baseline (zero) point for the survival-time stratification found in standard failure-time methods (such as Cox modeling), the additional stratification on allocation time may introduce or aggravate data sparsity, especially if there are more than a few allocation-time strata or there is stratification on center as well.

This sparsity is easily dealt with by modeling the risk trend, including allocation time as a regression covariate. Alternatively, one can adjust for possible trend confounding by inverse-probability-of-treatment weighting (IPTW) [18], which takes a particularly simple form in trials. With IPTW each patient record is weighted by the inverse of the patient’s allocation probability (the probability that the patient would have received the treatment actually given the patient). Thus a patient receiving active treatment when the allocation ratio was 1:1 (50% active) would receive a weight of 1/0.50 = 2, while a patient receiving treatment when the allocation ratio was 2:1 (67% active) would receive a weight of 1/0.67 = 1.5 and a patient receiving the control under 2:1 allocation would receive a weight of 1/.33 = 3. These weights can be further modified (stabilized) to improve precision [18].

IPTW adjustment has the advantage of not involving the patient outcomes, and thus (unlike data-based risk-model selection) will not distort type-I error rates or confidence-interval coverage. Risk regression and IPTW can however be combined to provide a more model-robust (“doubly robust”) analysis [19]. Furthermore, both can be combined with hierarchical (shrinkage) and Bayesian methods [20,21] to improve precision and further deal with problems of data sparsity.

The bias formulas for multiple time periods may be used for a continuously changing randomization proportion, which is an extreme form of block adaptive randomization. For both two time periods and multiple time periods, we simplified our formulas by assuming that the true risk ratio or risk difference was constant. Even if incorrect, these assumptions may be harmless if the resulting estimates are interpreted as averages over time [22]. If however there is concern that the true risk ratio or difference is indeed evolving, further analysis of the time trend is warranted. For example, if later data are more representative of future effects, more accurate predictions may be obtained by modeling effect trends and projecting them forward, rather than assuming constancy of effect [14]. Note that if background risk is changing, a constant risk ratio implies a changing risk difference and vice versa [13,15], so even if the constancy assumption appears to hold for one measure, that should not be taken as a basis for claiming or behaving as if other effects are constant.

Our formulas were further simplified by assuming that there are no type 2s in the population (i.e., that treatment never causes the outcome of interest); the formulas should therefore not be used in a clinical setting where that assumption is unreasonable. Finally, we note that our risk-ratio formulas may be applied to odds ratios when the outcome is infrequent (under 10%) in both the treated and control group, since then the odds ratio approximates the risk ratio [15]. When the outcome is more common, various authors recommend avoiding odds ratios due to interpretational problems [13,15,23].

Conclusion

A sequential trial that uses adaptive randomization attempts to merge serial subtrials into one large trial. Even if the true effect measure is constant across the component trials, differential weighting of the arms due to adaptive randomization may lead to confounding when there is a time trend in risk. Thus, when an adaptive randomization strategy is chosen, analysis must involve attention to or adjustment for possible trends in background risk. Numerous modeling strategies are available for that purpose, including stratification, trend modeling, IPTW, and hierarchical regression.