A Hierarchical Algorithm for Fast Debye Summation with Applications to Small Angle Scattering

Abstract

Debye summation, which involves the summation of sinc functions of distances between all pair of atoms in three dimensional space, arises in computations performed in crystallography, small/wide angle X-ray scattering (SAXS/WAXS) and small angle neutron scattering (SANS). Direct evaluation of Debye summation has quadratic complexity, which results in computational bottleneck when determining crystal properties, or running structure refinement protocols that involve SAXS or SANS, even for moderately sized molecules. We present a fast approximation algorithm that efficiently computes the summation to any prescribed accuracy ε in linear time. The algorithm is similar to the fast multipole method (FMM), and is based on a hierarchical spatial decomposition of the molecule coupled with local harmonic expansions and translation of these expansions. An even more efficient implementation is possible when the scattering profile is all that is required, as in small angle scattering reconstruction (SAS) of macromolecules. We examine the relationship of the proposed algorithm to existing approximate methods for profile computations, and show that these methods may result in inaccurate profile computations, unless an error bound derived in this paper is used. Our theoretical and computational results show orders of magnitude improvement in computation complexity over existing methods, while maintaining prescribed accuracy.

1 Introduction

Solution small-angle scattering (SAS) of X-ray and neutrons senses the size and shape of a molecular object, and therefore is a powerful analytical tool capable of providing valuable structural information [16, 35]. The ability to study molecules and their interactions under physiological conditions and with essentially no limitation on the size of the system under investigation makes SAS an extremely promising complement to high-resolution techniques such as X-ray crystallography and solution NMR. With the rise of computational power, SAS studies have become increasingly popular, with the applications covering a broad range of problems, including structure refinement of biological macromolecules (proteins, nucleic acids) and their complexes [24, 23, 22, 40], elucidation of conformational ensembles and flexibility in solution [6, 11, 34, 5], validation of the macromolecular structures observed in crystals [11], and even the structure of bulk water [10] and X-ray and neutron diffraction patterns of various powder samples [45]. At the heart of all SAS applications to structural studies in chemistry and biology is the ability to predict the scattering data from a given atomic-level structure. Performing this task accurately and efficiently is critical for successful use of SAS in chemistry and structural biology. Skipping over the less computationally challenging preprocessing involved in SAS, the main problem for computing the scattering profile, I, of a molecular object can be written as the summation of the sinc kernel between all pairs of atoms in N-atom system,

$$\begin{array}{l}I(q)=\sum _{j=1}^N{f}_j(q){\psi }_j(q),{\psi }_j(q)=\sum _{l=1}^N{f}_l(q)s({\mathbf{r}}_j-{\mathbf{r}}_l),\\ s({\mathbf{r}}_j-{\mathbf{r}}_l)=\text{sinc}({qr}_{jl})=\frac{sin({qr}_{jl})}{{qr}_{jl}},r_{jl}=\mid {\mathbf{r}}_j-{\mathbf{r}}_l\mid .\end{array}$$ (1)

where ψ_j are partial sums, q is the scattering wavenumber (q = (4π/λ) sin ϑ, with 2ϑ being the scattering angle and λ the wavelength), r_j is the coordinate of the jth atom, and f_j are the atomic form factors.

The computational cost of directly evaluating Eq. (1) for each q is O(N²). For larger molecular systems the number of atoms considered may be extremely large (N ≥ 10⁵), especially when large crystals, or large molecular complexes are considered. The quadratic computational cost becomes a prohibitive barrier for atomic level application of the Debye formula for such systems. This problem is further compounded, when the Debye sum has to be repeatedly calculated as part of a structural refinement protocol, e.g., [37, 18].

Due to the large computational cost of Eq. (1), numerous methods have been proposed for efficiently computing its approximation. Two approaches are most commonly used. In the first approach, the set distances between the point-sets are assigned to a predetermined number of buckets, and the value of the Debye sum is approximated by summing over the buckets instead of the full set of distances [46, 25, 45]. This approach is faster than direct evaluation if the number of q values is large relative to the number of unique {f_j(q)} values, or the {f_j(q)} dependence of q can be factored out of the summation, which is the case in small angle neutron scattering (SANS). In that case after the initial O(N²) computation of the buckets, each additional summation for a new q value results only in a linear increase in computation time. While faster for certain problems than direct evaluation, the method is still limited by the O(N²) cost of bucketization. Further, the error introduced by this approach has not been carefully ascertained.

The second widely used approach, is to expand the pre-orientationally-averaged scattering formula (from which the Debye formulation is analytically derived) in terms of infinite series of spherical harmonics and then analytically average the series using the orthogonality property of the basis functions [43, 36]. This series is truncated at a conveniently small truncation number p, reducing the computational complexity to O(p²N) [44]. As will be shown below, unless the truncation pP is correctly chosen based on the problem size D a computation that uses a preset constant cutoff can be divergent for the case of large qD, while at small qD the method may perform wasteful computation. As with the histogram (or bucketing) approach, the approximations introduced in the computation are not quantified a priori, and may be significant.

We present a method for computing the Debye sum which has a O(N log N) computational cost, while providing the user with the ability to bound the accuracy of the computation to an arbitrary precision ε. Our algorithm is related to the fast multipole method (FMM), first proposed by [19]. The FMM is a widely used method for solving large scale particle problems arising in many diverse areas (molecular dynamics, astrophysics, acoustics, fluid mechanics, electromagnetics, scattered data interpolation, etc.) because of its ability to achieve linear or O((N + M) log N) computation time for memory dense matrix vector products/sums,

$$\psi =\mathbf{\Psi }\mathbf{f}\iff {\psi }_j=\sum _{l=1}^N\mathrm{\Psi }({\mathit{\rho }}_j,{\mathbf{r}}_l)f_l,j=1,\dots ,M,$$ (2)

to within a prescribed accuracy ε. Here {r_l} and {ρ_j} are sets of N source and M evaluation points and Ψ (ρ, r) is the kernel function. It was first developed for the Coulomb kernel [19], which in 3D is Ψ (ρ, r) = |ρ − r|⁻¹, but has now been successively adapted for a multitude of other kernels, particularly, for the Green’s function of the Helmholtz equation (e.g. [29]). This is closely related to the present problem, since the function s (r) in Eq. (1) also satisfies the Helmholtz equation in three dimensions,

$${\nabla }^{2}s(\mathbf{r})+q^{2}s(\mathbf{r})=0,\mathbf{r}\in {\mathbb{R}}^3.$$ (3)

However, in comparison to the Green’s function for the Helmholtz equation the Debye function is regular, and this results in a significantly simplified and accelerated algorithm.

We provide complexity estimates and tests of the developed algorithms. In addition, we show that our method is significantly faster for even moderately large values of N than all previous methods described, while at the same time providing accurate results, and demonstrate when the methods presented by previous authors may yield incorrect results.

2 SAS intensity computations

Before describing the new algorithm, we establish notation and show the relation between the two basic methods for SAS intensity computations, first, based on the Debye sums, and, second, based on spherical harmonic expansions.

The measured scattering intensity from a system of molecules in solution is proportional to the averaged scattering of a sample volume:

$$I(q)={\langle {\mid A(\mathbf{q})\mid }^2\rangle }_{\mathrm{\Omega }}=\frac{1}{4\pi }{\int }_{S_u}{\mid A(\mathbf{q})\mid }^{2}dS(\mathbf{u}),\mathbf{q}=q\mathbf{u},$$ (4)

where A (q) is the scattering amplitude from the particle in vacuo, 〈〉_Ω denotes that the quantity is averaged over the unit sphere S_u (all orientations), and u is a unit orientation vector. For atomic coordinates r_j = r_js_j, |s_j| = 1, and the corresponding atomic form factors f_j(q), the scattering amplitude of a sample volume is

$$A(\mathbf{q})=\sum _{j=1}^N{f}_j(q)exp(i\mathbf{q}·{\mathbf{r}}_j).$$ (5)

2.1 Debye sums

The first method to compute I (q) is to just insert Eq. (5) into formula (4) and do the integration analytically

$$\begin{array}{l}I(q)=\frac{1}{4\pi }{\int }_{S_u}\sum _{l=1}^N{f}_l(q)exp(i\mathbf{q}·{\mathbf{r}}_l)\sum _{j=1}^N\overline{f_j(q)}exp(-i\mathbf{q}·{\mathbf{r}}_j)dS(\mathbf{s})\\ =\sum _{l=1}^N\sum _{j=1}^N{f}_l(q)\overline{f_j(q)}\frac{1}{4\pi }{\int }_{S_u}exp(i\mathbf{q}·({\mathbf{r}}_l-{\mathbf{r}}_j))dS(\mathbf{s})\\ =\sum _{l=1}^N\sum _{j=1}^N\overline{f_j}{f}_{l}s({\mathbf{r}}_j-{\mathbf{r}}_l)=\sum _{j=1}^N\overline{f_j}{\psi }_j,\end{array}$$ (6)

where ψ_j are provided by Eq. (1).

2.2 Spherical harmonic expansions

The second method exploits expansions over spherical harmonics (e.g. [44]). In this method for a given q we introduce regular spherical basis functions

$$R_n^m(\mathbf{r})=j_n(qr)Y_n^m(\mathbf{s})=j_n(qr)Y_n^m(\theta ,\varphi ),\mathbf{r}=r\mathbf{s}.$$ (7)

Functions $R_n^m(\mathbf{r})$ here are given in spherical coordinates (r, θ, ϕ), r = r (sin θ cos ϕ, sin θ sin ϕ, cos θ), where j_n(qr) are spherical Bessel functions, while $Y_n^m(\theta ,\varphi )$ are the normalized spherical harmonics of degree n and order m,

$$\begin{array}{l}{Y}_n^m(\theta ,\varphi )={(-1)}^m\sqrt{\frac{2n+1}{4\pi }\frac{(n-\mid m\mid )!}{(n+\mid m\mid )!}}{P}_n^{\mid m\mid }(cos\theta )e^{im\varphi },\\ n=0,1,2,\dots ;m=-n,\dots ,n.\end{array}$$ (8)

where $P_n^{\mid m\mid }(\mu )$ are the associated Legendre functions consistent with that in [1], or Rodrigues’ formulae

$$\begin{array}{l}{P}_n^m(\mu )={(-1)}^m{(1-{\mu }^2)}^{m/2}\frac{d^m}{d{\mu }^m}{P}_n(\mu ),n\ge 0,m\ge 0,\\ P_n(\mu )=\frac{1}{2^{n}n!}\frac{d^n}{d{\mu }^n}{({\mu }^2-1)}^n,n\ge 0,\end{array}$$ (9)

where P_n (μ) are the Legendre polynomials.

Using the Gegenbauer series

$$exp(i\mathbf{q}·{\mathbf{r}}_j)=4\pi \sum _{n=0}^{\infty }\sum _{m=-n}^n{i}^n\overline{R_n^m({\mathbf{r}}_j)}{Y}_n^m(\mathbf{u}),$$ (10)

one can rewrite Eq. (5) in the form

$$A(\mathbf{q})=\sum _{n=0}^{\infty }\sum _{m=-n}^n{A}_n^m(q)Y_n^m(\mathbf{u}),A_n^m(q)=4\pi i^n\sum _{j=1}^N{f}_j(q)\overline{R_n^m({\mathbf{r}}_j)}.$$ (11)

and determine the intensity after integration in Eq. (4)

$$I(q)=\frac{1}{4\pi }{\int }_{S_u}{\mid A(\mathbf{q})\mid }^{2}dS(\mathbf{u})=\frac{1}{4\pi }\sum _{n=0}^{\infty }\sum _{m=-n}^n{\mid A_n^m(q)\mid }^2.$$ (12)

In practice the number of modes n can be truncated to p (n = 0, …, p − 1), which provides summation of p² terms in Eq. (12). Hence, to compute directly all needed $A_n^m(q)$ using Eq. (11), one needs O(p²N) operations. Obviously, the second method should be faster than the direct Debye sum computation if p² < N. Note that p is a growing function of q and should be selected according to the error bounds given in this paper.

3 Algorithms for the Debye summation

3.1 Factored expansions of the 3D sinc kernel

3.1.1 Regular spherical basis functions

A regular solution of the Helmholtz equation, ψ(r), can be expanded into a series over spherical basis functions, Eq. (7),

$$\psi (\mathbf{r})=\sum _{n=0}^{\infty }\sum _{m=-n}^n{C}_n^m{R}_n^m(\mathbf{r}),$$ (13)

where $C_n^m$ are expansion coefficients.

In [29] a formula is provided that allows the basis function $R_n^m(\mathbf{r}+\mathbf{t})$ centered at r = −t to be expressed as an infinite series over the basis functions { $R_n^m(\mathbf{r})$} centered at the origin. The Debye function can be related to the regular spherical basis function of order and degree zero, $R_0^0$ as follows

$$s(\mathbf{r})=\frac{sin\mathit{qr}}{qr}=j_0(qr)=\sqrt{4\pi }{R}_0^0(\mathbf{r}).$$ (14)

Using the mentioned formula, the Debye function centered at r = r_s can be expressed over the regular basis functions as

$$s(\mathbf{r}-{\mathbf{r}}_s)=4\pi \sum _{n=0}^{\infty }\sum _{m=-n}^n{R}_n^{-m}({\mathbf{r}}_s)R_n^m(\mathbf{r}).$$ (15)

3.1.2 Error bounds

In practical computations the infinite series or integrals should be replaced by finite series,

$$s(\mathbf{r}-{\mathbf{r}}_s)=4\pi \sum _{n=0}^{p-1}\sum _{m=-n}^n{R}_n^{-m}({\mathbf{r}}_s)R_n^m(\mathbf{r})+{\epsilon }_p,$$ (16)

which create truncation errors ε_p, where p is the “truncation number.” Using the addition theorem for spherical harmonics and the fact that for the Legendre polynomials of arbitrary order |P_n (μ)| ≤ 1, |μ| ≤ 1, we can bound the |ε_p| as follows

$$\begin{array}{l}\mid {\epsilon }_p\mid =\left|4\pi \sum _{n=p}^{\infty }\sum _{m=-n}^n{R}_n^{-m}({\mathbf{r}}_s)R_n^m(\mathbf{r})\right|=\left|\sum _{n=p}^{\infty }{j}_n({qr}_s)j_n(qr)4\pi \sum _{m=-n}^n{Y}_n^{-m}({\theta }_s,{\varphi }_s)Y_n^m(\theta ,\varphi )\right|\\ =\left|\sum _{n=p}^{\infty }(2n+1)j_n({qr}_s)j_n(qr)P_n(cos{\theta }^{\prime })\right|\le \sum _{n=p}^{\infty }(2n+1)\mid j_n({qr}_s)\mid \mid j_n(qr)\mid ,\end{array}$$ (17)

where θ′ is the angle between vectors r_s and r. Let the source r_s and the evaluation point r be enclosed by a sphere of radius a centered at the origin, r ≤ a, r_s ≤ a. Because

$$\mid j_n(qr)\mid \le \frac{{(qr)}^n}{[(2n+1)!!]}\le \frac{{(qa)}^n}{[(2n+1)!!]}$$

(see [1]) the error can be bounded as

$$\begin{array}{l}\mid {\epsilon }_p\mid \le \sum _{n=p}^{\infty }(2n+1)\frac{{(qa)}^{2n}}{{[(2n+1)!!]}^2}\le \sum _{n=p}^{\infty }\frac{{(qa)}^{2n}}{(2n)!!(2n-1)!!}=\sum _{n=p}^{\infty }\frac{{(qa)}^{2n}}{(2n)!}\\ =\frac{{(qa)}^{2p}}{(2p)!}\sum _{n=0}^{\infty }\frac{(2p)!{(qa)}^{2n}}{(2n+2p)!}<\frac{{(qa)}^{2p}}{(2p)!}\sum _{n=0}^{\infty }\frac{{(qa)}^{2n}}{(2n)!}=\frac{{(qa)}^{2p}}{(2p)!}cosh(qa)\le \frac{{(qa)}^{2p}}{(2p)!}{e}^{qa}.\end{array}$$ (18)

Here we used the inequality

$$\frac{(2n)!(2p)!}{(2n+2p)!}=\frac{1}{C_{2n+2p}^{2n}}\le 1,$$ (19)

where $C_{2n+2p}^{2n}$ are the binomial coefficients.

The above estimate shows that for given qa the series converges absolutely. Although the estimate (18) can be applied for any qa, for qa ≫ 1 a tighter bound can be established. The spherical Bessel functions j_n(qa) decay exponentially as functions of η_n = (qa)^−1/3(n − qa + 1/2). Hence, for η_n ≫ 1 the principal term of the sum in the right hand side of Eq. (17) provides a good estimate of the entire sum, i.e.

$$\mid {\epsilon }_p\mid \lesssim 2\left(p+\frac{1}{2}\right)j_p^2(qa),{\eta }_p={(qa)}^{-1/3}(p-qa+\frac{1}{2})\gg 1.$$ (20)

In fact, the large η_n asymptotic behavior is achieved at moderate values of η_n ≳ 2.

The principal term of j_p(qa) of asymptotic expansion for η_p ≫ 1 is [1]

$$j_p(qa)={\left(\frac{\pi }{2qa}\right)}^{1/2}{J}_{p+1/2}(qa)~{\left(\frac{\pi }{2qa}\right)}^{1/2}{2}^{1/3}{\left(p+\frac{1}{2}\right)}^{-1/3}\text{Ai}\left(2^{1/3}{\eta }_p\right),$$ (21)

where J_ν and Ai are the Bessel function of order ν and the Airy function of the first kind. It is proven in [30] that

$$\text{Ai}(x)\le \text{Ai}(0)exp\left(-\frac{2}{3}{x}^{3/2}\right),\text{Ai}(0)=\frac{1}{3^{2/3}\mathrm{\Gamma }(2/3)}<0.3351,x\ge 0,$$ (22)

where Γ is the gamma-function. Combining Eqs (20)–(22), we obtain

$$\begin{array}{l}\mid {\epsilon }_p\mid \lesssim \frac{\pi }{qa}{2}^{2/3}{\text{Ai}}^2(0){\left(p+\frac{1}{2}\right)}^{1/3}exp\left(-\frac{1}{3}{2}^{5/2}{\eta }_p^{3/2}\right)\\ <\frac{1}{qa}{\left[qa+{\eta }_p{(qa)}^{1/3}\right]}^{1/3}exp\left(-\frac{1}{3}{2}^{5/2}{\eta }_p^{3/2}\right).\end{array}$$ (23)

The asymptotic region we are interested in is $p+\frac{1}{2}-qa\ll qa$, which provides η_p(qa)^1/3 ≪ qa. If the error is prescribed so that |ε_p| < ε, we obtain the following expression for p to achieve this error

$$p\gtrsim p_{hf}(\epsilon ,qa)=qa+\frac{1}{2}{\left[\frac{3}{2}log\frac{1}{\epsilon }-log(qa)\right]}^{2/3}{(qa)}^{1/3}.$$ (24)

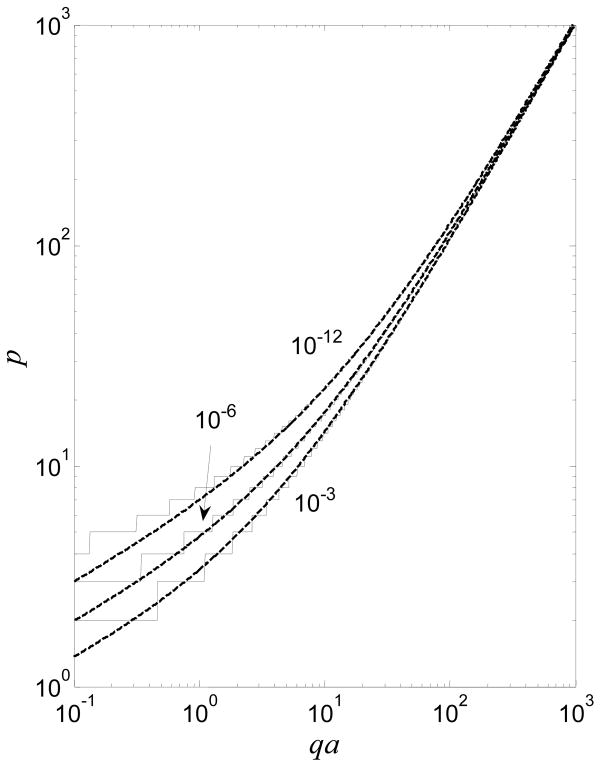
Figure 1 illustrates computations of the series truncation number p using the worst case (r_s = r = a) according to Eq. (17) and the high qa approximation (24). It is not difficult to compute ε_p exactly for arbitrary p, since for r_s = r = a and p = 0 the sum in the right hand side of Eq. (17) is equal to 1 [1], while the values for different p can be computed using the recursion ${\epsilon }_{p+1}={\epsilon }_p-(2p+1)j_p^2(qa)$. In the same figure, the dependence p_hf (ε, qa) provided by Eq. (24) is also plotted. Note that for the computed values of ε and range of qa shown in the figure, the maximum difference between the exact and approximate values of the truncation number p does not exceed 2. We also found that the equation for the truncation number,

Figure 1.

Minimum truncation number p(ε, qa) (solid lines) and its approximation, Eq. (24) (dashed lines) for prescribed values of error ε.

$$p=[p_{hf}(\epsilon ,qa)]+2,$$ (25)

where [] denotes the integer part, provides a value for p not less that the exact truncation number in the considered range of parameters. This demonstrates an excellent agreement with the exact value even at low frequencies, so Eq. (25) can be used for fast and accurate estimation of the truncation number.

Note that dependence of type p ~ qa + f(ε)(qa)^1/3 can be found in the FMM literature for the far field expansions of the Green’s function for the Helmholtz equation (see e.g. [29, 30]). Comparison with those expressions show that for the same error ε the truncation numbers for the Debye kernel are smaller. In fact, the present expression f(ε) is approximately equal to a similar expression g(ε^1/2) used in those publications.

3.2 Algorithm 1: “Middleman” method

The “Middleman” method (e.g. see [29]) is the simplest, but for some cases the fastest O(N + M) method to compute sums of type (2). The algorithm can be described in a few lines. Indeed, from Eqs (2) and (16) we have

$$\begin{array}{l}{\psi }_l=\sum _{j=1}^N{f}_{j}s({\rho }_l-{\mathbf{r}}_j)=\sum _{j=1}^N{f}_j\left[4\pi \sum _{n=0}^{p-1}\sum _{m=-n}^n{R}_n^{-m}({\mathbf{r}}_j)R_n^m({\rho }_l)+{\epsilon }_p\right]\\ =\sum _{n=0}^{p-1}\sum _{m=-n}^n{B}_n^m{R}_n^m({\rho }_l)+{\epsilon }_p^{(\mathit{tot})},B_n^m=4\pi \sum _{j=1}^N{f}_j{R}_n^{-m}({\mathbf{r}}_j),{\epsilon }_p^{(\mathit{tot})}=\sum _{j=1}^N{f}_j{\epsilon }_p.\end{array}$$ (26)

If the computational domain is bounded by a sphere of radius a, and the truncation number p is selected so that an error ${\epsilon }_p^{(\mathit{tot})}$ is tolerated, then O (p²N) operations are needed to compute $B_n^m$, n = 0, …, p − 1, m = −n, …, n and O (p²M) operations are needed to compute all ψ_l, l = 1, …, M. The computation of all required 2p² basis functions $R_n^m({\rho }_l)$ and $R_n^{-m}({\mathbf{r}}_j)$ is done via an O(p²) procedure (using recurrences for the spherical Bessel and associated Legendre functions) [29]. The total complexity of the algorithm is, therefore O(p²(N + M)).

This algorithm is faster than the brute force direct summation only if

$$p^2(N+M)\ll NM.$$ (27)

This condition holds when p is controlled, which means that qa is not very large (see Eq. (24)). More precisely, assuming M = N, and considering p ~ qa = qD/2 (D = 2a) we can rewrite condition (27) as

$$qD\ll {(2N)}^{1/2}.$$ (28)

3.3 Algorithm 2: Hierarchical summation

For larger qD the value of p according to Eq. (24) becomes large leading to increased computational cost. We propose to use a different algorithm, which subdivides the domain hierarchically using local expansions about multiple expansion centers, and achieves lower complexity than the “Middleman” method. Translation operators provide a mathematical foundation for merging expansions of smaller subdomains into a larger domain, while maintaining the validity of the overall expansion. The advantage of the hierarchical method is that only a low order representation of the subdomain is maintained. Optimal conditions on the number of subdomains, or levels of hierarchical space subdivision are obtained to minimize the cost at a given acceptable error, as is commonly done in the FMM.

3.3.1 Translations

In contrast to the FMM for singular kernels, here only local-to-local, or R|R- translations are used, thus significantly simplifying the algorithm. These translations can be expressed by the action of a linear operator that enables change of the origin of the expansions. Consider two expansions of the same function (see Eq. (13)),

$$\psi (\mathbf{r})=\sum _{n=0}^{\infty }\sum _{m=-n}^n{C}_n^m{R}_n^m(\mathbf{r}-{\mathbf{r}}_{\ast 1})=\sum _{n=0}^{\infty }\sum _{m=-n}^n{\widehat{C}}_n^m{R}_n^m(\mathbf{r}-{\mathbf{r}}_{\ast 2}),$$ (29)

where $C_n^m$ and ${\widehat{C}}_n^m$ are expansion coefficients for bases centered at r_*1 and r_*2 respectively. The basis functions centered at r = −t and r = 0 are related to each other via an infinite reexpansion matrix, (R|R)^T (t), whose entries, ${(R\mid R)}_{n^{\prime }{n}^{\prime }}^{m^{\prime }m}(\mathbf{t})$ are given in the appendix (e.g., see Eq. (52)). Knowing this operator one can represent a basis function centered at r = −t in terms of basis functions centered at the origin via

$$R_n^m(\mathbf{r}+\mathbf{t})=\sum _{n^{\prime }=0}^{\infty }\sum _{m^{\prime }=-n^{\prime }}^{n^{\prime }}{(R\mid R)}_{n^{\prime }n}^{m^{\prime }m}(\mathbf{t})R_{n^{\prime }}^{m^{\prime }}(\mathbf{r}),n=0,1,\dots ,m=-n,\dots ,n,$$ (30)

where t is the translation vector. Substituting this reexpansion into the first sum in Eq. (29) one finds that the coefficients ${\widehat{C}}_n^m$ in the new basis are related to the coefficients in the old basis $C_n^m$ as

$${\widehat{C}}_n^m=\sum _{n^{\prime }=0}^{\infty }\sum _{m^{\prime }=-n^{\prime }}^{n^{\prime }}{(R\mid R)}_{{nn}^{\prime }}^{{mm}^{\prime }}(\mathbf{t})C_{n^{\prime }}^{m^{\prime }},\mathbf{t}={\mathbf{r}}_{\ast 2}-{\mathbf{r}}_{\ast 1},n=0,1,\dots ,m=-n,\dots ,n,$$ (31)

since the expansion over the basis $R_n^m(\mathbf{r}-{\mathbf{r}}_{\ast 2})$ is unique. We will stack coefficients into a single vector and use a more compact notation for translation operator as a matrix

$$\widehat{\mathbf{C}}=(\mathbf{R}\mid \mathbf{R})(\mathbf{t})\mathbf{C}.$$ (32)

In a practical numerical realization the series and matrix should be appropriately truncated and the truncation error should be controlled to stay within the error bound.

3.3.2 Data Structures

The algorithm consists of two parts: an initial set-up stage where data structures and other precomputations are performed, followed by a stage where the actual sum is obtained at each evaluation point. In a practical implementation where the sum may be computed for many values of the momentum transfer parameter q, the hierarchical data structures may only need be set up once, while the sum computations done many times for the same distribution of atoms.

All sources and evaluation points are enclosed into a cube with side d and diagonal $D=d\sqrt{3}$, which is termed the “computational domain”. This cube is considered to be a box at level l = 0 in an octree structure [42]. Eight children cubes of level 1 are produced by division of each side of the initial cube by two. The process of division continues down to level l = l_max, whose value is determined from cost optimization considerations. At the end of the process we have an octree of depth l_max. All cubes at each level are indexed using Morton space-filling curve (spatial z–order) [42]. Such an indexing can be obtained using bit interleaving [29]. This indexing also enables fast determination of children and parents of all boxes. Boxes containing sources are called source boxes and boxes containing evaluation points are called receiver boxes.

To avoid wasteful computations, we make the algorithm adaptive, by skipping all empty boxes. Further adaptivity can be introduced as in the FMM [9, 29]; however, the space filling nature of atoms in macromolecules (or crystals) implies that these considerations are likely to be unimportant in practice for profile computation.

In the present problem, since the computation involves all atom pairs, the “sources” r_l and “receivers” ρ_j in Eq. (2) are the same point sets. At the stage of generation of data structure some precomputations of the entries of the translation operators can be performed, which can be stored and reused during the algorithm. We also determine truncation numbers for different levels, p₀, …, p_lmax, consistent with the prescribed computation error and an optimal tree depth. Note that the truncation numbers depend on parameter qD which is reduced by half as the boxes become finer. At level l this should be taken as qD_l, D_l = 2^−lD₀ = 2^−lD. The initial data-structure phase is then followed by the sum evaluation, where initial expansion, and hierarchical summation for aggregation, and dissemination of the intermediate results is performed.

3.3.3 Sum evaluation

The sum evaluation part of the algorithm consists of the following four stages.

1. Initial Expansion: for level l = l_max generate the local expansion for each source about the center, r_b, of box b to which this source belongs and consolidate all such expansions for a given box, to obtain the vector of coefficients C^(b) due to all sources in the box. This can be written formally as

   $${\mathbf{C}}^{(b)}=4\pi \sum _{{\mathbf{r}}_j\in b}{f}_j\overline{\mathbf{R}}({\mathbf{r}}_j-{\mathbf{r}}_b),b=1,\dots .,N_{sb}(l_{max}),$$ (33)

   where R̄ is the vector of complex conjugate basis functions with entries $\left\{R_n^{-m}\right\}=\left\{\overline{R_n^m}\right\}$ (see Eq. (26)) and N_sb(l) is the number of the source boxes at level l.

2. Upward pass (Aggregation): Recursively execute the following procedure for levels l = l_max, …, 1. Translate expansion coefficients for each source box, b′, of level l to its parent box, b, at level l − 1, and consolidate such expansions for each parent box. This can be written formally as

   $${\mathbf{C}}^{(b)}=\sum _{b^{\prime }\in \mathit{Children}(b)}(\mathbf{R}\mid \mathbf{R})({\mathbf{r}}_b-{\mathbf{r}}_{b^{\prime }}){\mathbf{C}}^{(b^{\prime })},b=1,\dots ,N_{sb}(l-1),l=l_{max},\dots ,1,$$ (34)

   where Children(b) is a set of all children boxes for box b.

3. Downward pass (Disaggregation): Recursively execute the following procedure for levels l = 0, …, l_max − 1. Translate expansion coefficients for each receiver box, b′, of level l to its children boxes, b, at level l. This can be written formally as

   $${\mathbf{C}}^{(b)}=(\mathbf{R}\mid \mathbf{R})({\mathbf{r}}_{b^{\prime }}-{\mathbf{r}}_b){\mathbf{C}}^{(b^{\prime })},b^{\prime }\in \mathit{Children}(b),b=1,\dots ,N_{rb}(l),l=l_{max},\dots ,1,$$ (35)

   where N_rb(l) is the number of the receiver boxes at level l.

4. Evaluation: for level l = l_max evaluate the local expansion for each receiver about the center, r_b, of box b to which this receiver belongs. This can be written formally as

   $${\psi }_{j^{\prime }}=\sum _{n=0}^{p-1}\sum _{m=-n}^n{C}_n^{(b)m}{R}_n^m({\rho }_{j^{\prime }}-{\mathbf{r}}_b),{\rho }_{j^{\prime }}\in b,{\mathbf{C}}^{(b)}=\left\{C_n^{(b)m}\right\},b=1,\dots .,N_{rb}(l_{max}).$$ (36)

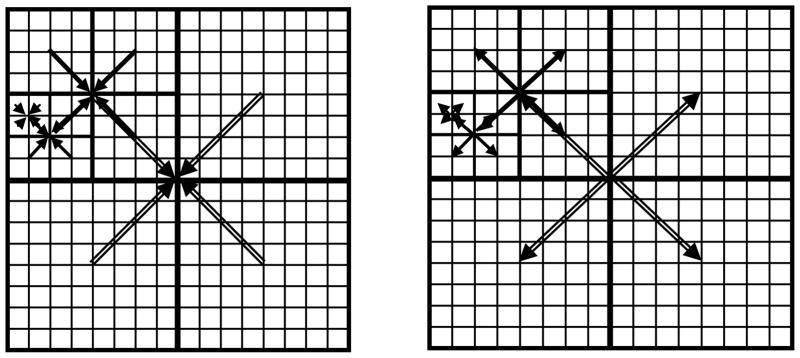
Figure 2 schematically shows (in 2D) the steps 2 and 3 of the above algorithm.

Figure 2.

Schematic illustration of the Upward pass (aggregation, on the left) and the Downward pass (disaggregation, on the right) of the proposed fast hierarchical algorithm.

3.3.4 Translation operators

Steps 2 and 3 of the above algorithm require translation operators. In general, since the translation operator is a matrix relating vectors of length p², in general form it is a p² × p² matrix, and its computation and application are both O(p⁴) operations. More efficient computations of the translation operators for the 3D Helmholtz equations can be found, e.g. in [41, 29, 8]. Using some symmetries of solutions of the Helmholtz equation, our algorithm achieves this in O(p³) operations. While there exist asymptotically faster translation methods (e.g. based on diagonal forms [41]), in the present problem the values of qD are usually not extremely large for which the O(p³) methods are faster than or are competitive with the O(p² log p) methods for these qD values. This is because the asymptotically faster methods have much larger constants associated with them. We first derive error bounds for R|R translation in order to determine proper cutoff for p in the representation of the operator, and then describe the O(p³) algorithm for the translation.

Error bounds

Before deriving more rigorous estimates of the translation errors, let us turn attention to Eq. (17). Assume that the source is located inside a domain of radius a centered at the origin, so that r_s ≤ a. The estimates of the truncation number obtained above for r ≤ a, obviously, are not valid if the evaluation point is far from the expansion center. However, even in this case we can bound the error for p > qa as follows

$$\mid {\epsilon }_p\mid \le \sum _{n=p}^{\infty }(2n+1)\mid j_n({qr}_s)\mid \mid j_n(qr)\mid \le \sum _{n=p}^{\infty }(2n+1)j_n(qa)\mid j_n(qr)\mid .$$ (37)

Since |j_n(qr)| ≤ 1 for any values of n and qr, and for n ≥ p > qa the functions j_n(qa) decay exponentially as functions of η_n, we still can use the principal term for estimation of the entire sum. This provides

$$\mid {\epsilon }_p\mid \lesssim 2\left(p+\frac{1}{2}\right)j_p(qa),{\eta }_p={(qa)}^{-1/3}(p-qa+\frac{1}{2})\gg 1.$$ (38)

This can be compared with Eq. (20). We can slightly modify the high qa error bound to obtain

$$\begin{array}{l}\mid {\epsilon }_p\mid \lesssim {\left(\frac{\pi }{qa}\right)}^{1/2}{2}^{5/6}\text{Ai}(0){\left(p+\frac{1}{2}\right)}^{2/3}exp\left(-\frac{1}{3}{2}^{3/2}{\eta }_p^{3/2}\right)\\ \approx \frac{1}{{(qa)}^{1/2}}{\left[qa+{\eta }_p{(qa)}^{1/3}\right]}^{2/3}exp\left(-\frac{1}{3}{2}^{3/2}{\eta }_p^{3/2}\right).\end{array}$$ (39)

From this we obtain, similarly to Eq. (24),

$$p\gtrsim p_{hf}(\epsilon ,qa)=qa+\frac{1}{2}{\left(3log\frac{1}{\epsilon }+\frac{1}{2}log(qa)\right)}^{2/3}{(qa)}^{1/3}.$$ (40)

This coincides with the result obtained in [29] for the expansion of an arbitrary incident field.

Accurate analysis of the effect of application of truncated translation matrix is provided in Appendix A. This result shows that this error is consistent with (40), while just a small correction to the coefficient of log(qa) may be needed (see Eq. (61)). Such a correction slightly changes p as normally ε < (qa)⁻¹ and 3 log ε⁻¹ is the dominating term. The practical rule is to use Eqs (40) or (61) where p can be increased by a small value, e.g., unity, from the computed value p_hf (ε, qa). Moreover, practical errors are usually two orders of magnitude smaller than those provided by theoretical error bounds, since not all sources and evaluation points are located in the worst positions.

Summarizing, we can state that translations can be performed using truncated rectangular p² × p′² translation matrices, where p and p′ are truncation numbers assigned to levels of the octree to which and from which the translation occurs respectively.

RCR-decomposition

To perform translation by direct matrix-vector multiplication from level to level O(p⁴) operations are needed, assuming that the matrix is precomputed. As it is shown in [29] this method is not fast enough to provide overall O(N log N) fast summation algorithm for 3D spatial distributions, as are encountered here, and at least O(p³) translation methods are needed. Several methods of this complexity are discussed and presented in [29], while we focus on the so-called RCR-decomposition (Rotation - Coaxial translation - Rotation), which first was introduced for the Laplace equation in [47], and further successfully implemented for the Laplace and Helmholtz equation in several FMM realizations (e.g. [29, 28]).

Formally, the RCR-decomposition of the translation matrix can be represented as

$$(\mathbf{R}\mid \mathbf{R})(\mathbf{t})=\mathbf{Ro}{\mathbf{t}}^{-1}(\mathbf{t}/t)(\underset{\_}{\mathbf{R}\mid \mathbf{R}})(t)\mathbf{Rot}(\mathbf{t}/t),$$ (41)

where operator Rot(t/t) provides rotation in the way that the unit vector t/t becomes the z-axis basis vector of the new reference frame, operator (R|R)(t) provides coaxial translation by distance t along the z-axis, and Rot⁻¹ (t/t) is inverse to Rot(t/t) (back rotation). Each of these operators has O (p³) complexity. For a rectangular p² × p′² matrix (R|R) (t) matrices Rot(t/t) and Rot⁻¹ (t/t) are truncated to square matrices p′² × p′² and p² × p², respectively, while matrix (R|R ) (t) has size p² × p′². The saving comes from the fact that all these matrices are block-sparse, as they act only on subspaces of expansion coefficients { $C_n^m$} invariant to rotation (n) and invariant to coaxial translation (m), so the total number of non-zero elements is O(p³) for each matrix. Entries of these matrices can be computed for cost O(p³) using recursive procedures described in [26, 29]. Improved versions of these procedures are provided in Appendix B and C. Note that we found that the recursive process for rotation coefficients described in the above references is unstable for large p ( p ≳ 80). We provide in the appendix an improved process, which we found to be stable even for very large p (tested up to several thousands).

3.3.5 Algorithm complexity and optimization

The algorithm for sum of non-singular functions described above has different complexity and optimization than the FMM which involves summation of singularities. The singularities in the FMM are avoided by building neighborhood data structures, matrix decomposition to sparse (local) and dense (far) parts and a balance between the major costs of the local summation and translations. Translation costs are heavily dominated by the many multipole-to-local translations. These expensive parts of the FMM are all removed in the present algorithm. Also the data structure for the present algorithm is much simpler, since the elimination of multipole to local translation means that we do not need neighborhood lists.

In Step 1, the cost of generation of the initial p_lmax-truncated local-expansion for a single source in the domain of size qD_lmax is $B_{exp}{p}_{l_{max}}^2$, where B_exp is some constant. Similarly, the cost of evaluation of the expansion, in Step 4, is the same for a single receiver point. The total cost of the expansion generation and evaluation for N sources and M receivers is $B_{exp}{p}_{l_{max}}^2(N+M)$.

Cost of a single translation from level l to l − 1 can be estimated as $B_{\text{trans}}{p}_l^3$ using the O(p³) algorithms. (Truncation numbers for levels l and l − 1 are of the same order – for large qD they differ by a factor of two). Here B_trans is some constant of order 1, which for simplicity is taken to be the same for all levels, and which is asymptotically correct for large qD. For estimations we can assume that all boxes in the octree are occupied, as is expected in the macromolecular scattering. In this case at level l we have 8^l boxes. We note then that if all boxes are occupied then the cost of translations in the upward and downward passes of the algorithm are the same, and so the total complexity of the algorithm can be estimated as

$$C_{\text{tot}}=C_{exp}+C_{\text{trans}},C_{exp}=B_{exp}{p}_{l_{max}}^2(N+M),C_{\text{trans}}=2B_{\text{trans}}\sum _{l=1}^{l_{max}}{8}^l{p}_l^3,$$ (42)

where C_exp and C_trans are total expansion and translation costs.

The hierarchical algorithm is appropriate for large qD, where p_l ~ qD_l/2. Since D_l = 2^−lD we have

$$\begin{array}{l}{C}_{\text{trans}}~\frac{1}{4}{B}_{\text{trans}}\sum _{l=1}^{l_{max}}{8}^l{2}^{-3l}{(qD)}^3=\frac{1}{4}{B}_{\text{trans}}{l}_{max}{(qD)}^3,\\ C_{exp}~\frac{1}{4}{B}_{exp}(N+M)2^{-2l_{max}}{(qD)}^2,\\ C_{\text{tot}}=\frac{1}{4}{(qD)}^2\left[B_{exp}(N+M)2^{-2l_{max}}+B_{\text{trans}}{l}_{max}qD\right].\end{array}$$ (43)

It is seen then that for a given qD, N, and M, the function C_trans (l_max) is growing, while the function C_exp (l_max) is decaying, so that there is an optimal value for their sum, C_tot. This minimum can be found simply from the condition that the derivative of C_tot with respect to l_max is zero. This provides the optimum maximum level, $l_{max}^{(\mathit{opt})}$, and the cost of the optimized algorithm, $C_{\text{tot}}^{(\mathit{opt})}(l_{max})$:

$$\begin{array}{l}{l}_{max}^{(\mathit{opt})}=\frac{1}{2}{log}_2\frac{(2log2)B_{exp}(N+M)}{B_{\text{trans}}qD},\\ C_{\text{tot}}^{(\mathit{opt})}=\frac{1}{8}{(qD)}^3{B}_{\text{trans}}{log}_2\frac{(2elog2)B_{exp}(N+M)}{B_{\text{trans}}qD}.\end{array}$$ (44)

So for fixed qD the optimal algorithm is scaled as O(log(N + M)), while for fixed N the scaling is approximately O((qD)³).

Now, if we consider a system of N = M atoms with typical interatomic distance d_a, which occupies a cube with diagonal D and edge $D/\sqrt{3}$ then $D^3=3^{3/2}{Nd}_a^3$ and the above estimates for optimum settings become

$$\begin{array}{l}{l}_{max}^{(\mathit{opt})}=\frac{1}{2}{log}_2\frac{(4log2)B_{exp}{N}^{2/3}}{\sqrt{3}{B}_{\text{trans}}{qd}_a}=O\left(log\left(\frac{N}{{({qd}_a)}^{3/2}}\right)\right),\\ C_{\text{tot}}^{(\mathit{opt})}=\frac{3\sqrt{3}}{8}{({qd}_a)}^3{B}_{\text{trans}}N{log}_2\frac{(4elog2)B_{exp}{N}^{2/3}}{\sqrt{3}{B}_{\text{trans}}{qd}_a}\\ =O\left({({qd}_a)}^{3}Nlog\left(\frac{N}{{({qd}_a)}^{3/2}}\right)\right).\end{array}$$ (45)

This shows that for fixed qd_a and increasing N the number of levels should increase as O(log N ) and the algorithm scales as O(N log N). Another asymptotic behavior is also interesting – for fixed N and increasing qd_a the number of levels should decrease (!), while the total algorithm complexity is approximately scaled as O((qd_a)³). The first fact is only due to the p³ translation scheme, where for large qD the amount of translations (and so the levels) should be reduced in a scheme of minimal complexity. Formally, for qd_a ≳ N^2/3 the number of levels becomes less than 1, in which case one should use the “Middleman” scheme. In practical applications of the small angle scattering qd_a usually does not exceed qd_a ~ 10², which shows that the high qa switch to the “Middleman” algorithm may happen only for relatively small N ≲ 10³. On the other hand, the “Middleman” scheme is not practical for large qD (see Eq. (28)), and such a switch may never happen in practice. For larger systems several levels (l_max ≥ 1) are required.

We note that for small or moderate qD the truncation number does not depend strongly on qD, which affects the optimization estimates. If, for these values of qD we take the truncation number to be some constant that is used for all levels, we can see from Eq. (42) that C_exp does not depend on l_max, while C_trans is a monotonically increasing function of l_max. This means that $C_{\text{tot}}^{(\mathit{opt})}$ is reached for l_max, which is as small as possible, i.e. l_max = 0 and we revert to the “Middleman” scheme.

3.3.6 Combined algorithm

The above complexity consideration shows that a combined algorithm which includes a switch between the “Middleman” and the hierarchical algorithm can perform better for certain values of N and qd_a. Practical values for such a switch depend on the algorithm implementation, hardware, etc. However, we can estimate this region of parameters qualitatively, using Eq. (42), where we can put more accurate estimates for the truncation number and study the parametric dependencies C_tot(qD, N ) numerically. We note then that if the “Middleman” scheme is used, then Eq. (24) should be used, which is different from Eq. (40) (which shows up for small and moderate qD). So, for the qualitative model we assume B_exp = B_trans = 1, M = N, ε = 10⁻⁶, compute cost $C_{\text{tot}}^{(M)}$ of the “Middleman” method as C_exp for l_max = 0 and p provided by Eq. (24), while compute the cost of the hierarchical scheme as C_tot with p_l determined by a = D_l−1/2 and Eq. (40) for optimal l_max (this always overestimates C_trans), which we determine by finding the minimum of C_tot over a range of l_max (we will add const p = 1 to both Eq. (24) and (40) to have at least one term in the expansion even for qa → 0). The switch for any particular values in the parametric space (qD, N) then is determined by the comparison of C_tot and $C_{\text{tot}}^{(M)}$. We note that we also have a “brute force” algorithm of complexity $C_{\text{tot}}^{(B)}=N^2$. In the comparison shown in Fig. 3 we also indicate the cases when this is faster.

Figure 3.

Qualitative map in parameter space (qD, N) of the region of best performance for the three different algorithms to compute Debye sums. The numbers in the graph indicate the optimal maximum level of the octree for the hierarchical algorithm.

For qD ≲ 10 the difference in performance between the Middleman and Hierarchical algorithms is small. Fig. 3 also shows, as expected, that the brute force computations are more efficient than methods based on expansions for large qD and not very large N.

Fig. 4 shows that more accurate estimation of the truncation number substantially affects the scaling of the algorithm with respect to qD (and, in fact to N). While asymptotically the scaling should be close to O((qD)³), such scaling is realized only for very high qD ≳ 10³. For qD ≪ 10³ the dependence of the complexity on this parameter is weaker.

Figure 4.

The cost C_tot of the algorithm for different N and varying qD. The dashed lines are computed using Eq. (44) (M = N) for N = 10⁴, 10⁵, and 10⁶, while the solid lines are computed using dependence (40) of the truncation number on qD.

4 Faster versions for SAS profile computation

The SAS intensity computations based on the Debye sums can be accelerated at least two times (in fact, even more) due to the following facts: 1) for these computations the source and receiver sets are the same; 2) the final result are not the Debye sums, but sums (6). Let us consider modifications of the Middleman method and the Hierarchical algorithm in this case.

4.1 Modified Middleman method for profile computation

Substituting ψ_j from Eq. (26) into Eq. (6) and neglecting the error term, we obtain

$$\begin{array}{l}I(q)=\sum _{i=1}^N\overline{f_i}\sum _{n=0}^{p-1}\sum _{m=-n}^n{B}_n^m{R}_n^m({\mathbf{r}}_i)=\sum _{n=0}^{p-1}\sum _{m=-n}^n{B}_n^m\sum _{i=1}^N\overline{f_i}{R}_n^m({\mathbf{r}}_i)\\ =\frac{1}{4\pi }\sum _{n=0}^{p-1}\sum _{m=-n}^n{B}_n^m\overline{B_n^m}=\frac{1}{4\pi }\sum _{n=0}^{p-1}\sum _{m=-n}^n{\mid B_n^m\mid }^2.\end{array}$$ (46)

It is also not difficult to see by comparison of Eqs. (26) and (11) that

$$A_n^m(q)=4\pi i^n\sum _{j=1}^N{f}_j(q)j_n({qr}_j)\overline{Y_n^m({\mathbf{s}}_j)}=4\pi i^n\sum _{j=1}^N{f}_j(q)R_n^{-m}({\mathbf{r}}_j)=i^n{B}_n^m.$$ (47)

Obviously, due to these relations Eq. (12) turns into identity.

Hence, the Middleman method is simply equivalent to the spherical harmonic expansion method, with properly chosen truncation numbers. To compute the intensity there is no need to evaluate ψ_j, but simply sum up the norms of the expansion coefficients $B_n^m$. The procedure of obtaining these coefficients is twice as cheap as the computation of the Debye sums ψ_j since generation of the expansion has approximately the same cost as its evaluation. In practice the savings may be more substantial, since there is no need to store and retrieve ψ_j from memory to provide a summation of N terms. This equivalency of the methods also establishes the error bound for the spherical expansion method, as p can be selected exactly as for the Middleman method and the error bound (25) can be applied.

4.2 Hierarchical algorithm for profile computation

It should be noticed that the upward pass (34) ends up with expansion coefficients C for the entire domain, which are nothing but coefficients { $B_n^m$} in the Middleman method, since the expansion over the regular basis functions is unique (we note that in all methods we can select the center of the entire domain as the center of the minimal sphere containing all atomic centers r_j to reduce the radius of the domain). Hence, we can use Eq. (46) to compute the intensity. In this case we do not need the downward pass, as all { $B_n^m$} are obtained in the upward pass results. Because the costs of the upward and downward passes are approximately the same, this reduces the computational time by factor 2. As mentioned above the actual savings can be larger, since in this case we do not need to store N quantities ψ_j and provide an additional summation (which for large N may also introduce additional roundoff errors). Such savings can be especially significant at large N (e.g. for N ~ 10⁶ – 10⁷ we observed 3–4 times acceleration of the algorithm).

5 Numerical examples

We implemented the algorithms described above and conducted performance tests in several settings, including random distributions, and profile computation of SAS for randomly generated proteins and for several real biomacromolecules. Since our algorithms were adapted from previous FMM implementations [32] they were already parallelized for shared memory multicore architectures, and it is the setting we describe our results in. The parallelization efficiency was high (≳90%), so the reported computation times can be scaled to different configurations and clusters. In all test cases the source and evaluation points were the same, and double precision computations were used for all algorithms.

5.1 Random distribution tests

In the first test we distributed N = 10³ – 10⁷ source points uniformly and randomly inside a cube, and measured the wall clock time and errors for different qD = 0.1 – 300 and prescribed accuracy ε = 10⁻¹² – 10⁻³. The upper limit for qD is mainly related to the memory of the PC used, while for qD ≳ 400 we also observed an increase in the error due to lack of precision in the computation of the expansions and translation operators. These errors reduced to below the theoretical bounds if the algorithms are executed quadruple-precision. However this increases the time and memory needed, and qD must be selected within this limit for the present code.

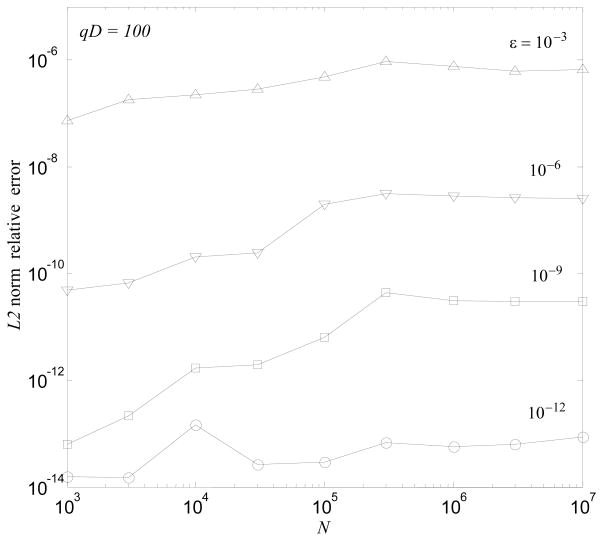
For comparisons and error computations, we compute the exact solution for N_eval ~ 10² randomly selected points from the total set and computed a relative L₂ error for these points. The experimental error performance is always better than the prescribed tolerance, which is based on a worst case analysis, as is confirmed by Fig. 5. The performance depends on the prescribed accuracy and we observed a 2 to 3 times increase of the computational time between the extreme cases of ε = 10⁻³ and 10⁻¹². The cases presented in the figure are the ones typically used in applications. We do not provide the errors for the “Middleman” method, for which the computation time is much larger. However, it is worth mentioning that the errors for that method were usually a few orders of magnitude smaller than for the hierarchical algorithm. In both cases we used a truncation number p = 2 + [p_hf ], where p_hf is provided by Eq. (24) for the former case and Eq. (61) for the latter case.

Figure 5.

Actual L₂-norm relative error of the hierarchical algorithm measured over 100 random sample points. Different curves correspond to different prescribed algorithm errors, ε, shown near the curves.

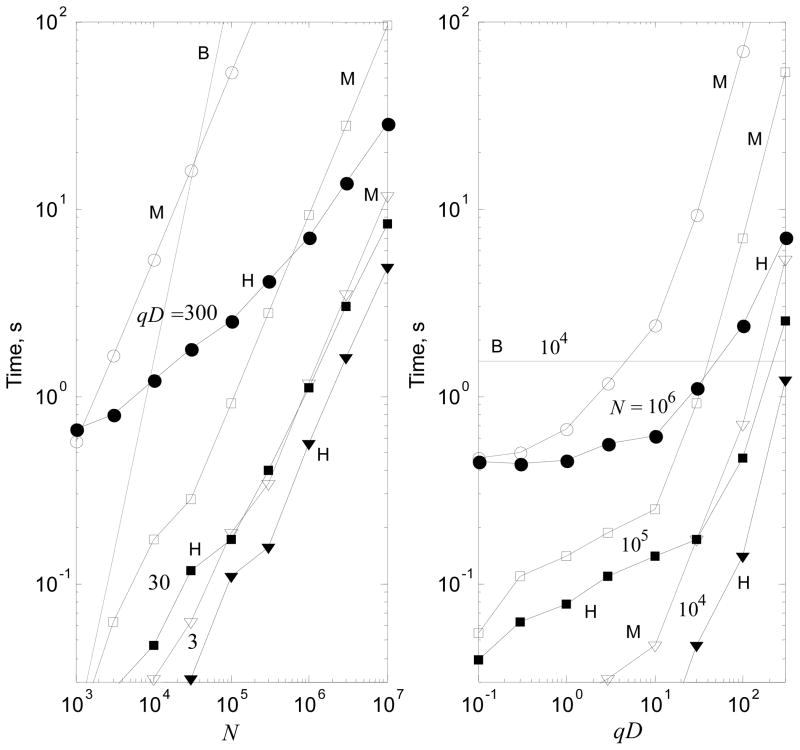
Table 1 shows the wall clock time in seconds for some cases measured for a 4 core PC (Intel Core 2 Extreme QX6700, 2.66GHz, 8GB RAM, all algorithms were parallelized via OpenMP). The prescribed accuracy was ε = 10⁻³. For all these cases the hierarchical algorithm (H) outperforms the “Middleman” (M) and the brute force (B) methods. The two slowest methods have almost perfect time scaling of O(N) and O(N²), respectively, at large run times (the estimated times are shown in the parentheses). In the reported times we excluded the times for computing the data structure and for precomputations which are done separately, and the cost of which is amortized over a set of computations. In any case, such times never exceeded the run time of the algorithm. The times for the hierarchical algorithm were computed for the optimal octree depth, l_max, which was found experimentally. The relation $l_{max}=\left[l_{max}^{(\mathit{opt})}\right]-1$, restricted by l_max < 7 with $l_{max}^{(\mathit{opt})}$ from Eq. (44) for B_exp = B_trans = 1 is in good agreement with the experimentally observed optimal l_max – in almost all cases the difference between them does not exceed 1 (a slight increase is seen for large qD and a decrease for small qD). Fig. 6 displays computed data for an extended range.

Table 1.

Wall clock time (in seconds) for the hierarchical (H), “Middleman” (M), and brute force (B) algorithms. Numbers in italics are estimated rather than computed.

	qD = 0.3			qD = 3			qD = 30			qD = 300
N	H	M	B	H	M	B	H	M	B	H	M	B
104	<0.01	0.023	1.55	0.016	0.031	1.55	0.047	0.17	1.55	1.23	5.38	1.55
105	0.062	0.11	158	0.11	0.19	158	0.17	0.92	158	2.52	53.3	158
106	0.44	0.50	15800	0.56	1.17	15800	1.11	9.22	15800	7.05	533	15800

Figure 6.

The wall clock time for the hierarchical (H), “Middleman” (M), and brute force (B) algorithms at different N and qD. The empty and filled markers correspond to the “M” and “H” algorithms at the same fixed parameter values shown near the curves.

It is seen from Table 1 and Figure 6 that for qD ≲ 10 the performance of the Middleman algorithm is comparable with that of the hierarchical algorithm, while the hierarchical algorithm becomes significantly faster for large qD. Scaling with respect to N of the hierarchical algorithm for a fixed large qD is sublinear (theoretically, O(log N) for large N, but this is not realized). It is also seen in Figure 6 that the qD dependence (for fixed N) in the computed range of parameters does not scale as O((qD)³), but is weaker. Qualitatively, this is consistent with the model shown in Fig. 4 and explainable by the nonlinear dependence of the truncation number on the domain size and momentum transfer parameter for qD ≪ 10³. We also note that the largest time demonstrated by the hierarchical algorithm in the tested range was a relatively quick 28.6 s, even for an extremely large problem size with N = 10⁷ and qD = 300.

5.2 Error in the existing profile computation approaches

We compare our theoretical and computational results to several previously proposed methods for approximate computation of the Debye formula. These methods rely on pseudo-uniform sampling, quadrature integration over a sphere, or harmonic expansion in order to avoid O(N²) computation of the Debye formula. For all these methods a constant value of samples or expansions has been given, which gives them an O(N) complexity. For example, in both SoftWAXS [2] and AquaSAXS [39] a constant value of 900 has been suggested as adequate for most problems sizes, while in AXES [21] a value of 1589 has been used.

The error in these methods can be understood as follows. The integrand for averaging over the sphere in Eq. (12) can be approximated by a p = O(qD) band limited function in a spherical harmonic basis (the value of p appears as a critical value, p = qD/2, of the order of spherical Bessel functions, j_p(qD/2) at which they change behavior from being oscillatory to exponentially decaying functions). This is a natural basis in the space of square integrable functions on a unit sphere. We observe that it is insufficient to use p smaller than qD/2 as this violates Nyquist sampling for an oscillatory function. Since the number of the spherical harmonic basis functions of bandwidth less than p is p², one can see that at least p² = O(q²D²) sampling points are needed to provide an accurate integration for bandwidth p (this is actually a well known result, e.g. see [29] and references cited there). Hence, any accurate quadrature method applied for computation of the intensity for N atoms has complexity O(q²D²N).

The most popular method for solving Eq. (6) is harmonic expansion, introduced in the program CRYSOL [44]. CRYSOL expands the integrand using spherical harmonics, and uses their orthogonality property to analytically account for averaging over all possible orientations. The method assumes a constant cutoff for harmonic order (set to 15 by default, and capped at a maximum of 50), giving the method a complexity of O(N). We demonstrate the potential magnitude of the errors in Table 2 for proteins of various sizes for the harmonic expansion approach suggested in [44], though the error could appear in any of the methods with a fixed sampling in either the order of expansion, or the number of quadrature samples.

Table 2.

The relative errors in the computation of the scattering profile using the “Harmonic” method on our example proteins (no water layer), for a single value of q in Å⁻¹ and prescribed tolerance ε = 10⁻³. p_hf + 2 is the order of the spherical harmonic expansion that should be used in the computation in order to guarantee a relative error of less than ε. The values p = 15 and p = 50, are the default and maximum possible order of spherical expansion in CRYSOL.

	phf + 2			p=15			p=50			p= phf + 2
PDB	q=0.3	q=0.5	q=1.0	q=0.3	q=0.5	q=1.0	q=0.3	q=0.5	q=1.0	q=0.3	q=0.5	q=1.0
6LYZ	14	19	33	1.0e-9	2.0e-4	0.30	0	0	0	9.2e-9	1.9e-7	1.3e-7
2R8S	31	48	89	0.17	0.48	0.79	0	3.5e-9	0.12	7.5e-8	6.8e-8	2.7e-7
3R8N	44	70	132	0.53	0.81	0.94	7.7e-12	0.02	0.48	6.5e-8	2.3e-8	6.5e-8
1FFK	43	68	129	0.60	0.85	0.95	4.5e-13	0.02	0.50	6.0e-8	2.7e-8	3.7e-8
1AON	42	66	124	0.74	0.88	0.98	4.6e-14	0.01	0.59	5.0e-8	1.8e-8	7.4e-8

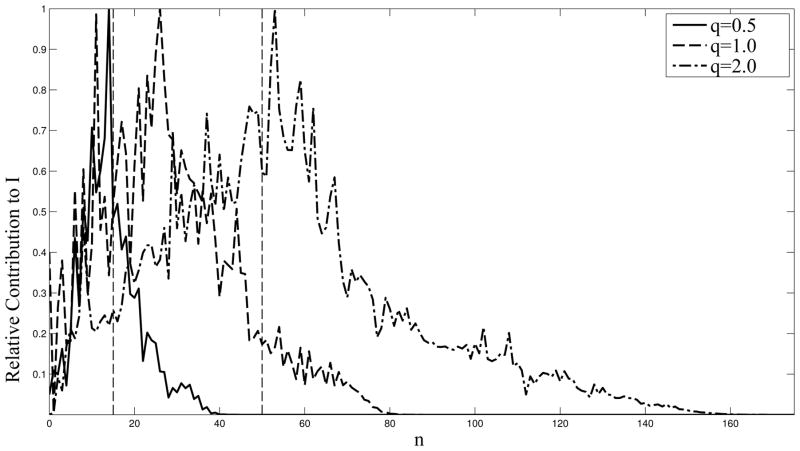
From Table 2 we see that for p = 15 the error becomes significantly larger than experimental errors in the q ≤ 0.5Å ⁻¹ region of the profile, even for relatively small molecules. Note that the errors are related to the maximum distance between atoms, so a sparse pseudo-molecule, like the one used in DAMMIF [18] or in coarse amino-acid level representation, would have large errors even for small N. Increasing the value of p to 50 moves the region of the error to higher values of q and larger proteins, but the error can still be seen. Using the proper value of p as derived in this paper ensures that a low error is achieved throughout. The reason for this error is that terms which are neglected may be non-ngeligible. In Figure 7 we plot the relative contributions to profile values of components for a given value of the spherical harmonic degree for different values of q for a given molecule. It is seen that for q = 0.5Å⁻¹ p = 15 is inadequate, while p = 50, while ensuring accurate computations, pays a penalty of over 50 % of wasteful computations, since a value of p = 40 would have sufficed. A value of p = 80 would have been sufficient for q = 1.0Å⁻¹, but not for q = 2.0 where the right p is about 160. The scaling of p with qD is also seen here.

Figure 7.

The relative contribution (scaled such that the maximum contribution is unity) to profile values by coefficients corresponding to different values of n (the degree of the expansion, n ≤ p, where p is the truncation number). For this particular molecule, a value of p = 15 causes an error for all values of q, while a value of p = 50 is adequate (but wasteful of computations) for the q = 0.5Å ⁻¹ case, but inadequate for q = 1.0Å ⁻¹ or q = 2.0Å ⁻¹. A properly chosen truncation number can ensure accurate computations, while ensuring that no wasteful computations are performed.

Therefore, all the previously described methods, if implemented accurately using the presented error bounds, would have a fundamental theoretical complexity of at least O(q²D²N), which is higher than the theoretical complexity of our proposed hierarchical method, and is identical to our proposed middleman approach.

5.3 Performance Results for Profile Computation

When we compute the SAXS or SANS scattering profile of a molecule, the relation between qD and N is constrained by the atomic density of protein/RNA/DNA complexes in solution, and the range 0Å⁻¹ < q < 0.5Å⁻¹, for which the experimental data are usually collected. In the typical ab initio reconstruction of the scattering profile 50 uniformly spaced samples of q in that range are used. The number of atoms in a molecule can range from around 1000 for small molecules like ubiquitin, to 1, 000, 000+ for ribosomal systems, with the atomic density of such systems being around d = 0.02Å⁻³ (assuming a uniformly packed structure inside a bounding sphere).

In order to show that the performance of the present hierarchical method is orders of magnitude faster for the SAS experimental domain, we first demonstrate the speed of the method on randomly generated proteins as well as several real structures from the PDB database, similar or identical to those which have been previously analyzed by SAS. To generate an N size random protein we randomly assign N atom in a sphere of radius (3N/4dπ)^1/3, while avoiding steric collisions. All proteins structures include the associated hydrogen atoms, which are treated explicitly in the computation.

Below we compare the performance of our hierarchical algorithm at computing an ab initio SAS profile relative to two popular approaches. The first method is a direct summation of Eq. (1) (what we previously referred to as the brute force method) as provided by the function “calculate profile reciprocal” in the IMP v1.0 software package [33], we refer to this method as “IMP”. This method is exact, to within machine precision. The second method is our implementation of the direct harmonic expansion method, similar to the one used in the ATSAS software package, primarily in the popular CRYSOL [44] and DAMMIN/F [18] programs. However, to avoid the errors introduced by a fixed order of expansion, we vary the truncation number according to the value of qD by using Eq. (25). This is denoted as our “Middleman” method for SAS profiles.

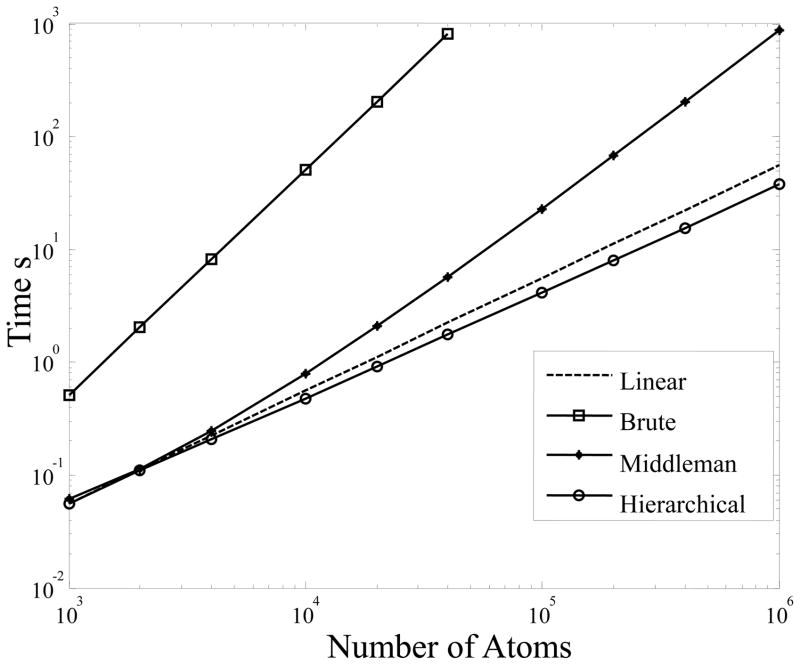
Note that in the performance tests shown below we used IMP as is, without parallelizing the code. The hierarchical and Middleman methods were parallelized. The benchmark cases were executed on a Dual Quad-Core Intel Xeon X5560 CPU @ 2.80GHz 64bit Linux machine with 24GB ECC DDR3 SDRAM (8 cores). The wall clock time was measured for generating a SAS profile made out of 50 uniformly spaced evaluations in the range 0.01Å⁻¹ ≤ q ≤ 0.5Å⁻¹, for randomly generated molecule with atomic density of d = 0.02Å⁻³. The results for the randomly generated data are presented in Fig. 8, while the results for real PDB structures are shown in Table 3.

Figure 8.

Timing results for computation of uniformly spaced 50 point SAS profile on uniformly dense, spherical, randomly generated proteins, with 0.01Å−1 ≤ q ≤ 0.5Å⁻¹ and ε = 10⁻³. “Linear” line represents an ideal O(N) linearly scaled algorithm.

Table 3.

Timing results (in seconds) for (H) Hierarchical, (M) Middleman, (B) Brute force IMP for various sized molecules, where N is the number of atoms. “None” columns represent the molecule without any additional solvation layers. “Layer” includes additional atoms that form an 8Å water layer around the molecule. “Sphere” includes additional atoms from an 8Å water sphere around the molecule. Numbers in italics are estimated. Numbers written as a(b) indicate a number a × 10^b.

	None					Layer					Sphere
PDB	N	D	H	M	B	N	D	H	M	B	N	D	H	M	B
6LYZ	1959	53	0.1	0.5	1.8	6785	70	0.4	2.2	22	16207	69	0.8	5.0	122
2R8S	11556	161	1.0	12.7	65	35923	179	2.0	46	620	329765	178	12	419	5.2(3)
3R8N	93263	246	5.4	206	4.2(3)	214840	263	9.5	533	2.2(4)	1029628	262	40	2532	5.1(5)
1FFK	94876	240	5.7	201	4.3(3)	256100	258	11	606	3.1(4)	880941	256	37	2143	3.7(5)
1AON	118923	230	6.0	235	6.7(3)	255198	247	11	565	3.1(4)	845460	247	33	1875	3.4(5)

From Fig. 8 we can see that our hierarchical method (“H”) is order of magnitude faster than the two previous approaches described here. In fact, the hierarchical method exhibits sub-linear performance for the tested problem domains, while maintaining prescribed accuracy. Table 3 confirms similar performance on actual molecular structures. Overall, the hierarchical method is about 10 to 60 times faster than the Middleman method (“M”) on the benchmark problem domains, while the brute force IMP method (“B”) is computationally infeasible on all but the very small molecules. It is seen that the “H” algorithm for cases with large enough N substantially outperforms the “M” algorithm (which in its turn outperforms the “B” algorithm).

Note that the timing results did not include the translation operators or setting of the data structure for the hierarchical algorithm, since it is amortized over the set of computations or, in the case of translation operators, can be precomputed and stored in a lookup table. Comparison to other existing software requires additional analysis of the pre-processing and post-processing modules, and is therefore outside the scope of this paper.

6 Conclusion

We have developed and demonstrated a fast new algorithm for Debye summations based on hierarchical decomposition of the molecule, coupled with local harmonic expansion and translation. The developed hierarchical algorithm, in all computed cases, is faster and provides significantly better scaling than two of the popular methods tested, while at the same time providing accurate and theoretically provable results to within any prescribed accuracy. In addition, we have provided the theoretical framework for analyzing the accuracy and computational cost of several of the previously proposed methods and demonstrated their computational dependence on N as well as, previously unpublished, dependence on qD. The dependence on qD is critical for computing accurate results, as well as determining the computationally optimal sampling/cutoff value. As shown here, in the harmonic expansion approach (proposed in [44]) an incorrect cutoff introduces significant error in the computation.

Since this is only a prototype, we anticipate further improvements, such as further optimization for our specific problem type, GPU parallelization [31], and algorithmic improvement in local-to-local translations, could further significantly speedup the computation, and are the focus of our future research. The above software is being made part of a new high performance software package, ARMOR, which will also include additional NMR restraints [3, ?]. We hope that the computational improvement of our fast Debye summation method will lead to tighter integration of SAS into current structure refinement protocols.

A Appendix

A.1 Error bounds for translation

Assume that we perform translation from domain of radius a′ centered at r = 0 for which we have truncation number p′ to domain of radius a centered at r = t for which the truncation number is p. We will estimate the translation matrix truncation error for a single sinc source. According to Eq. (16) the expansion coefficients for a single source are $C_{n^{\prime }}^{m^{\prime }}=4\pi R_{n^{\prime }}^{m^{\prime }}({\mathbf{r}}_s)$, n′ = 0, …, p′ − 1, m′ = −n′, …, n′. So for translation of this expansion we have

$${\widehat{C}}_n^m=\sum _{n^{\prime }=0}^{p^{\prime }-1}\sum _{m=-n^{\prime }}^{n^{\prime }}{(R\mid R)}_{{nn}^{\prime }}^{{mm}^{\prime }}(\mathbf{t})C_{n^{\prime }}^{m^{\prime }}=4\pi \sum _{n^{\prime }=0}^{p^{\prime }-1}\sum _{m^{\prime }=-n^{\prime }}^{n^{\prime }}{(R\mid R)}_{{nn}^{\prime }}^{{mm}^{\prime }}(\mathbf{t})R_{n^{\prime }}^{-m^{\prime }}({\mathbf{r}}_s),\mid {\mathbf{r}}_s\mid \le a^{\prime }.$$ (48)

The error in the sinc function computed at point r and its approximation obtained via the truncated translation of the truncated expansion then is

$$\begin{array}{l}{\epsilon }_{{pp}^{\prime }}=s(\mathbf{r}-{\mathbf{r}}_s)-\sum _{n=0}^{p-1}\sum _{m=-n}^n{\widehat{C}}_n^m{R}_n^m(\mathbf{r}-\mathbf{t})\\ =s(\mathbf{r}-{\mathbf{r}}_s)-4\pi \sum _{n=0}^{p-1}\sum _{m=-n}^n\sum _{n^{\prime }=0}^{p^{\prime }-1}\sum _{m^{\prime }=-n^{\prime }}^{n^{\prime }}{(R\mid R)}_{{nn}^{\prime }}^{{mm}^{\prime }}(\mathbf{t})R_{n^{\prime }}^{-m^{\prime }}({\mathbf{r}}_s)R_n^m(\mathbf{r}-\mathbf{t}).\end{array}$$ (49)

Substituting here expansion (16) about center r = t, we obtain

$${\epsilon }_{{pp}^{\prime }}=4\pi \sum _{n=0}^{p-1}\sum _{m=-n}^n\left[R_n^{-m}({\mathbf{r}}_s-\mathbf{t})-\sum _{n^{\prime }=0}^{p^{\prime }-1}\sum _{m^{\prime }=-n^{\prime }}^{n^{\prime }}{(R\mid R)}_{{nn}^{\prime }}^{{mm}^{\prime }}(\mathbf{t})R_{n^{\prime }}^{-m^{\prime }}({\mathbf{r}}_s)\right]R_n^m(\mathbf{r}-\mathbf{t})+{\epsilon }_p.$$ (50)

Note now that by definition of the translation coefficients and symmetry ${(R\mid R)}_{{nn}^{\prime }}^{-m,-m^{\prime }}(-\mathbf{t})={(R\mid R)}_{n^{\prime }n}^{m^{\prime }m}(\mathbf{t})$ (see [29]), we have

$$R_n^{-m}({\mathbf{r}}_s-\mathbf{t})=\sum _{n^{\prime }=0}^{\infty }\sum _{m^{\prime }=-n^{\prime }}^{n^{\prime }}{(R\mid R)}_{{nn}^{\prime }}^{-{mm}^{\prime }}(-\mathbf{t})R_{n^{\prime }}^{m^{\prime }}({\mathbf{r}}_s)=\sum _{n^{\prime }=0}^{\infty }\sum _{m^{\prime }=-n^{\prime }}^{n^{\prime }}{(R\mid R)}_{n^{\prime }n}^{m^{\prime }m}(\mathbf{t})R_{n^{\prime }}^{m^{\prime }}({\mathbf{r}}_s).$$ (51)

We also have the following integral representation of the translation coefficients [29]

$${(R\mid R)}_{{nn}^{\prime }}^{{mm}^{\prime }}(\mathbf{t})=i^{n-n^{\prime }}{\int }_{S_u}{e}^{iq\mathbf{s}·\mathbf{t}}{Y}_{n^{\prime }}^{m^{\prime }}(\mathbf{s})Y_n^{-m}(\mathbf{s})dS(\mathbf{s}).$$ (52)

Substituting Eqs (51) and (52) into Eq. (50) and using the addition theorem for spherical harmonics, we obtain

$${\epsilon }_{{pp}^{\prime }}=\frac{1}{4\pi }\sum _{n=0}^{p-1}\left[\sum _{n^{\prime }=p^{\prime }}^{\infty }(2n^{\prime }-1)j_{n^{\prime }}({qr}_s)i^{n-n^{\prime }}(2n+1)j_n(q\mid \mathbf{r}-\mathbf{t}\mid ){\int }_{S_u}{e}^{iq\mathbf{s}·\mathbf{t}}{P}_{n^{\prime }}(\mathbf{s}·\frac{{\mathbf{r}}_s}{r_s})P_n\left(s·\frac{\mathbf{r}-\mathbf{t}}{\mid \mathbf{r}-\mathbf{t}\mid }\right)dS(\mathbf{s})\right]+{\epsilon }_p.$$ (53)

Since

$$\left|\frac{1}{4\pi }{\int }_{S_u}{e}^{iq\mathbf{s}·\mathbf{t}}{P}_{n^{\prime }}(\mathbf{s}·\frac{{\mathbf{r}}_s}{r_s})P_n\left(\mathbf{s}·\frac{\mathbf{r}-\mathbf{t}}{\mid \mathbf{r}-\mathbf{t}\mid }\right)dS(s)\right|\le \frac{1}{4\pi }{\int }_{S_u}\left|e^{iq\mathbf{s}·\mathbf{t}}{P}_{n^{\prime }}(\mathbf{s}·\frac{{\mathbf{r}}_s}{r_s})P_n\left(\mathbf{s}·\frac{\mathbf{r}-\mathbf{t}}{\mid \mathbf{r}-\mathbf{t}\mid }\right)\right|dS(\mathbf{s})\le 1,$$ (54)

the error can be bounded as

$$\mid {\epsilon }_{{pp}^{\prime }}\mid \le \sum _{n=0}^{p-1}(2n+1)\mid j_n(q\mid \mathbf{r}-\mathbf{t}\mid )\mid \sum _{n^{\prime }=p^{\prime }}^{\infty }(2n^{\prime }+1)\mid j_{n^{\prime }}({qr}_s)\mid +\mid {\epsilon }_p\mid .$$ (55)

Since qr_s ≤ qa′, p′ > qa′ the second sum can be bounded by |ε_p′| given by Eq. (38) (where primes should be placed near a and p). The first sum can be bounded using |j_n(q |r − t|)| ≤ 1, in which case the sum of odd numbers from 0 to 2p − 1 is p² and we obtain

$$\mid {\epsilon }_{{pp}^{\prime }}\mid \le p^2\mid {\epsilon }_{p^{\prime }}\mid +\mid {\epsilon }_p\mid .$$ (56)

Note that the last term here, |ε_p|, can be ignored, since for p given by Eq. (40) actual expansion error (23) is approximately square of error (39). We also note that coefficient p² of the first term can be improved due to the following lemma.

Lemma 1

For x ≥ 0 the following bound holds ${\sum }_{n=0}^{\infty }(2n+1)\mid j_n(x)\mid <C_1+C_{2}x$, where C₁ and C₂ are some real positive numbers.

Proof

For n > x functions j_n(x) decay exponentially and the series converges. So

$$\begin{array}{l}\sum _{n=0}^{\infty }(2n+1)\mid j_n(x)\mid =\sum _{n=0}^{[x]}(2n+1)\mid j_n(x)\mid +\epsilon (x),\epsilon (x)\\ =\sum _{n=[x]}^{\infty }(2n+1)\mid j_n(x)\mid <C(2x+1)j_x(x),\end{array}$$ (57)

where C is some constant of order 1. Since j_x(x) is a monotonic decaying function of x, we have j_x(x) < j₀(0) = 1. The first sum can be bounded since the function in the right hand side is continuous and has some maximum on the interval [0, 1], while for x > 1, 0 < n ≤ [x] we have |j_n(x)| < B/x, where B is some constant. Hence,

$$\sum _{n=0}^{[x]}(2n+1)\mid j_n(x)\mid <\frac{B}{x}\sum _{n=0}^{[x]}(2n+1)=\frac{B}{x}{([x]+1)}^2<Bx+B_1,x>1.$$ (58)

This completes the proof.

Remark 2

We computed this function numerically for 10⁻² < x < 10³ and found that C₁ < 2, C₂ < 1.

So, the error can be bounded as

$$\mid {\epsilon }_{{pp}^{\prime }}\mid \le (C_1+C_{2}p)\mid {\epsilon }_{p^{\prime }}\mid ~p\mid {\epsilon }_{p^{\prime }}\mid .$$ (59)

where C₁ and C₂ are some constants of order 1. For large qa we have p ~ qa which is two times larger or smaller than p′ ~ qa′. Using Eq. (39) we have then

$$\mid {\epsilon }_{{pp}^{\prime }}\mid \lesssim {(q{a}^{\prime })}^{5/6}exp\left(-\frac{1}{3}{2}^{3/2}{\eta }_{p^{\prime }}^{3/2}\right),$$ (60)

which provides a slightly larger truncation number for a region of size a (we replaced p′ with p and qa′ with qa).

$$p\gtrsim p_{hf}(\epsilon ,qa)=qa+\frac{1}{2}{\left(3log\frac{1}{\epsilon }+\frac{5}{2}log(qa)\right)}^{2/3}{(qa)}^{1/3}.$$ (61)

A.2 The coaxial translation

Coaxial translation can be described as

$${\widehat{C}}_n^m=\sum _{n^{\prime }=\mid m\mid }^{p^{\prime }-1}{\left(\underset{\_}{R\mid R}\right)}_{{nn}^{\prime }}^m(t)C_{n^{\prime }}^m,m=0,\pm 1,\dots ,\pm (min(p,p^{\prime })-1),n=0,1,\dots ,p-1.$$ (62)

(in the general matrix ${\left(\underset{\_}{R\mid R}\right)}_{{nn}^{\prime }}^{{mm}^{\prime }}=0$ for m′ ≠ m). Recursive computations of ${\left(\underset{\_}{R\mid R}\right)}_{{nn}^{\prime }}^m(t)$ can be performed only for non-negative |m| and for n ≥ n′ (or n′ ≥ n) due to symmetries

$${\left(\underset{\_}{R\mid R}\right)}_{{nn}^{\prime }}^m(t)={\left(\underset{\_}{R\mid R}\right)}_{{nn}^{\prime }}^{-m}(t)={(-1)}^{n+n^{\prime }}{\left(\underset{\_}{R\mid R}\right)}_{n^{\prime }n}^m(t).$$ (63)

The recursive process starts with the initial values

$${\left(\underset{\_}{R\mid R}\right)}_{n0}^0(t)={(-1)}^n\sqrt{2n+1}{j}_n(qt),n=0,1,\dots$$ (64)

Advancement in m can be performed using

$$b_{m+1}^{-m-1}{\left(\underset{\_}{R\mid R}\right)}_{n,m+1}^{m+1}=b_n^{-m-1}{\left(\underset{\_}{R\mid R}\right)}_{n-1,m}^m-b_{n+1}^m{\left(\underset{\_}{R\mid R}\right)}_{n+1,m}^m,n=m+1,m+2,\dots$$ (65)

Advancement in n′ can be performed using

$$a_n^m{\left(\underset{\_}{R\mid R}\right)}_{n,n^{\prime }+1}^m=a_{n^{\prime }-1}^m{\left(\underset{\_}{R\mid R}\right)}_{n,n^{\prime }-1}^m-a_n^m{\left(\underset{\_}{R\mid R}\right)}_{n+1,n^{\prime }}^m+a_{n-1}^m{\left(\underset{\_}{R\mid R}\right)}_{n-1,n^{\prime }}^m,n^{\prime }=m,m+1,\dots$$ (66)

In Eqs (65) and (66) the recursion coefficients are

$$\begin{array}{l}{a}_n^m=\{\begin{array}{c}\sqrt{\frac{(n+1+m)(n+1-m)}{(2n+1)(2n+3)}},n\ge \mid m\mid ,\\ 0,n<\mid m\mid ,\end{array},\\ b_n^m=\{\begin{array}{c}sgn(m)\sqrt{\frac{(n-m-1)(n-m)}{(2n-1)(2n+1)}},0\le m\le n,\\ 0,n<\mid m\mid .\end{array}\end{array}$$ (67)

where sgn(m) is defined as

$$sgn(m)=\{\begin{array}{cc}1,& m\ge 0,\\ -1,& m<0.\end{array}$$ (68)

A.3 Expressions for the rotation of coefficients

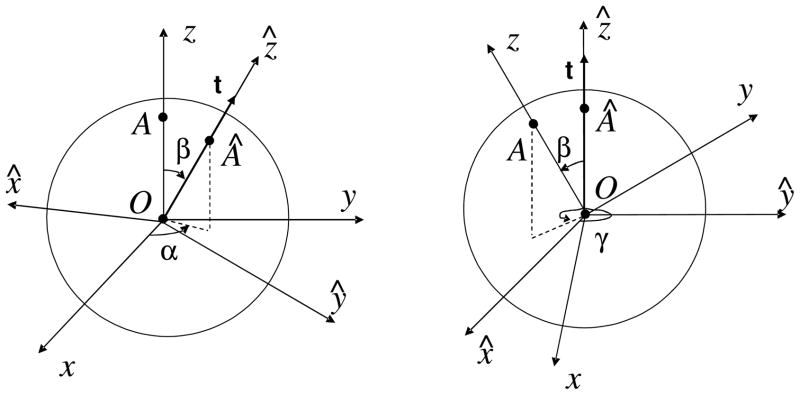
In general, an arbitrary rotation transform can be specified by three Euler angles of rotation. For rotation of spherical harmonics it may be more convenient to use slightly modified Euler angles, and use angles α, β, γ which are related to the spherical polar angles (θ_t, ϕ_t) of the unit vector t/t = (sin θ_t cos ϕ_t, sin θ_t sin ϕ_t, cos θ_t) as β = θ_t, α = ϕ_t (see Fig. 9). The original axis z in the rotated reference frame has spherical polar angles (β, γ), which is the definition of the third rotation angle. Since the rotation transform is a function of the rotation matrix Q(α, β, γ) for which Q⁻¹(α, β, γ) = Q(γ, β, α), we describe only the forward rotation, since the inverse rotation simply exchanges angles α and γ.

Figure 9.

Rotation specified by angles α, β, and γ, where α and β are the spherical polar angles of the translation vector t in the original reference frame.

The rotation transform can be described by

$${\stackrel{\sim }{C}}_n^m=e^{-im\gamma }\sum _{m^{\prime }=-n}^n{H}_n^{{mm}^{\prime }}(\beta )e^{{im}^{\prime }\alpha }{C}_n^{m^{\prime }},n=0,1,\dots ,p-1,m^{\prime }=-n,\dots ,n,$$ (69)

where $H_n^{{mm}^{\prime }}(\beta )$ are the entries of a real dense matrix that can be computed recursively.

The basic recursion used for computation is derived in [29]

$$\begin{array}{l}{d}_n^{m-1}{H}_n^{m-1,m^{\prime }}-d_n^m{H}_n^{m+1,m^{\prime }}=d_n^{m^{\prime }-1}{H}_n^{m,m^{\prime }-1}-d_n^{m^{\prime }}{H}_n^{m,m^{\prime }+1},\\ d_n^m=\frac{1}{2}sgn(m){[(n-m)(n+m+1)]}^{1/2},m=-n,\dots ,n,\end{array}$$ (70)

and sgn(m) is provided by Eq. (68). This recursion, however, should be applied carefully, due to potential recursion instabilities. For angles 0 < β < π/2 the maximum values of $H_n^{{mm}^{\prime }}(\beta )$ are reached on the main diagonal m′ = m and subdiagonals m′ = m ± 1. Figure 10 illustrates organization of the recursive process in this case (for the boundary points, m = n, recursion coefficients $d_n^m=0$). The values on the diagonals and subdiagonals are computed via the axis flip transform, which corresponds to β = π/2:

$$H_n^{{mm}^{\prime }}(\beta )=\sum _{\nu =-n}^n{H}_n^{m\nu }\left(\frac{\pi }{2}\right)H_n^{m^{\prime }\nu }\left(\frac{\pi }{2}\right)cos\left(\nu \beta +\frac{\pi }{2}(m+m^{\prime })\right).$$ (71)

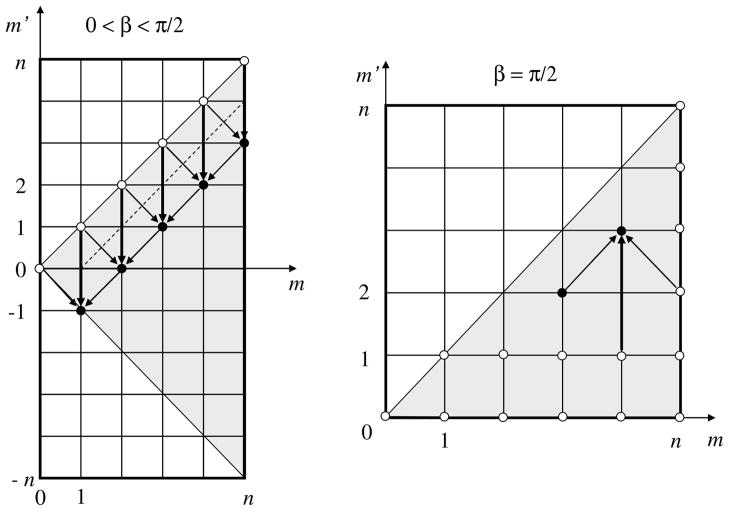
Figure 10.

A scheme for stable recursive computation of the rotation coefficients. On the left, the process of recursive computation of the values of the coefficient for different values of m, m′ (displayed on a grid) is shown. The ● values are computed from the main diagonal for which the values are directly obtained. These are indicated by ○. To compute values at all nodes in the shaded area one needs the values on the subdiagonal (the dashed line). These values are obtained via the flip transform from the rotation coefficients for β = π/2, which are computed recursively via the process shown on the right. Initial values at the nodes marked by ○ are computed using analytical formulae. The values of the rotation coefficients in the entire domain m′, m = −n, …, n can be obtained from the values in the shaded domains using symmetry relations.

Even though we could use this equation to compute all $H_n^{{mm}^{\prime }}(\beta )$, because the cost of computation will be O (p⁴), we only use it for computation of the diagonal and subdiagonal coefficients for an O (p³) procedure. This requires knowledge of the coefficients $H_n^{{mm}^{\prime }}(\pi /2)$. A stable recursive process based on Eq. (70) can be applied (Fig. 10). To start this process the values of $H_n^{{mm}^{\prime }}(\pi /2)$ are needed for m′ = 0, 1 and m = 0, …, n, as well as the values for m = n and m′ = 0, …, n. These can be found from analytical expressions for $H_n^{{mm}^{\prime }}(\beta )$

$$\begin{array}{l}{H}_n^{m^{\prime }0}={(-1)}^{m^{\prime }}\sqrt{\frac{(n-\mid m^{\prime }\mid )!}{(n+\mid m^{\prime }\mid )!}}{P}_n^{\mid m^{\prime }\mid }(cos\beta ),n=0,1,\dots ,m^{\prime }=-n,\dots ,n,\\ H_n^{m^{\prime }n}={\epsilon }_n{\epsilon }_{-m^{\prime }}{\left[\frac{(2n)!}{(n-m^{\prime })!(n+m^{\prime })!}\right]}^{1/2}{cos}^{n+m^{\prime }}\frac{1}{2}\beta {sin}^{n-m^{\prime }}\frac{1}{2}\beta ,{\epsilon }_m=\{\begin{array}{c}1,m\ge 0\\ {(-1)}^m,m\ge 0\end{array},\end{array}$$ (72)

and the recurrence [29]

$$\begin{array}{l}{H}_{n-1}^{m^{\prime },m+1}=\frac{1}{b_n^m}\left\{\frac{1}{2}\left[b_n^{-m^{\prime }-1}(1-cos\beta )H_n^{m^{\prime }+1,m}-b_n^{m^{\prime }-1}(1+cos\beta )H_n^{m^{\prime }-1,m}\right]-a_{n-1}^{m^{\prime }}sin\beta H_n^{m^{\prime }m}\right\}\\ n=2,3,\dots ,m^{\prime }=-n+1,\dots ,n-1,m=0,\dots ,n-2,\end{array}$$ (73)

where $a_n^m$ and $b_n^m$ are provided by Eq. (67). For small and moderate n this recursion can be used to obtain all rotation coefficients immediately, as it was done in [29], but for large n this is not stable. So we use Eqs (72) and (73) only for β = π/2 and Eq. (73) only for m = 0 to obtain $H_n^{m^{\prime }1}(\pi /2)$. Note than that the following symmetries are used for faster computations

$$H_n^{m^{\prime }m}(\beta )=H_n^{{mm}^{\prime }}(\beta ),H_n^{m^{\prime }m}(\beta )=H_n^{-m^{\prime },-m}(\beta ),H_n^{m^{\prime }m}(\pi -\beta )={(-1)}^{n+m+m^{\prime }}{H}_n^{-m^{\prime },m}(\beta ).$$ (74)

The last equation provides an additional symmetry for β = π/2, while for other β it can be used to reduce all computations to the range 0 ≤ β ≤ π/2. In fact, for the present algorithm only rotations with β = π/4 and β = 3π/4 are needed. So the latter can be reduced to the former case, and only the constant coefficients $H_n^{m^{\prime }m}(\pi /4)$ are needed. In principle, these coefficients can be precomputed and stored to reduce the run time.