Kinetic signatures of microRNA modes of action

MicroRNAs (miRNAs) are important regulators of gene expression affecting a great variety of biological processes. A variety of mechanisms have been proposed to explain the mechanism by which miRNAs exert their role. In this paper, the authors describe a mathematical tool to discriminate between different mechanisms of action of microRNAs (translational inhibition and/or target mRNA decay). This mathematical model combines nine known mechanisms of miRNA action and estimated the model parameters from the literature. They propose a model in which several mechanisms may operate at the same time, the resulting apparent mechanism depending on the “sensitive” or “dominant” parameters of the target mRNA system itself. Furthermore, the authors developed a computational tool for discriminating among different possible individual mechanisms of miRNA action based on translation kinetics data that can be experimentally measured. Their results highlight the need to consider miRNA binding to its mRNA targets as well as translation kinetics to interpret data on the mechanism of miRNA action.

Abstract

MicroRNAs (miRNAs) are key regulators of all important biological processes, including development, differentiation, and cancer. Although remarkable progress has been made in deciphering the mechanisms used by miRNAs to regulate translation, many contradictory findings have been published that stimulate active debate in this field. Here we contribute to this discussion in three ways. First, based on a comprehensive analysis of the existing literature, we hypothesize a model in which all proposed mechanisms of microRNA action coexist, and where the apparent mechanism that is detected in a given experiment is determined by the relative values of the intrinsic characteristics of the target mRNAs and associated biological processes. Among several coexisting miRNA mechanisms, the one that will effectively be measurable is that which acts on or changes the sensitive parameters of the translation process. Second, we have created a mathematical model that combines nine known mechanisms of miRNA action and estimated the model parameters from the literature. Third, based on the mathematical modeling, we have developed a computational tool for discriminating among different possible individual mechanisms of miRNA action based on translation kinetics data that can be experimentally measured (kinetic signatures). To confirm the discriminatory power of these kinetic signatures and to test our hypothesis, we have performed several computational experiments with the model in which we simulated the coexistence of several miRNA action mechanisms in the context of variable parameter values of the translation.

INTRODUCTION

MicroRNA (miRNAs) are short (21–23-nt-long) noncoding RNAs that negatively regulate gene expression. MiRNAs are currently considered to be modulators of a wide variety of biological pathways, including development, differentiation, and oncogenesis. Mature miRNAs are processed from long transcripts and are incorporated into the RISC complex, whose key component is an Argonaute protein. MiRNAs regulate gene expression by guiding the RISC complex toward specific target mRNAs. The exact mode of action of the RISC complex is still a matter of debate. Several distinct mechanisms have been reported in many studies (Esquela-Kerscher and Slack 2006; Kloosterman and Plasterk 2006; Jackson and Standart 2007; Pillai et al. 2007; Eulalio et al. 2008a; Filipowicz et al. 2008; Bartel 2009; Carthew and Sontheimer 2009; Chekulaeva and Filipowicz 2009; Ghildiyal and Zamore 2009; Moazed 2009; and others) (summarized in Table 1; Fig. 1), the experimental data and subsequent conclusions of which are highly controversial. Several attempts to resolve the contradictions have been made, but they do not provide satisfactory explanations for all published observations (Valencia-Sanchez et al. 2006; Jackson and Standart 2007; Eulalio et al. 2008a; Farazi et al. 2008; Filipowicz et al. 2008; Kozak 2008; Iwasaki et al. 2009).

TABLE 1.

Main experimental data supporting the proposed mechanisms of microRNA action

FIGURE 1.

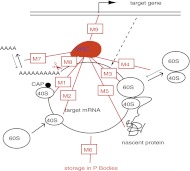
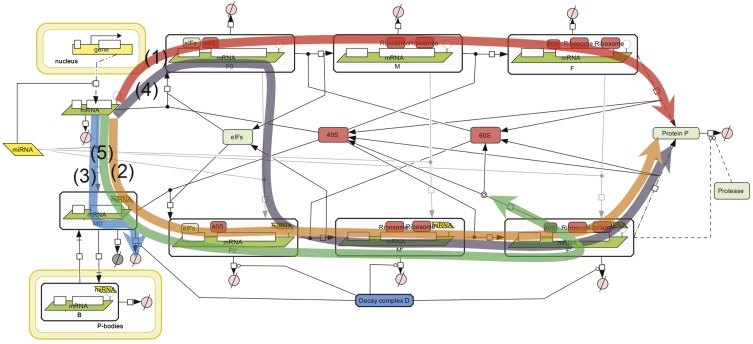
Possible mechanisms of microRNA action. (Black) The main steps of gene expression from DNA to protein. (Red) The RISC complex and the various levels at which it can inhibit gene expression; the mechanisms (M) are numbered as in Table 1 and are described in detail there.

We will outline the proposed mechanisms and contradictory experimental results from different published reports. Our analysis begins with the arguable premise that multiple miRNA mechanisms of action can coexist.

Firstly, the level at which the microRNA acts (transcriptional, translational, etc.) is still debated. Gene repression by microRNAs at the level of mRNA translation is the most frequently reported mechanism and includes repression of initiation and/or elongation, ribosome drop-off, and nascent polypeptide degradation. Gene repression by microRNAs at the level of mRNA stability (before translation) includes microRNA-mediated mRNA decay, sequestration of target mRNAs in P-bodies (cytoplasmic structures in which the mRNA degradation machinery is enriched), and rarely in animals, but frequently in plants, target mRNA cleavage. Moreover, some observations suggest that miRNAs can also act at the transcriptional level by mediating chromatin reorganization, which involves mechanisms strikingly different from the repression modes already mentioned. Finally, transcriptional (Kim et al. 2008; Place et al. 2008) and translational (Vasudevan and Steitz 2007; Orom et al. 2008) activation by microRNAs have also been reported. However, currently the best-documented mechanisms are the action of microRNAs at the level of initiation of translation and target mRNA decay (degradation).

Second, the issue of miRNA mode(s) of action is controversial due to the fact that the ground on which some of the conclusions are based is shaky. Here we list some of the most striking illustrations of this:

1. Though inhibition of translation initiation is the most frequently proposed mode of microRNA action, the experimental data supporting this mechanism are discordant. For example, it has been proposed that repression of initiation may occur through the binding of AGO proteins to the mRNA cap sequence, which would physically exclude the initiation factor eIF4E (Kiriakidou et al. 2007). However, this interpretation has been weakened by recent findings indicating that the eIF4E-like domain in AGO proteins cannot be involved in cap binding, because it is occupied by an AGO partner protein, GW182; moreover, crystallographic analysis has suggested that the folding of AGO proteins precludes an interaction with the cap sequence (Eulalio et al. 2008b; Kinch and Grishin 2009).

   The observations that mRNAs with an IRES (internal ribosome entry site) or A-caps are insensitive to microRNAs, which provided strong support for this model, have also been challenged, as some mRNAs were shown to be repressed by a microRNA even though their translation is cap independent (Petersen et al. 2006; Lytle et al. 2007; Baillat and Shiekhattar 2009; Karaa et al. 2009). The issue looks especially controversial in the case of VEGF protein, which is endogenously regulated by miR-16. VEGF protein was shown to be translated from two possible IRES, but only one of these IRES allows inhibition by miR-16, whereas the other does not (Karaa et al. 2009). Furthermore, Kozak (2008) is very critical about the results of IRES experiments and any conclusions arising from them, instead proposing that different IRES might affect mRNA translation at the upstream level of splicing, rather than by providing alternative initiation sites.

2. It was shown that eIF6, an inhibitor of 60S joining (a later step of translation initiation), is required for microRNA action (Chendrimada et al. 2007), thus supporting a mechanism of microRNAs action at the level of 60S subunit joining, but this conclusion has been called into question by other studies (Eulalio et al. 2008b).

3. Kong et al. (2008) reported that the same mRNA targeted by a given microRNA was found to be regulated either at the initiation or at the elongation level, depending on the promoter from which the mRNA was transcribed. However, other investigators (Gu et al. 2009) later concluded that repression occurs at the level of elongation with the “initiation” promoter used by Kong and colleagues.

4. In Lytle et al. (2007), different mechanisms were found to be implicated when different transfection methods were used.

5. According to Olsen and Ambros (1999), analysis of the polysomal distribution of target mRNAs supports a silencing mechanism operating during the elongation step of translation. Based on the same analysis, degradation of nascent polypeptide has also been proposed (Nottrott et al. 2006). However, the polysomal profiles in these two studies were very similar.

6. Several groups have reported that degradation and translational arrest can be coupled in various experimental systems (Pillai et al. 2005; Wu et al. 2006; Eulalio et al. 2007b, 2008b, 2009), but the details of this combination are not completely understood: Some mRNA are repressed mostly at the translational level, others mostly at the stability level (with or without a requirement for concurrent translation inhibition), and some at both levels (Aleman et al. 2007). However, mRNA decay might be a consequence of translational repression, or alternatively, the two mechanisms might function in parallel (Eulalio et al. 2008a,b; Zipprich et al. 2009). Eulalio et al. (2008b) have concluded that the relative contributions of translational repression and decay depend on the length of the poly(A) tail. Whether deadenylation is the cause or consequence of silencing is another unresolved issue (Standart and Jackson 2007).

The experimental data and summarizing conclusions about the mechanisms of microRNA action thus may be considered to be highly controversial. We believe that mathematical modeling can help to systematize the available information and to suggest a computational biology tool for discriminating among all proposed mechanisms of miRNA action and their combinations. Using this tool, some of the contradictory experimental findings may be explained in the framework of the unifying model of microRNA action, whereas others may be discarded as being highly unlikely.

We suggest that “kinetic signatures” (i.e., characteristic time-course patterns to attain protein and mRNA steady-state levels, as well as the number of ribosomes per mRNA molecule after microRNA application) computed for each proposed mechanism could be a good indicator to discriminate between alternative mechanisms. This tool could be useful for proving the existence of the mechanism claimed in a given system or for selecting between several alternative suggested mechanisms.

Repression of protein translation by miRNA has already been the subject of mathematical modeling (Nissan and Parker 2008; Zinovyev et al. 2010). However, a computational tool for discriminating among all proposed mechanisms of miRNA action remains to be developed.

In this work we provide kinetic signatures of microRNA action for each proposed mechanism and also for combinations of mechanisms. To generate these kinetic signatures, we created a complete mathematical model of microRNA action, taking into account all previously described mechanisms, and analyzed this model using the methodology developed in our previous work (Zinovyev et al. 2010), where a rigorous mathematical analysis of dynamical behavior of the systems involving microRNA action was performed. This analysis led us, in particular, to formulate a new hypothesis for microRNA action that underlies the unifying model of microRNA action presented in this work. This new hypothesis, if validated, could reconcile the contradictory interpretations of existing data.

RESULTS

Complete Model based on unifying hypothesis of microRNA action

In our previous work (Zinovyev et al. 2010) we suggested an analytical approach to study important characteristics of miRNA action based on a chemical kinetics mathematical model considering the most important reactions involved in protein translation. In that work, using the simplest model system involving only three possible mechanisms of microRNA action, we worked out methods for analyzing the system of equations corresponding to complex networks of such reactions. As a result, we showed that by using this method we can discriminate between three different mechanisms if we have the experimental data reflecting mRNA and protein dynamics in time-course experiments. Additionally, we found that a given mechanism of microRNA action can be detected experimentally only if it targets parameters of the dominant system (a generalization of the concept of a rate-limiting step to complex networks) of the translation mechanism. This led us to hypothesize that what appears experimentally as a single mechanism may in fact be the result of multiple mechanisms running at the same time, but with only one of these mechanisms eventually affecting the protein translation because it affects the rate-limiting step(s). As a further development of this hypothesis, we suggest here a model in which all mechanisms of microRNA action coexist in a cell, while the apparent mechanism X, i.e., that which will be detected experimentally, depends on the kinetic rate constants of the different steps of mRNA translation, mRNA or protein degradation, and others, both internal and external to microRNA pathways. We think that this postulate can be considered as representing a unifying hypothesis of microRNA action, because, if confirmed, it gives us the possibility to reconcile the apparently contradictory interpretations of previous results in the framework of a single model of microRNA action. In the Discussion section we revisit the controversial studies cited in the Introduction section in the framework of our model. This analysis provides an explanation for most of the discrepancies in the literature, and we propose an experimental approach for validating the model.

The interplay between the kinetic rates of different steps of mRNA translation and degradation depends on a set of intrinsic characteristics of the given experimental system, such as the content of target mRNA, the set of mRNA-binding proteins, the mRNA degradation rate, and other details of the translational machinery. Differences in these parameters between various experimental systems or changing some of these parameters within a given experimental system will result in implementation of the dominant systems corresponding to different mechanisms.

Indeed, many studies underscore the importance of the intrinsic characteristics of mRNAs for the final outcome of miRNA action. For example, RNA-binding proteins not related to the miRNA pathway have been shown to have a strong influence on the regulation by miRNA (Yang et al. 2003; Moore 2005; Sandberg et al. 2008; Mayr and Bartel 2009).

Another argument in favor of the unifying hypothesis is that the possibility of coexistence of two or more mechanisms has already been discussed and proven in the literature (Pillai et al. 2005; Valencia-Sanchez et al. 2006; Wu et al. 2006; Eulalio et al. 2007b, 2008a; Leung and Sharp 2007; Filipowicz et al. 2008; Zipprich et al. 2009). At the biological level, the molecular mechanisms enabling miRNAs to interact with a variety of distinct proteins in order to affect various steps of protein synthesis remain to be explored. However, the RISC complex appears to be formed by a number of proteins, and it is conceivable that each of these proteins itself interacts with other proteins belonging to different regulatory pathways.

In the present work we apply our analytical approach to the Complete Model containing all (or most) of the proposed mechanisms of microRNA action, with the main goal to obtain a tool for discriminating between all of these mechanisms on the basis of the experimental kinetic data. Namely, we introduce here the idea of kinetic signatures of mechanisms of microRNA action as a tool for discriminating between them. The kinetic signature of each mechanism is a chart representing experimental data on the dynamics of three measurable biological parameters: (1) the amount of the target mRNA, (2) the amount of the corresponding protein, and (3) the average number of ribosomes on the target mRNA (which could be determined from the polysomal profile). Following our results, in those cases when only one given mechanism is responsible for the observed result of microRNA application, these charts will be unique for each mechanism.

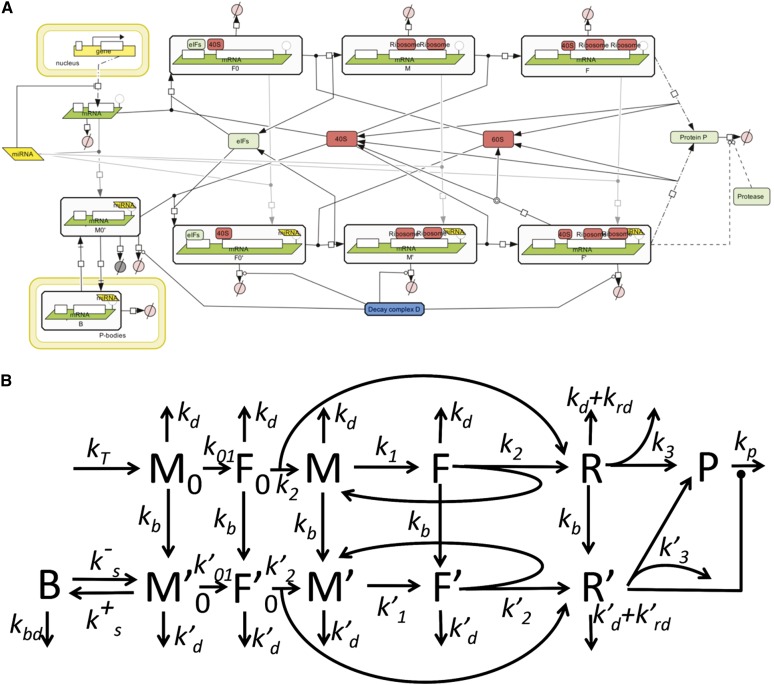
We based our Complete Model on nine distinct mechanisms of microRNA action that have been described in the literature; the main experimental data supporting each proposed mechanism are summarized in Table 1, and the schematic illustration of the mechanisms are presented in Figure 1. Following our unifying hypothesis, the Complete Model is created as a network of reactions involved in protein production, with nine possible mechanisms of microRNA action (Fig. 2) that can potentially coexist. In the framework of this model we can model the situation where any combination of proposed mechanisms of microRNA action acts simultaneously. We can also study individual mathematical models for each proposed mechanism, which can thus be considered as particular cases of the Complete Model, where only the kinetic rate constant (or several constants) corresponding to a given mechanism is changed as a result of microRNA application. For our analysis, we assumed that the initiation factors and ribosomal subunits are always available in excess, and that their concentration is constant. This allowed us to simplify the model to 12 chemical species and 31 reactions, the detailed descriptions of which are given in the Materials and Methods section. All steps of the mathematical analysis and the process of creating the charts for kinetic signatures are also described in the Materials and Methods section. The corresponding MATLAB code for the model is provided in the Supplemental File.

FIGURE 2.

The unifying mathematical model taking into account all nine mechanisms of miRNA action. (A) Created in Systems Biology Graphical Notation (SBGN) standard using CellDesigner 4.1 software (Funahashi et al. 2003). (B) Simplified schematic model presentation in the assumption that ribosomal subunits, initiation factors and miRNA are present in excess and their concentrations are fixed. The description of the reaction graph is given in the Materials and Methods section.

Determination of the kinetic rate constants for dynamical modeling

For simulations, we needed the numerical values of 18 kinetic coefficients, which were estimated from published reports, recapitulated in Tables 2 and 3. Although it is obvious that the values of the rate constants can vary considerably for different mRNAs, experimental data mining allowed us to make plausible assumptions for most of the kinetic rate constants used in the model. For example, mRNA half-lives vary from several minutes to >24 h, with a mean value at 10 h (Yang et al. 2003), which we selected as the corresponding rate. It is nevertheless possible that highly regulated mRNAs, such as most miRNA targets, have shorter half-lives. The same reasoning also applies to protein half-lives.

TABLE 2.

Parameters of translation and miRNA action

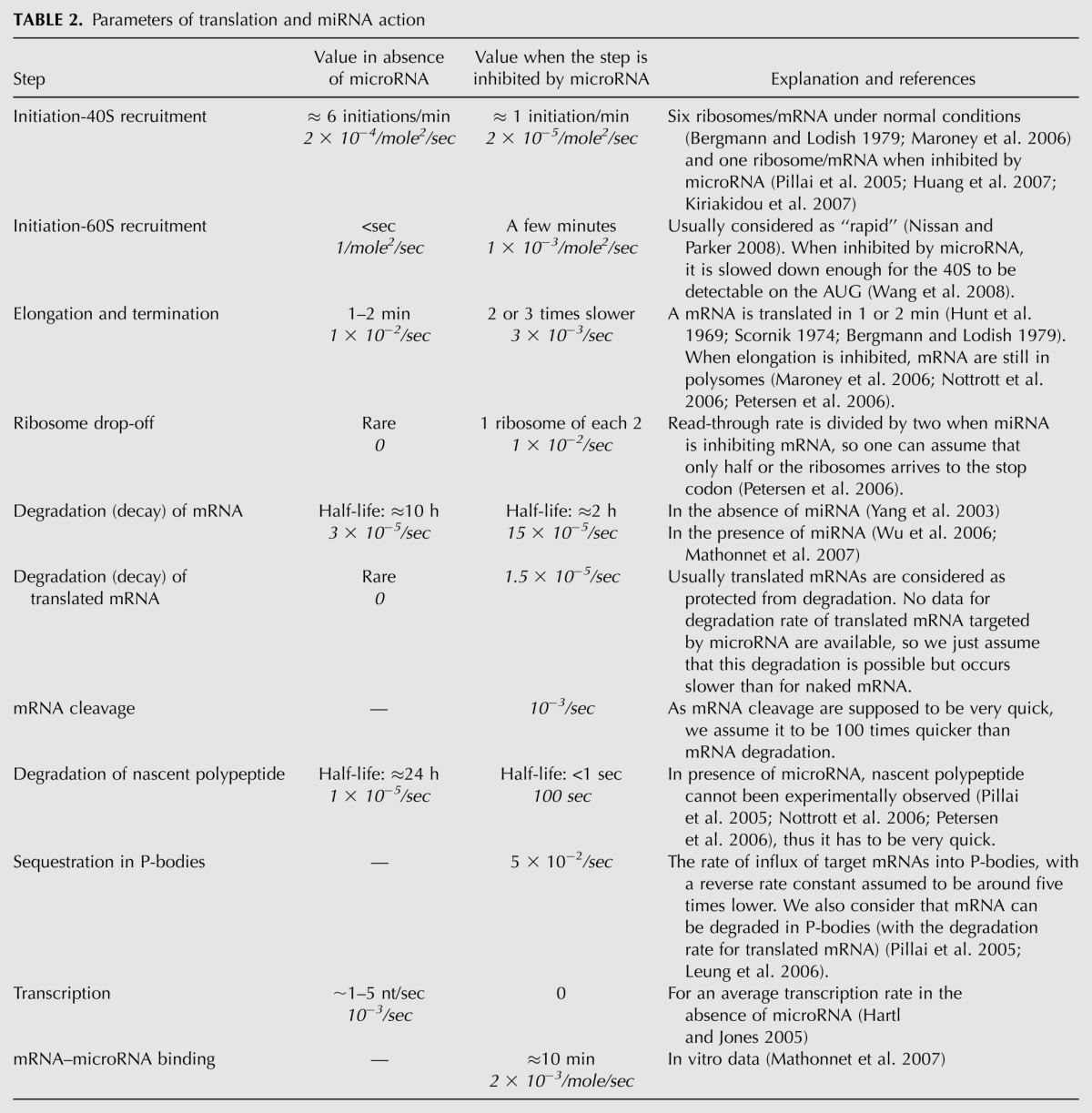
TABLE 3.

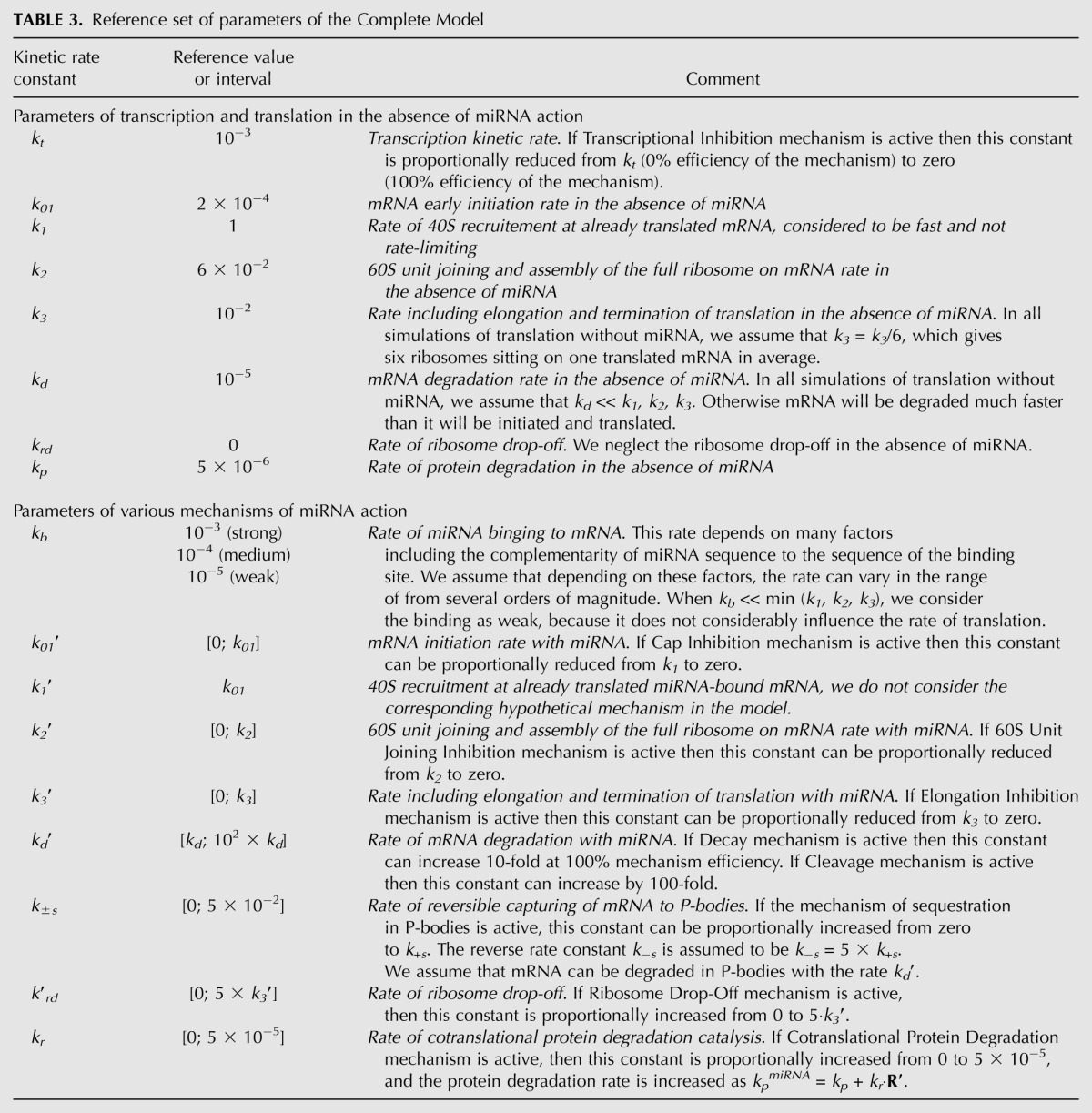
Reference set of parameters of the Complete Model

Similarly, we estimated the elongation time for mRNA translation as 1–2 min (Hunt et al. 1969; Scornik 1974; Bergmann and Lodish 1979), even though it depends on the mRNA length: at 10–15 aa/sec (Gilchrist and Wagner 2006); 1–2 min corresponds to a mean length of 1.8–3.6 kb (Hartl and Jones 2005, page 410). Likewise, the numbers of ribosomes per mRNA molecule are highly variable, from four to five to more than 10 (Bergmann and Lodish 1979; Maroney et al. 2006; A Polesskaya, pers. comm.). We considered six ribosomes per mRNA as being a reasonable assumption representing normal translation conditions. We therefore postulated that six initiation events occur during a cycle of elongation, which leads to an estimate of six initiations/minute, and is of the same order of magnitude as what has been proposed previously (Bergmann and Lodish 1979). All information concerning the kinetic coefficients that we used for our modeling is summarized in Table 2, and the corresponding values of kinetic coefficients for the MATLAB program is given in Table 3.

In addition, we provide a qualitative analytical solution of the model, which is valid for any distribution of parameters and can be used as a guide in analysis.

Kinetic signatures for nine proposed mechanisms (modes) of microRNA action

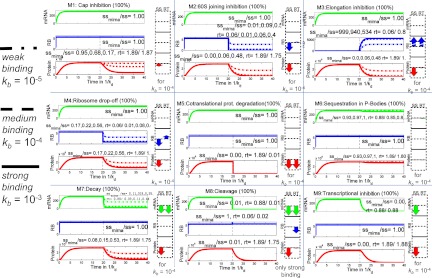
After introducing the kinetic parameters into the mathematical model and running the numerical simulations, specific kinetic signatures were obtained (Fig. 3), which provide a practical recipe for distinguishing between nine different mechanisms of miRNA action by studying the dynamical behavior of three measurable biological parameters: the amount of target mRNA, the amount of the corresponding protein, and the average number of ribosomes on the target mRNA. The time courses of these three measures are quantified by the relative change of their steady state (SS) and relaxation times (RT). The relaxation time is the time between microRNA application to the system and stabilization of the system, meaning reaching new steady-state levels of mRNA and protein. This parameter can be determined from the kinetic signature plots (for a more detailed explanation, see Zinovyev et al. 2010) and the experimental data, and then compared.

FIGURE 3.

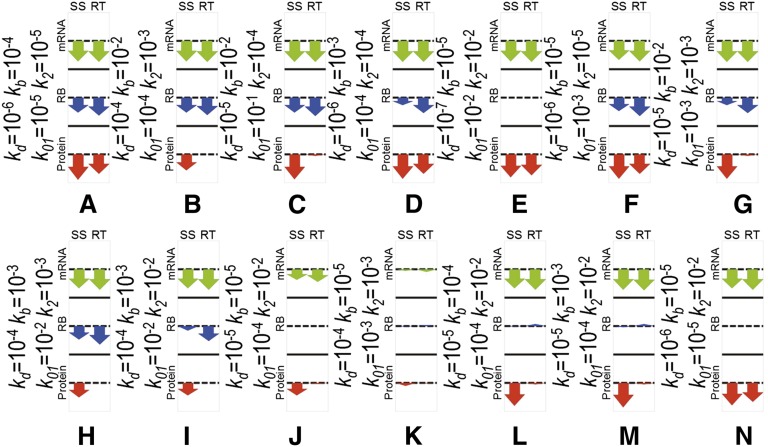
Kinetic signatures for nine individual mechanisms of microRNA action. Each plot shows a dynamics of three quantities: amount of mRNA (mRNA), average number of ribosomes per translated mRNA (RB), total amount of protein (Protein) in the time units measured in 1/k_d, where k_d is the equilibrium dissociation constant characterizing the intrinsic degradation rate of the mRNA in the absence of miRNA. Numbers on the y axis for mRNA and protein levels are arbitrary and should be interpreted based on the steady-state levels of mRNA amount, protein amount, and number of ribosomes per mRNA in the absence of miRNA. The left part of each plot corresponds to translation without miRNA, which is added at the time point 20 (shown by the dashed line). Three scenarios are simulated for each signature: strong, medium, and weak binding strength of miRNA to mRNA. The numbers on the graphs show relative change in the steady-state (ss_miRNA/ss) and change in the relaxation time (rt, measured in 1/k_d). If three numbers are shown separated by a comma, they correspond to weak, medium, and strong miRNA binding. If only one number is shown, it means that the binding strength does not affect this quantity significantly. The arrow diagrams show relative changes in steady-state (SS) and relaxation time (RT) for three quantities: amount of mRNA (mRNA), number of ribosomes per mRNA (RB), and amount of protein (Protein).

Figure 3 presents kinetic signatures of particular miRNA action mechanisms, obtained for those cases when only one individual mechanism is active in the biological system investigated, and at maximum, i.e., 100% efficiency (which means, for example, a complete block of mRNA elongation in the presence of miRNA, for the Elongation Inhibition mechanism). These signatures are also equivalent to the situation where the effect of one particular mechanism is dominant over all of the others (in other words, the inhibiting effect of miRNA on the rate of the target reaction is at least an order of magnitude greater than its effect on any other reaction). All kinetic parameters corresponding to the process of translation in the absence of miRNA, as well as general kinetic parameters corresponding to microRNA action, were taken from publications (Table 2) and considered to be the same for all simulations. An exception was the kinetic coefficient of microRNA–mRNA binding, for which we studied three cases: weak, medium, and strong miRNA-binding strengths (Fig. 3). The time points on the x axis are given in 1/k_d units, where k_d is the equilibrium dissociation constant characterizing the degradation rate of the mRNA. The figure shows that the proper time intervals for obtaining the kinetic signatures of a particular mRNA of interest must be chosen taking into account its specific half-life. The numbers on the y axis for mRNA and protein levels are arbitrary and depend on their steady-state levels without microRNA action.

Each kinetic signature plot on Figure 3 is supplemented with arrow diagrams, visualizing the six numbers characterizing the corresponding simulation. These numbers are the relative changes of steady state (SS) and relaxation time (RT) of the three main measurable parameters: amount of mRNA (mRNA), amount of protein (Protein), and number of ribosomes per mRNA (RB). One can see that the kinetic signatures of the nine mechanisms are qualitatively different, which means that alternative or controversial mechanisms can be reliably distinguished by using this modeling approach. For example, the difference between microRNA-driven cap inhibition and 60S joining (both influencing the process of translation initiation) or between Elongation inhibition, Ribosome drop-off, and Nascent protein degradation (all influencing the post-initiation steps of translation) can be distinguished using the kinetic signatures (Fig. 3). It is important to note that not all mechanisms can be distinguished based solely on the steady-state value analysis. Some of the relaxation time relative changes should be measured as well in order to distinguish, for example, Ribosome Drop-Off from 60S Unit Joining Inhibition. Finally, one can observe that some of the signature components strongly depend in a quantitative fashion on the order of magnitude of the miRNA-binding constant, and some are completely insensitive. This suggests a further computational experiment in which several sequences of miRNA would be utilized having different (weak, medium, tight) affinities to the target mRNA-binding site. Observing how the dynamics of the observable quantities vary with the binding affinity, one can distinguish the mechanisms more reliably. For example, in the case of Cap Inhibition, the protein profile should be more sensitive to changing miRNA affinity than is Cotranslational protein degradation. Our modeling shows that, given the rate of recycling of target mRNAs in P-bodies (Pillai et al. 2005; Leung et al. 2006), the influence of this sequestration on total protein level is very small and will not be detected if we take into account sequestration alone, i.e., without mRNA degradation within P-bodies. The influence of this sequestration on total mRNA levels also will not be detected due to the experimental procedure for total mRNA preparation, which disrupts P-bodies. As a result, the kinetic signature proposed here (using our estimation of the kinetic rate constants) shows only a minor effect of miRNA, which might not allow detecting the case where miRNA acts only through sequestration in P-bodies.

Of course, specific mechanisms such as transcriptional inhibition or mRNA cleavage have specific biological features and can be distinguished without kinetic signatures, but even for these cases the kinetic signatures can also be very useful if one needs to elucidate a possible combination of these mechanisms with others.

Kinetic signatures for combinations of multiple mechanisms of miRNA action

We formalize the coexistence of several miRNA action mechanisms in the following way. We characterized a situation when a miRNA can interfere with several steps of translation (and transcription) by a strength spectrum of nine “pure” mechanisms. The spectrum is a nine-dimensional vector S = {s₁,s₂,…,s₉} with components corresponding to the strengths (contributions) of “pure” mechanisms M1, M2,…, M9. Each component s_i of this vector can vary from 0.0 (absence of the mechanism) to 1.0 (or 100%, maximum strength of the mechanism). We call this situation a “combined” mechanism of miRNA action. The “pure” mechanisms acting at maximum strength (1.0) are basis vectors in the space of “combined” mechanisms. For example, the spectrum S = {0,1.0,0,0,0,0,0,0,0} corresponds to the blockage of 60S unit joining by miRNA without affecting any other step of translation, while S = {0.8,0,0,0.5,0,0,0,0,0} corresponds to the coexistence of Cap Inhibition (at 80% of its maximal strength) and Ribosome drop-off (at 50% of its maximal strength). Also, there are seven normal translation parameters (without miRNA), k_t, k_01, k₁, k₂, k₃, k_d, k_p, which allow us to consider a vector of parameters P = {k_t, k₀₁, k₁, k₂, k₃, k_d, k_p} in a seven-dimensional space of parameters (see Materials and Methods section for details).

In one computational experiment we studied the effect of the coexistence of various mechanisms of microRNA action as an effect of varying S given P fixed at reference parameters (set of standard translation parameters) (Tables 2, 3).

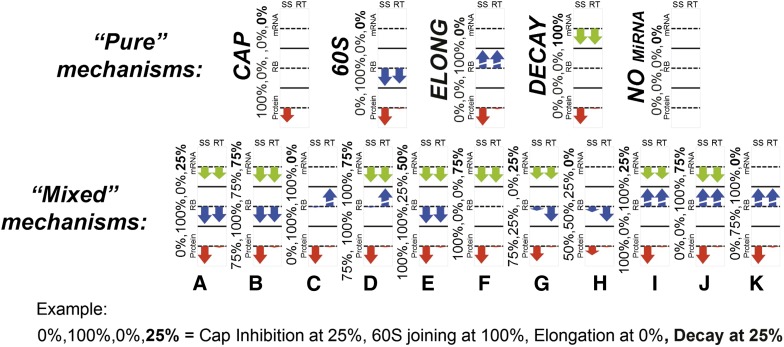
For the combination of the four most frequently referenced mechanisms: Cap Inhibition, 60S Unit Joining Inhibition, Elongation Inhibition, and Decay, we computed 625 kinetic signatures corresponding to all possible combinations of four mechanism strengths (s₁, s₂, s_3, s₇) at the level of 0%, 25%, 50%, 75%, and 100%. The results of the computation are given in Figure 4 as arrow diagrams, where we show the most representative cases around which other signatures have been grouped.

FIGURE 4.

Combination of multiple mechanisms of miRNA action. Combination of Cap Inhibition, 60S unit joining inhibition, Elongation, and Decay mechanisms are considered for the reference set of translation parameters and k_b = 10⁻³. The arrow diagrams show relative changes in steady-state (SS) and relaxation time (RT) for three quantities: amount of mRNA (mRNA), number of ribosomes per mRNA (RB), and amount of protein (Protein). Four numbers on the left of each diagram show the strengths of four miRNA action mechanisms (Cap Inhibition, 60S Unit Joining Inhibition, Elongation Inhibition, and Decay, bottom-up).

The first important conclusion that can be made from Figure 4 is that the presence of Decay mechanism in the spectrum (s₇ > 0) can mask the effect of other mechanisms, leading to the very early blockage of translation. Indeed, it might not matter that translation in the presence of miRNA is completely blocked at a later stage if the increased degradation will destroy mRNA even before it can arrive at this blocked later stage. In some cases (such as the mixed mechanism F, coexistence of complete Cap Inhibition, and Decay) the kinetic signature of the mixed mechanism is indistinguishable from Decay.

The kinetic signature K (mix of 60S Unit Joining Inhibition and Elongation Inhibition) is indistinguishable from the pure signature of Elongation Inhibition. The kinetic signature H (mix of three first mechanisms without Decay) looks similar to the pure 60S Unit Joining Inhibition mechanism. Cases F, K, and H are three examples of kinetic signature masking (or domination) of one mechanism by another.

In other cases the resulting kinetic signature of a mixed mechanism does not look similar to any signature of the four pure mechanisms: In contrast, certain superimposition of the kinetic signatures happens. Thus, the mixed mechanisms A (coexistence of complete 60S Unit Joining Inhibition and some induction of Decay) and C (coexistence of complete 60S Unit Joining Inhibition and Elongation inhibition) give the signature that looks like a superimposition of the kinetic signatures of the initial mechanisms. However, further addition of miRNA action mechanisms does not change the signature qualitatively. Thus, the mix of all four mechanisms together (cases B and E) still looks like a mix of 60S Unit Joining Inhibition and Decay. Hence, one can say that in this case a superimposition of two kinetic signatures masks signatures of other mechanisms.

Interestingly, the kinetic signature in the mixed mechanism I (mix of Cap Inhibition, Elongation Inhibition, and Decay) can be still interpreted as a mix of three signatures of the initial pure mechanisms. This is an example, when three mechanisms are superimposed and leave their “traces” in the final mix.

Kinetic signatures strongly depend on the parameters of the translation system

The next very important conclusion from our modeling is that each possible mechanism will have an impact on the final kinetic output only if it targets a sensitive parameter of the system (except in the rare cases of almost complete inhibition by miRNA). The mathematical analysis underlying this point is given in the Materials and Methods section and in Table 4 and illustrated in Figure 5, where it is shown that in the situation of several possibly coexisting mechanisms of miRNA action, the actually observed mechanism will be determined by the direction of the dominating flux through the reaction network (dominant path). The latter will in turn depend on the relative orders of the kinetic parameters. This theoretical consideration was supported by direct numerical simulation experiment.

TABLE 4.

Dominant paths of the simplified model of microRNA action mechanisms

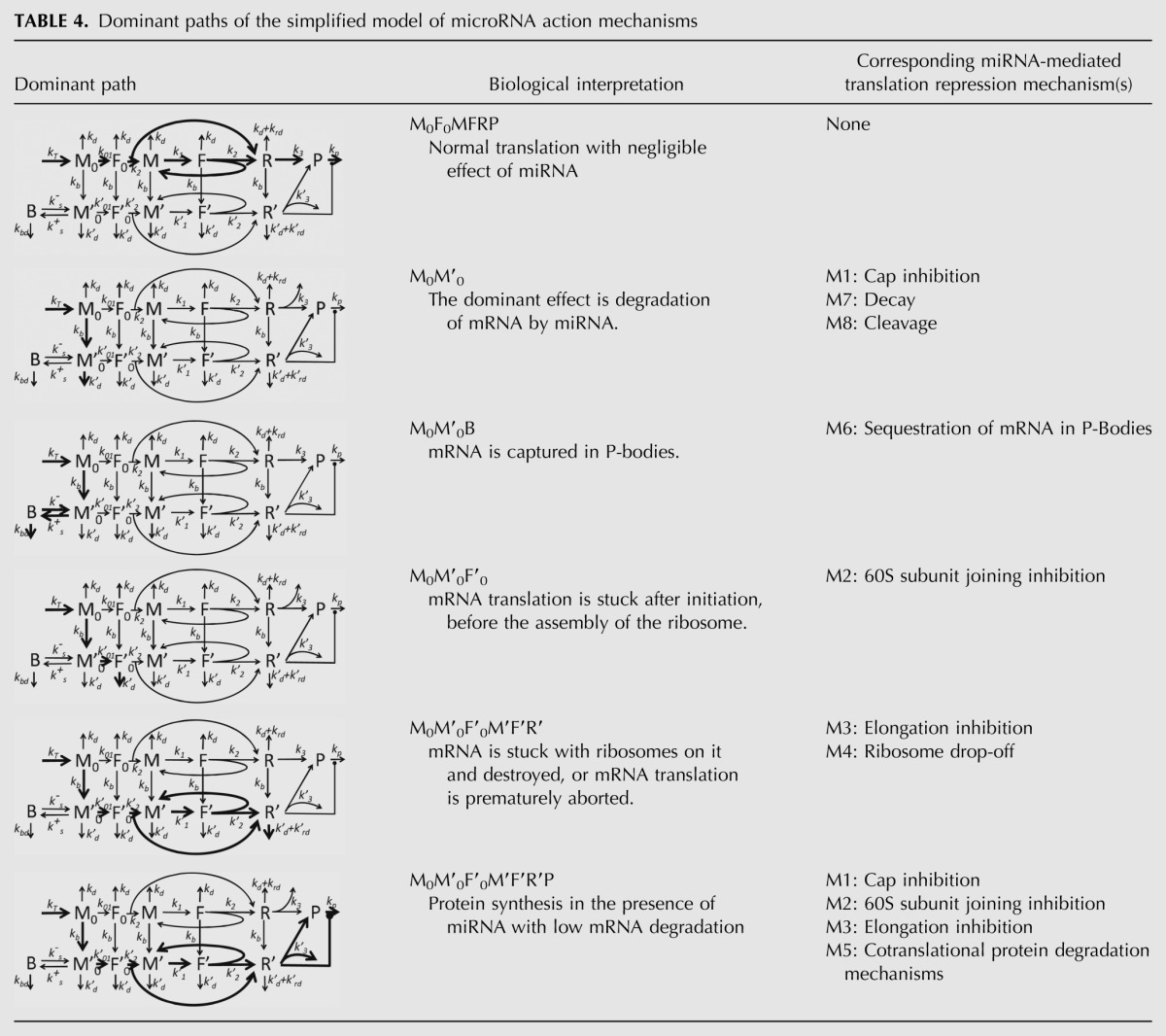
FIGURE 5.

Illustration of the hypothesis of microRNA action. In the same system, depending on the ratios of system parameters and consequent dominant system realization, a biochemist will arrive at different conclusions: (1) Protein is translated “normally,” microRNAs do not interfere (in red); (2) protein translation is inhibited by microRNA at the initiation step (in orange); (3) protein translation is inhibited by microRNA via degradation of mRNA (in blue); (4) protein translation is inhibited by microRNA by slowing down ribosome assembly (in purple); (5) protein translation is inhibited by microRNA through ribosome drop-off (in green).

Changing the kinetic parameters of translation influenced the results (signatures) of our simulations with several possible mechanisms of microRNA action operating simultaneously

This observation led us to suggest the following hypothesis: The differences in conclusions drawn from experimental data arise from physiological mRNA differences and depend on intrinsic parameters of the processing steps for the target mRNA in question. In other words, we propose that the relative abundance and activity of factors not directly related to the miRNA pathways, but rather to the processing of the specific mRNA, can be responsible for the apparent inhibition mechanism(s) detected. The effect will be measurable only on the limiting, sensitive steps of target mRNA processing. If two or more steps are sensitive, then two or more mechanisms of microRNA action will be apparent experimentally.

To illustrate this idea, we performed the second computational experiment, where we considered a combination of four mechanisms (Cap Inhibition, 60S Unit Joining, Elongation Inhibition, and Decay) acting simultaneously, with the fixed strengths 50% of each one, i.e., we consider the combined mechanism of miRNA action characterized by the spectrum S = {0.5, 0.5, 0, 0.5, 0.5, 0, 0, 0, 0, 0}. We study the resulting kinetic signatures of this mixed mechanism when the kinetic parameters of the normal translation are varied in very large intervals (five orders of magnitude), or in other words, we study the effect of varying P given S. We varied four kinetic rate constants k_d, k_b, k₀₁, k₂, leaving k_t and k_p fixed at the reference values and putting k₃ = k₂/6 to provide a constant average number of about six ribosomes sitting on one mRNA. The parameters took the following range of values: k_d∈{10⁻³,10⁻⁴,10⁻⁵,10⁻⁶,10⁻⁷}, k_b,k₀₁,k₂∈{10⁻¹,10⁻²,10⁻³,10⁻⁴,10⁻⁵} in all possible combinations. From these combinations those were excluded that violated the condition of efficient translation (not dominated by degradation) k_d << k₀₁, k₂, k₃. As a result, we have tried 440 different simulations for which we created kinetic signatures, characterized by six numbers, as for the previous computational experiment. To illustrate the results of these simulations, in Figure 6 we provide 14 particular representative cases, shown as arrow diagrams.

FIGURE 6.

Variation of internal parameters of the translational machinery. Cap Inhibition at 50%, 60S Unit Joining Inhibition at 50%, Elongation Inhibition at 50%, and Decay at 50%, and a variable set of internal translation parameters. The arrow diagrams show relative changes in steady-state (SS) and relaxation time (RT) for three quantities: amount of mRNA (mRNA), number of ribosomes per mRNA (RB), and amount of protein (Protein).

Several important conclusions can be made from this computational experiment, and the first one concerns the role of miRNA-binding strength. Evidently, if k_b is much smaller than the normal translation parameters k_d, k₀₁, k₂, then miRNA binding does not affect the dynamics significantly and the “normal” M₀F₀MFRP dominant path is functional (e.g., case K). In the case when the binding is significant but not very strong and comparable to k_d, k₀₁, k₂ parameters, the signature is masked by a Decay-like pattern (e.g., case J). The Decay mechanism masks all other mechanisms also in those combinations of parameters where k₂ is faster than k_d by several (three) orders of magnitude (cases L and M). In this case, the ribosomal profile is not perturbed by miRNA.

The protein relaxation time is affected in the signatures when the mRNA degradation rate constant becomes less than the degradation rate constant of the protein: k_d << k_p = 5 × 10⁻⁶. This explains a significant change in the protein relaxation time for the signatures A, D, E, F, and N. This explains also the quantitative differences in some of the signatures, such as F and H, which correspond to the same dominant path M₀F₀MFRR′, or D and G which both correspond to the dominant path M₀M′₀F′₀M′F′R′P. Note that for the reference set of parameters, the protein is assumed to be more stable than the transcript, and the only “pure” signature where the relaxation time of the protein is affected by miRNA is Cotranslational Protein Degradation. If the protein is less stable than a transcript, then this might create confusion in interpreting the signatures by suggesting activation of this mechanism while it is not functional in reality.

The signatures A, B, C, D, F, G, H, and I can be interpreted as a superimposition of 60S Unit Joining Inhibition with Decay, with the possible role of Cap Inhibition. Elongation Inhibition mechanism leading to the increase of both RB steady-state and relaxation time never manifests itself in this particular situation. A simple explanation for this is that due to the equal strength (50% and 50%) of Elongation Inhibition and 60S Unit Joining Inhibition in the mix S, k₃′ always stays smaller than k₂′ or k₂ and it never leads to accumulation of ribosomes on the transcript. Hence, for this particular mixed mechanism, the Elongation Inhibition contribution is always masked, which might not be the case for other mixed miRNA action mechanisms.

From the expressions (1) and (2) in the Materials and Methods section one can qualitatively understand which parameter modifications of mRNA translation can lead to changes in observable values. For example, decrease in k₀₁ value caused by the Cap Inhibition mechanism can affect only the steady-state rate of protein synthesis and the relaxation time of RB. In order to change the steady-state and the relaxation time of MT, miRNA has to act through k_d (Decay or Cleavage mechanisms) or k_t (Transcriptional Inhibition mechanism).

Dominant paths of the model of miRNA action

Dynamic limitation theory for modeling biochemical reaction networks

The main mathematical approach used in this work relies on the theory of dynamical limitation for biochemical reaction networks. The name “asymptotology” was coined by Kruskal (1963) for the area of science dealing with rigorous separation of “small” and “big” terms in mathematical models, where small terms are small enough to neglect them. This approach, based on a theory of dynamic and static limitation in multiscale reaction networks (Gorban and Radulescu 2008; Gorban et al. 2010), allows computing the simplest network that can substitute for a multiscale reaction network, in order to approximate its steady-state and relaxation times. This simple network is called the dominant system (White 2006). In the simplest case, the dominant system can be represented as a subnetwork of the initial complex reaction network, though this is not necessarily a general case.

Knowledge of the dominant system can be used to answer an important question: Which parameters are sensitive in a given network model? Sensitive parameters of the dominant system indicate putative targets that will change the behavior of the large network. Some applications of this approach to systems biology were presented in Radulescu et al. (2008) and Zinovyev et al. (2010).

Here, we apply the methodology of determining asymptotic solutions for the system of dynamical equations. Every asymptotic solution can correspond to one or many mechanisms of miRNA action. To characterize a kinetic signature as a time series of three observable variables, MT, PR, and RB, we can predict the change of expression of their steady-states and relaxation times after adding miRNA to the system. The relaxation time t_rel is an important dynamical characteristic, which defines the time needed to achieve the steady-state rate after a perturbation; for example, after microRNA addition. For further analysis, it is important to mention that in a cycle or in a linear chain of chemical reactions with well-separated constants, the steady-state rate is limited (determined) by the slowest reaction, while the relaxation time is limited by the second slowest reaction (Gorban and Radulescu 2008).

Dominant paths of miRNA action

Accordingly to the methodology of asymptotology (Gorban et al. 2010), let us consider the case of well-separated constants, i.e., when any two kinetic constants in the graph in Figure 2B have different orders of magnitude at each fork (i.e., a node with several outgoing reactions). Each such a (partial) ordering of kinetic constants will generate a path on the graph (possibly cyclic), starting at M₀ node. We will call it the dominant path. Each path corresponds to one (if it does not contain cycles) or several (if it contains a cycle) dominant systems and to a distinguishable biochemical scenario. For example, the partial ordering (k_b >> k₁, k_d ; k₀₁ >> k_-s, k′_d ; k′₂ << k_d) corresponds to the dominant path describing the process of translation inhibition via 60S subunit joining repression (see Table 4, path M₀M′₀F′₀).

A dominant path is connected to a dominant system (whose solution of the corresponding dynamics equations provides an asymptotic approximation of the whole system dynamics) in the following way. If the path does not contain cycles, then it represents the dominant system. If the path contains cycles, then the cycles should be glued and represented by single nodes (which will represent quasistationary distribution of chemical species concentrations inside the cycle). Then one should find the dominant path for the new graph with glued cycles and continue until an acyclic dominant path can be found. Depending on the ordering of kinetic rate constants inside each cycle, one cyclic dominant path can lead to several different dominant systems. The dominant system in general represents a hierarchy of glued cycles. The details of constructing dominant systems are provided in Gorban and Radulescu (2008) and Radulescu et al. (2008).

It is convenient to designate each dominant path by the nodes through which it passes. There are many possible reaction graph traversals leading to multiple possible dominant paths if one considers all partial orderings of the constants in the reaction forks. However, some of them are biologically nonrelevant. For example, the ordering k_d >> k₀₁ (dominant path M₀) will not lead to any translation (the mRNA will be degraded before it will be initiated). In the same way, k_d >> k₂ (dominant path M₀F₀) will terminate the normal translation prematurely. Thus, we postulate k_d << k₀₁, k₂, k_3. Also, for simplicity we assume that binding of miRNA to mRNA is more rapid than normal initiation, i.e., k_b >> k₀₁, k₂, k₃ if there is miRNA in the system, and k_b = 0, if not. Also we assume that k₀₁ << k₁, because k₁ corresponds to recruiting 40S subunit on already initiated and translated mRNA (which we assume never be rate-limiting), while k₀₁ includes both mRNA initiation and 40S subunit recruiting. This leads to six biologically relevant dominant paths, all of which are listed in Table 4.

Table 4 shows that the types of dynamical behavior (dominant paths) can be mapped onto the biologically characterized mechanisms of miRNA action, but this mapping is not one-to-one: Several biological mechanisms can correspond to one dynamical type (for example, M₀M′₀ dominant path corresponds to M1, M7, and M8 biological mechanisms and, conversely, biological mechanism M1 can correspond to M₀M′₀ or M₀M′₀F′₀M′F′R′P dominant paths).

DISCUSSION

The mode/mechanisms of microRNA action have generated considerable discussion, and remain a controversial issue. In this work we (1) propose a unifying model of microRNA mechanisms stating that all known mechanisms can potentially coexist and work simultaneously; (2) create a complete mathematical model of microRNA action based on this hypothesis; (3) suggest a set of “kinetic signatures” for individual mechanisms to be used as a tool for discriminating between different mechanisms. The signatures are obtained from analysis of this mathematical model in the particular case where each mechanism is considered as the only one acting in the system. It is important to note that, though tightly connected, these three parts of the study have independent meaning, significance, and novelty.

It is of utmost significance that the proposed unifying hypothesis of microRNA action explains how apparently contradictory and/or controversial conclusions about the mechanism(s) of microRNA action in different experimental systems/approaches can be reconciled. Below, we will demonstrate several examples of such reconciliation of controversial interpretations in the light of this hypothesis, using publications mentioned in the Introduction section.

The proposed unifying hypothesis of miRNA modes of action postulates that all (or many) possible modes of microRNA action may coexist in the cell and operate simultaneously, and that the observed mode of miRNA action in a particular biological system depends on a set of intrinsic parameters of this system that influence the interplay between the kinetic rates of the different steps of mRNA translation, mRNA or protein degradation, and others. These parameters/factors are not necessarily related to miRNA pathways, but, in the first place, intrinsically determine the sensitive parameters of the system and can depend on the characteristics of the target mRNA under study (e.g., mRNA content, mRNA-binding proteins, special marks of mRNA processing, mRNA degradation rate) and the details of its translation.

The following examples show how changes in the kinetic rates of different steps of mRNA translation may lead to differences in the final interpretation of the data, resulting in different conclusions about the microRNA mode of action, and how this depends on the relative abundance and/or activity of a set of factors intrinsic to any given biological experimental system.

First of all, it can be noted that in most of the studies showing initiation inhibition, in vitro-transcribed mRNAs (transfected into cells or studied directly in vitro) were used. In contrast, almost all data supporting elongation inhibition were obtained in living cells (in vivo) (Humphreys et al. 2005; Pillai et al. 2005; Kiriakidou et al. 2007; Mathonnet et al. 2007; Thermann and Hentze 2007; Wang et al. 2008), with only one very specific exception (Lytle et al. 2007).

In the framework of our model, the first possible explanation of this experimental bias could be, for example, the influence of splicing marks that are attached to mRNA in vivo during its processing in the nucleus (“mRNA nuclear history”). The process of mRNA splicing leaves protein marks on mRNA, which promotes the first round of translation at the initiation step (Le Hir and Seraphin 2008; Moore and Proudfoot 2009). Though these marks are dissociated during the first round of translation, speeding up the initial initiations during the first round of translation can lead, in the “closed-loop” model, to increasing efficiency of reinitiation (Kapp and Lorsch 2004). This could explain higher initiation rates on intron-containing mRNA in vivo, when elongation becomes a critical step. In contrast, in vitro-transcribed mRNAs lack splicing marks, resulting in a decreased initiation rate, which becomes limiting.

Another very important point explaining the contradictory findings is that the elongation efficiency depends on codon usage. In particular, we observe that microRNA has been reported to act on initiation steps when codon usage is optimized for human translation (Pillai et al. 2004; Kiriakidou et al. 2007), whereas with nonoptimized codons, microRNA was found to act on elongation (Nottrott et al. 2006, Petersen et al. 2006; Lytle et al. 2007; Gu et al. 2009). This means that characteristics of mRNAs that decrease elongation rates cause elongation to become the limiting step in translation, so that interference with elongation becomes the mode of microRNA action that is detected.

Finally, the most trivial explanation for discrepancies between in vitro and in vivo studies is that under in vitro conditions, initiation is highly dependent on the concentration of initiation factors, thus making initiation the limiting step, with the result that it is detected as the apparent mode of microRNA action in in vitro studies.

Next, reviewing the publications reporting a mechanism of translational inhibition via the 40S-cap, one can note that most of the experiments proving this mechanism were done in systems with a very slow, critical initiation rate (A-capped mRNA or mRNA with IRES). For this reason, the correct interpretation of results showing that cap modifications are refractory to miRNA action may be that cap modifications (A-capped mRNA or mRNA with IRES) lead to such a strong, critical, decrease of the initiation rate, that the system becomes insensitive to any additional decrease caused by miRNA action.

As all IRES are different, some of them can have initiation efficiencies similar to “canonical” initiation, whereas others may be less efficient. This could explain, in the framework of our model, the data concerning two IRES in the same gene (VEGF), one of which allows inhibition of this gene by miR16, whereas the other does not (Karaa et al. 2009). Additionally, most of the studies showing IRES-driven mRNAs to be refractory to microRNAs were carried out either in vitro (Mathonnet et al. 2007) or using in vitro-transcribed mRNAs transfected into cells (Humphreys et al. 2005; Pillai et al. 2005; Kiriakidou et al. 2007), whereas the studies showing IRES-driven mRNAs to be repressed by miRNAs were carried out with mRNAs transcribed in situ, i.e., inside cells (Petersen et al. 2006; Karaa et al. 2009). Thus, the difference might come from the status of the target mRNA, or from the absence in in vitro systems of the specific factors influencing (increasing or decreasing) the efficiency of cap initiation or other steps, thus conditioning the final outcome.

The proposed unifying hypothesis also explains the observations that the same microRNA apparently uses distinct mechanisms on different targets (e.g., for let7, Pillai et al. 2005; Maroney et al. 2006; Chendrimada et al. 2007; Mathonet et al. 2007; Wakiyama et al. 2007; for CXCR4 microRNA, Humphreys et al. 2005; Petersen et al. 2006; Wang et al. 2006, 2008; for miR16, Huang et al. 2007; Karaa et al. 2009; for miR122, Jopling et al. 2008); and that the status of the cell affects the final observable mode of miRNA action (Bhattacharyya et al. 2006; Leung et al. 2006; Valencia-Sanchez et al. 2006).

Finally, our hypothesis predicts that the different experimental procedures used might lead to “pre-existing” differences in the rates of translation, degradation, and other processes essential for microRNA action. This would imply different parameter sensitivities and, hence, different “observed” mechanisms. This analysis is supported by the article by Kong et al. (2008), who showed that the same microRNA can act on the initiation or the elongation step according to the promoter used for its transcription. This phenomenon, not explained in the original article, could be explained by our model. For a reporter mRNA with intron(s) and nonoptimized codons, different promoters may “promote” the accumulation of different “mRNA nuclear history” marks (e.g., splicing marks, or possibly other modifications), or lead to different amounts of mRNA being transcribed, thus changing the whole set of critical parameters of the system in such a way that the critical step appears to be initiation in one case, and elongation in the other.

Also, the report about the dependence of microRNA mode of action on the experimental procedure used for the transfection (Lytle et al. 2007) becomes understandable in the framework of the unifying model. The transfection procedure is likely to influence the association of the target mRNA with mRNA-binding proteins, which, in turn, changes the sensitive parameters of the system and, hence, the final outcome of microRNA action.

For experimental validation of the unifying model hypothesis, we propose the design of an experiment for studying the influence of codon frequency on detection of the mechanism of microRNA action. It is well known that elongation efficiency is dependent on the codons used: Some tRNAs are more frequent than others in the cell, and therefore the corresponding codons will be translated faster. mRNAs enriched in “frequent codons” will consequently be translated faster than mRNAs enriched in “rare codons.” We therefore propose the construction of two mRNA reporters with identical microRNA-binding sites, promoters, introns, 5′UTR, 3′UTR, and protein products. The only difference between the two reporters would be the codon usage: one would be enriched in rare codons, whereas the other would be optimized for human translation. We predict that in this case, elongation inhibition will be observed for the “optimized codons” mRNA, and initiation inhibition for the “rare codons” mRNA. According to our model, in those systems for which the initiation inhibition mechanism has already been proved, the decreased elongation efficiency (in the case of “rare codons”) should convert the initially observed initiation inhibition mode to an elongation inhibition mode. Inversely, any increase in elongation efficiency (in the case of “optimized codons”) should favor detection of an initiation inhibition mechanism.

The mathematical model developed and analyzed in this work presents a set of new approaches for analysis of complex systems. The mathematical approach we have developed here for analysis of the complete model of microRNA action is based on the general theory of dynamical limitation (Gorban and Radulescu 2008) and uses the notion of a dominant dynamical system, itself a generalization of the rate-limiting step concept to complex networks (Gorban and Radulescu 2008; Gorban et al. 2010; Zinovyev et al. 2010). The idea that microRNA action will not have a visible impact on inhibition of translational initiation unless this is the rate-limiting step in protein translation has already been mentioned in the work by Nissan and Parker (2008). However, the notion of a rate-limiting step becomes nontrivial when we consider complex networks (more complex than a linear chain or a cycle of monomolecular reactions). In our previous work (Zinovyev et al. 2010), by analyzing the complex network model of miRNA action, we arrived at an essential conclusion that miRNA action has an impact on the final kinetic output only if it targets sensitive parameters of the system. Given the parameter distribution, we can determine the sensitive parameter set by computing the dominant system of the protein translation process. Here we have applied this strategy to construct and analyze the complete model of microRNA action, which gives us a possibility to consider each proposed mechanism individually, all proposed mechanisms simultaneously, or any combination of several proposed mechanisms.

The main practical result of the modeling is a set of “kinetic signatures” for each of the proposed mechanisms/modes of microRNA action. Namely, analysis of the mathematical model has revealed a characteristic kinetic signature for each individual mechanism of miRNA action. A kinetic signature is the predicted dynamics of three measurable variables, namely, the accumulation of protein, mRNA, and the number of ribosomes per mRNA after microRNA application, during a time-course experiment. Two quantitative measures of the dynamics were shown to be necessary in characterizing the kinetic signatures: (1) relative change of the steady-state and (2) relative change of the relaxation time. We believe that these kinetic signatures represent a useful tool for experimental discrimination between distinct mechanisms or for detecting the actual mechanism of microRNA action in different experimental systems, independently of the experimental “kitchen” applied. Also, the kinetic signatures for combinations of several proposed mechanisms have been created, first of all for those cases that are under most active debate, such as the combination of cap-dependent inhibition of initiation and mRNA degradation mechanisms.

In summary, our results provide a mathematical tool to discriminate between different miRNA modes of action. Moreover, we propose a unifying model in which the observed mode of action of a particular miRNA is dictated by the relationships among the intrinsic characteristics of its target mRNA. We anticipate that the tool we have developed will promote better analysis of experimental data and that our model will permit a better understanding of microRNA action.

MATERIALS AND METHODS

Description of the mathematical model of microRNA action

As the first approximation, we postulate that the concentrations of ribosomal subunits, initiation factors, and miRNA are in excess, fixed and only included in the final kinetic parameters as multipliers. In this way, the model can be simplified to a linear model, which can be represented in a simplified schematic way (Fig. 2B). The values of the corresponding parameters can be found in Table 2.

This model was used to derive and analyze the kinetic signatures. Below we give a detailed model description. The model contains 12 variables corresponding to chemical species and 31 reactions, including 12 reactions of degradation. We will use the following notations for the amounts of corresponding molecules in the system (in a cell or in an experimental tube):

• [M₀]—newly synthesized and not yet initiated mRNA

• [F₀]—newly initiated mRNA, with initiation complex, including 40S ribosomal subunit

• [M]—initiated mRNA with free translation initiation site

• [F]—initiated mRNA with translation initiation site occupied by 40S ribosomal subunit

• [R]—number of ribosomes fully assembled on miRNA-free mRNA

• [M′₀]—newly synthesized not initiated mRNA with one or more miRNAs bound

• [F′₀]—new mRNA with initiation complex, including 40S ribosomal subunit, with miRNA(s) bound to mRNA

• [M′]—initiated miRNA-bound mRNA with free translation initiation site

• [F′]—initiated miRNA-bound mRNA with translation initiation site occupied by 40S ribosomal subunit

• [R′]—ribosomes fully assembled on miRNA-bound mRNA

• [P]—protein, completely translated from the given mRNA

• [B]—mRNA sequestered in P bodies

Let us make a notice on interpretation of some of the model variables. Explicit description of mRNA:ribosome complexes would require separate dynamical variables for the amounts of mRNA with one ribosome, mRNA with two ribosomes, mRNA with three ribosomes, and so on (potentially, a large number of variables). To avoid this complexity, we apply lumping of the detailed model, described in Gorban et al. (2012). According to this schema, newly produced mRNA (state M₀) is first initiated and prepared for the first round of translation (state F₀). After that, the initiated mRNA alternates between states M (state ready for the next round of translation) and F (mRNA prepared for the next ribosome assembly). During each round, a new assembled ribosomal complex (R) appears in the system. Thus, we explicitly separate the process of mRNA initiation (which can include capping, adenylation, circularization, mRNA transport to specific cellular regions) and the process of recruiting a 40S ribosomal subunit at already initiated mRNA for the next round of translation. In our model, these two processes proceed with different speeds.

In our interpretation, we consider mRNAs as places for a catalytic reaction (protein translation). These places (amount of catalyzer) in our model can be synthesized or destroyed and present in four states (noninitiated, initiated, in “translating” state ready for assembling new ribosome, and in “translating” state with a new ribosome assembling). To take into account miRNA, we say that there are two types of catalyzer: miRNA-free and miRNA-bounded, with different rate constants of degradation. miRNA-free catalyzer can be irreversibly transformed into a miRNA-bounded type of catalyzer.

Importantly, [R] in our interpretation is not the amount of mRNA translating proteins but the amount of ribosomes bound to mRNA and translating proteins, i.e., the number of sites where the catalysis takes place. Dividing the number of these sites by the amount of the catalyzer in the initiated state [M] + [F] gives the average number of ribosomes per mRNA, which we denote as [RB].

The definition of the kinetic rate constants used further in the study is as follows:

• 1. null → M₀, the free mRNA is transcribed in the system with the rate constant k_t

• 2. M₀ → F₀, assembly of initiation complex and 40S ribosomal subunit with mRNA occurs with the rate constant k₀₁

• 3. F₀ → M+R, assembly of the first ribosome on the initiation site with the rate constant k₂

• 4. M → F, initiation of the translation (recruitment of 40S subunit) on already translated mRNA, with the rate constant k₁

• 5. F → M + R, assembly of full ribosome (S80) on mRNA occurs with the rate constant k₂

• 6. R → P, translation of the protein with consequent release of ribosomes occurs with the rate constant k₃

• 7. R → null, degradation of mRNA leads to release of ribosomes with the rate constant k_d, same reaction describes premature ribosome drop-off from mRNA with the rate constant k_rd

We will assume that the process of microRNA binding to mRNA can occur at various stages of translation and that its rate k_b will be the same in each of the following reactions:

• 8. M₀ → M₀′

• 9. F₀ → F₀′

• 10. M → M′

• 11. F → F′

• 12. R → R′

The same way we will assume that the rate of degradation of mRNA not driven by microRNA action (k_d) can be considered as the same one at all stages of translation:

• 13. M₀ → null

• 14. F₀ → null

• 15. M → null

• 16. F → null

The degradation rate of mRNA bound to microRNA could occur with or without direct action of microRNA on its degradation. For the beginning we will assume that this rate constant (k_d′) is different from the free mRNA degradation and is the same one for all stages of translation:

• 17. M′₀ → null

• 18. F′₀ → null

• 19. M′ → null

• 20. F′ → null

• 21. R′ → null

Next, we assume that the reaction corresponding to the assembly of initiation complex and 40S ribosomal subunit with mRNA in the presence of miRNA (M′₀ → F′₀) will occur with the rate constant k₀₁′.

• 22. M′₀ → F′₀

Recruitment of 40S subunit on already translated miRNA-bound mRNA occurs with the rate constant k₁′:

• 23. M′ → F′

Reactions of assembly of the full ribosome (S80) on mRNA in the presence of microRNA occur with the rate constant k₂′:

• 24. F′₀ → M′+R

• 25. F′ → M′+R

The rate of protein production in the case of microRNA action is described by the following reaction:

• 26. R′ → P, with the rate constant k₃′

• 27. R′ → null, describes possible mechanism of ribosomal drop-off (without protein production), with the rate constant k_rd′, and mRNA degradation with ribosome release, with the rate constant k_d′.

Reactions 28 and 29 describe the reverse process of mRNA sequestration in P-bodies, with rates k_+s and k_−s correspondingly:

• 28. M₀′ → B,

• 29. B → M₀′

The mRNA in P-bodies is degraded with specific rate k_bd′:

• 30. B → null

• 31. P+R′ → null, the rate of protein degradation by microRNA-independent mechanisms is k_p, while it can be increased in the presence of miRNA by k_r × R′.

The system of equations dx/dt = K₀ + Kx (where x is the vector of 12 dynamic variables, K is the kinetic matrix, and K₀ is the vector of production with only one non-zero component corresponding to the transcriptional synthesis of mRNA) has the following form:

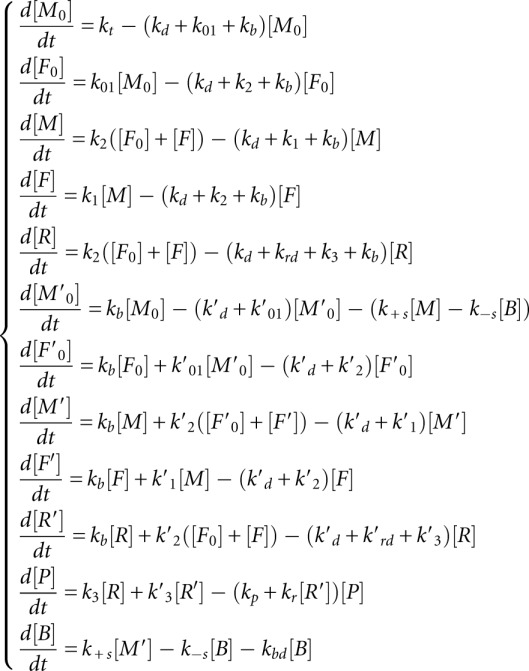For this simplified linear model we need to define the proper values for 18 coefficients corresponding to the rates of reactions.

The dynamical variables that can be observed and measured in the experiment are

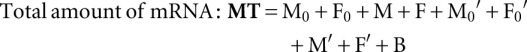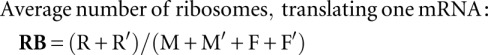These expressions were used to define the kinetic signatures.

First, the solution of model equations and expression for [MT], [PR], [RB] for the trivial case without miRNA in the system were obtained. This can be modeled by putting to zero the binding constant k_b = 0.

For this case the steady-state values for the measurable quantities are

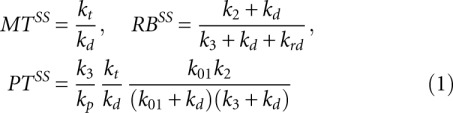and the relaxation times are

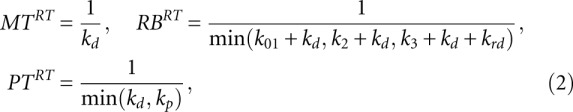where we have assumed that k₁ >> k₀₁, k₂, k₃.

These formulas allow qualitative understanding of the effect of miRNA on various steps of translation and the corresponding kinetic signatures. They can also help to decipher experimentally observed kinetic signatures when multiple mechanisms are present simultaneously and the translation parameters are not known. The exact recipe for doing this will be a subject of our future work.

Simulating the kinetic signatures

The mathematical model of miRNA-mediated translation regulation is encoded in MATLAB’s SBTOOLBOX and provided as a Supplemental File. The corresponding values of kinetic coefficients for the MATLAB program are given in Table 3. The MATLAB code used to draw and classify kinetic signatures is available on demand from the investigators.

The simulation for the kinetic signatures was performed in the following way:

• (1) First, the system was simulated from zero initial conditions without the presence of miRNA (k_b = 0) in the time interval [0; 20/k_d]. The steady-state and relaxation time values for MT, RB, and PR values were estimated from the simulation.

• (2) The miRNA-binding constant was changed to the corresponding value and the simulation was continued from the steady-state obtained before in the time interval [20/k_d; 40/k_d]. New steady-state and relaxation time values were estimated from the simulation.

The model includes a vector of parameters P = {k_t, k_01, k₁, k₂, k₃, k_d, k_p} and of a strength spectrum S = {s₁,s₂,…,s₉}, which can vary. Each computational experiment is defined by the corresponding vectors P and S, binding constant for miRNA (k_b), and the rest of the model parameters are computed using the following formulas:

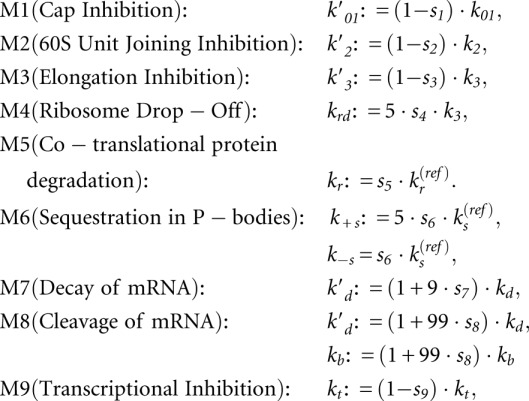The result of the simulation is a kinetic signature for a mixed mechanism of miRNA action, characterized by six numbers: relative changes of the steady states 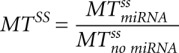, , 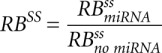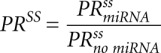and relative changes of relaxation times , , .

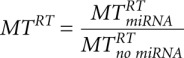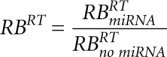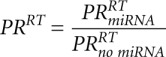SUPPLEMENTAL MATERIAL

Supplemental material is available for this article.