SUMMARY
Identification of homogeneous subsets of images in a macromolecular electron microscopy (EM) image data set is a critical step in single-particle analysis. The task is handled by iterative algorithms, whose performance is compromised by the compounded limitations of image alignment and K-means clustering. Here we describe an approach, iterative stable alignment and clustering (ISAC) that, relying on a new clustering method and on the concepts of stability and reproducibility, can extract validated, homogeneous subsets of images. ISAC requires only a small number of simple parameters and, with minimal human intervention, can eliminate bias from two-dimensional image clustering and maximize the quality of group averages that can be used for ab initio three-dimensional structural determination and analysis of macromolecular conformational variability. Repeated testing of the stability and reproducibility of a solution within ISAC eliminates heterogeneous or incorrect classes and introduces critical validation to the process of EM image clustering.
INTRODUCTION
Macromolecular cryo-electron microscopy (EM) is a structural determination technique that uses the ability of the transmission electron microscope to record near-atomic resolution projection images of proteins preserved in close-to-native form. A typical EM project progresses in a well-defined sequence of steps (Penczek, 2008). Following biochemical characterization and purification of the biological specimen and optimization of EM grid preparation conditions, a set of electron microscope images is recorded. These two-dimensional (2D) projection images of individual complexes are windowed and subjected to a multistage computational analysis that proceeds through 2D alignment (registration) and clustering by similarity, followed by ab initio determination of an initial three-dimensional (3D) structure and its subsequent refinement. The final spatial resolution of a 3D EM structure is dictated by a number of factors, notably the number and quality of input projection images, and the structural homogeneity of the sample. Whereas EM image analysis protocols can be complex, the two basic algorithms used in both the 2D and 3D phases of analysis are alignment and clustering of the 2D images.
EM image analysis is intrinsically challenging because a data set will generally include a variety of images that arise from projecting a macromolecule from various directions, which results in a mixture of similar and quite different patterns. The ultimate goal is to extract subsets of similar images that have to be brought into register within each group. This presents a conundrum because images within a group should ideally be similar in order to be properly aligned, but extracting groups (clusters) of similar images using clustering techniques requires that the images be properly aligned. In addition, determining the proper number of image clusters (corresponding to the number of different projection directions of the structure represented in a data set) and evaluating the homogeneity of images assigned to a given cluster, are essential for accurate completion of the analysis. Failure to obtain well-defined, homogeneous image groups would prevent proper determination of a 3D structure and could signal selection of an inappropriate number of clusters, improper preservation of the specimen, or structural variability of the macromolecule under study.
Various strategies have been proposed to deal with the problem of alignment and clustering of large sets of 2D single-particle EM images (Penczek, 2008). The most general approach is known as multireference alignment (MRA; van Heel, 1984), a process in which the data set is presented with K seed templates, and all images are aligned to and compared with all templates and assigned to the one they most resemble. The process is iterative; a new set of templates is computed by averaging images based on results from the initial grouping (including transformations given by alignment of the data in the previous step), and the whole procedure is repeated until a stable solution is reached. Even if the method has not been formalized as such, it can be recognized as a version of K-means clustering, in which distance is defined as a minimum over all possible orientations of an image with respect to a template (Penczek, 2008). Thus, MRA can be seen as a combination of two algorithms: K-means clustering applied on top of 2D image alignment. Neither of the two algorithms has a satisfying solution, and this represents an intrinsic limitation of this approach.
The goal of the K-means algorithm, minimizing the sum of within-class square errors, is directly connected to the overall goal of single-particle EM analysis, namely, finding a 3D structure for which the overall square discrepancy between reprojections of the structure and 2D experimental projection (input images) is minimized (Penczek, 2008). This explains why K-means is prevalent in single-particle EM applications. However, the standard implementations of K-means suffer from four important limitations.
Results depend strongly on the choice of number of clusters K, and the correct value of the parameter is initially unknown. Hence, the only sensible solution is to apply the algorithm repeatedly to the same data set using different K values and try to identify a most reasonable result.
Because cluster size is not monitored during execution of the K-means algorithm, some clusters may become empty (“collapse”), and this will cause premature termination of the algorithm (a phenomenon often observed when the number of clusters is not chosen properly or when additional degrees of freedom due to alignment are introduced). Whereas it is possible to “reseed” empty clusters, doing so rarely restores the balance between cluster sizes.
Because the K-means algorithm converges only to a local minimum of the goal function, the results are not necessarily reproducible in that the composition of the final clusters depends strongly on the initialization conditions. This undermines the reliability of subsequent ab initio structural determination and structure refinement.
In EM applications it is difficult (if not impossible) to assess the “purity” (homogeneity) of K-means clusters as images are very noisy and appropriate similarity measures are not trivial to define (Sorzano et al., 2010).
Some simple refinements to the basic MRA protocol that try to address alignment limitations have been also introduced. For example, the alignment results can be iteratively improved by refining the orientation parameters for individual images within a group with respect to the current approximation of the average for the group. This works remarkably well when images are very similar to each other and the amount of noise is modest, but it can be easily shown that this “average correction” modification will cause MRA to converge in a finite number of steps to a local extremum of a goal function, causing the outcome of the alignment to be strongly biased toward the initial guess of the average. Therefore, the overall results of MRA will still depend on the initial guess about the number of clusters, on the method employed to construct initial 2D templates, and on the order in which images are processed. Lack of average validation also remains a problem in this modified MRA approach. The most commonly used “validation” is based on the assessment of resolution using the Fourier ring correlation (FRC) methodology, which is a measure of the reciprocal space self-consistency of the aligned data set (Penczek, 2010). However, the FRC is not a very sensitive measure, and it is well known that (1) widely different alignment results will yield virtually indistinguishable FRC curves, and (2) simply increasing the size of an image group, irrespective of its actual homogeneity, can improve the “resolution” measured by the FRC criterion. Similarly, the correlation coefficient computed between group members and group average is not particularly informative. It can be shown that individual images have higher correlations with featureless group averages obtained from heterogeneous sets of images than with averages of homogeneous groups that have relatively few members.
Here, we propose an approach to alignment and clustering of heterogeneous sets of EM projection images, iterative stable alignment and clustering (ISAC), that relies on the use of a new clustering algorithm (EQK-means) that delivers equal-size classes, and on the concept (unprecedented to our knowledge) of evaluating the stability and reproducibility of the alignment solution. ISAC is capable of extracting nearly homogenous subsets of 2D images that are distinguished by their high degree of reproducibility, addressing all of the limitations of MRA. Application of ISAC to a human RNA polymerase II (RNAPII) image data set indicates that ISAC averages are precise enough to detect structural heterogeneity in this asymmetric, relatively small (molecular mass ~500 kDa) macromolecule and can lead to an ab initio structure of the polymerase that can be convincingly matched to a known atomic-resolution X-ray structure.
RESULTS
The Design of the Iterative Stable Alignment and Clustering
The aim of iterative stable alignment and clustering (ISAC) is to produce meaningful averages from a large and potentially very heterogeneous data set of 2D EM projection images by employing a new clustering algorithm, EQual-size group K-means (EQK-means), and the principle of evaluation of the stability and reproducibility of results. Whereas ISAC is a form of multireference alignment, validation of outcomes at key stages of the analysis improves its performance and, most importantly, results in clustering of images into highly homogeneous groups.
We developed EQK-means to address a known limitation of the standard K-means algorithm that results from the combination of clustering and image alignment in EM applications; differences in groups sizes tend to progressively increase, leading to “collapsing” of smaller groups and unchecked increase in the size of larger groups. This problem is caused by the large number of degrees of freedom, that is, the overall algorithm has to concurrently determine image orientation parameters and cluster membership. Groups tend to increase in size rapidly as their averages build up low frequency information, become relatively featureless, and thus correlate well with all images in the data set irrespective of their high frequency features. In contrast, small groups yield low SNR averages, which do not correlate well with very noisy individual images. At its root, this problem might relate to a peculiarity of single-particle projection data sets; very often, projections corresponding to a small number of projection directions (or even just one) dominate the data set. EQK-means successfully addresses these issues by forcing all clusters to have the same number of members. Whereas EQK-means will divide very large groups into smaller groups generating very similar cluster averages, it will also bring up small groups that otherwise would be absorbed by predominant groups, and will prevent the collapse of smaller groups.
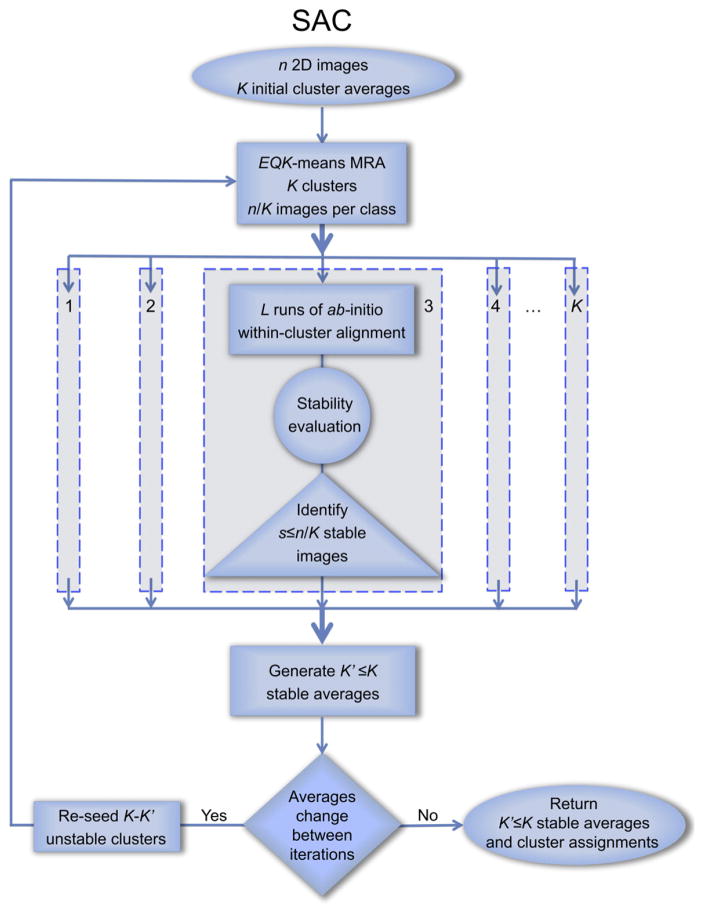
In the context of ISAC, “stability” and “reproducibility” refer to the stability of alignment parameters and the reproducibility of multireference clustering results. The stability of alignment for a 2D image is defined in the context of its group membership and is assessed by comparing the outcome of L reference-free alignments (Penczek et al., 1992) of the group of images initialized with randomized orientation parameters. L repeats of the reference-free alignment procedure yield L sets of orientation parameters, that is, for each image we have L resulting transformations defined by a rotation angle, two translations, and a mirroring flag (Joyeux and Penczek, 2002). After bringing all alignment results into register, we assess the stability of images by computing the value of a dedicated alignment error measure, the pixel error. Images whose pixel errors are below a predefined threshold are deemed stable within the respective group. EQK-means and the stability test constitute the backbone of our stable alignment and clustering (SAC) design (Figure 1).
Figure 1. Flowchart of Stable Alignment and Clustering.
Only clusters comprising images with alignment parameters that are stable (at a given pixel error threshold) across several independent rounds of within-cluster alignment are retained. Images in unstable clusters are sent back to the unassigned image pool for reclustering.
See also Figure S5.
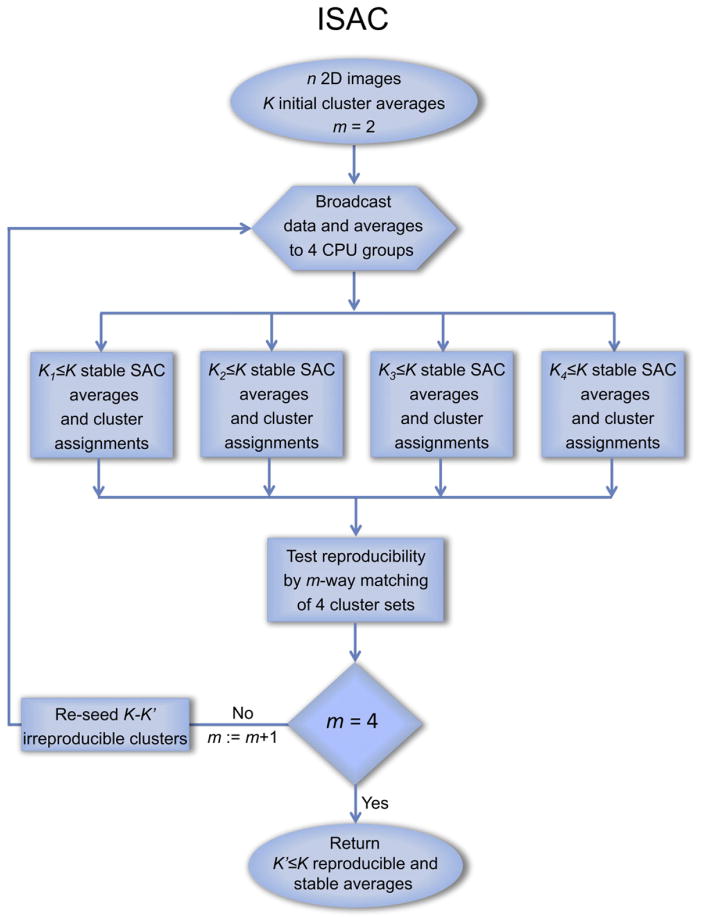
Although SAC is capable of producing stable groups of particle images, the algorithm does not guarantee convergence to a global minimum and, because of its intrinsic randomness (specifically in alignment initialization), the results will differ when SAC is reapplied to the same data set. Moreover, some groups containing stable images, and thus considered stable, might be so due to coincidental grouping of images that will have this property without actually being similar. This problem is addressed by evaluating the reproducibility of SAC results. We postulate that the results of SAC should be considered “correct” only if they can be reproduced in quasi-independent runs of the algorithm. Thus, we apply the SAC algorithm repeatedly to the entire data set. After each SAC reaches convergence, we compare the resulting cluster assignments using a dedicated multipartition matching algorithm. We retain images in clusters, whose assignment is reproduced over a number of quasi-independent SAC runs, and the corresponding group averages serve as input to the next iteration, whereas clusters (and thus averages) deemed irreproducible are reseeded. As the program progresses, the reproducibility test becomes increasingly stringent, beginning from testing selected pairs of SAC runs, through comparison of triplets of SAC result, and to full agreement between four SAC runs. Addition of this validation completes the design of the ISAC method (Figure 2).
Figure 2. Flowchart of Iterative Stable Alignment and Clustering.
The membership of clusters generated by four semi-independent SAC runs is compared, and only clusters with reproducible membership are retained. Images in clusters with low reproducibility are sent back to the unassigned image pool for reclustering.
In order to optimize the performance of ISAC, the input images must be well centered. Precentering decreases the time of calculations and eliminates the possibility of obtaining very similar clusters that differ only by their position within the image window. ISAC progresses by analyzing a set of particle images, identifying and setting aside image subsets that can be aligned in a stable and reproducible manner, and finally reporting these clusters (and associated cluster averages) as a result. We call one application of ISAC to the data set a pass. Typically, only a subset of the input particle images will be assigned to classes that are alignment stable and reproducible in one pass. This subset of input images are set aside, and ISAC is applied to the remaining images, producing a second set of clusters (and averages). The number of particles accounted for in subsequent passes decreases rapidly (from an initial ~50% of the data set to as few as <10%). The process is terminated after no new alignment stable and reproducible groups are identified, which usually takes about ten passes. Within each pass, the ISAC program is divided into two phases. During the initialization phase of the procedure, suitable candidates for cluster averages are randomly generated from the available set of image. The second phase includes the actual ISAC calculations, with the initial cluster averages being used as a starting point for identification of subsets of particle images that can be stably and reproducibly aligned. The only difference between the two phases is that during initialization the reproducibility test is relaxed so that the number of candidate averages is increased at the expense of their reliability.
Properties of ISAC
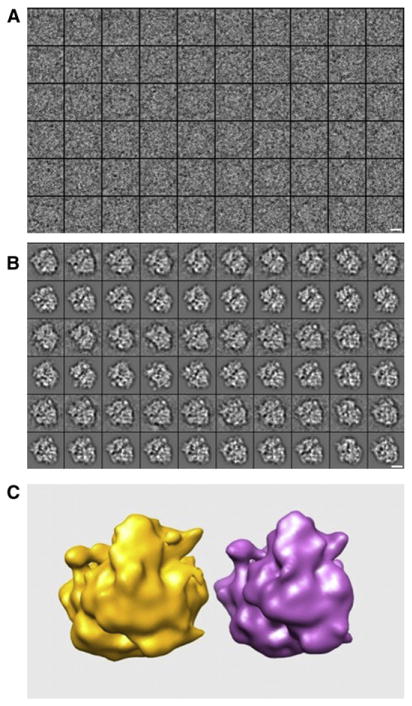
In order to investigate the properties of the ISAC method, we used it to analyze an exceptionally well-defined and well-characterized set of actual EM images: 50,000 cryo-EM projection images drawn from a data set of a ribosomal Thermus Thermophilus 70S·tRNA·EF-Tu·GDP·kirromycin complex, where the ternary complex (EF-Tu·aminoacyl-tRNA·GDP) was stalled on the ribosome using the antibiotic kirromycin (further referred to as EF-Tu ribosomal complex). The high quality of the EF-Tu data is evidenced by the 6.5 Å structure it yielded (Schuette et al., 2009). The original images were recorded on film using a Tecnai G2 Polara (FEI) at 300 kV and 39,000x magnification under low dose conditions (19 e−/Å2) and scanned on a D8200 Primscan drum scanner (Heidelberger Druckmaschinen, Kennesaw, GA, USA) with a step size of 4.758 μm, corresponding to 1.26 Å on the specimen scale. For the purpose of the present work, we decimated the windowed particle images to 64×64 pixels and a pixel size 5.2 Å (Figure 3A).
Figure 3. ISAC Results Obtained for the Data Set of EF-Tu Ribosomal Complex.
(A) Raw EM images.
(B) Selection of ISAC cluster averages matched to projections of the X-ray structure.
(C) Common lines volume compared with a map derived from the X-ray model. Scale bar corresponds to 10 nm. See also Figures S1–S3 and S6–S11.
Newly developed computational methods are ordinarily tested on simulated data, but we decided to use actual images because it is difficult to properly account for all the idiosyncrasies and complexity of actual images in simulated data. In particular, the properties of non-Gaussian random effects are not well characterized, as they stem from factors like sample contamination by objects other than the specimen, various artifacts found in a presumably uniform amorphous ice layer, damage to the frozen specimen, partial disassociation of the imaged complex, and nonuniformity of imaging conditions. As a result of these factors, tests performed on simulated data often reflect the quality of the simulation, rather than the quality of the method being tested. In addition, a pseudo-atomic model based on the X-ray structure of the 70S ribosome is available and could be used for assessment and validation of ISAC results.
The parameters for ISAC analysis of the 50,000 EF-Tu particle images were set as follows:
The expected number of images per cluster was set to 200. Should this number be too high, the resulting groups could be heterogenous, whereas too small a number may cause difficulties with reference-free alignment due to insufficient SNR of the resulting average. The selected number was ultimately based on the fact that the angular distribution of EF-Tu ribosomal projection images is nonuniform, that is, the images are dominated by 3–4 main groups with small angular dispersion (~60% of data), and the reminder of the images are thinly distributed among other angular directions. Taking this into consideration, we decided that 200 images per class would be a good tradeoff between the expected resolution, the SNR of the data, and the angular distribution of projection images.
The minimum number of images per cluster was set to 20. This value is determined mainly by the SNR of individual particle images. Since the EF-Tu data set was collected on a microscope operated at 300 kV, the contrast and SNR of data were low. Therefore, in order to be aligned successfully, a group has to be sufficiently large to overcome the low SNR of individual images. The exact value of 20 was ultimately determined by trial and error.
The pixel error threshold for alignment stability tests was set to , which follows from the requirement that the maximum pixel error in three orientation parameters (rotation and two translations) should not simultaneously exceed one pixel.
The number of independent reference-free alignments L in SAC was set to five. The value was selected as a reasonable compromise between the strictness of stability tests and time of calculations (alignment accounts for most of the time required to run ISAC).
With these parameter settings, ISAC yielded 471 groups that accounted for 37,356 images (or 75% of the entire EF-Tu image set; Figure 3B). The number of images per cluster varied between 21 and 141, and the majority of clusters contained 60 to 100 images (the average number of images per cluster was 79; Figure S1, available online). We confirmed the validity of ISAC group averages by 3D projection matching to reprojections of the X-ray crystallographic atomic model of the 70S EF-Tu ribosomal complex (Schuette et al., 2009). ISAC averages proved to match reprojections of the X-ray model faithfully, revealing virtually identical details (Figure S2). Next, we selected by visual inspection a subset of 111 averages with possibly different projection views of the ribosome, and we obtained an ab initio 3D structure using the SPARX implementation of a common-lines-based structure determination program (http://sparx-em.org/sparxwiki/sxfind_struct; Penczek et al., 1996). The resulting 3D map faithfully represents the structure of the ribosome at a resolution limited by the number of averages used (Figure 3C). In further tests, we determined that two main factors explain why 25% of images were not assigned to stable clusters by ISAC. First, the unaccounted for images tend to have lower defocus values and thus comparably lower SNR. Second, unaccounted images mostly correspond to ribosome orientations represented only infrequently in the data set (Figure S3). Selecting adequate values for ISAC parameters determining the expected and minimum number of images per cluster (Supplemental Experimental Procedures, S3) and the superior performance of EQK-means, result in improved alignment and clustering of images corresponding to rare view of a structure, as evidenced by comparing ISAC results with those from standard MRA; ISAC is able to extract more clusters that are alignment stable and these clusters are far more homogenous and fairly more reproducible than those resulting from MRA (Supplemental Experimental Procedures, S4). Nonetheless, we find that the assignment of rare views to stable clusters is hampered by the conflicting requirements of alignment (which performs better with a larger number of images that have higher SNR) and stability (which is lowered when rare views are mixed with similar projections to assemble a group large enough to be properly aligned).
In summary, these results demonstrate that from a high-quality data set of 50,000 projection images of EF-Tu ribosomal complex, ISAC is capable of extracting a large set of homogeneous image groups whose averages faithfully represent the structure of EF-Tu, and these averages can be used for ab initio determination of an initial 3D map of the complex.
ISAC Analysis of a Human RNA Polymerase II cryo-EM Data Set
To test the performance of ISAC on an EM data set of more “typical,” medium-resolution quality, we used ISAC to process 28,805 cryo-EM projection images of human RNA polymerase II (hRNAPII; Figure 4A) drawn from a data set of images recorded on film at a magnification of 66,000 using a Philips CM200 (FEI/ Philips, Hillsboro, OR, USA) microscope equipped with a field emission source, operating at 120 kV. Micrographs were digitized on a Zeiss SCAI flat-bed scanning densitometer (ZI/Carl Zeiss, New York, NY, USA) with a step size of 7 μm. For the purpose of the ISAC analysis, the digitized images were decimated to a pixel size of 4.11 Å on the specimen scale. Parameters for ISAC were similar to those used for analysis of the ribosome images. The minimum and maximum number of images per cluster were set to 20 and 200, respectively; the pixel error threshold was higher, at , and the number of independent reference-free alignments within SAC was kept at five. ISAC yielded 13,516 hRNAPII images included in 316 clusters (Figure S4), which accounted for 46.9% of the total data set, with the number of images per cluster ranging from 21 to 81 and with an average value of 43. The polymerase ISAC cluster averages do not show the degree of detail observed in the ribosome averages, but they closely resemble reprojections of the highly homologous yeast RNAPII X-ray structure (Protein Data Bank [pdb] 1WCM; Armache et al., 2005), demonstrating that ISAC is capable of producing detailed averages of this relatively small (~500 kDa) macromolecule (Figure 4B). Furthermore, as with the ribosome averages, the quality of the hRNAPII ISAC averages allowed us to obtain an ab initio 3D map of the enzyme after determining the relative orientations of a subset of averages by common lines analysis (Figure 4C).
Figure 4. ISAC Analysis of hRNAPII EM Images.
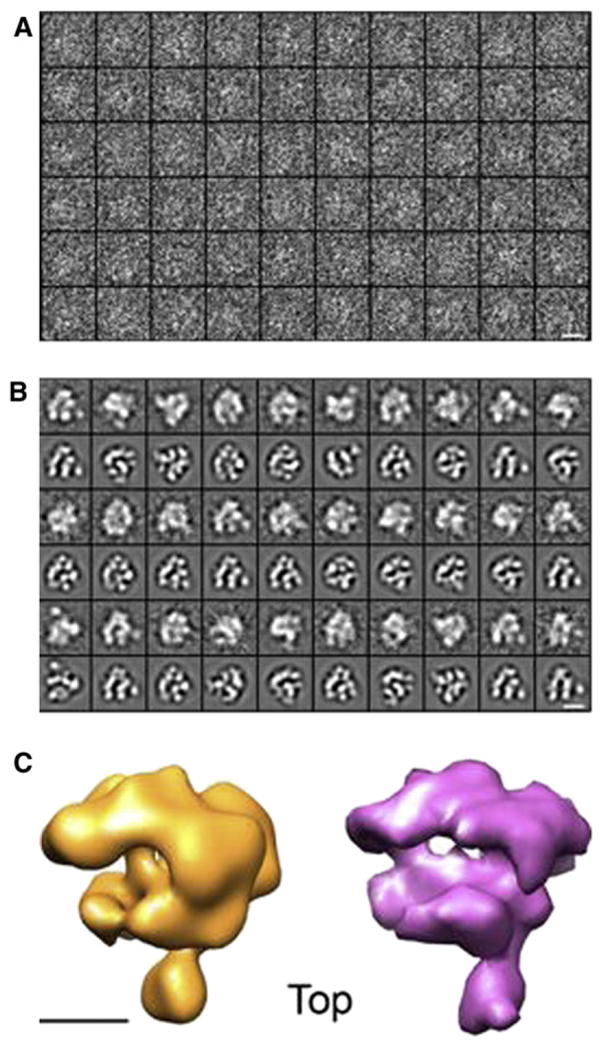
(A) Raw EM images of hRNAPII.
(B) A selection of hRNAPII ISAC cluster averages matched to projections of the X-ray structure of yeast RNAPII (pdb 1WCM).
(C) A 3D map of hRNAPII derived by applying common lines to the ISAC averages shown in (B) (left), compared to a map of the homologous yeast RNAPII (right) derived from its X-ray structure.
Scale bars correspond to 10 nm in (A and B) and 5 nm in (C).
See also Figure S4.
Whereas the salient feature of the ribosome averages was the high degree of structural detail, the most striking observation about the hRNAPII ISAC averages is that ISAC was able to discriminate between images differing only in small features indicative of the presence of different polymerase conformations. Perhaps the best example of this are averages corresponding to the same projection direction, which display different conformations of the clamp domain that defines the active site cleft of RNAPII (Figure 5A). We explored this further by determining the relative orientation of hRNAPII ISAC averages and performing resampling and codimensional principal component analysis (CD-PCA; Penczek et al., 2011). Clustering of ISAC averages indicates that, in agreement with previous reports (Kostek et al., 2006), the position of the clamp region in the hRNAPII structure can vary (Figures 5B and 5C). Our hRNAPII results demonstrate the feasibility of using the very reliable class averages generated by ISAC for characterization of macromolecular conformational variability directly from low-contrast cryo-data.
Figure 5. Conformational Variability of hRNAPII Revealed by ISAC Cluster Averages.
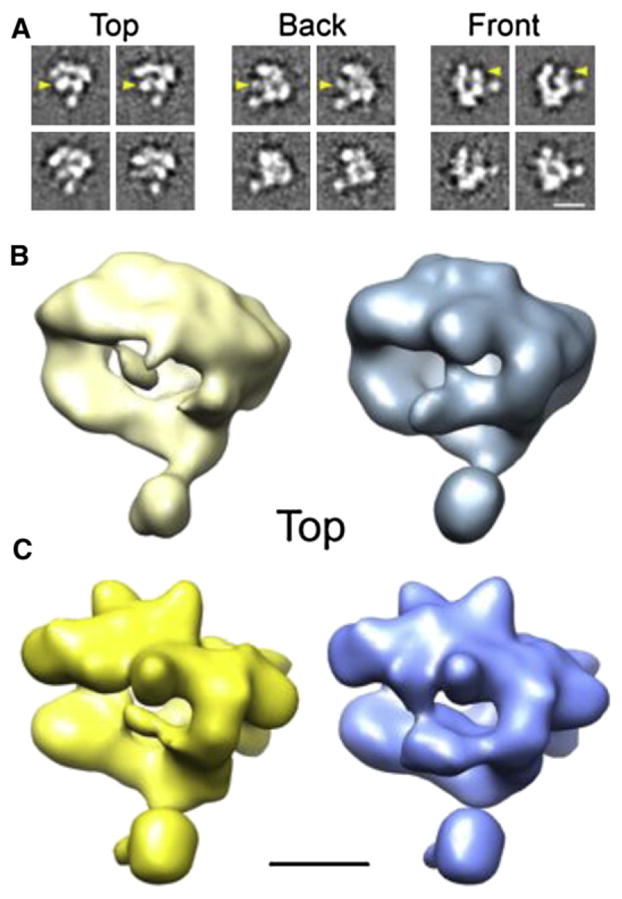
(A) Selected hRNAPII ISAC averages showing changes in the position/ appearance of the clamp domain (marked by yellow arrowheads).
(B) hRNAPII volumes obtained after CD-PCA analysis of resampled ISAC averages show variability in clamp structure.
(C) Two 3D maps obtained by competitive refinement of hRNAPII images using the volumes in (B) as initial references show alternative conformations of the hRNAPII clamp domain. Scale bars correspond to 10 nm in (A) and 5 nm in (B and C).
Conclusions
Iterative stable alignment and clustering (ISAC) represents a novel, simple, and intuitive approach for multireference alignment of single-particle EM images, a critical step in the multistage process that culminates with determination of a 3D EM map. Through the use of a new clustering algorithm (EQK-means), ISAC will extract homogenous subsets of images, validated through repeated evaluation. The stability and reproducibility tests that underlie ISAC’s performance result in homogeneous image groups whose averages faithfully represent the structure of a macromolecular complex with considerable detail. Because of their reliability, ISAC averages can be used for such fundamental tasks as ab initio determination of a 3D map of a complex, or analysis of conformational variability. ISAC operates exclusively on parameters and labels, eliminating the need to consider image similarities that are unreliable and hard to evaluate consistently. As a result, using only basic data-set-specific parameters and a minimal number of additional settings, ISAC can generate dependable and validated 2D averages with minimal external intervention.
The design of ISAC introduces to single particle cryo-EM image processing an integrated approach that combines data analysis and outcome validation. The novelty of the approach is directly related to the use of validation tests to provide feedback to both the alignment and clustering steps of the algorithm. By iteratively accumulating particle images into stable and reproducible groups, ISAC is capable of arriving at highly homogeneous groups of images. The final cluster averages are validated in the sense that the possibility of obtaining accidental results is kept within user-specified bounds. Particle images that do not form stable groups are excluded and group averages are reproducible within a predefined pixel error level.
EXPERIMENTAL PROCEDURES
Reference-free Alignment and Its Stability
Alignment is a prerequisite for clustering of 2D images, as the latter requires similar images to have similar orientations. In reference-free alignment of N images, we seek a set of orientation parameters such that a well-defined goal function, such as the L2 norm of the average, is maximized (Penczek et al., 1992). Reference-free alignment comprises two phases. First, a “random approximation” of the global average is found (originally it was suggested to align individual images in a random order using cumulatively updated average of already aligned images). Second, this global average is improved by individually aligning images using the current average as a template. The orientation parameters are determined using a 2D alignment method based on resampling into polar coordinates (Joyeux and Penczek, 2002). Each iteration of reference-free alignment is completed with an update of the global average using the alignment parameters found. Here, in agreement with the stability concept used in SAC, we initialize the algorithm by setting rotation angles and a mirroring flag to random values and translations to zero.
Reference-free alignment is a greedy algorithm that quickly converges to a local extremum of its goal function (Penczek et al., 1992). In practice, this means that if the data set is heterogeneous (contains particle projections with unrelated features), or the level of noise is excessive, the result of the alignment will strongly depend on the initialization, that is, the alignment will be unstable. Hence, we introduce the notion of alignment stability of an image determined within the context of a group of images. For the purpose of this work, we say that 2D alignment is stable if perturbation of initial alignment parameters does not produce dramatically different results. We observed that for a homogeneous set of EM images (i.e., all images represent projections of a 3D molecule in approximately the same direction), reference-free alignment is extremely robust (stable), even for very low contrast and SNR of the data, and the ability to align a homogeneous data set has an almost binary relation to SNR, that is, the alignment results are either stable or not (Supplemental Experimental Procedures, S1). We postulate that the converse is true, that is, if we can extract from a larger data set a subset of images whose alignment is stable, this provides strong evidence that this subset is homogeneous. In other words, we equate alignment stability of a group of images with their homogeneity (Supplemental Experimental Procedures, S2). As a consequence, by making determination of stable data subsets an integral part of the alignment procedure, we can simultaneously accomplish two major goals of 2D EM data analysis: stable alignment and extraction of homogeneous subsets of images (i.e., clustering).
EQK-Means
Standard K-means is one of the most popular clustering algorithms because of its simplicity, versatility, and fast convergence. Given a set of N objects represented by vectors in p-dimensional space, and assuming a desired K number of clusters, one begins with selection of K seeds (typically either K randomly selected objects from the given set or averages of K equal-sized randomly drawn subsets). These initial guesses are iteratively refined using two alternating steps:
For each object compute distances (typically Euclidean) to current averages, and assign it to the class with the most similar average;
Given assignments for all objects, compute a new set of averages.
If any object changed its assignment the procedure goes back to step 1; otherwise it stops.
The algorithm lends itself to a very efficient parallel implementation: as in step 1, all objects can be processed simultaneously. The same holds for computation of averages in step 2. It can be shown that the algorithm terminates in a finite number of iterations, even though it does not necessarily converge to the global minimum of the clustering problem (Duda et al., 2001). Many protocols developed for single-particle EM structure determination, notably multireference alignment and 3D projection matching, can be seen as versions of standard K-means algorithm, even though they are rarely formalized in these terms (Penczek, 2008; Spahn and Penczek, 2009).
In the sum of square errors (SSE) version of the K-means algorithm, an explicitly formulated clustering criterion of the total squared distances from cluster averages is minimized (Duda et al., 2001). This is accomplished by processing the objects sequentially and accepting a reassignment to the nearest averages only if the move results in decrease of the SSE criterion value. The two averages that would require modification, should the reassignment be accepted, are updated immediately. Whereas this algorithm has better convergence properties than the standard version, the lack of a high-performance parallel implementation makes it less appealing for tasks with high computational demands. Both the standard and SSE versions of K-means algorithm share the fundamental problem of “collapsing” of classes: there is nothing in step 1 that would prevent some classes from being left without assigned objects. This normally happens when the selected value for K is too large or, as stated before, in application to EM data and in combination with alignment, when some clusters start acquiring disproportionally large portions of the data. An obvious remedy is to reseed empty classes in step 2, but usually it is difficult to bring the algorithm back to balance.
To solve the problem of class collapse, we propose the equal-sized group K-means (EQK-means) algorithm, with distance defined as a minimum discrepancy over range of orientations between a 2D image and a template constitutes a foundation of ISAC. EQK-means is initiated by deciding on the desired number of images per cluster k = N/K and selecting a set of K seeds. The algorithm comprises two alternating steps:
Compute a matrix DK×N whose elements dki are distances of i′ th image to k′ th average;
-
Determine assignments of images to clusters by iterating:
-
2.1
set K̃ = K and Ñ = N,
-
2.2
find the smallest element of matrix DK̃×Ñ, say dk̃ĩ, and assign ĩ′ th image to k̃′ th class,
-
2.3
delete ĩ′ th row of matrix DK̃×Ñ and set Ñ: = Ñ − 1,
-
2.4
if k̃′ th class reached k images, delete k̃′ th column of matrix DK̃×Ñ and set K̃: = K̃ − 1,
-
2.5
if K̃ > 0 and Ñ > 0 go to step 2.2, else stop;
-
2.1
Given assignments of all objects, compute a new set of averages;
If any object changed its assignment, go to 1; otherwise stop.
For n divisible by K the algorithm guarantees that all clusters will have exactly the same number of objects. If not, the remaining objects are evenly distributed among clusters, so their number is either k or k + 1.
The EQK-means algorithm as previously outlined does converge in a finite number of steps but has relatively poor convergence properties. Depending on the choice of initial seeds, it may fail to find a solution, even for a simple noise-free test data set. A significant improvement that greatly increases the likelihood that a global minimum will be reached is to implement a simulated annealing version, in which in step 2.2, we consider the probability (whose distribution depends both on the distribution of distances within a given row and on the iteration number) for images to be assigned to classes other than those given by the minimum distance criterion. However, in the context of ISAC, we use EQK-means in conjunction with within-group alignment of images that, as we will describe, replaces step 3. Randomization is built into the alignment step, and we determined that this sufficiently improves the convergence of EQK-means. Therefore, simulated annealing was not incorporated in the final version of ISAC.
Determination of Alignment Stability
We evaluate alignment stability using a Monte Carlo approach; we apply the reference-free alignment algorithm (Penczek et al., 1992) independently L times (typically 4–10) to the same data set using randomized initial orientation parameters. The rotation angle is drawn from a uniform distribution (0°, 360°), a flag indicating whether the image has to be mirrored is randomly set to either true or false, and translations are all set to zero. Randomization of initial parameters is necessary because it is required to compute the first approximation of the average. At the same time, because the alignment parameters are used to indicate the initial orientation of particle images, randomization of translations would unnecessarily complicate the alignment of a given data set.
Comparison of orientation alignment parameters would make sense only if the mirroring flag values were the same in all trials, so we first consider mirror stability (discussed in the next section). Images that are mirror-stable are then tested for orientation stability, where we consider only rotation and translation parameters. In order to determine orientation stability of individual images we first have to bring all L sets of alignment parameters into register, that is, determine the overall rotation and translation for each set such that some measure of alignment parameters’ consistency is optimized. Regrettably, for more than two sets, the problem does not have a closed-form solution, nor is it even well posed, so in what follows we propose an approximation that yields the needed transformations with accuracy entirely sufficient for our purposes.
Let be the 2D transformation of i’th image during l’th alignment (Baldwin and Penczek, 2007):
| (1) |
such that for an arbitrary coordinate vector x within the image field we have
| (2) |
where N is the number of images and L is the number of independent alignments. Our goal is to find a set of L transformations Gl that minimize the variance of Cartesian grid points due to mismatch of the alignment transformations :
| (3) |
where is the squared pixel error of the i’th image evaluated over an image area D. E2 is thus a global measure of misalignment for a set of images that is based on comparisons of orientation parameters resulting from alignment, not comparisons of images, as the latter are unreliable because of the very low SNR of EM data. Since we are interested in the variance of alignment parameters, we need an average position of each image transformation after L alignments; this is given by Hix, and thus Hi is an “average” transformation of i’th image. For a set of 2D rotations, the notion of “average” rotation is ill-defined. However, the ultimate goal is to identify a subset of images whose pixel error is “small,” and, in this case, we expect the dispersion of rotation angles to be small and hence the average rotation to be well defined and meaningful.
For a number of alignments L > 2 Equation 3 does not have a closed-form solution, so we find a solution using the quasi-Newton optimization method LBFGSB (Zhu et al., 1997). We initialize the LBFGSB algorithm by first finding an approximate solution for each matrix Gl independently. Since the problem is overdetermined, we arbitrarily set the first transformation to identity G1 = I and then take advantage of the fact that for two sets of transformations the closed form solution is given by (Penczek et al., 1995)
| (4) |
| (5) |
Given initial parameter values θ̂ (1,l), x̂(1,l), ŷ(1,l) that specify matrices Ĝl l = 2, ···, L, “average transformations” Hi are computed as the “averages” of transformations , l = 1, ···, L. Here we take advantage of the fact that for D being a circle with a diameter d, the closed-form solution for Hi exists (Joyeux and Penczek, 2002). Barring the unlikely case , we have
| (6) |
where
| (7) |
The transformations, Gl, l = 1, ···, L, and average transformations, Hi, i = 1, ···, N, are found using the LBFGSB optimization algorithm initialized with parameter values given by Eq. (4)–(6), which yields the final set of parameters, that is, transformations Gl, l = 1, ···, L. We use them to compute pixel errors for each of the N images in the analyzed set. Images whose pixel errors are lower than a preselected threshold are designated as a stable set, which ultimately forms the output of the procedure.
Determination of Multireference Alignment Reproducibility
We evaluate EQK-means MRA reproducibility by taking advantage of the fact that within ISAC, SAC is applied to the same data set in a semi-independent manner for a predefined number of times (currently set to 4). Each application of SAC yields a set of cluster assignments (Figure 2). Each cluster contains image numbers (labels) assigned to it by EQK-means. Four applications of SAC result in four such sets, and in order to determine the reproducibility of individual outcomes, we have to establish which clusters in different sets of cluster assignments match, that is, share the largest possible number of labels. If SAC results were perfectly reproducible, each application of SAC would result in the same assignments of images to clusters, and one would only have to determine which pairs of clusters matched, which for 100% assignment agreement would be a simple task. In other words, if all sets were identical with the only possible trivial difference arising from different labeling of the clusters (e.g., cluster number 1 in the first partition may appear as cluster number 6 in the second), one would have 100% matching percentage for all clusters. If assignments of images to clusters were entirely random, the percentage of matched images would depend on the number of clusters K and would be 100=KL−1%. Thus, in practice we must find a correspondence or “matching” among clusters in different partitions such that the total number of objects that co-occur in matched clusters is maximized.
To this end, we implemented a dedicated multipartition matching algorithm, which finds the overall solution by maximizing the total number of matched labels, that is, the total number of labels shared in all matched clusters. The higher the percentage of matched labels, the higher the reproducibility of EQK-means. In addition, we consider the reproducibility of individual clusters; given the outcome of the multipartition matching algorithm, we use a preselected threshold T to form a set of reproducible clusters, that is, clusters that contain at least T reproducible images (T has to be less or equal to the number of expected images per group set in ISAC). Note that the number of reproducible clusters returned by the algorithm is usually smaller than the number of groups resulting from SAC runs, and this number depends on the user-selected threshold T.
The solution to the matching problem just described is nontrivial. For two partitions, a polynomial time combinatorial optimization algorithm known as the Hungarian or Kuhn-Munkres assignment algorithm exists and is capable of finding optimum matching. Regrettably, optimum matching of a number of partitions larger than two is equivalent to an axial multi-index assignment problem, which is known to be NP-complete. Most existing solutions are tailored either to data sets with limited size and scale or data sets satisfying special conditions enabling an efficient or subexponential solution (Burkard et al., 2009). To the best of our knowledge, existing data sets for which known solutions are given do not compare in size and scale with the data processed in ISAC (four partitions and the number of groups per partition on the order of 102; for comparison, see Grundel and Pardalos, 2005 and Karapetyan et al., 2008).
Our solution to the multipartition matching problem within ISAC can be categorized as a branching algorithm. The goal of the matching algorithm is to construct correspondences among groups in different partitions that maximize the total number of objects shared among corresponding groups. Consider L partitions with K groups each, where the number of objects in each group can vary. We first define a match as an L-element set that contains one group from each partition. The weight of a match is the number of elements that are shared by all the groups in the match. We only consider collection of matches such that no group appears in more than one match. We call this a feasible collection of matches. The weight of a collection of matches is the sum of the weights of the matches in the collection. Given L partitions with K groups each, the aim is to find a feasible collection of matches with the largest weight. As noted previously, finding an exact solution to this problem is NP-hard.
In our approach, feasible collections of matches are constructed iteratively beginning with the empty collection. More specifically, let the partial solution computed in the 0-th step be the empty collection. In each subsequent step, for each partial solution P computed in the previous step, we determine J matches that have the largest weights out of all matches m, which result in a feasible collection when added to the collection P. The parameter J is user-defined. For each match m′ in a subset S of the J matches, we construct a new partial solution from P by adding m′ to P. We require that S contains the match with the largest weight out of the J matches, so our approach will perform at least as well as the greedy approach in which, at each step, the partial solution is the feasible collection with the largest weight that can be obtained by adding a match to the partial solution of the previous step. Also, S should be chosen so as to avoid computing two partial solutions that are identical, except for the order in which the matches are added. One way to achieve this is by selecting S so that no two matches in S comprise a feasible collection. Lastly, to ensure a reasonable running time, we limit the number of partial solutions that can be constructed using a user-defined threshold. When this threshold is exceeded, S can consist of only one match. By construction, partial solutions are feasible collections of matches. The algorithm terminates when no new partial solutions can be constructed from existing ones, and the solution is given by the partial solution with the largest weight.
To find J matches with the largest weights, we use a simple pruning strategy based on a user-provided threshold T specifying that the solution should only consist of matches with weights larger than T. More specifically, consider a sequence of n < L possible moves, where the i-th move in the sequence corresponds to selecting a group from the i-th partition. If the number of objects that are shared by all n groups does not exceed T, then there is no need to explore the possibilities for the next move on this sequence of n moves since they cannot result in a match with weight exceeding T. This pruning strategy allows us, under most conditions, to avoid explicitly enumerating all possible matches m in order to find the one with the largest weight.
Our algorithm performs at least as well as the greedy algorithm, but the solution cannot be guaranteed to be globally optimal. The running time of the algorithm depends on the parameters J and T and on an additional user defined parameter max_branch, which is used to calculate the number of partial solutions that can be constructed. Importantly, its runtime is negligible within the context of ISAC.
In ISAC, the multipartition matching algorithm is primarily used to identify reproducible groups based on the results obtained from several independent SAC runs. These groups found are further analyzed using the stability test to find a subset of particles that are both reproducible and stable. Averages resulting from these subsets of particles are either output as the final results or used as seeds for the next round of SAC. The multipartition matching algorithm is also used to determine the mirror stability of 2D reference-free alignment runs (see the previous section). Mirror flags resulting from alignment form a string of zeroes and ones indicating whether or not a given image should be mirrored when the average is computed. Mirroring of the average does not change the value of its quality criterion, which means that a given zero-one representation can be inverted to form a quality-equivalent one with zeroes becoming ones and vice versa. With that in mind, for a given alignment outcome we create a partition with two subsets. The first subset contains image numbers that were assigned a zero-mirroring flag, whereas the second subset contains images with a mirroring flag that equals one. Given partitions from several alignments, we use the multipartition matching algorithm to establish the correspondence of subsets in different partitions. The images that are shared by all corresponding subsets are the mirror-stable images.
Implementation
We implemented the ISAC method in the SPARX system (http://sparx-em.org/sparxwiki/) with CPU-intensive components written in low-level C++ and the overall protocol written in high-level Python (Hohn et al., 2007). The code was parallelized using the distributed memory paradigm of message passing interface (MPI; Pacheco, 1996), and we took advantage of the MPI concept of groups of processors to simplify the design of the program. Given a total number of processors assigned to an MPI program, these can be further subdivided into groups that independently execute some code in a distributed memory parallel mode. In our case, SAC is independently executed within ISAC, that is, there is no communication between four runs of SAC, even though each analyzes the same data set. Therefore, we divide all available processors into four equal-sized groups, each executing a single SAC. This design greatly simplifies the ISAC program and, in the event that groups coincide with multicore nodes of a computer cluster, minimizes internode communication and accelerates calculations.
The total number of parameters within ISAC is large, but only few that are data-dependent (e.g., desired number of images per group, particle diameter and such) have to be set by the user. There are other parameters that could be modified by the user but whose default values work well for a broad variety of data sets (e.g., pixel error threshold). Finally, there are parameters that could be in principle modified by the user but which we consider to be an integral part of the ISAC design (e.g., number of ab initio alignment runs L for stability tests currently set to five or the number of SAC runs currently set to four). ISAC settings can be conveniently organized with the help of a GUI command editor that generates a SPARX command line to be executed on a computer cluster under the MPI regime (Figure S5). The design of the GUI reflects the grouping of parameters into the three categories previously outlined.
ISAC analysis of the EF-Tu ribosomal data set (comprising 50,000 64×64 pixel images) took ~74 hr using 256 processors of a distributed memory cluster using MPI. ISAC analysis of the RNAPII data set (28,805 images 64×64 pixel images) took ~44 hr using 512 processors of the same cluster. The time of calculations thus depends on the quality of the data set. High-quality ribosome images require fewer passes of ISAC to identify homogeneous classes, whereas the more challenging RNAPII images yield fewer classes per pass of ISAC and thus require a relatively longer time to process.
Supplementary Material
Acknowledgments
The authors acknowledge the Texas Advanced Computing Center (TACC) at The University of Texas at Austin for providing access to high performance computing resources that enabled us to develop and test the ISAC program and obtain the results we report here. This work was supported by the National Institutes of Health (grants R01 GM60635 to P.A.P. and R01 GM67167 to F.J.A.).
Footnotes
Supplemental Information includes eleven figures and Supplemental Experimental Procedures and can be found with this article online at doi:10.1016/j.str.2011.12.007.
References
- Armache KJ, Mitterweger S, Meinhart A, Cramer P. Structures of complete RNA polymerase II and its subcomplex, Rpb4/7. J Biol Chem. 2005;280:7131–7134. doi: 10.1074/jbc.M413038200. [DOI] [PubMed] [Google Scholar]
- Baldwin PR, Penczek PA. The transform class in SPARX and EMAN2. J Struct Biol. 2007;157:250–261. doi: 10.1016/j.jsb.2006.06.002. [DOI] [PubMed] [Google Scholar]
- Burkard RE, Mauro D, Martello S. Assignment Problems. Philadelphia: Society for Industrial and Applied Mathematics; 2009. [Google Scholar]
- Duda RO, Hart PE, Stork DG. Pattern Classification. New York: Wiley; 2001. [Google Scholar]
- Grundel DA, Pardalos PM. Test problem generator for the multidimensional assignment problem. Comput Optim Appl. 2005;30:133–146. [Google Scholar]
- Hohn M, Tang G, Goodyear G, Baldwin PR, Huang Z, Penczek PA, Yang C, Glaeser RM, Adams PD, Ludtke SJ. SPARX, a new environment for Cryo-EM image processing. J Struct Biol. 2007;157:47–55. doi: 10.1016/j.jsb.2006.07.003. [DOI] [PubMed] [Google Scholar]
- Joyeux L, Penczek PA. Efficiency of 2D alignment methods. Ultramicroscopy. 2002;92:33–46. doi: 10.1016/s0304-3991(01)00154-1. [DOI] [PubMed] [Google Scholar]
- Karapetyan D, Gutin G, Goldengorin B. Empirical evaluation of construction heuristics for the multidimensional assignment problem. In: Chan JDJ, Rahman MS, editors. London Algorithmics 2008: Theory and Practice. London: College Publications; 2008. pp. 107–122. [Google Scholar]
- Kostek SA, Grob P, De Carlo S, Lipscomb JS, Garczarek F, Nogales E. Molecular architecture and conformational flexibility of human RNA polymerase II. Structure. 2006;14:1691–1700. doi: 10.1016/j.str.2006.09.011. [DOI] [PubMed] [Google Scholar]
- Pacheco PS. Parallel Programming with MPI. San Francisco: Morgan Kaufmann; 1996. [Google Scholar]
- Penczek P, Radermacher M, Frank J. Three-dimensional reconstruction of single particles embedded in ice. Ultramicroscopy. 1992;40:33–53. [PubMed] [Google Scholar]
- Penczek P, Marko M, Buttle K, Frank J. Double-tilt electron tomography. Ultramicroscopy. 1995;60:393–410. doi: 10.1016/0304-3991(95)00078-x. [DOI] [PubMed] [Google Scholar]
- Penczek PA. Single Particle Reconstruction. In: Shmueli U, editor. International Tables for Crystallography. New York: Springer; 2008. pp. 375–388. [Google Scholar]
- Penczek PA. Resolution measures in molecular electron microscopy. Methods Enzymol. 2010;482:73–100. doi: 10.1016/S0076-6879(10)82003-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Penczek PA, Zhu J, Frank J. A common-lines based method for determining orientations for N > 3 particle projections simultaneously. Ultramicroscopy. 1996;63:205–218. doi: 10.1016/0304-3991(96)00037-x. [DOI] [PubMed] [Google Scholar]
- Penczek PA, Kimmel M, Spahn CMT. Identifying conformational states of macromolecules by eigen-analysis of resampled cryo-EM images. Struct. 2011;19:1582–1590. doi: 10.1016/j.str.2011.10.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schuette JC, Murphy FVT, 4th, Kelley AC, Weir JR, Giesebrecht J, Connell SR, Loerke J, Mielke T, Zhang W, Penczek PA, et al. GTPase activation of elongation factor EF-Tu by the ribosome during decoding. EMBO J. 2009;28:755–765. doi: 10.1038/emboj.2009.26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sorzano CO, Bilbao-Castro JR, Shkolnisky Y, Alcorlo M, Melero R, Caffarena-Fernández G, Li M, Xu G, Marabini R, Carazo JM. A clustering approach to multireference alignment of single-particle projections in electron microscopy. J Struct Biol. 2010;171:197–206. doi: 10.1016/j.jsb.2010.03.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spahn CM, Penczek PA. Exploring conformational modes of macromolecular assemblies by multiparticle cryo-EM. Curr Opin Struct Biol. 2009;19:623–631. doi: 10.1016/j.sbi.2009.08.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Heel M. Multivariate statistical classification of noisy images (randomly oriented biological macromolecules) Ultramicroscopy. 1984;13:165–183. doi: 10.1016/0304-3991(84)90066-4. [DOI] [PubMed] [Google Scholar]
- Zhu C, Byrd RH, Lu P, Nocedal J. L-BFGS-B: Algorithm 778: L-BFGS-B, FORTRAN routines for large scale bound constrained optimization. ACM Trans Math Softw. 1997;23:550–560. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.