Abstract
The Michaelis–Menten (M–M) approximation of the target-mediated drug disposition (TMDD) pharmacokinetic (PK) model was derived based on the rapid binding (RB) or quasi steady-state (QSS) assumptions that implied that the target and drug binding and dissociation were in equilibrium. However, the initial dose for an IV bolus injection for the M–M model did not account for a fraction bound to the target. We postulated a correction to an initial condition that was consistent with the assumptions underlying the M–M approximation. We determined that the difference between the injected dose and one that should be used for the initial condition is equal to the amount of drug bound to the target upon reaching the equilibrium. We also observed that the corrected initial condition made the internalization rate constant an identifiable parameter that was not for the original M–M model. Finally, we performed a simulation exercise to check if the correction will impact the model performance and the bias of the M–M parameter estimates. We used literature data to simulate plasma drug concentrations described by the RB/QSS TMDD model. The simulated data were refitted by both models. All the parameters estimated from the original M–M model were substantially biased. On the other hand, the corrected M–M is able to accurately estimate these parameters except for equilibrium constant Km. Weighted sum of square residual and Akaike information criterion suggested a better performance of the corrected M–M model compared with the original M–M model. Further studies are necessary to determine the importance of this correction for the M–M model applications to analysis of TMDD driven PK data.
Keywords: Michaelis–Menten, Target-mediated drug disposition, Rapid binding, Quasi steady-state, Equilibrium
Introduction
Target-mediated drug disposition (TMDD) pharmacokinetic (PK) models apply to drugs exhibiting a clearance mechanism due to binding to their targets followed by internalization and degradation [1]. They account for processes such as target binding and dissociation, receptor turnover, and internalization of the drug-receptor complex. Identification of all model parameters becomes impossible for PK data lacking information about the target binding process due to the receptor saturation, infrequent sampling, or other reasons. To enable estimation of the TMDD parameters different from a second order rate binding constant kon and a first-order dissociation rate constant koff, approximations of the TMDD model based on the rapid binding (RB) [2] or quasi steady-state (QSS) assumptions [3] were proposed. These models utilize the equilibrium equation replacing kon and koff with the equilibrium constant KD (RB) or KSS (QSS). Additionally, the free drug plasma concentration C is expressed by an algebraic equation as a function of the total drug concentration Ctot and total receptor concentration Rtot. Both Ctot and Rtot are described by a system of differential equations. Further simplifying assumptions reduced the RB and QSS TMDD models to a single differential equation for C where the target-mediated binding is represented by the Michaelis– Menten (M–M) clearance [3, 4]. The M–M approximation of the TMDD model becomes mathematically identical for both RB and QSS TMDD models. In the case of the IV bolus dose administrations the initial value for C for the M–M model has been proposed as Dose/V where V is the drug central compartment volume of distribution [3, 4]. This is inconsistent with the algebraic equation describing C for the RB/QSS TMDD models at time 0.
A primary objective of this report is to propose the initial condition for the M–M model with an IV bolus drug administration that is consistent with the assumptions underlying M–M approximation. A secondary objective is to determine if the correction of the initial dose affects the M–M model parameter identifiability and the parameter estimates.
Theoretical
The Michaelis–Menten approximation of the TMDD model consists of the differential equations describing the concentration of the free (unbound) drug in the plasma:
| (1) |
| (2) |
with the initial conditions
| (3a, b) |
where C denotes the drug concentration in the central (plasma) compartment, AT is the drug amount in the peripheral (tissue) compartment, V is the volume of distribution, kel is the first-order elimination rate constant from the central compartment, ktp and kpt are the first-order distribution rate constants, and Vmax and Km denote the M–M elimination rate parameters. For both rapid binding and quasi-steady state approximations of the TMDD model the Vmax and Km parameters have the same interpretation as Vmax = Rtot0kintV and Km = Keq, where Rtot0 is the steady-state concentration of the target, kint is the first-order internalization rate constant, and Keq is the equilibrium dissociation rate constants equal to KD for RB and KSS for QSS TMDD models. The M–M approximation (1) was derived from the RB and QSS models which describe the time courses of the total drug and target (receptor) concentrations Ctot and Rtot, respectively [2, 3] (see Appendix A). The free drug concentration is calculated from the equilibrium assumptions (Appendix B):
| (4) |
This implies that the correct initial condition for the differential Eq. 1 should be
| (5) |
where the original initial values Dose/V and Rtot0 for Ctot and Rtot were used, respectively. The expression (5) is the logical initial value for (1) that is consistent with the assumptions underlying the M–M approximation. Using (3a) as an initial condition, although intuitively straightforward, ignores the assumptions leading to the M–M approximation which basically assume that the (1) operates for conditions where the receptor binding and dissociation reached equilibrium. This implies that a fraction of the initial dose that has been bound to the receptors needs to be subtracted from Dose in order to be the initial dose of the free drug. Indeed, one can show that (see Appendix B)
| (6) |
Equation 6 states that initially the total drug concentration Dose/V consists of the free drug concentration Ccorr(0) and bound drug concentration expressed by the last term. This difference can be observed in Fig. 1 as a gap between the simulated time courses of the solutions to M–M approximation with C(0) and Ccorr(0) initial conditions. Consequently, the correct initial condition for (1) can be expressed in terms of the M–M parameters as follows:
| (7) |
The corrected initial condition introduces one more parameter kint into the model structure, which offers a more mechanistic interpretation of the M–M approximation, but on the other hand it raises a question of identifiability of the corrected M–M model.
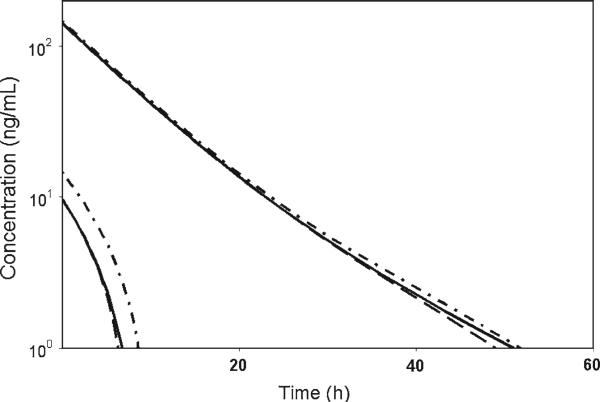
Fig. 1.
Simulation of the pharmacokinetic profile with 1 and 10 μg kg–1 IV doses using the RB/QSS TMDD model (solid line), the corrected M–M model (dash line), and the original M–M model (dash-dot line). Parameters for TMDD model are listed in Table 1. M–M profiles were simulated with the following parameter values: kel = 0.0382 h–1, V = 68.3 ml kg–1, kpt = 0.0806 h–1, ktp = 0.0148 h–1, Vmax = 59.0795 ng kg–1 h–1, Km = 0.131 ng ml–1
In the following section we demonstrate the impact of correcting the initial condition for the M–M approximation on the model performance and parameter estimation. We also provide evidence that kint parameter is identifiable and can be estimated based on the data following into the scope of the M–M approximation.
Methods
To demonstrate the influence of initial condition on the M–M approximation of TMDD model, M–M approximations with different initial conditions were simulated and compared with the TMDD profile. Model parameter values were adopted from the PK/PD model of romiplostim, a TPO mimetic peptibody exhibiting TMDD PK [5]. The M–M parameter Vmax was calculated as Rtot0kintV and Km was equal to KD. Simulations were conducted at IV bolus doses of 1 and 10 μg/kg. The kdeg value was fixed at kint value and the simulated concentrations were truncated at concentration of 1 ng/ml to satisfy the equivalent conditions between M–M model and TMDD model [4].
To demonstrate the influence of correction of initial condition on parameter estimations, residual error was further introduced to the simulated TMDD profile for romiplostim according to a proportional error model:
| (8) |
where Y denotes the simulated value, Ŷ is the predicted concentration and ε is the residual error, which is assumed to be a normally distributed random variable with mean zero and standard deviation σ = 0.15. Simulated data were fitted with the original M–M and corrected M–M models. Minimization was performed using the Gauss–Newton with Levenberg and Hartley algorithm. The squared residuals were weighted by the inverse of squared model predicted values (1/Ŷ2). This simulation and estimation procedure was repeated 100 times. The metrics of weighted sum of square residual (WSSR) and Akaike information criterion (AIC) were reported along with the parameter estimates. Computer simulations and model fittings were conducted using Phoenix WinNonlin 6.0 (Pharsight Corporation, Cary, NC).
Sensitivity analysis was performed for the M–M model with corrected initial condition (Eqs. 1 and 7) with perturbation in kint. A series of simulations were conducted with differing kint values, which were 10-time lower and higher than the adopted literature value. IV bolus doses of 1 and 10 μg/kg were used.
Results
The parameters obtained from the TMDD PK model for romiplostim in humans were used to generate data mimicking IV bolus administration at doses high enough to ensure applicability of the M–M approximation (see Fig. 1). The M–M approximation with and without corrected initial condition was simulated with Vmax = Rtot0kintV and Km = KD, and compared with the simulated TMDD profile (Fig. 1). It can be seen that the original M–M approximation systematically over-predicted the data especially for lower dose level, where the fraction of drug bound to target is relatively large.
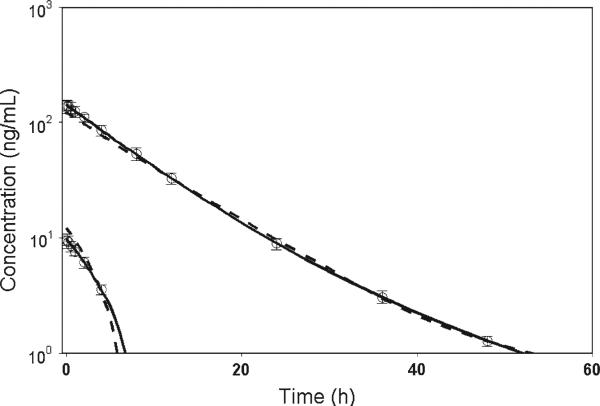
Then, residual error was introduced into simulated data to generate 100 replicates. Both original M–M model and initial condition corrected M–M model were fitted to 100 data sets. The purpose of this exercise was to compare two M–M models in terms of model performance, parameter bias and parameter identifiability. Both AIC and WSSR indicated that the performance of the corrected M–M model is superior to the original M–M model. The original M–M model also exhibited an imprecise estimate of kel. The estimate of volume of distribution V was positively biased for the original M–M model with percent bias of 20%, but the corrected M–M model was able to accurately estimate this parameter (Table 1). Sizeable biases of Km estimates were observed for both models. For the rest of the parameters, the estimates from the original M–M model were substantially biased, but the estimates from the corrected M–M model were fairly accurate. A model misfit for the original M–M model was demonstrated in Fig. 2, while the corrected M–M was able to successfully describe the data.
Table 1.
Parameter values, WSSR and AIC obtained from fitting of the M–M model models to the simulated 100 replicates
| Parameter | Description | Estimate (IQR) |
Parameter bias (%) |
|||
|---|---|---|---|---|---|---|
| True value | Original M–M | Corrected M–M | Original M–M | Corrected M–M | ||
| kel (h–1) | First-order elimination | 0.0382 | 0.00143 (0.0003, 0.00386) | 0.0423 (0.0147, 0.0725) | –96.2 | 10.6 |
| Vc (ml kg–1) | Volume of distribution | 68.3 | 81.9 (78.7, 84.8) | 68.3 (64.6, 72.3) | 20 | 0.027 |
| kcp (h–1) | Tissue distribution | 0.0806 | 0.0979 (0.0918, 0.105) | 0.078 (0.0594, 0.0962) | 21.4 | –3.24 |
| kpc (h–1) | Tissue distribution | 0.0148 | 0.0224 (0.0194, 0.0258) | 0.0157 (0.0115, 0.0254) | 51 | 5.75 |
| kint (h–1) | Receptor internalization | 0.173 | N/A | 0.167 (0.107, 0.223) | N/A | –3.64 |
| kdeg (h–1) | Receptor degradation | 0.173a | N/A | N/A | N/A | N/A |
| Keq (ng ml–1) | Dissociation constant | 0.131 | N/A | N/A | N/A | N/A |
| Rtot0 (ng ml–1) | Baseline free receptor | 5 | N/A | N/A | N/A | N/A |
| Vmax (ng kg–1 h–1) | Maximum elimination rate | 59.1b | 144.5 (122.2, 157.7) | 56.9 (43.8, 72.1) | 145 | –3.7 |
| Km (ng ml–1) | Michaelis constant | 0.131c | 1.06 (0.616, 1.3) | 0.29 (0.0685, 0.664) | 711 | 121 |
| WSSR | Weighted sum of squared residuals | N/A | 0.567 (0.436, 0.748) | 0.243 (0.173, 0.321) | N/A | N/A |
| AIC | Akaike information criterion | N/A | 2.63 (–2.11, 7.07) | –10.0 (–15.8, –5.32) | N/A | N/A |
The median value and interquartile range were calculated and reported. Parameter bias was calculated based on median values IQR interquartile range, N/A not applicable
Fixed at kint value
Calculated as Rtot0kintV
Same to KD
Fig. 2.
Simulated PK data fitted with the original and corrected M–M models. Open circle represents simulated median data from 100 replicates. Error bar represents the interquartile range. Parameter values for simulations and model estimates are listed in Table 1. Model predictions are shown for the corrected M–M model (solid lines) and original M–M model (dashed lines)
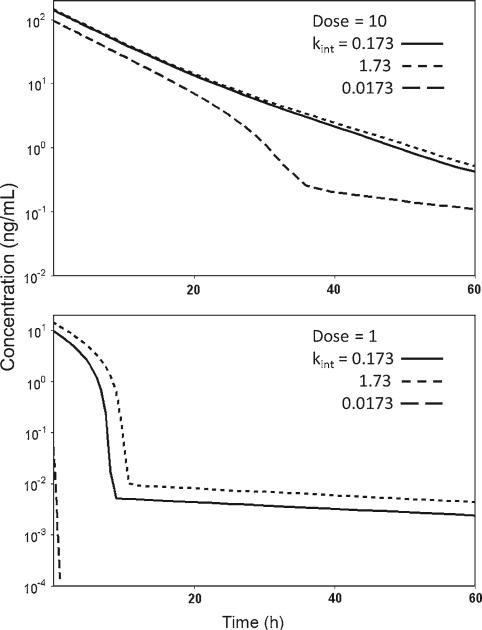
The identifiability of the kint parameter for the corrected M–M model was supported by the sensitivity analysis shown in Fig. 3. The tenfold change in the parameter value resulted in observable changes in the initial free drug concentrations Ccorr(0) which increased for later times. This implies that despite of the absence of the kint in the differential equation describing C(t), this parameter has a profound impact on the behavior of the C(t) vs. t curve, especially for lower doses.
Fig 3.
Simulation of concentration–time profiles for perturbations in kint with values of 0.173 h–1 (solid line), 1.73 h–1 (short dash line) and 0.0173 h–1 (long dash line), for dose amount of 10 μg kg–1 (upper panel) and 1 μg kg–1 (lower panel). Other parameter values are same as in Fig. 1 for the corrected M–M model
Discussion
The correction of the initial condition for the M–M approximation of the TMDD model is a logical consequence of the assumptions underlying the derivations of this model. The difference between corrected initial concentration and Dose/V is equal to the concentration of the drug bound to the target upon reaching the equilibrium. This implies that the correction of the IV bolus dose by the fraction of drug amount is of significance only at concentration levels that do not saturate the target. For higher concentrations the difference between Ccorr(0) and Dose/V will be negligible. At lower doses the M–M approximation becomes invalid due to a relatively slow target binding process that should be accounted by the full TMDD model. However, if the data in the lower concentrations region are sparse, the M–M approximation might be the only viable modeling option and the importance of the correct initial condition becomes immanent.
The volume of distribution V estimated from the original M–M model is positively biased. The estimate of linear clearance pathway kel is severely negatively biased and approaches zero for some data sets. On the other hand, the corrected M–M model produced fairly accurate estimates for these parameters. These observations imply that the lack of the dose correction may lead to an overestimation of the volume of distribution and underestimation of the clearance. Consequently, model based inferences about dose and dosing interval selections for clinical trial designs might be inaccurate. Our simulations assessing estimability of the parameters for the corrected M–M model were based on 100 replicates of the data with 15% residual error. The point of this exercise was a demonstration of an impact of the dose correction on model performance and parameter estimation. The results demonstrated better performance of the corrected M–M model than the original M–M model as well as estimability of the kint parameter.
We have presented a dose correction for a single IV bolus dose. For multiple IV doses, analogous corrections are required for each bolus. This creates an additional complexity to the presented correction in this report at the initial time where there is no drug in the system. A dose correction after multiple bolus administration has to account for the drug amount already present in the system at the time of administration. As in a single dose case, one might expect the correction to be of importance if the drug plasma concentrations prior to injections (troughs) are at levels that do not saturate the target. Further studies are necessary to determine the impact of the dose correction of the M–M approximation of the TMDD model applications to the multiple dose data.
The dose correction for IV bolus inputs can be calculated because of the instantaneous changes in free drug concentrations that this kind of inputs implies. However, such calculation is challenging for inputs that extend over the equilibration time for the drug-target interaction such as IV infusions or absorptions from extravascular sites. This time is meant to be negligible for the RB/QSS models, but if a substantial drug amount is bound to the target during the equilibration, a correction of the initial conditions for these models seems to be necessary. Analysis of TMDD models with non-instantaneous inputs has yet to be performed.
In summary, we postulated a correction to an initial condition for the M–M approximation of the TMDD PK model with an IV bolus input that was consistent with the assumptions underlying this approximation. We determined that the difference between the injected dose and one that should be used for the initial condition is equal to the amount of drug bound to the target upon reaching the equilibrium. We also observed that the corrected initial condition made the internalization rate constant kint an identifiable parameter that was not for the original M–M model. Finally, we performed a simulation exercise to check if the correction will impact the bias of the M–M parameter estimates. All the parameters estimated from the original M–M model were substantially biased. On the other hand, the corrected M–M model is able accurately estimate these parameters except for Km. WSSR and AIC suggested the better performance of corrected M–M model compared with the original M–M model. Further studies are necessary to determine the importance of the dose correction for the M–M model applications to analysis of TMDD driven PK data.
Acknowledgment
This work was supported by the National Institutes of Health Grant GM 57980.
Appendices
Appendix A: Equations describing the RB/QSS TMDD PK model
The following equations were proposed as RB and QSS approximations of the TMMD PK model and adopted for the IV bolus drug administration [2, 3]:
| (9) |
| (10) |
| (11) |
| (12) |
| (13a, b, c) |
Here ksyn denotes the zero-order rate constant for production of the target, and kdeg is the first-order rate constant for the degradation of the target.
Appendix B: Derivation of Eq. 6
The free drug plasma concentration described by (4) is a solution to the equilibrium equation [2, 3]:
| (14) |
where Keq = KD (RB) and Keq = KSS (QSS). Upon multiplying both sides of (14) by Ctot – C and rearranging the terms of the equation one can arrive at
| (15) |
Dividing both sides of (15) by Keq + C yields
| (16) |
For the RB/QSS TMDD model at time 0, Ctot(0) = Dose/V and R(0) = Rtot0. Therefore the correct initial condition for the M–M approximation C(0) = Ccorr(0) satisfies the following relationship:
| (17) |
which proves Eq. 6.
References
- 1.Mager DE, Jusko WJ. General pharmacokinetic model for drugs exhibiting target-mediated drug disposition. J Pharmacokinet Pharmacodyn. 2001;28:507–532. doi: 10.1023/a:1014414520282. [DOI] [PubMed] [Google Scholar]
- 2.Mager DE, Krzyzanski W. Quasi-equilibrium pharmacokinetic model for drugs exhibiting target-mediated drug disposition. Pharm Res. 2005;22:1589–1596. doi: 10.1007/s11095-005-6650-0. [DOI] [PubMed] [Google Scholar]
- 3.Gibiansky L, Gibiansky E, Kakkar T, Ma P. Approximations of the target-mediated drug disposition model and identifiability of model parameters. J Pharmacokinet Pharmacodyn. 2008;35:573–591. doi: 10.1007/s10928-008-9102-8. [DOI] [PubMed] [Google Scholar]
- 4.Yan X, Mager DE, Krzyzanski W. Selection between Michaelis–Menten and target-mediated drug disposition pharmacokinetic models. J Pharmacokinet Pharmacodyn. 2010;37:25–47. doi: 10.1007/s10928-009-9142-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Wang Y-MC, Krzyzanski W, Doshi S, Xiao JJ, Perez-Ruixo JJ, Chow AT. Pharmacodynamics-mediated drug disposition (PDMDD) and precursor lifespan model for single dose of romiplostim in healthy subjects. AAPS J. 2010;12:729–740. doi: 10.1208/s12248-010-9234-9. [DOI] [PMC free article] [PubMed] [Google Scholar]