Simulation tools for two-dimensional experiments in x-ray computed tomography using the FORBILD head phantom

Abstract

Mathematical phantoms are essential for the development and early-stage evaluation of image reconstruction algorithms in x-ray computed tomography (CT). This note offers tools for computer simulations using a two-dimensional (2D) phantom that models the central axial slice through the FORBILD head phantom. Introduced in 1999, in response to a need for a more robust test, the FORBILD head phantom is now seen by many as the gold standard. However, the simple Shepp-Logan phantom is still heavily used by researchers working on 2D image reconstruction. Universal acceptance of the FORBILD head phantom may have been prevented by its significantly-higher complexity: software that allows computer simulations with the Shepp-Logan phantom is not readily applicable to the FORBILD head phantom. The tools offered here address this problem. They are designed for use with Matlab^®, as well as open-source variants, such as FreeMat and Octave, which are all widely used in both academia and industry. To get started, the interested user can simply copy and paste the codes from this PDF document into Matlab^® M-files.

1 Introduction

Mathematical phantoms are essential for the development and early-stage evaluation of image reconstruction algorithms in x-ray computed tomography (CT). An important phantom was developed for this purpose in the initial years of CT. This phantom, called the Shepp-Logan phantom [1] has been heavily used, as well as a three-dimensional (3D) version of it that can be found in [2]. However, by the mid-nineties, it was recognized that this phantom and its 3D version were too simple for the evaluation of advanced reconstruction theories; more challenging phantoms were needed to improve the robustness of evaluations. In 1999, a solution to this problem was proposed by a group of CT researchers at the Institute of Medical Physics (Erlangen, Germany). Working together with scientists from Siemens Healthcare, this group developed the FORBILD phantoms [3], which model different parts of the anatomy. Among these phantoms, the models of the head and the thorax were quickly adopted by CT researchers, particularly for early-stage evaluations of new image reconstruction algorithms; for examples, see [4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18].

Unfortunately, the Shepp-Logan phantom is still largely used in papers that focus on 2D image reconstruction [19, 20, 21, 22, 23, 24, 25, 26, 27, 28]. We attribute this situation to the fact that software for data simulation with the Shepp-Logan phantom is not readily applicable to the FORBILD head phantom. Two difficulties must be overcome, and handling these typically requires a significant investment in software development. The first difficulty stems from the fact that the primitive objects forming the phantom are not merely ellipsoids; elliptical cylinders, cones, and truncated ellipsoids are also needed. Second, these objects are not combined together with the common addition formula: a precedency rule is used instead. That is, the order of the objects matters, because each object in the list is assigned the entire space it occupies, so that it can hide portions of objects that are listed prior to it.

In this paper, we present a 2D phantom that models the central axial slice through the FORBILD head phantom, and we offer simulation tools for 2D experiments with this phantom. This slice exhibits much of the complexity of the FORBILD head phantom and has been extensively employed in the development of 2D reconstruction algorithms [29, 30, 31, 32, 33, 34]. In particular, it includes more sophisticated features than the Shepp-Logan phantom, allowing the evaluation of low-contrast object detectability in the presence of artifact-inducing, high-contrast objects. The tools are designed for use with Matlab^®, as well as any open-source versions of Matlab^®, such as Octave and FreeMat.

2 Phantom definition

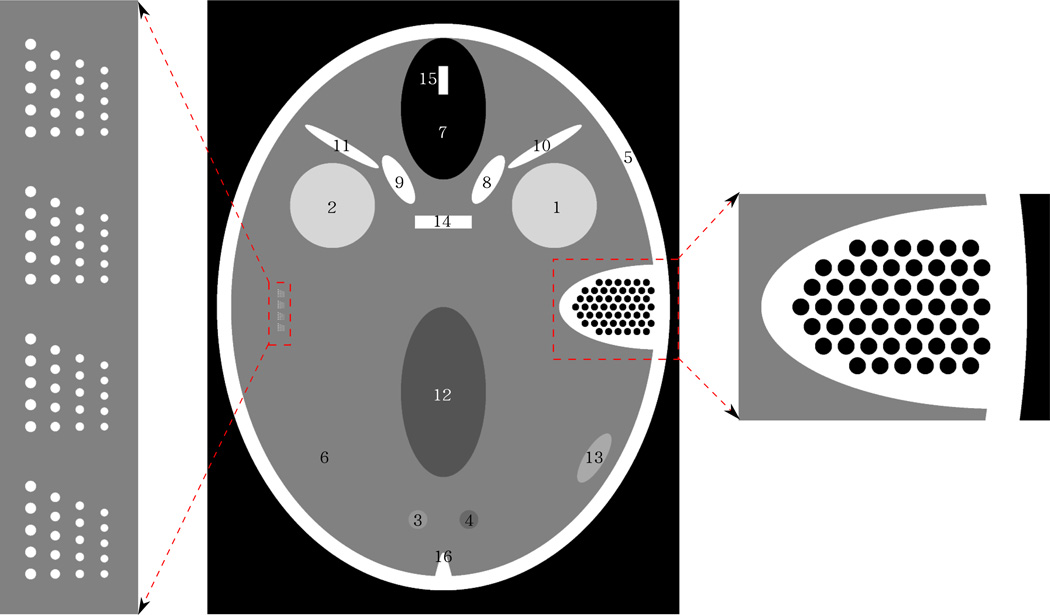
The FORBILD head phantom consists of 17 objects plus two inserts, which we refer to as the left and right ears. Each of the 17 objects is either an ellipsoid, a cylinder, or a cone, or a portion thereof. The left ear is a resolution pattern built from ellipsoids of various sizes. The right ear is a model of the temporal bone, defined as a set of spherical air cavities within a high-density (bone-like) material. A depiction of how the 17 objects and the two inserts appear within the central axial plane through the phantom is given in Figure 1. Note that only 16, not 17 objects are seen in this figure, because the two cones that model the petrous bone cannot be distinguished from each other in this plane; they are reduced to the object labelled as number 16.

Figure 1.

Central axial slice through the FORBILD head phantom. In this slice, only 16 of the 17 objects forming the phantom can be seen. These objects are each labelled with a number between 1 and 16. The phantom also includes two inserts: the left and right ears, a magnified version of which is shown. Display window: [35, 65]HU.

The goal of this paper is to provide simulation tools for a 2D phantom that models the image displayed in Figure 1. A proper name for this phantom may be “The 2D FORBILD head phantom”. The tools are offered with the option of including or leaving out either of the two ears. Our description is based on Cartesian coordinates, x and y, that are measured along the minor and major axes of the outer ellipse in Figure 1. The origin (x, y) = (0, 0) is at the center of this ellipse.

3 Modeling technique

We present here our mathematical model for the 2D FORBILD head phantom. We start by discussing the overall design, then provide details on the most important aspects of the model. Note that lengths are always expressed in centimeters.

3.1 Design

The 2D FORBILD head phantom is built as a linear combination of functions that are each equal to one within an ellipse or the portion of an ellipse and zero outside. Whenever the portion of an ellipse is involved, this portion is identified through the use of a clipping line, as discussed later. This construction has the advantage of yielding a simple description and of enabling fast data simulation, particularly in comparison with using object superposition with a precedency rule (which is the method employed in the definition of the FORBILD phantom). However, these advantages come with a cost: our model is not an exact representation of the central axial slice through the FORBILD head phantom — it is a slight approximation. The misrepresentation issue is linked to the petrous bone (object 16), which is created from a cone in such a way that its boundary is a parabola that cannot be exactly described by an ellipse. In our model, the petrous bone is approximately represented, whereas all other features of the FORBILD phantom are accurately reproduced.

3.2 Ellipses and clipping lines

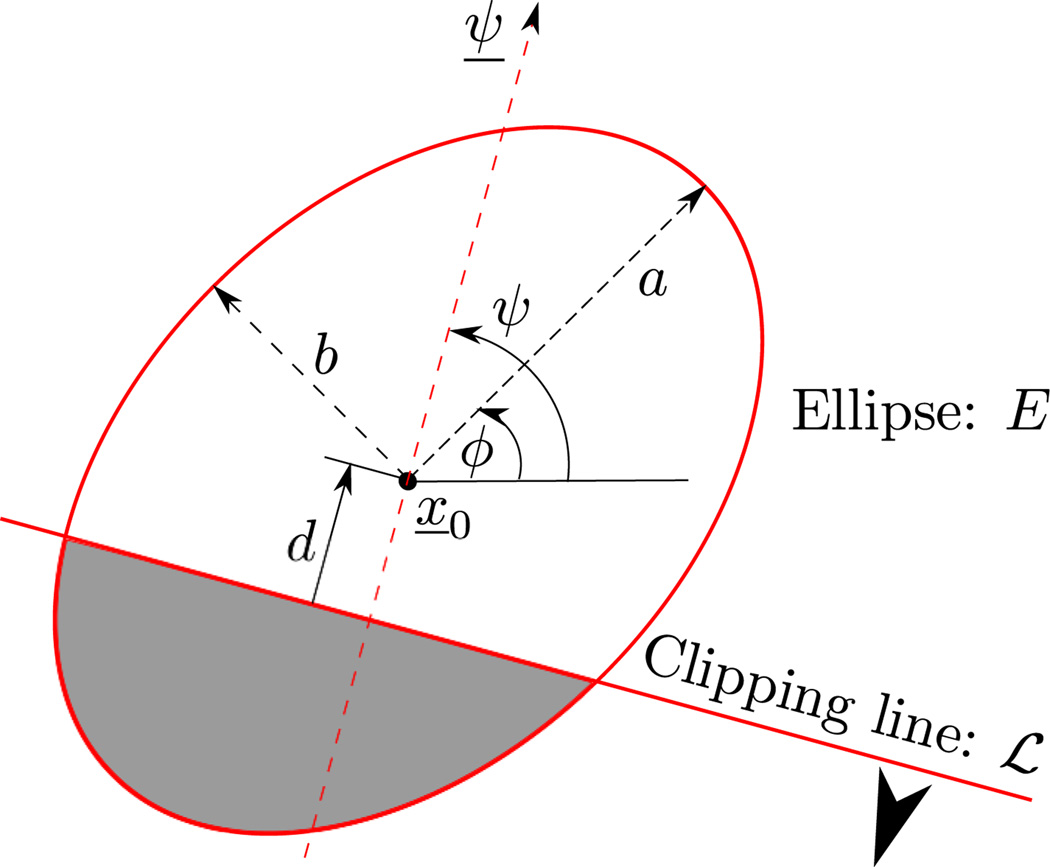
Let E be the ellipse of half axes a and b that is centered at x̱₀ and makes an angle ϕ with the x-axis, as shown in Figure 2. By definition, any point x̱ within E satisfies the equation

$${(\mathrm{x̱}-{\mathrm{x̱}}_0)}^T{\mathbf{Q}}^T{\mathbf{D}}^2\mathbf{Q}(\mathrm{x̱}-{\mathrm{x̱}}_0)\le 1,$$ (1)

where

$$\mathbf{D}=\left[\begin{array}{cc}\hfill 1/a\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1/b\hfill \end{array}\right],\mathbf{Q}=\left[\begin{array}{cc}\hfill \text{cos }\varphi \hfill & \hfill \text{sin }\varphi \hfill \\ \hfill -\text{sin }\varphi \hfill & \hfill \text{cos }\varphi \hfill \end{array}\right].$$ (2)

Figure 2.

Illustration of an ellipse together with a clipping line. The portion retained after clipping is indicated by the arrow and the shaded area. Note that d is a signed distance that is negative in this drawing.

Next, let ℒ be the line that is at signed distance d from the center of the ellipse in the direction of a given vector ψ̱ = (cos ψ, sin ψ), as illustrated in Figure 2. When the magnitude of d is small enough relative to the size of the ellipse, line ℒ intersects the ellipse and can be used to single out a portion of it. When perfoming this role, we say that ℒ is a clipping line. The portion of the ellipse that is identified as the object of interest is the set of points x̱ such that

$${(\mathrm{x̱}-{\mathrm{x̱}}_0)}^T\mathrm{\psi ̱}<d.$$ (3)

Given an ellipse E and a number K of clipping lines, described with d_i and ψ̱_i = (cos ψ_i, sin ψ_i), where i = 1, …, K, we introduce a characteristic function:

$$f(\mathrm{x̱})=\{\begin{array}{cc}1\hfill & \text{if }\mathrm{x̱}\in E\text{ and }{(\mathrm{x̱}-{\mathrm{x̱}}_0)}^T{\mathrm{\psi ̱}}_i<d_i,i=1,\dots ,K\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}.$$ (4)

Our description of The 2D FORBILD head phantom without ears involves 17 objects that are each defined as one ellipse together with a number of clipping lines. The n^th object is associated with a relative density value, μ_n, as well as with a function f_n(x̱) that is defined in the same way as f(x̱) in (4), so that the mathematical expression for the phantom with no ears is

$$\mu (\mathrm{x̱})={\displaystyle \sum _{n=1}^{17}}{\mu }_n{f}_n(\mathrm{x̱}).$$ (5)

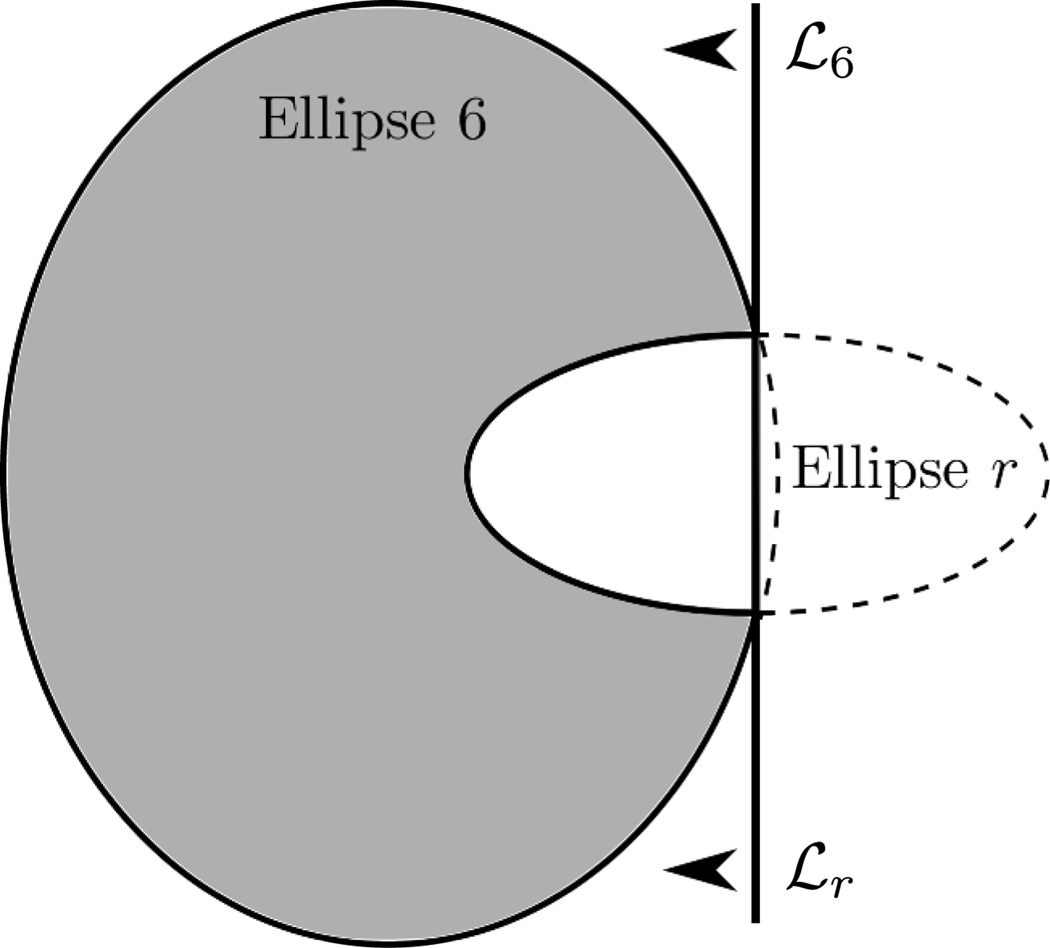
When desired, the right ear (see Figure 1) is included using the following transformations. First, object number 6 is truncated, and a new clipped ellipse is introduced, as drawn in Figure 3, to create the main body of this ear. The relative density assigned to this new ellipse is such that the value of μ(x̱) within the ear is equal to that of the skull (object 5) before adding the air cavities. Next, the air cavities are inserted within the ear as 53 small circular disks. The inclusion of the left ear is much simpler, as it amounts to just adding 80 circular disks.

Figure 3.

Construction of the right ear body. Object 6, which represents the brain matter, is clipped by a vertical line denoted as ℒ₆, and a new ellipse, called ellipse r, is introduced. This new ellipse is clipped by line ℒ_r, which is geometrically identical to ℒ₆, and is added with a relative density such that the overall density of the right ear body is equal to that of object 5, which depicts the skull.

Note that the full description of all objects involved in the phantom is embedded within the first Matlab^® function that we supply. Note also that the values taken by μ(x̱) are to be interpreted as attenuation factors relative to that of water, so that 1000 (μ(x̱)−1) is in Hounsfield units. To perform simulations with noise or a polychromatic x-ray beam, some corrections must be applied, which will be discussed later.

3.3 Modeling of the petrous bone

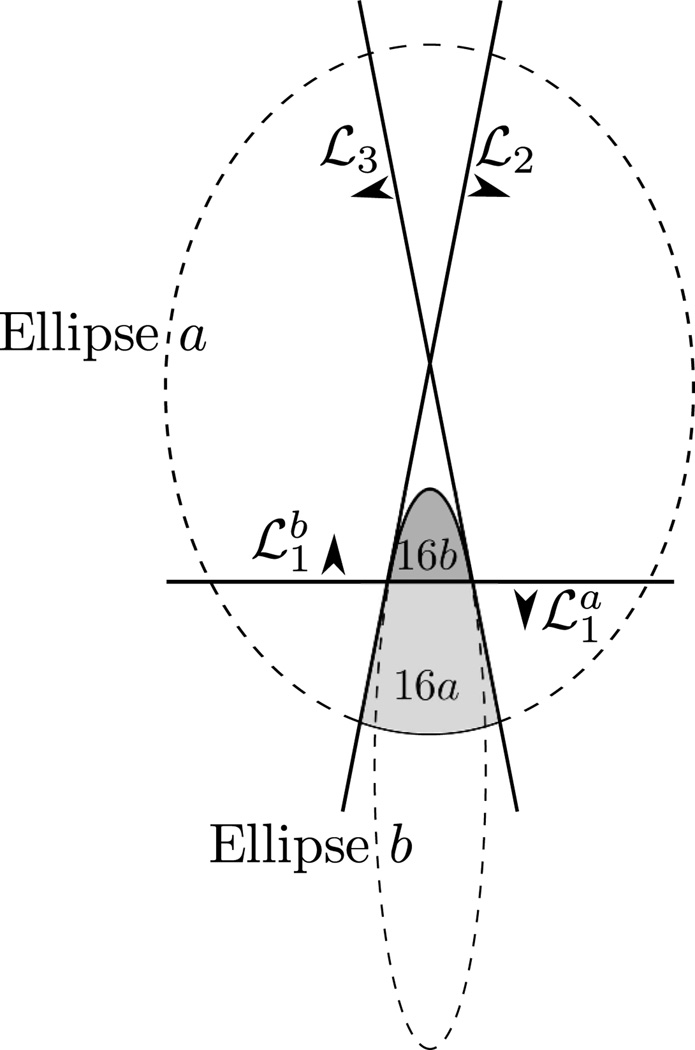
As discused earlier, our model involves an approximation because the petrous bone (object number 16 in Figure 1) could not be exactly represented using ellipses. We have represented this object using a combination of two clipped ellipses, denoted as objects 16a and 16b in Figure 4, where Ellipse a is the same ellipse as that describing object 6. Note that Figure 4 is not drawn to scale: objects 16a and 16b are magnified for visibility purpose. Object 16a is the portion of Ellipse a that remains after it is clipped by lines ${ℒ}_1^a$, ℒ₂ and ℒ₃. Object 16b is the portion of another ellipse, called Ellipse b, that is clipped by line ${ℒ}_1^b$. The major axis of Ellipse a is colinear with that of Ellipse b, and lines ℒ₂ and ℒ₃ are mirror images of each other relative to this major axis. Moreover, these two lines are tangent to Ellipse b, and lines ${ℒ}_1^a$ and ${ℒ}_1^b$, which are on top of each other, pass through the two tangency points, so that the boundary of the union of objects 16a and 16b is both continuous and differentiable.

Figure 4.

Modeling of the petrous bone (object number 16 in Figure 1). Our model is based on two ellipse portions: 16a from Ellipse a and 16b from Ellipse b.

The level of approximation involved in our representation of the petrous bone can be appreciated through inspection of images given in Figure 5. A very good approximation is achieved near the points where ℒ₂ and ℒ₃ meet Ellipse b, as well as near the tip of the bone. Away from these regions, the size of our pretrous bone slightly differs from that of the original bone: see the plot in Figure 5, which shows the width difference in x as a function of y.

Figure 5.

Approximation in our representation of the petrous bone. From left to right: the original bone; our approximation; mask highlighting the locations where the representation differs from the original; difference in width (in cm) as a function of y, from baseline to tip, between the representation and the original.

Since the approximation involved in our representation of the petrous bone is fairly smooth and small in size, it is not expected to affect image quality evaluations in x-ray CT experiments.

4 Simulation Tools

We provide the reader with four Matlab^® functions. The first function creates a matrix-based analytical representation of the phantom, and it must be executed before running the other functions. When executing this first function, the user gets the opportunity to decide which, if any, of the two ears should be included. The second function changes the attenuation value within the description of the phantom; it is only needed for experiments involving a polychromatic x-ray beam. The last two functions allow the user to obtain a discretized version of the phantom and to compute exact line integrals through the phantom, both with freely-selectable sampling conditions.

This section is divided into three subsections that provide guidance on how to use each of the four Matlab^® functions, as well as specific details on how these functions are built. Note that all four functions can be copied and pasted directly from the PDF version of this paper into Matlab^® M-files, naming each file with the name of the function it contains.

4.1 Analytical representation

The function to generate the analytical representation of the 2D FORBILD head phantom is

$$[\mathbf{\text{phantom}}]=\mathbf{\text{analytical}}\_\mathbf{\text{phantom}}\mathbf{(}\mathbf{\text{oL}},\mathbf{\text{oR}}\mathbf{)},$$

where [oL] and [oR] are two input parameters acting on the inclusion or not of the left and right inner ears. By setting [oL = 1] (resp. [oR = 1]), the left inner ear (resp. the right inner ear) is added to the phantom, whereas any other value chosen for [oL] (resp. [oR]) results in the corresponding ear being left out.

The output of this function, called phantom above, is a structure containing two elements, phantom.E and phantom.C, which are both matrices containing the parameters for the ellipses and clipping lines forming the phantom, respectively. Each row of phantom.E defines one ellipse and the number of lines clipping it; the elements of any row successively correspond to the (x, y) coordinates of the ellipse center, the half lengths, the orientation angle, the relative attenuation coefficient, and the number of clipping lines. (Note that the correspondance between the object labels in Figure 1 and the rows of E is highlighted in the Matlab^® function using a comment (number) at the end of each row of E.)

The columns of phantom.C each define one clipping line. The first element of each column specifies the signed distance d, whereas the second element gives the orientation angle, ψ, in degrees. The order of the columns is critical and defined in agreement with the rows in phantom.E. Since there are no clipping lines associated with the first 12 rows in phantom.E, the first four columns of phantom.C define the clipping lines for the ellipse described in the 13th row of phantom.E (object 14), whereas the next four columns are the clipping lines for the ellipse in the 14th row, and so on.

As discussed earlier, the attenuation values within the phantom are expressed relative to that of water. There are two options to perform experiments with physical attenuation values. The first option is straightforward and generally sufficient for experiments assuming a monochromatic beam: simply multiply any line integral computed from phantom with the linear attenuation coefficient of water at some energy of interest. For example, a multiplication factor of 0.183 can be used when the energy of interest is 80 keV, which is close to the average energy of the beam for a diagnostic CT scan performed at 120kVp. In defining this factor, recall that all lengths are expressed in centimeters; the attenuation coefficient for water at 80keV is 0.183/cm.

This first option discussed above to create physical line integrals is a minimal requirement to perform experiments with noise, which can be peformed as explained, for example, in [33]. To perform experiments that involve a polychromatic x-ray beam, it is better to adopt another option, which accounts for the fact that the linear attenuation coefficients for water and bone change with the photon energy, denoted as E_p. This second option corresponds to using the function

$$[\mathbf{\text{physphantom}}]=\mathbf{\text{physical}}\_\mathbf{\text{value}}\mathbf{(}\mathbf{\text{phantom}}\mathbf{,}\mathbf{\text{muW}}\mathbf{,}\mathbf{\text{muB}}\mathbf{)},$$

which transforms all attenuation coefficients within the phantom into physical values based on two materials, water and bone, so that any line integral computed from the output of this function, physphantom, has a physical meaning. The second and the third arguments are the linear attenuation coefficients for water and bone, respectively, at a given value for E_p. Conceptually, physical_value changes all attenuation values of 1.8 to muB, and replaces all other attenuation values by their product with muW (e.g., a value of 1.05 becomes 1.05 muW). Thus, all attenuation values that are equal to 1.8 are assumed to represent bone; and all attenuation values that differ from 1.8 are assumed to represent materials that behave like water, except for a relative change in mass density. A typical procedure for an experiment with a polychromatic x-ray beam is to compute the line integrals of interest for a number of energy values and combine those afterwards using energy spectrum information [35].

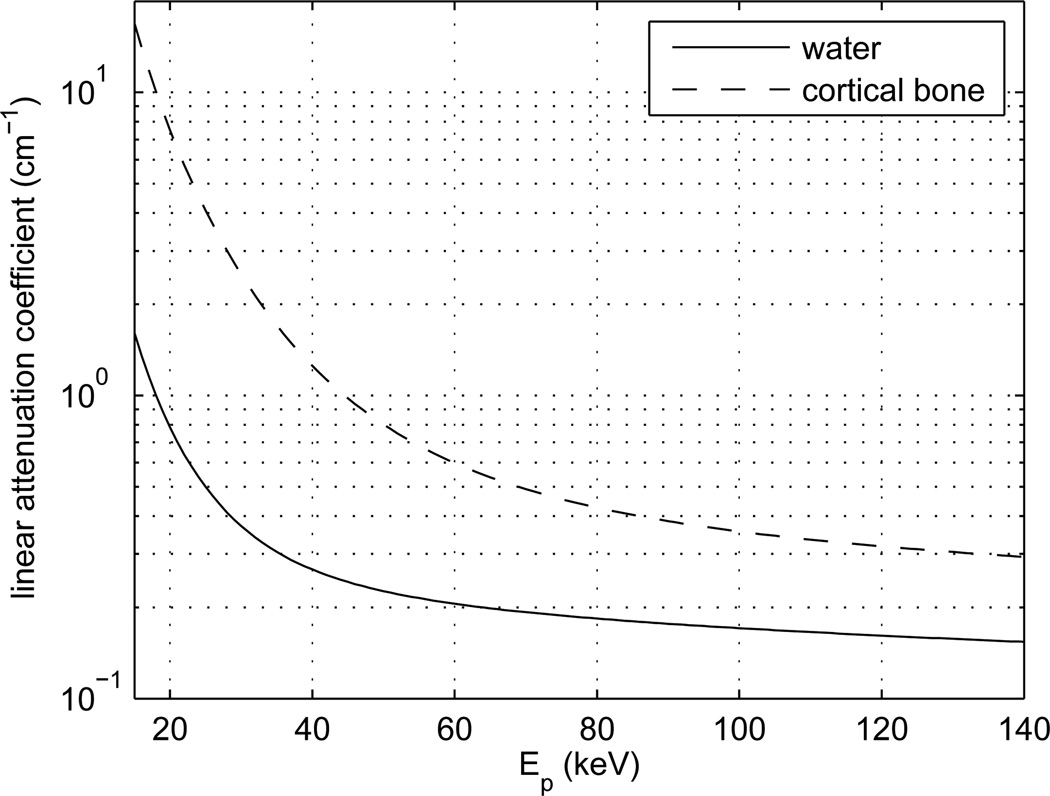
Figure 6 shows how the linear attenuation coefficients for water and cortical bone vary with E_p. These two curves were obtained using the cross-section databases from NIST [36]. They are well approximated using the following polynomial-based expression:

$$\mu \simeq \text{exp }\{p_1{\epsilon }^4+p_2{\epsilon }^3+p_3{\epsilon }^2+p_4\epsilon +p_5\}$$ (6)

where ε = ln E_p, i.e., ε is the natural logarithm of E_p. The coefficients that appear in this expression are given in table (1). Note that μ and E_p are expressed in cm⁻¹ and keV, respectively. Note also that the fitting is only accurate for E_p between 15 keV and 140 keV. The maximum relative error within this range is 2.5%. Finally, observe that the ratio between the attenuation coefficients of cortical bone and water at 80 keV is not 1.8, as could be expected; it is 2.32. Technically-speaking, the human skull is not made of cortical bone only: the inner portion of the skull is made of less attenuating material, but the FORBILD head phantom does not allow for this level of detail. If a lower attenuation effect is desired, the third input of physical_value may be chosen as 0.77 times the linear attenuation coefficient of cortical bone. Either way, the most important issue is to clearly report in any research paper the expression that was used for muB.

Figure 6.

Linear attenuation coefficients for water and cortical bone as a function of the photon energy, E_p.

Table 1.

Coefficients for the polynomial-based approximation of curves in figure (6); see equation (6).

	p1	p2	p3	p4	p5
water	−0.014027	−0.045959	2.366105	−13.683202	21.867818
cortical bone	−0.179564	2.851439	−16.055087	35.924159	−23.704935

4.2 Phantom discretization

A discrete version of the 2D FORBILD head phantom can be obtained using the following Matlab^® function:

$$[\mathbf{\text{image}}]=\mathbf{\text{discrete}}\_\mathbf{\text{phantom}}\mathbf{(}\mathbf{\text{xcoord}}\mathbf{,}\mathbf{\text{ycoord}}\mathbf{,}\mathbf{\text{phantom}}\mathbf{)}.$$

In this function, the third input argument is the output of analytical_phantom, or the output of physical_value, whereas the first and the second inputs are two matrices of the same size that respectively specify the x and the y coordinates corresponding to all desired samples. By construction, the ouput result, image, is a matrix that has the same size as the first two input arguments, with element (k, l) of this matrix being the value taken by the phantom at location (x, y) with x and y given by element (k, l) of the first and the second input arguments, respectively.

For example, suppose that we wish to create a 400 × 400 image of the phantom that is centered on the origin with a sampling step of 0.075 cm in both x and y. This task can be performed using the following Matlab^® command lines to generate the first two input arguments:

x      = ((0:399)−199.5)*0.075;
y      = ((0:399)−199.5)*0.075;;
xcoord = ones(400,1)*x;
ycoord = transpose(y)*ones(1,400);

From these inputs, the output, image, will be a 400 × 400 matrix that contains pixel values for a fixed y in each row, with the first row corresponding to the most negative value of y. Within each row, x increases from left to right.

4.3 Line integrals

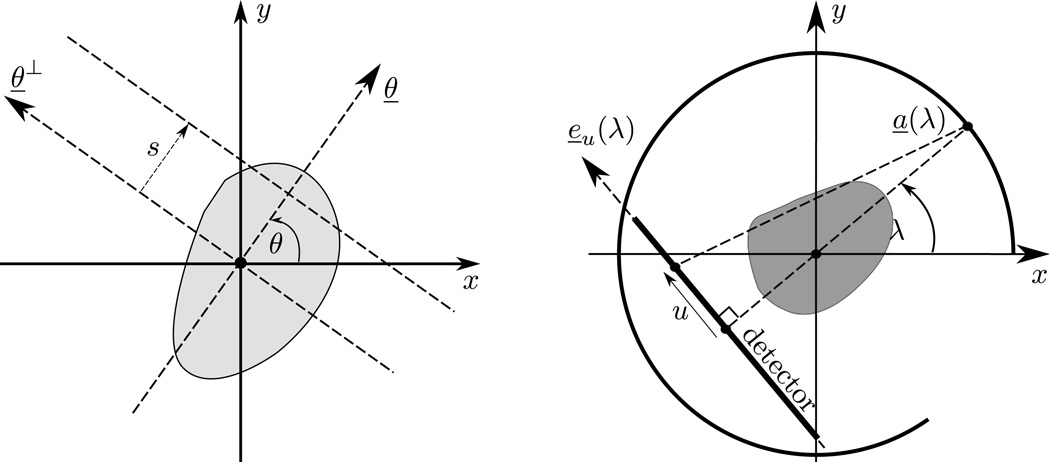
The second Matlab^® function is for computation of line integrals through the phantom. We describe lines using the Radon transform notation, i.e., any line L through the object is specified using a scalar, s, and an angle, θ. By definition, line L(θ, s) is orthogonal to vector θ̱ = (cos θ, sin θ) at signed distance s from the origin, with s measured positively in the direction of θ̱, as shown on the left side of Figure 7.

Figure 7.

Circular scan geometries using flat detector. Left: the parallel beam geometry; right: the fan beam geometry with radius of R and source-to-detector distance of D.

Any sets of line integrals through The 2D FORBILD head phantom can be obtained using the following function:

$$[\mathbf{\text{sino}}]=\mathbf{\text{line}}\_\mathbf{\text{integrals}}\mathbf{(}\mathbf{\text{scoord}}\mathbf{,}\mathbf{\text{theta}}\mathbf{,}\mathbf{\text{phantom}}\mathbf{)}.$$

In this function, the third input is the output of analytical_phantom, or the output of physical_value, whereas the first and the second inputs are two matrices of the same size that respectively specify the parameters s and θ corresponding to all desired lines. By construction, the ouput result, sino, is a matrix that has the same size as the first two input arguments, with element (k, l) of this matrix being the integral of the phantom along the line L(θ, s) that results from using the element (k, l) of the first and the second input arguments to define s and θ, respectively.

For example, suppose that we wish to obtain a set of 1160 non-truncated parallel-beam projections, with a sampling step of 0.075 cm in s, and with the first projection in the direction of y. Given that the phantom fits within a disk of radius 12 cm centered on the origin, a minimum of 320 rays per view is needed. Suppose that we set out for 351 rays evenly distributed across the origin s = 0. Then, the following command lines in Matlab^® yield the inputs for lines_integrals:

s      = ((0:350)−175)*0.075;
theta  = (0:1159)*pi/1160−pi/2;
scoord = ones(1160,1)*s;
theta  = transpose(theta)*ones(1,351);

From these inputs, the output, sino, will be a matrix of size 1160 × 351, with each row yielding one of the desired parallel-beam projections.

Our Matlab^® function can also be used to create fan-beam data. For illustration, consider a fan-beam data acquisition geometry with a linear detector array, as shown on the right side of Figure 7. The distance from the source to the rotation center is R, and angle λ describes the rotation, so that the source position is a̱(λ) = (Rcos λ, Rsin λ). Also, the detector is parallel to e̱_u (λ) = (−sin λ, cos λ) at distance D from the source, with each point on the detector identified using a coordinate u that is measured positively in the direction of e̱_u (λ), and with u = 0 coinciding with the orthogonal projection of the source onto the detector. In this geometry, any line that connects the source to a point on the detector is given by

$$\{\begin{array}{c}\theta =\lambda +\pi /2-\text{arctan}(u/D)\hfill \\ s=\mathit{\text{uR}}/\sqrt{D^2+u^2}\hfill \end{array}.$$ (7)

Therefore, the following Matlab^® command lines will create the two inputs required to obtain M fan-beam projections over 360 degrees with N rays per view sampled with a stepsize W in u:

u       = ((0:N−1)−(N−1)/2)*W;
lambda  = (0:M−1)*2*pi/M; %lambda
uc      = ones(M,1)*u;
lambdac = transpose(lambda)*ones(1,N);
scoord  = R*uc./sqrt(D^2+uc.^2);
theta   = lambdac+pi/2−atan(uc/D);

For the interested reader, Appendix I provides details on the method and the associated notation used to compute the line integrals. There is however one important numerical aspect that we wish to highlight here. This aspect regards our handling of cases where L(θ, s) is parallel to one of the clipping lines. For any such line, we decided to add a tiny increment to the value of θ (specifically, 10⁻¹⁰) to circumvent any mathematical singularity that could appear at some values of s. While having a negligible effect on the accuracy of simulations, this increment avoids errors that could occur when L(θ, s) is identical to one of the clipping lines used to define the petrous bone or the right ear. Moreover, it regularizes the output in cases where the line integral through an object is undefined, which occurs when the boundary of an object includes a segment of line and the line integral is to be taken along this line segment, as with object 14.

5 Conclusions

The primary purpose of this note was to offer simulation tools for 2D experiments in x-ray CT using a phantom that models the central slice through the FORBILD head phantom. These tools consist of four different Matlab^® functions, the first two of which are dedicated to the phantom definition, whereas the other two are for phantom discretization and line integral computation. The reader might have noticed that the last two functions are not restricted to the 2D FORBILD phantom. They apply to any 2D phantom that is built by addition of clipped ellipses. The tools offered here should enable more widespread use of the FORBILD head phantom, thereby facilitating the development of modern 2D image reconstruction theories.

Appendix I: computation of line integrals

Here, we describe the technique used to compute a line integral through the object described by equation (4). Any line integral through The 2D FORBILD head phantom is a weighted sum of such line integrals, obtained using equation (5).

By definition, any point x̱ on L(θ, s) can be written in the form

$$\mathrm{x̱}=s\mathrm{\theta ̱}+t{\mathrm{\theta ̱}}^{\perp }$$ (8)

for some t ∈ ℝ, with θ̱ = (cos θ, sin θ) and θ̱^⊥ = (−sin θ, cos θ). To get the integral of the function f in (4) on L(θ, s), we determine if L(θ, s) intersects the support of f or not, and at what values of t. If there are no intersections, the integral is zero. Otherwise, since the support of f is convex, there is only one entrance point and one exit point, and these two points fully determine the value for the desired integral, given that f is constant within its support. To determine the locations where L(θ, s) possibly meets the support of f, we first examine the intersections between L(θ, s) and the ellipse E forming (4), then we refine the results by examining the impact of each clipping line, as explained hereafter.

Assuming that x̱ is on the boundary of the ellipse, which is given by (1), we obtain a quadratic equation for t:

$${({\mathrm{s̱}}_0+t{\mathrm{\theta ̱}}^{\perp })}^T{\mathbf{Q}}^T{\mathbf{D}}^2\mathbf{Q}({\mathrm{s̱}}_0+t{\mathrm{\theta ̱}}^{\perp })=1,$$ (9)

where s̱₀ = sθ̱ − x̱₀. For the Matlab^® function, this equation is rewritten in the form:

$${\mathit{\text{At}}}^2+\mathit{\text{Bt}}+C=0,\text{ with }\{\begin{array}{cc}A\hfill & ={\Vert \mathbf{\text{DQ}}{\mathrm{\theta ̱}}^{\perp }\Vert }^2\hfill \\ B\hfill & =2(\mathbf{\text{DQ}}{\mathrm{\theta ̱}}^{\perp })·(\mathbf{\text{DQ}}{\mathrm{s̱}}_0)\hfill \\ C\hfill & ={\Vert \mathbf{\text{DQ}}{\mathrm{s̱}}_0\Vert }^2-1.\hfill \end{array}$$

When B² > 4AC, there exist two solutions t_P and t_Q, which indicates two intersection points between E and L(θ, s), denoted as P and Q, with t_Q > t_P. When B² ≤ 4AC, the line integral is zero.

Once t_P and t_Q are known, the impact of each clipping line is determined by evaluating whether t_P and t_Q corresponds to points within the retained portion of the ellipse or not. For clipping line ℒ(ψ_i, d_i), this evaluation is performed using the following inequality test:

$$t{\mathrm{\theta ̱}}^{\perp }·{\mathrm{\psi ̱}}_i<d_i-{\mathrm{s̱}}_0·{\mathrm{\psi ̱}}_i.$$ (10)

If t_Q fails to satisfy this inequality, then t_Q is replaced by

$$t_Z=(d_i-{\mathrm{s̱}}_0·{\mathrm{\psi ̱}}_i)/({\mathrm{\theta ̱}}^{\perp }·{\mathrm{\psi ̱}}_i),$$ (11)

and the same operation is applied to t_P. Geometrically, t_Z corresponds to the intersection point between L(θ, s) and ℒ(ψ_i, d_i). Once all clipping lines have been considered, the line integral is attributed the value of t_Q − t_P, which may be zero if both t_Q and t_P satisfy none of the clipping-line inequalities.

Naturally, the expression for t_Z is only well-defined when the denominator in (11) is non-zero, which is always the case when L(θ, s) and ℒ(ψ_i, d_i) are non-parallel. In our Matlab^® function, this geometrical arrangement is enforced through the addition of a tiny increment to θ whenever L(θ, s) is parallel to one of the clipping lines (recall the discussion at the end of section 4.3).

Appendix II: Matlab^® functions

function [ phantom ] = analytical_phantom(oL, oR)
if (oL~=1) oL=0; end; if (oR~=1) oR=0; end;
 sha   = 0.2*sqrt(3);            y016b = −14.294530834372887;
a16b   = 0.443194085308632;       b16b =   3.892760834372886;
E=[−4.7    4.3      1.79989    1.79989     0       0.010   0; %1
    4.7    4.3      1.79989    1.79989     0       0.010   0; %2
   −1.08  −9        0.4        0.4         0       0.0025  0; %3
    1.08  −9        0.4        0.4         0      −0.0025  0; %4
    0      0        9.6        12          0       1.800   0; %5
    0      8.4      1.8        3.0         0      −1.050   0; %7
    1.9    5.4      0.41633    1.17425   −31.07698 0.750   0; %8
   −1.9    5.4      0.41633    1.17425    31.07698 0.750   0; %9
   −4.3    6.8      1.8        0.24      −30       0.750   0; %10
    4.3    6.8      1.8        0.24       30       0.750   0; %11
    0     −3.6      1.8        3.6        0       −0.005   0; %12
  6.39395 −6.39395  1.2        0.42      58.1      0.005   0; %13
    0      3.6      2          2          0        0.750   4; %14
    0      9.6      1.8        3.0        0        1.800   4; %15
    0      0        9.0        11.4       0        0.750   3; %16a
    0     y016b     a16b       b16b       0        0.750   1; %16b
    0      0        9.0        11.4       0       −0.750  oR; %6
    9.1    0        4.2        1.8        0        0.750   1];%R_ear
%generate the air cavities in the right ear
cavity1     = transpose(8.8:−0.4:5.6);    cavity2 = zeros(9,1);
cavity3_7   = ones(53,1)*[0.15 0.15   0  −1.800 0];
for j = 1:3    kj = 8−2*floor(j/3);    dj = 0.2*mod(j,2);
cavity1 = [cavity1; cavity1(1:kj)−dj;  cavity1(1:kj)−dj];
cavity2 = [cavity2; j*sha*ones(kj,1); −j*sha*ones(kj,1)]; end
E_cavity    = [cavity1 cavity2 cavity3_7];
%generate the left ear (resolution pattern)
x0    = −7.0;y0 = −1.0;d0_xy = 0.04;
d_xy  = [0.0357, 0.0312, 0.0278, 0.0250];
x00   = zeros(0,0);      y00 = zeros(0,0);
ab  = 0.5*ones(5,1)*d_xy; ab = ab(:)*ones(1,4);
leftear4_7 = [ab(:) ab(:) ones(80,1)*[0 0.750 0]];
for i = 1:4 y00 = [y00; transpose(y0+(0:4)*2*d_xy(i))];
x00 = [x00; (x0+2*(i−1)*d0_xy)*ones(5,1)]; end
x00 = x00*ones(1,4);
y00 = [y00;y00+12*d0_xy; y00+24*d0_xy; y00+36*d0_xy];
leftear = [x00(:) y00 leftear4_7];
C=[ 1.2     1.2     0.27884  0.27884         0.60687  0.60687  0.2 ...
    0.2    −2.605  −2.605  −10.71177  y016b+10.71177  8.88740 −0.21260;
    0       180     90       270             90       270      0   ...
  180       15      165      90              270      0        0     ];
if    (oL==0&oR==0) phantom.E=E(1:17,:);           phantom.C=C(:,1:12);
elseif(oL==0&oR==1) phantom.E=[E;E_cavity];        phantom.C=C;
elseif(oL==1&oR==0) phantom.E=[leftear;E(1:17,:)]; phantom.C=C(:,1:12);
else                phantom.E=[leftear;E;E_cavity];phantom.C=C;     end
end

function [ physphantom ] = physical_value(phantom,muW,muB)
physphantom.E=phantom.E;
physphantom.C=phantom.C;
nrows=size(phantom.E,1);
shift=0;if (nrows > 71) shift=80;end
if (nrows >= 97) physphantom.E(1:80,6)=muB−1.05*muW;end
if (nrows == 71 || nrows == 151)
     physphantom.E(18+shift,6)=muB−1.05*muW;
     physphantom.E((19:71)+shift,6)=−muB;
end
physphantom.E(5+shift,6)=muB;
physphantom.E(17+shift,6)=1.05*muW−muB;
physphantom.E(6+shift,6)=−1.05*muW;
physphantom.E(14+shift,6)=muB;
physphantom.E([7 8 9 10 13 15 16]+shift,6)=muB−1.05*muW;
j=[1 2 3 4 11 12];
physphantom.E(j+shift,6)=muW*phantom.E(j+shift,6);
end

function [ image ] = discrete_phantom(xcoord,ycoord,phantom)
image   = zeros(size(xcoord));
nclipinfo = 0;
for k   = 1:length(phantom.E(:,1))
    Vx0 = [transpose(xcoord(:))−phantom.E(k,1); transpose(ycoord(:))−phantom.E(k,2)];
    D   = [1/phantom.E(k,3) 0;0 1/phantom.E(k,4)];
    phi =  phantom.E(k,5)*pi/180;
    Q   = [cos(phi) sin(phi); −sin(phi) cos(phi)];
    f   = phantom.E(k,6);
    nclip     = phantom.E(k,7);
    equation1 = sum((D*Q*Vx0).^2);
    i   = find(equation1<=1.0);
    if (nclip > 0)
        for j = 1:nclip
            nclipinfo = nclipinfo+1;
            d         = phantom.C(1,nclipinfo);
            psi       = phantom.C(2,nclipinfo)*pi/180;
            equation2 = ([cos(psi) sin(psi)]*Vx0);
            i         = i(find(equation2(i)<d));
        end
end
image(i)  = image(i)+f;
end

function [ sino ] = line_integrals(scoord,theta,phantom)
sinth = sin(transpose(theta(:)));costh = cos(transpose(theta(:)));
meps  = 1e−10; nclipinfo = 0;     mask  = zeros(size(theta));
for k=1:size(phantom.C,2)
    psi = phantom.C(2,k)*pi/180;    tmp = −sinth*cos(psi)+costh*sin(psi);
    kk  = find(abs(tmp)<meps); mask(kk) = meps;
end
theta= theta+mask;               sino =  zeros(1,length(scoord(:)));
sinth = sin(transpose(theta(:)));costh =  cos(transpose(theta(:)));
sx    = transpose(scoord(:)).*costh;  sy = transpose(scoord(:)).*sinth;
for k=1:length(phantom.E(:,1))
    x0    = phantom.E(k,1);          y0    = phantom.E(k,2);
    a     = phantom.E(k,3);          b     = phantom.E(k,4);
    phi   = phantom.E(k,5)*pi/180;   f     = phantom.E(k,6);
    nclip = phantom.E(k,7);          s0    = [sx−x0;sy−y0];
    DQ = [cos(phi)/a sin(phi)/a;  −sin(phi)/b cos(phi)/b];
    DQthp = DQ*[−sinth;costh];       DQs0  = DQ*s0;
    A  = sum(DQthp.^2);                 B  = 2*sum(DQthp.*DQs0);
    C  = sum(DQs0.^2)−1;          equation = B.^2–4*A.*C;
    i = find(equation>0);
    tp = 0.5*(−B(i)+sqrt(equation(i)))./A(i);
    tq = 0.5*(−B(i)−sqrt(equation(i)))./A(i);
    if (nclip>0)
       for j = 1:nclip
         nclipinfo = nclipinfo+1;
         d  = phantom.C(1,nclipinfo);
         psi= phantom.C(2,nclipinfo)*pi/180;
         xp = sx(i)−tp.*sinth(i);     yp = sy(i)+tp.*costh(i);
         xq = sx(i)−tq.*sinth(i);     yq = sy(i)+tq.*costh(i);
         tz = d−cos(psi)*s0(1,i)−sin(psi)*s0(2,i);
         tz = tz./(−sinth(i)*cos(psi)+costh(i)*sin(psi));
         equation2 = ((xp−x0)*cos(psi)+(yp−y0)*sin(psi));
         equation3 = ((xq−x0)*cos(psi)+(yq−y0)*sin(psi));
         m1 = find(equation3>=d); tq(m1) = tz(m1);
         m2 = find(equation2>=d); tp(m2) = tz(m2);
       end
    end
    sinok = f*abs(tp−tq); sino(i) = sino(i)+sinok;
end
sino = reshape(sino,size(theta));
end