Abstract
The intraclass correlation coefficient (ICC) is a fundamental parameter of interest in cluster randomized trials as it can greatly affect statistical power. We compare common methods of estimating the ICC in cluster randomized trials with binary outcomes, with a specific focus on their application to community-based cancer prevention trials with primary outcome of self-reported cancer screening. Using three real data sets from cancer screening intervention trials with different numbers and types of clusters and cluster sizes, we obtained point estimates and 95% confidence intervals for the ICC using five methods: the analysis of variance estimator, the Fleiss-Cuzick estimator, the Pearson estimator, an estimator based on generalized estimating equations and an estimator from a random intercept logistic regression model. We compared estimates of the ICC for the overall sample and by study condition. Our results show that ICC estimates from different methods can be quite different, although confidence intervals generally overlap. The ICC varied substantially by study condition in two studies, suggesting that the common practice of assuming a common ICC across all clusters in the trial is questionable. A simulation study confirmed pitfalls of erroneously assuming a common ICC. Investigators should consider using sample size and analysis methods that allow the ICC to vary by study condition.
Keywords: cancer screening, cluster randomized trials, correlated binary data, intervention trials, intraclass correlation coefficient
Introduction
In cluster or group randomized trials, clusters of individuals such as primary care practices, geographic regions, families or community organizations are randomized to study conditions. Methodological research on such trials has increased dramatically in recent years as challenging issues are increasingly recognized for such trials [1, 2].
A key feature of cluster randomized trials is that outcomes of individuals within a cluster are correlated rather than independent. The intraclass correlation coefficient (ICC), usually denoted ρ, provides a quantitative measure of within-cluster correlation. The ICC is variously defined as the Pearson correlation between two members of the same cluster or the proportion of the total variance in the outcome attributable to the variance between clusters.
The ICC is a fundamental parameter of interest in cluster randomized trials. A cluster randomized trial typically has lower power than an individually randomized trial with the same number of subjects; the decrease in power depends on ρ through the variance inflation factor 1+(m − 1)ρ, where m is average cluster size [2]. Estimates of the ICC are needed at the design stage for sample size and power calculations, which are greatly affected by the value of ICC. The method of analysis must also account for correlation of responses. In some situations, the ICC itself may be an object of inference. For these reasons, it is important to have reliable estimation procedures for the ICC.
Studies that randomize geographical communities or primary care practices have become common and have been relatively well studied; study of the ICC and its estimation in trials that randomize other types of clusters have received less attention. Examples include the Korean Healthy Life Study [3], in which Korean churches in Los Angeles County, California were randomly assigned to intervention or control conditions, and the outcome, self-reported receipt of hepatitis B testing, was assessed among church members. Another example is the hepatitis B control trial among Cambodian Americans conducted by Taylor el at. [4], which randomly sampled households from an electronic database of telephone listings and attempted to recruit one man and one woman from each household, with the primary outcome being self-reported receipt of hepatitis B testing. Further examples of diverse cluster types are in [5]. The nature of the clusters and outcome measures may affect the ICC. The ICC may be expected to be higher in families or small community-based organizations than in large geographical regions where members of the cluster may have little direct interaction with one another. The ICC may also be related to the outcome variable; e.g., self-reported outcomes and objectively measured outcomes may have different ICCs.
In this paper, we compare methods of estimating the ICC for binary data, with a focus on application of these methods to community-based cluster randomized trials of cancer prevention interventions with self-reported screening outcomes. There is a profusion of point and interval estimators of the ICC for binary data in the literature; examples include Pendergast et al [6], Ridout el at.[7], Zou and Donner [8], Turner et al. [9] and Chakraborty et al.[10]. A number of authors have compared the performance of various estimators. They include Ridout el at.[7], Evans et al. [11] and Turner et al. [12]. We compare five methods of estimating the ICC for binary data. Three have closed-form asymptotic variance formulae [8] and two are based on regression models. Three of these methods have been previously compared [7, 8] and our work here to further compare them with estimates from the generalized estimating equation (GEE) model and the random effects logistic model is new. Our work to compare arm-specific ICC estimates to overall ICC estimates by these methods also adds to the literature. We apply the methods to three real data sets from cluster randomized trials to promote cancer screening and compare their point and confidence interval estimates for the ICC. We use simulation studies to compare performance of the methods and discuss the practical implications of our findings for the design and analysis of cluster randomized trials.
Methods
Methods of Estimating the ICC
Suppose there are k clusters and the ith cluster has ni individuals. The response of the jth individual in the ith cluster is a binary variable Yij with Yij = 1 for success and Yij = 0 for failure. For example, in the context of the Korean Healthy Life Study, we have Yij =1 if the subject is screened for hepatitis B by six months after baseline interview and Yij = 0 if the subject is not. Let be the total number of successes from the ith cluster and let N = Σni be the total number of observations in the data set.
The five estimators of the ICC that we consider are: (1) the analysis of variance (ANOVA) estimator, (2) the Fleiss-Cuzick estimator, (3) the Pearson estimator, (4) the GEE estimator, and (5) an estimator from the random intercept logistic model. The first three estimators are based on the common correlation model [7, 8, 13], which assumes that the probability of success is the same for all individuals, Pr(Yij = 1) = π for all i and j, and that the responses of subjects from different clusters are independent but responses of any two subjects in the same cluster have a common correlation, Corr(Yij, Yil) = ρ for j ≠ l, where the value of ρ is the same for all clusters. The formulae for these three estimators are reported in Ridout et al. [7].
(1) The ANOVA estimator
The ANOVA estimator was originally proposed for continuous data but is also used for binary data. The ANOVA point estimator for the ICC is given by
| (1) |
where
and
Here, MSB and MSW are between-group and within-group mean squares from a one-way analysis of variance of the binary data. The variance of the estimated ICC is given by
| (2) |
where λ = (N − k)[N − 1 − nA (k − 1)]ρ + N(k − 1)(nA − 1).
(2) The Fleiss-Cuzick estimator
The Fleiss-Cuzick estimator is a kappa-type estimator. Suppose that two individuals from the same cluster have probability α of having the same response and two individuals from different clusters have probability β of having the same response. It can be shown that the ICC is
The estimated value of β is β̂ = 1 − 2π̂ (1 − π̂ ) where and an unbiased estimator of α using data from the ith group is . A weighted average of these estimates with weights proportional to (ni − 1) is used to estimate α. The Fleiss-Cuzick estimator for the ICC is
| (3) |
and its variance is given by
| (4) |
(3) The Pearson estimator
The Pearson estimator is based on direct calculation of the correlation between observations within each cluster. For binary data, this estimator is given by
where and the weight wi is user-selected and satisfies Σni (ni − 1)wi = 1. If we give equal weight to each pair of observations, this estimator becomes
| (5) |
where and its variance is given by
| (6) |
Confidence intervals for the above three estimators can be directly computed using their asymptotic standard errors as . However, previous studies have shown that linear confidence intervals do not perform well with extreme values of π and ρ or when cluster size is small [8, 14]. An alternative is to use a modified Wald test based on the equality
| (7) |
where Vãr(ρ̂) is the variance expression with π̂ instead of π [8, 15, 16]. This equation provides two roots which are the lower and upper bounds of the confidence interval. We calculate confidence intervals using both the linear method and the modified Wald test method for the ANOVA, Fleiss-Cuzick and Pearson estimators.
Multiple regression is sometimes used in cluster randomized trials in order to obtain an estimate of the treatment effect controlling for other covariates and thus it is desirable to have an estimate of the ICC from a regression model. Let Yij be the binary response and let Xij be a vector of covariates from the jth individual in the ith cluster. We consider two popular regression modeling approaches, generalized estimating equations and random effects logistic regression.
(4) ICC Estimation from the GEE Method
The GEE method is an extension of the generalized linear model. The model has three parts: (1) μij = E(Yij | Xij), the conditional expectation of the response given the covariates; (2) a link function linking the conditional expectation to the covariates, ; and (3) the conditional variance of Yij, given by Var(Yij| Xij) = φv(μij), where φ is a scalar parameter. In the general case, the conditional within-cluster association is assumed to be a function of a set of association parameters α. It can be shown that {k1/2 (β̑ − β)T}, k1/2 (α̑ − α)T} has an asymptotic normal distribution [17] and the estimates of α and β can be iteratively solved using a modified scoring algorithm. Details can be found in [17–19].
For binary outcomes, a logistic link function is typically used, such that we have
where pij = E(Yij | Xij) = Pr (Yij = 1 | Xij) and Var(Yij |Xij) = pij (1 − pij) and the scalar parameter is set to one, i.e., φ = 1. In cluster randomized trials, it is typically assumed that subjects from different clusters are independent and the correlation between pairs of subjects in the same cluster is identical, which implies an exchangeable correlation structure for responses within cluster. Hence we have a simple with-cluster association structure conditional on cluster, Corr(Yij, Yik) = αi for cluster i. We obtain estimates assuming that either overall or within each study arm, αi = α. The estimated ICC is obtained as the estimated Pearson correlation among the residuals of the cluster members:
| (8) |
where . We note that the ICC estimates given by GEE can be negative; this is also true of the ANOVA, Fleiss-Cuzick and the Pearson estimates for the ICC. We also note that these methods do not make an assumption regarding the distribution of the cluster-level proportions.
(5) ICC Estimation from the Random Intercept Logistic Model
The random intercept logistic model is given by
where it is typically assumed that the random effect bi is normally distributed with mean 0 and unknown variance . The random intercept logistic model can be viewed as a latent-response model,
where Yij = 1 if and 0 otherwise, and εij is assumed to have a logistic distribution with mean 0 and variance π2/3. ICC is defined as the ratio of between-cluster variance to total variance, with the estimated ICC given by
| (9) |
where is the estimated variance of the random intercept bi. From equation (9), we can see that unlike the other ICC estimators we discuss, the estimated ICC from the random intercept logistic model cannot be negative. In addition, whereas the other estimators are on the proportion scale, this ICC is on the logistic scale. On this scale, cluster and individual effects are assumed additive and the within-cluster variance π2/3 does not depend on within-cluster prevalence.
The random intercept logistic model is a type of generalized linear mixed model (GLMM), for which there are several methods of estimation, including penalized quasi-likelihood, Laplace approximation, Gauss-Hermite quadrature and Markov chain Monte Carlo [20]. These methods yield a point estimate for , from which a point estimate of the ICC can be obtained using equation (9). Methods for obtaining a standard error or confidence interval for or the ICC, however, are less well-developed. The sampling distribution of variance estimates in GLMMs is in general strongly asymmetric [20, 21]; even if a standard error is produced by an estimation method, it may be a poor characterization of uncertainty and linear confidence intervals are likely to have poor coverage properties. Given this difficulty and the fact that this ICC is on a different scale than the others, in this paper we confine our attention to estimating and reporting point estimates of the ICC from the random intercept logistic model for comparison to the point estimates of the ICC obtained from the other methods.
Data Sets
We apply these five estimation methods to three data sets collected from cancer screening intervention trials conducted through the Jonsson Comprehensive Cancer Center at the University of California, Los Angeles.
(1) The Breast Cancer Education Program for Samoan Women (“Samoan” study)
This study was a cluster-randomized trial designed to increase rates of mammogram usage in women of Samoan ancestry [22]. In the trial, Samoan churches in southern California were randomized to intervention and control arms. Women at intervention churches participated in a culturally appropriate breast cancer education program that included specially developed English and Samoan language breast cancer educational booklets and skill building and behavioral exercises delivered through four interactive group sessions. The control condition was usual care. The outcome was self-reported receipt of a mammogram at follow-up.
(2) The High Risk Colon Study (“Colon” study)
This study was a cluster-randomized trial designed to increase colorectal cancer (CRC) screening among high-risk individuals [23, 24]. In this study, CRC cases were identified through the California Cancer Registry and asked to provide contact information for their first-degree relatives aged 40 to 80 years; relatives who were not adherent to CRC screening guidelines were then recruited into the study. Relatives within the same family composed clusters, which were randomized to intervention or control arms. Subjects assigned to the intervention condition received a tailored print intervention and, if not screened within 6 months, brief telephone counseling. The control group received a generic CRC screening pamphlet. The outcome was self-reported receipt of CRC screening at follow-up.
(3) The Filipino American Health Study (“Filipino” study)
This trial was designed to increase CRC screening among Filipino Americans [25–27]. Subjects recruited from community organizations were organized into smaller groups and these groups were randomized to either of two intervention arms or a control arm. Technically, this study design may be classified as an individually randomized group treatment trial [28] rather than a cluster randomized trial; however, the importance and estimation of the ICC in such trials are similar. The intervention consisted of a small-group educational session to encourage CRC screening along with take-home print materials, a reminder letter and a letter to participants’ providers (Intervention1). One intervention arm (Intervention2) additionally received a free fecal occult blood test kit. The control arm received small-group education about the health benefits of physical activity. Here, we model clustering by group. The outcome was self-reported receipt of CRC screening.
Computation
R software [29] was used for computations. For the ANOVA, Fleiss-Cuzick and Pearson estimators, we wrote R functions to calculate point estimates and confidence intervals, using formulae provided by [8]; both Wald and linear confidence intervals were constructed. For the GEE model, we used the geese command in the R package geepack [30] to obtain point estimates and standard errors for the ICC, which were used to construct linear confidence intervals. For the random intercept logistic model, the R package lme4 [21] was used to obtain the variance of the random intercept term, from which a point estimate of the ICC was obtained using equation (9).
For each study, we obtained an estimate of the ICC for the overall data set and estimated the ICC for each study arm separately; for the latter, we applied the method to subsets of the data corresponding to the study arm. When obtaining estimates of the ICC for the overall data set using GEE or the logistic model, covariates indicating treatment arm were included in the linear predictor.
Results
Characteristics of the three data sets are provided in Table 1. The numbers of clusters and cluster sizes varied among the studies. The Samoan study had a moderate number of clusters of moderate size, the Colon study had a large number of small clusters, and the Filipino study had a moderate number of small to moderate sized clusters. In the Samoan and Colon studies, the estimated success probability (proportion screened) in the control group was similar to that in the intervention group. In the Filipino data set, the estimated success probability was higher in the two intervention groups than the control group.
Table 1.
Characteristics of the three example data sets
| Study arm | Number of subjects | Number of clusters | Mean cluster size | Success probability (proportion screened) |
|---|---|---|---|---|
| Samoan study | ||||
| Combined | 769 | 55 | 14.0 | 0.430 |
| Intervention | 389 | 30 | 13.0 | 0.473 |
| Control | 380 | 25 | 15.2 | 0.387 |
| Colon study | ||||
| Combined | 1304 | 834 | 1.6 | 0.350 |
| Intervention | 674 | 440 | 1.5 | 0.395 |
| Control | 630 | 394 | 1.6 | 0.302 |
| Filipino study | ||||
| Combined | 431 | 103 | 4.2 | 0.278 |
| Intervention1 | 146 | 36 | 4.1 | 0.308 |
| Intervention2 | 155 | 37 | 4.2 | 0.394 |
| Control | 130 | 30 | 4.3 | 0.108 |
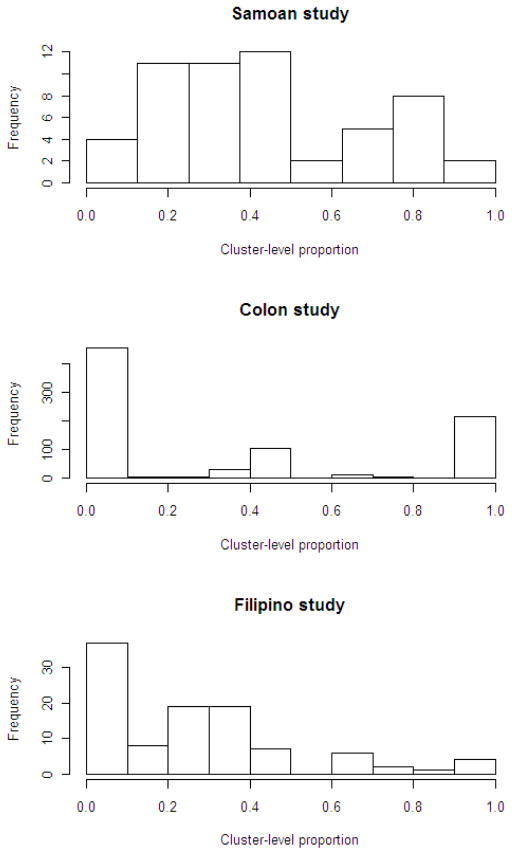
As displayed in Figure 1, the distributions of the cluster-level proportions varied among the data sets. The cluster-level proportions were well-dispersed over the possible range in the Samoan study, bimodal in the Colon study with frequent occurrences of 0’s and 1’s, and skewed in the Filipino study. A distribution with peaks at 0 and/or 1 may be expected when many clusters are of size 1. This suggests violation of the assumption of normality of the random effect in the logistic model.
Figure 1.
Distribution of cluster-level proportions in the three data sets
The estimated ICCs for the three data sets and their standard errors and 95% confidence intervals obtained using the five methods are provided in Tables 2–4. For all three data sets, there was little difference in point estimates for the overall ICC from the ANOVA, Fleiss-Cuzick and Pearson estimators (Tables 2–4, Overall ICC rows). More divergence between these three estimators was observed when calculating arm-specific ICCs. In particular, the arm-specific ICCs from the Pearson estimator were different from those given by the other two methods for the Samoan and Colon data sets. The Pearson estimate was sometimes higher and sometimes lower.
Table 2.
Results of different ICC estimation methods: Samoan data set
| Study arm | Estimation method | ρ̂ | SE(ρ̂) | Wald 95% CI | Linear 95% CI |
|---|---|---|---|---|---|
| Overall | ANOVA | 0.204 | 0.070 | (0.100, 0.367) | (0.067,0.341) |
| Fleiss-Cuzick | 0.200 | 0.068 | (0.098, 0.357) | (0.067,0.333) | |
| Pearson | 0.199 | 0.092 | (0.077, 0.420) | (0.019,0.379) | |
| GEE model | 0.192 | 0.051 | -- | (0.092,0.292) | |
| Random intercept logistic model | 0.255 | 0.056 | -- | -- | |
| Intervention | ANOVA | 0.314 | 0.105 | (0.152, 0.534) | (0.108,0.520) |
| Fleiss-Cuzick | 0.303 | 0.102 | (0.146, 0.519) | (0.103,0.503) | |
| Pearson | 0.341 | 0.143 | (0.136, 0.625) | (0.061,0.621) | |
| GEE model | 0.340 | 0.057 | -- | (0.228,0.452) | |
| Random intercept logistic model | 0.372 | 0.088 | -- | -- | |
| Control | ANOVA | 0.083 | 0.080 | (0.011, 0.340) | (−0.074,0.240) |
| Fleiss-Cuzick | 0.077 | 0.072 | (0.011, 0.314) | (−0.064,0.218) | |
| Pearson | 0.052 | 0.080 | (0.003, 0.381) | (−0.105,0.209) | |
| GEE model | 0.061 | 0.043 | -- | (−0.023,0.145) | |
| Random intercept logistic model | 0.103 | 0.054 | -- | -- |
Table 4.
Results of different ICC estimation methods: Filipino data set
| Study arm | Estimation method | ρ̂ | SE(ρ̂ ) | Wald 95% CI | Linear 95% CI |
|---|---|---|---|---|---|
| Overall | ANOVA | 0.113 | 0.067 | (0.021, 0.278) | (−0.018,0.244) |
| Fleiss-Cuzick | 0.110 | 0.060 | (0.024, 0.252) | (−0.008,0.228) | |
| Pearson | 0.127 | 0.072 | (0.033, 0.303) | (−0.014,0.268) | |
| GEE model | 0.033 | 0.045 | -- | (−0.055,0.121) | |
| Random intercept logistic model | 0.070 | 0.061 | -- | -- | |
| Intervention1 | ANOVA | 0.072 | 0.100 | (−0.030, 0.351) | (−0.124,0.268) |
| Fleiss-Cuzick | 0.064 | 0.088 | (−0.030, 0.305) | (−0.108,0.236 | |
| Pearson | 0.072 | 0.102 | (−0.014, 0.381) | (−0.128,0.272) | |
| GEE model | 0.077 | 0.103 | -- | (−0.125,0.279) | |
| Random intercept logistic model | 0.102 | 0.105 | -- | -- | |
| Intervention2 | ANOVA | 0.073 | 0.083 | (−0.030, 0.288) | (−0.090,0.236) |
| Fleiss-Cuzick | 0.065 | 0.078 | (−0.031, 0.270) | (−0.088,0.218) | |
| Pearson | 0.066 | 0.083 | (−0.019, 0.312) | (−0.097,0.229) | |
| GEE model | 0.072 | 0.069 | -- | (−0.063,0.207) | |
| Random intercept logistic model | 0.095 | 0.095 | -- | -- | |
| Control | ANOVA | −0.070 | * | * | * |
| Fleiss-Cuzick | −0.076 | * | * | * | |
| Pearson | −0.070 | * | * | * | |
| GEE model | −0.067 | 0.037 | -- | (−0.141, 0.006) | |
| Random intercept logistic model | 0.000 | † | -- | -- |
Valid variance estimate could not be obtained; standard error and confidence interval are not available.
Point estimate is truncated to be 0; corresponding standard error and confidence interval are not available.
The point estimates of the overall ICC from the GEE model were lower than the ANOVA, Fleiss-Cuzick and Pearson estimates in all three data sets. This was most striking for the Filipino data set, which had an overall ICC of 0.033 by the GEE estimator but 0.113, 0.110 and 0.127 by the ANOVA, Fleiss-Cuzick and Pearson estimators, respectively. For the arm-specific ICCs, the GEE model gave point estimates similar to the Pearson estimator, which is expected based on their similar method of calculation. In most cases, the random intercept logistic model ICC was larger than the proportion-scale ICCs, with a few exceptions.
Patterns of variation in the ICC by study arm differed among the studies. In the Samoan study (Table 2), for all methods, the estimated ICCs for the overall sample, intervention arm and control arm were very different, with the intervention arm showing the highest ICCs (range of 0.303 to 0.372), the control arm showing much lower ICCs (0.052–0.103) and the overall ICCs being intermediate between the two (0.192–0.255). In the Colon data set (Table 3), the overall and arm-specific ICCs were similar. In the Filipino data set (Table 4), the overall ICCs given by the ANOVA, Fleiss-Cuzick and Pearson estimators were unexpectedly higher than the arm-specific ICCs from these estimators. In addition, in the Filipino study, the control group was distinctive in having negative ICCs by the ANOVA, Fleiss-Cuzick, Pearson and GEE estimators. Only the GEE method could provide a valid standard error and confidence interval in the case of negative ICC. The ICC from the random intercept logistic model was set to 0 because the ICC from such models cannot be negative.
Table 3.
Results of different ICC estimation methods: Colon data set
| Study arm | Estimation method | ρ̂ | SE(ρ̂ ) | Wald 95% CI | Linear 95% CI |
|---|---|---|---|---|---|
| Overall | ANOVA | 0.037 | 0.051 | (−0.072, 0.128) | (−0.063,0.137) |
| Fleiss-Cuzick | 0.036 | 0.044 | (−0.044, 0.126) | (−0.050,0.122) | |
| Pearson | 0.037 | 0.042 | (−0.029, 0.133) | (−0.045,0.119) | |
| GEE model | 0.033 | 0.024 | -- | (−0.014,0.080) | |
| Random intercept logistic model | 0.042 | 0.053 | -- | -- | |
| Intervention | ANOVA | 0.029 | 0.063 | (−0.127, 0.124) | (−0.094,0.152) |
| Fleiss-Cuzick | 0.028 | 0.060 | (−0.079, 0.153) | (−0.090,0.146) | |
| Pearson | 0.020 | 0.056 | (−0.066, 0.152) | (−0.090,0.130) | |
| GEE model | 0.020 | 0.034 | -- | (−0.047,0.087) | |
| Random intercept logistic model | 0.027 | 0.074 | -- | -- | |
| Control | ANOVA | 0.022 | 0.086 | (−0.138, 0.188) | (−0.147,0.191) |
| Fleiss-Cuzick | 0.020 | 0.064 | (−0.090, 0.157) | (−0.105,0.145) | |
| Pearson | 0.043 | 0.062 | (−0.038, 0.201) | (−0.079,0.165) | |
| GEE model | 0.046 | 0.034 | -- | (−0.021,0.113) | |
| Random intercept logistic model | 0.057 | 0.077 | -- | -- |
The standard errors and confidence intervals were roughly similar for the ANOVA, Fleiss-Cuzick and Pearson estimators. Throughout, the GEE model gave the smallest standard errors and narrowest confidence intervals with a single exception, for the first intervention arm of the Filipino data set (Table 4). In general, confidence intervals by the various methods were wide and overlapped. The linear confidence intervals tended to have lower limits that ranged more deeply into negative values.
Simulation Studies
We investigated the performance of the ICC estimation methods using two simulation studies. The aim of Study 1 was to assess the performance of the methods in terms of bias of point estimates and coverage probability of confidence intervals when π and ρ are homogeneous across clusters, which is the assumed underlying model for the ANOVA, Fleiss-Cuzick and Pearson methods, and for the GEE method when conditioning on covariates. The scenario of homogeneous π and ρ could be encountered when estimating the ICC for a single study arm, or for the overall data when the ICC and success probability are the same in the study arms. The aim of Study 2 was to investigate the ICC estimates yielded by the methods in the context of a two-arm trial in which π, ρ or both vary between treatment arms but the method is asked to estimate a single ICC value over the entire data set, as is common in practice.
We simulated correlated binary data using the method of Emrich and Piedmonte [31], which is an indirect method of generating correlated binary data from a multivariate normal distribution. Suppose we want to simulate a J -dimensional vector Y with binary elements Y1, …., YJ with E(Yj) = πj and Corr(Yj, Yk) = ρjk, j ≠ k. The first step of the method is to solve the equation
where Θ denotes the cumulative distribution function for a standard bivariate normal random variable with correlation coefficient δ jk and w(π) denotes the π th quantile of the standard normal distribution, for δjk. The second step is to simulate a J -dimensional multivariate normal random variable W = (W1, …, WJ)T with mean 0 and correlation matrix Σ = (δjk). The third step is to generate the vector Y with components Yj = I (Wj ≤ w(πj )) for j = 1, …, J. It can be shown that under this set-up, E(Yj) = πj and Corr(Y j, Yk) = ρjk. To generate data following the common correlation model, we set πj = π and ρjk = ρ.
In Study 1, each simulation scenario had 10 clusters each of size 5, 10 and 15, for a total of 30 clusters. The true ICC values were ρ = 0.02,0.05,0.10,0.25; for each value of ρ, we considered π = 0.1,0.2,0.3,0.4 and 0.5; higher values of π are not presented due to symmetry about 0.5. We generated 2000 simulated data sets for each combination of π and ρ and estimated the ICCs using the various methods. We estimate bias as the mean of ρ̂ − ρ over 2000 replications and relative bias as the mean of (ρ̂ − ρ)/ρ. The empirical coverage probability (ECP) for 95% confidence intervals for ρ was calculated as the percentage of replications in which the confidence interval contained the true value. For the ANOVA, Fleiss-Cuzick and Pearson methods, we obtained both Wald and linear confidence intervals. For GEE, only linear confidence intervals were available. Since the ICC from the random effects logistic model is on the logistic scale but data were simulated on the proportion scale, we did not assess bias of the random intercept logistic model ICC in the simulation study. However, we obtained and report the mean ρ̂ for the random intercept logistic model for each setting for comparison with the other estimates.
In Study 2, each simulation scenario had two arms, with each arm having 10 clusters each of size 5, 10 and 15, for a total of 30 clusters in each arm and 60 total. The specified parameters were (π1, π2, ρ1, ρ2) where there were three groups of settings: same π different ρ (π1 = π2, ρ1 ≠ ρ2); different π same ρ (π1≠ π2, ρ1 = ρ2); and different π different ρ (π1 ≠ π2, ρ1, ≠ ρ2). We used success probabilities of 0.1, 0.2 and 0.5 and ICCs of 0.02, 0.05, 0.10 and 0.25, and generated 2000 simulated data sets for each scenario.
Table 5 provides results for Study 1. Almost all methods exhibited a small negative bias, tending to underestimate the ICC. The ANOVA method had the least bias; the GEE method had the most, underestimating the ICC by 20–25% when the ICC was 0.02. Bias decreased as π approached 0.5. The Fleiss-Cuzick, Pearson and GEE methods showed more relative bias for lower values of ICC than for higher values; for the ANOVA method, relative bias varied little with the value of ρ. The ICCs from the random intercept logistic model were strikingly higher than the ICCs from the other methods; they decreased as π approached 0.5. The 95% confidence intervals constructed using the Wald method tended to have higher than the nominal coverage probability; coverage was closest to the nominal rate for π = 0.5. The ANOVA, Fleiss and Pearson methods had similar patterns of coverage of linear intervals: for ρ = 0.02 or 0.05, coverage of the linear confidence intervals was lower than the nominal rate, and for ρ = 0.25, coverage was higher than the nominal rate. For the GEE method, the coverage of linear confidence intervals was lower than the nominal rate for all combinations of ρ and π.
Table 5.
Results of Simulation Study 1 to assess performance of ICC estimation methods when data follow a common correlation model, with same (ρ, π) for all clusters using 2000 simulated data sets
| A. Bias and mean estimated values
| ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| True ρ | True π | Estimated mean bias | Estimated mean relative bias | Mean ρ̂ | ||||||||||
|
| ||||||||||||||
| ano | fc | pe | gee | ano | fc | pe | gee | ano | fc | pe | gee | re | ||
|
| ||||||||||||||
| 0.02 | 0.1 | −0.001 | −0.003 | −0.004 | −0.005 | −0.05 | −0.15 | −0.20 | −0.25 | 0.019 | 0.017 | 0.016 | 0.015 | 0.056 |
| 0.2 | −0.001 | −0.003 | −0.003 | −0.004 | −0.05 | −0.15 | −0.15 | −0.20 | 0.019 | 0.017 | 0.017 | 0.016 | 0.033 | |
| 0.3 | −0.001 | −0.003 | −0.003 | −0.004 | −0.05 | −0.15 | −0.15 | −0.20 | 0.019 | 0.017 | 0.017 | 0.016 | 0.025 | |
| 0.4 | 0.000 | −0.002 | −0.002 | −0.004 | 0.00 | −0.10 | −0.10 | −0.20 | 0.020 | 0.018 | 0.018 | 0.016 | 0.023 | |
| 0.5 | 0.000 | −0.002 | −0.002 | −0.004 | 0.00 | −0.10 | −0.10 | −0.20 | 0.020 | 0.018 | 0.018 | 0.016 | 0.022 | |
|
| ||||||||||||||
| 0.05 | 0.1 | −0.002 | −0.004 | −0.005 | −0.008 | −0.04 | −0.08 | −0.10 | −0.16 | 0.048 | 0.046 | 0.045 | 0.042 | 0.125 |
| 0.2 | −0.001 | −0.003 | −0.003 | −0.006 | −0.02 | −0.06 | −0.06 | −0.12 | 0.049 | 0.047 | 0.047 | 0.044 | 0.079 | |
| 0.3 | −0.001 | −0.003 | −0.003 | −0.005 | −0.02 | −0.06 | −0.06 | −0.10 | 0.049 | 0.047 | 0.047 | 0.045 | 0.063 | |
| 0.4 | 0.000 | −0.002 | −0.002 | −0.005 | 0.00 | −0.04 | −0.04 | −0.10 | 0.050 | 0.048 | 0.048 | 0.045 | 0.057 | |
| 0.5 | 0.000 | −0.002 | −0.002 | −0.004 | 0.00 | −0.04 | −0.04 | −0.08 | 0.050 | 0.048 | 0.048 | 0.046 | 0.055 | |
|
| ||||||||||||||
| 0.10 | 0.1 | −0.003 | −0.006 | −0.007 | −0.011 | −0.03 | −0.06 | −0.07 | −0.11 | 0.097 | 0.094 | 0.093 | 0.089 | 0.234 |
| 0.2 | −0.002 | −0.005 | −0.005 | −0.008 | −0.02 | −0.05 | −0.05 | −0.08 | 0.098 | 0.095 | 0.095 | 0.092 | 0.159 | |
| 0.3 | −0.001 | −0.004 | −0.004 | −0.007 | −0.01 | −0.04 | −0.04 | −0.07 | 0.099 | 0.096 | 0.096 | 0.093 | 0.132 | |
| 0.4 | 0.000 | −0.003 | −0.003 | −0.005 | 0.00 | −0.03 | −0.03 | −0.05 | 0.100 | 0.097 | 0.097 | 0.095 | 0.121 | |
| 0.5 | 0.001 | −0.002 | −0.002 | −0.005 | 0.01 | −0.02 | −0.02 | −0.05 | 0.101 | 0.098 | 0.098 | 0.095 | 0.118 | |
|
| ||||||||||||||
| 0.25 | 0.1 | −0.009 | −0.013 | −0.016 | −0.026 | −0.04 | −0.05 | −0.06 | −0.10 | 0.241 | 0.237 | 0.234 | 0.224 | 0.510 |
| 0.2 | −0.004 | −0.008 | −0.009 | −0.014 | −0.02 | −0.03 | −0.04 | −0.06 | 0.246 | 0.242 | 0.241 | 0.236 | 0.393 | |
| 0.3 | −0.001 | −0.005 | −0.006 | −0.010 | 0.00 | −0.02 | −0.02 | −0.04 | 0.249 | 0.245 | 0.244 | 0.240 | 0.350 | |
| 0.4 | 0.001 | −0.004 | −0.005 | −0.008 | 0.00 | −0.02 | −0.02 | −0.03 | 0.251 | 0.246 | 0.245 | 0.242 | 0.329 | |
| 0.5 | 0.001 | −0.004 | −0.004 | −0.008 | 0.00 | −0.02 | −0.02 | −0.03 | 0.251 | 0.246 | 0.246 | 0.242 | 0.324 | |
| B. Empirical coverage probability of 95% confidence intervals for ρ
| ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| True ρ | True π | Wald interval ECP | Linear interval ECP | |||||||||||
|
| ||||||||||||||
| ano | fc | pe | ano | fc | pe | gee | ||||||||
|
| ||||||||||||||
| 0.02 | 0.1 | 1.000 | 1.000 | 1.000 | 0.718 | 0.666 | 0.654 | 0.871 | ||||||
| 0.2 | 0.999 | 0.998 | 0.998 | 0.754 | 0.711 | 0.705 | 0.858 | |||||||
| 0.3 | 0.997 | 0.996 | 0.996 | 0.790 | 0.754 | 0.722 | 0.858 | |||||||
| 0.4 | 0.990 | 0.991 | 0.994 | 0.834 | 0.796 | 0.777 | 0.860 | |||||||
| 0.5 | 0.987 | 0.991 | 0.993 | 0.839 | 0.812 | 0.786 | 0.869 | |||||||
|
| ||||||||||||||
| 0.05 | 0.1 | 1.000 | 1.000 | 1.000 | 0.876 | 0.842 | 0.852 | 0.797 | ||||||
| 0.2 | 1.000 | 1.000 | 1.000 | 0.910 | 0.884 | 0.878 | 0.835 | |||||||
| 0.3 | 0.999 | 0.999 | 0.998 | 0.915 | 0.887 | 0.884 | 0.858 | |||||||
| 0.4 | 0.996 | 0.995 | 0.996 | 0.926 | 0.909 | 0.902 | 0.865 | |||||||
| 0.5 | 0.992 | 0.993 | 0.996 | 0.922 | 0.905 | 0.900 | 0.872 | |||||||
|
| ||||||||||||||
| 0.10 | 0.1 | 1.000 | 1.000 | 1.000 | 0.963 | 0.949 | 0.953 | 0.793 | ||||||
| 0.2 | 0.999 | 0.999 | 0.998 | 0.976 | 0.965 | 0.965 | 0.839 | |||||||
| 0.3 | 0.999 | 0.999 | 0.998 | 0.976 | 0.962 | 0.965 | 0.860 | |||||||
| 0.4 | 0.995 | 0.996 | 0.997 | 0.969 | 0.955 | 0.956 | 0.873 | |||||||
| 0.5 | 0.996 | 0.996 | 0.997 | 0.968 | 0.952 | 0.958 | 0.879 | |||||||
|
| ||||||||||||||
| 0.25 | 0.1 | 1.000 | 0.998 | 0.998 | 0.994 | 0.989 | 0.992 | 0.872 | ||||||
| 0.2 | 0.999 | 0.998 | 0.998 | 0.997 | 0.991 | 0.994 | 0.867 | |||||||
| 0.3 | 0.998 | 0.998 | 0.998 | 0.994 | 0.988 | 0.991 | 0.882 | |||||||
| 0.4 | 0.996 | 0.996 | 0.996 | 0.988 | 0.980 | 0.988 | 0.898 | |||||||
| 0.5 | 0.992 | 0.992 | 0.994 | 0.984 | 0.978 | 0.982 | 0.898 | |||||||
ECP, empirical coverage probability; ano, ANOVA; fc, Fleiss-Cusick; pe, Pearson; gee, generalized estimating equations; re, random intercept logistic regression
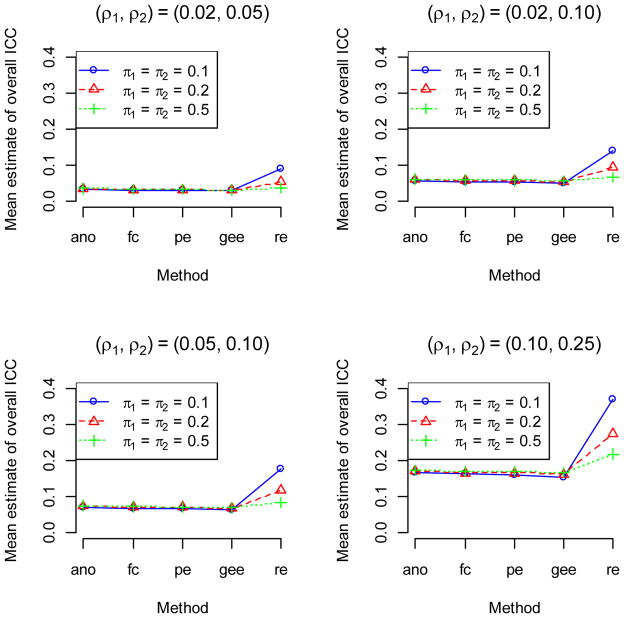
For Study 2, in the scenarios in which the two arms had the same π but different ρ (Figure 2), the ANOVA, Fleiss-Cuzick, Pearson and GEE methods all gave estimates of the overall combined ICC that were intermediate between the two values of ρ, and the estimates had little dependence on the value of π. The ICCs from the random effects logistic model were higher than the proportion scale ICCs, and were highest when π was 0.1 and lowest when π was 0.5.
Figure 2.
Results of Simulation Study 2 to compare point estimates of overall ICC from five ICC estimation methods (ano, ANOVA; fc, Fleiss-Cusick; pe, Pearson; gee, generalized estimating equations; re, random intercept logistic regression) when data arise from a two-arm trial with same π but different ρ in each arm using 2000 simulated data sets for each scenario
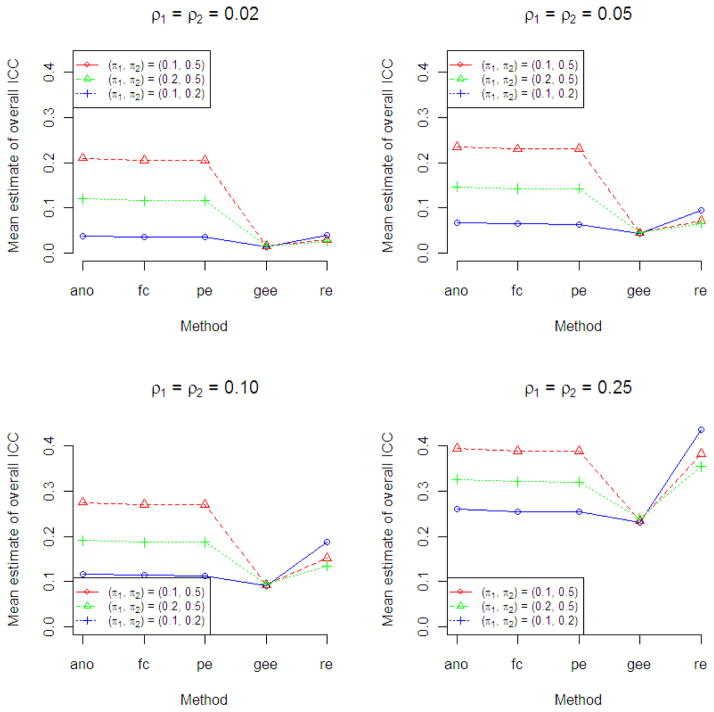
In scenarios in which the two arms had the same ρ but different π (Figure 3), the ANOVA, Fleiss-Cuzick and Pearson methods were striking in their overestimation of the ICC. The overestimation was highest when the success probabilities in the two arms were the most divergent. In contrast, the GEE method gave estimates of the ICC close to the true value. The random effects logistic model ICCs were also highest when the success probabilities were the most divergent.
Figure 3.
Results of Simulation Study 2 to compare point estimates of overall ICC from five ICC estimation methods (ano, ANOVA; fc, Fleiss-Cusick; pe, Pearson; gee, generalized estimating equations; re, random intercept logistic regression) when data arise from a two-arm trial with same ρ but different π in each arm using 2000 simulated data sets for each scenario
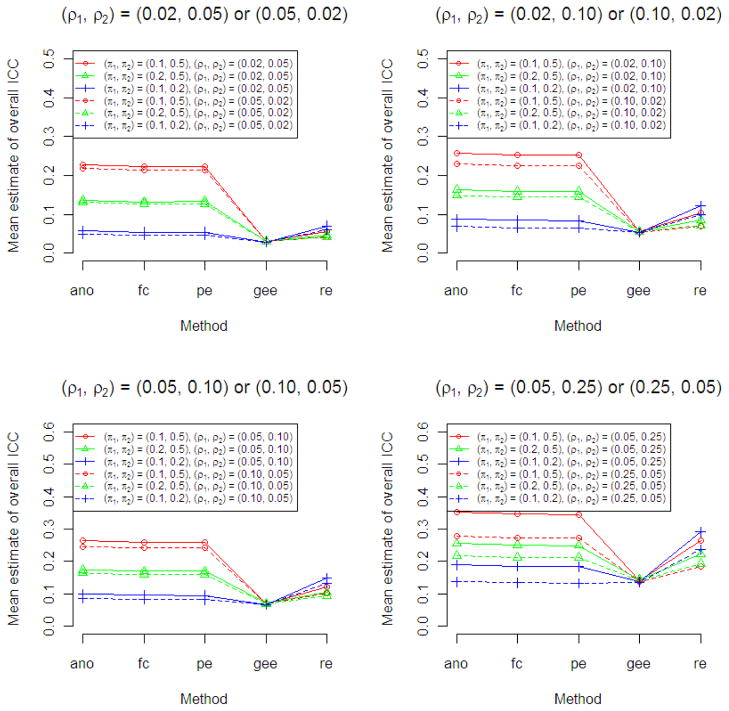
Scenarios in which the two arms had both different ρ and different π (Figure 4) showed an similar pattern of overestimation of the ICC for the ANOVA, Fleiss-Cuzick and Pearson methods when the success probabilities in the two arms were divergent, consistently yielding estimates of the overall ICC than exceeded either of the two values when (π1, π2) = (0.1,0.5) or (0.2,0.5). The overestimation was somewhat less when the higher ICC was associated with the lower success probability. In contrast, the GEE method gave estimates of the overall ICC that were close to the average of the values in the two arms. For the random intercept logistic model, the ICCs for the combined data were higher when the arm with the higher success probability had the higher ICC.
Figure 4.
Results of Simulation Study 2 to compare point estimates of overall ICC from five ICC estimation methods (ano, ANOVA; fc, Fleiss-Cusick; pe, Pearson; gee, generalized estimating equations; re, random intercept logistic regression) when data arise from a two-arm trial with different ρ and different π in each arm using 2000 simulated data sets for each scenario
Discussion
Our results from estimating the ICC using five different methods for the overall sample and specific study conditions have several practical implications.
Our results show that ICC estimates obtained using different methods can be quite different, although confidence intervals were wide and overlapped. Thus the four different proportions scale methods could lead to different conclusions if the uncertainty is not recognized. This illustrates the difficulties of relying on a single point estimate in sample size calculations. Uncertainty in estimating the ICC and overlapping intervals by different methods have been recognized by several authors [9, 11, 12, 32].
Several patterns could be discerned in the real data sets. For the Samoan and Colon studies, the four proportion-scale estimators gave similar results for the overall ICC; however, for the Filipino study, the GEE estimate of the overall ICC was quite different from the other three estimates. This may be due to the fact that the ANOVA, Fleiss-Cuzick and Pearson estimators assume the success probability is the same for all individuals, whereas the GEE estimator was able to incorporate the effect of treatment arm on success probability. In the Samoan and Colon studies, success probabilities were similar across arms; in the Filipino study, the probabilities were quite different across arms. In the latter case, the assumption of the same success probability may not hold and therefore estimates from the ANOVA, Fleiss-Cuzick and Pearson estimators may be misleading. The assumptions of these estimators may be more valid in the case of arm-specific ICCs, for which it may be reasonable to assume equal success probability across clusters, and therefore we would expect the four estimators to agree more on arm-specific ICCs. This was indeed observed for the Filipino study. Overall, this indicates that in a cluster-randomized trial, if the outcome probabilities are very different between study conditions, the GEE estimator may be preferred over the ANOVA, Fleiss-Cuzick or Pearson estimators when estimating the overall ICC for the study. In addition, the ANOVA method can be extended to an analysis of covariance (ANCOVA) to adjust for covariates, as was recently done in [33].
A common practice is to assume a constant ICC across study conditions in both sample size calculations and analyses. However, we found clear evidence that the ICC varied substantially by study condition in two of our real studies. Since the ICC is a function of the outcome prevalence, it follows that ICC values will generally differ between study arms with different outcome prevalences [34]. In such situations, the assumption of a common ICC for the whole sample is questionable, and investigators should consider sample size calculation and analytic methods that allow the ICC to vary by study condition. Thomson et al [35] and Roberts and Roberts [36] have also noted problems with assuming constant ICC across intervention groups. Sample size calculation formulae that allow the ICC to vary by condition are provided in [1, 34]. For analysis, the GEE method implemented in the R package geepack can be used; see, for example, Crespi et al [37]. Other alternatives are alternating logistic regression [38], a special type of GEE for binary outcomes in which the within-cluster association is modeled using odds ratios, and mixed logistic models with two between-cluster variance components, as in [39]. In choosing an estimator, it is important to be aware that the sandwich estimator of the standard error for the GEE model is biased in small samples [40]. While the sample sizes in our simulation study were not small by the definition of [40], their relatively greater negative bias in our simulation studies suggests that some bias may have been occurring.
An important finding was that the ICC estimate for the combined data could be higher than the arm-specific ICCs when using the ANOVA, Fleiss-Cuzick or Pearson estimators. We observed this in the Colon and Filipino studies, and confirmed this in the simulation study. The estimates were especially high when the difference in outcome proportions across conditions was large. Again, this phenomenon is probably attributable to the erroneous assumption of these models of a common success probability across all clusters.
There were several additional cautionary tales from our simulation studies. We observed negative bias in many settings, suggesting that investigators should be concerned about ICC underestimation. In addition, confidence intervals generally did not have the nominal coverage probability for any of the methods.
The distribution of the cluster-level proportions, which was quite different among our three studies, may also affect the performance of the estimation methods. The random intercept logistic model in particular typically assumes that the cluster-level random effect is normally distributed, which may not be true in practice. This may especially be the case for clusters of small size such as we observed in the Colon study, which had a bimodal distribution with frequent occurrence of 0’s and 1’s. Future studies should examine the sensitivity of ICC estimates to violations of the normality assumption of the random effects.
When comparing ICC estimates obtained using different methods, it is important to note that the ICC from a random/mixed effects logistic regression is on a logistic scale and is therefore a different entity than the other ICCs, which are on a proportion scale [13]. There is no simple formula for converting a random effect logistic ICC to the common correlation model ICC. Table 1 of Eldridge et al [13] provides values of the ICC on the logistic scale for specific proportion-scale ICC and outcome prevalence values.
One of our datasets yielded estimates of the ICC that were negative for the control condition. Other examples of negative ICC are in Cochran ([41], pp.124–127) and Hanley [42]. Truly negative ICCs are thought to be rare in cluster randomized trials [2]. The practical implication is that if the true ICC is negative, analysis using GEE may be preferred. We agree with the general recommendation that negative ICCs should not be used in sample size and power calculations [43]. In this situation, standard practice is to use 0 or a small positive value. Interestingly, our negative ICC estimates occurred in the control arm of an individually randomized group treatment trial, in which the clusters were not naturally constituted. Investigators designing individually randomized group treatment trials should consider how expectations of correlation may differ for such trials as compared to cluster randomized trials; Pals et al. [28] provide some guidance.
Our findings imply that investigators should be aware of the different assumptions and limitations of ICC estimators and use caution in selecting an estimator appropriate for their data, as has been noted by other authors [9, 11, 12, 32]. In particular, the common practice of assuming a common ICC for the whole sample may be questionable, in sample size calculations and in analyses. Investigators should consider using methods that allow the ICC to vary by study condition.
Acknowledgments
Crespi was supported by National Institutes of Health grants CA137827 and CA16042. Wong was supported by National Institutes of Health grant CA109091.
Abbreviations
- ANOVA
analysis of variance
- CRC
colorectal cancer
- GEE
generalized estimating equations
- ICC
intraclass correlation coefficient
References
- 1.Hayes RJ, Moulton LH, editors. Cluster randomized trials. Chapman and Hall/CRC; 2009. [Google Scholar]
- 2.Donner A, Klar N, editors. Design and analysis of cluster randomized trials in health research. A Hodder Arnold Publication; 2000. [Google Scholar]
- 3.Bastani R, Glenn BA, Taylor VM, Chen MS, Jr, Nguyen TT, Stewart SL, et al. Integrating theory into community interventions to reduce liver cancer disparities: The Health Behavior Framework. Prev Med. 2010;50:63–7. doi: 10.1016/j.ypmed.2009.08.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Taylor VM, Talbot J, Do HH, Liu Q, Yasui Y, Jackson JC, et al. Hepatitis B knowledge and practices among Cambodian Americans. Asian Pac J Cancer Prev. 2011;12:957–61. [PMC free article] [PubMed] [Google Scholar]
- 5.Crespi CM, Maxwell AE, Wu S. Cluster randomized trials of cancer screening interventions: are appropriate statistical methods being used? Contemp Clin Trials. 2011;32:477–84. doi: 10.1016/j.cct.2011.03.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Pendergast JF, Gange SJ, Newton MA, Lindstrom MJ, Palta M, Fisher MR. A survey of methods for analyzing clustered binary response data. Int Stat Rev. 1991;64:89–118. [Google Scholar]
- 7.Ridout MS, Demetrio CG, Firth D. Estimating intraclass correlation for binary data. Biometrics. 1999;55:137–48. doi: 10.1111/j.0006-341x.1999.00137.x. [DOI] [PubMed] [Google Scholar]
- 8.Zou G, Donner A. Confidence interval estimation of the intraclass correlation coefficient for binary outcome data. Biometrics. 2004;60:807–11. doi: 10.1111/j.0006-341X.2004.00232.x. [DOI] [PubMed] [Google Scholar]
- 9.Turner RM, Omar RZ, Thompson SG. Constructing intervals for the intracluster correlation coefficient using Bayesian modelling, and application in cluster randomized trials. Stat Med. 2006;25:1443–56. doi: 10.1002/sim.2304. [DOI] [PubMed] [Google Scholar]
- 10.Chakraborty H, Moore J, Carlo WA, Hartwell TD, Wright LL. A simulation based technique to estimate intracluster correlation for a binary variable. Contemp Clin Trials. 2009;30:71–80. doi: 10.1016/j.cct.2008.07.008. [DOI] [PubMed] [Google Scholar]
- 11.Evans BA, Feng Z, Peterson AV. A comparison of generalized linear mixed model procedures with estimating equations for variance and covariance parameter estimation in longitudinal studies and group randomized trials. Stat Med. 2001;20:3353–73. doi: 10.1002/sim.991. [DOI] [PubMed] [Google Scholar]
- 12.Turner RM, Omar RZ, Thompson SG. Bayesian methods of analysis for cluster randomized trials with binary outcome data. Stat Med. 2001;20:453–72. doi: 10.1002/1097-0258(20010215)20:3<453::aid-sim803>3.0.co;2-l. [DOI] [PubMed] [Google Scholar]
- 13.Eldridge SM, Ukoumunne OC, Carlin JB. The intra-cluster correlation coefficient in cluster randomized trials: A review of definitions. Int Stat Rev. 2009;77:378–94. [Google Scholar]
- 14.Altaye M, Donner A, Klar N. Inference procedures for assessing interobserver agreement among multiple raters. Biometrics. 2001;57:584–8. doi: 10.1111/j.0006-341x.2001.00584.x. [DOI] [PubMed] [Google Scholar]
- 15.Donner A, Zou G. Interval estimation for a difference between intraclass kappa statistics. Biometrics. 2002;58:209–15. doi: 10.1111/j.0006-341x.2002.00209.x. [DOI] [PubMed] [Google Scholar]
- 16.Donner A, Eliasziw M. A goodness-of-fit approach to inference procedures for the kappa statistic: confidence interval construction, significance-testing and sample size estimation. Stat Med. 1992;11:1511–9. doi: 10.1002/sim.4780111109. [DOI] [PubMed] [Google Scholar]
- 17.Prentice RL, Zhao LP. Estimating equations for parameters in means and covariances of multivariate discrete and continuous responses. Biometrics. 1991;47:825–39. [PubMed] [Google Scholar]
- 18.Prentice RL. Correlated binary regression with covariates specific to each binary observation. Biometrics. 1988;44:1033–48. [PubMed] [Google Scholar]
- 19.Yan J, Fine J. Estimating equations for association structures. Stat Med. 2004;23:859–74. doi: 10.1002/sim.1650. discussion 75-7,79-80. [DOI] [PubMed] [Google Scholar]
- 20.McCulloch CE, Searle SR. Generalized, linear, and mixed models. New York: John Wiley & Sons; 2001. [Google Scholar]
- 21.Bates DM. lme4: Mixed-effects modeling with R. Springer; 2010. Available online at http://lme4.r-forge.r-project.org/book/ [Google Scholar]
- 22.Mishra SI, Bastani R, Crespi CM, Chang LC, Luce PH, Baquet CR. Results of a randomized trial to increase mammogram usage among Samoan women. Cancer Epidemiol Biomarkers Prev. 2007;16:2594–604. doi: 10.1158/1055-9965.EPI-07-0148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Bastani R, Glenn BA, Maxwell AE, Ganz PA, Mojica CM, Chang LC. Validation of self-reported colorectal cancer (CRC) screening in a study of ethnically diverse first-degree relatives of CRC cases. Cancer Epidemiol Biomarkers Prev. 2008;17:791–8. doi: 10.1158/1055-9965.EPI-07-2625. [DOI] [PubMed] [Google Scholar]
- 24.Glenn BA, Herrmann AK, Crespi CM, Mojica CM, Chang LC, Maxwell AE, et al. Changes in risk perceptions in relation to self-reported colorectal cancer screening among first-degree relatives of colorectal cancer cases enrolled in a randomized trial. Health Psychol. 2011;30:481–91. doi: 10.1037/a0024288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Maxwell AE, Bastani R, Crespi CM, Danao LL, Cayetano RT. Behavioral mediators of colorectal cancer screening in a randomized controlled intervention trial. Prev Med. 2011;52:167–73. doi: 10.1016/j.ypmed.2010.11.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Maxwell AE, Bastani R, Danao LL, Antonio C, Garcia GM, Crespi CM. Results of a community-based randomized trial to increase colorectal cancer screening among Filipino Americans. Am J Public Health. 2010;100:2228–34. doi: 10.2105/AJPH.2009.176230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Maxwell AE, Crespi CM, Danao LL, Antonio C, Garcia GM, Bastani R. Alternative approaches to assessing intervention effectiveness in randomized trials: application in a colorectal cancer screening study. Cancer Causes Control. 2011;22:1233–41. doi: 10.1007/s10552-011-9793-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Pals SL, Murray DM, Alfano CM, Shadish WR, Hannan PJ, Baker WL. Individually randomized group treatment trials: a critical appraisal of frequently used design and analytic approaches. Am J Public Health. 2008;98:1418–24. doi: 10.2105/AJPH.2007.127027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Team RDC. R: A language and environment for statistical computing. Vienna, Austria: R Foundation for Statistical Computing; 2010. [Google Scholar]
- 30.Halekoh U, Hojsgaard S, Yan J. The R Package geepack for Generalized Estimating Equations. J Stat Softw. 2006;15:1–11. [Google Scholar]
- 31.Emrich LJ, Piedmonte MR. A Method for Generating High-Dimensional Multivariate Binary Variates. American Statistician. 1991;45:302–4. [Google Scholar]
- 32.Turner RM, Thompson SG, Spiegelhalter DJ. Prior distributions for the intracluster correlation coefficient, based on multiple previous estimates, and their application in cluster randomized trials. Clin Trials. 2005;2:108–18. doi: 10.1191/1740774505cn072oa. [DOI] [PubMed] [Google Scholar]
- 33.Hade EM, Murray DM, Pennell ML, Rhoda D, Paskett ED, Champion VL, et al. Intraclass correlation estimates for cancer screening outcomes: estimates and applications in the design of group-randomized cancer screening studies. J Natl Cancer Inst Monogr. 2010;2010:97–103. doi: 10.1093/jncimonographs/lgq011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Crespi CM, Wong WK, Wu S. A new dependence parameter approach to improve the design of cluster randomized trials with binary outcomes. Clin Trials. 2011;8:687–98. doi: 10.1177/1740774511423851. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Thomson A, Hayes R, Cousens S. Measures of between-cluster variability in cluster randomized trials with binary outcomes. Stat Med. 2009;28:1739–51. doi: 10.1002/sim.3582. [DOI] [PubMed] [Google Scholar]
- 36.Roberts C, Roberts SA. Design and analysis of clinical trials with clustering effects due to treatment. Clin Trials. 2005;2:152–62. doi: 10.1191/1740774505cn076oa. [DOI] [PubMed] [Google Scholar]
- 37.Crespi CM, Wong WK, Mishra SI. Using second-order generalized estimating equations to model heterogeneous intraclass correlation in cluster-randomized trials. Stat Med. 2009;28:814–27. doi: 10.1002/sim.3518. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Carey V, Zeger SL, Diggle P. Modeling Multivariate Binary Data with Alternating Logistic Regressions. Biometrika. 1993;80:517–26. [Google Scholar]
- 39.Omar RZ, Thompson SG. Analysis of a cluster randomized trial with binary outcome data using a multi-level model. Statistics in Medicine. 2000;19:2675–88. doi: 10.1002/1097-0258(20001015)19:19<2675::aid-sim556>3.0.co;2-a. [DOI] [PubMed] [Google Scholar]
- 40.Mancl LA, DeRouen TA. A covariance estimator for GEE with improved small-sample properties. Biometrics. 2001;57:126–34. doi: 10.1111/j.0006-341x.2001.00126.x. [DOI] [PubMed] [Google Scholar]
- 41.Cochran W. Sampling Techniques. New York: Wiley; 1953. [Google Scholar]
- 42.Hanley JA, Negassa A, Edwardes MD. GEE analysis of negatively correlated binary responses: a caution. Stat Med. 2000;19:715–22. doi: 10.1002/(sici)1097-0258(20000315)19:5<715::aid-sim342>3.0.co;2-t. [DOI] [PubMed] [Google Scholar]
- 43.Donner A, Klar N. Cluster Randomization Trials in Epidemiology - Theory and Application. Journal of Statistical Planning and Inference. 1994;42:37–56. [Google Scholar]