Measurement of distance with the nSPIRO (nanoScale Precise Imaging by Rapid beam Oscillation) method

Abstract

We discuss here the principles of a novel optical method in which the scanning of a laser spot around a fluorescent object is used to determine its shape, orientation and fluorophore distribution. The scanning pattern is adapted to the shape of the object according to a feedback principle based on intensity modulation measurements. The modulation of the intensity with respect to the angular coordinate is used to keep the orbit centered on the object. The modulation induced by rapid oscillations of the orbit radius is used to measure the local distance from the surface with nanometer precision. We provide a model to describe the fundamental relationship between modulation and distance and discuss the range of validity of several approximate expressions. According to this model the distance can be measured with a precision dependent on the steepness of the Point Spread Function and the total number of detected photons. To test our findings we performed experiments with one or two channels on fluorescent spheres of known size and characterized the modulation function of our microscope setup. We conclude that the method can be used to measure distances in the range 10–200nm between two surfaces labeled with two different probes.

Introduction

We have recently introduced a laser scanning imaging method in which the scanning pattern is adapted to the shape of the object (Lanzano et al., 2011a). This method, called nSPIRO (nanoScale Precise Imaging by Rapid beam Oscillation), uses a feedback principle to produce 3D images of sparse and small features in live cells. Examples of these features include apical membrane microvilli or cellular protrusions extending out of the main cell body. The efficient imaging of these subcellular structures can be challenging due to the fact that they move and/or extend sparsely in 3D. To overcome these issues the laser spot is moved around the object to be imaged forming a light envelope around it. The scanning pattern is continuously adapted in order to track changes in shape or in position of these structures using a feedback algorithm. The feedback is based on the determination of the center of mass of the fluorescent object and the determination of the distance between the laser spot and the object surface.

The determination of the center of mass is performed by sending the laser beam in an orbit around the object and using an algorithm previously developed for tracking point-like particles in 3D in live cells with nanometer precision (Kis-Petikova and Gratton, 2004; Levi et al., 2005a). This algorithm allows the real-time repositioning of the scanner in such a way as to follow the particle movement in different types of environments (Hellriegel and Gratton, 2009; Katayama et al., 2009; Levi et al., 2005a; Levi et al., 2005b; Levi et al., 2006). The use of a simple circular orbit provides the fastest way (down to about 1 ms) to obtain information about the coordinates of the center of mass in a plane with a mechanical scanning system since the galvo-mirrors can be driven at resonant frequency. We extended this method to track the motion of entire subcellular structures like microvilli or nuclear pore complexes in live cells (Cardarelli et al., 2011; Lanzano et al., 2011a; Lanzano et al., 2011b). We also showed that this form of line scanning is compatible with fluctuation analysis techniques like Fluorescence Correlation Spectroscopy (FCS) (Elson, 2011) and Raster Image Correlation Spectroscopy (RICS) (Digman et al., 2005) to detect the local diffusion of molecules.

The size and shape of the object can be determined by measuring the distance between the laser spot and the object surface. As the object is kept at the center of the scanned orbit we measure at each angle of the orbit the distance from the surface along the radial direction. The distance is not given by the fluorescence intensity along the circular orbit because the intensity at each point is a function not only of the distance from the surface but also of the local concentration of fluorophores. To overcome this indetermination, while performing the orbit, we locally oscillate the laser spot also in the radial direction and measure the modulation of the fluorescence due to this rapid oscillatory motion. The modulation is a quantity dependent almost exclusively on the distance from the surface. Using the modulation value we are able to track the local distance of the surface at each position along the orbit while we ‘sit’ in the coordinate system of the center of mass of the fluorescence distribution. The nSPIRO nanoimaging method generalizes the principles of the orbital tracking method, previously developed for point-like particles, to track the surface (shape) of finite size objects.

A basic principle in this nanoimaging method is the distance measurement used as a feedback to track the shape of the object. The fundamental relationship between modulation and distance is represented by the modulation function which depends on the Point Spread Function (PSF) of the microscope. The modulation function relative to a given fluorescent object can be always calculated using simulations of the surface distribution of fluorophores if we know the PSF of the microscope. For some simple cases the modulation function can also be calculated analytically.

Here we show in mathematical detail how the distance can be measured from the modulation and under which conditions the modulation depends only on the distance of the laser spot from the surface. We find an analytical expression for the modulation in the simple case of a uniform cylindrical surface which still represents a good model for a variety of cell membrane protrusions. We show measurements performed on fluorescent spheres of known size to test the validity of our method and to calibrate the modulation function of our microscope setup.

Materials and Methods

Microscope setup

nSPIRO measurements were performed using a home-built microscope capable of Single Particle Tracking (SPT), whose technical details have been already described (Hellriegel and Gratton, 2009; Levi et al., 2005a). This microscope is built around an Olympus X71 body. Multi-photon excitation was provided by a tunable Chameleon Ultra II Ti:Sapphire laser (Coherent, Santa Clara, CA) tuned at λ=930nm. Fluorescence emission was collected by an Olympus 0.9-NA 60x air objective. Two GaAs detectors H7422-40 (Hamamatsu, Bridgewater, NJ) were used to acquire the fluorescence in the 500–550nm and 575–645nm spectral range for the two channels, respectively. The galvano xy-scanner (Cambridge Technology, Lexington, MA) as well as the piezo z-scanner (Phisik Instrumente, Auburn, MA) were driven by the ISS-3axis card (ISS, Champaign, IL).

During orbital tracking, the two scanning mirrors are moved independently by π/2-phase shifted sine wave voltages generated in the card so that the laser beam moves in a circular path around the particle. The position of the scanning center is determined by the offset values of the sine waves (Kis-Petikova and Gratton, 2004). For the modulated pattern the coordinates of the scanner were modified as follows:

$$\begin{array}{l}x=x_0+[R+\mathrm{\Delta }Rsin(n\omega t)]cos(\omega t)\\ y=y_0+[R+\mathrm{\Delta }Rsin(n\omega t)]sin(\omega t)\end{array}$$ (1)

The fluorescence intensity at 128 points along the orbit was collected at a sampling rate of 15625Hz so that the period of one orbit was T=8.192ms. The modulation of the radius was set at a period of 1.024ms, so that we had n=8 radial oscillations for each orbit. The orbital pattern was stored in the memory of the ISS-3axis card and the center offset in the xy plane position was updated according to the tracking mechanism every 8 orbits (t=8T=65.5ms) using the Fast Fourier Transform (FFT)-based algorithm described previously(Kis-Petikova and Gratton, 2004). This algorithm updates the values of the coordinates (x₀, y₀) in such a way as to minimize the modulation of the first harmonic in the Fourier spectrum of the intensity trace along the orbit. The modulation induced by the oscillation of the orbit radius is extracted from the modulation of the n^th harmonic component of the intensity (n=8).

Fluorescent spheres

nSPIRO measurements were performed on yellow-green fluorescent microspheres (excitation/emission = 505/515 nm, Invitrogen, Carlsbad, CA) of known diameter (φ=0.11±0.01μm). The spheres were diluted, sonicated and then fixed on a microscope slide.

Simulations, data acquisition and data processing

Simulations were performed using Global for Images (SimFCS), a software developed at the Laboratory for Fluorescence Dynamics (http://www.lfd.uci.edu/globals/). The same software was used for data acquisition and for data processing.

Results

Orbital modulation and radial modulation

In the orbital tracking method, the position of the center of mass is determined by scanning an orbit around the object and measuring the asymmetry of the intensity profile along the orbit. As described in detail in previous publications (Hellriegel and Gratton, 2009; Kis-Petikova and Gratton, 2004; Levi et al., 2005a), from the Fast Fourier Transform (FFT) of the intensity trace along the orbit, we get the average intensity or DC as the 0^th order term of the Fourier series and the AC as the coefficient of the 1^st harmonic term. The angular coordinate of the particle is provided by the phase of the AC term, and its distance from the center can be calculated from the modulation of the signal, defined as the ratio AC/DC. We will call this ratio orbital modulation, to avoid confusion with the concept of radial modulation which is one of the novelties introduced recently by our group (Lanzano et al., 2011a) and the main focus of this paper. We show here that we can use the orbital modulation to track particles of finite size.

The orbital modulation is related to the asymmetry of the intensity trace along the orbit and can be defined as the relative variation of the intensity along the angular coordinate:

$${mod}_{\varphi }=\left|\frac{\mathrm{\Delta }I}{I}\right|=\frac{1}{I}\left|\int \frac{\partial I}{\partial \varphi }d\varphi \right|$$ (2)

The tracking algorithm updates the position of the center of the scanning orbit in such a way as to minimize the asymmetry of the intensity profile. The orbital modulation is minimized when the center of mass of the fluorescent intensity distribution is located at the center of the orbit. Indeed, if a point-particle is off center of a given amount δ in the direction ϕ₀ (Fig. 1A) the intensity will have a maximum at this angle instead of being uniform along the orbit (Fig 1B). This is because the distance R_p between the spot and the particle is a function of the angle ϕ:

$$R_p^2=R^2+{\delta }^2-2R\delta cos(\varphi -{\varphi }_0)$$ (3)

and the intensity is a function of the angle ϕ through the square distance R_p²:

$$\frac{\partial I}{\partial \varphi }=\frac{\partial I}{\partial R_p^2}\frac{\partial R_p^2}{\partial \varphi }=\frac{\partial I}{\partial R_p^2}[2Rsin(\varphi -{\varphi }_0)\delta ]$$ (4)

Fig. 1.

Concept of orbital modulation for a point-like particle. A particle is shifted with respect to the center of a scanned orbit (A). As a result the intensity shows a modulation along the angular coordinate (B).

The orbital modulation of the intensity can be evaluated integrating between ϕ₀-π and ϕ₀:

$${mod}_{\varphi }=\left|\frac{\mathrm{\Delta }I}{I}\right|\approx \frac{\frac{1}{2}\underset{{\varphi }_0-\pi }{\overset{{\varphi }_0}{\int }}\frac{\partial I}{\partial \varphi }d\varphi }{\frac{1}{2\pi }\underset{-\pi }{\overset{\pi }{\int }}Id\varphi }=\frac{\underset{{\varphi }_0-\pi }{\overset{{\varphi }_0}{\int }}\frac{\partial I}{\partial R_p^2}\frac{\partial R_p^2}{\partial \varphi }d\varphi }{\frac{1}{\pi }\underset{-\pi }{\overset{\pi }{\int }}Id\varphi }=\frac{\underset{{\varphi }_0-\pi }{\overset{{\varphi }_0}{\int }}\frac{\partial I}{\partial R_p^2}[2Rsin(\varphi -{\varphi }_0)\delta ]d\varphi }{\frac{1}{\pi }\underset{-\pi }{\overset{\pi }{\int }}Id\varphi }$$ (5)

Considering a Gaussian shape of the PSF, $I=I_0{e}^{-\frac{2R_p^2}{w^2}}$ and ignoring for simplicity the variation of $\frac{\partial I}{\partial R_p^2}=-\frac{2}{w^2}I$ with respect to the sinusoidal term, then the modulation of the signal is dependent on the shift δ in a simple linear form:

$${mod}_{\varphi }\approx \frac{4R}{w^2}\delta =k\delta$$ (6)

which can be used as a feedback function to keep the particle at the position δ ≈ 0.

If instead of a single particle we have N particles each one shifted in the direction ϕ_i of an amount δ_i respectively, we can still show that the modulation is related to the shift of the center of mass of the distribution.

Orbital Modulation for a small cluster of particles

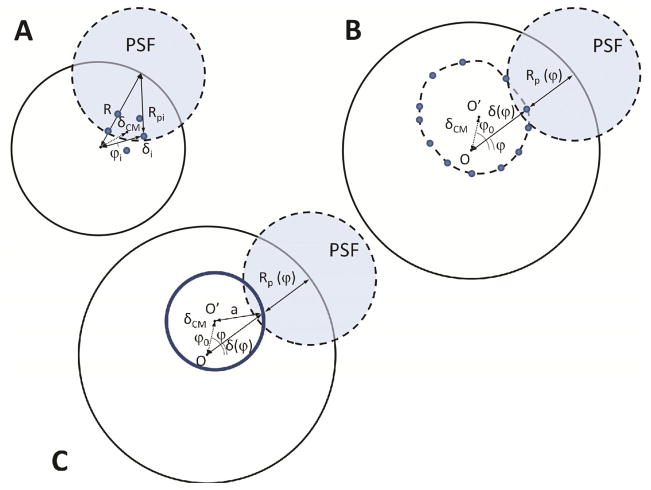
Let’s consider first a small group of N particles (Fig. 2A), each one shifted in the direction ϕ_i of an amount δ_i respectively, for which we can define the position of the center of mass as:

$${\overrightarrow{\delta }}_{CM}=\frac{\sum {\overrightarrow{\delta }}_i}{N}$$ (7)

Fig. 2.

Orbital Modulation for a small cluster of particle (A), a large distribution of particle (B) and a fluorescent circle (C).

In this case the derivative of the total intensity as a function of the angle along the orbit is given by:

$$\frac{\partial \left(\sum I_i\right)}{\partial \varphi }=\sum \frac{\partial \sum I_i}{\partial R_{pj}^2}\frac{\partial R_{pj}^2}{\partial \varphi }=\sum \frac{\partial I_j}{\partial R_{pj}^2}\frac{\partial R_{pj}^2}{\partial \varphi }=\sum \frac{\partial I_j}{\partial R_{pj}^2}\left[2Rsin\left(\varphi -{\varphi }_j\right){\delta }_j\right]=-\frac{4R}{w^2}\sum I_j\left[sin\left(\varphi -{\varphi }_j\right){\delta }_j\right]$$ (8)

If the center of mass is shifted at a distance δ_CM in the direction ϕ₀ with respect to the center of the orbit, we can quantify the modulation of the signal as:

$${mod}_{\varphi }=\left|\frac{\mathrm{\Delta }I}{I}\right|=\frac{\underset{{\varphi }_0-\pi }{\overset{{\varphi }_0}{\int }}\frac{\partial \left(\sum I_i\right)}{\partial \varphi }d\varphi }{\frac{1}{\pi }\underset{-\pi }{\overset{\pi }{\int }}\left(\sum I_i\right)d\varphi }=\frac{-\frac{4R}{w^2}\underset{{\varphi }_0-\pi }{\overset{{\varphi }_0}{\int }}\sum I_j\left[sin\left(\varphi -{\varphi }_j\right){\delta }_j\right]d\varphi }{\frac{1}{\pi }\underset{-\pi }{\overset{\pi }{\int }}\left(\sum I_i\right)d\varphi }$$ (9)

Ignoring again the variation of I_i with respect to the sinusoidal term we get:

$${mod}_{\varphi }\approx \frac{2R}{w^2}\underset{{\varphi }_0-\pi }{\overset{{\varphi }_0}{\int }}sin(\varphi -{\varphi }_0){\delta }_{CM}d\varphi =\frac{4R}{w^2}{\delta }_{CM}=k{\delta }_{CM}$$ (10)

Orbital Modulation for a large cluster of particles

If we have a large distribution of particles (Fig. 2B), we can approximate the intensity at each angle ϕ with the intensity generated by only the particles located at the angle ϕ:

$$I(\varphi )=\sum I_i(\varphi )\approx I_0(\varphi )e^{-\frac{2R_p^2(\varphi )}{w^2}}$$ (11)

Then we can write:

$$\frac{\partial I(\varphi )}{\partial \varphi }\approx \frac{\partial I_0(\varphi )}{\partial \varphi }{e}^{-\frac{2R_p^2(\varphi )}{w^2}}-\frac{2}{w^2}{I}_0(\varphi )e^{-\frac{2R_p^2(\varphi )}{w^2}}\frac{\partial R_p^2(\varphi )}{\partial \varphi }=\frac{\partial I_0(\varphi )}{\partial \varphi }{e}^{-\frac{2R_p^2(\varphi )}{w^2}}-\frac{2}{w^2}I(\varphi )\frac{\partial R_p^2(\varphi )}{\partial \varphi }=I_0(\varphi )e^{-\frac{2R_p^2(\varphi )}{w^2}}\left[\frac{1}{I_0(\varphi )}\frac{\partial I_0(\varphi )}{\partial \varphi }-\frac{2}{w^2}\frac{\partial R_p^2(\varphi )}{\partial \varphi }\right]$$ (12)

For a constant orbit radius R we have:

$$R_p^2={[R-\delta (\varphi )]}^2=R^2+\delta ({\varphi }^2)-2R\delta (\varphi )$$ (13)

and

$$\frac{\partial R_p^2}{\partial \varphi }=2[R-\delta (\varphi )]\frac{\partial \delta (\varphi )}{\partial \varphi }$$ (14)

Where δ(ϕ) is the distance of the particle from the center of the orbit. Considering for simplicity fluorophores distributed uniformly on a circle of radius a (Fig. 2C) then we have the following relationships:

$$\begin{array}{l}\delta {(\varphi )}^2={\phi }^2+{\delta }_{CM}^2-2a{\delta }_{CM}cos(\varphi -{\varphi }_0)\\ \frac{\partial \delta (\varphi )}{\partial \varphi }=\frac{a{\delta }_{CM}sin(\varphi -{\varphi }_0)}{\delta (\varphi )}=\frac{2a{\delta }_{CM}sin(\varphi -{\varphi }_0)}{2\sqrt{a^2+{\delta }_{CM}^2-2a{\delta }_{CM}cos(\varphi -{\varphi }_0)}}\approx {\delta }_{CM}sin(\varphi -{\varphi }_0)\end{array}$$ (15)

Under these conditions:

$$\frac{\partial I(\varphi )}{\partial \varphi }\approx I_0(\varphi )e^{-\frac{2R_p^2(\varphi )}{w^2}}\left[-\frac{2}{w^2}\frac{\partial R_p^2(\varphi )}{\partial \varphi }\right]=-\frac{4I(\varphi )}{w^2}(R-\delta (\varphi ))\frac{\partial \delta (\varphi )}{\partial \varphi }\approx -\frac{4I(\varphi )}{w^2}(R-\delta (\varphi )){\delta }_{CM}sin(\varphi -{\varphi }_0)$$ (16)

For the modulation we have:

$${mod}_{\varphi }=\left|\frac{\mathrm{\Delta }I}{I}\right|=\frac{\underset{{\varphi }_0-\pi }{\overset{{\varphi }_0}{\int }}\frac{\partial \left(\sum I_i\right)}{\partial \varphi }d\varphi }{\frac{1}{\pi }\underset{-\pi }{\overset{\pi }{\int }}\left(\sum I_i\right)d\varphi }\approx \frac{\underset{{\varphi }_0-\pi }{\overset{{\varphi }_0}{\int }}\frac{\partial I(\varphi )}{\partial \varphi }d\varphi }{\frac{1}{\pi }\underset{{\varphi }_0-\pi }{\overset{{\varphi }_0}{\int }}I(\varphi )d\varphi }\approx \frac{-\frac{4}{w^2}\underset{{\varphi }_0-\pi }{\overset{{\varphi }_0}{\int }}[R-\delta (\varphi )]I(\varphi )sin(\varphi -{\varphi }_0){\delta }_{CM}d\varphi }{\frac{1}{\pi }\underset{{\varphi }_0-\pi }{\overset{{\varphi }_0}{\int }}I(\varphi )d\varphi }$$ (17)

Ignoring the variation of δ(ϕ) ≈ a and I(ϕ), the modulation can be finally expressed approximately as:

$${mod}_{\varphi }\approx \frac{4(R-a)}{w^2}{\delta }_{CM}=k{\delta }_{CM}$$ (18)

According to the formula (18) the sensitivity for the feedback increases with increasing distance (R − a) from the object surface, and the formula (6) valid in the case of a point-like particle is recovered as a limit when a ≈ 0. If we also take into account the measurement noise we find that for larger distance the sensitivity is limited by the level of the signal. As discussed thoroughly in Ref. (Kis-Petikova and Gratton, 2004), the optimal orbit radius for tracking a point-like particle is obtained when the particle is in correspondence of the steepest region of the PSF. For a large particle we can restate the same principle saying that the surface of the particle must correspond to the region of maximum slope of the PSF.

Radial Modulation

The minimization of the orbital modulation keeps the system around the position δ_CM ≈ 0, so that the orbit is centered on the center of mass of the distribution of fluorophores. From the measurement of the orbital modulation, which is related to variations of the intensity in the angular coordinate, we don’t have access to information on the size of the object being tracked. In order to get this information we need to measure variations of the intensity in the radial direction. For this purpose we compute the derivative of the intensity with respect to the radial coordinate to measure the distance of the laser spot from the surface of the object.

The distance between the laser spot and the object surface at a given angle ϕ is determined by oscillating the scanner position in the radial direction of a given amount Δr (Fig. 3) and measuring the relative variation of the intensity, or radial modulation, defined as:

$${mod}_r=\left|\frac{\mathrm{\Delta }I}{I}\right|\approx \left|\frac{\partial I}{\partial r}\frac{\mathrm{\Delta }r}{I}\right|$$ (19)

Fig. 3.

Radial modulation in the nSPIRO method. The radius of the scanned orbit is oscillated rapidly instead of being constant (A). The intensity shows a modulation pattern which is related to the local distance from the surface (B).

If we know the modulation function

$${mod}_r=f(d)$$ (20)

which describes how the radial modulation is related to the distance d between the laser spot and the surface, we can recover the local radius ρ(ϕ) of an object by the simple relationship:

$$\rho (\varphi )=R-d(\varphi )$$ (21)

Alternatively, the modulation function can also be used as a feedback to maintain constant the value of the modulation and make the spot ‘surf’ at constant distance d(ϕ)=D from a surface in a way similar to the tip of an AFM microscope. Then the local radius of the object is recovered using the following relationship:

$$\rho (\varphi )=r(\varphi )-D$$ (22)

In both cases we need to make use of the modulation function to assign unequivocally a value of distance to any measured value of the modulation.

Radial modulation for a generic fluorescent surface

For a confocal or 2-photon microscope the intensity detected from a fluorescent particle is a function of its distance from the center of the focal spot. This spatial dependence is expressed through a function called the Point Spread Function (PSF) of the microscope. The detected fluorescence intensity depends also on other factors, namely the excitation intensity, the excitation probability, the quantum yield, the instrument efficiency. The intensity generated by a spatial distribution of fluorescent particles C(r′,ϕ′,z′) can be expressed in general as:

$$I(r,\varphi ,z)=I_0\int \mathit{dVC}(r^{\prime },\varphi ,z^{\prime })\mathit{PSF}(r-r^{\prime },\varphi -{\varphi }^{\prime },z-z^{\prime })$$ (23)

Consider the particles distributed randomly over a surface. Our aim is to reconstruct the shape of this surface through the detection of a fluorescent signal. In the nSPIRO method we orbit around a section of the surface, and reconstruct the shape of this section. The section of the surface is tracked (as described in the previous section) so that the center of the orbit coincides with the center of mass of the distribution. Then we want to measure also the local radius of the object ρ(ϕ) at any given angle ϕ.

First we will solve the problem in 2 dimensions and consider later the axial coordinate z. The detected signal at each position (r,ϕ) of the orbit will be, approximately, a function of the distance from the surface and of the local concentration of molecules according to the following relationship:

$$I(r,\varphi )=I_0\int \mathit{dVC}(r^{\prime },\varphi )\mathit{PSF}(r-r^{\prime },\varphi -{\varphi }^{\prime })\cong I_0(\varphi )\mathit{PSF}(r-\rho (\varphi ))$$ (24)

With this approximation we are only considering the contribution of the fluorescent surface to the measured intensity for a small area around the coordinate (ρ(ϕ),ϕ). This approximation is not valid if the surface is too small with respect to the PSF or if the spatial variations in concentration along the surface are larger than the variation of the PSF between opposite sides of the surface. We will analyze the validity of this approximation later in the derivation of an exact expression for the modulation of a uniform fluorescent empty cylinder.

Clearly the evaluation of the intensity alone is not enough to measure the distance of the focal spot from the fluorescent surface. To obtain a measurable quantity which depends solely on the distance between the spot and the fluorescent surface we need to build a function independent from the local amount of fluorophores. In order to do this we evaluate the radial modulation of the intensity upon a variation Δr of the radial coordinate:

$${mod}_r=\left|\frac{\mathrm{\Delta }I}{I}\right|\approx \left|\frac{\partial I}{\partial r}\frac{\mathrm{\Delta }r}{I}\right|\approx \frac{\left|\frac{\partial [I_0(\varphi )\mathit{PSF}(r-\rho (\varphi ))]}{\partial r}\mathrm{\Delta }r\right|}{I_0(\varphi )\mathit{PSF}(r-\rho (\varphi ))}=\frac{\left|\frac{\partial \mathit{PSF}(r-\rho (\varphi ))]}{\partial r}\mathrm{\Delta }r\right|}{\mathit{PSF}(r-\rho (\varphi ))}$$ (25)

As the non-spatial terms cancel out from the equation, the final expression shows that the modulation is a function only of the relative distance between the focal spot and the surface.

The first of the two approximations which have been used in the above formula is rigorously valid only for values of the variation Δr small enough with respect to the characteristic size of the PSF. The validity of the second approximation will be analyzed in more detail later.

For instance for a Gaussian shape of the PSF characterized by a waist w:

$$\mathit{PSF}=e^{-\frac{2{(r-\rho (\varphi ))}^2}{w^2}}$$ (26)

the modulation will be given by:

$${mod}_r\approx \frac{4(r-\rho (\varphi ))}{w^2}\mathrm{\Delta }r=\left(\frac{4\mathrm{\Delta }r}{w^2}\right)d(\varphi )$$ (27)

i.e. the modulation varies linearly with the radial distance from the surface:

$$d(\varphi )=r-\rho (\varphi )$$ (28)

The modulation is also proportional to the variation of the orbit radius Δr. For large values of Δr we expect deviations from this linear behavior. In fact, when Δr>d the maximum of the PSF penetrates the surface and we do not expect any additional gain in the modulation of the signal. The formula shows also that the sensitivity of the modulation function is inversely proportional to the square of the PSF waist w². It is easy to show that the formula (27) holds rigorously for an infinitely small cylinder as well as for a flat surface. The behavior for cylinders of finite size is analyzed in the next section.

Modulation function for a uniform cylinder and a Gaussian PSF

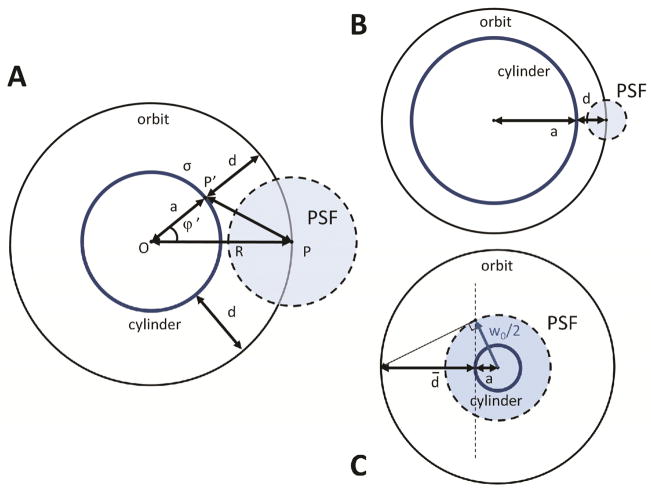
Consider now a cylindrical surface of radius ρ(ϕ′)=a and uniform density of fluorophores σ as shown in Fig. 3. Given a point P along the orbit of constant radius R, and a point P′ on the cylinder section, their distance is given by: ${\overline{{PP}^{\prime }}}^2=a^2+R^2-2\mathit{aR}cos{\varphi }^{\prime }$. Since every surface element dS′=adz′dϕ′ hosts an amount of fluorophores dN=σdS, the total fluorescence intensity collected in P will be proportional to the integral:

$$\underset{S}{\int }\mathit{PSF}(R-a,{\varphi }^{\prime },z^{\prime })\sigma {dS}^{\prime }=\sigma a\underset{-\infty }{\overset{\infty }{\int }}{dz}^{\prime }{e}^{-\frac{2{z^{″}}^2}{w_z^2}}\underset{-\pi }{\overset{\pi }{\int }}d{\varphi }^{\prime }{e}^{-\frac{2}{w_0^2}\left(a^2+R^2-2\mathit{aR}cos{\varphi }^{\prime }\right)}=\sqrt{2{\pi }^3}\sigma {aw}_z{e}^{-\frac{4}{w_0^2}\left(a^2+R^2\right)}·I_0\left(\frac{4aR}{w_0^2}\right)$$ (29)

Thus we can write the intensity as:

$$I=F_0{e}^{-\frac{2}{w_0^2}\left(a^2+R^2\right)}{I}_0\left(\frac{4aR}{w_0^2}\right)$$ (30)

where I₀(x) is the modified Bessel function of 0^th order and F₀ is a constant. Similarly we find for the derivative:

$$\frac{\partial I}{\partial R}=F_0{e}^{-\frac{2}{w_0^2}\left(a^2+R^2\right)}\left[-\frac{4R}{w_0^2}·I_0\left(\frac{4aR}{w_0^2}\right)+\frac{4a}{w_0^2}{I}_1\left(\frac{4aR}{w_0^2}\right)\right]$$ (31)

where I₁(x) is the modified Bessel function of the 1^st order.

The modulation can then be calculated as:

$$mod\cong \frac{\left|\frac{\partial I}{\partial R}\mathrm{\Delta }R\right|}{I}=\frac{F_0{e}^{-\frac{2}{w_0^2}\left(a^2+R^2\right)}\left|-\frac{4R}{w_0^2}·I_0\left(\frac{4aR}{w_0^2}\right)+\frac{4a}{w_0^2}{I}_1\left(\frac{4aR}{w_0^2}\right)\right|·\mid \mathrm{\Delta }R\mid }{F_0{e}^{-\frac{2}{w_0^2}\left(a^2+R^2\right)}{I}_0\left(\frac{4aR}{w_0^2}\right)}=\left|-\frac{4R}{w_0^2}+\frac{4a}{w_0^2}\frac{I_1\left(\frac{4aR}{w_0^2}\right)}{I_0\left(\frac{4aR}{w_0^2}\right)}\right|·\mid \mathrm{\Delta }R\mid$$ (32)

We can rewrite the modulation as a function of the distance d=R−a between the orbit and the surface:

$$mod=\frac{4\mid \mathrm{\Delta }R\mid }{w_0^2}\mid d+a[1-I_1(\gamma )/I_0(\gamma )]\mid$$ (33)

with $\gamma =4(d+a)a/w_0^2$.

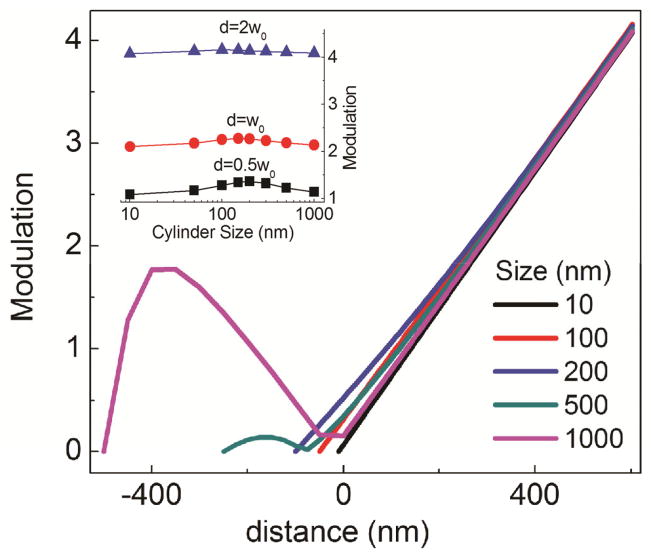
The modulation obtained from equation (33) is plotted in Fig. 5 as a function of the distance, for different cylinder sizes, for w₀=300nm and Δr=0.5w₀. We analyze now the asymptotic behavior of the modulation for small and large values of the parameter γ respectively.

Fig. 5.

Calculated modulation as a function of the distance for cylinders of different sizes. The insert shows the modulation at a given distance (as indicated) as a function of the size of the cylinder. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

Point-like particle approximation

For γ → 0, the Bessel functions ratio $\frac{I_1(\gamma )}{I_0(\gamma )}\to 0$, and the modulation can be approximated by the formula: $mod\approx \frac{4\mid \mathrm{\Delta }R\mid }{w_0^2}\mid d+a\mid$. This approximation holds when $(d+a)a\ll w_0^2/4$, i.e. for the two cases:

1. d ≈ −a (for an infinitely small orbit radius, the modulation is zero because the PSF is at the center of the cylinder)

2. a ≈ 0 (infinitely small cylinder radius) for which we can also write $mod\approx \frac{4\mid \mathrm{\Delta }R\mid }{w_0^2}\mid d\mid$.

In both conditions we are not able to measure the size of the cylinder, which will appear as a point-like structure.

Nearest-surface approximation

On the other hand, when γ ≫ 0 the Bessel function ratio $\frac{I_1(\gamma )}{I_0(\gamma )}\to 1$, and the modulation can be expressed in the linear form:

$$mod\approx \frac{4\mid \mathrm{\Delta }R\mid }{w_0^2}\mid d\mid$$ (34)

It follows that within the range of validity of this approximation, namely when:

$$(d+a)a\gg w_0^2/4,$$ (35)

the modulation can be considered a linear function only of the distance d from the surface. Under this condition the size of the cylinder can be recovered using the relation (34). We can distinguish two cases:

1. In the limit of a quasi-flat surface (Fig. 4B), i.e. for large cylinder radii a ≫ w₀/2, this condition is fulfilled for every positive distance d (and also for negative distances d for which is |d| ≪ a) (Fig. 5).

2. For a generic cylinder of radius a the condition above is still valid for sufficiently large positive distances d such that: $(d+a)\gg w_0^2/4a$, or, equivalently: d ≫ d̄ with $(\overline{d}+a)=w_0^2/4a$ (Fig. 4C and 5)

Fig. 4.

Derivation of the formula of the radial modulation for a uniform cylinder (A). Special cases of a large cylinder (B) and a small cylinder (C).

The figure 4C shows a geometrical construction for d̄ when we have a cylinder diameter smaller than the PSF waist. This condition expresses the fact that we have to orbit at large enough distance in order to resolve the two opposite sides of a small cylinder. This condition is equivalent to ignoring the intensity contribution of a fluorescent point at a distance d+2a with respect to one at a distance d:

$$\frac{I(d+2a)}{I(d)}=\frac{e^{-\frac{2{(d+2a)}^2}{w_0^2}}}{e^{-\frac{2{(d)}^2}{w_0^2}}}=e^{-\frac{2{(d+2a)}^2}{w_0^2}+\frac{2{(d)}^2}{w_0^2}}=e^{-\frac{2(4ad+4a^2)}{w_0^2}}=e^{-\frac{2a(d+a)}{w_0^2/4}}\approx 0.$$ (36)

Though in principle we could use an arbitrary large orbit radius to resolve the opposite sides of an arbitrary small cylinder, in a real case we are limited by other factors, the most important of which is the decrease of the signal to noise ratio as we move far away from the surface.

We note that at large enough distances the modulation is largely independent on the size of the cylinder (Fig 5 and inset). For instance, at a distance d=w₀, the calculated modulation for cylinders of 500nm and 1000nm size respectively differs by only 2%. This translates into a systematic error of about 6nm in the measured distance from the surface which is generally comparable or lower than the uncertainty due to S/N. This systematic error can be corrected if one uses equation (33) as the modulation function at any given orbit radius, instead of the simple equation (34).

Modulation for a cylinder at an angle

We consider now the modulation of a cylinder which is not exactly perpendicular to the plane of the orbit but oriented at an angle Θ with respect to the z-axis, along a direction Φ with respect to the x-axis (Fig. 6). As we orbit at constant radius around the cylinder, the distance d from its elliptical section will be a function of the phase ϕ−Φ, d=d(ϕ−Φ). In order to reconstruct the section we have to determine the relationship between the measured modulation and the distance d at each angle ϕ.

Fig. 6.

Cylinder at an angle with respect to the plane of the orbit.

For simplicity we will assume that the nearest-surface approximation is valid within a region along the z-axis of the order of w_z, the size of the Gaussian PSF along this axis. If this is the case, in order to calculate the modulation at a given angle ϕ along the orbit, it is equivalent to consider the plane tangent to the cylinder at that angular position. This plane is found at radial distance d and is oriented at an angle θ(ϕ) with respect to the z-axis. The angle θ is given by the relationship:

$$tan\theta =tan\mathrm{\Theta }cos(\varphi -\mathrm{\Phi }).$$ (37)

The absolute value of the angle θ is maximum (|θ|=Θ) for ϕ =Φ, Φ+π and has a minimum (|θ|=0) for ϕ = Φ±π/2.

Calculation of the modulation

As we oscillate the spot along the radial direction, we can separate this motion in a parallel and a perpendicular component with respect to the axis of the cylinder (Fig. 6). Only the perpendicular component yields a variation of the fluorescence intensity with an effective oscillation of the radius along this direction given by Δr′= Δrcosθ. The effective distance is given by d′=dcosθ. The effective waist w′, due to the asymmetry of the PSF, is given by:

$$\frac{1}{{w^{\prime }}^2}=\frac{{cos}^2\theta }{w_0^2}+\frac{{sin}^2\theta }{w_z^2}$$ (38)

We can approximate the modulation as:

$$mod\cong \frac{4d^{\prime }·\mid \mathrm{\Delta }{r}^{\prime }\mid }{{w^{\prime }}^2}=4d·\mid \mathrm{\Delta }r\mid {cos}^2\theta ·\left(\frac{{cos}^2\theta }{w_0^2}+\frac{{sin}^2\theta }{w_z^2}\right)=\frac{4d·\mid \mathrm{\Delta }r\mid }{w_0^2}{cos}^4\theta ·\left[1+\frac{w_0^2}{w_z^2}{tan}^2\theta \right]=\frac{4d·\mid \mathrm{\Delta }r\mid }{w_0^2}\frac{1+\frac{w_0^2}{w_z^2}{tan}^2\theta }{{[1+{tan}^2\theta ]}^2}$$ (39)

From which we see that the condition w_z>w₀ causes an additional reduction in the measured modulation with respect to the case of a perfectly spherical PSF (w_z=w₀):

$$mod(w_z=w_0)=\frac{4d·\mid \mathrm{\Delta }r\mid }{w_0^2}\frac{1}{1+{tan}^2\theta }$$ (40)

due to the increase in the effective waist for any angle θ>0.

The modulation depends on the phase ϕ through tanθ as defined above. Moreover the distance d depends also on the phase ϕ according to the shape of the section, namely an ellipse of minor and major axis b=R and a=R/cosΘ respectively:

$$d(\varphi )=r_{\mathit{orbit}}-r_{\mathit{cylinder}}(\varphi )=r_{\mathit{orbit}}-\frac{ab}{\sqrt{{(bcos\varphi )}^2+{(asin\varphi )}^2}}=r_{\mathit{orbit}}-\frac{R^2/cos\mathrm{\Theta }}{\sqrt{{(Rcos\varphi )}^2+{\left(R\frac{sin\varphi }{cos\mathrm{\Theta }}\right)}^2}}=r_{\mathit{orbit}}-R\frac{1}{\sqrt{{cos}^2\mathrm{\Theta }{cos}^2\varphi +{sin}^2\varphi }}$$ (41)

where we have assumed Φ=0 for simplicity.

Putting the equations together we obtain:

$$mod\cong \frac{4d(\varphi )·\mid \mathrm{\Delta }r\mid }{w_0^2}\frac{1+\frac{w_0^2}{w_z^2}{tan}^2\mathrm{\Theta }{cos}^2\varphi }{{\left[1+{tan}^2\mathrm{\Theta }{cos}^2\varphi \right]}^2}$$ (42)

This formula links the modulation to the distance d(ϕ) along the radial direction. If we explicit the dependence of d(ϕ) on the phase ϕ we obtain:

$$mod(\mathrm{\Theta },\varphi )\cong \frac{4·\mid \mathrm{\Delta }r\mid }{w_0^2}\left[r_{\mathit{orbit}}-R\frac{1}{\sqrt{{cos}^2\mathrm{\Theta }{cos}^2\varphi +{sin}^2\varphi }}\right]\frac{1+\frac{w_0^2}{w_z^2}{tan}^2\mathrm{\Theta }{cos}^2\varphi }{{\left[1+{tan}^2\mathrm{\Theta }{cos}^2\varphi \right]}^2}$$ (43)

Calculation of the intensity

The orientation of the cylinder away from the perpendicular to the orbit will cause a modulation of the intensity along the orbit even though the concentration of fluorophores is uniform. It follows that the intensity has to be corrected for this geometrical factor. To calculate an approximate expression of the intensity at a given point we can use the ‘nearest surface’ approximation, i.e. calculate the intensity at the point of the cylinder which gives the maximum contribution to the total intensity. This is the point T (Fig. 6) where the cylinder is tangent to the elliptical isosurface defined by the PSF shape, which, in the plane formed by the radial and z direction, we can write as:

$$e^{-2\left(\frac{r^2}{w_0^2}+\frac{z^2}{w_z^2}\right)}=e^{-2k}$$ (44)

or equivalently:

$$\frac{r^2}{w_0^2}+\frac{z^2}{w_z^2}=k$$ (45)

Using $\frac{\partial r}{\partial z}=tan\theta$ we obtain the angle θ′ formed between the direction r and the line connecting the center of the spot O to the point T:

$$tan{\theta }^{\prime }=\left|\frac{z}{r}\right|=\frac{w_z^2}{w_0^2}tan\theta$$ (46)

The distance d″(ϕ)=OT can then be calculated using the formula:

$$d^{″}(\phi )=\frac{d(\phi )cos\theta }{cos({\theta }^{\prime }-\theta )}$$ (47)

The intensity will depend on the distance d″(ϕ) and the effective waist w″ at the angle θ′:

$$\frac{1}{{w^{″}}^2}=\frac{{cos}^2{\theta }^{\prime }}{w_0^2}+\frac{{sin}^2{\theta }^{\prime }}{w_z^2}$$ (48)

So that finally the intensity will be given by:

$$I=F_0{e}^{-\frac{2{d^{″}}^2(\phi )}{{w^{″}}^2}}=F_0{e}^{-2d^2(\phi )\frac{{cos}^2\theta }{{cos}^2({\theta }^{\prime }-\theta )}\left[\frac{{cos}^2{\theta }^{\prime }}{w_0^2}+\frac{{sin}^2{\theta }^{\prime }}{w_z^2}\right]}$$ (49)

It is worth noting that the modulation of the intensity due to the cylinder orientation will be more evident at increasing distances from the surface. For small values of the distance d(ϕ), the variation of the intensity along the orbit can be approximated as:

$$I\approx F_0-2F_0{d}^2(\phi )\frac{{cos}^2\theta }{{cos}^2({\theta }^{\prime }-\theta )}\left[\frac{{cos}^2{\theta }^{\prime }}{w_0^2}+\frac{{sin}^2{\theta }^{\prime }}{w_z^2}\right]$$ (50)

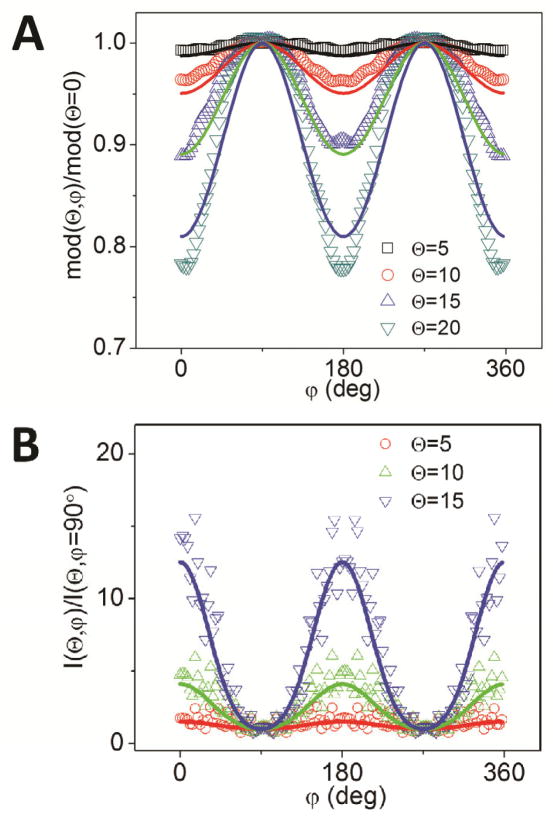
To check the validity of these formulas we performed simulations of uniform empty cylinders oriented at different angles, for a PSF with an axial waist w_z>w₀. In Fig. 7 we report the simulated variation of the modulation (Fig. 7A) and of the intensity (Fig. 7B) along the orbit for a cylinder of radius a=750nm and length L=2μm when we scanned the PSF (w₀=300nm, w_z=900nm) in an orbit of radius R=1250nm. The formulas approximate quite well the simulated data, at least for angles of orientation up to about 20°. Provided that the PSF parameters w₀ and w_z are known from calibration and the angle θ is known from the 3D trajectory (Lanzano et al., 2011a), the formulas can be used to correct the values of measured modulation and intensity from the effects due to orientation and obtain the proper shape and fluorophore concentration along the surface.

Fig. 7.

Simulated (symbols) versus calculated (lines) modulation (A) and intensity (B) for a cylinder at an angle. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

We note that in the experimental setup we can vary the orbital plane as to be perpendicular to the axis of the cylinder. Therefore this complication can be avoided by proper feedback of the plane of the orbit.

Error in the measurement of modulation

From the definition of the modulation:

$$mod=\frac{\mid \mathrm{\Delta }I\mid }{I}=\frac{\mid I(r+\mathrm{\Delta }r)-I(r)\mid }{I}$$ (51)

We can estimate the uncertainty on the modulation using the error propagation formula:

$${\left|\frac{\delta (mod)}{mod}\right|}^2={\left|\frac{\delta (\mathrm{\Delta }I)}{\mathrm{\Delta }I}\right|}^2+{\left|\frac{\delta I}{I}\right|}^2$$ (52)

$${\mid \delta (mod)\mid }^2={\left|\frac{\delta (\mathrm{\Delta }I)}{I}\right|}^2+{\left|\frac{\delta I}{I}\right|}^2{mod}^2={\left|\frac{\delta I}{I}\right|}^2+{\left|\frac{\delta (I+\mathrm{\Delta }r)}{I}\right|}^2+{\left|\frac{\delta I}{I}\right|}^2{mod}^2\approx \frac{1}{N}\left[2+{(mod)}^2\right]$$ (53)

where N is the total number of photon collected at a given distance d from the surface. The relative error can be expressed as:

$$\left|\frac{\delta (mod)}{mod}\right|\approx \frac{1}{\sqrt{N}}{\left[1+\frac{2}{{mod}^2}\right]}^{\frac{1}{2}}$$ (54)

Equation (54) shows that the precision in the measurement of modulation is dependent on the number N of collected photons as 1/√N, so that, for instance, to reduce the error by a factor of 10 one needs to increase the intensity by a factor of 100.

Substituting $N=N_0{e}^{-\frac{2d^2}{w_0^2}}$ and $mod=\frac{4d·\mid \mathrm{\Delta }r\mid }{w_0^2}$, we obtain:

$$\left|\frac{\delta (mod)}{mod}\right|\approx \frac{e^{\frac{d^2}{w_0^2}}}{\sqrt{N_0}}{\left[1+\frac{w_0^4}{8d^2{(\mathrm{\Delta }r)}^2}\right]}^{\frac{1}{2}}$$ (55)

Expression (55) shows that for small distances $d^2\ll \frac{w_0^4}{8{(\mathrm{\Delta }r)}^2}$ the error is dominated by the second term in parenthesis (related to the uncertainty on ΔI) and is larger than the photon-limited noise:

$$\left|\frac{\delta (mod)}{mod}\right|\approx \frac{e^{\frac{d^2}{w_0^2}}}{\sqrt{N_0}}{\left[\frac{w_0^4}{8d^2{(\mathrm{\Delta }r)}^2}\right]}^{\frac{1}{2}}>\frac{1}{\sqrt{N}},$$ (56)

On the other hand, for large enough distance the uncertainty depends only on the number of photons collected at distance d:

$$\left|\frac{\delta (mod)}{mod}\right|\approx \frac{1}{\sqrt{N}}$$ (57)

since the uncertainty arises mainly from the evaluation of the intensity value I.

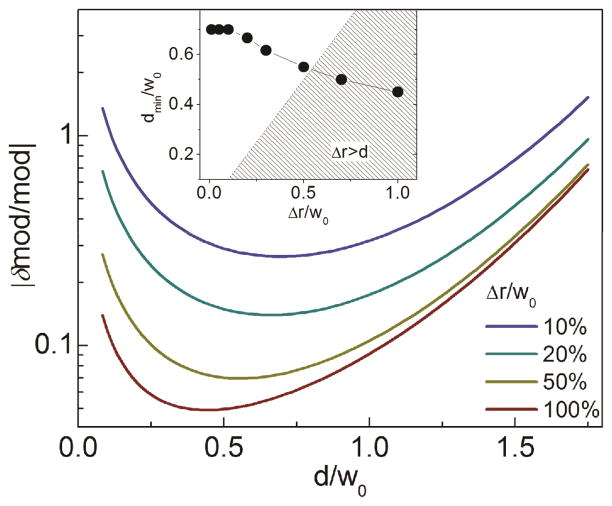
In order to show how the uncertainty varies with the distance we plotted the expression (55) in Fig. 8 for the value N₀=1000. According to the graph there seems to be an optimal distance d_min for which the relative error reaches a minimum. The value of the optimal distance d_min decreases down to the value ~ 0.5w₀ for increasing amount of modulation Δ;r (Fig. 8, inset). For values of Δr larger than ~0.5w₀, we are limited by the condition d>Δr, meaning that we have to orbit far enough for the PSF not to penetrate into the surface and, as we orbit at a larger distance, the uncertainty tends to increase due to the √N component.

Fig. 8.

Calculated uncertainty in the measure of the modulation as a function of the distance. The value of d_min is plotted in the inset for different amount of input modulation. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

Variations along the optical axis

So far we have ignored the effect of being off-focus along the optical axis or z-axis. If a particle is smaller than the PSF dimension along z, and is located at a given z distance from the focal point, it will probe the PSF shape at this coordinate. For a Gaussian profile:

$$\mathit{PSF}(r,z)=e^{-\left(\frac{2r^2}{w^2}+\frac{2z^2}{w_z^2}\right)}$$ (58)

the modulation is independent of z. This is not true for a general shape of the PSF. For instance, under the 2-photon excitation, the intensity profile is well approximated by a squared Gaussian-Lorentzian function (Berland et al., 1996; Chen et al., 1999):

$$\mathit{PSF}(r,z)=\frac{4w_0^4}{{\pi }^2{w}^4(z)}{e}^{-\left(\frac{4r^2}{w^2(z)}\right)}$$ (59)

with

$$\begin{array}{l}{w}^2(z)=w_0^2\left(1+{\left(\frac{z}{z_R}\right)}^2\right)\\ z_R=\frac{\pi w_0^2}{\lambda }\end{array}$$ (60)

In this case, being the waist of the radial PSF a function of the z-axis distance, the modulation is expected to decrease with z.

If we have a cylinder of length greater than the PSF then its surface will probe an average of the function (59) along the z. As a result the modulation will be smaller for a Gaussian-Lorentzian PSF compared to a Gaussian PSF having a radial waist w₀ equal to the effective waist $w_{\mathit{eff}}=w(0)/\sqrt{2}$ of the Gaussian-Lorentzian measured at the focal plane. Numerical simulations indicate that the modulation for a Gaussian-Lorentzian PSF is reduced roughly by a factor of 2.

Experiments with fluorescent spheres

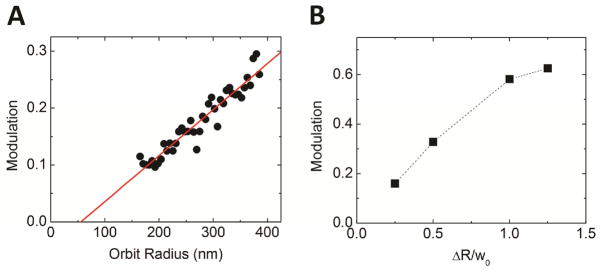
In order to confirm the predictions based on calculations and simulations we performed experiments on fluorescent beads of known size. In Fig. 9 we show the variation of modulation measured for a 110nm fluorescent bead fixed on a slide. The bead is tracked using different scanning orbit radius and different amount of modulation. Within the reported range the modulation varies linearly with the orbit radius and hence with the distance (Fig. 9A). The value of the modulation increases also as a function of the radial oscillation amplitude ΔR but tends to saturate for values of ΔR larger than about 50% of the PSF width (Fig. 9B).

Fig. 9.

Calibration of the modulation function of the microscope setup: (A) Experimental modulation functions for a 110nm-diameter fluorescent sphere as a function of the orbit radius. (B) Modulation at R=275nm for different values of radius oscillation Δr.

The experimental points in Fig. 9A can be interpolated by a linear fit which represents the modulation function at a given percentage of oscillation of the orbit radius. The slope of the modulation function ultimately determines the sensitivity of the setup to measure differences in distance. The radial size of the particle can be extrapolated from the point where the linear fit of the modulation takes the value 0. The histograms of the slope and particle radius values recovered from the measurement on N=11 spheres are reported on Fig. 10. The slope has an average value of 0.00081±0.00004nm⁻¹ (mean±s.d.). For the particle radius, if we consider a bimodal distribution, we obtain the two center values R_p1=59±4nm and R_p2=73±1nm. The smaller value is in agreement with the size of single beads (φ/2=55±5nm) while the larger value could be associated to the apparent size of clusters of two particles (√2·φ/2=78±7nm) that did not dissociate during sonication.

Fig. 10.

Histogram of the recovered values of the slope (A) and particle radius (B) for several (N=11) 110nm-size fluorescent spheres.

We then performed acquisition in two channels to show that the modulation is not dependent on the intensity level of the signal. We report in Fig. 11 the tracking of a fluorescent bead for which the intensity of the signal in the green channel is significantly higher than the intensity in the red channel (I_green~6·I_red). For an increasing orbit radius the intensity decreases in both channels due to the increasing distance from the particle and following the PSF profile (Fig 11A). In contrast the modulation of the intensity increases with the distance from the particle and has the same value for both channels (Fig 11B). On the other hand the precision in the measure of modulation is different for the two channels, as is dependent on the intensity level of the signal (Fig 10C). In fact, as expected from equation (54) the modulation error in the red channel is increased of a factor given by the ratio of the inverse square root of the intensities in the two channels (√I_green/√I_red ~2.4).

Fig. 11.

Two-channels experiment with 110nm fluorescent spheres, showing how the intensity (A), the modulation (B) and the uncertainty in the modulation (C) vary with the distance in the two channels. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

The two channels acquisition setup opens up the possibility to perform differential measures of distance between two surfaces labeled with two different probes. In this case the distance between the two surfaces can be determined measuring the difference of modulation in the two channels, and the sensitivity of this distance measurement depends on the steepness of the modulation function. For instance, if the slope of the modulation function is of the order of 0.001nm⁻¹ and we measure the modulation at a distance from the surface of about 200nm, then a measured difference of 10% between the modulation values in the two channels translates into a measured distance of about 20nm. This super-resolution range is especially interesting since it represents a range not accessible by other techniques, as for instance FRET (Forster Resonance Energy Transfer), which probes distances between molecules which are in the order of only a few nanometers.

Discussion

In this paper we have introduced a mathematical model to describe the concept of intensity modulation which is at the base of the nSPIRO method. In this method, the simultaneous tracking and imaging of an object are possible through the real-time measurement of the modulation of the fluorescence intensity. We have shown here that, while the minimization of the orbital modulation keeps an object at the center of the orbit, the radial modulation induced by the rapid oscillation of the beam in the radial direction provides a direct measure of the distance between the laser spot and the object.

The mathematical model shows under which conditions the modulation can be considered a quantity dependent on the distance from the object, but largely independent from the shape of the surface and the concentration of fluorophores. The model takes in to account how the sensitivity of the modulation function is related to the parameters describing the PSF and which are the experimental factors affecting the precision with which the modulation itself can be measured.

The main findings of the model have been confirmed by the experiments performed on fluorescent spheres of known size. The results of these experiments show that is possible to measure the size of the particles and to determine how sensitive the microscope setup is to the measurement of distances. In particular the possibility of performing simultaneous acquisition in two channels looks very promising as a method to measure the distance between surfaces in the range 10–200nm which is complementary to the typical range observable by FRET.

In our opinion the results presented in this work help understanding the principles of the nSPIRO method and the advantages and limitations of this technique in view of its current and future applications to the imaging of biological structures.