On the electrophysiological response of bone cells using a Stokesian fluid stimulus probe for delivery of quantifiable localized picoNewton level forces

Abstract

A Stokesian fluid stimulus probe (SFSP), capable of delivering quantifiable pN level hydrodynamic forces, is developed to distinguish the electrophysiological response of the cell process and cell body of osteocyte-like MLO-Y4 cells without touching the cell or its substrate. The hydrodynamic disturbance is a short lived (100 ms), constant strength pressure pulse that propagates nearly instantaneously through the medium creating a nearly spherical expanding fluid bolus surrounding a 0.8 µm micropipette tip. Laboratory model experiments show that the growth of the bolus and the pressure field can be closely modeled by quasi-steady Stokes flow through a circular orifice provided the tip Reynolds number, Re_t<0.03. By measuring the deflection of the dendritic processes between discrete attachment sites, and applying a detailed ultrastructural model for the central actin filament bundle within the process, one is able to calculate the forces produced by the probe using elastic beam theory. One finds that forces between 1 and 2.3 pN, are sufficient to initiate electrical signaling when applied to the cell process, but not the much softer cell body. Even more significantly, cellular excitation by the process only occurs when the probe is directed at discrete focal attachment sites along the cell process. This suggests that electrical signaling is initiated at discrete focal attachments along the cell process and that these sites are likely integrin-mediated complexes associated with stretch-activated ion channels though their molecular structure is unknown.

1. Introduction

There has been a longstanding debate summarized in a recent review (Fritton and Weinbaum, 2009) as to bone mechanotransduction. The two fundamental questions are: 1) whether the osteocyte cell body or its dendritic processes serve as the mechanosensor of fluid flow in the lacunar-canalicular porosity, and 2) if the cell process is the sensing component, whether intracellular signaling is initiated at discrete attachment sites along the cell process, as hypothesized in (Wang et al., 2007) and (McNamara et al., 2009) or at the much more numerous flexible tethering attachments described in (You et al., 2001; You et al., 2004). It has proved extremely challenging to resolve these issues because of the difficulty of separately exposing the cell body and its dendritic processes to fluid flow. To address these questions, we have developed a new hydrodynamic force probe, the Stokesian fluid stimulus probe (SFSP). The SFSP was based on pressurized fluid delivery through fine pipettes, a methodology in routine use by pharmacologists studying single cell responses. A drawback to other currently used force probe techniques is that all require physical contact to deform membranes and may alter the system through this contact in a live single-cell experiment (Appendix A summarizes: biomembrane force probe, magnetic pullers and twisters, the atomic force microscope (AFM), and optical tweezers.

Generally, micropipette ejection systems operate in a tip Reynolds number (Re_t) regime where a vortex-shedding axial jet is produced that breaks up into turbulence (Hanani, 1997). To produce not a jet, but a nearly spherical reproducible bolus, whose growth and pressure field can be theoretically predicted and experimentally measured, required operating in a much lower Re_t regime than, heretofore, examined. An initial series of experiments was performed with tracers ejected at low pressure from a micropipette with a 0.8 µm tip diameter to visualize the fluid bolus. However, diffusional blurring prevented clear demarcation of the edge of the growing bolus, and vastly improved results were obtained using a 1,000 fold larger laboratory scale model employing hydrodynamic similarity. This laboratory scale model clearly demonstrated that a nearly spherical bolus, closely corresponding to Sampson flow through a circular orifice, could be achieved provided Re_t < 0.03, and that Sampson’s solution could be used to describe the velocity and pressure field in the vicinity of the micropipette tip.

The SFSP does not actually touch the cell or its substrate, yet creates tensile forces on focal attachments of the same magnitude as the tensile forces predicted in (Wang et al., 2007) for very small focal contacts observed at the apex of the canalicular protuberances described in (McNamara et al., 2009). These forces, which are in the range of < 1–10 pN, involve just a few integrins and are roughly three orders of magnitude smaller than the mechanical forces one typically exerts in touching a cell with a micropipette tip or AFM to elicit a Ca²⁺ response (Huo et al., 2010).

We have combined this physiological force stimulus with highly sensitive whole-cell voltage-clamp recordings to elucidate the mechanism of signal initiation in single osteocyte-like MLO-Y4 cells. The SFSP is used on single MLO-Y4 cells to identify the region where a mechanotransdution event is initiated in the cell, and whether this intracellular signaling is adhesion dependent. Our results strongly support the hypothesis that the cell process rather than the cell body is the site of mechanosensation. In addition, because response was correlated with focal attachment of cell processes to substrate, these findings indicate that the discrete attachment sites along the cell process are indeed sites of early osteocyte mechanotransduction.

2. Method

2.1. MLO-Y4 culture

MLO-Y4 osteocyte-like bone cells were maintained in α-MEM (Invitrogen) supplemented with 5% fetal bovine serum (Invitrogen), 5% bovine serum (Invitrogen), and 1% penicillin-streptomycin solution (Meditech). MLO-Y4s were plated on 12 mm glass microscope coverslips (Fisher Scientific) at low density and cultured for two days before performing whole-cell voltage-clamp experiments.

2.2. Probe characterization and performance

2.2.1. Tracer studies

Epi-fluorescent image sequences of spreading dye, Lucifer Yellow CH dilithium salt (Sigma-L0259) or Dextran Conjugated Fluorescein (MW 70k, Molecular Probes-D1822) diluted in extracellular solution, were obtained at an acquisition interval of 20ms or 50ms during SFSP application at 20psi for 100ms. Micropipettes were pulled with a P-97 Pipette Puller (Sutter Instruments) to achieve an initial tip resistance of 2–3MΩ when backfilled with extracellular solution. For composition of solutions, see Appendix B.

2.2.2. Tip Reynolds number relationship

It was apparent from initial tracer studies that there were two key Re in the problem:

$${\text{Re}}_{\mathrm{t}}=\frac{2\mathrm{\rho }{\mathrm{U}}_{\mathrm{t}}{\mathrm{R}}_{\mathrm{t}}}{\mu },$$ (1)

where R_t and U_t are the internal radius and average velocity at the tip exit, and

$${\text{Re}}_{\mathrm{s}}=\frac{2\mathrm{\rho }{\mathrm{U}}_{\mathrm{s}}{\mathrm{R}}_{\mathrm{s}}}{\mu },$$ (2)

where R_s and ${\mathrm{U}}_{\mathrm{s}}=\frac{{\text{dR}}_{\mathrm{s}}}{\text{dt}}$ are the instantaneous radius and expansion velocity of the bolus corresponding to a constant ejection rate, Q, at the micropipette tip. From continuity,

$${\mathrm{Q}}_{\mathrm{t}}=\mathrm{\pi }{{\mathrm{R}}_{\mathrm{t}}}^2{\mathrm{U}}_{\mathrm{t}}=4\mathrm{\pi }{{\mathrm{R}}_{\mathrm{s}}}^2{\mathrm{U}}_{\mathrm{s}}\text{ or }{\mathrm{U}}_{\mathrm{t}}=4{\left(\frac{{\mathrm{R}}_{\mathrm{s}}}{{\mathrm{R}}_{\mathrm{t}}}\right)}^2{\mathrm{U}}_{\mathrm{s}}.$$ (3)

Substituting the relationship between U_t and U_s from the continuity equation (3) into the foregoing definitions of Re_t and Re_s one finds that

$${\text{Re}}_{\mathrm{t}}=4\left(\frac{{\mathrm{R}}_{\mathrm{s}}}{{\mathrm{R}}_{\mathrm{t}}}\right){\text{Re}}_{\mathrm{s}}.$$ (4)

2.2.3. Laboratory model

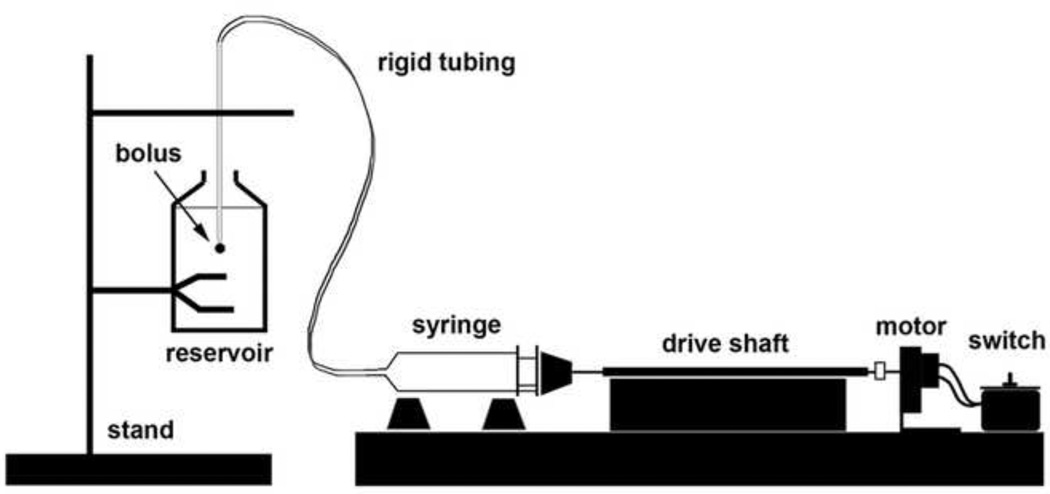
A screw-actuated syringe pump was constructed to eject fluid at constant flow rate from a large-scale pipette using a 20mL syringe (BD Biosciences) inline with a motor (RF-310TA, Mabuchi) (Fig. 1), more details in Appendix B. Four drive shaft revolutions advanced the syringe to expel 1mL of fluid over 31.2s. Newtonian fluid (Pantene Pro-V shampoo) was used in the reservoir and pipette, but the latter differed in color to clearly demarcate the advancing border of the ejected fluid bolus. To determine the time dependent variation of the fluid bolus shape as a function of Re_t from 0.03–20.4, four different viscosities were investigated where the fluid viscosity was changed by dilution with water over a 600 fold range. Images at four time points, t = 0 s through t = 31.2 s at 7.8 s intervals, were extracted (HandyAvi) for each viscosity and compared.

Figure 1.

A schematic of the scaled-up laboratory model built to visualize expansion of the ejected fluid bolus. The screw-actuated syringe pump ejects Newtonian fluid at a constant flow rate of Q = 32 mm³/s. The same Newtonian fluid is used to fill the pipette tip and the reservoir, but differed in color to clearly distinguish the leading edge of the expanding bolus. One mL of fluid is expelled from the pipette tip into a 500 mL reservoir and imaged for 31 s.

2.2.4. Sampson solutions for velocity and pressure field

Laboratory model experiments showed that the growth of the bolus is closely approximated by Sampson flow through a circular orifice in a zero thickness plane wall. Solutions for the velocity and pressure field for Sampson flow are given in Appendix C.

2.3. Osteocyte electrophysiology experiments

In order to test whether osteocyte activation originates at cell processes or the cell body or at discrete locations along the cell processes, we have performed the first electrophysiological experiments to measure the focal activation of ion channels in the dendritic processes of osteocytes using our newly developed SFSP. A unique aspect of the experiment is that the SFSP can apply pN level forces locally along the length of the dendritic process. One could accurately determine local attachment sites along the length of the dendritic processes.

2.3.1. Micropipette setup and placement

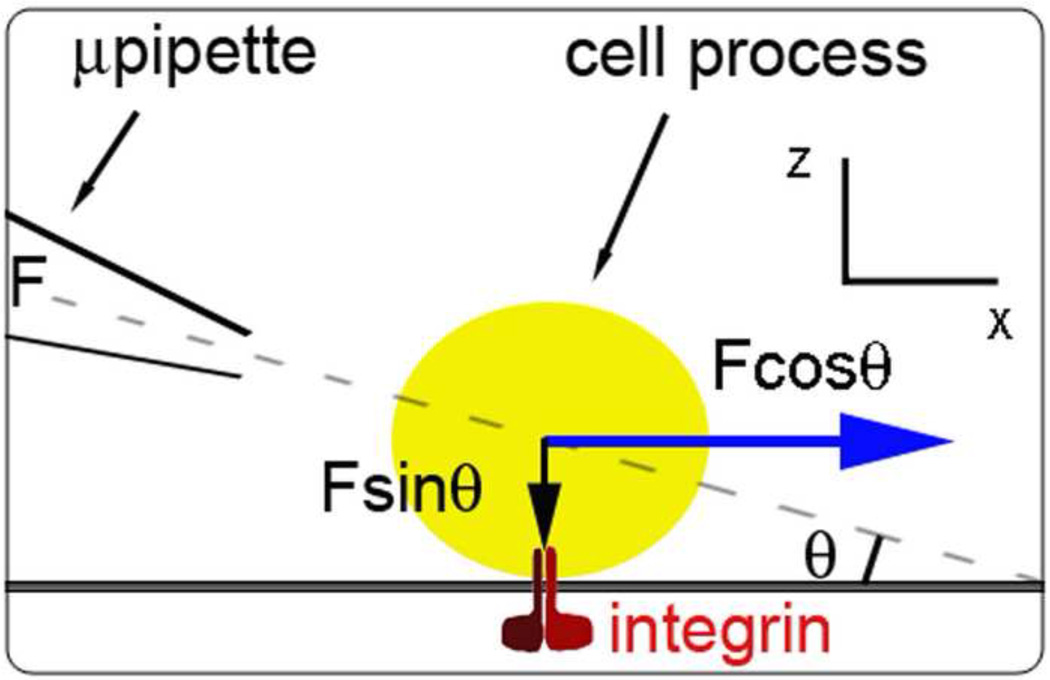
SFSP micropipettes were prepared as described in Methods Section 2.2.1, filled with extracellular solution, and placed at 2–5 µm distance from the cell body or its processes at a 37 degree angle from the substrate. A single SFSP pressure pulse is applied at 20psi and held constant for a duration of 100ms. The quasi-steady state velocity and pressure field are established nearly instantaneously and motion ends abruptly with the termination of pulse. Sketch of the force diagram and pipette placement are shown in Figure 2.

Figure 2.

Force diagram showing vectors of SFSP force: traction force, F_x (Fcosθ), and compression force, F_z (Fsinθ). Only F_x creates tensile force on integrin attaching cell process to its substrate. Line of action is through the center of the cell process cross-section. Positioning of the SFSP micropipette was achieved by using the coarse and fine adjustment of a 3-axis hydraulic micromanipulator.

2.3.2. Measurements of process deflections and predictions of forces

The determination of the force acting on the processes is subtle since the flow geometry is fully three dimensional and unbounded and, thus, not easily amenable to a computational solution at low Re. It is easy to observe and measure the deflection of the process and the separation distance L between discrete attachment sites where there was no visible deflection, Video S1. Thus, if one can estimate the flexural rigidity EI of the central actin filament bundle in the process, one can apply elastic beam theory to relate the force on the process to the displacement at its center. The detailed structure of the fimbrin cross-linked actin filament bundle is a highly organized hexagonal structure, five actin filaments across, and described in detail (Han et al., 2004). This structure is based on the electron microscopic observations of dendritic process cross-sections (You et al., 2004), and exposed actin filament bundles in which the process’ membrane has been enzymatically removed (Tanaka-Kamioka et al., 1998). The Young’s modulus of individual actin filaments, E = 2.6×10³ pN/nm², has been accurately measured by in vitro nanomanipulation (Kojima et al., 1994), and I is the area moment of inertia of the central actin bundle, where the effective cross-sectional area of an individual actin filament is 25nm². The theory for determining EI and relating the force to the deflection of the process is described in more detail in Appendix D.

2.3.3. Whole-cell voltage-clamp experiments

Patch microelectrodes were pulled as described in Methods Section 2.2.1., but to an initial electrode resistance of 4–5MΩ. Conventional whole-cell voltage-clamp recordings were performed on individual MLO-Y4 cells held at −60mV with high resistance seals >1GΩ. The electric charge and peak conductance in response to SFSP stimulation directed to the cell process at attached sites or the cell body was calculated and analyzed using a two-tailed paired Student’s t-test. All values were expressed as means±s.e.m. See Appendix B for more details.

3. Results

3.1. Probe characterization and performance

3.1.1. Tracer studies

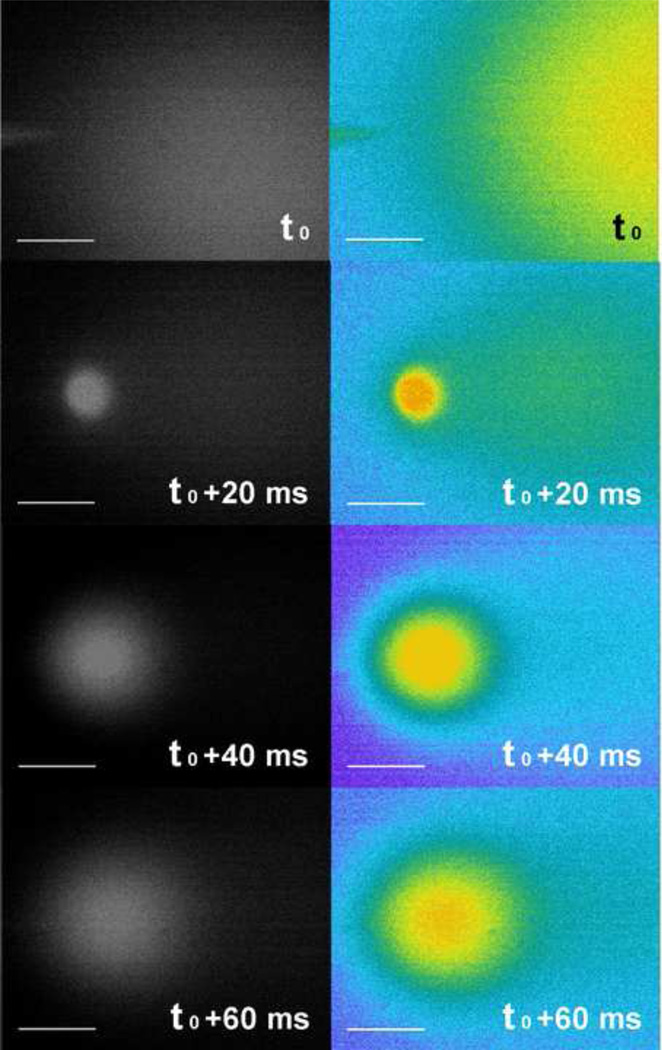
The Lucifer yellow tracer results (Fig. 3) clearly demonstrated the feasibility of ejecting a reproducible nearly spherical fluid bolus. However, the Lucifer yellow images did not clearly demarcate the edge of the growing bolus because of diffusional spreading of this low MW tracer. The blurring of the image is roughly estimated from the characteristic diffusion length, $\mathrm{\delta }=\sqrt{4\mathrm{D}\mathrm{t}}$, where D, the diffusion coefficient for Lucifer yellow, is 3×10⁻⁶ cm²/s (Imanaga et al., 1987). For t = 100ms, δ ~ 11 µm. Experiments were also conducted with a high molecular weight fluorescein conjugated dextran, which provided a much clearer series of images (Appendix E), but it still remained difficult to track the leading edge of the expanding bolus as a function of time with the current experimental set-up. The shortest acquisition interval, 20ms, was too long to accurately capture the evolving bolus shape.

Figure 3.

FSP experiment using Lucifer yellow dye (MW 457) showing growth of bolus with diffusion in extracellular solution. The picospritzer applied a back pressure of 20 psi for 100 ms to a micropipette with a tip diameter 0.8 µm. A 20 ms image acquisition interval was used to capture a series of bolus expansion images. Both greyscale fluorescent and pseudo color images are shown. Scale bar is 50 µm.

3.1.2. Tip Reynolds number relationship

In Table 1, the diameter of the bolus after 100ms is roughly estimated from the tracer images (Fig. 3), and this growth rate is used to estimate Re_s. Re_t is then calculated from the relation in equation (4), derived from equation (3). For an applied pressure of 10–20 psi, the expelled bolus was nearly spherical. However, for pressures > 25psi the bolus started to distort.

Table 1.

Measurement of Q at back pressures of 10 and 20 psi and determination of sphere and tip Reynolds numbers Re_s and Re_t, from equations (1) and (2). Lucifer yellow (MW 457) was used to image the expanding SFSP bolus, but diffusional blurring prevented accurate observation of the bolus shape and its growth. Thus, a laboratory model (Fig. 1) was developed to more clearly observe the leading edge of the expanding bolus and its changing shape.

Pressure (psi)	Q (µm3/ms)	Dt (µm)	Res	Ret
10	23	0.8	0.0003	0.04
20	51	0.8	0.0006	0.10

3.1.3. Laboratory model

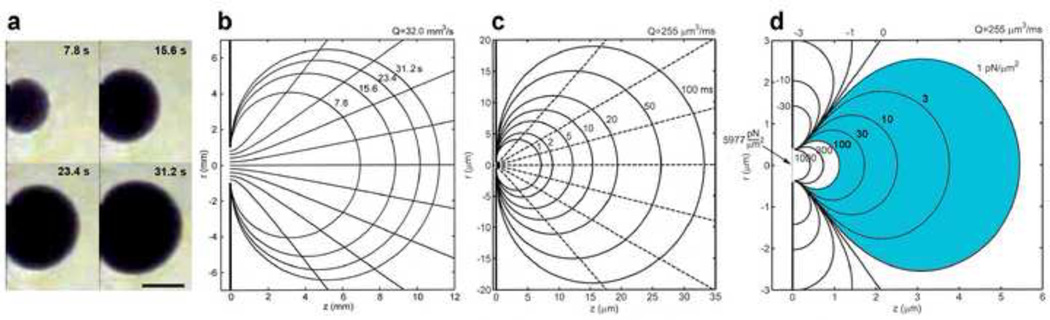
A laboratory model, 1,000 fold larger than the SFSP experiment, was developed to observe the expansion of the ejected bolus over a much longer timescale of 31.2s (Fig. 4). One observes in this figure that a fully developed laminar jet has started to break up into turbulence about its rolled up vortex at Re_t = 20.4 (Fig. 4e), and remnants of this behavior are clearly evident at Re_t = 0.5 (Fig. 4d). A pear-like distortion in the spherical bolus is also observed at Re_t = 0.1 (Fig. 4c), but a nearly spherical bolus is achieved at Re_t = 0.03 (Fig. 4b), a value close to the first entry in Table 1. Note that the bolus growth for the flow from a circular orifice in a plane wall (Fig. 4a) closely approximates the pipette flow at the same Re_t.

Figure 4.

Laboratory model results were presented to illustrate the time dependent change in bolus shape obtained by varying solution viscosity from 0.01 to 6.71 cm²/s. For all experiments, the reservoir solution and the bolus solution were identical in viscosity but differ in color. The laboratory pipette tip diameter was 0.2 cm. The reservoir size and pipette tip position were chosen to minimize the influence of the boundaries and the bolus was considered to expand into free space. (a,b) The nearly spherical bolus shape was preserved at a Re_t of 0.03, and (c) pear-like bolus distortions are observed at a Re_t as small as 0.1. (d) Large distortions are observed at Re_t = 0.5 and (e) for Re_t > 1 an axial jet develops. When the pipette exit was replaced by a circular orifice in a plane wall, the bolus shape closely resembled a Sampson flow. Scale bar is 1.5 cm.

3.1.4. Sampson solutions for velocity and pressure profiles

While there are no analytical solutions for Stokes flow at the exit of a hollow bore circular cylinder, there is a closed form solution for creeping flow through a circular orifice in a wall of zero thickness, Sampson flow (Happel and Brenner, 1973). Since the length of the bore has little effect on the exit velocity profile (Dagan et al., 1982), one would expect that the exit flow at the pipette tip is very similar to Sampson flow. This similarity is clearly observed when Re_t = 0.03 (Fig. 5a from Fig. 4a) in which the growth of the bolus is nearly identical to Sampson flow predictions (Fig. 5b) at equivalent time points with only minor differences in overall bolus shape. Thus, Sampson’s solution for the bolus growth for the laboratory model, Q = 32 mm³/s, and the micropipette, Q_t = 255 µm³/ms (Fig. 5c), and its associated pressure field in the vicinity of the micropipette exit (Fig. 5d) provide a remarkably good description of the bolus expansion and pressure field.

Figure 5.

(a) Laboratory model of growing bolus for Sampson flow through a circular orifice, from Figure 4a where Re_t = 0.03. Scale bar is 0.5 cm. (b) Theoretical prediction for the laboratory model bolus growth for Q = 32.0 mm³/s in which the pipette tip diameter was 0.2 cm and Re_t = 0.03. The Sampson solution closely predicts the leading edge of the bolus expansion over time, and closely approximates the bolus growth in the laboratory model pipette experiment (Fig. 4a). (c) Theoretical prediction of bolus shape for Sampson flow for a micropipette with a tip diameter of 1 µm where Q = 255 µm³/ms. (d) Theoretical predictions of the pressure field (isobars) in the vicinity of the micropipette tip exit corresponding to the bolus expansion. This pressure field describes the decay in the velocity field from the plane of the orifice.

Although the flow starts from rest and there is an initial transient, this is short lived. If the characteristic vorticity diffusion distance, $\sqrt{4\mathrm{\nu }\mathrm{t}}$, is 10µm and ν = 0.01 cm²/s (water 20 °C), the duration of this initial transient, t = 6×10⁻⁴ s. Thus, the steady state pressure field is set up almost instantaneously, and the velocity field is a quasi-steady Stokes flow and does not change during the entire pressure pulse. A key observation is that although the bolus has an approximate diameter of 35µm at the end of the pressure pulse (Fig. 5c), the region of interest in the pressure diagram, shaded blue in Figure 5d, is confined to 1–5 µm from the orifice exit. Here the pressure rapidly decays from approximately 100 to 1 pN/µm² along the axis of the bolus.

3.2. Measurements of process deflections and predictions of forces

In Table 2, we have summarized the detailed measurements of the maximum deflection δ_m of the cell process at the central location between firm attachment sites on the process for five cell process deflections. Radii a and distance between attachments L are shown for each process. The maximum deflection of the process varies inversely as the third power of the distance L and the value of ⊟ = 2.2×10⁸ pN nm². Here I = 8.6×10⁴ nm⁴ is calculated using the detailed theoretical model for the central actin filament bundle described in Appendix D, Figure S1. In general, the distance L is significantly larger than the radial spread of the pressure profile in Figure 5d, which depends on the distance of the probe tip from the centerline of the process d_t where the maximum deflection δ_m is measured (Appendix D, Figure S2). This distance d_t was typically in the range 4.4–6.3 µm and the radial pressure profiles along the process estimated from the solutions for Sampson flow are shown in Appendix D, Figure S3. The rapid lateral decay allows us to treat the force as a concentrated load applied midway between firm attachment sites on the cell process. Predicted forces on processes are shown in the last column of Table 2 and are based on equation (D6) in Appendix D where the force is related to δ_m by $\mathrm{F}=\frac{48\boxminus {\mathrm{\delta }}_{\mathrm{m}}}{{\mathrm{L}}^3}$. Note that the predicted forces all fall in the range 1 to 2.3 pN, well within the range of forces predicted by (Wang et al., 2007) for the hypothesized integrin attachments at canalicular projections.

Table 2.

Measurements of radius a, distance between SFSP tip and center of cell process d_t, length between two firm attachment sites on the cell process L, maximum deflection δ_m,, and predicted force F for five different cell process deflections are given. Predictions of F acting at the midpoint of L are in the range of 1 to 2.3 pN, and are within the range of forces predicted to occur at focal attachment sites along the cell process in vivo (Wang et al., 2007). Details of bending analysis and force predictions are in Appendix D.

	a (µm)	dt (µm)	L (µm)	δm (µm)	F (pN)
cell A	0.7	4.4	28.9	5.2	2.3
cell B	0.7	4.8	35.2	4.1	1.0
cell C	0.9	5.0	26.2	3.3	2.0
cell D	1.6	6.3	26.9	3.8	2.1
cell E	1.3	6.3	28.0	3.3	1.6

3.3. Whole-cell voltage-clamp experiments

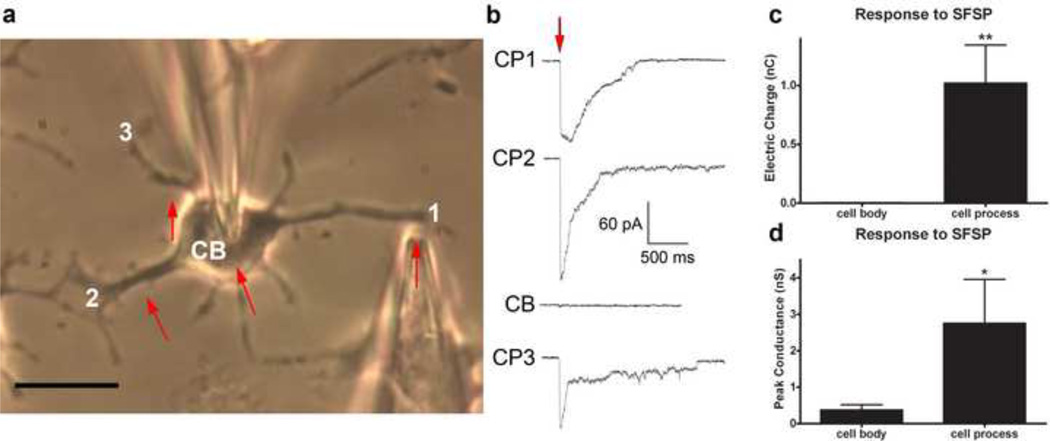
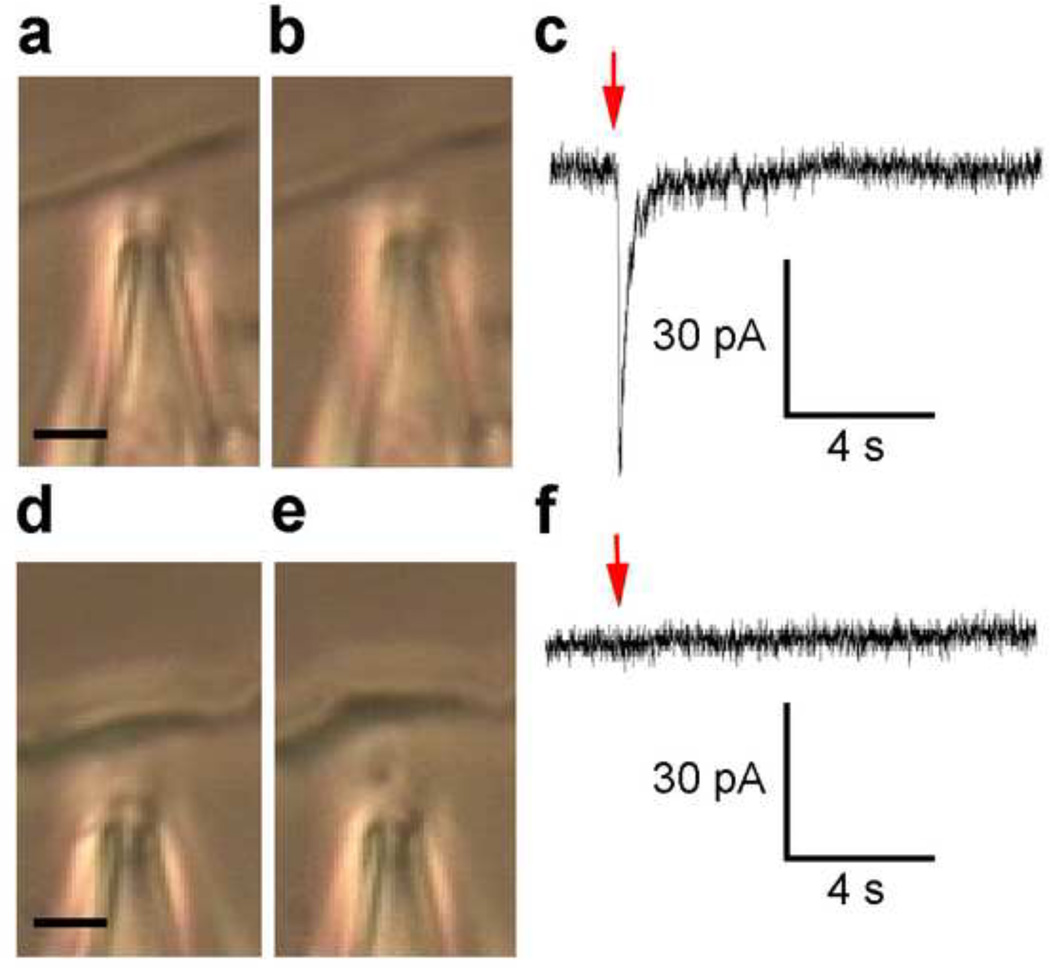
The whole-cell voltage-clamp technique has been used to measure membrane currents in cells subjected to SFSP stimulation at different locations along the cell process and on the cell body. In the case of the cell process, two strikingly different traces were obtained depending on whether the probe tip was directed precisely at an attachment site or midway between attachment sites. A single-cell was loaded at different locations in series, Figure 6a, and its whole-cell voltage-clamp recordings in response to a head-on impingement at attachment sites of the cell process and on the cell body, at comparable SFSP tip distance, are shown in Figure 6b. Collectively, out of 10 cells and 31 cell processes, significantly larger electric charge was observed when local pN level forces were directed at focal attachment sites along the cell process, 1.02±0.32nC, than when directed at the cell body, 0.0032±0.0011nC, where p=0.004 (Fig. 6c). Much larger peak conductance in response to SFSP stimulation was also observed when the bolus was directed at a cell process attachment, 2.76±1.20nS, compared to impingement on the cell body, 0.38±0.14nS, (Fig. 6d) where p=0.041. Only data from high resistance seals of 1–3GΩ were included in the analysis; however, data from lower resistance seals of ~300 MΩ provided evidence of similar osteocytic polarity where n = 105, data not shown. Most important is the observation that traces for CP1,2,3 were all collected at points where there was little to no deflection of the cell process indicating that these were loci of discrete attachments. A vivid comparison of cellular responses at a strong adhesion site (Fig. 7b) compared to a weak adhesion site (Fig. 7e), where process deflection occurs, is compared in Figures 7c,f. Deflections observed in Figure 7e yielded a similar deflection seen in Video S1, and corresponding current traces were similar to those of the cell body indicating that in the absence of firm attachment there was no change in electrical conductance.

Figure 6.

Prior to SFSP stimulation, seals ≥ 1GΩ are formed at the cell body (CB) with a patch microelectrode and the SFSP tip is positioned perpendicular to and 2–5 µm away from the cell process (CP). (a) A light micrograph of a MLO-Y4 cell with SFSP tip 3 µm from CP1. Red arrows indicate remaining SFSP tip positions during this experiment. (b) Whole-cell voltage-clamp recordings during SFSP stimulation of the MLO-Y4 cell at CP1, CP2, CB, and CP3 consecutively. SFSP application is indicated by the red arrow. (c) SFSP stimulation at the CP induced larger electric charge, 1.02 ± 0.32 nC, through the membrane than when the SFSP is directed at the CB, 0.0032 ± 0.0011 nC, and (d) conductance amplitudes were larger in response to SFSP stimulation at the CP, 2.76 ± 1.20 nS, compared to those from SFSP stimulation at the CB, 0.38 ± 0.14 nS. (n = 31, two-tailed paired Student’s t-test, **p < 0.01 and *p < 0.05, mean ± s.e.m) Scale bar is 20 µm.

Figure 7.

Comparison of cellular responses when stimulated by the SFSP at two separate locations along the same cell process. (a) First location along cell process (b) is stimulated by the SFSP without deflecting, and (c) a change in cellular conductance is detected. (d) Second location along the same cell process (e) is stimulated by the SFSP with visual deflection of the cell process that (f) yielded no change in cellular conductance. Scale bar is 5 µm, red arrow indicates SFSP application, cell was held at −60 mV with a seal > 1GΩ.

4. Discussion

The SFSP was developed to deliver highly focal hydrodynamic forces to single osteocyte-like bone cells in culture of comparable magnitude to the pN level forces that (Wang et al., 2007) predicted to occur in vivo due to physiological loading to address whether intracellular signaling is initiated at discrete attachment sites along the cell process, as hypothesized in (Wang et al., 2007) and (McNamara et al., 2009), or at the much more numerous flexible tethering attachments described in (You et al., 2004). Our present electrophysiological experiments in Figure 6 indicate that dendritic processes induce a far greater mechanosensitive response than the cell body when stimulated by the SFSP at comparable distances. By contrast, observed membrane deformations of the cell body were larger than those of the cell process when subjected to the SFSP stimulus. This demonstrates that the soft cell body, which easily dimples in response to pN level forces (Video S2), is a poor force transducer and that membrane deformation alone is not sufficient to initiate a detectable change in cellular conductance.

Even more important than the polarization of the cell, is the observation that electrical signaling (Fig. 7) is initiated only when the probe is directed at focal attachment sites along the cell process (Fig. 7b). There was no response when the SFSP is directed at locations along the process where there were no focal attachments and discernable cell process deflection (Fig. 7e) or when the SFSP is applied on top of the process putting it in compression (results not shown), indicating that only tensile forces trigger a response.

While the molecular structure of the attachment complex is uncertain, likely candidates for the attachment are β₁ and β₃ integrins. (Litzenberger et al., 2010) have stably transfected a dominant negative form of β₁ integrin into MLO-Y4 cells and consequently have observed a reduction in PGE₂ release. (McNamara et al., 2009) used immunostaining in vivo and observed β₁ integrins on both the cell body and cell process membranes, but only β₃ on the cell process. More specifically, in vitro studies on rat osteocytes using echistatin to demonstrate its positive affect on SA-cation channel and Ca²⁺ signaling suggested the functional importance of α_Vβ₃ integrin (Miyauchi et al., 2006). Collectively, these results indicate that the electrical response we have observed is most likely mediated by an integrin-associated complex whose identity at present is unknown.

Two-dimensional culture systems using MLO-Y4 cells were crude approximations of osteocytes in the lacunar canalicular system in vivo One of the most important differences is that there are numerous tethering fibers attaching the cell process to the canalicular walls in vivo (You et al., 2004). These tethering fibers when subject to fluid flow through the lacunar-canalicular sytstem are put in tension and create a hoop strain on the cell process membrane, which mathematical models predict can be more than an order of magnitude larger than whole tissue strains. It would be very difficult to distinguish experimentally in vivo whether the electrophysiological response observed herein originated from axial strains associated with focal integrin attachments or from these hoop strains in vivo. In contrast, the hoop strains in culture are absent since there are no tethering fibers and the response is clearly due to the discrete focal attachments.

The foregoing results strongly support the observations of two recent cell culture studies. (Adachi et al., 2009) observed that slender dendritic processes were more sensitive to mechanical deformation than the cell body when coated microparticles were attached to the cell membrane and subject to measured displacements. (Burra et al., 2010) showed that intact integrin attachments on the processes were required for entry of Lucifer yellow tracer into the cell after hydrodynamic stimulation of dendritic processes. Stimulating forces in these studies were in the nN range rather than in the pN range, and exceeded the force range predicted to occur at integrin attachment sites in vivo.

Our results in Figures 6c,d and the results in Table 2 indicate that physiological forces between 1–2.3 pN applied at focal attachment sites on cell processes led to responses that were 300 times the average electrical charge and 7 times the average peak conductance of those of the cell body. These observed changes in cellular conductance in MLO-Y4s are indicative of molecular and ionic fluxes passing through the cell membrane in response to external stimulation occurring upstream or independent of signaling pathways such as Ca²⁺ release, and only detected by the whole-cell voltage-clamp technique of high sensitivity. Studies are currently underway to determine the components of the complex, possibly containing α_vβ₃ integrin and a mechanically sensitive ion channel permeable to molecules such as ATP, PGE₂, and other signaling molecules pertinent to osteogenesis and bone maintenance.