Improved precision of syndesmophyte measurement for the evaluation of ankylosing spondylitis using CT: a phantom and patient study

Abstract

Ankylosing spondylitis is a disease characterized by abnormal bone formation (syndesmophyte) at the margins of intervertebral disk spaces. Syndesmophyte growth is currently typically monitored by visual inspection of radiographs. The limitations inherent to the modality (2D projection of a 3D object) and rater (qualitative human judgment) may compromise sensitivity. With newly available treatments, more precise measures of syndesmophytes are needed to determine if treatment can slow rates of syndesmophyte growth. We previously presented a computer algorithm measuring syndesmophyte volumes and heights in the 3D space of CT scans. In this study we present improvements to the original algorithm and evaluate the gain in precision as applied to an anthropomorphic vertebral phantom and patients. Each patient was scanned twice in one day, thus providing two syndesmophyte volume and height measures. The difference between those two measures (ideally zero) determines our algorithm’s precision. The technical improvements to the algorithm decreased the mean volume difference (standard deviation) between scans from 3.01% (2.83%) to 1.31% (0.95%) and the mean height difference between scans from 3.16% (2.99%) to 1.56% (1.13%). The high precision of the improved algorithm holds promise for application to longitudinal clinical studies.

1. Introduction

Ankylosing Spondylitis (AS) is an inflammatory arthritis affecting primarily the spine. Its progression can be characterized by abnormal bone structures (syndesmophytes) that slowly grow at the margins of inter-vertebral disk spaces (IDS) and over decades may lead spinal fusion (Braun and Sieper, 2007). A reliable way to monitor this structural damage would be highly desirable for clinical studies of AS. New drugs have been shown to considerably reduce signs of inflammation but it remains unclear if they also reduce syndesmophyte formation (van der Heijde et al., 2008a; van der Heijde et al., 2008b). Considerable research effort has been aimed at understanding the molecular mechanisms of bone formation in AS. Correlation between syndesmophyte growth and the expression of certain genes is typically sought (Appel et al., 2009; Daoussis et al., 2010). However, the current standard for assessing the presence and growth of syndesmophytes is visual inspection of plain radiographs (van der Heijde et al., 2008a; van der Heijde et al., 2008b; Appel et al., 2009; Daoussis et al., 2010). The main limitations associated with this method are: 1) use of 2D images to assess 3D structures arrayed in space; 2) poor visualization due to the superimposition of extraneous anatomical objects on the same 2D space; 3) qualitative scoring system. Those limitations compromise sensitivity in determining syndesmophyte formation. Figure 1 shows a vertebra with two lateral syndesmophytes on a coronal CT view and a radiographic view. Lateral syndesmophytes are difficult to visualize on a radiograph, resulting in their exclusion from the most commonly used radiographic scoring system (Creemers et al., 2005).

Figure 1.

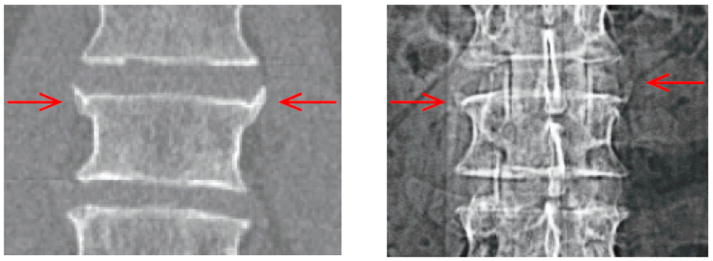
CT (left) and radiographic (right) view of the same vertebra with two lateral syndesmophytes.

We previously proposed a method designed to overcome those limitations: a computer algorithm that quantitatively measures syndesmophytes in the 3D space of CT scan (Tan et al., 2008a). The algorithm is highly automated with the user only providing the rough locations of the vertebral bodies. It starts with the segmentation of vertebral bodies using a method based on level sets. The syndesmophytes must then be separated from the vertebral bodies. Consistency in operating this syndesmophyte extraction is an important and unique challenge which we have addressed by using registration. Corresponding vertebrae are then registered so that syndesmophytes can be cut from vertebral bodies using the same reference level. This reference level is provided by the ridgelines of vertebral bodies.

The first objective of this paper is to present additional processing introduced to improve the original algorithm. Those improvements refine the segmentation of the syndesmophytes and address the problems of partial volume effect and of differing levels of image blur. We then provide a comprehensive set of measurements: in addition to volumes and heights, we also, for the first time, computed the masses of the syndesmophytes.

Our second objective is to present a precision/reliability study of our method. When a new method is proposed, its validity and reliability should ideally be tested. We previously provided evidence of our algorithm’s validity by comparing its measures to a physician’s visual rating (Tan et al., 2008a). A precision study is particularly important when a method is to be applied to longitudinal investigations, as in our case. A precision study allows one to distinguish true change from the variability associated with the measurement.

Because our method is highly automated, measurement variability is primarily related to scan acquisition and algorithm performance. Every imaging device suffers from specific distortion and artifacts. CT artifacts such as beam hardening depend on the relative position of the patient to the imaging system, which is usually subject to unavoidable variations in a longitudinal study. For this reason it is necessary to evaluate this variability using repeat scans. Our precision study was carried out on a specifically designed anthropomorphic phantom that was scanned in slightly different positions to mimic variation in patient positioning. Crucially we were also able to assess this precision with patient data. This is the first time that short-term repeat scans of patients have been used to evaluate the precision of syndesmophyte measurement using CT. We evaluated the gain in precision brought by the improvements to the original algorithm.

2. Materials and Protocol

The phantom, manufactured by CIRS (Norfolk, VA), consists of 5 anthropomorphic vertebral bodies forming 4 IDSs. It is made of epoxy resin, with cortical and trabecular bone represented by different densities (respectively 1200mg/cc in a soft tissue matrix and 250mg/cc of calcium hydroxyapatite in a marrow equivalent matrix). Syndesmophytes were made with the cortical bone density. One IDS had a syndesmophyte that bridged across the IDS connecting the 2 vertebrae, the 3 others each have 2 non-bridging syndesmophytes. The phantom is contained in an acrylic tank. The tank was filled with water to provide an interface with the epoxy resin similar to that between cortical bone and soft tissue in patients. Figure 2(a)-(b) show photographic views of the phantom, figure 2(c) a coronal slice of a scan of the phantom where 4 syndesmophytes are visible (the top one is the bridging syndesmophyte).

Figure 2.

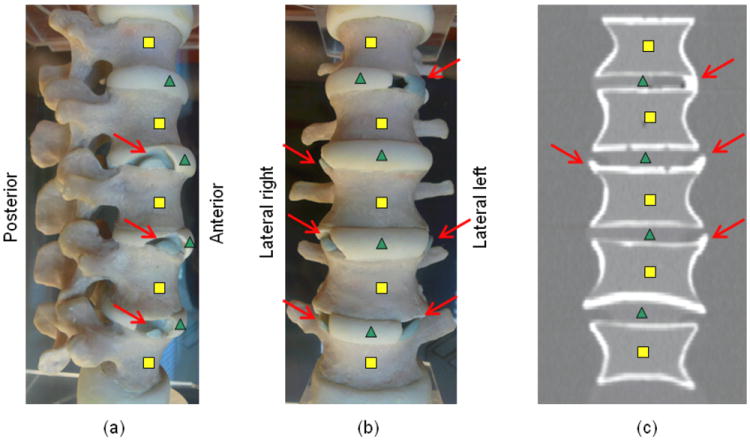
Syndesmophytes (arrows) on a (a) lateral left photograph of the phantom (b) anterior photograph of the phantom (c) coronal slice of a scan of the phantom. Squares and triangles respectively indicate vertebral bodies and intervertebral disks. Not all syndesmophytes are visible on the photographs or CT slice shown.

The patient study protocol was approved by the institutional review board and all subjects provided written informed consent. The subjects were 6 men with Ankylosing Spondylitis (mean age of 62 years ranging from 54 to 71). Each patient had syndesmophytes in at least 2 of the 4 IDSs that were processed.

The scanners used were a Philips Brilliance 64 and a GE Lightspeed Ultra. For both scanners voltage and current parameters were 120 kVp, 300 mAs respectively. Slice thickness was 1.5 and 1.25 mm respectively for the Philips and GE. The reconstruction kernel used for the Philips scanner, kernel B, is the equivalent of the “standard” kernel that was used for the GE. Spacing between slices was 0.7 and 0.625 mm for the Philips and GE respectively. For each scan, three reconstructions were made at field of view (FOV) diameters 25, 40 and 48 cm, corresponding to axial in-plane pixel sizes of about 0.49, 0.78 and 0.94 mm, which we respectively call high, medium and low resolutions. The image matrix is 512 by 512.

The anthropomorphic phantom was scanned 12 times, 6 times on each scanner. After each scan the phantom was slightly moved. Each patient was scanned twice with only a few minutes between the 2 scans. 3 patients were scanned on the Philips scanner and 3 on the GE scanner. After the first scan, patients were made to get out of the scanner and stand up before lying down again for the second scan. This ensured that they did not lie in exactly the same position and that the variation is in the range expected for patients in a longitudinal study. Each patient was scanned from the middle of the T10 vertebra to the middle of the L4 vertebra so that for each of them 4 IDS and 5 vertebral bodies could be processed.

3. Methods

The complete algorithm, summarized in figure 3, consists of three parts. We concentrate on the third stage where substantial improvements have been made and only provide a summary of the first two parts. First, vertebral bodies are segmented using a 3D multi-stage level set method. Triangular meshes representing the surfaces of the segmentations are obtained using the Marching Cubes algorithm (Lorensen and Cline, 1987). Such meshes are shown in figure 3. The vertebral surfaces of corresponding vertebrae are then registered. The purpose of the registration is to extract the syndesmophytes of both vertebrae using the same reference level. Syndesmophytes are cut from the vertebral body using the end plate’s ridgeline (shown in yellow in the lowest part of figure 3) as the reference level.

Figure 3.

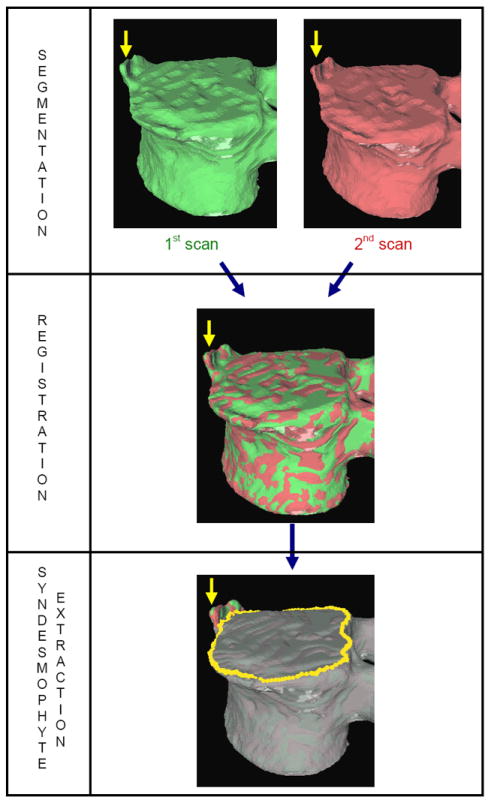
Overview of the method.

3.1. Segmentation of the vertebral bodies

Many image processing segmentation techniques have previously been applied to the extraction of vertebral bodies in CT (Yao et al., 2006; Aslan et al., 2010; Stern et al., 2011). Our algorithm is based on level sets. Level sets are evolving contours or surfaces that can expand, contract and even split or merge (Sethian, 1999). For the purpose of segmentation they are designed to deform so as to match an object of interest and stop at its edges. In the present work, the main level set used was the geodesic active contour (GAC). Its evolution equation can be written (Caselles et al., 1997):

$$\frac{d\psi }{\mathit{dt}}=\alpha g(\overrightarrow{x})c|\nabla \psi |+\beta g(\overrightarrow{x})\kappa |\nabla \psi |+\gamma \nabla g(\overrightarrow{x})\nabla \psi$$ (1)

The evolving contour is encoded as the zero level set of the distance function ψ( $\overrightarrow{x}$, t). In other words points that verify ψ( $\overrightarrow{x}$, t) = 0 form the contour. By convention the distance is negative for points inside the contour and positive for the ones outside:

$$\psi (\overrightarrow{x},t)=\pm d$$ (2)

where d is the distance from point $\overrightarrow{x}$ to the zero level set contour. Our algorithm is 3D and $\overrightarrow{x}$ here represent the 3 space coordinates.

The first term on the right-hand side of the Equation 1 is the propagation term that makes the contour move with velocity c. The second term, the curvature term, controls the smoothness of the contour using the mean curvature κ. The third term, the advection term, locks the contour to the boundary. The spatial function $g(\overrightarrow{x})$, derived from the images to be segmented, contains information about the objects’ boundaries and is called the speed function. The parameters α, β and γ weight the importance of each term. Those parameters were optimized using a previously published method (Tan et al., 2008a).

The speed function $g(\overrightarrow{x})$ should ideally have values close to 1 where there are no boundaries (so that the level set can expand rapidly) and values close to 0 where boundaries are present (so that the level set stops). This can be achieved for instance by writing (Ibanez et al., 2003):

$$g(\overrightarrow{x})=1-\frac{1}{1+\exp \left(-\frac{I-\xi }{\eta }\right)}$$ (3)

where I is the gradient magnitude of the grey level image at voxel $\overrightarrow{x}$. The two parameters ξ and η are typically computed using the equations (Ibanez et al., 2003):

$$\eta =\frac{K_1-K_2}{6}\xi =\frac{K_1+K_2}{2}$$ (4)

where K₁ is the minimum gradient magnitude value along the object’s boundary and K₂ the average gradient magnitude inside the object where the level set is initialized. Those definitions ensure that the level set advances over internal gradients but stops at the minimum gradient along the boundary, as Equation 3 maps gradients values up to K₂ to approximately 1 and gradient values equal or larger than K₁ to approximately 0. An algorithm for evaluating K₁ and K₂ has been described (Tan et al., 2008a).

To segment the different parts of a vertebral body (trabecular and cortical bone), successive level sets were used. The segmentation starts from a seed manually placed roughly in the center of the vertebral body. Detail on the implementation of the algorithm can be found in (Tan et al., 2008a).

3.2. Segmentation of the vertebral body ridgelines

The segmentation of vertebral body ridgelines is a preliminary step to both the registration stage (section 3.3) and the syndesmophyte extraction stage (section 3.4). The vertebral body ridgelines are instrumental in our method. They provide the landmarks that aid the registration process and the reference level from which syndesmophytes are cut (figure 3, bottom). We extract the ridgelines from the triangular meshes representing the surfaces of the vertebrae using the same level set as Equation 1, but transposed from the Cartesian domain of rectangular grids to the domain of a surface mesh. The most important adjustment is that, while in section 3.1 the relevant features are grey level gradients, on a surface mesh, useful features are curvature measures (the vertebral body surface is more curved at the ridgelines than on the end plates). The curvature measure we used is curvedness (C) (Koenderink, 1990):

$$C=\sqrt{\frac{{\kappa }_1^2+{\kappa }_2^2}{2}}$$ (5)

where κ₁ and κ₂ are the principal curvatures. The equations for the speed function remain the same as Equation (3)-(4) except that grey level gradients are replaced by gradients of curvature measures. The level contour starts from the center of the end plates, grows and stops at the ridgelines. This algorithm allows the segmentation of the end plates and the extraction of the ridgelines. Figure 4 shows examples of end plates (white) and ridgelines (green) obtained using the algorithm. A complete description of the method including implementation details can be found in (Tan et al., 2008a).

Figure 4.

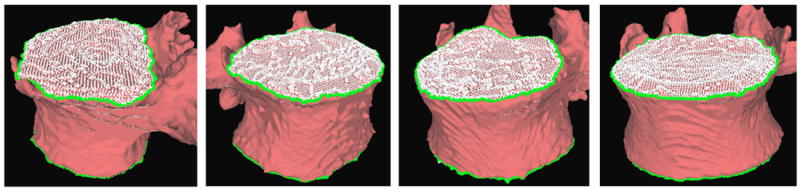
Examples of end plate (white) and ridgeline (green) segmentation.

3.3. Vertebral body registration

Ideally, ridgelines detected on different scans of the same vertebra should be located at identical positions at the junctions where the syndesmophytes merges with the end plates. In reality, this position can be subject to variations especially for syndesmophytes that do not grow at a right angle in respect to the end plate but laterally and merge with the end plate in a smooth gradual junction. In such cases, the curvature at the junction can be low and the level set might for instance stop at the syndesmophyte’s base at high resolution but leak into the syndesmophyte at low resolution, where the more blurred image makes the junction smoother. Figure 5 shows such an example. If the syndesmophytes at high and low resolutions were cut from their respective ridgelines, the low resolution syndesmophytes would have a smaller volume because of the leaks. We use registration to compensate for such inconsistencies. Registration aligns the vertebral bodies of two longitudinal scans (middle of figure 3). Once the vertebral bodies are registered, either of the two ridgelines can be used. The important point is to use only one of the ridgelines so that the same syndesmophyte is cut from the exactly the same level on two longitudinal scans.

Figure 5.

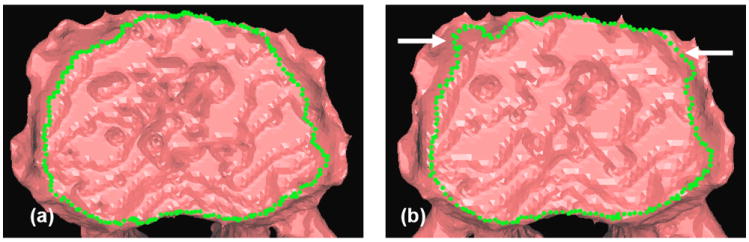
Ridgeline detection on the lower end plate of a vertebra based on a (a) high and (b) low resolution mesh. Arrows indicate segmentation errors (leaks).

The most commonly used algorithm for vertebral surface registration is the iterative closest point algorithm (ICP) (Besl and McKay, 1992; Herring and Dawant, 2001; Tamura et al., 2005). We added landmark matching to address its limitations. Given 2 sets of points, the ICP algorithm determines the rigid transformation that minimizes the mean square distance between them. It however suffers from the problem of local minima that make the algorithm stop before it reaches the correct solution. This happens in particular when initialization is far from the solution and/or when the symmetries of the surfaces to register allow many false matches. We made the ICP algorithm more robust by designing a multi-stage method using landmarks. ICP registration is performed successively on the ridgelines, end plates and the complete surface. The result of each stage is the initialization for the following stage. It was shown that this method yielded better results than the ICP used alone without landmark matching (Tan et al., 2008b).

3.4. Syndesmophyte extraction

Once corresponding pairs of vertebrae are registered, syndesmophytes can be cut from the vertebral bodies using the ridgeline of either vertebra. In the present work the ridgeline of the first scan was used. In the following, we describe the improvements to the original algorithm. Those improvements allow us to operate this cutting with subvoxel accuracy, address problems of differing degrees of blurring in the scans and partial volume effect, and refine the segmentation of syndesmophytes.

3.4.1. Syndesmophyte cutting

From the previous section, we have extracted the 2 end plates and ridgelines of each vertebral body. We now consider the IDSs, the spaces between the vertebral bodies where syndesmophytes are located. Each IDS is bounded by the lower end plate of the superior vertebra, that we note EP1, and the upper end plate of the inferior vertebra, noted EP2. The corresponding ridgelines are respectively noted RL1 and RL2. The cutting algorithm marks as syndesmophyte those previously segmented voxels that are between those 2 end plates. Each candidate voxel is considered in relation to the local ridgelines. If it is below the level of the local level of EP 1/RL1 and above the local level of EP2/RL2 it is marked as syndesmophyte.

However the representation of a continuous space by discrete voxels can introduce inaccuracies in this algorithm. In our previous work a whole voxel was considered either above or below the local ridgeline level (Tan et al., 2008a). However, in reality, most voxels close to the ridgeline level are neither completely above nor completely below that level. Rather, part of the voxel is above while the other part is below. The following algorithm achieves syndesmophyte cutting with subvoxel accuracy. We show how to determine the proportion of a voxel above the local level of EP2/RL2. Determining the proportion of a voxel below the local level of EP1/RL1 is straightforwardly similar.

First we extract the normal to the end plate EP2, $\overrightarrow{N}$, using a least square estimate method (Tan et al., 2008a). Let V be a voxel under consideration. We determine the local ridgeline/end plate level in the following way. The point of RL2 closest to V is found. Neighboring points of EP2/RL2 are averaged to form the point R_V, which, as an average, is an estimate more robust to noise. R_V and $\overrightarrow{N}$ define a plane P, that can be used to cut syndesmophyte from vertebral body. We now determine the position of V relative to this plane. V is a rectangle defined by 8 vertices V_i with i ∈ {1,…,8}. The sign of the scalar product:

$$s(V_i)=\mathit{sign}(\overrightarrow{R_V{V}_i}·\overrightarrow{N})$$ (6)

tells us if V_i is above or below the plane P. If all signs are positive or negative, then voxel V is either completely a syndesmophyte voxel or not. If we have a mix, then V is a partial syndesmophyte voxel. To determine what proportion of V is syndesmophyte, we subdivide V into smaller rectangles. A voxel V of dimensions p_x, p_y and p_z can be subdivided into M³ equal subvoxels of dimensions $\frac{p_x}{M},\frac{p_y}{M}$ and $\frac{p_z}{M}$. For this, we simply take as locations of the vertices of the new subvoxels the coordinates $\left(i·\frac{p_x}{M},j·\frac{p_y}{M},k·\frac{p_z}{M}\right)$ where M is an integer controlling the number of subdivisions and (i, j, k) are integers. Here we chose M=10, which means each voxel is divided into M³=1000 subvoxels. Then, for each subvoxel, it is straightforward to determine if it is above or below P using the same scalar product (Equation 6). However, since we do not want to pursue the subdivision process further, it is not necessary to test all 8 vertices. We only test one, corresponding to the smallest (i, j, k). For every subvoxel of V, if the test is positive in sign we increment N_S that we define as the number of subvoxels of V found to be syndesmophyte (conversely to determine the proportion of a voxel below the local level of EP1/RL1, we would increment when the test is negative in sign). The corresponding partial syndesmophyte volume is:

$$\mathit{PSV}=\frac{N_S}{M^3}·p_x·p_y·p_z$$ (7)

The number of subdivision M is a matter of choice constrained by the trade-off between precision and computing time. The better results produced by more subdivisions (larger M) comes at the price of a larger computational burden and is limited by diminishing returns in terms of gain in precision. We performed an optimization with 3 patients. The numbers of subdivisions tested were 0, 2³, 4³, 6³, 8³, 10³, and 12³. The mean error in interscan volume measurements dropped from 3.4% to 1.9% with 6³ subdivisions. With 10³ subdivisions, the error was further reduced to 1.8%. With 12³ subdivisions, the error stayed at 1.8%. The decrease from 1.9% to 1.8% is marginal but, at this stage where our algorithm has not yet been optimized for speed, we chose the number of subdivisions that gave us the best precision.

Figure 6 illustrates the difference between whole voxel and subvoxel cutting.

Figure 6.

Comparison between subvoxel and whole voxel cutting. (a) Coronal view of a CT scan of an IDS. (b) Lateral view of the 3D surface reconstruction of the registered right-hand side syndesmophytes. View of the registered syndesmophyte upper surfaces after (c) subvoxel and (d) whole voxel cutting from the vertebral body. The view is from the direction of the blue arrow in (a) and (b).

3.4.2. Equalization of image blurring

Images from different scanners and/or at different resolutions have different levels of blurring. This has an impact on the apparent size of the syndesmophytes. In general, the more blurred an image is, the larger the syndesmophyte will appear. To compensate for this effect we devised an algorithm for harmonizing the degree of blurring of two images. Blur equalization for the reduction of measurement variability was previously performed in function magnetic resonance imaging (Friedman et al., 2006). They estimated the full width at half maximum (FWHM) of the Gaussian kernels that produced the blur in their data. They then blurred all their data to match the most blurred image. Our method is simpler in that we do not seek to model the Gaussian that produced the blur in our images. We did not blur all our images to the level of our most blurred image. Instead we equalized blur in pairs of scans.

We first devised a measure of image blur. We tested two measures. The first is the standard deviation of grey levels in a homogeneous region containing only trabecular bone. A region containing both trabecular and cortical bone could produce misleading results. The computation of the standard deviation involves an estimation of the mean grey level of that region. Our second blur measure is more local in that it does not use any quantity pertaining to the region as a whole. Instead, for each voxel in the region, a mean difference with its neighbors is computed. All those voxel-wise differences are then averaged across the region. This measure can be written:

$$B=\sum _{j=1}^M\sum _{i=1}^{N_j}\frac{|G{L}_j-G{L}_i|}{M{N}_j}$$ (8)

where GL_j is the grey level of voxel j in the region, GL_i is the grey level of voxel i in the neighborhood of j. M is the total number of voxels in the region. N_j is the total number of neighbors of j that are also in the region. N_j is 26 unless voxel j is at the boundary of the region. Both those measures of image blurring need to be taken in a region that is homogeneous. To extract such a region we make use of the segmentations of the vertebral bodies (part 1 of the complete algorithm). Eroding those with a structuring element of 5 voxels we obtain homogeneous regions in the trabecular bone. The syndesmophyte precisions obtained using both measures proved to be very similar, with the second one performing marginally better. Henceforth “blur measure” will refer to the second one (Equation 8).

Our procedure for equalizing the blurring of two images is as follows. We first compute the blur measures of the 2 images. The more blurred image has the lower measure, which we call B_min. We call the blur measure of the other image B. We convolve the least blurred image with Gaussians of increasing standard deviations. We start with a standard deviation of 0.025 mm and increase it by increments of 0.025 mm. We used the ITK implementation of the Gaussian filter (Ibanez et al., 2003). After each convolution we compute B. When B becomes smaller than B_min we stop the process. Let us call that measure B_n and the previous one B_n-1. We compute the differences |B_min − B_n| and |B_min − B_n−1|. If the first difference is smaller we use the Gaussian associated with B_n to equalize the blurring of the two images. Otherwise we use the Gaussian associated with B_n-1. Figure 7 shows an example of the procedure. The standard deviation of the Gaussian needed to blur (a) to the level of (b) was 0.125 mm. This stage is a pre-processing step for the following refinement technique.

Figure 7.

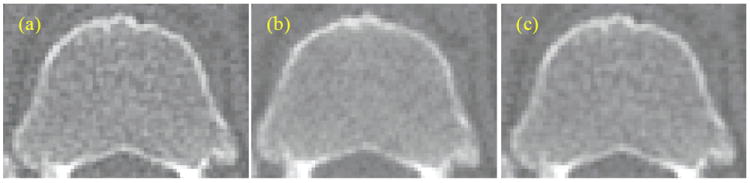
Blur equalization: the least blurred image (a) is convolved with a Gaussian (c) to match the blur level of (b).

3.4.3. Density and Laplacian based correction

Once blur equalization is performed, the segmentation of the syndesmophyte can be refined. In this new stage, syndesmophytes on less blurred images can add voxels and those on more blurred images can lose voxels.

Partial volume effect is taken into account. At the boundary between bone and soft tissue, the representation of a continuous space by discrete voxels leads to the creation of voxels containing both materials. Depending on the position of the syndesmophyte relative to the discrete grid, voxel intensity at the boundary will vary and a binary segmentation will arbitrarily include or leave out partial voxels, which will affect the precision of syndesmophyte measurement. Our algorithm incorporates partial voxels, assigning them a partial volume value depending on their “density”, that is, their grey level intensity. The density criterion is obtained in the following manner. From the initial rough syndesmophyte segmentation we estimate the mean voxel intensity for syndesmophyte, GL_S. Syndesmophytes are surrounded by soft tissue. Considering the neighbors of syndesmophyte voxels we mark the first soft tissue layer, T₁ and second soft tissue layer T₂. From those layers (T₁ and T₂) we extract the mean voxel intensity for soft tissue, GL_T. For a voxel i labeled as syndesmophyte or belonging to T₁ or T₂, our density criterion is based on the measure D_i defined as:

$$D_i=\frac{G{L}_i-G{L}_T}{G{L}_S-G{L}_T}$$ (9)

where GL_i is the grey level of voxel i. The higher the bone content of the voxel, the higher D_i is. The labeling of voxels as syndesmophyte or belonging to T₁ or T₂ can be performed by creating an auxiliary image where the grey level of each voxel corresponds to its label.

Another criterion based on the Laplacian operator is also used to distinguish bone from soft tissue. The action of the Laplacian operator on image I is defined as:

$$\mathrm{\Delta }I=\frac{{\partial }^{2}I}{\partial x^2}+\frac{{\partial }^{2}I}{\partial y^2}+\frac{{\partial }^{2}I}{\partial z^2}$$ (10)

The bone/soft tissue interface can be modeled as a smooth step function. Its Laplacian is positive on one side of the step and negative on the other. The Laplacian can therefore be used to divide the interface between 2 materials of different densities with the zero-crossing roughly in the middle. Figure 8 shows an IDS processed with a Laplacian. The color code is green for negative values and red for positive ones. Cortical bone is mainly green. Cortical bone is thin and can be seen as two step functions back to back. We used the ITK implementation of the Laplacian filter (Ibanez et al., 2003).

Figure 8.

(a) Original image. (b) Laplacian of image (a), color-coded with green (negative values) and red (positive values).

The density and Laplacian criteria are combined in the following manner:

1. First we consider all syndesmophyte, T₁ and T₂ voxels. If a voxel i (syndesmophyte, T₁ or T₂) verifies the conditions:

   $$D_i>D_1\mathit{and}{L}_i<0$$ (11)

   where D₁ is a threshold, it is classified as syndesmophyte (L_i is the Laplacian at voxel i). Otherwise it is labeled as soft tissue. This first step mainly corrects leaks. An example is shown in Figure 9.
2. The labeling of soft tissue layers T₁ and T₂ and the computing of GL_S and GL_T are redone based on the new segmentation resulting from step (a). We then process the first soft tissue layer T₁. If a voxel i of T₁ verifies the conditions:

   $$D_i>D_2\mathit{and}{L}_i<0$$ (12)

   where D₂ is a threshold, it is classified as partial syndesmophyte with proportion of bone corresponding to D_i. This second step adds a layer at the bone/soft tissue boundary where, due to partial volume effect, voxels are likely to contain both types of tissues.

Figure 9.

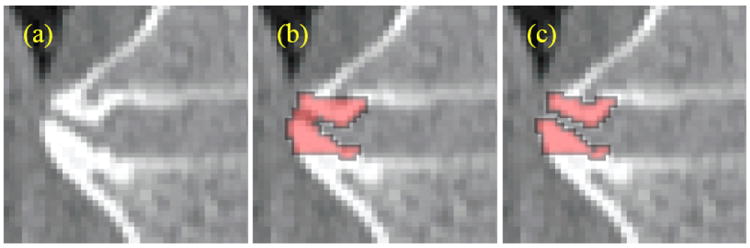
First stage of the syndesmophyte refinement algorithm: (a) Original image (b) Initial segmentation (c) Leak correction.

The thresholds D₁ and D₂ control how selective the algorithm is in admitting syndesmophyte voxels. They can be used to add partial bone voxels that were not segmented or exclude soft tissue voxels that were mistakenly labeled as syndesmophyte. Both thresholds can be set between 0 and 1. Lower thresholds are more permissive in syndesmophyte selection. To determine the optimal values for D₁ and D₂, we assigned them every pair of values on a 2D grid of size 1×1 and sampled at an interval of 0.2. D1 and D2 can take any value from the set: 0, 0.2, 0.4, 0.6, 0.8 and 1, making a total of 36 pairs. For all pairs, we computed the coefficient of variation (CV) for syndesmophyte volume, which is the measure most important to us. The data of 3 of the 6 patients were used for this optimization procedure. We found that the optimal set of parameters, defined as the one that minimized CV, was (0.8, 0). In a small neighborhood around this point {(0.8, 0.2), (0.6, 0) and (0.6, 0.2)}, CV did not vary substantially. In this neighborhood, we optimized the 2 thresholds for syndesmophyte height, our secondary measure. This led us adopt the set of threshold (0.8, 0.2).

3.5. Syndesmophyte volume, height and mass computation

It is straightforward to compute syndesmophyte volumes by adding complete voxels and partial voxels. We computed the height of each syndesmophyte individually. To group syndesmophyte voxels into separate syndesmophytes we use a simple blob labeling technique. Heights are measured along the normal to the end plate with the center of the end plate serving as the 0 level (figure 10). The height of voxel S can be written:

$$h=\frac{\overrightarrow{N}·\overrightarrow{\mathit{CS}}}{|\overrightarrow{N}|}$$ (13)

where $\overrightarrow{N}$ is the normal to the end plate and C its center. The center C is estimated as the average of all the contour points. Although figure 10 only shows the height computation of one voxel, to compute the height of a syndesmophyte we averaged its top 5% highest voxels. We recorded the height of each individual syndesmophyte in the 4 IDSs.

Figure 10.

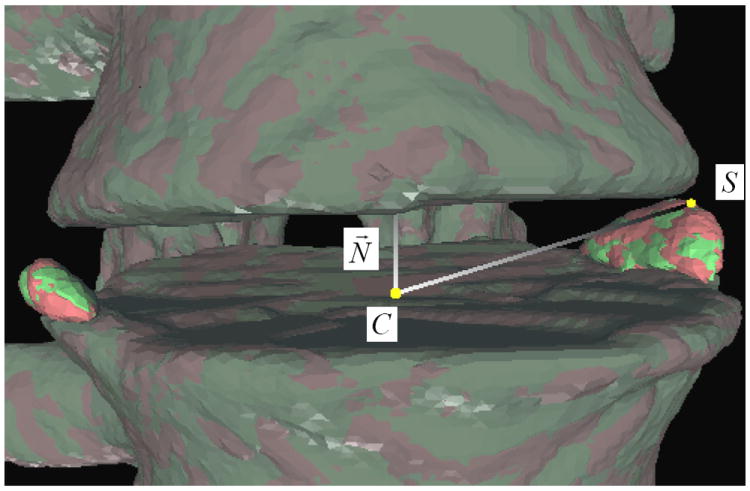
Evaluation of syndesmophyte height.

To compute syndesmophyte mass, patients were scanned with a QCT phantom (Mindways Software Inc., Austin, TX). The QCT phantom consists of 5 tubes of K₂HPO₄ of different densities. Those tubes were segmented in the CT scans and a mean grey level computed for each tube. Those 5 values were used to derive a linear relationship between grey level intensity and density using a method devised by Mindways Software. The mass of each individual voxel can be computed by multiplying the density corresponding to its grey level intensity by its volume. Adding the masses of all voxels segmented as part of a syndemophyte we obtain the mass of this syndesmophyte. Blur equalization was not used when processing for mass computation. Because blur equalization modifies the grey level values of voxels, the relationship to density might no longer be valid.

3.6. Accuracy, precision evaluations, effects of the improvements and statistical analysis

We evaluated the accuracy of the syndesmophyte segmentations by comparing them to manual segmentations performed using the ITK-SNAP software (Yushkevich et al., 2006). Although the software includes computer-aided segmentation features, we only used the manual tool. One operator manually segmented syndesmophytes in the 2 lowest IDSs for all patients in the medium resolution reconstructions. The agreement between manually and automatically segmented syndesmophytes was evaluated using the overlap similarity index (OSI) which is also called the Dice similarity coefficient (Zou et al., 2004):

$$\mathit{OSI}=\frac{2(V_1\cap V_2)}{V_1+V_2}$$ (14)

where V₁ and V₂ are the two volumes compared. OSI is always comprised between 0 and 1. The closer to 1 the better the similarity between the two volumes.

For each scan, syndesmophyte volume and mass were computed in the 4 IDSs. Those measures were then added to give a single total volume and mass estimate. We selected the height of the tallest syndemophyte for each of the 4 IDSs. The 4 maximal heights thus obtained were then added to yield one single total height measure per scan. To assess precision, we compared paired scans: random pairs for the phantom and consecutive scans of each patient. We computed the difference in total volume, mass and height for each pair of scans. The smaller the difference, the more precise the method. We considered this difference in absolute value (we changed the sign of negative differences). We also considered this difference as a percentage of syndesmophyte volume/mass/height (we divided the difference by the total syndesmophyte volume/mass/height of the first scan). For each set of difference measures, we computed the mean and standard deviation. For the anthropomorphic phantom, volume and height were computed. For patients, volume, height and mass were computed. We also evaluated the coefficient of variation (CV) as the root mean square of individual CVs (Glüer et al., 1995).

To assess the impact of the improvements, we compared the precision results obtained by the original algorithm with those of the final algorithm and those of intermediate stages. Those intermediate stages are: 1) The original algorithm with only subvoxel accuracy syndesmophyte cutting. 2) The original algorithm with only Laplacian and density based correction. 3) The original algorithm with only Laplacian and density based correction preceded by image blur equalization. Image blur equalization was designed as a pre-processing step for the Laplacian and density based correction and not for use on its own. Those intermediate stages allow us to evaluate the impact of each of the improvements separately.

Finally we performed a multivariate analysis of variance to test for the statistical significance of the gains in precision brought by the additional algorithmic steps. This analysis was conducted for the interscan differences in each IDS using the SAS software (version 9.2, Cary, N.C.) with adjustment for resolution and IDS level (T11-T12, T12-L1, L1-L2, L2-L3), and accounting for the correlation of within-patient measures.

4. Results

We first present the results for the study of syndesmophyte segmentation accuracy. For the precision study, we first provide the results for the final algorithm for the anthropomorphic phantom and the patients. We then present the results of the study investigating the impact of the improvements on the initial algorithm.

The anthropomorphic phantom was scanned 12 times, 6 times on the Philips scanner and 6 times on the GE scanner, providing 3 pairs for the Philips scanner and 3 pairs for the GE scanner. Six patients were scanned twice, also providing 12 scans in 6 pairs.

For both patients and phantom, each scan was reconstructed at 3 resolutions. For each pair, each of the 3 reconstructions of one scan can be compared to the three reconstructions of the other scan. It is important to do all possible comparisons because in longitudinal clinical settings, only one reconstruction might be available at a certain time point, so it may be necessary to compare syndesmophyte measurements based on high and low resolution reconstructions. For each pair of scans, we therefore performed all 9 possible comparisons, 3 with same resolutions and 6 with different resolutions. To investigate the effects of non-matching resolutions, the results were stratified into 2 groups, same resolution and cross resolution. For same resolution, the total number of comparisons is n=3×6=18, for cross resolutions n=6×6=36. The total number of comparisons is thus n=54.

4.1. Accuracy study

For this study, manual segmentation of the syndesmophytes was performed for the 2 lowest IDSs of the first scan of all 6 patients using the medium resolution reconstructions. The total number of comparisons with the automated segmentation technique is n=2×6=12. We found that the mean (standard deviation) OSI was 0.76 (0.06). Figure 11 shows an example of syndesmophyte segmentations by the manual and automated methods.

Figure 11.

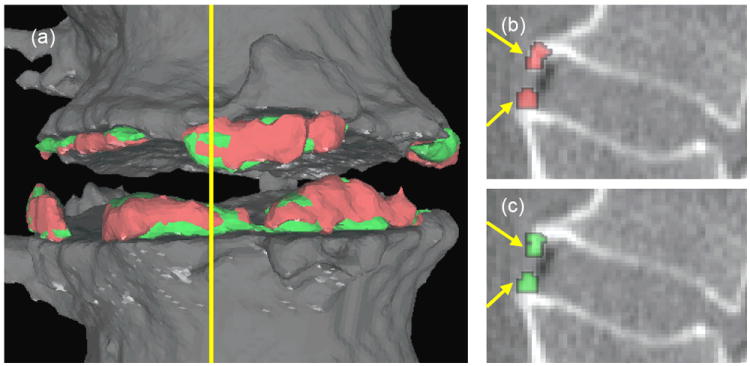
Comparison between manual (red) and automated (green) segmentation of syndesmophytes. (a) is a 3D surface reconstruction. (b) is a sagittal slice showing the manual segmentation and (c) is the same sagittal slice showing the automated segmentation. The yellow line in (a) indicates the position of the sagittal slice. The overlap similarity index in this example is 0.77.

4.2. Precision results for the anthropomorphic phantom

The total syndesmophyte volume and maximal height, as measured by our algorithm, were about 488 mm³ and 15.5 mm respectively (Table 1). Table 2 presents the results for volume and height differences between paired scans. For volume, the mean (standard deviation) of interscan differences are 5.19 (3.72) mm³ in absolute value and 1.07 (0.77) % in percentage. For height, the same are 0.18 (0.14) mm and 1.18 (0.88) %. The CV for volume and height are respectively 0.932% and 1.04%.

Table 1.

Volume and height measurements for the phantom.

		1st scan	2nd scan
VOLUMES (mm3)	n	54	54
	min	441	446
	max	517	525
	mean	488	488
	std	19.7	20.2
HEIGHTS (mm)	n	54	54
	min	15.0	14.7
	max	15.9	15.9
	mean	15.5	15.4
	std	0.21	0.24

Table 2.

Syndesmophyte volume and height differences for the anthropomorphic phantom.

		n	Mean +/- Std		CV
			mm3	%	%
VOLUMES	Same Resolution	18	4.60 +/- 3.43	0.96 +/- 0.71	0.842
	Cross Resolution	36	5.49 +/- 3.82	1.13 +/- 0.79	0.974
	All	54	5.19 +/- 3.72	1.07 +/- 0.77	0.932
			mm	%	%
HEIGHTS	Same Resolution	18	0.20 +/- 0.14	1.31 +/- 0.91	1.12
	Cross Resolution	36	0.17 +/- 0.13	1.12 +/- 0.86	1.00
	All	54	0.18 +/- 0.14	1.18 +/- 0.88	1.04

For both volume and height, cross and same resolution differences exhibit similar precision. In terms of percentage, the interscan differences obtained for height are slightly larger than for volume.

4.3. Precision results for patients

In contrast with the anthropomorphic phantom, patients were scanned with a QCT phantom that allowed us to compute syndesmophyte masses. However, in the high resolution reconstructions, the more restricted field of view meant that the QCT phantom was often not visible. For this reason, the results for syndesmophyte mass are limited to medium and low resolutions. Consequently, for mass, the number of comparisons for same and cross resolutions is n=2×6=12.

The total syndesmophyte volume, height and mass for the patients, as measured by our algorithm, ranged from about 242 to 4455 mm³ (mean of 1783 mm³), from 9.09 to 25.8 mm (mean of 16.8 mm) and from 83.4 to 2564 mg (mean of 989 mg) respectively (Table 3).

Table 3.

Volume, height and mass measurements for patients.

		1st scan	2nd scan
VOLUMES (mm3)	n	54	54
	min	248	242
	max	4426	4455
	mean	1781	1786
	std	1573	1571
HEIGHTS (mm)	n	54	54
	min	9.18	9.09
	max	25.4	25.8
	mean	16.8	16.7
	std	4.63	4.59
MASSES (mg)	n	24	24
	min	87.3	83.4
	max	2564	2548
	mean	989	989
	std	902	901

Table 4 provides the results for volume, height and mass differences between successive scans. For volume, the mean (standard deviation) of interscan differences are 19.0 (17.6) mm³ in absolute value and 1.31 (0.95) % in percentage. For height, the same are 0.25 (0.19) mm and 1.56 (1.13) % and for mass, 14.6 (17.9) mg and 2.16 (1.75) %. The CV for volume, height and mass are respectively 1.14%, 1.37% and 1.99%.

Table 4.

Syndesmophyte volume, height and mass differences for patients.

		n	Mean +/- Std		CV
			mm3	%	%
VOLUMES	Same Resolution	18	17.3 +/- 17.0	0.93 +/- 0.63	0.790
	Cross Resolution	36	19.9 +/- 17.9	1.50 +/- 1.03	1.28
	All	54	19.0 +/- 17.6	1.31 +/- 0.95	1.14
			mm	%	%
HEIGHTS	Same Resolution	18	0.24 +/- 0.18	1.46 +/- 1.05	1.28
	Cross Resolution	36	0.26 +/- 0.19	1.62 +/- 1.16	1.42
	All	54	0.25 +/- 0.19	1.56 +/- 1.13	1.37
			mg	%	%
MASSES	Same Resolution	12	7.35 +/- 7.42	1.44 +/- 1.58	1.54
	Cross Resolution	12	21.9 +/- 21.9	2.88 +/- 1.61	2.34
	All	24	14.6 +/- 17.9	2.16 +/- 1.75	1.99

For heights, same and cross resolutions have similar results. For volumes, same resolution measures are more precise, especially in percentage terms. The difference between the two groups is the most apparent for mass, with same resolution measurements being more than twice as precise as cross resolution measurements in absolute term.

In terms of percentage, the most precise measurements were for volume and the least for mass. However the results for mass are based on fewer measures as high resolution reconstructions were not considered.

4.4. Impact of the improvements

In this section, we present results without distinguishing between same resolution and cross resolution. Table 5 shows the results for volume and height for the initial and final algorithms as well as intermediate stages for the phantom. Table 6 shows the corresponding results for volume, height and mass for patients.

Table 5.

Impact of the technical improvements on syndesmophyte volume and height differences for the phantom.

		n	Mean +/- Std		CV
			mm3	%	%
VOLUMES	Initial algorithm	54	12.5 +/- 8.73	2.08 +/- 1.45	1.79
	With subvoxel cutting only	54	6.25 +/- 4.61	1.15 +/- 0.85	1.01
	With density and Laplacian only	54	12.5 +/- 7.10	2.34 +/- 1.31	1.90
	With density and Laplacian and blur equalization only	54	12.3 +/- 6.98	2.29 +/- 1.28	1.86
	Final algorithm	54	5.19 +/- 3.72	1.07 +/- 0.77	0.932
			mm	%	%
HEIGHTS	Initial algorithm	54	0.18 +/- 0.12	1.21 +/- 0.81	1.03
	With subvoxel cutting only	54	0.17 +/- 0.12	1.12 +/- 0.80	0.972
	With density and Laplacian only	54	0.19 +/- 0.14	1.28 +/- 0.97	1.14
	With density and Laplacian and blur equalization only	54	0.19 +/- 0.15	1.26 +/- 0.98	1.13
	Final algorithm	54	0.18 +/- 0.14	1.18 +/- 0.88	1.04

Table 6.

Impact of the technical improvements on syndesmophyte volume, height and mass differences for patients.

		n	Mean +/- Std		CV
			mm3	%	%
VOLUMES	Initial algorithm	54	40.2 +/- 38.2	3.01 +/- 2.83	3.03
	With subvoxel cutting only	54	37.0 +/- 42.6	1.88 +/- 1.42	1.68
	With density and Laplacian only	54	29.3 +/- 30.9	2.05 +/- 1.62	1.82
	With density and Laplacian and blur equalization only	54	22.2 +/- 20.0	1.86 +/- 1.58	1.70
	Final algorithm	54	19.0 +/- 17.6	1.31 +/- 0.95	1.14
			mm	%	%
HEIGHTS	Initial algorithm	54	0.50 +/- 0.48	3.16 +/- 2.99	3.14
	With subvoxel cutting only	54	0.47 +/- 0.42	3.04 +/- 2.91	2.96
	With density and Laplacian only	54	0.27 +/- 0.23	1.62 +/- 1.26	1.46
	With density and Laplacian and blur equalization only	54	0.27 +/- 0.22	1.64 +/- 1.21	1.44
	Final algorithm	54	0.25 +/- 0.19	1.56 +/- 1.13	1.37
			mg	%	%
MASSES	Initial algorithm	24	15.6 +/- 18.9	2.57 +/- 2.30	2.49
	With subvoxel cutting only	24	15.0 +/- 17.7	2.15 +/- 1.75	1.98
	With density and Laplacian only	24	16.4 +/- 20.4	2.74 +/- 2.69	2.79
	Final algorithm	24	14.6 +/- 17.9	2.16 +/- 1.75	1.99

For the phantom volumes, all the algorithmic modifications together have improved the precision by about a factor of 2. In terms of percentage, the mean (standard deviation) volume difference between scans decrease from 2.08 (1.45) % to 1.07 (0.77) %. However total maximal height differences do not seem affected. It can be seen that the most important improvement in the precision of volume measurement comes from the subvoxel cutting. When adding it, the mean difference in volume nearly halves in absolute value. The effects of blur equalization or density and Laplacian based correction are more modest. Total maximal height differences do not seem affected by the different improvements.

For patients, the impact of all the modifications together is even larger. For volumes, the mean (standard deviation) volume differences between scans decrease from 3.01 (2.83) % to 1.31 (0.95) %. For heights, the decrease is from 3.16 (2.99) % to 1.56 (1.13) %. For masses, the impact of the technical improvements together seems negligible.

For patients’ syndesmophyte volumes and heights, the most important improvement in precision comes from density and Laplacian based correction associated with blur equalization. With it, the mean and standard deviation of the differences nearly halve in absolute value. Subvoxel cutting leads to substantial gains only in percentage terms and only for volumes. For volumes, adding the blur equalization pre-processing step to density and Laplacian based correction yields an appreciable improvement, reducing the mean (standard deviation) interscan volume differences from 29.3 (30.9) to 22.2 (20.0) mm³.

For masses, the impact of all technical improvements seems small.

4.5. Significance of the improvements

To evaluate the significance of the gains in precision brought by the additional algorithmic steps we considered interscan differences in each IDS rather than per patient. Since 4 IDSs were measured for each patient, the number of sample measurements is multiplied by 4, making the statistical analysis more robust.

First, in Table 7, we present results for volume, height and mass measurements by the initial and final algorithms. Statistics about the interscan differences for the initial and final algorithms are provided in Table 8. When considering all possible resolution combinations, the total number of differences is n=4×54=216 for volume and height and n=4×24=96 for mass. Comparing CV of table 8 with those in table 6, the CVs are larger for individual IDSs than for sums of values for individual patients.

Table 7.

Volume, height and mass measurements for patient intervertebral disk spaces.

		Initial Algorithm		Final Algorithm
		1st scan	2nd scan	1st scan	2nd scan
VOLUMES (mm3)	n	216	216	216	216
	min	0	0	0	0
	max	2274	2250	1780	1783
	mean	559	561	445	447
	std	614	616	492	493
HEIGHTS (mm)	n	216	216	216	216
	min	0	0	0	0
	max	7.96	8.05	8.02	8.17
	mean	4.07	4.02	4.20	4.18
	std	2.06	2.03	2.09	2.10
MASSES (mg)	n	96	96	96	96
	min	0	0	0	0
	max	1092	1093	994	993
	mean	266	267	247	247
	std	315	317	290	290

Table 8.

Syndesmophyte volume, height and mass differences for patients’ intervertebral disk spaces. The asterisk indicates the precision of the final algorithm is statistically different from the precision of the initial algorithm.

	Algorithm	n	Mean +/- Std		CV
			mm3	%	%
VOLUMES	Initial	216	14.3 +/- 18.0	4.12 +/- 6.05	5.63
	Final*	216	7.55 +/- 8.99	2.54 +/- 3.38	2.94
			mm	%	%
HEIGHTS	Initial	216	0.17 +/- 0.28	3.72 +/- 5.43	4.92
	Final*	216	0.099 +/- 0.11	2.23 +/- 2.44	2.38
			mg	%	%
MASSES	Initial	96	5.75 +/- 7.51	3.64 +/- 4.44	4.10
	Final	96	4.43 +/- 6.13	2.59 +/- 2.87	2.74

As for patients, the gains in precision brought by the algorithmic refinements are more substantial for volume and height than for mass. Using multivariate analysis of variance with adjustment for resolution and IDS level, and accounting for the correlation of within-patient measures we found that the gain in precision with the final algorithm was statistically significant for volume (p<0.003) and height (p<0.02) but not mass (p=0.14).

5. Discussion

We have presented improvements to a highly automated computer algorithm that segments syndesmophytes from the 3D space of CT scans, which permits their full quantification in terms of volume, height and mass. This represents a substantial improvement on the current standard assessment which uses radiography and a crude semi-quantitative scoring system.

We investigated the precision of our method using a specifically designed anthropomorphic spine phantom and patients. For volume and height respectively, we observed CVs of 0.932 and 1.04% for the phantom and 1.14 and 1.37% for patients. These numbers indicate high precision. For comparison, a recent carpal bone volume measurement method reported an interscan CV of 3.0% (Duryea et al., 2008).

We investigated the impact of the technical refinements on our original algorithm. For the phantom volume, precision improved by about a factor of 2 in terms of percentage. For patient volume and height, the gain in precision is even larger.

We observed important differences between the results of the phantom and those of patients. In absolute value, the precision of volume measurements was found to be lower for patients than for the phantom. The mean (standard deviation) of interscan differences were respectively 19.0 (17.6) mm³ for patients compared to 5.19 (3.72) mm³ for the phantom. This disparity is caused by several factors. First, patients had considerably larger syndesmophytes than the phantom (mean volume of 2000 mm³ compared to 500 mm³). Larger syndesmophyte volumes lead to larger absolute volume differences (heteroskedasticity). We propose a plausible explanation. Consider a small inaccuracy in the registration process. Syndesmophytes would subsequently be cut from slightly different levels. For a narrow, extremely localized syndesmophyte the difference would be small. However for a larger syndesmophyte that runs the whole length of the ridgeline, the error is multiplied by the length of the ridgeline.

However, heteroskedasticity can only partly explain the difference between phantom and patient. Even in terms of percentage, patient volume measurements are less precise than phantom measurements: 1.31 (0.95)% for patients compared to 1.07 (0.77) % for the phantom. Moreover we observed the same trend for height: 1.56 (1.13) % for patients compared to 1.18 (0.88)% for the phantom. Height measures did not exhibit heteroskedasticity, probably because for each IDS we only considered the maximal height, which is localized, rather than the total height along the whole length of the ridgeline. The mean heights for phantom and patients are in fact similar: 15.5 and 17 mm respectively.

We also observed that the patient results are more precise for same resolution than cross resolution reconstructions, especially for mass. The difference between same and cross resolution reconstructions was not appreciable for the phantom.

An important factor explaining the higher precision of the phantom measurements as well as their robustness to resolution mismatch is likely the simplicity of the phantom design compared to the complexity of real syndesmophytes. The diversity of syndesmophyte shapes and densities is much greater in patients than in the phantom. Cortical bone, trabecular bone and surrounding soft tissue are more homogeneous in the phantom than in patients. The boundary between cortical bone and soft tissue is also more clearly defined in the phantom because of a higher density difference.

We also observed that the technical improvements had a larger impact on the precision of patient scans than on the phantom’s. This is especially true for height. This is also probably due to differences in structural complexity between the two. In particular, segmentation errors due to leaking are much less frequent for the phantoms’ syndesmophytes than for patients’. For instance, in the case depicted in figure 9, without the algorithmic refinements, the 2 syndesmophytes are merged as one whose height spans the whole IDS. With the refinements, the syndesmophytes are correctly measured as 2 separate syndesmophytes of lesser heights. Density and Laplacian based correction is crucial when the segmentation of the syndesmophytes is prone to mistakes due to unclearly defined boundary between bone and soft tissue, proximity between two distinct syndesmophytes (figure 9), or any other reason for confusion that are present in complex patient data.

For the anthropomorphic spine phantom, the most important precision improvement was related to subvoxel cutting, while for patients it was density and Laplacian based correction with blur equalization. This again could be explained by the lack of complexity in the cortical bone/soft tissue boundary in the phantom.

We also observed that, for patients, subvoxel cutting led to appreciable gains in percentage terms but not in absolute terms. This suggests that subvoxel cutting improves precision for small syndesmophytes but not for large ones. For large syndesmophytes with extended areas of contact with the vertebral bodies, the errors incurred by considering whole voxels could compensate each other. Such mitigation of errors is less likely for smaller syndesmophytes. This could also help explain why subvoxel cutting is so effective for the phantom. Its syndesmophytes are small compared those of patients.

The difference in precision estimates between patients and phantom underscores the importance of testing using patient data obtained in the same manner in which the method would be used clinically. Measurement precision would have been overestimated if only phantom experiments had been available. In particular, it could have led us to consider the original algorithm adequate for height measurement while with realistic data it is prone to segmentation errors.

The present work is limited by the small number of patients enrolled in the study. A one day repeat CT scan entails considerable radiation exposure that few patients are willing to submit to for a study that advances knowledge but offers no clinical benefit. The parameters for Laplacian and density based correction were mainly optimized for volumes, which is the measure most important to us. It is possible that higher precision for heights and masses could be obtained with other sets of parameters. Our main future work is a longitudinal study monitoring syndesmophyte evolution over a period of 3 years in a group of AS patients.

6. Conclusion

In our previous work (Tan et al., 2008a) we presented what was the first computerized method to fully quantify syndesmophytes in 3D space with the aim of improving on 2D radiographic scoring. The method was validated in a cross-sectional study. In anticipation of longitudinal studies, we have now investigated the precision of this algorithm using an anthropomorphic vertebral phantom and patients. The original algorithm was substantially improved to refine the segmentation of the syndesmophytes and address the problems of varying scanner performance. We were able to characterize the syndesmophytes in 3 quantifiable ways: volume, height and mass. We evaluated the precision of those 3 measures by computing the differences between pairs of scan reconstructions. Volume and height had better precision than mass and the phantom’s measurements had better precision than the patients’.

The improvements resulted in a gain in precision of more than a factor of 2 for patient volume and height measurements. The best final results were for volumes with a mean difference of 1.31% (standard deviation 0.95%) and a coefficient of variation of 1.14%. These results provide the basis for using this method to detect changes in syndesmophyte size over time in longitudinal clinical data. In addition, these results can serve as an example for other quantitative bone measurement applications using CT. Our method highlights how precision can be optimized by addressing problems posed by segmentation errors and differing image blur.