Laminar analysis of visually evoked activity in the primary visual cortex

Abstract

Studying the laminar pattern of neural activity is crucial for understanding the processing of neural signals in the cerebral cortex. We measured neural population activity [multiunit spike activity (MUA) and local field potential, LFP] in Macaque primary visual cortex (V1) in response to drifting grating stimuli. Sustained visually driven MUA was at an approximately constant level across cortical depth in V1. However, sustained, visually driven, local field potential power, which was concentrated in the γ-band (20–60 Hz), was greatest at the cortical depth corresponding to cortico-cortical output layers 2, 3, and 4B. γ-band power also tends to be more sustained in the output layers. Overall, cortico-cortical output layers accounted for 67% of total γ-band activity in V1, whereas 56% of total spikes evoked by drifting gratings were from layers 2, 3, and 4B. The high-resolution layer specificity of γ-band power, the laminar distribution of MUA and γ-band activity, and their dynamics imply that neural activity in V1 is generated by laminar-specific mechanisms. In particular, visual responses of MUA and γ-band activity in cortico-cortical output layers 2, 3, and 4B seem to be strongly influenced by laminar-specific recurrent circuitry and/or feedback.

Based on anatomy and neurophysiology, our view of the cerebral cortex has changed. Instead of viewing the cortex as a single network, we now conceive of the cortical laminae as a stack of loosely interconnected but distinct neuronal networks (1–5). Each lamina has different specific inputs, projection targets, and feedback connections.

The goal of this study is the determination of the spatial distribution of stimulus-driven neural activity throughout the depth of the cortex and across cortical laminae. Pursuing this goal, we chose to study Macaque primary visual cortex (V1), because V1 is a cortical area where the experimenter has control of the neuronal input by controlling visual stimulation. V1 laminar inputs, outputs, and local connections are well-known (1, 3, 6). Signals come from the thalamus [lateral geniculate nucleus (LGN)] into V1 layers 4C and 6. After intracortical processing, neuronal signals are routed to other cortical areas from cells in superficial layers 2, 3, and 4B of V1; subcortical targets receive cortical outputs from cells in layers 5 and 6. Extrastriate cortical feedback targets layers 2, 3, and 6 (1, 3, 7). The visual functional properties of cells in different layers are markedly different (2, 8–13), reflecting local circuitry that is layer-specific (1, 3, 6). Because of the similarities of laminar cortical circuitry throughout the cerebral cortex (14–16), we used V1 as a test bed to study laminar patterns of stimulus-driven responses.

To sample from many neurons in each layer, we measured multiunit spike activity (MUA) and the local field potential (LFP) with multiple microelectrodes (Methods details the operational definitions of MUA and LFP). We measured the power in the LFP at frequencies < 100 Hz, because the largest changes in LFP power in response to visual stimulation occur in the γ-band of frequencies between 30 and 80 Hz (17–28).

The pattern of visually driven activity as a function of depth in V1 cortex was different for MUA and the γ-band of the LFP. Visually driven MUA per unit depth was approximately constant across the depth of V1. However, the amount of visually driven γ-band power per unit depth varied in different V1 depths and laminae. The mismatched laminar patterns for LFP power and MUA suggest a functional dissociation between LFP γ-power and MUA (22, 29–32). The results also imply that there are laminar-specific mechanisms for the generation of neural activity.

Results

At each recording site, we measured the visually driven responses of MUA and the LFP to sinusoidal gratings drifting at 4 Hz for 2–4 s (details in Methods). Data from the 514 sites that had significant visually evoked LFPs or MUA were used for this study.

A typical MUA waveform in response to visual stimulation is shown in Fig. 1A. The visually driven MUA response was quantified as MUA(driven) − MUA(background), averaging MUA over all stimulus directions, where the units of MUA are impulses per millisecond. We analyzed the initial transient spike activity in the first 200 ms after stimulus onset, and separately, we analyzed the sustained MUA response from 300 ms after stimulus onset to the end of the 2-s stimulus.

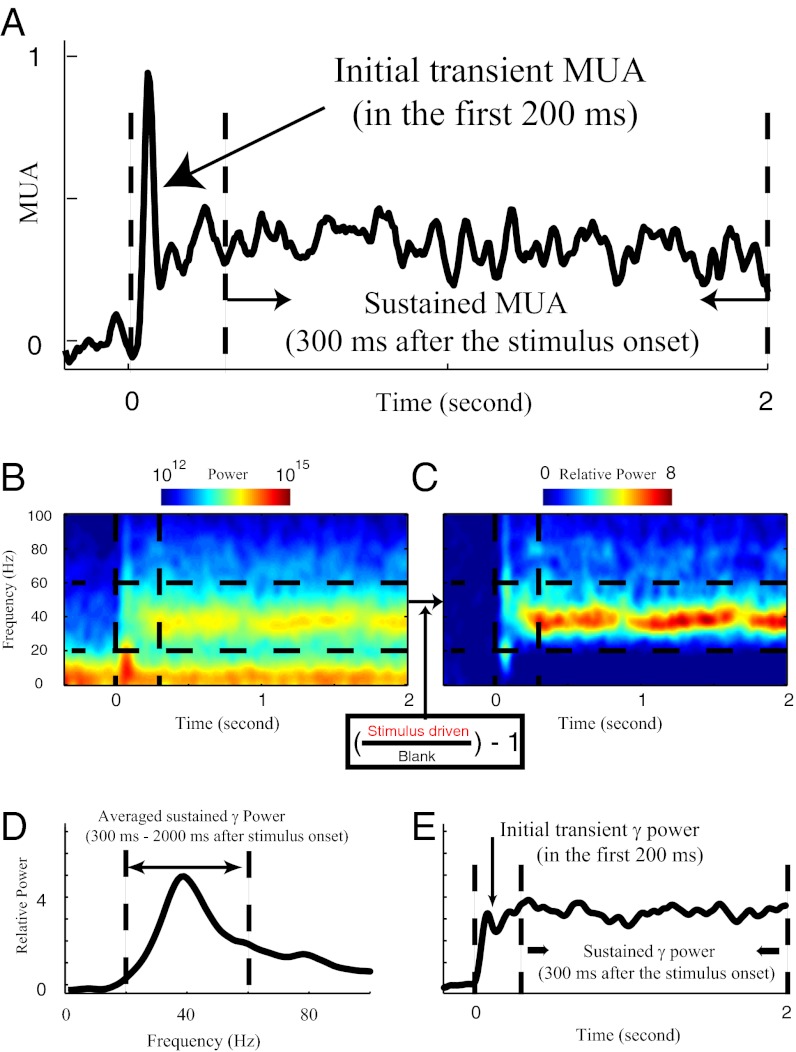
Fig. 1.

Population activity measured in V1. (A) Multiunit activity (MUA) to the drifting grating stimulus. The MUA averaged from 300 to 2,000 ms after stimulus onset was taken to be the steady-state MUA. The MUA response over the first 200 ms after stimulus onset was termed the MUA transient response. (B) Absolute spectrogram of the LFPs to the drifting grating stimulus is coded by color. Between 20 and 60 Hz (marked by two horizontal dashed lines), there is sustained power after stimulus onset (marked by the first vertical dashed line). (C) The raw power spectrum was converted into the relative power spectrum by normalizing by the power during the blank period at each frequency (Inset). (D) Sustained power spectrum of the LFP to the drifting grating stimulus. We defined the average power in the LFP from 300 to 2,000 ms after stimulus onset as the sustained power spectrum. (E) Dynamics of γ-power. We defined the power between 20 and 60 Hz at each time as the instantaneous γ-power.

The LFP was recorded simultaneously. Time frequency analysis of the LFP was performed on each individual trial. We calculated the relative spectrogram of the LFP (Fig. 1C) from the absolute spectrogram (Fig. 1B). The average relative spectrogram was formed by averaging individual spectrograms over all individual trials from all stimulus directions. The most significant visually driven LFP component below 100 Hz was in the γ-band around 40 Hz (Fig. 1 B–D). Like MUA (Figs. 1A and 2), the γ-band visual response was sustained throughout visual stimulation (Fig. 1 B, C, and E). To average MUA and LFP data across sites and electrodes, it was essential to use the relative LFP spectrum as in Fig. 1C to normalize for amplitude differences caused by extraneous factors like electrode impedance. The definition of MUA ensured that it was also a signal normalized against extraneous amplitude variations. This technique was an essential computational technique of data analysis that enabled us to perform the population averages of MUA and LFP signals needed for this study.

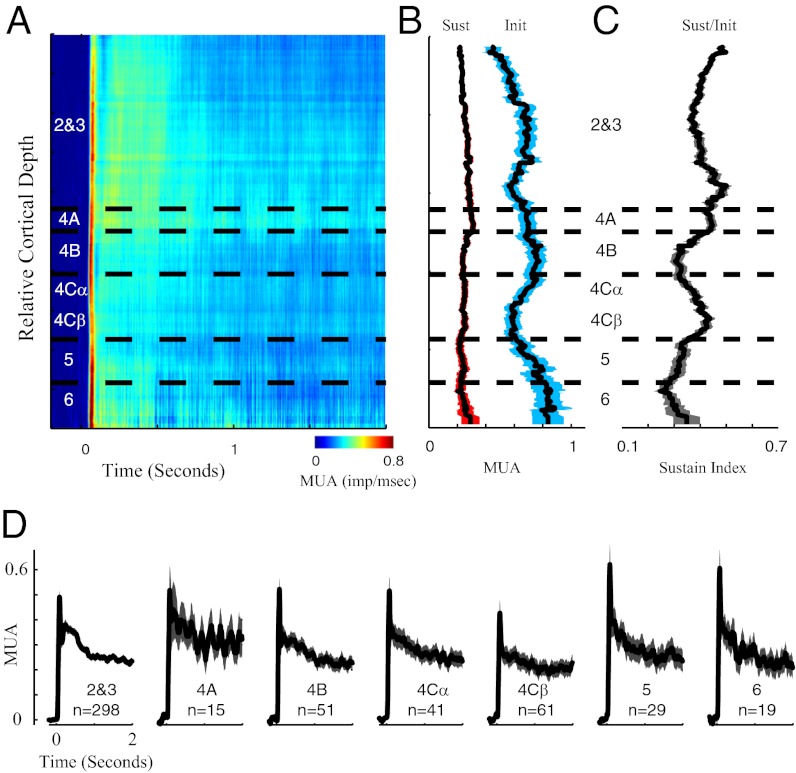
Fig. 2.

Laminar pattern of MUA dynamics in V1. (A) Dynamics of MUA plotted as a function of cortical depth; x axis represents the time after stimulus onset, and colors represent the MUA. Horizontal dashed lines define the borders of V1 cortical laminae. (B) Running averages of the sustained (red-shaded curve) and transient (blue-shaded curve) MUA. The length of sliding window is 100 μm in cortical space, and the shaded regions represent the SEM. MUA activity is in units of impulses per millisecond. (C) Sustain indices (sustained MUA divided by transient MUA) are plotted as a function of cortical depth. The length of sliding window is 100 μm in cortical space, and the shaded regions represent the SEM. (D) Population-averaged MUA time waveforms are plotted for different cortical layers. The colored shaded regions in D represent the SEM.

Visually Driven Spike Activity (MUA) at Different Depths in V1.

Stimulus-driven, steady-state MUA was distributed uniformly with cortical depth (Fig. 2). In Fig. 2B, the black curve with the red band around it indicates the average sustained, visually driven MUA. The red band around the black line represents the SEM across many sites recorded at each depth. The first row in Table 1 presents the mean sustained MUA in each cortical layer. One-way ANOVA was used to test the significant mean differences for MUA among seven layers; the variation of the mean of the sustained MUA across layers was not statistically significant (P > 0.05 for ANOVA).

Table 1.

Mean values of the MUA and γ-power and their Sustain Index

	Layers 2 and 3	Layer 4A	Layer 4B	Layer 4Cα	Layer 4Cβ	Layer 5	Layer 6	P (one-way ANOVA)
Sustained MUA	0.26 ± 0.01	0.33 ± 0.06	0.25 ± 0.03	0.26 ± 0.04	0.21 ± 0.03	0.26 ± 0.05	0.25 ± 0.04	0.52
Transient maximum MUA	0.49 ± 0.03	0.55 ± 0.12	0.52 ± 0.05	0.52 ± 0.07	0.43 ± 0.05	0.62 ± 0.08	0.61 ± 0.07	0.12
MUA Sustain Index	0.52 ± 0.01	0.60 ± 0.04	0.48 ± 0.02	0.51 ± 0.03	0.49 ± 0.02	0.43 ± 0.03	0.41 ± 0.04	0.2
Sustained-γ (relative)*	2.13 ± 0.11	1.90 ± 0.34	2.42 ± 0.29	1.61 ± 0.20	1.08 ± 0.15	1.08 ± 0.15	1.06 ± 0.12	1.7 × 10−5
Transient-γ†	4.78 ± 0.35	3.38 ± 0.79	3.48 ± 0.37	3.18 ± 0.40	2.59 ± 0.35	4.21 ± 0.82	4.01 ± 0.83	0.015
γ-Sustain Index‡	0.45 ± 0.01	0.57 ± 0.04	0.70 ± 0.03	0.51 ± 0.04	0.42 ± 0.03	0.26 ± 0.03	0.27 ± 0.04	3.3 × 10−5
Layer thickness (fraction)	0.442	0.058	0.108	0.083	0.083	0.11	0.116

Population means and SEs of MUA and γ-power and the Sustain Index for MUA and γ-power in different cortical layers are shown in rows 1–6. For the mean values in each row, one-way ANOVA was used for testing whether the average values for MUA, γ-power, and their sustained indices are the same among the seven cortical layers. Row 7 shows the fractional thickness of seven different cortical layers in V1.

*For sustained γ-power, the average γ-power in layers 2 and 3 or 4B is significantly larger than the average γ-power in layer 4Cβ, 5, or 6; other pairs are not significantly different.

^†For transient γ-power, only the mean difference between layers 2 and 3 and 4Cβ is significant.

^‡The Sustain Index of γ-power is significantly larger in layers 2 and 3, 4A, or 4Cα than layer 5; the Sustain Index of layer 4B is significantly larger than in layers 4Cβ, 5, and 6.

At all cortical depths in V1 (Fig. 2A) there was an initial transient MUA response and then steady state impulse firing that lasted throughout stimulation (Fig. 2 A, B, D). There was a tendency for the MUA to be more sustained in the output layers 2 and 3, as quantified by the sustained/init response ratio (Fig. 2C), but this trend was not statistically significant (P > 0.05 for ANOVA in Table 1).

Visually Driven LFP γ-Power at Different Cortical Depths in V1.

Relative γ-band power in the LFP is a measure of cortical activity that captures an aspect of stimulus-driven neural activity that is approximately independent of or only weakly related to spike activity (22, 29–32). Note that the relative γ-band signal (as defined in Fig. 1) is the component of the LFP modulated most by a visual stimulus (17–28). Although the absolute power in lower-frequency components (<20 Hz) of the LFP is higher than γ-band power (Fig. 1), the power in frequencies < 20 Hz is not well-driven by the visual stimuli that we used. We investigated relative γ-band power with the intention of studying stimulus-driven activity in the subthreshold responses of cortical neurons.

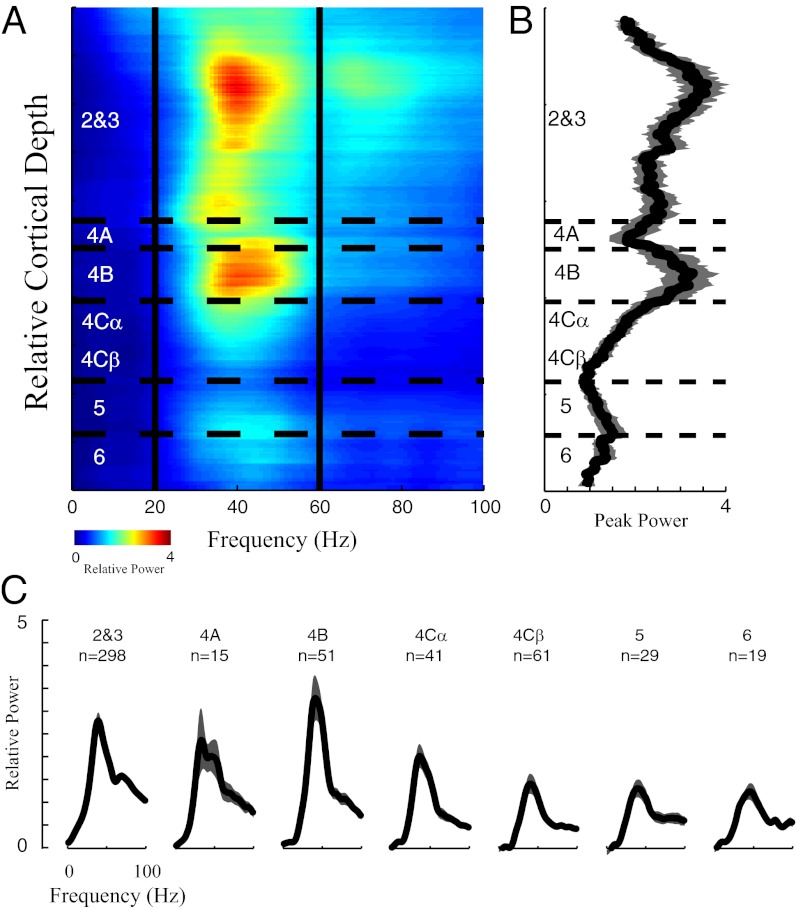
There was a clear laminar pattern of relative γ-band power per unit depth in the cortex. The γ-peak power in the sustained power spectrum was greatest at sites in layers 2, 3, and 4B (particularly layer 2), and it was generally lower in deeper layers (Fig. 3). Fig. 3B plots the running average across cortical depth of the peak amplitude in the power spectrum for each site during the sustained period, and Fig. 3C shows the power spectra averaged over the depth of each layer. Both indicate the highest γ-band activity in layers 2, 3, and 4B.

Fig. 3.

Laminar pattern of LFP power spectrum in V1. (A) Power spectrum of the LFP plotted as a function of cortical depth; x axis represents the frequencies, and colors represent the power at each frequency. Horizontal dashed lines define the borders of different cortical layers in V1. Two vertical lines mark 20 and 60 Hz. Power spectrum was the averaged relative power in the period of 300–2,000 ms after stimulus onset. (B) Running average of the peak γ-band in different layers. The length of the sliding window is 100 μm in cortical space, and the gray-shaded region represents the SEM within the corresponding sliding window. (C) Population-averaged power spectra of the LFP are plotted for different cortical layers. The gray-shaded regions in C represent the SEM.

To make quantitative comparisons of the γ-band power during the sustained period in different V1 layers, we defined sustained γ-band power (sustained-γ in Table 1) at each recording site as relative power averaged over the frequency band of 20–60 Hz (Fig. 1 B–D) during the sustained period of visual stimulation. The difference between the layers in sustained γ-band power was significant (P < 0.05 in Table 1 for sustained-γ). The sustained γ-band power per unit depth in layers 2, 3, and 4B was at least two times larger than the power in layers 4Cβ, 5, and 6 of V1 (Fig. 4 and Table 1, P < 0.05 for posthoc test after ANOVA).

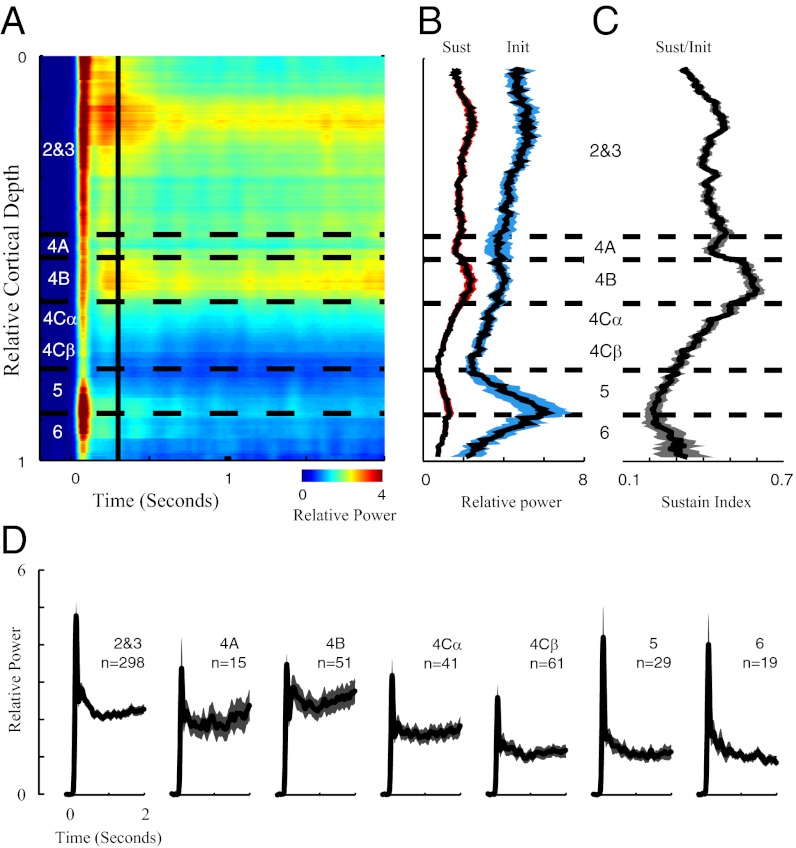
Fig. 4.

Laminar pattern of γ-band dynamics in V1. (A) Dynamics of γ-power plotted as a function of cortical depth; x axis represents the time after stimulus onset, and colors represent the γ-power. Horizontal dashed lines define the borders of V1 cortical laminae. The vertical line marks 300 ms after stimulus onset. (B) Running averages of the sustained (red-shaded curve) and transient (blue-shaded curve) LFP γ-power. The length of sliding window is 100 μm in cortical space, and the shaded regions represent the SEM. (C) Sustain indices (sustained γ-power divided by transient γ-power for the LFP) are plotted as a function of cortical depth. The length of sliding window is 100 μm in cortical space, and the shaded regions represent the SEM. (D) Population-averaged γ-dynamics are plotted for different cortical layers. The shaded regions represent the SEM.

Dynamics of γ-Band Power at Different Cortical Depths in V1.

Transient and sustained responses.

The dynamics of γ-band activity revealed additional information about laminar function (Fig. 4). Fig. 4A plots the average γ-band power as a function of time and depth. Average γ-band power was computed as the average power between 20 and 60 Hz (Fig. 1 B–D). Fig. 4A shows that γ-band activity was more sustained in layers 2 and 4B (yellow colored region to the right of the vertical black line in Fig. 4A). Fig. 4B plots average γ-band power in the transient (labeled Init) and sustained (labeled Sust) periods (Fig. 1E) as a function of depth. Transient γ-power was observed in all layers. It was weakest in layer 4Cβ, with the highest values in layers 2, 5, and 6 (Fig. 4 A, B, and D). Similar to the results in Fig. 3B, sustained γ-power varied with cortical depth, with the highest values in layers 2, 3, and 4B. The laminar differences in sustained and transient γ-power were significant (P < 0.05 for ANOVA), and the difference in transient power between layers 2, 3, and 4Cβ also was statistically significant (posthoc test for ANOVA).

Sustain Index reveals differences in laminar processing.

Making the comparison between transient and steady-state responses is important, because it is conceivable that the interlaminar differences in Fig. 3 might have been a result of different input strengths to the different layers. The initial transient mainly reflected the strength of synaptic inputs to each layer before recurrent interactions had time to work (33). To normalize for synaptic input to each layer, we calculated a Sustain Index = sustained/initial response ratio (29) (Fig. 4C and Table 1). The mean Sustain indices across V1 depth were significantly different (P < 0.05 for ANOVA). Layers 2, 3, 4A, and 4Cα have significantly larger sustain indices than layer 5, and layer 4B has a significantly larger index than layers 4Cβ, 5, and 6 (posthoc test for ANOVA).

Neuronal Activity in Different Cortical Layers of V1.

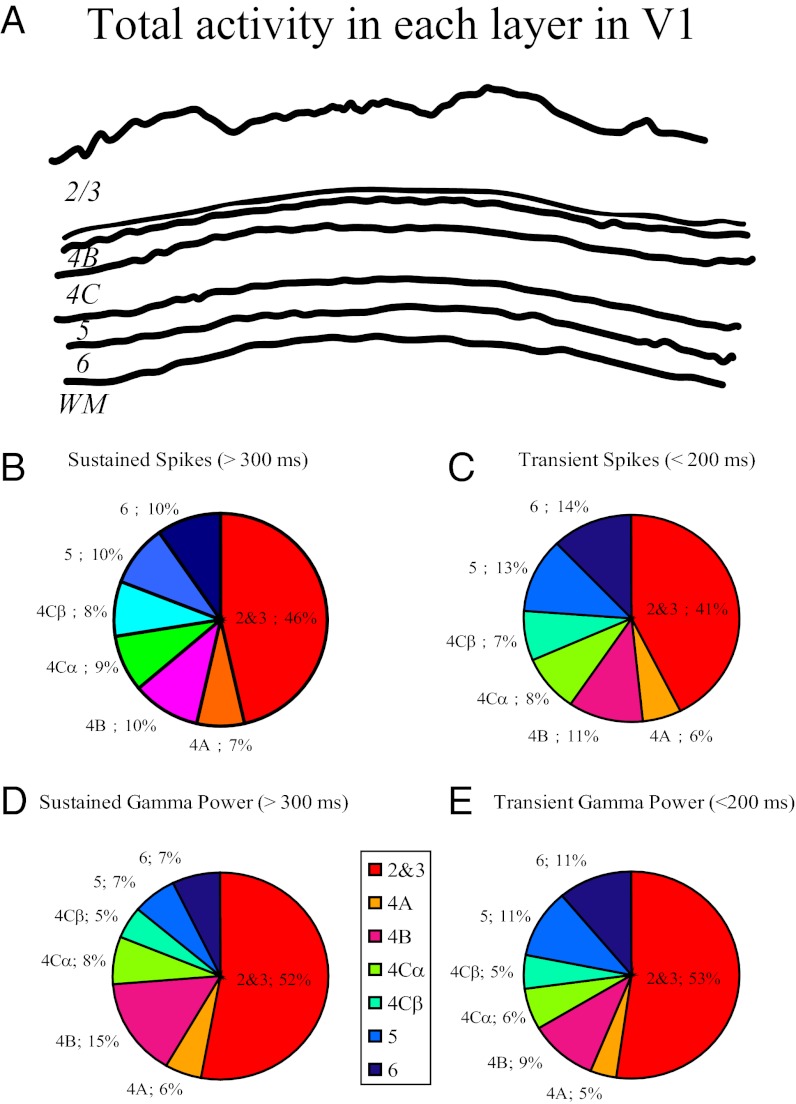
Figs. 2, 3, and 4 show how neuronal activity depends on cortical depth. Another method of analysis is to calculate neuronal activity in each cortical layer. Fig. 5A is a diagram of the laminar thicknesses in a slice of V1 cortex. Summing the activity per unit depth of MUA and LFP γ-band (Table 1) across each layer gives us an estimate of the laminar contribution to total cortical activity in V1. We calculated the fractional activity distribution (FAD), which is the fraction that each layer contributes to total cortical activity for MUA and γ-power separately. We defined the FAD as (thickness × local activity per unit length)/sum (thickness × local activity per unit length), where the sum is taken across all layers (Methods). The reason for this definition of FAD is that the local microelectrode measurements are of activity per unit depth, and we need to sum the local measurements across the thickness of the layer to estimate the contribution of each layer (Methods).

Fig. 5.

Laminar pattern of population activity in V1. (A) Demonstration of the laminar structure of Macaque V1. (B) FAD of sustained spike activity in different layers. (C) FAD of transient spike activity in different layers. (D) FAD of the sustained γ-power in different layers. (E) FAD of the transient γ-power in different layers.

MUA measurements (Fig. 2D and Table 1) allowed us to estimate how many spikes are fired in different V1 layers (23) for both the sustained (Fig. 5B) and initial transient components (Fig. 5C). Visually driven spike activity was roughly constant per unit depth (Fig. 2), and therefore, the FAD for MUA approximately followed laminar thickness (given in Table 1). Fig. 5 B and C shows that cortico-cortical output layers (layers 2, 3, and 4B) contributed 56% of the total V1 spike activity.

We calculated FADs for γ-power in the LFP for both sustained (Fig. 5D) and transient components (Fig. 5E). Cortico-cortical output layers 2, 3, and 4B generated 67% of the sustained power in the γ-band (Fig. 5 D and E).

Discussion

Visually Evoked Neural Activity in V1: Laminar Distribution.

The measurements of transient and sustained responses of MUA and the LFP γ-band activity in each layer have implications for the mechanisms that lead to the laminar patterns of activity per unit depth. For instance, the initial transient peak of the γ-band response in each layer reflects input to the layer where it is recorded. The pattern that we found, shown in Fig. 4B as the blue curve, indicates this laminar input. The transient γ-power per unit depth was statistically significantly different between cortical layers, with the highest values in layers 2, 3, 5, and 6 and the lowest values in layer 4C (Fig. 4B and Table 1). The data indicate that the LGN input into layer 4C is amplified within the cortex, and therefore, transient γ-power is larger in output vs. input layers. However, transient MUA is relatively constant across layers as seen in Fig. 2B and Table 1. The results on γ-band activity and MUA taken together suggest that the amplification of synaptic currents in the output layers is an amplification of both excitatory and inhibitory inputs that balance each other to cause the approximately constant size of the transient spike rate response.

The sustained responses of MUA and the γ-power also can be used to track signal flow in the cortical network. The sustained γ-power per unit depth varies significantly across the cortical layers, with highest values in layers 2, 3, and 4B (Fig. 4B and Table 1). The even larger (and significant) variation of the Sustain Index with cortical depth (Fig. 4C and Table 1) indicates that the sustained LFP γ-responses in the output layers are likely to be generated by recurrent or feedback interactions that are layer-specific. The smaller and not statistically significant variations of the MUA Sustain Index suggest that recurrent excitatory and inhibitory signals in the output layers must be roughly balanced to keep the cortical spike activity approximately constant in the sustained visual responses as in the transient responses.

There are other factors that change between the layers that do not influence our measurements and conclusions. For instance, cell density varies with layer, with the highest cell density in the input or granular layers. Nevertheless, our measurement of MUA per unit depth will take the density variation into account, because a higher density of spiking neurons will be reflected in a higher MUA. Similarly, the size of pyramidal neurons varies across layers, with the largest pyramidal cells with the largest volume/surface areas in layer 5. This finding will be reflected in the LFP measurements that integrate synaptic currents over a small volume in the cortex (34, 35).

γ-Band Activity Is a Measure of Network Recurrency.

LFP γ-band activity is an important feature of cortical activity that can be used for evaluating V1 models. Peaks in the LFP power spectrum, including γ-band activity, can be generated by a recurrent network (36–39)—feedforward networks do not generate such spectral peaks. Therefore, neurons in a V1 layer with strong γ-band activity are not modeled adequately by simple feedforward models like an LN model (40–42) (a model with a linear filter followed by a static nonlinear function). Our results on the dynamics of γ-band activity could be used for indicating the recurrency of the different laminar networks (39, 43–45). The dynamics measurements allowed us to estimate separately the input, which represents the early feedforward input to a cortical layer, and its sustained γ-band response, which represents the recurrent interaction. The higher Sustain Index in layers 2, 3, and 4B suggests that intralaminar interactions, rather than the amplitude of the input, determine the amount of sustained activity in these layers. The cortico-cortical output layers, with high sustain indices, are those layers with the densest recurrent connections (3, 46). It is also possible that cortico-cortical feedback to V1 contributed to the higher sustained visual responses in the γ-band (7).

Comparisons with Earlier Work on Laminar Neural Activity.

Several groups have studied V1 laminar variation (5, 8, 9, 25, 47–49) by using spike-field coherence analysis (25), current source density analysis (5, 49, 50), or the BOLD signal in functional MRI (47). In this study, we used drifting gratings with spatial frequency equal to two cycles per degree, which are optimal stimuli for stimulating neurons in the V1 network (20, 51). The work by Schroeder et al. (5) used diffuse light, which is very low spatial frequency, as a visual stimulus, and this use is probably the main reason that they found MUA mainly in the input layer 4. The work by Maier et al. (49) also used visual stimuli of low spatial frequency, similar to the work in ref. 5. Because V1 neurons are usually tuned to stimulus spatial frequency, diffuse light and low spatial frequency stimuli are not effective stimuli in driving V1. Based on results in the work by Jia et al. (20), we know that visual stimuli of low spatial frequency induce relatively little γ-band activity.

FAD, the Fraction of Total Cortical Activity Contributed from Each Cortical Layer.

We measured visually driven spike activity as well as the LFP γ-power as a function of cortical depth, and we used these data to compute the FAD, the fraction of total cortical activity contributed from each cortical layer. Cortico-cortical output layers accounted for 67% of total sustained γ-band activity and 56% of the total sustained spike activity summed across the depth of V1 (Fig. 5). Therefore, sustained γ-band activity in the output layers, which comprises 55% of the depth of V1, was two times as strong (67% vs. 33%) as γ-band activity summed over all other V1 layers. However, the number of sustained spikes in the output layers was 27% (56% vs. 44%) more than sustained spike activity summed over all other layers. It is likely that different stimulus regimens (17–20, 24, 52) or brain states (53, 54) could lead to different multilayer patterns of activation.

Methods

Surgery and Preparation.

Acute experiments were performed on nine adult Old World monkeys (Macaca fascicularis). After surgery, anesthesia was maintained with a continuous infusion of sufentanil citrate (6–12 μg/kg h⁻¹ i.v.), and the animal was paralyzed with verucuronium bromide (0.1 mg/kg h⁻¹ i.v.) (details in SI Methods).

Electrophysiological Recordings and Data Acquisition.

A matrix of seven independently moveable electrodes (Thomas Recording) was used to record simultaneously from multiple cortical sites in V1. The seven electrodes were arranged in a straight line, with each electrode separated from its neighbor by ∼300 μm (details in SI Methods).

Visual Stimulation.

At each recording site, an experiment was run with drifting sinusoidal gratings (at high contrast > 90%, spatial frequency at two cycles per degree, temporal frequency at 4 Hz, and 12 directions of drift between 0° and 360°) within a circular patch of radius 4° visual angle, covering the visual field locations of all recording sites (details in SI Methods).

Time Frequency Analysis.

The continuous Gabor transform was used for time frequency analysis of the LFP. The continuous Gabor transform is a short-time or windowed Fourier transform (also called a spectrogram) (details in SI Methods).

Absolute and Relative Power in the LFP.

Time frequency analysis of the LFP was performed on each individual trial, and the absolute power spectrum (Fig. 1B) was averaged over all individual trials from all conditions (all 12 directions). The raw, visually stimulated LFP power spectrum (Fig. 1B) was converted into a relative power spectrum by normalizing by the power during the blank period (defined as the absolute power in the γ-frequency band of the LFP during the stimulus condition divided by the absolute power in the corresponding frequency band without any stimulus, minus one). We defined the averaged power between 0 and 200 msec in the relative power spectrum as the transient γ-power (Fig. 1E), and we defined the average power from 300 to 2,000 ms after stimulus onset as the sustained power spectrum (Fig. 1D).

Multiunit Activity.

Multiunit activity (MUA in Fig. 1A) was computed as follows: (i) the raw signal was high-pass filtered (1,000 Hz); (ii) the high-frequency signal was half-wave rectified in the negative direction; (iii) the mean and SD for the half-wave rectified signal were estimated; (iv) MUA was defined as the number of events 3 SDs more negative than the mean in each 1-ms time bin.

Statistical Analysis on the Laminar Patterns (One-Way ANOVA and Its Posthoc Test).

We conducted one-way ANOVA to test the statistically significant differences of the mean values for MUA, γ-power, and the sustain indices for both signals among seven layers in V1. Significance levels (P values) are shown in Table 1. We concluded that a significant difference existed between different layers when the P value was less than 0.05. For a one-way ANOVA with P < 0.05, we also conducted a posthoc test based on the result of the ANOVA (multiple comparison of means provided by Matlab) to tell which pair of means was different.

Local Activity per Unit Depth.

We defined the local activity per unit depth for different measurements as the mean value of the measurements around a cortical depth (Figs. 2 A–C, 3 A and B, and 4 A–C). For example, the local activity per unit depth for transient γ-band power at a cortical depth (Fig. 4B, black line) was calculated by averaging the transient γ-band power from all recording sites within 100 μm of that cortical depth. We used a depth window of 100 μm in cortical distance (equivalent to 0.05 unit length in a normalized V1, with total depth set to 1 unit length). MUA and γ-band power in Figs. 2, 3, and 4 are abbreviations to represent the local activity per unit depth for MUA and γ-band power, respectively. The average local activity per unit depth in a cortical layer (Figs. 2D, 3C, and 4D and rows 1–6 in Table 1) was calculated as the population average in that layer.

Calculation of the Total Activity in Each Layer.

For the computations displayed in Fig. 5, we calculated the FAD. The contribution of each layer to the total activity will be thickness × local activity per unit length, where local activity per unit length is the average of our measurements of the signal recorded by our microelectrodes from all of the sites within a given layer. We defined the FAD of a given layer as (Eq. 1)

The summation was taken over all seven cortical layers (layers 2 and 3, 4A, 4B, 4Cα, 4Cβ, 5, and 6). The mean relative thickness of each layer is 0.442 for layers 2 and 3, 0.058 for layer 4A, 0.108 for layer 4B, 0.083 for layer 4Cα, 0.083 for layer 4Cβ, 0.11 for layer 5, and 0.116 for layer 6 (8). The time window for the transient FADs was the first 200 ms after stimulus onset, and the time window for sustained FADs was between 300 and 2,000 ms after stimulus onset.

Histology.

Recording sites were assigned to different layers of V1 based on the results of track reconstruction (SI Methods).