Long-range exciton dissociation in organic solar cells

Abstract

It is normally assumed that electrons and holes in organic solar cells are generated by the dissociation of excitons at the interface between donor and acceptor materials in strongly bound hole-electron pairs. We show in this contribution that excitons can dissociate tens of angstroms away from the interface and generate partially separated electrons and holes, which can more easily overcome their coulombic attraction and form free charges. We first establish under what conditions long-range exciton dissociation is likely (using a kinetic model and a microscopic model for the calculation of the long-range electron transfer rate). Then, defining a rather general model Hamiltonian for the donor material, we show that the phenomenon is extremely common in the majority of polymer:fullerene bulk heterojunction solar cells.

In all organic solar cells with respectable efficiency, the majority of absorbed photons generate free holes and electrons in the donor and acceptor materials that constitute the cell’s active components (1–3). This fact is surprising and not well understood. It is generally assumed that the photon absorption generates an exciton in the donor that, after reaching the donor-acceptor interface by diffusion, dissociates in a coulombically bound hole-electron pair. However, simple theories (4, 5) indicate that the hole-electron attraction is too strong for the hole-electron pair to separate before de-excitation, considering the very low dielectric constant of the media. Understanding why the generation of free charges can be so efficient is clearly a key prerequisite to understand the difference between good and bad solar cells and to design better ones.

According to some authors (5), the dissociation of the exciton at the interface generates a hole-electron pair with an excess of vibrational energy that can be used to overcome the coulombic attraction. An alternative hypothesis is that the exciton leads directly to relatively delocalized charges (still not free charges), a hypothesis that allows a satisfactory modeling of the device (6). This latter idea was explored with microscopic models that assume the delocalization of the hole along a polymer chain (7) and include the possible effect of an interface potential between donor and acceptor materials that further reduces the attraction between the two (8).

Unlike the models above, which assume that the hole-electron pair is generated at the donor-acceptor interface, in this paper we explore the possibility that an exciton, located at a certain distance from the interface, can also dissociate into a hole and electron that are already partially separated to start with. This idea is suggested by a simple analogy with electron transfer reactions in single molecules composed by a donor and an acceptor fragment, chemically connected by a bridging medium. In these systems (9), an electron in the photoexcited donor can be transferred to the acceptor over very long distances, and this phenomenon has been investigated particularly carefully in the context of long-range electron transfer in biomolecules (10). Phenomenologically, the electron transfer rate k_ED (exciton dissociation in the solar cell speak), decreases exponentially with the distance between donor and acceptor R, k_ED(R) ∼ k⁰ exp(-βR), with an attenuation factor β that varies from approximately 1 Å^-1 when donor and acceptor are separated by an alkane bridge [high Highest Occupied Molecular Orbital–Lowest Unoccupied Molecular Orbital (HOMO–LUMO) gap] to values as low as approximately 0.2 Å^-1 for a connection made by a pi-conjugated fragment (small HOMO–LUMO gap) (9). The physics is very elementary: The electron can tunnel from the donor to the acceptor and the probability of this happening depends (exponentially) on the distance between donor and acceptor and on the barrier for tunneling which is high for large HOMO–LUMO gaps and small for small HOMO–LUMO gap bridges. For low β, charge separation over distances of many tens of angstroms has been observed (9).

In an organic solar cell, the exciton can (i) migrate within the donor material, (ii) dissociate, or (iii) relax to the ground state (Fig. 1, Top). The importance of (long-range) dissociation is determined by the (distance-dependent) dissociation rate in relation with the rates of migration and de-excitation. In this paper, we first describe a suitable model of distance dependence of the dissociation rate, and then we study under what parameter range this long-range dissociation is possible. The conclusion of this work is independent from the material considered, but the results are exemplified with data suitable for the benchmark system where the polymer poly(3-hexylthiophene) (P3HT) is the donor and the molecular solid formed by the fullerene derivative [6,6]-phenyl-C⁶¹-butyric acid methyl ester (PCBM) is the acceptor (11).

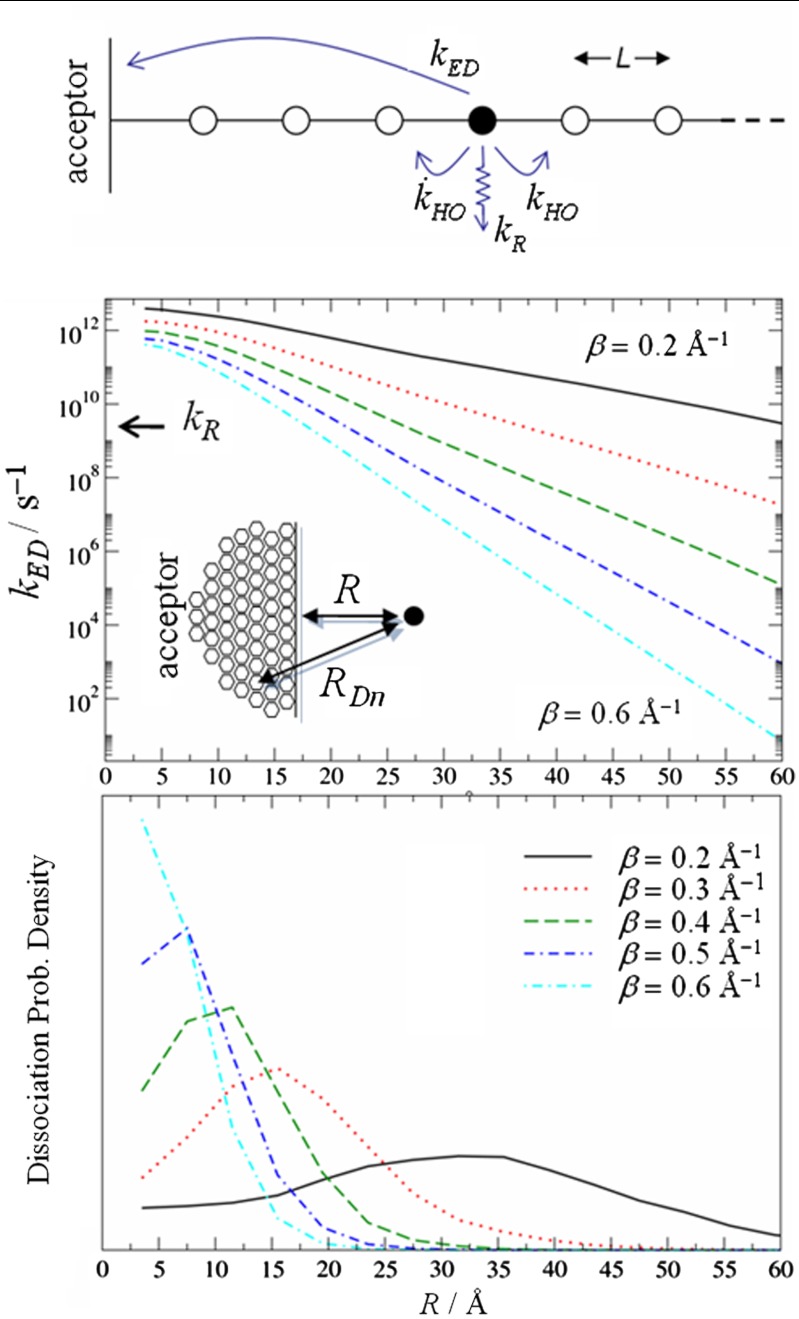
Fig. 1.

(Top) A simple 1D lattice model where the exciton can hop to neighboring sites with rate k_HO, dissociate with rate k_ED(R), and relax to ground state with rate k_R. (Middle) Exciton dissociation rate for an exciton at distance R from a cluster of acceptor molecules computed using Eq. 3 for different values of the attenuation factor β. (Bottom) Results of the kinetic model analyzed in terms of the probability that, when the electron dissociates, it dissociates at a given distance R.

Model

The electron transfer rate between a weakly coupled molecular donor and acceptor can be expressed as (12):

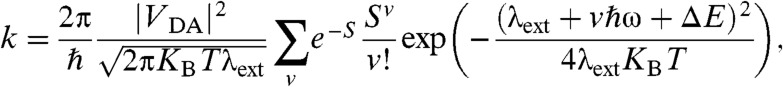[1]

where V_DA is the electronic coupling between the donor and acceptor (initial and final) states, λ_ext is the external reorganization energy, S is the effective Huang-Rhys factor, ω is frequency of one effective mode that incorporates in an average way the effect of all quantum modes, ΔE is the energy difference between initial and final states, K_BT is the thermal energy, and ℏ is the reduced Planck constant. This formula provides quantitatively correct rates for the process of generation of the charge separated state in a model containing a short polymer chain (where the exciton is initially localized) and a PCBM molecule in contact with the polymer chain (13). Eq. 1 should be generalized to the case where the exciton is far from the donor-acceptor interface, and many states in the acceptor material may be occupied by the electron. As the hole and electron are generated at larger distances, the energy of the exciton dissociation process ΔE becomes less negative, the electron can be more delocalized in the acceptor material, and the coupling between donor and acceptor states decreases.

We describe the acceptor as a cluster of N molecules, with one orbital 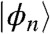per molecule such that an electron in the acceptor is described by a wave function 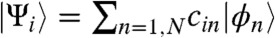. A tight-binding Hamiltonian describes the acceptor so that 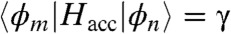if m and n are neighbors and 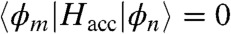otherwise. The diagonal matrix elements are influenced by the presence of a hole generated in the donor material and take the form of

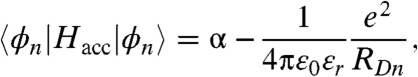[2]

where ε₀ and ε_r are the vacuum and relative dielectric constants, e is the electric charge, R_Dn is the distance between the donor and acceptor molecule n; α was set to zero; i.e., the origin of our energy scale, and γ was set to 0.0125 eV based on computations of bulk PCBM (14). The interface between donor and acceptor is assumed to be planar and the acceptor molecules are arranged in a semispherical cluster with face centered cubic packing (the PCBM molecule is approximately spherical). Diagonalization of H_acc provides the orbital energies E_i and the coefficient c_in needed for the evaluation of k_ED(R).

The total exciton dissociation rate k_ED is the sum of the electron transfer rate k_i to each of the acceptor orbitals:

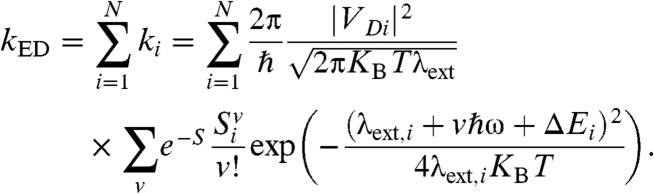[3]

Each rate k_i is different because the energy difference, the electronic coupling, the intramolecular, and polarization reorganization energy are different. We define ΔE_i = E_i - E_D, where E_D is the energy of the donor state. In this work, E_D was set to 0.399 eV so that for an exciton-acceptor distance of R = 3.5 Å and a cluster formed of a single acceptor ΔE₁ matches the energy difference (-0.969 eV) computed from electronic structure calculation of a model containing a single donor and acceptor (13). In a system with many acceptors, an electron in state i of the acceptor is shared approximately by 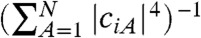molecules (the inverse participation ratio) so that both the Huang-Rhys factor (S_i) and the external reorganization energy λ_ext,i are to be evaluated for each acceptor state (SI Materials and Methods). The electronic coupling between donor and acceptor orbitals can be decomposed in terms of the coupling between donor orbital and each individual acceptor 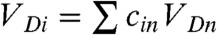. Since the donor orbital is assumed to be exponentially localized, V_Dn depends on the distance R_Dn between donor and acceptor as 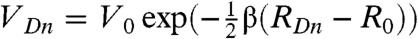where V₀ and R₀ were set to 0.0136 eV and 3.5 Å, based on the computation in (13), and β is the attenuation factor initially taken as a parameter.

Results

The decrease of the rate with the distance, illustrated in the central panel of Fig. 1, follows an exponential ∼ exp(-β^′R) with an apparent attenuation factor β^′ < β. This weaker distance dependence is due to ΔE becoming less negative as the distance increases (because opposite charges are separated further away), and the charge transfer rate increases with less negative ΔE. This latter effect is observed because the charge separation takes place in the so-called Marcus inverted regime, as discussed more extensively in ref. 13, a feature that turns out to be crucial to promote long-range exciton dissociation. Additional calculations with varied parameters are included in the SI Materials and Methods to illustrate that the distance dependence of k_ED(R) is similar for the majority of donor-acceptor interfaces.

A simple kinetic model that can be used to describe the possible fate of the exciton is illustrated in the top panel of Fig. 1. In this 1D lattice model, the exciton occupies one of the lattice sites j(j > 0), and it is assumed that site 1 is in contact with the acceptor material. Each exciton can hop to one of the neighbor sites with rate k_HO, relax to ground state with de-excitation rate k_R, or dissociate into a hole and electron with rate k_ED(R) as determined from Eq. 3. The rest of the parameters are set to be appropriate for the P3HT:PCBM cell. The k_R was set to 2.5 ∗ 10⁹ s^-1, as determined from the exciton lifetime in bulk P3HT (15). The closest distance between donor and acceptor was taken to be R₀ = 3.5 Å. The reported values of the exciton diffusion coefficient D_E for P3HT range between 10^-8 (16) and 10^-7 m ²s^-1 (15), meaning that if we set the distance between lattice sites to L = 4 Å, the hopping rate can be set in the range k_HO = [10¹¹∶10¹²]s^-1 from the relation D_E = k_HOL².

The model can be studied numerically with a straightforward kinetic Monte Carlo algorithm. Considering all the exciton dissociation events, the bottom panel of Fig. 1 gives the probability that the dissociation takes place at a particular distance from the acceptor. As expected, the smaller the value of β, the larger the probability that the exciton dissociates far away from the interface. The average distance of exciton dissociation events is 10.6, 15.2, and 34.4 Å for β values of 0.6, 0.4, and 0.2 Å^-1, respectively. Albeit these values are slightly modulated by the value chosen for k_HO (SI Materials and Methods), the model indicates that for β ∼  < 0.6Å^-1 long-range charge separation is possible and, indeed, very likely.

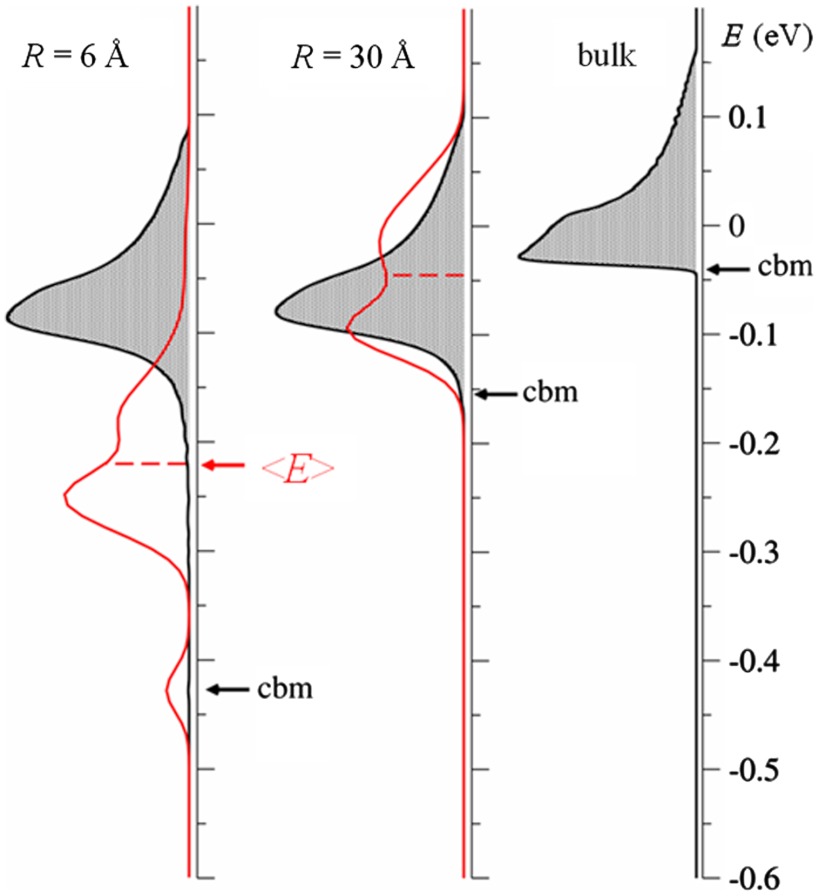
The energy distributions of the final acceptor state [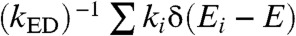] for different distances R are illustrated in Fig. 2, where they are compared with the density of states (DOS) in the presence of a hole at distance R. For small R (Fig. 2, 6 Å), following the exciton dissociation, the electron is transferred to very low energy states, localized near the hole and, therefore, more strongly bound. These states correspond to the conventional strongly bound electron-hole pair and the dissociation energy required to move the electron to the bottom of the conduction band in bulk states is approximately 0.4 eV. However, for R = 30 Å, the distribution of final states for the electron is completely different, and the electron is injected toward the center of the conduction band of the acceptor. The average energy of the final state is larger than the conduction band minimum of the acceptor in the absence of a hole. An electron with this energy can dissociate from the hole, reaching the bottom of the conduction band of the bulk (without barrier), or it can relax to one of the lower energy interface states stabilized by the hole. Even in the latter scenario, however, the dissociation barrier would be just approximately 0.13 eV; i.e., only a few times larger than the thermal energy and much smaller than the dissociation energy of a bound electron-hole pair.

Fig. 2.

The filled curve represents the DOS of the conduction band for a cluster of 1,000 acceptors in the presence of a positive charge (the hole) at either 6 or 30 Å from the interface with the donor and in the absence of a hole (bulk). The red curve is the distribution of final energies of the electron upon charge separation. The average energy of the separated electron and the conduction band minimum (cbm) are indicated by a dashed horizontal line and a black arrow, respectively.

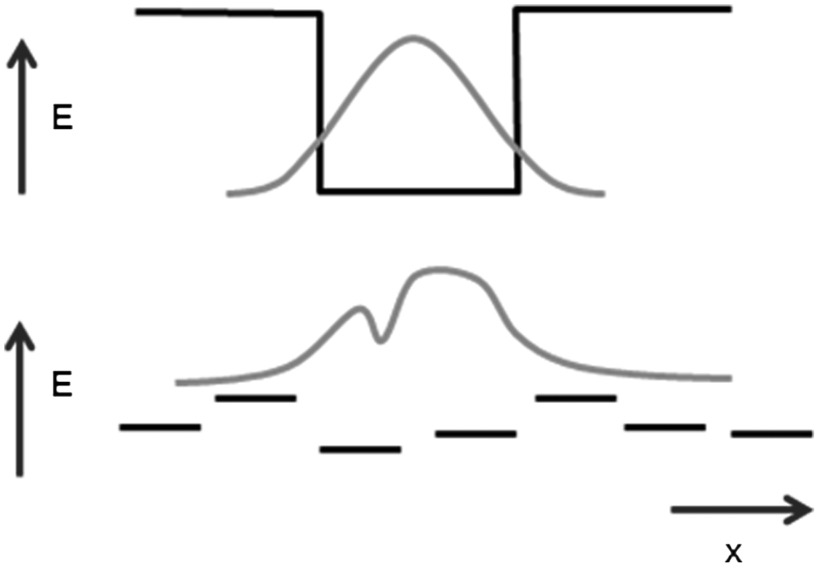
We conclude our investigation by evaluating the plausible range of β values for a realistic donor. For a particle in a 1D potential energy well, the attenuation factor β is just the logarithmic slope of the exponentially localized wave function; i.e., 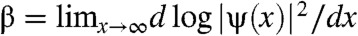. Orbitals in a disordered system are localized by static disorder (Anderson localization) (17), and the probability of tunneling to other states decreases exponentially with the distance following the decrease of |ψ|² (Fig. 3). The range of states accessible by tunneling is determined by the tail of the wave function, and this property is commonly used to describe transport in disordered materials (18). Unlike in donor-bridge-acceptor molecules, we therefore define the attenuation factor without defining localized donor and acceptor states coupled by a bridge. The tunneling range is determined by the localization of the eigenstates of the system.

Fig. 3.

The tunneling range (and attenuation factor β) of a particle in a 1D well is determined by the tail of the wave function. In a polymeric material, there is no well, but the single electron states are similarly localized by static disorder and display an exponential tail that can be used to compute β. The typical standard deviation of the on-site energies is of the order of 0.1–0.2 eV.

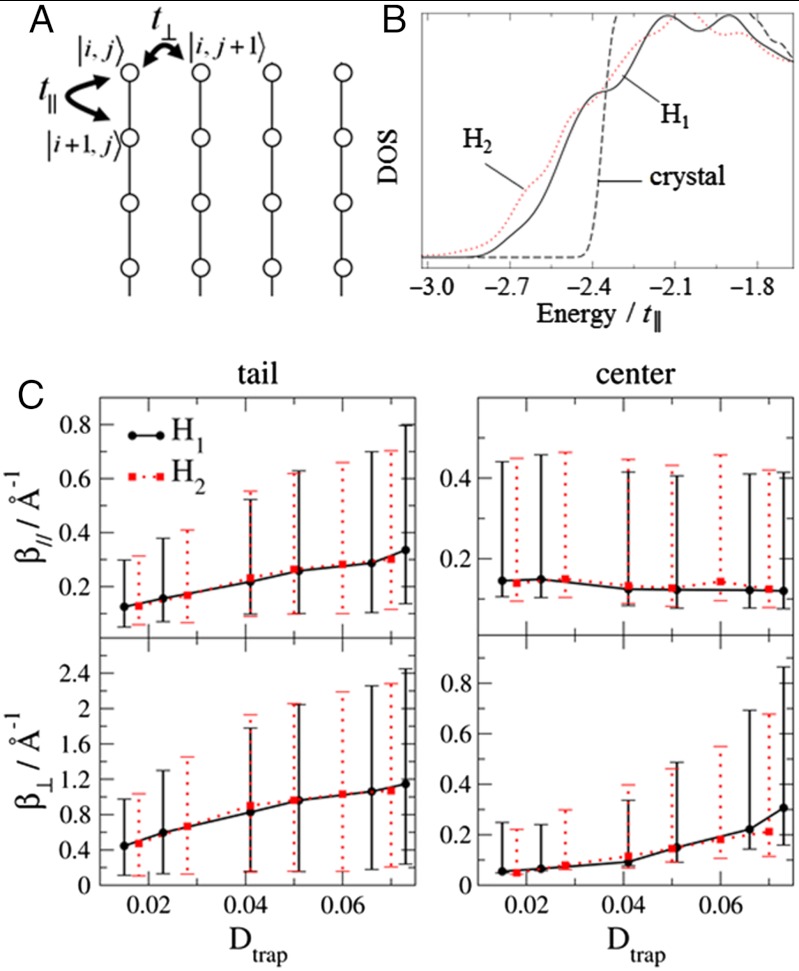
To estimate β for a typical solar cell donor, we need a model of the donor Hamiltonian that correctly describes the localization of its conduction band orbitals. The best polymers for photovoltaics form partially ordered lamellar phases (19) so that a suitable model Hamiltonian for the conduction band of this system is made by a 2D lattice, where there is a one-electron state 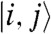per site, which can be identified with the monomer (Fig. 4A). We considered a model Hamiltonian H₁ where the disorder is present in the off-diagonal elements of the tight-binding Hamiltonian and a model H₂, where the disorder is present in the diagonal matrix elements. They give similar results as more general models with both types of disorder:

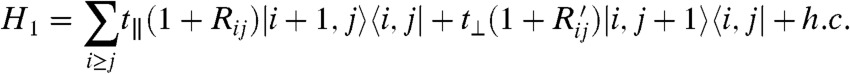[4]

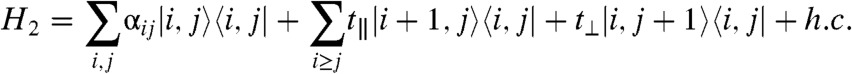[5]

The t_∥ and t_⊥ are the intermonomer coupling along the polymer chain and between chains for a perfectly crystalline sample. The α_ij and R_ij (or 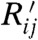) are normally distributed random variables modulating diagonal and off-diagonal disorder, respectively. The parameters of the Hamiltonian should be chosen to reproduce the localization and DOS of the realistic system (Fig. 4B). We start setting t_∥ as the unit of energy and t_⊥/t_∥ = 0.08, based on the approximate ratio between the bandwidth perpendicular and parallel to chain direction (20, 21). The DOS of the disordered system is broader than that of the crystalline system. The integrated DOS below the conduction band edge for the crystalline system corresponds to trap states generated by the disorder of the electronic Hamiltonian, and we define this density as D_trap. The approximate value of D_trap is known for semicrystalline polymers from device analysis (22, 23) and from simulation (24); i.e., it is possible to set the level of disorder within a physically plausible range for a semiconducting polymer. The width of the random variables α_ij and R_ij was set to have D_trap in the range 0.015–0.070 states per monomer; the experimental range is 0.028–0.045 (22, 24).

Fig. 4.

(A) A scheme of the model tight-binding disordered Hamiltonian. (B) The tail of the DOS for model H₁ and H₂ compared with the DOS of the perfect crystal. The disorder parameters were tuned to have the DOS below the conduction band D_trap comparable with experiment and numerical simulations. (C) Computed values of attenuation factor from the two considered models, H₁ and H₂. For each model, the attenuation factor was evaluated at the tail of the DOS (Left) and at the center (Right), both in the parallel (Top) and perpendicular (Bottom) direction. As the βs are non-normally distributed, their median and interquartile range are represented by the filled symbols and the error bars in the plot.

The numerical diagonalization of H₁ or H₂ gives a set of localized eigenfunctions for which it is possible to compute the attenuation factor β_∥ in the direction of the polymer chain and β_⊥ in the direction perpendicular to the chains as a numerical derivative of log |Ψ|² along the corresponding direction. Further details are given in SI Materials and Methods, including the non-normal distribution of β values obtained. The conduction band orbitals are more localized near the band edge, and so we present our evaluation of β separately for orbital in the DOS tail (E < -2.36t_∥) and DOS center (-2.0t_∥ < E < -1.0t_∥). In practice, excitons where the electron occupies all these conduction band states are initially generated by incoming photons, but it was experimentally observed that excitons rapidly migrate toward lower energy states (25) corresponding very roughly to the electron occupying lower energy conduction band orbitals; we are assuming a single electron picture to estimate the value of β_⊥,∥. Unsurprisingly (Fig. 4C), we find β_∥ < β_⊥; i.e., the exciton is more likely to dissociate at a long distance from the interface if the polymer chain is aligned perpendicular to the donor-acceptor interface. The structure of the interface is not known, and one should expect a variety of orientations (and β values) to be occurring.

Both model Hamiltonians indicate that, in the majority of cases, the coupling between exciton and surface decrease exponentially with an attenuation factor smaller than 0.6 Å^-1. The exception is, for the most, localized excitons and the polymer chains parallel to the interface. For β ∼  < 0.6 Å^-1, our microscopic model of charge separation shows that the majority of charge dissociation events takes place with the exciton far from the interface; i.e., hole and electron are generated already with a separation larger than 15–20 Å.

It should be remarked that we have used a single electron picture to describe the attenuation factor, assuming that the exponential decay of the excitonic wave function follows that of the unoccupied orbitals. This approximation seems justified by the similarity between electronic coupling computed between orbitals and multi-electron states in donor-bridge-acceptor systems (26). However, the energy ΔE in Eq. 1 must reflect the energy of the initial and final multi-electron states (not orbitals) and that is how the parameters of the model used to compute k_ED(R) have been chosen. Keeping this in mind, it is not possible for the electron to hop from the SOMO of the exciton into one of the unoccupied orbitals in the region of space between the exciton and the acceptor (even if initial and final orbitals have similar energy) because this state would be a high-energy charge-separated state within the donor material. Free hole and electron can be formed within the bulk material directly upon excitation, but there is no evidence that they can be formed spontaneously from the exciton (16).

Discussion

The hypothesis of this work was that an electron can tunnel at long distances if the barrier for tunneling is sufficiently low and that this long-range electron transfer may facilitate the separation of charges in organic solar cell. The tunneling barrier is very controllable in metal-insulator-metal junctions and, to some extent, controllable in donor-bridge-acceptor molecular systems. It is very well-known for the latter that, if the bridge is a conjugated fragment with relatively small HOMO–LUMO gap, the tunneling barrier can be very low, and the attenuation parameter β can be as low as 0.2 Å^-1 (9). In a semiconducting polymer, the medium is a material with relatively low band gap, possessing a number of partially delocalized orbital levels which are nearly degenerate with the donor and should, therefore, promote long-range electron tunneling. The analogy between tunneling from a conduction band orbital of a polymeric semiconductor and from the LUMO of the donor cannot be pushed too far though. In fact, what causes the localization of the conduction band orbitals of a solar cell is the disorder in the semiconducting polymer while, in donor-bridge-acceptor molecules, the donor’s orbitals are localized because formed by a chemically distinct unit, generally with smaller HOMO–LUMO gap than the bridge.

To translate this analogy into a quantitative theory, we have divided the problem into two. First, we have described the kinetics and energetics of long-range exciton dissociation, assuming relatively low value of the attenuation factor 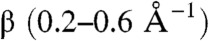. When the exciton is not in contact with the interface, there are many acceptor orbitals that the electron can tunnel into and the energy distribution of the final charge transfer state is not trivial. The electron, in fact, prefers to tunnel into one of the higher energy unoccupied orbitals; i.e., part of the exciton energy remains available to escape from the interface region. While we have not described the fate of the charge transfer state formed by a long-range electron transfer, we observed that the barrier for the formation of fully separated holes and electrons is of the order of magnitude of thermal energy or smaller. Long-range exciton dissociation is therefore an efficient way of using the energy difference between donor and acceptors conduction band states to separate hole and electrons. It should be noted that the proposed model is fully consistent with the available experimental data on the charge separation rate at the interface and exciton diffusion, but it is currently not possible to discriminate between the conventional mechanism of exciton dissociation at the interface and the long-range exciton dissociation proposed here.

For the second part of the problem, evaluating the actual attenuation factor, we have resorted to rather general model Hamiltonians where the single electron states are localized by disorder. It is not difficult to tune the disorder parameters of the Hamiltonian to reproduce the localization and density of state of realistic polymers. From a statistical analysis of the polymer orbitals, it was possible to estimate a plausible range of the attenuation factor β, which was (maybe not too surprisingly, given the analogy we started with) typically less than 0.6 Å^-1; i.e., sufficiently low to allow long-range exciton dissociation.

In conclusion, this paper has shown that, in the majority of cases, an exciton that dissociates into a hole and electron does so without reaching the interface first. This mechanism explains the efficient formation of free holes and electrons observed in the best available organic solar cells.