Abstract
The evolution of anisogamy (the production of gametes of different size) is the first step in the establishment of sexual dimorphism, and it is a fundamental phenomenon underlying sexual selection. It is believed that anisogamy originated from isogamy (production of gametes of equal size), which is considered by most theorists to be the ancestral condition. Although nearly all plant and animal species are anisogamous, extant species of marine green algae exhibit a diversity of mating systems including both isogamy and anisogamy. Isogamy in marine green algae is of two forms: isogamy with extremely small gametes and isogamy with larger gametes. Based on disruptive selection for fertilization success and zygote survival (theory of Parker, Baker, and Smith), we explored how environmental changes can contribute to the evolution of such complex mating systems by analyzing the stochastic process in the invasion simulations of populations of differing gamete sizes. We find that both forms of isogamy can evolve from other isogamous ancestors through anisogamy. The resulting dimensionless analysis accounts for the evolutionary stability of all types of mating systems in marine green algae, even in the same environment. These results imply that evolutionary trajectories as well as the optimality of gametes/zygotes played an important role in the evolution of gamete size.
Keywords: convergent evolution, evolutionarily stable strategy, fertilization kinetics
Almost all extant plant and animal species that reproduce sexually form anisogametes of two different sizes and mating types (1). It is generally agreed that the evolutionary antecedents of anisogamy can be traced to isogamy with small gametes (1–6). The evolution of anisogamy is one of the most fundamental issues in evolutionary biology, because (i) anisogamy underlies sexual selection and (ii) anisogamy incurs the twofold cost of sex (2, 7). However, the precise trajectory of the evolution of anisogamy remains poorly understood.
There are three theories describing selection pressures for the evolution of anisogamy (8). The pioneering theory of Parker, Baker, and Smith (known among evolutionary biologists as PBS) considered the tradeoff between gamete size and gamete number. Parker, Baker, and Smith proposed that anisogamy is an evolutionarily stable strategy (ESS) caused by disruptive selection for search efficiency and postzygotic survival (3). Subsequent theory focused on gamete search and the ability of highly motile sperm to overcome sperm limitation for large immobile eggs (4, 9). Finally, a third theoretical approach attempts to explain the evolution of anisogamy as an adaptation for preventing nuclear–cytoplasmic conflict through uniparental inheritance of organelles (10). The work by Billiard et al. (11) presented an excellent review of the hypotheses to explain the evolution of mating types and gamete size, mainly focusing on another interesting biological group, fungi, because their mating types vary from zero to thousands. Comparing the models proposed so far, the work by Billiard et al. (11) suggested that the “gamete size model” (Parker, Baker, and Smith's model) is the most applicable to fungi (11). However, none of these models successfully account for the evolution of all known forms of isogamy and anisogamy in extant marine green algae (12).
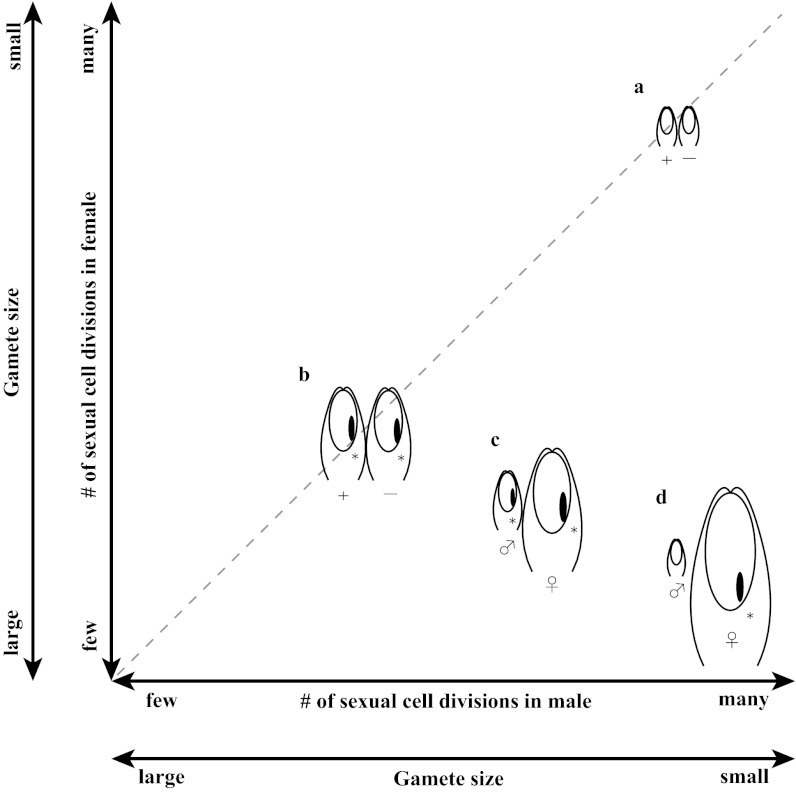
Marine green algae are characterized by a variety of mating systems linked to their habitats (Fig. 1, Fig. S1A, size of isogametes, and Fig. S1B, size of anisogametes, and Table S1). Two different types of isogamy occur. Some species produce isogametes of medium size, which possess a phototactic system in the form of eyespots, whereas other species produce extremely small isogametes devoid of eyespots. The existence of these two different types of isogamy raises the question of whether either form of isogamy is, in some sense, atavistic, representing a primitive mating system similar to that used by ancestral species, or whether they represent evolutionary advancements.
Fig. 1.
Schematic of mating systems observed in marine green algae. a, Small isogamy; b, large isogamy; c, slight anisogamy; d, marked anisogamy. *With an eyespot.
Two forms of anisogamy also occur. Some marine green algal species are characterized by slight anisogamy in which the size differences between the large and small gametes are subtle. Previous analyses indicate global evolutionary stability for anisogamy with small regions of local stability for isogamy; slight anisogamy is not predicted to be an ESS under these previous theories (1, 4, 13). Other marine green algal species are profoundly anisogamous.
Most previous theories depend on the impact of environmental differences on zygote survival to explain the evolution of anisogamy (8). However, both isogamous and slightly anisogamous species of marine green algae occupy similar environments and sometimes coexist in shallow waters (14). They might have evolved under the same types of environment. We, thus, cannot find the difference in zygote survival in their environments. Their zygote fitness functions might be the same or very similar, particularly among closely related species. It has been suggested that variable mortality through differential survival or metabolic damage acting on both zygotes and gametes may affect the evolution of gamete size by recent studies (15, 16). We have previously found strongly anisogamous species to generally inhabit relatively deeper waters (12).
In this study, we develop a model based on individual selection that tracks the fate of individual gametes and zygotes to explain these observations of different mating systems in extant marine green algae. Using an individual-based population genetic model, it has been proposed that gamete contact rates may explain isogamy and anisogamy that emerge as alternative outcomes in different ecological conditions (17). We predict fertilization success based on collision kinetics theory, and then, we assess the survival of the zygotes produced by the resultant fusions. By calculating the relative fitness of each intermediary mutant form, we are able to identify all possible evolutionary trajectories. This analysis leads to a theory for gamete size evolution that explains the simultaneous existence of all known forms of isogamy and anisogamy in extant taxa.
Model
Based on the reproductive biology of marine green algae, we examined whether mutants with gametes of a different size gain numerical advantage over the course of the life cycle, where in the current generation, (i) the life cycle begins with spawning of gametes, which are formed through synchronized cell divisions during gametogenesis and specialize in sexual fusion from haploid dioecious gametophytes of each sex, (ii) zygotes are formed when gametes of opposite sex collide (fertilization), (iii) zygotes develop into diploid sporophytes, (iv) sporophytes produce zoospores through meiosis, and (v) each zoospore germinates into an individual gametophyte of each sex in the next generation (18). We compared the ratio of mutants that are introduced in one of two mating types at a very low rate in the current generation with the whole population between the two successive generations to evaluate whether invasion is successful (19). If different mutations are invadable, the next step depends on chance. The evolutionary trajectory might not necessarily go to the direction with the highest fitness. In accordance with observations from nature, phenotypic variance in size of gametes produced within each mating type is constrained (20, 21), and loci that determine gamete size are linked to loci that determine mating types (22, 23). To keep the model as simple as possible, we use a haploid model that excludes the possibility of simultaneous (i.e., double) mutations in both sexes.
Results
We examined all of the invadabilities of mutants with gametes of a different size in terms of synchronized cell division that commonly occurs during gametogenesis and considered the evolutionary trajectories of gamete size (see also Fig. S2). As infrequent mutants appeared in the WT population, their evolutionary trajectories were plotted (Figs. 2 and 3). In Figs. 2 and 3, an evolutionary trajectory is symbolized by an arrow. Each arrow indicates net flow and not deterministic flow. For example, (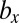 ,
, 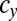 ) → (
) → (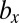 ,
, 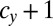 ) means that, (i) when a mutant of type c with a gene that determines the number of sexual cell divisions as
) means that, (i) when a mutant of type c with a gene that determines the number of sexual cell divisions as 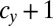 appears in the WT population consisting of individuals of type b and c, which have different mating types with genes that determine the numbers of sexual cell divisions as
appears in the WT population consisting of individuals of type b and c, which have different mating types with genes that determine the numbers of sexual cell divisions as 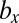 and
and 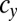 , respectively, such mutants spread in this WT population and finally, replace the individuals of type c with a gene for
, respectively, such mutants spread in this WT population and finally, replace the individuals of type c with a gene for 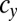 cell divisions and (ii) conversely, a mutant with a gene for
cell divisions and (ii) conversely, a mutant with a gene for 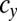 cell divisions cannot invade the WT population of b and c types with genes for
cell divisions cannot invade the WT population of b and c types with genes for 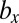 and
and 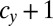 cell divisions. Note that there is no intermediate state between any two neighboring points in these figures (Figs. 2 and 3). In this lattice space with the maximum number of cell divisions in each sex, the invadability determines the convergent stability as well as the evolutionary stability. We define a convergently stable solution as a point with an area where strategies converge at this point (surrounded by solid and dotted lines in Figs. 2 and 3). A point with no outgoing arrow is the ESS, an evolutionarily stable and convergently stable point is the continuously stable strategy (CSS), a point with both incoming and outgoing arrows is a transient strategy, and a point with only outgoing arrows is a possible starting point (origin).
cell divisions. Note that there is no intermediate state between any two neighboring points in these figures (Figs. 2 and 3). In this lattice space with the maximum number of cell divisions in each sex, the invadability determines the convergent stability as well as the evolutionary stability. We define a convergently stable solution as a point with an area where strategies converge at this point (surrounded by solid and dotted lines in Figs. 2 and 3). A point with no outgoing arrow is the ESS, an evolutionarily stable and convergently stable point is the continuously stable strategy (CSS), a point with both incoming and outgoing arrows is a transient strategy, and a point with only outgoing arrows is a possible starting point (origin).
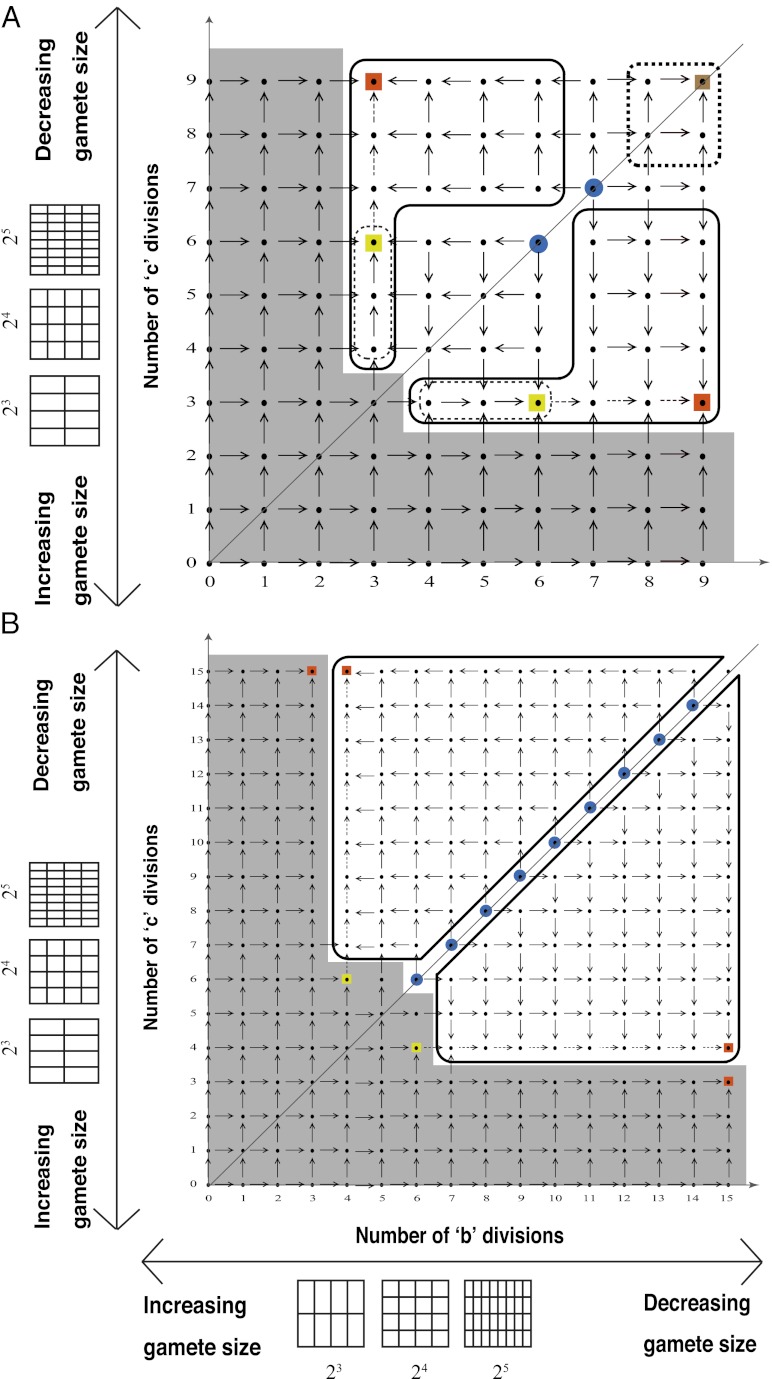
Fig. 2.
The evolutionary trajectories of gamete size. Note that if the number of cell divisions during gametogenesis increases, the size of gametes formed is decreased, and vice versa. The zygote survival probability function is Eq. S16, in which the individual zygote mortality rate depends directly on provisioning of resources from its constituent gametes. The contribution of gametic resources per unit volume to the zygote survival is equal between the sexes. Provisioning of resources of a zygote from its constituent gametes is just proportional to the sum of the male and female gamete volumes (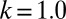 ) (Fig. 3B defines
) (Fig. 3B defines 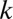 ).
). 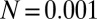 and (A)
and (A) 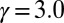 ,
, 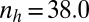 (B)
(B) 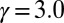 ,
, 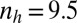 .
. 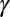 , the slope of the zygote survival probability function (Eq. S16) at the 50% point, where the volume of zygote
, the slope of the zygote survival probability function (Eq. S16) at the 50% point, where the volume of zygote 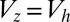 ;
; 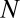 , the proportion of invaders;
, the proportion of invaders; 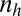 , the number of gametes that are produced by an individual gametophyte and that have one-half of the volume of
, the number of gametes that are produced by an individual gametophyte and that have one-half of the volume of 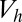 . A is under a better environmental condition than B. Depending on the direction of gamete size mutation, the evolutionary trajectories are allowed to move one grid either horizontally or vertically. Each pair between b and c types is the WT population. A mutant one point away can arise. If an invasion of such a mutant is successful (i.e., invadable), it is indicated by an arrow. The dotted arrows indicate an evolutionary trajectory with the additional evolution of pheromonal attraction systems. Under the line of number of b divisions is the number of c divisions. Above this line, each arrow that is symmetrically located centering the line has the same color. Stable strategies are indicated using squares. Green square, larger isogamy; brown square, extremely small isogamy; orange square, marked anisogamy; yellow square, slight anisogamy; blue circle, possible starting point (origin). Note that (i) in an area surrounded by a thin dotted line, strategies converge at a yellow square, (ii) in an area surrounded by a thick dotted line, they converge at a brown square, and (iii) in an area surrounded by a thick solid line, they converge at an orange square. An area that cannot be reached from the origins (blue circles) is shaded. For the conditional convergently stable strategy, the maximum number of sexual cell divisions to retain the phototactic device is assumed to be six (throughout the study).
. A is under a better environmental condition than B. Depending on the direction of gamete size mutation, the evolutionary trajectories are allowed to move one grid either horizontally or vertically. Each pair between b and c types is the WT population. A mutant one point away can arise. If an invasion of such a mutant is successful (i.e., invadable), it is indicated by an arrow. The dotted arrows indicate an evolutionary trajectory with the additional evolution of pheromonal attraction systems. Under the line of number of b divisions is the number of c divisions. Above this line, each arrow that is symmetrically located centering the line has the same color. Stable strategies are indicated using squares. Green square, larger isogamy; brown square, extremely small isogamy; orange square, marked anisogamy; yellow square, slight anisogamy; blue circle, possible starting point (origin). Note that (i) in an area surrounded by a thin dotted line, strategies converge at a yellow square, (ii) in an area surrounded by a thick dotted line, they converge at a brown square, and (iii) in an area surrounded by a thick solid line, they converge at an orange square. An area that cannot be reached from the origins (blue circles) is shaded. For the conditional convergently stable strategy, the maximum number of sexual cell divisions to retain the phototactic device is assumed to be six (throughout the study).
Fig. 3.
Typical evolutionary trajectories of gamete size when (A) the zygote survival is not related to the individual zygote mortality rate and (B) the per unit volume male gamete contribution to the zygote survival is smaller than the female contribution. (A) Eq. S17 is used instead of Eq. S16. The contribution of gametic resources per unit volume to the zygote survival is equal between the sexes (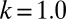 ) as in Fig. 2. Parameter conditions:
) as in Fig. 2. Parameter conditions: 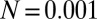 ,
, 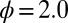 , and
, and 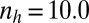 .
. 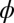 , an environmental parameter of the zygote survival probability function (Eq. S17). Fig. 2 explains the other parameters. (B) The zygote survival probability function is Eq. S16. Parameter conditions:
, an environmental parameter of the zygote survival probability function (Eq. S17). Fig. 2 explains the other parameters. (B) The zygote survival probability function is Eq. S16. Parameter conditions: 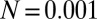 ,
, 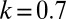 ,
, 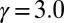 , and
, and 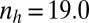 .
.  , the ratio of the contribution of resources of a male gametes per unit volume to the contribution of a female gamete.
, the ratio of the contribution of resources of a male gametes per unit volume to the contribution of a female gamete. 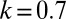 means that provisioning of resources of a zygote from a male gamete is 70% of the rate of provisioning of a female gamete per unit volumes. Fig. 2 explains the arrows, symbols, and areas surrounded by solid and dotted lines.
means that provisioning of resources of a zygote from a male gamete is 70% of the rate of provisioning of a female gamete per unit volumes. Fig. 2 explains the arrows, symbols, and areas surrounded by solid and dotted lines.
We implemented a zygote survival probability function (Eq. S16 and Fig. S3A) to analyze the effects of favorable environmental conditions, such as shallow water and rocky upper intertidal zones (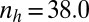 ) (Fig. 2A), as well as unfavorable conditions, such as deep tide pools or deep open water (
) (Fig. 2A), as well as unfavorable conditions, such as deep tide pools or deep open water (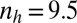 ) (Fig. 2B) for marine green algae.
) (Fig. 2B) for marine green algae.
For invasion of mutant strategies, we found one unique ESS in each environment (Fig. 2, green squares). Because strategies do not converge at this point, this ESS point (Fig. 2, green squares) is not a CSS. Therefore, we distinguish two types of ESS: non-CSS (Fig. 2, green squares) and CSS (Fig. 2, yellow, orange, and brown squares).
We also found convergently stable strategies. There is an area where, even if both the strategy pairs are displaced from the orange square (marked anisogamy), they converge back to this point (Figs. 2 and 3, thick line). It is caused by the existence of the maximum number of cell divisions assumed in our model and plausible in nature as well as random mutations. Multiple routes are allowed for this convergence. Similarly, the brown square (thick dotted line shows small isogamy) and the yellow squares (thin dotted lines show slight anisogamy) in Fig. 2B can be convergently stable strategies. These strategies are also ESSs. Thus, when they are convergently stable, they are CSSs.
Probabilities of each stable strategy from given starting points can be calculated in our model if mutations to produce gametes of a different size derived from one more (+1) or one less (−1) numbers of cell divisions during gametogenesis than WTs are equally likely to occur in either mating type. For example, in Fig. 2A, the probabilities of large isogamy and slight anisogamy are both one-half if the starting point is 7, 7. The probability of marked anisogamy is one if the starting point is 8, 7 or 7, 8. The probabilities of marked anisogamy and small isogamy are both one-half if the starting point is 8, 8. These probabilities may be changed if simultaneous (i.e., double) mutation or polymorphism is allowed.
Given random mutations, any mating system is possible. However, only the mating systems indicated by these squares are selected as stable strategies. The evolutionary outcomes depend on three factors: (i) whether the environmental conditions are favorable or unfavorable, (ii) the evolutionary starting point (e.g., the precise mating system of the ancestor), and (iii) the evolutionary trajectories in which previous mutations were channelized. Our results indicate that historical effects of these factors—and thus, phylogenetic trajectories—are important in the diversified evolution of gamete size. Although the sequence of environments experienced by algal ancestors can have a direct impact on the eventual mating systems, we found the environment not to be solely deterministic in mating system evolution, because multiple evolutionary trajectories can exist in the same environment and are actually observed in extant marine green algae.
From the extensive analyses, we select the most important quantitatively differing examples from the main results in Fig. 2. When the function for zygote survival probability is modified (as described in detail in Model Specifications), the stable large isogamy (green square) disappears (Fig. 3A). When the male gamete contribution is reduced to a certain threshold (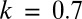 or less), the marked anisogamy becomes the only stable strategy; all of the other stable strategies disappear (Fig. 3B).
or less), the marked anisogamy becomes the only stable strategy; all of the other stable strategies disappear (Fig. 3B).
Gamete fusions resulting in insufficient zygote provisioning and gametes too small to be viable were excluded from additional analysis (Fig. S4). Note that our dimensionless analysis requires only the five independent parameters (SI Text, Evolutionary Dynamics) to provide a generalized solution that explains a wide spectrum of individual cases (see also Fig. S5).
Discussion
As an example of evolutionary dynamics of gamete size, consider the ultimate ancestor of marine green algae in shallow water (represented by 7, 7; 8, 7; 7, 8; and 8, 8 in Fig. 2A). The most primitive gametes should have a simple structure without an additional organ like an eyespot. Strictly simultaneous (i.e., double) mutations that occur at a very low probability might not be necessary for the evolution of phototactic devices, including an eyespot. In some circumstances (e.g., shallow tide pools), even nonphototactic gametes without an eyespot in both sexes might effectively encounter near the 2D surface. If they are large gametes, they would soon obtain an eyespot, because not only do such gametes have sufficient space for an eyespot but also, phototactic devices are closely related to the large chloroplasts that they have. Three evolutionary trajectories are possible: (i) large isogamy (to 5, 5), (ii) smaller isogamy (to 9, 9), and (iii) anisogamy (by 7, 4 to 9, 4).
The first evolutionary trajectory, isogamy with larger gametes, leads to evolutionary stability (i.e., an ESS but not CSS). Here, the optimal size of gamete is determined solely by its fertilization kinetics and zygote survival. In the second evolutionary trajectory, isogamy with extremely small gametes, minimum gamete size is not determined by the fertilization kinetics and zygote survival but instead, the minimum provisioning volume necessary for gamete viability.
The third evolutionary trajectory, anisogamy, depends on ecological conditions necessary for successful fertilization in marine green algae. Slight anisogamy, the first step in this trajectory, requires fertilization on the water surface. Encounter rates of gametes in a 2D surface are disproportionately higher than in 3D (4), and we observe the evolution of phototaxis in many green algal species (18). Therefore, the minimum size of male (smaller) gametes must remain relatively large because of the need for phototactic devices to find the surface (e.g., eyespots) (represented by 6, 4 in Fig. 2A). Thus, slight anisogamy is an evolutionarily convergent state. This finding may be the reason why we find so many slightly anisogamous species in marine green algae, although slight anisogamy has been assumed to be evolutionarily unstable in previous theoretical studies (1, 4, 13).
The second step in this evolutionary trajectory is additional size reduction (and thus, increased motility) in male gametes gained by the loss of phototactic devices (represented by 9, 4 in Fig. 2A). The loss of an eyespot in male gametes and the resultant decline in gamete encounter rates, however, can be compensated for by the evolution of pheromonal attraction by female gametes. Here, larger female gametes might be better suited not only to maintain phototactic devices but also, to produce sexual pheromones needed to attract male gametes (5). In some Bryopsis species (Bryopsidales), large female gametes with phototactic devices release pheromones that attract small and nonphototactic male gametes (20). This finding could be considered as an example of an evolutionary transition to strict anisogamy.
The third step in this evolutionary trajectory is the environmental shift from shallow to deep water. The advantages of phototaxis are negated in water of sufficient depth, because gametes released from gametophytes on the bottom are unable to ascend to the water surface. Gametes of several profoundly anisogamous Derbesia species (Bryopsidales) that inhabit water of 9–12 m in depth (24) have lost their phototactic systems, even in females (25).
Not only can gamete encounter rates be reduced by deep water, but zygote survival can also be adversely affected by the reduction of photosynthesis efficiency. Thus, there is selection for large female gametes (from 9, 4 in Fig. 2A by 9, 4 in Fig. 2B to 9, 2 in Fig. 2B). This finding implies that the deeper the water, the more extreme the gamete size dimorphism.
Additional enlargement of female gametes in anisogamy can be achieved by the evolution of the mulitinucleate (coenocytic) female gametophyte. Female gametes of strongly anisogamous species are often much larger than the gametes of isogamous species, which has been observed in Bryopsidales (e.g., >250 μm in length) (26). It is impossible to produce gametes larger than the biomass of a single cell allocated to gamete production by the gametophyte. However, to our knowledge, all members of the Bryopsidales have a multinucleate unicellular structure (18) that allows large gametes to be produced.
Here, we apply a haploid model and find all of the variations of gamete size in marine green algae. By adopting a diploid model that includes simultaneous (i.e., double) mutations in both sexes, we may be able to evaluate the probability (plausibility) for these evolutionary goals quantitatively. Double mutations might play a role in the evolution of additional devices, such as an eyespot and pheromones.
In the past, the evolutionary choice between isogamy and aniosgamy was treated as an asymmetric evolutionary game under PBS (8, 15, 27). Isogametes with minimum size should have evolved when the increased zygote volume yielded diminishing zygote fitness. Disruptive selection on gamete size leading to extreme anisogamy can occur only if the zygote fitness function gives increased returns. Thus, the evolution of isogamy with small gametes and extreme anisogamy was explained but only if different zygote fitness functions were used in the two circumstances. In our analyses, which include fertilization kinetics and historical effect, both isogamy and anisogamy are stable (Fig. 2) under the same zygote fitness function (Eq. S16).
In previous models, no ESS was found for large isogametes; for example, in the work by Cox and Sethian (4), only small isogametes were stable. Note that the zygote survival probability function (Eq. S16 and Fig. S3A) that we used in Fig. 2 is derived from assuming that the probability of mortality of an individual zygote per unit time is a function of its volume. An ESS for large isogametes is not observed (Fig. 3A) when using another zygote survival probability function (Eq. S17 and Fig. S3B). Thus, the volume-correlated mortality seems necessary in the zygote survival function.
Currently, we have no direct measurement of zygote survival. However, we have strong indirect evidence of the effects of zygote size on its survival. First, if zygote survival is not affected by its size, algae should produce as many smaller gametes (resulting zygotes) as possible, because the total reproductive output is limited. However, the observed zygotes exhibited the minimum output (Fig. S1C); this finding proves that there is the minimal survival size in zygotes. Second, the size of zygotes increases with the degree of anisogamy (Fig. S1C). This finding indicates clearly that the survival of zygotes is definitely affected by the size of zygotes in anisogamous species.
Why is isogamy not more common among other species with external fertilization? First, note that the stability of large isogamy will disappear in worse environments (Fig. 2). This finding explains that such a mating system is scarcely observed in many other biological groups and that strong anisogamy and small isogamy are often found. Second, less adaptive strategies might go to extinction, particularly under worse conditions. Third, recent empirical studies reveal that, even in isogamous marine green algae, organelles of one mating type are uniparentally inherited (28). This finding suggests that, at least in this group, selection for uniparental inheritance of organelles does not initiate the evolution of anisogamy. However, the contribution of resources of a male gamete per unit volume to the zygote survival might actually become less than the contribution of a female gamete because of (i) uniparental inheritance of organelles, (ii) cytoplasmic parasites, or (iii) conflicts between organelles derived from different parents (10). In such cases, our results predict that anisogamy would be favored (Fig. 3B). This finding might be a reason why anisogamy is common in many biological groups.
In conclusion, our theory provides a single integrated explanation for the existence of different types of gamete dimorphism and gamete monomorphism in marine green algae. This theory allows for the evaluation of multiple competing hypotheses governing the evolution of gamete size. A reason why we find these various stable solutions (especially large isogamy and slight anisogamy) is that we use discrete cell division as optimizing trait values instead of continuous gamete volumes. We suggest that the evolutionary outcomes are dependent on random mutations and precise ecological conditions at the time of evolutionary divergence of the different mating types. This interplay between chance (i.e., mutations) and necessity (i.e., gamete encounter rates and selection for zygote survival) provides a better understanding of the evolution of anisogamy as well as the persistence of different types of isogamy in extant marine green algae (29). Our theory is well-supported by recent empirical studies on sex-specific genes in green algae, which suggest that maleness evolved from the dominant sex (mating type minus) of its isogamous ancestor (23, 30).
Model Specifications
Gametophytes use equal amounts of biomass that determine the number of gametes spawned. There is, therefore, a tradeoff between the size (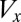 ) and the number (
) and the number (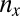 ) of gametes produced (that is,
) of gametes produced (that is, 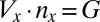 , where
, where 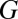 is the fixed amount of gametic materials in the both sexes) (20, 31, 32). As commonly observed in marine green algae (20), gametes are produced through synchronized cell divisions during gametogenesis. Thus, gamete size (
is the fixed amount of gametic materials in the both sexes) (20, 31, 32). As commonly observed in marine green algae (20), gametes are produced through synchronized cell divisions during gametogenesis. Thus, gamete size (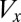 ) takes only discrete values and increases when the number of cell divisions (
) takes only discrete values and increases when the number of cell divisions (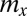 ) decreases, and vice versa (i.e.,
) decreases, and vice versa (i.e., 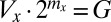 ).
).
The number of zygotes formed during a generation depends on the number of collisions between gametes of the opposite sex. The gametes are assumed to be spherical. Gametes are not generally spherical, but the spherical approximation is appropriate for gamete movement in a viscous medium at low Reynolds numbers (4). Gametes move in a random and uncorrelated fashion throughout the water at a speed inversely proportional to their radius because of Stokes law at low Reynolds numbers hydrodynamics (20, 21). We use methods of collision kinetics similar to those methods used for hard sphere gases to calculate the number of collisions (details in ref. 33). The three fundamental controlling factors are the collision cross-section with a radius of the sum of the radii of the two gametes, relative gamete velocities, and gamete concentrations. Spherical gametes collide with their partners in the cylindrical water column if they get closer than the collision cross-section according to their relative speed. Zygotes do not participate in additional fusions. By introducing the relative collision rate function (Eq. S9), our model simply embodies the entire collision kinetics of the gametes (Eq. S10 and Fig. S2) and thus, predicts the zygote formation rate for any specific conditions.
We introduce one type of infrequent mutants in one of two mating types. Only mutations with small effects are viable (34). We specifically assume that mutants that produce gametes of a different size derived from one more (+1) or one less (−1) numbers of cell divisions during gametogenesis than WT arise in either mating type. Which of the mutations (i.e., +1, −1) occurs depends on chance. The rates of zygote formation are different between the mutant and the WT, because their cross-sections are different (Eq. S5).
After a sufficiently long time for virtually all zygotes to form, the zygotes are subjected to a nonlinear survival process. Survival in a population of zygotes is described by a logistic function (Eq. S13). The probability that a zygote will survive to become a breeding adult depends on the specific or individual zygote mortality rate and time duration. The individual zygote mortality rate, 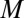 , depends linearly on provisioning of resources from its constituent gametes, consisting of cytoplasm, mitochondria, and chloroplasts, etc., in addition to environmental properties, such as temperature, pressure, etc. This assumption would be plausible, for instance, if the number of chloroplasts in a gamete increases as gamete size increases, which is often observed in marine green algae. The survival probability of zygotes and provisioning for one generation then take a sigmoidal form with the two parameters determined by the environment (i.e.,
, depends linearly on provisioning of resources from its constituent gametes, consisting of cytoplasm, mitochondria, and chloroplasts, etc., in addition to environmental properties, such as temperature, pressure, etc. This assumption would be plausible, for instance, if the number of chloroplasts in a gamete increases as gamete size increases, which is often observed in marine green algae. The survival probability of zygotes and provisioning for one generation then take a sigmoidal form with the two parameters determined by the environment (i.e., 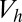 is the zygote volume for which the survival probability is 50%, and
is the zygote volume for which the survival probability is 50%, and 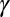 is the slope of the survival rate curve at the 50% point) (Eq. S16 and Fig. S3A). We also consider a function that has a shape similar but without the above relationship between the individual zygote mortality rate,
is the slope of the survival rate curve at the 50% point) (Eq. S16 and Fig. S3A). We also consider a function that has a shape similar but without the above relationship between the individual zygote mortality rate, 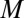 , and provisioning of resources (Eq. S17 and Fig. S3B). A good measure of the degree of provisioning is given by the volume of the zygote, which in turn, is usually taken to be the sum of the constituent male and female gamete volumes. However, it is often the case that some of the provisions originating from the male gamete are damaged or destroyed to avoid spread of cytoplasmic parasites (e.g., viruses and bacteria) and conflicts between organelles derived from different parents through uniparental inheritance of organelles (10). Therefore, the per unit volume contribution of male gametes may be smaller than the contribution of female gametes. Here, we introduce the parameter
, and provisioning of resources (Eq. S17 and Fig. S3B). A good measure of the degree of provisioning is given by the volume of the zygote, which in turn, is usually taken to be the sum of the constituent male and female gamete volumes. However, it is often the case that some of the provisions originating from the male gamete are damaged or destroyed to avoid spread of cytoplasmic parasites (e.g., viruses and bacteria) and conflicts between organelles derived from different parents through uniparental inheritance of organelles (10). Therefore, the per unit volume contribution of male gametes may be smaller than the contribution of female gametes. Here, we introduce the parameter 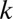 , which is the ratio of the contribution of male gametes to the contribution of female gametes. We first analyze the case of equal contributions between male and female gametes (
, which is the ratio of the contribution of male gametes to the contribution of female gametes. We first analyze the case of equal contributions between male and female gametes (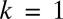 ) (Figs. 2 and 3A). We then analyze the cases when the contributions of male gametes are smaller than the contributions of female gametes, reducing
) (Figs. 2 and 3A). We then analyze the cases when the contributions of male gametes are smaller than the contributions of female gametes, reducing 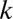 (<1;
(<1; 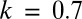 ) (Fig. 3B). Each diploid sporophyte that is developed from a survived zygote produces the same number of haploid zoospores with a 1:1 ratio of one mating type to another (35). Each zoospore germinates into an individual gametophyte of each sex that begins the life cycle in the next generation.
) (Fig. 3B). Each diploid sporophyte that is developed from a survived zygote produces the same number of haploid zoospores with a 1:1 ratio of one mating type to another (35). Each zoospore germinates into an individual gametophyte of each sex that begins the life cycle in the next generation.
Now, we are ready to evaluate whether an invasion by mutants with gametes of a different size is successful. A successful invasion by mutants is defined to be when the proportion of mutant gametophytes to WT in a succeeding generation is larger than the proportion in the current generation (19). If an invasion of such mutants is successful, we initialize the generation with gametes of this size (Figs. 2 and 3). The evolution of gamete size is shown by the stochastic process.
Supplementary Material
Acknowledgments
We thank anonymous referees for perceptive comments and discussion on this work. This work was funded by a grant-in-aid from the Japan Science and Technology Agency (to T.T.).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission. G.A.P. is a guest editor invited by the Editorial Board.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1203495109/-/DCSupplemental.
References
- 1.Matsuda H, Abrams PA. Why are equally sized gametes so rare? The instability of isogamy and the cost of anisogamy. Evol Ecol Res. 1999;1:769–784. [Google Scholar]
- 2.Maynard Smith J. The Evolution of Sex. Cambridge, UK: Cambridge Univ Press; 1978. [Google Scholar]
- 3.Parker GA, Baker RR, Smith VGF. The origin and evolution of gamete dimorphism and the male-female phenomenon. J Theor Biol. 1972;36:529–553. doi: 10.1016/0022-5193(72)90007-0. [DOI] [PubMed] [Google Scholar]
- 4.Cox PA, Sethian JA. Gamete motion, search, and the evolution of anisogamy, oogamy, and chemotaxis. Am Nat. 1985;125:74–101. [Google Scholar]
- 5.Hoekstra RF. In: The Evolution of Sex and Its Consequences. Stearns SC, editor. Basel: Birkhauser; 1987. pp. 59–91. [Google Scholar]
- 6.Maynard Smith J, Szathmáry E. The Major Transitions in Evolution. San Francisco: Freeman; 1995. [Google Scholar]
- 7.Darwin CR. The Descent of Man, and Selection in Relation to Sex. London: J. Murray; 1871. [Google Scholar]
- 8.Randerson JP, Hurst LD. The uncertain evolution of the sexes. Trends Ecol Evol. 2001;16:571–579. [Google Scholar]
- 9.Levitan DR. The importance of sperm limitation to the evolution of egg size in marine invertebrates. Am Nat. 1993;141:517–536. doi: 10.1086/285489. [DOI] [PubMed] [Google Scholar]
- 10.Cosmides LM, Tooby J. Cytoplasmic inheritance and intragenomic conflict. J Theor Biol. 1981;89:83–129. doi: 10.1016/0022-5193(81)90181-8. [DOI] [PubMed] [Google Scholar]
- 11.Billiard S, et al. Having sex, yes, but with whom? Inferences from fungi on the evolution of anisogamy and mating types. Biol Rev Camb Philos Soc. 2011;86:421–442. doi: 10.1111/j.1469-185X.2010.00153.x. [DOI] [PubMed] [Google Scholar]
- 12.Togashi T, Bartelt JL. In: The Evolution of Anisogamy: A Fundamental Phenomenon Underlying Sexual Selection. Togashi T, Cox PA, editors. Cambridge, UK: Cambridge Univ Press; 2011. pp. 194–242. [Google Scholar]
- 13.Cox PA. In: The Evolution of Anisogamy: A Fundamental Phenomenon Underlying Sexual Selection. Togashi T, Cox PA, editors. Cambridge, UK: Cambridge Univ Press; 2011. pp. 1–16. [Google Scholar]
- 14.Togashi T, Motomura T, Ichimura T, Cox PA. Gametic behavior in a marine green alga, Monostroma angicava: An effect of phototaxis on mating efficiency. Sex Plant Reprod. 1999;12:158–163. [Google Scholar]
- 15.Bulmer MG, Parker GA. The evolution of anisogamy: A game-theoretic approach. Proc Biol Sci. 2002;269:2381–2388. doi: 10.1098/rspb.2002.2161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Bonsall MB. The evolution of anisogamy: The adaptive significance of damage, repair and mortality. J Theor Biol. 2006;238:198–210. doi: 10.1016/j.jtbi.2005.05.007. [DOI] [PubMed] [Google Scholar]
- 17.Iyer P, Roughgarden J. Gametic conflict versus contact in the evolution of anisogamy. Theor Popul Biol. 2008;73:461–472. doi: 10.1016/j.tpb.2008.02.002. [DOI] [PubMed] [Google Scholar]
- 18.van den Hoek C, Mann DG, Jahns HM. Algae: An Introduction to Phycology. Cambridge, UK: Cambridge Univ Press; 1996. [Google Scholar]
- 19.Togashi T, et al. Evolution of gamete size in primitive taxa without mating types. Popul Ecol. 2009;51:83–88. [Google Scholar]
- 20.Togashi T, Motomura T, Ichimura T. Production of anisogametes and gamete motility dimorphism in Monostroma angicava. Sex Plant Reprod. 1997;10:261–268. [Google Scholar]
- 21.Togashi T, Motomura T, Ichimura T. Gamete dimorphism in Bryopsis plumosa. Phototaxis, gamete motility and pheromonal attraction. Bot Mar. 1998;41:257–264. [Google Scholar]
- 22.Charlesworth B. The population genetics of anisogamy. J Theor Biol. 1978;73:347–357. doi: 10.1016/0022-5193(78)90195-9. [DOI] [PubMed] [Google Scholar]
- 23.Ferris P, et al. Evolution of an expanded sex-determining locus in Volvox. Science. 2010;328:351–354. doi: 10.1126/science.1186222. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Chapman VJ, Edmonds AS, Drogmoole FI. Halicystis in New Zealand. Nature. 1964;202:414. [Google Scholar]
- 25.Ziegler JR, Kingsbury JM. Cultural studies on the marine green alga Halicystis parvula – Derbesia tenuissima. I. Normal and abnormal sexual and asexual reproduction. Phycologia. 1964;4:105–116. [Google Scholar]
- 26.Clifton KE, Clifton LM. The phenology f sexual reproduction by green algae (Bryopsidales) on Caribbean coral reefs. J Phycol. 1999;35:24–34. [Google Scholar]
- 27.Bulmer MG. Theoretical Evolutionary Ecology. Sunderland, MA: Sinauer; 1994. [Google Scholar]
- 28.Kagami Y, et al. Sexuality and uniparental inheritance of chloroplast DNA in the isogamous green alga Ulva compressa (Ulvophyceae) J Phycol. 2008;44:691–702. doi: 10.1111/j.1529-8817.2008.00527.x. [DOI] [PubMed] [Google Scholar]
- 29.Monod J. Chance and Necessity. New York: Vintage Books; 1971. [Google Scholar]
- 30.Nozaki H, Mori T, Misumi O, Matsunaga S, Kuroiwa T. Males evolved from the dominant isogametic mating type. Curr Biol. 2006;16:R1018–R1020. doi: 10.1016/j.cub.2006.11.019. [DOI] [PubMed] [Google Scholar]
- 31.Charnov EL. The Theory of Sex Allocation. Princeton: Princeton Univ Press; 1982. [PubMed] [Google Scholar]
- 32.Graham AL, et al. Fitness correlates of heritable variation in antibody responsiveness in a wild mammal. Science. 2010;330:662–665. doi: 10.1126/science.1194878. [DOI] [PubMed] [Google Scholar]
- 33.Togashi T, Cox PA, Bartelt JL. Underwater fertilization dynamics of marine green algae. Math Biosci. 2007;209:205–221. doi: 10.1016/j.mbs.2006.08.025. [DOI] [PubMed] [Google Scholar]
- 34.Fisher RA. The Genetical Theory of Natural Selection. Oxford: Clarendon; 1930. [Google Scholar]
- 35.Togashi T, Cox PA. Equal sex ratios of a marine green alga, Bryopsis plumosa. J Integr Plant Biol. 2008;50:648–652. doi: 10.1111/j.1744-7909.2008.00665.x. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.